Методические указания
Задача 1.
Графическое
решение матричных игр.
1. Найдем оптимальные
стратегии игроков в игре, заданной
платежной матрицей
![]() .
.
Сначала проверим,
есть ли в данной игре седловая точка.
Нижняя цена игры
равна
![]() max
max
{4, 3} = 4.
Верхняя цена этой
игры равна
![]() min
min
{7, 9, 9, 9} = 7.
Поскольку
![]() ,
,
то седловой точки у данной игры нет, и
решение нужно искать в смешанных
стратегиях.
Графически решаются
те матричные игры, в которых хотя бы у
одного из игроков есть лишь две чистые
стратегии. Задача именно этого игрока
и решается графически. В задаче 1 у
первого игрока две чистых стратегии, а
у второго − четыре, поэтому будем решать
графически задачу первого игрока.
Смешанная стратегия
первого игрока задается вектором
![]() .
.
Построения осуществляются следующим
образом. На горизонтальной прямой
откладывается отрезок единичной длины,
характеризующий вероятность применения
чистых стратегий первым игроком. Каждой
точке этого отрезка сопоставляется
смешанная стратегия первого игрока по
следующему правилу: расстояние от точки
до правого конца отрезка задает величину![]() ,
,
а расстояние до левого его конца −
величину![]() (см. рисунок 1.1). Для определенных таким
(см. рисунок 1.1). Для определенных таким
образом величин![]() и
и![]() выполняются соотношения
выполняются соотношения![]()
![]() ,
,![]() ,
,
поэтому, согласно (5), вектор![]() задает смешанные стратегии первого
задает смешанные стратегии первого
игрока.

Тогда точка 0 задает
вектор (1, 0), т. е. первую чистую стратегию
первого игрока, а точка 1 задает вектор
(0, 1), т. е. вторую чистую стратегию первого
игрока. Далее через концы единичного
отрезка проводятся вертикальные линии.
На этих линиях откладываются выигрыши
первого игрока при применении вторым
игроком его различных чистых стратегий.
При этом выигрыши в случае применения
первым игроком его первой чистой
стратегии располагаются на левой
вертикальной линии, а соответствующие
второй чистой стратегии первого игрока
− на правой вертикали. Точки левой и
правой вертикали, соответствующие одной
и той же чистой стратегии второго игрока,
соединяются отрезками. На рисунке 1.2
изображены выигрыши первого игрока при
применении вторым игроком первой чистой
стратегии. Римскими цифрами указано,
что второй игрок применяет именно первую
чистую стратегию.

Любая точка K
этого отрезка с координатами
![]() и
и![]() показывает, что если первый игрок будет
показывает, что если первый игрок будет
применять свою смешанную стратегию![]() ,
,
а второй игрок − свою первую чистую
стратегию, то средний выигрыш первого
игрока будет равен![]() .
.
Аналогичные
построения выполняются для остальных
чистых стратегий второго игрока (рисунок
1.3). Римские цифры указывают на номер
его чистой стратегии.

Жирным шрифтом
выделена ломаная, соответствующая
нижней границе выигрыша первого игрока,
т.е. дающая его средний гарантированный
выигрыш. В точке М находится наибольший
гарантированный выигрыш первого игрока
(так как М − наивысшая точка ломаной).
Эта точка является пересечением
отрезков, соответствующих первой и
второй чистым стратегиям второго
игрока. Эти стратегии называются
активными.
Второй игрок будет использовать их в
своей оптимальной смешанной стратегии
с ненулевой вероятностью. Отрезки,
соответствующие третьей и четвертой
чистым стратегиям второго игрока, не
проходят через точку М, поэтому эти
стратегии в оптимальную смешанную
стратегию второго игрока войдут с
нулевыми вероятностями, так как их
реализация приведет к большему проигрышу
второго игрока. Такие стратегии называют
пассивными.
При определении
оптимальной смешанной стратегии первого
игрока и цены игры используется следующее
утверждение:
Утверждение 3.
Если один
из игроков применяет свои оптимальные
смешанные стратегии, то его выигрыш
будет равен цене игры, независимо от
того, с какими вероятностями применяет
другой игрок свои стратегии, вошедшие
в оптимальную смешанную стратегию.
Выпишем соотношения
для нахождения оптимальной смешанной
стратегии первого игрока, основываясь
на утверждении 3. В нашем примере платежная
функция, согласно (7), имеет вид:
![]()
Пусть оптимальная
смешанная стратегия первого игрока
равна
![]() .
.
По утверждению 3 он получит выигрыш,
равный цене игры![]() ,
,
с какими бы вероятностями не применял
второй игрок свои активные стратегии.
Мы рассмотрим случаи, когда второй игрок
применяет свои активные чистые стратегии,
т.е. либо первую, либо вторую.
Итак, пусть
![]() ,
,![]() .
.
Тогда![]() .
.
Пусть
![]() ,
,![]() .
.
Тогда![]() .
.
Приравняем эти значения к цене игры![]() и добавим уравнение
и добавим уравнение![]() ,
,
получим систему уравнений:
 (9)
(9)
Решив эту систему,
получаем
![]()
![]()
![]()
Теперь найдем
оптимальную смешанную стратегию второго
игрока. Пусть она задается вектором
![]() .
.
Здесь мы учли тот факт, что третья и
четвертая чистые стратегии второго
игрока являются пассивными. Выпишем
величину проигрыша второго игрока, если
он применяет свою оптимальную смешанную
стратегию, а первый игрок − свои чистые
стратегии.
Пусть
![]()
![]() .
.
Тогда![]() .
.
Пусть
![]()
![]() .
.
Тогда![]() .
.
Применяем утверждение
3, учитывая, что цена игры найдена и равна
![]() получим систему уравнений:
получим систему уравнений:

Решив эту систему,
получаем
![]()
![]() .
.
Итак, оптимальная смешанная стратегия
второго игрока задается вектором![]() .
.
Ответ к данной
задаче запишем в виде:
![]()
![]() ,
,
![]()
![]() .
.
2. Рассмотрим теперь
матричную игру, платежная матрица
которой является транспонированной к
матрице задачи 1, т.е. игра задается
матрицей

В новой игре первый
игрок имеет четыре чистые стратегии, а
второй − две. Нижняя цена игры
![]() а верхняя цена игры
а верхняя цена игры![]() .
.
Так как
![]() ,
,
то у этой игры нет седловой точки, поэтому
нужно искать ее решение в смешанных
стратегиях. Пусть![]() − вектор смешанных стратегий первого
− вектор смешанных стратегий первого
игрока, а![]() −
−
вектор смешанных стратегий второго
игрока. Платежная функция данной игры
равна:
![]()
Второй игрок имеет
две чистые стратегии, поэтому графически
будет решаться задача второго игрока.
Построения выполняются аналогично п.1,
если поменять местами первого и второго
игроков (см. рисунок 1.4). Цель второго
игрока, согласно его осторожному
поведению, состоит в минимизации его
возможного риска. Риск второго игрока
(т.е. максимально возможный проигрыш
второго игрока при применении им той
или иной смешанной стратегии) на рисунке
1.4 показан жирной линией. Точка M
обозначает минимальный риск второго
игрока. Она лежит на пересечении отрезков,
соответствующих второй и четвертой
чистым стратегиям первого игрока.

Обозначим оптимальную
смешанную стратегию второго игрока
![]() .
.
Для нахождения значений![]() и
и![]() воспользуемся утверждением 3. Активными
воспользуемся утверждением 3. Активными
стратегиями первого игрока являются
вторая и четвертая. Тогда
1)
![]() ,
,![]() =>
=>![]() .
.
2)
![]() ,
,![]() =>
=>![]() .
.
Приравняем эти
значения к цене игры
![]() и добавим уравнение
и добавим уравнение![]() ,
,
получим систему уравнений:
 Решив
Решив
эту систему, получаем![]()
![]()
![]()
Теперь найдем
оптимальную смешанную стратегию первого
игрока,
![]() .
.
Так как его активные стратегии − вторая
и четвертая, а первая и третья пассивные,
то![]() .
.
Следовательно,![]() .
.
Применяя утверждение 3 и учитывая, что
цена игры уже найдена, получим систему
уравнений:

Решая эту систему,
получаем
![]()
![]()
Итак, решение
матричной игры задается векторами
![]()
![]() и ценой игры
и ценой игры![]() :
:
![]() ,
,
![]()
![]()
![]() .
.
Задача 2. Об
оптовой закупке при неопределенности
розничной продажи.
1. Составим платежную
матрицу игры, описывающей предложенную
в задаче ситуацию. Эта задача является
примером так называемых «игр с природой».
Торговая фирма выступает в качестве
первого игрока. У нее есть две чистые
стратегии: делать закупки, рассчитывая
на холодную и дождливую погоду (первая
стратегия) или на жаркую солнечную
(вторая стратегия). Вторым игроком
является природа. У нее также две чистые
стратегии. Первая стратегия − установить
холодную и дождливую погоду, вторая
стратегия − установить жаркую солнечную
погоду. Элементы платежной матрицы −
это прибыль, которую будет получать
фирма в той или иной ситуации. Прибыль
рассчитывается как разница между
выручкой фирмы от розничной реализации
продукции и ежедневными затратами
фирмы. Затраты в свою очередь есть сумма
средств, направленных на оптовую закупку
товаров, и издержек на розничную
реализацию продукции.
Рассмотрим первую
чистую стратегию фирмы. Пусть фирма
планирует закупить товары А и В в
количествах kA
и kB
соответственно. Предполагается, что
завтра будет холодная погода. Исходя
из статистических данных, на каждые 2
ед. товара А реализуется 3 ед. товара В.
Следовательно, фирма должна закупить
продукты таким образом, чтобы выполнялось
соотношение на их количество. Это значит,
что должно выполняться соотношение:
![]()
На закупки фирма
предполагает тратить 9775 руб. ежедневно.
Поэтому, исходя из оптовых цен продуктов,
она может купить продукты в количествах,
для которых выполнено:
![]()
Итак, для нахождения
количеств закупаемых в расчете на
холодную погоду продуктов, необходимо
решить следующую систему уравнений:
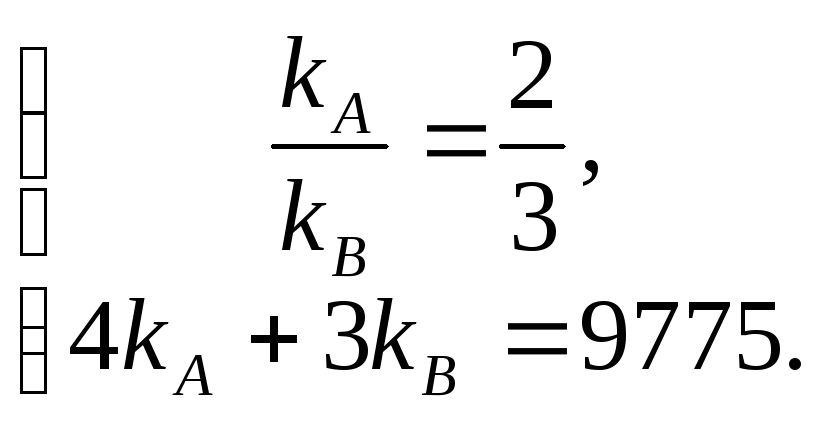
Отсюда получаем:
kA
= 1150 kB
= 1725, т.е.
необходимо закупить 1150 ед. товара А и
1725 ед. товара В.
Пусть фирма
применяет свою вторую чистую стратегию,
т.е. делает покупки в расчете на солнечную
погоду. Это значит, что фирма предполагает
на каждые 5 ед. товара А продать 1 ед.
товара В. Следовательно, для количеств
nA
и nB
закупаемых
товаров должно выполняться соотношение:
![]()
Учитывая оптовые
цены товаров и планируемую сумму трат
на их закупку, получаем систему уравнений:

Решение этой
системы: kA
= 2125, kB
= 425. Итак,
при второй своей чистой стратегии фирма
должна закупить 2125 ед. товара А и 425 ед.
товара В.
Теперь рассчитаем
ожидаемую прибыль фирмы при различных
погодных условиях. Может быть четыре
ситуации:
-
фирма применяла
свою первую чистую стратегию, т.е. делала
закупки в расчете на холодную погоду
и угадала; -
фирма делала
закупки в расчете на холодную погоду
(применяла первую чистую стратегию), а
погода была жаркой; -
фирма применяла
свою вторую чистую стратегию, т.е. делала
закупки в расчете на жаркую погоду, а
погода была холодной; -
фирма применяла
свою вторую чистую стратегию, т.е. делала
закупки в расчете на жаркую погоду, и
погода была действительно жаркой.
Рассмотрим отдельно
каждую из этих ситуаций.
1) Фирма совершает
покупки в расчете на холодную погоду,
т.е. закупает 1150 ед. товара А и 1725 ед.
товара В. При холодной погоде (т.е. первой
чистой стратегии природы) продукты
продаются в выбранном фирмой соотношении,
т. е. фирма продаст
все продукты, которые закупила (т.е.
товар А в количестве 1150 ед., а товар В в
количестве 1725 ед.). Учитывая издержки,
связанные с розничной продажей, прибыль
П фирмы в данном случае равна:
П = 1150*7 + 1725*6 –
1150*4 – 1725*3 – 1900 = 6725 (руб.).
2) Фирма по-прежнему
закупает 1150 ед. товара А и 1725 ед. товара
В, рассчитывая на холодную погоду. При
жаркой погоде товара А можно было бы
продать 2125 ед., но фирма купила только
1150. Товара В фирма купила 1725 ед., но при
жаркой погоде можно продать только 425
ед. Излишек товара В в количестве 1725 –
425 = 1300 ед. можно сдать на пищевую
переработку по цене на 75 % меньше оптовой,
т.е. по 0,25*3 = 0,75 (руб.). Итого, прибыль фирмы
в данной ситуации равна
П = 1150*7 + 425*6 – 1150*4
– 1725*3 + 1300*0,75 – 1900 = – 100 (руб.).
Заметим, что
отрицательная прибыль фирмы означает,
что фирма несет убытки, если не угадала
погоду на завтра.
3) Фирма применяет
свою вторую чистую стратегию, т.е.
закупает 2125 ед. товара А и 425 ед. товара
В, рассчитывая на жаркую погоду. Если
в действительности погода оказалась
холодной, то фирма сможет продать только
1150 ед. товара А. Остаток в 2125 – 1150 = 975 ед.
можно будет сдать на пищевую переработку
по цене на 75% меньше оптовой, т.е. по 0,25*
4 = 1 руб.
Товара В фирма
сможет продать только 425 ед. вместо
возможных 1725 ед. Итак, если фирма применит
свою вторую чистую стратегию против
первой стратегии природы, то прибыль
ожидается равной
П = 1150*7 + 425*6 – 2125*4
– 425*3 + 975*1 – 1900 = – 100 (руб.).
4) Фирма совершает
покупки в расчете на жаркую погоду, т.е.
закупает 2125 ед. товара А и 425 ед. товара
В. Если погода угадана, то фирма продаст
все продукты, которые закупила (т.е.
товар А в количестве 2125 ед., а товар В в
количестве 425 ед.). Данная ситуация
соответствует второй чистой стратегии
природы. Учитывая издержки, связанные
с розничной продажей, прибыль П фирмы
в данном случае равна:
П = 2125*7 + 425*6 – 2125*4
– 425*3 – 1900 = 5750 (руб.).
Таким образом,
платежная матрица игры имеет вид:
![]()
Найдем решение
полученной матричной игры графическим
способом. Пусть вектор
![]() − вектор смешанных стратегий фирмы, а
− вектор смешанных стратегий фирмы, а![]() − вектор смешанных стратегий природы.
− вектор смешанных стратегий природы.
Тогда платежная функция игры имеет вид:
![]() (10)
(10)
Оптимальной
смешанной стратегии фирмы на рисунке
2.1 соответствует точка K.

Применим к данной
игре утверждение 3. Обе чистые стратегии
природы являются активными. Обозначим
оптимальную смешанную стратегию фирмы
![]() .
.
Итак, пусть
![]() ,
,![]() .
.
Тогда![]() .
.
Пусть
![]() ,
,![]() .
.
Тогда![]() .
.
Приравняем эти значения к цене игры![]() и добавим уравнение
и добавим уравнение![]() ,
,
получим систему уравнений:

![]()
Решением этой
системы будет
![]()
![]()
![]() .
.
Итак, оптимальная
стратегия фирмы состоит в том, чтобы
делать закупки, рассчитывая на завтрашний
дождь в 46% случаев, а в 54% случаев − на
солнечную погоду. Средняя ожидаемая
выручка фирмы при этом должна составить
3050 руб. ежедневно.
Снова применяя
утверждение 3, составим систему для
нахождения оптимальной смешанной
стратегии природы.

Отсюда
![]()
![]()
-
Предположим, что
вероятность завтрашнего дождя известна
и составляет 40%. Тогда смешанная стратегия
природы оказывается равной
 .
.
Найдем ожидаемую прибыль фирмы с учетом
этой информации, если применяется
оптимальная смешанная стратегия фирмы.
Подставим оптимальную смешанную
стратегию фирмы и
и в выражение для платежной функции (10):
в выражение для платежной функции (10):
![]()
![]() (руб.).
(руб.).
Заметим, что
согласно теореме 3, ожидаемая прибыль
фирмы должна была оказаться равной цене
игры, т.е. 3050 руб. Отклонение рассчитанной
величины от данного значения вызвано
погрешностью вычисления оптимальной
смешанной стратегии фирмы.
Найдем оптимальную
стратегию фирмы на завтрашний день,
если администрации известна вероятность
завтрашнего дождя, равная 40%. Возможные
стратегии фирмы на завтрашний день −
это делать закупки в расчете либо на
дождливую, либо на солнечную погоду.
Смешанная стратегия природы равна
![]() .
.
Если фирма будет
делать закупки в расчете на дождливую
погоду, т.е. применять свою первую чистую
стратегию
![]() ,
,
то ее ожидаемая выручка, согласно (10),
составит:
![]() (руб.).
(руб.).
Если фирма будет
делать закупки в расчете на жаркую
погоду, т.е. применять свою вторую чистую
стратегию
![]() ,
,
то ее ожидаемая выручка составит:
![]() (руб.).
(руб.).
Итак, поскольку
![]() ,
,
то оптимальной стратегией фирмы на
следующий день является ее вторая чистая
стратегия, т.е. выполнение закупок в
количествах ед. товара А и ед. товара В
соответственно. При этом на следующий
день ожидается прибыль, равная 3410 руб.
Задача 3. Задача
о структуре посевов.
-
Составим платежную
матрицу игры, которая описывается
заданной ситуацией. В данной игре
принимают участие два игрока. Первый
игрок − агрофирма. У нее две чистые
стратегии: засеять всю площадь культурой
А или всю площадь культурой В. Второй
игрок − природа. У нее три чистые
стратегии: установить засушливое,
нормальное или дождливое лето. Поэтому
у платежной матрицы
 будет две строки и три столбца. Выигрыш
будет две строки и три столбца. Выигрыш
агрофирмы − это ее выручка, полученная
с 1 га от продажи выращенных культур.
Умножив урожайность культуры А в тех
или иных условиях на ожидаемую цену 1
ц данной культуры, получим ожидаемую
выручку агрофирмы с 1 га пашни, засеянного
культурой А. В случае засушливого лета
ожидаемая выручка составит 1 тыс.
руб./ц*18 ц/га = 18 тыс. руб./га, в случае
нормального лета ожидаемая выручка
составит 1 тыс. руб./ц *12 ц/га = 12 тыс.
руб./га, случае дождливого лета − 1 тыс.
руб./ц*32 ц/га = 32 тыс. руб./га. Аналогично
рассчитывается ожидаемая выручка в
случае применения агрофирмой ее второй
чистой стратегии. Итак, игра задается
следующей платежной матрицей:
![]() (11)
(11)
2. Пусть
![]() −
−
доля имеющейся у агрофирмы пашни,
засеянная культурой А, а![]() −
−
доля имеющейся у агрофирмы пашни,
засеянная культурой В. Если считать,
что будет засеяна вся площадь, то![]()
![]() ,
,![]() ,
,
т.е. вектор![]() задает смешанную стратегию агрофирмы.
задает смешанную стратегию агрофирмы.
Пусть![]() −
−
вероятность засушливого лета,![]() −
−
вероятность нормального лета,![]() −
−
вероятность дождливого лета. Тогда
вектор![]() задает смешанную стратегию природы.
задает смешанную стратегию природы.
Обозначим через![]() ожидаемую выручку агрофирмы с одного
ожидаемую выручку агрофирмы с одного
га пашни при применении ей своей смешанной
стратегии. Найдем оптимальные смешанные
стратегии агрофирмы и природы и цену
игры. В отличие от задач 1 и 2 рассмотрим
еще один способ решения матричных игр
− сведение задач теории игр к задачам
линейного программирования. Опишем
сначала процедуру сведения в общем
виде.
Рассмотрим игру,
определяемую матрицей

Утверждение 4.
Для того,
чтобы число
![]() было ценой игры, а векторы
было ценой игры, а векторы![]() и
и![]() − оптимальными смешанными стратегиями
− оптимальными смешанными стратегиями
первого и второго игроков соответственно
необходимо и достаточно выполнение
неравенств
![]()
![]() ,
,
(12)
![]()
![]() .
.
(13)
Согласно утверждению
4 для оптимальной стратегии первого
игрока должно выполняться неравенство
(12). Предположим для определенности, что
![]() .
.
Этого всегда можно добиться, прибавив
ко всем элементам матрицы![]() одно и то же число
одно и то же число![]() .
.
Подобная операция не изменит оптимальных
стратегий игроков, а только увеличит
цену игры на![]() .
.
Разделим обе части
неравенства (12) на
![]() (так как
(так как![]() ,
,
то знак неравенства сохраняется):
![]() ,
,
![]() .
.
Положим
![]() ,
,
тогда
![]() ,
,
![]() .
.
(14)
Кроме того, так
как по определению смешанных стратегий
![]() ,
,![]() ,
,
то и![]() ,
,![]() .
.
Сумма компонент вектора смешанных
стратегий, согласно (5), должна быть равна
1:
![]()
![]()
![]()
Так как первый
игрок стремится получить максимальный
в среднем выигрыш, то он должен
минимизировать величину
![]() .
.
Учитывая это, а также (14), получаем, что
для нахождения оптимальной смешанной
стратегии первого игрока необходимо
решить задачу линейного программирования:
![]()
![]() ,
,
![]() (15)
(15)
![]() ,
,
![]() .
.
Аналогично можно
показать, что для нахождения оптимальной
смешанной стратегии второго игрока
необходимо решить задачу линейного
программирования:
![]()
![]() ,
,
![]() (16)
(16)
![]() ,
,
![]() .
.
Здесь
![]() ,
,![]() ,
,
где![]() − вектор смешанных стратегий второго
− вектор смешанных стратегий второго
игрока.
Заметим, что задача
(15) является двойственной к задаче (16).
Поэтому для того, чтобы найти решение
матричной игры, необходимо найти
оптимальное решение пары двойственных
задач (15) и (16). Пусть
![]() − оптимальное решение задачи (16),
− оптимальное решение задачи (16),![]() − оптимальное решение задачи (15),
− оптимальное решение задачи (15),![]() −
−
оптимальные значения целевых функций.
Формулы для определения оптимальных
стратегий и цены игры имеют вид:
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
(17)
Теперь выпишем
задачи линейного программирования,
соответствующие игре, описываемой
матрицей (11).
|
Задача |
Задача |
|
|
|
Найдем оптимальное
решение каждой из этих задач. Задача
агрофирмы имеет две переменные, поэтому
ее можно решить графически. На рисунке
3.1 представлено графическое решение
задачи агрофирмы.

Область допустимых
решений задачи на рисунке 3.1 представлена
неограниченным четырехугольником ABCD,
вектор
![]() дает направление вектора-градиента
дает направление вектора-градиента
целевой функции, линия![]() изображает линию уровня целевой функции.
изображает линию уровня целевой функции.
Точкой минимума является точкаC,
лежащая на пересечении первой и второй
граничной прямых. Ее координаты найдем,
решив систему уравнений:
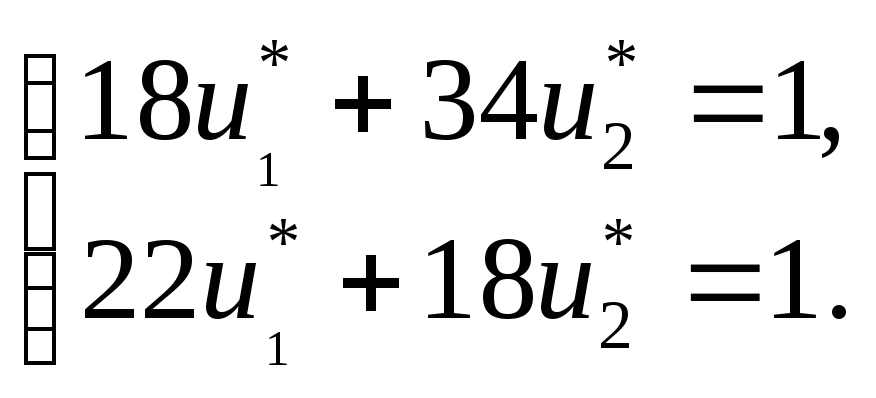
Отсюда
![]() ,
,![]() .
.
Тогда![]()
![]() .
.
Оптимальное решение
задачи природы найдем, используя условия
«дополняющей нежесткости».
Первая группа
условий: xjvj=0,
![]() ,
,
где
v1
=![]() ,
,
v2
=![]() ,
,
v3
=![]() .
.
Тогда
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]() .
.
Вторая
![]() группа
группа
условий:![]()
![]() где
где
![]()
![]()
Тогда
![]()
![]()
![]() ,
,
![]()
![]()
![]() .
.
Отсюда получаем

Решение этой
системы:
![]()
![]()
![]() .
.
![]() Далее,
Далее,
используя найденные оптимальные решения
пары двойственных задач, по формулам
(17) найдем цену игры и оптимальные
смешанные стратегии игроков.
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом,
оптимальная смешанная стратегия
агрофирмы равна
![]() .
.
Это означает, что для получения
максимальной ожидаемой выручки агрофирме
необходимо 80% площади имеющейся пашни
засеять культурой А и 20 % пашни засеять
культурой В. Ожидаемая выручка при этом
должна составить 21,2 тыс. руб./га.
Оптимальная
смешанная стратегия природы
![]() т. е. наиболее неблагоприятной для фирмы
т. е. наиболее неблагоприятной для фирмы
погодой будет − с вероятностью 20%
засушливое лето, с вероятностью 80%
нормальное лето, а дождливое лето − с
вероятностью 0.
Соседние файлы в папке Все ИДЗ 2 курс(Задания)
- #
20.06.201540.45 Кб196Задача 1.xls
- #
20.06.201539.42 Кб132Задача 2.xls
- #
20.06.2015155.65 Кб108Задача 4.xls
- #
- #
- #
- #
- #
20.06.201552.74 Кб61Назначение_напарников.xls
- #
- #
20.06.201540.45 Кб67ПОСЕВ2007.xls
- #
20.06.201562.98 Кб81РаспредСырья 2007.xls
Решение матричной игры в смешанных стратегиях
Краткая теория
Для игры без седловой точки оптимальные стратегии игроков
находятся в области смешанных стратегий. Смешанной стратегией игрока
называют вектор
,
компоненты которого удовлетворяют условиям
Смешанной стратегией игрока
называют вектор
где
и
– вероятности, с которыми игроки
и
выбирают свои чистые стратегии
и
.
При использовании смешанных стратегий игра приобретает случайный характер,
случайной становится и величина выигрыша игрока
(проигрыша игрока
).
Эта величина является функцией смешанных стратегий
и
и определяется по формуле:
Функцию
называют платежной или функцией выигрыша.
Смешанные стратегии
и
называются оптимальными, если они образуют
седловую точку для платежной функции
,
то есть удовлетворяют неравенству
.
Пользуются и другим определением оптимальных смешанных стратегий; стратегии
и
называют оптимальными, если
Величину
называют ценой игры.
Поиск оптимальных стратегий начинают с
упрощения платежной матрицы. Если в платежной матрице элементы
-й
строки не меньше соответствующих элементов
-й
строки, то есть
,
то говорят, что стратегия
доминирует над стратегией
.
Аналогично, если элементы
-го
столбца не превосходят элементы
-го
столбца, то есть
,
то говорят, что стратегия
доминирует над стратегией
.
Частным случаем доминирования является дублирование стратегий, когда
или
.
Исключение из платежной матрицы заведомо доминируемых стратегий (ими игрокам
пользоваться заведомо невыгодно) позволяет уменьшить ее размерность, а это
упрощает решение игры. Вероятность применения доминируемых стратегий равна
нулю.
Оптимальные смешанные стратегии
в игре с платежной матрицей
и ценой
остаются оптимальными и для игры с платежной
матрицей
(где
)
и ценой
.
На этом основании платежную матрицу можно всегда преобразовать так, что ее
элементы будут целыми неотрицательными числами, а это упрощает расчеты.
Решение матричной игры сведением к
задаче линейного программирования
Пусть имеем игру размерности
с матрицей:
Обозначим через
оптимальные смешанные стратегии игроков
к
.
Стратегия
игрока
гарантирует ему выигрыш не меньше
,
независимо от выбора стратегии
,
игроком
.
Это можно записать так:
где
.
Аналогично стратегия
игрока
гарантирует ему проигрыш не больше
,
независимо от выбора стратегии
,
игроком
,
т. е.:
где
.
Поскольку элементы платежной матрицы на
основании всегда можно сделать
положительными, то и цена игры
(оптимальные смешанные стратегии
и
соответственно игроков
и
в матричной игре
с ценой
будут оптимальными и в матричной игре
с ценой
,
где
).
Преобразуем системы неравенств, разделив обе части
каждого неравенства на положительное число
,
и введем новые обозначения
;
.
Получим:
где:
и
где
Так как игрок А стремится максимизировать цену игры
,
то обратная величина
будет минимизироваться, поэтому оптимальная
стратегия игрока А определится из задачи линейного программирования следующего
вида:
найти минимальное значение функции
при
ограничениях (1) и (2).
Оптимальная смешанная стратегия игрока
определится решением задачи следующего вида:
найти максимальное значение функции
при
ограничениях (3) и (4).
Решив пару двойственных задач графическим (для
случая двух переменных) или симплексным методом, далее определим:
Поскольку задачи (1)(2) и (3)(4) образуют пару
симметричных двойственных задач линейного программирования, нет необходимости
решать обе задачи. Получив решение одной из них, достаточно воспользоваться
соответствием между переменными в канонических записях задач.
и из строки целевой функции последней
симплекс-таблицы, содержащей компоненты оптимального вектора, выписать значения
компонент оптимального вектора двойственной задачи.
При поиске оптимальных стратегий в
матричных играх размерностей
и
целесообразно
использовать графический метод решения ЗЛП и свойства оптимальных планов пары
двойственных задач: если в оптимальном плане задачи переменная положительна, то
соответствующее ограничение двойственной задачи ее оптимальным планом
обращается в равенство; если оптимальным планом задачи ограничение обращается в
строгое неравенство, то в оптимальном плане двойственной задачи соответствующая
переменная равна нулю.
Пример решения задачи
Задача
Отрасли
и
осуществляют капитальные вложения в четыре
объекта. С учетом особенностей вкладов и местных условий прибыль отрасли
в зависимости от объема финансирования
выражается элементами платежной матрицы
. Для упрощения
задачи принять, что убыток отрасли
равен прибыли отрасли
. Найти
оптимальные стратегии отраслей.
Требуется:
1)
свести исходные данные в таблицу и найти решение матричной игры в чистых
стратегиях, если оно существует (противном случае см. следующий пункт 2);
2)
упростить платежную матрицу;
3)
составить пару взаимно двойственных задач, эквивалентную данной матричной игре;
4)
найти оптимальное решение прямой задачи (для отрасли
)
симплекс-методом;
5)
используя соответствие переменных, выписать оптимальное решение двойственной
задачи (для отрасли
.
6)
используя соотношение между оптимальными решениями пары двойственных задач,
оптимальными стратегиями и ценой игры, найти решение в смешанных стратегиях;
7)
дать рекомендации по каждой отрасли.
Решение
1)
Сведем исходные данные в таблицу:
Так
как
, то седловая
точка отсутствует, и оптимальное решение следует искать в смешанных стратегиях
игроков:
и
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
2)
Упростим платежную матрицу, отбросив стратегии, заведомо невыгодные или
дублирующие.
2-я
стратегия (2-й столбец) является невыгодной для игрока
– элементы 2-го столбца не меньше элементов
3-го.
4-я
стратегия (4-й столбец) является невыгодной для игрока
– элементы 4-го столбца не меньше элементов
3-го.
2-я
стратегия (2-я строка) является невыгодной для игрока
– элементы 2-й строки не больше элементов 1-й
4-я
стратегия (4-я строка) является невыгодной для игрока
– элементы 4-й строки не больше элементов 1-й
Получили
матрицу размером 2х2
3) Составим пару взаимно двойственных задач, эквивалентных
данной матричной игре.
Так
как платёжная матрица содержит отрицательные числа, то лучше перейти к новой
матрице с неотрицательными элементами; для этого к элементам платёжной матрицы
достаточно добавить соответствующее положительное число, в данном случае 2.
Решение игры при этом не изменится, а цена игры увеличится на 2. Платёжная матрица примет вид:
Обозначив
и
,
составим две взаимно двойственные задачи
линейного программирования:
4)
Найдем оптимальное решение задачи для отрасли
симплекс-методом.
На другой странице сайта есть задача, решенная симплекс-методом очень подробно, а в этом примере, для краткости, из расчетов приведены только симплексные таблицы.
Приведем
задачу к каноническому виду.
Заполняем
симплексную таблицу 0-й итерации.
Получаем таблицу 1-й итерации:
Получаем таблицу 2-й итерации:
В
индексной строке все члены неотрицательные, поэтому получено следующее решение
задачи линейного программирования (выписываем из столбца свободных членов):
5)
Соответствие между переменными исходной и двойственной задачи:
На
основании симплексной таблицы получено следующее решение 1-й задачи:
6)
Найдем решение игры в смешанных стратегиях.
Цена
игры:
Находим
оптимальную стратегию
Учтем,
что 2-я и 4-я строка матрицы были отброшенные, как невыгодные для игрока
:
Находим
оптимальную стратегию
Учтем,
что 2-й и 4-й столбец матрицы были отброшенные, как невыгодные для игрока
:
Цена
игры
7) Дадим рекомендации по каждой отрасли.
Отрасли
необходимо вложить 37,5% средств в 1-й объект и 62,5% средств во 3-й
объект. Во 2-й и 4-й объект капитальные вложения осуществлять невыгодно.
Отрасли
необходимо вложить 25% средств в 1-й объект и 75% средств во 3-й
объект. Во 2-й и 4-й объект капитальные вложения осуществлять невыгодно.
Двойственная задача линейного программирования
Время на прочтение
9 мин
Количество просмотров 26K

Обычно с задачей линейного программирования (ЗЛП) связана другая линейная задача, называемая двойственной. Обе эти задачи можно считать двойственными одну по отношению к другой, считать равносильными. Первая задача называется обычно исходной, или прямой, другая – обратной. Переменные, используемые в двойственной задаче называются двойственными или множителями Лагранжа. На них не накладывается ограничений по знаку. Рассматриваются двойственные критерии оптимальности. Специальные случаи называют симметричными двойственными задачами линейного программирования. Связь между оптимальными решениями двойственных задач устанавливается теоремой двойственности.
Теорема двойственности
Важнейшие свойства пары двойственных задач математического программирования сформулированы в трех основных теоремах.
Теорема двойственности
Допустимый вектор решения прямой задачи программирования оптимален тогда и только тогда, когда существует такой допустимый вектор решения двойственной задачи, что целевые функции прямой и двойственной задачи равны. Допустимый вектор двойственной задачи оптимален тогда и только тогда, когда существует допустимый вектор прямой задачи и целевые функции обеих задач равны.
Теорема существования решения
Если существуют допустимые векторы решений прямой и двойственной задач, то обе задачи имеют оптимальные векторы. Если одна из двух задач не имеет допустимого вектора, то ни одна из них не имеет оптимального вектора решения.
Теорема (принцип) дополняющей нежесткости
-
Если (xQ , xL) – оптимальное решение прямой задачи, а (yQ, yL) – решение двойственной задачи, то (xQ , xL, yQ , yL) – решение задачи Лагранжа. В частности, в этом случае удовлетворяются соотношения между переменными прямой и двойственной задач и условия дополняющей нежесткости.
-
Оптимальное решение прямой задачи программирования получается только при одном значении xQ. Это справедливо и для переменной yQ в двойственной задаче.
Теоремы двойственности
Основное неравенство двойственности. Для любых допустимых решений Х<n> и Y<n>пары двойственных ЗЛП имеет место неравенство
Экономически это означает, что для любого допустимого плана производства и любого дополнительного вектора оценок ресурсов (на складе) стоимость изготовленного продукта не превосходит оценки ресурсов.
Теорема существования (малая тероема двойственности)
Чтобы прямая и двойственная задачи имели opt решения, необходимо и достаточно, чтобы существовали допустимые решения для каждой из них.
Теорема 1 двойственности.
Если одна из пары двойственных задач имеет opt решение, то и другая его имеет. Причем экспериментальные решения их целевых ф. равны; если же ЦФ одной из задач не ограничена, то система ограничений другой противоречива. Интерпретация: оптимальное использование ресурсов – opt план. Суммарная оценка ресурсов = оценке продукта полученного при opt плане. Любой другой план не рентабелен. Cj – стоимость единицы продукции (внешняя оценка) yi – стоимость единицы ресурса (внутренняя оценка). Эти двойственные оценки выступают как инструменты балансирования затрат и результатов. Имеет место xj <-> ym +j ; xn+i <-> yi.
Теорема 2 двойственности (о дополняющей нежесткости)
Для того, чтобы допустимые решения X и Y пары двойственных задач были оптимальными, необходимо и достаточно выполнить условия:
То есть, если какое-либо ограничение одной ЗЛП обращается ее opt планом в строгое равенство, то соответствующая переменная двойственной задачи в ее opt плане равна нулю; если же какая-либо переменная opt-го решения одной ЗЛП положительна, то соответствующее ограничение в двойственной ЗЛП ее opt планом обращается в точное равенство.
Теорема Кёнига хорошо иллюстрирует использование принципа двойственности ЗЛП.
Формулирование теоремы. Максимальное число попарно неколлинеарных единиц любой булевой матрицы равно минимальному числу линий, покрывающих все единицы матрицы.
Доказательство. Для нахождения максимального числа попарно неколлинеарных единиц булевой матрицы достаточно сформулировать и решить линейную задачу:
Минимальное число линий, покрывающих все единицы матрицы [Cij], найдем, решив линейную задачу:
Оптимальному решению (u*i, v*j) последней задачи отвечает минимальное покрытие, состоящее из множества строк I, для которых u*i = 1 и столбцов J, для которых u*j =1.
Матрицы А и АТ коэффициентов (*), (**), (***) являются абсолютно унимодулярными, как матрицы двудольного графа. Поэтому условия целочисленности переменных заменяем на условие их неотрицательности, и тогда получаем пару двойственных задач линейного программирования и согласно теореме двойственности имеем:
Линией матрицы называется ее строка или столбец. Два элемента матрицы называются неколлинеарными, если они не лежат на одной линии.
Матрица называется абсолютно унимодулярной, если все ее ненулевые миноры равны 1, либо -1.
Следствие. Матрица инциденций неориентированного графа G абсолютно унимодулярна тогда и только тогда, когда G – двудольный граф. В двудольном графе все простые циклы имеют четкую длину
Принцип двойственности в задачах линейного программирования.
Предположим, что руководство предприятия из анализа конъюнктуры рынка продукции приняли решение: производство сократить, а от запасов сырья избавиться, (продать на рынке) и при этом не нанести себе убытков.
С этой целью руководство должно назначить стоимости yi за единицу сырья вида Si, стремясь при этом минимизировать общую стоимость сырья (чтобы быстрее продать сырье): Ф = Σ4i=1 biyi
Выручка предприятия от продажи сырья, расходуемого на единицу продукции Пi, составит: Σ4i=1 aij yi
И по условию она не должна быть меньше Сj (в противном случае предприятию выгоднее не продавать сырье, а использовать его для нужд производства, выпуска продукции).
Сформулируем исходную и двойственную задачи:
Обе задачи по отношению друг к другу называются двойственными или сопряженными. Анализ таблицы позволяет сделать выводы:
-
Если первая задача сформулирована на поиск максимума, то вторая формулируется на поиск минимума линейной функции.
-
Коэффициенты ЦФ первой задачи являются свободными членами системы ограничений второй.
-
Свободные члены системы ограничений первой задачи являются коэффициентами линейной системы во второй задаче.
-
Матрица коэффициентов второй задачи является транспонированной к матрице коэффициентов ограничений первой задачи.
-
Знаки неравенств в ограничениях второй задачи противоположны знакам неравенств в ограничениях первой задачи.
Оптимальный план Xopt<n> одной из задач тесно связан с оптимальным планом Yopt<n> другой. Если одна из задач имеет решение, то другая также разрешена, причем для оптимальных клонов Xopt<n> =<x1, x2,…xn> и Yopt<m> =<y1, y2,…ym> справедливо равенство Q( Xopt ) =Q’( Yopt ). Если линейная форма одной из задач неограниченна, то условия другой задачи несовместны. Если A-1 обратная матрица к матрице В, состоящей из векторов базиса оптимального плана исходной задачи, то оптимальный план двойственной задачи равен Yopt<m> =СВ -1, здесь С – вектор базисных переменных. Решение двойственной задачи получается в последней симплексной таблице исходной задачи, в (m+1) строке, в столбцах, соответствующих дополнительным параметрам.
Для того чтобы векторы Xopt<n> =<x1, x2,…xn> и Yopt<m> =<y1, y2,…ym> были решениями пары задач, необходимо и достаточно, чтобы их компоненты удовлетворяли следующим условиям:
Эти условия называют принципом дополняющей нежесткости. Если исходная (прямая) задача задана в канонической форме, то двойственная к ней называется несимметричной. Для несимметричной двойственной задачи соблюдается условие yi ≥ 0.
Теория ЗЛП доказывает, что компоненты оптимальных планов взаимно двойственных задач, приведенных к каноническому виду, соответствуют одни другим. То есть базисные переменные основной задачи соответствуют свободным переменным двойственной задачи и наоборот, j = 1(1)n, x*j y*m +j ; x*n+i y*i ; i = 1(1)m.
Размерности в табличке m и n берутся в задаче для y-ков записанной в канонической форме.
Пример. Двойственный симплекс метод.
Исходная задача. Имеется три вида продуктов Пj, причем единица веса каждого из видов продуктов содержит aij единиц (питательных веществ). Для нормальной жизнедеятельности человек должен потреблять не менее bi единиц вещества Bi в сутки. Стоимость единицы продукта Пj равняется Cj. Требуется составить оптимальный суточный рацион питания, т.е. найти количество xj продукта, которое должен потреблять человек, чтобы стоимость питания была бы минимальной, если известно, что
такие значения его компонентов xj, j = 1(1)3, которые минимизируют целевую функцию (Ц) Q = 3x1 + 2x2 + x3 и удовлетворяют ограничениям неравенствам
0,3x1 + 0,2x2 + 0, 4x3 ≥ 0,2;
0,4x1 + 0,3x2 + 0,45x3 ≥ 0,5;
0,2x1 + 0,3x2 + 0, 1 x3 ≥ 0,6;
0,1x1 + 0,2x2 + 0,05x3 ≥ 0,1;
xj ≥ 0; j = 1(1)3 = n
Для приведения задачи к каноническому виду введем дополнительные переменные x4, x5, x6, x7, переменных стало больше чем уравнений n – m = 7 – 4 = 3, следовательно, части из них (трем любым,) для получения решения можно задать произвольные значения (задают, как правило, нулевые значения), возникает число сочетаний из n по m вариантов. Система ограничений примет вид равенств
0,3x1 + 0,2x2 + 0,4x3 – x4 = 0,2;
0,4x1 + 0,3x2 + 0,45x3 – x5 = 0,5;
0,2x1 + 0,3x2 + 0,1x3 – x6 = 0, 6;
0,1x1 + 0,2x2 + 0,05x3 – x7 = 0, 1;
xj ≥ 0; j = 1(1)3 = n, i = 1(1)4 = m.
Назначаем опорный план. Выбор в качестве базисных переменных x4, x5, x6, x7 приводит к недопустимому опорному плану. Так как знаки левой и правой частей различны. (Свободные переменные x1 = x2 = x3 = 0) Метод искусственного базиса приводит к увеличению числа неизвестных задач, что нежелательно. Анализ задачи показывает, что число уравнений в системе ограничений больше числа переменных. Поэтому попытаемся применить принцип двойственности, т.е. вначале решим двойственную ЗЛП, а затем найдем решение исходной.
Двойственная задача. Коэффициентами линейной формы в двойственной задаче выступают правые части bi , i = 1(1)4 = m, исходной основной задачи. Переменные получают другие имена y1, y2, y3, y4, и формулируется двойственная задача иначе. Найти максимум линейной формы Q’:
Q’=0,2y1 + 0,5y2 + 0,6y3 + 0,1y4;
при ограничениях
0,3y1 + 0, 4y2 + 0,2y3 + 0,1y4 ≤ 3;
0,2y1 + 0, 3y2 + 0,3y3 + 0,2y4 ≤ 2;
0,4y1 + 0,45y2 + 0,1y3 + 0,05y4 ≤ 1;
yi ≥ 0; i = 1(1)4.
Приведем задачу к каноническому виду, вводим дополнительные неотрицательные переменные y5 , y6 , y7 :
Найти минимум ЦФ (знаки у коэффициентов ЦФ поменяли на противоположные): Q’= – 0,2y1 – 0,5y2 – 0, 6y3 – 0,1y4;
при ограничениях (в ограничения добавили новые переменные):
0,3y1 + 0, 4y2 + 0,2y3 + 0, 1y4 + y5 = 3;
0,2y1 + 0, 3y2 + 0,3y3 + 0, 2y4 + y6 = 2;
0,4y1 + 0,45y2 + 0,1y3 + 0,05y4 + y7 = 1,
yi ≥ 0; i = 1(1)7.
Задача решается симплекс методом. Исходный опорный план в качестве переменных может иметь y5, y6, y7 и свободные переменные y1 = y2 = y3 = y4 = 0, т.е. Y<7> = [0, 0, 0, 0, 3, 2, 1] .
Базисные переменные y5, y6, y7 и ЦФ выражаем через свободные переменные, т.е. из свободных членов (правых частей, обозначенных γi ) вычитаем левые части ограничений
y5 = 3 – (0,3y1 + 0,4y2 + 0,2y3 + 0,1y4);
y6 = 2 – (0,2y1 + 0,3y2 + 0,3y3 + 0,2y4);
y7 = 1 – (0,4y1 + 0,45y2 + 0,1y3 + 0,05y6);
Q’1=γ0 – Σ4i=1 γi yi = 0 -(0,2y1 + 0,5y2 + 0, 6y3 + 0,1y4);
γ0 =0, так как ЦФ не содержит свободного члена.
и строим симплекс таблицу с двумя полуклетками. Направляющий столбец y3, направляющая строка y6.
Анализ таблицы показывает, что все коэффициенты ЦФ при свободных переменных положительны. Следовательно, план Y<7> не является оптимальным, ЦФ можно уменьшить, увеличивая значения соответствующих свободных переменных.
Находим γ = max{γi} =max {0,2; 0,5; 0,6; 0,1} = 0,6. Переменную y3 надо ввести в базис. После этого устанавливаем, существует ли оптимальный план. В направляющем столбце все коэффициенты положительны, следовательно, оптимальный план существует. В базисе есть переменные, которые можно уменьшать до нуля увеличивая значения y3, тем самым минимизируя ЦФ. Раньше других в нуль обратиться переменная y6 и ее исключаем из базиса.
После замены переменных в базисе переходим к новой симплексной таблице.
Анализ этой таблицы показывает, что все коэффициенты в выражении ЦФ свободных переменных отрицательны. Следовательно, опорный план Y<7>= [0, 0, 20/3, 0, 5/3, 0, 1/3] является оптимальным. ЦФ при этом Q’1 = – 4 достигла наименьшего значения. Возвращаемся к двойственной задаче. Используя соответствие между оптимальными планами двойственных задач ЛП, определяем: базисными переменными в оптимальном плане будут x2 x4 x5 x7; их значения с противоположным знаком записаны в последней строке таблицы. Таким образом, Xopt<n> =<0; 2; 0; 0; 2; 0; 1; 0; 1/30>, т.е. оптимальный рацион из двух единиц продукта П2. Стоимость такого рациона минимальна и составляет 4 единицы. Это значение с противоположным знаком записано в той же таблице.
Литература
-
Ваулин А. Е. Методы цифровой обработки данных.– СПб.: ВИККИ им. А. Ф. Можайского, 1993.– 106 с.
-
Гэри М., Джонсон Д. Вычислительные машины и трудно решаемые задачи. М.: Мир, 1982.
-
Квейд Э. Методы системного анализа // Новое в теории и практике управления производством в США.–М.: Прогресс, 1971.– с.78-99. .
-
Корбут А.А., Финкельштейн Ю. Ю. Дискретное программирование М. Наука. Гл. ред. физ.-мат. лит. 1969.
-
Макаров И. М. и др. Теория выбора и принятия решений.– М.: Наука, 1982.– 328 с.
-
Пфанцагль И. Теория измерений. – М.: Наука, 1988.–384 с.
-
Таха Х. А. Введение в исследование операций. 7-е изд. М.: Изд. дом «Вильямс», 2005.
-
Фишберн П. С. Теория полезности для принятия решений. – М.: Наука,1978. –352 с.
УДК 512.83 В.М. Упит, В.И. Бутылкин
МАТРИЧНОЕ МОДЕЛИРОВАНИЕ ПРИ ПОИСКЕ ОПТИМАЛЬНЫХ РЕШЕНИЙ
В статье рассмотрена процедура нетрадиционного оптимального поиска на примере матричного сопоставления нескольких вариантов возможных к применению средств формирования и накопления продукции у сортировочных устройств.
При многообразии технических средств, используемых на обработке и переработке исходного сырья, выбор одного, лучшего из возможных к применению машин и механизмов, сложен. Принимаемые решения в значительной мере носят отпечаток субъективного подхода, обусловленного уровнем квалификации, производственного опыта или степенью знакомства с существующими методами оптимального поиска или, иначе, поиска оптимальных решений. Немаловажную роль играет и способность исследователя оторваться от инерции использования апробированных методов.
Наряду с традиционными методами оптимизации, позволяющими численно установить полезность каждого исхода [1], применяют и нетрадиционные методы [2]. Например, убедителен и прост метод «отношения предпочтений», основанный на формализации связи результатов (исходов) с обеспечивающими исход средствами.
Особенно эффективен метод комплексной оценки соответствия состояний заданным критериям-требованиям [3-4], благодаря возможности формализации поиска и перевода его на язык логики (алгебры высказываний), с представлением системы в виде автомата А (Р, Х, У, Л, 8), где Р – конечное множество состояний, Х – конечное множество входов в систему, У – единичное множество выходов, Л и 8 – функции перехода.
Рассматриваемая упрощенная модификация метода «комплексной оценки соответствия состояний …», основанная на матричном моделировании, является удобным в работе, эффективным и, главное, простым средством решения задач оптимизации поиска лучших из множества возможных технических и технологических решений.
Порядок использования этого метода может быть прослежен на рассмотрении процедуры выбора из заведомо ограниченного числа средств накопления продукции у сортировочного устройства (продольного или поперечного конвейера), лучшего из возможных к применению накопителя, на основе установления его соответствия задаваемым критериям-требованиям.
Совокупность технических средств накопления и формирования у сортировочного конвейера продукции аграрного, лесопромышленного или какого-либо иного производства может рассматриваться как производственный автомат типа А (Р, Х, У), где Р (Р1, Р2, …) – возможные состояния предмета, орудия или, в общем случае, средства труда; Х (Х1, Х2, …) – входы в систему оценки состояний, или критериев – требований к состоянием; У (У1, У2, …) – выходы системы, или оценочные характеристики каждого из состояний, число которых в итоге оптимального поиска равно единице У (У, = 1).
Из множества применяемых и возможных и применению состояний Р (Р1, Р2, Р3, …) рассмотрим лесонакопители Гипролестранса Р1, накопители СибНИИЛПа Р2 и накопителя КГТУ Р3 [5].
Р1 – лесонакопитель Гипролестранса (рис., а), представляет собой емкость для размещения формируемых пачек, пакетов или пучков бревен, ограниченную, с одной стороны, источником поступления бревен (продольным или поперечным лесотранспортером), с противоположной стороны – парой неподвижных или, реже, подвижных стоек, и снизу – двумя опорными лежнями.
Р2 – лесонакопитель СибНиИЛП (рис., б), выполнен с наклонными, под углом к горизонту 30-45″, балками основания и подвижными стойками, с возможностью их перемещения по мере заполнения лесона-копителя бревнами и возврата в исходное положение после заполнения и освобождения от бревен.
Р3 – лесонакопитель КГТУ (рис., в) с полноповоротными стойками.
а
в
Лесонакопители: а – с неподвижными стойками; б – с подвижными стойками; в – с полноповоротными стойками
Требования Х (Х1, Х2, ….) к состояниям Р определяют исходя из оценки соответствия последних условиям обеспечения безотказного функционирования системы:
Х1 – бревна не должны перекрещиваться и перехлестываться в процессе заполнения лесонакопите-
ля;
Х2 – разбег между торцами в пачке бревен должен быть минимальным;
Х3 – емкость лесонакопителя должна соответствовать параметрам грузозахватных устройств лесопе-регружателей (кранов, погрузчиков);
Х4 – характер перемещения стоек лесонакопителя должен быть односторонним;
Х5 – форма направляющих, по ходу перемещения груза в лесонакопителе, должна быть вогнутой. Матрица соответствия (табл.) в координатах РХ с отображением состояний Р и Х, соответственно по осям ординат и абсциссе, замыкается размещаемыми по вертикали показателями соответствия ПС и качества ПК.
Матрица соответствия состояний требованиям эффективного функционирования системы
Состояния Р Входы Х в систему Выходы У
Х1 Х2 Х3 Х4 Х5 ПС ПК
Р1 Нет Нет Да – Нет 0,25 0,5
Р2 Да Да Да Нет Нет 0,60 1,0
Р3 Да Да Да Да Да 1,00 1,0
При матричной оценке соответствия состояний требованиям эффективного функционирования системы для каждого из состояний Р, устанавливают степень его соответствия ПС предъявляемым требованиям путем установления отношения числа позитивных оценок «да» к общему их количеству (табл.). Так, для состояния Р1 (лесонакопитель Гипролестранса) показатель соответствия равен 0,25, поскольку лишь ] часть критериев-требований является позитивной; для состояния Р2 (лесонакопитель СибНИИЛП) ПС = 0,60; для состояния Р2 (лесонакопитель КГТУ) показатель ПС=1,00.
Для установления ценности, важности каждого из состояний, вводится новый показатель – качества состояния, путем выделения из общего числа доминирующих критериев-требований. В рассматриваемом примере такими доминирующими критериями-требованиями являются: Х1, предусматривающий необходимость исключения возможности перекрещивания бревен в лесонакопителе, и Х3, предусматривающий соответствие параметров груза (пачки, пакета, пучка бревен) техническим характеристикам кранов или погрузчиков, используемых на освобождении лесонакопителей. Этим условиям (критериям-требованиям), определяемым отношением числа позитивных оценок доминирующих критериев-требований, к общему числу доминирующих критериев-требований отвечают состояния Р2 и Р3.
Таким образом, из рассмотренных и оцениваемых состояний Р1, Р2 и Р3 только состояние Р3 (лесонакопитель КГТУ с полноповоротными стойками (рис., в)) обеспечивает равенство показателя качества единице (ПК=1) и показателя соответствия ПС=0,75 ^ 1,0.
Результаты матричной оценки совпадают с результатами алгебраической оценки.
НДФ: (Р1 д Р2 д Р3)у(Р1 V Р2 V Рз) = Р3.
Литература
1. Фергин, В.Р. Методы оптимизации в лесопильно-деревообрабатывающем производстве / В.Р. Фергин. -М.: Лесн. пром-сть, 1975. – 216 с.
2. Розен, В.В. Цель – оптимальность – решение: математические модели принятия решений / В.В. Розен. -М.: Радио и связь, 1982. – 168 с.
3. Гуслицер, И.И. Основы эффективного функционирования поточных линий по первичной обработке древесного сырья: моногр. / И.И. Гуслицер, В.П. Шмаков, А.П. Меньшиков. – Красноярск: Изд-во КГУ, 1993. -184 с.
4. Каверзин, С.В. Обеспечение работоспособности гидравлического привода при низких температурах / С.В. Каверзин, В.П. Лебедев, Е.А. Сорокин. – Красноярск, 1998. – 240 с.
5. Бутылкин, В.И. Накопители для лесных грузов. Создание и совершенствование / В.И. Бутылкин, В.М. У пит // Проблемы машиностроения и новые материалы: мат-лы Всерос. науч. конф. – Красноярск: ИПЦ КГТУ, 2006. – С. 171-175.
———-♦’————
УДК 519.622 Е.А. Новиков, Ю.А. Шитов
ВНУТРЕННЯЯ УСТОЙЧИВОСТЬ ЯВНЫХ МЕТОДОВ РУНГЕ-КУТТА1
Для произвольного т получены коэффициенты явных т -стадийных методов типа Рунге-Кутта с первого по третий порядок точности, у которых области устойчивости промежуточных численных формул согласованы с областью устойчивости основной схемы. Построены неравенства для контроля точности и устойчивости.
Введение. Для численного решения задачи Коши для жестких систем обыкновенных дифференциальных уравнений
У = /(*, У У(*о) = Уо. *о < * < *к, (1)
в [1] предлагается применять явные методы типа Рунге-Кутта
т г-1
уи+1 = у» + Е Рт&, К = ¥ (*п + аА Уп+Е ДА)> (2)
г=1 }=1
где у и I – гладкие вещественные N -мерные вектор функции; * – независимая переменная;
К,1 < г < т, – стадии метода; ц, Рт ,1 < г < т, 1 < } < г -1 – коэффициенты, определяющие свой-
ства точности и устойчивости схемы (2). В [1] для произвольного т получены коэффициенты методов с первого по третий порядок, а в [2] – коэффициенты методов четвертого порядка с максимальным интервалом устойчивости. Там же численно показано значительное повышение эффективности алгоритмов интегрирования за счет комбинирования таких численных формул в процессе вычислений на основании критерия
устойчивости. Заметим, что в [1] и [2] не рассмотрен вопрос о выборе коэффициентов , которые влияют
на устойчивость промежуточных численных схем и, в конечном счете, на эффективность алгоритма интегрирования. Авторы ограничились замечанием, что устойчивости промежуточных формул можно добиться за
счет выбора данных коэффициентов достаточно малыми.
Численные схемы. Для упрощения выкладок далее рассмотрим задачу Коши для автономной системы обыкновенных дифференциальных уравнений
У=1 (УХ У(*о) = Уо> *о < * < *к> (3)
для решения которой применим методы типа Рунге-Кутта, записанные в следующем виде:
г т
Упг = Уп + Е в+1,А * 1 < г < т – 1 Уп+1 = Уп + Е РтК , (4)
}=1 г=1
1 Работа выполнена при финансовой поддержке РФФИ (грант №05-01-00579-а).
Еще одна из выделенных задач линейного программирования, о которой важно упомянуть — это задача о назначениях. Вообще говоря, можно считать, что это частный случай транспортной задачи, для которой мощности поставщиков и потребности клиентов равны 1 (и обычно совпадает размерность). Если на примерах, это может быть задача назначения работников на должности (с достижением максимальной эффективности, или, может, минимальных затрат на зарплату), назначение машин на производственные линии и т.п., при этом один исполнитель (человек, машина, орудие и т.п.) может выполнять только одну работу.
Так же как для решения транспортной задачи был модифицирован симплекс-метод и разработан метод потенциалов, так и для задачи о назначениях был создан более подходящий (более краткий) метод решения. Чаще всего используется так называемый венгерский метод (см. решение примера 1 ниже).
Ниже выложены примеры задач о назначениях, решенные разными способами — изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении заданий, перейдите в раздел: Решение задач линейного программирования для студентов.
Задача 1. Решить задачу об оптимальном назначении с матрицей эффективностей A.
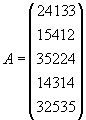
Задача 2. Решить задачу о назначениях.
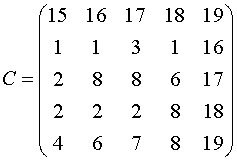
Задача 3. Четыре работника должны выполнять четыре вида работ. Назначить работников на работы методами динамического программирования и ветвей и границ таким образом, чтобы затраты труда были минимальны.
Типичное задание:
В цехе предприятия имеются 5 универсальных станков, которые могут выполнять 4 вида работ. Каждую работу единовременно может выполнять только один станок, и каждый станок можно загружать только одной работой.
В таблице даны затраты времени при выполнении станком определённой работы. Определить наиболее рациональное распределение работ между станками, минимизирующее суммарные затраты времени.
Задача. Служба занятости имеет в наличии четыре вакантных места по разным специальностям, на которые претендуют шесть человек. Проведено тестирование претендентов, результаты которого в виде баллов представлены в матрице
Распределить претендентов на вакантные места таким образом, чтобы на каждое место был назначен человек с наибольшим набранным по тестированию баллом.
Пример решения задачи о назначении с минимальной стоимостью;
Пример решения задачи о назначении с максимальной стоимостью;
В таблице 1 приводятся оценки возможных транспортных издержек.
Таблица 1 — Оценки транспортных издержек
| R j Q i |
25 | 32 | 5 | 4 |
| 30 | 5 | М | 25 | 26 |
| 35 | 10 | 3 | 30 | 31 |
| 5 | М | М | 0 | 1 |
| 5 | М | М | 0 | 1 |
Сделаем математическую постановку задачи о назначениях.
Переменные. В качестве переменной введем величину

Все предполагаемые алгоритмы поиска решения задачи о назначениях базируются на следующем утверждении: оптимальное решение задачи не изменится, если к любой строке или столбцу матрицы издержек прибавить (или вычесть) постоянную величину в силу того, что приоритет назначения не изменится. И весь алгоритм ведется на матрице издержек с соответствующими преобразованиями для получения в ней нулевых элементов, образующих систему так называемых «независимых нулей». Число независимых нулей равно размерности матрицы, а их расположение таково, что каждый из них встречается один раз в строке и один раз в столбце. Если такие независимые нули будут найдены, то в матрице решения в соответствии с их положением будут проставлены единицы. В матрице 1 нулевые элементы получены вычитанием наименьшего элемента в каждой строке. (1)
Как только будут получены нулевые элементы, применяют различные алгоритмы: Мака, венгерский, минимальных линий. Рассмотрим процедуру вычеркивания нулевых элементов минимальным числом прямых линий. В матрице 2 показано, как используется это правило. Могут быть и другие варианты вычеркивания. 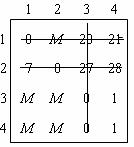
Если все нулевые элементы в матрице будут вычеркнуты, а минимальное число линий будет равно размерности матрицы, то независимые нули в матрице существуют, и решение найдено. В противном случае выбирается наименьший элемент из невычеркнутых элементов (он равен 1). Этот элемент вычитается из каждого невычеркнутого элемента и прибавляется к каждому элементу, стоящему на пересечении проведенных прямых.
В результате получается матрица (3), которая указывает на два оптимальных решения (матрицы решений 4 и 5).
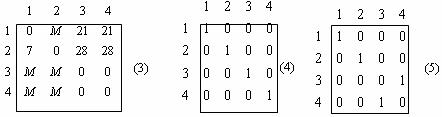
Следует заметить, что, если на последнем шаге оптимальное решение не достигнуто, то процедуру проведения прямых следует повторять до тех пор, пока не будет получено допустимое решение.
Модель назначений
Пример . Руководство фирмы приняло решение произвести инспекцию своих предприятий в Лейпциге, Нанси, Льеже и Тилбурге, направляя туда своих вице-президентов, каждый из которых в компании возглавляет одно из направлений (финансы, маркетинг, производство и персонал). Хотя может существовать большое число факторов, которые нужно учесть при таком назначении (знание языка, узкая специализация, невозможность оторваться от прямых обязанностей и т. д.), руководство компании решило оптимизировать в качестве первого шага только суммарные затраты на командировку вице-президентов. Таблица командировочных расходов в различные города (тыс. долларов) приведена ниже.
| Вице-президенты | Лейпциг | Нанси | Льеж | Тилбург |
| По финансам | 24 | 10 | 21 | 11 |
| По маркетингу | 14 | 22 | 10 | 15 |
| По производству | 15 | 17 | 20 | 19 |
| По персоналу | 11 | 19 | 14 |
Требуется составить схему распределения вице-президентов по филиалам, минимизирующую командировочные расходы.
Решение. Табличная модель этой задачи после проведенной оптимизации приведена на рис.
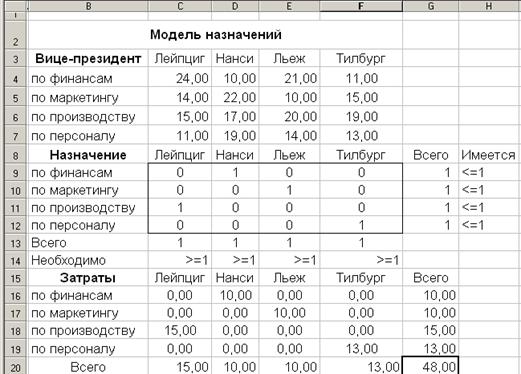
Модель назначений является разновидностью транспортной модели. От последней она отличается только тем, что в ней единица предложения не может распределяться по нескольким местам назначения (ср. рис.).
Таким образом, модель назначений всегда можно построить в виде транспортной модели, в которой предложение в каждой исходной точке и спрос в каждом конечном пункте равны единице.
Точно так же, как и транспортная модель, модель назначений может быть несбалансированной, содержать недопустимые назначения, иметь альтернативные решения при одном и том же значении целевой функции. Эти варианты моделей назначения строятся в полной аналогии с соответствующими транспортными моделями.
Оптимальное распределение продавцов по торговым точкам
Задание. Существует 4 продавца А1, А2, А3, А4 и 4 торговые точки В1, В2, В3, В4. Эффективность работы продавцов на торговых точках задаётся следующей матрицей:
| 9 | 3 | 4 | 8 |
| 4 | 6 | 7 | 11 |
| 5 | 8 | 8 | 4 |
| 6 | 12 | 15 | 9 |
Найти оптимальное распределение продавцов по торговым точкам.
Поскольку задана матрица эффективности, то искать необходимо максимальные значения, следовательно, целевая функция стремится к максимуму. Именно поэтому при решении выбираем вид Максимальная прибыль .
Модифицируем матрицу умножением всех элементов на (-1) и затем сложением их с максимальным элементом матрицы (15) так, чтобы матрица не содержала бы отрицательных элементов:
| 6 | 12 | 11 | 7 |
| 11 | 9 | 8 | 4 |
| 10 | 7 | 7 | 11 |
| 9 | 3 | 0 | 6 |
Шаг №1.
1. Проводим редукцию матрицы по строкам. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль.
| 0 | 6 | 5 | 1 | 6 |
| 7 | 5 | 4 | 0 | 4 |
| 3 | 0 | 0 | 4 | 7 |
| 9 | 3 | 0 | 6 | 0 |
Затем такую же операцию редукции проводим по столбцам, для чего в каждом столбце находим минимальный элемент:
| 0 | 6 | 5 | 1 |
| 7 | 5 | 4 | 0 |
| 3 | 0 | 0 | 4 |
| 9 | 3 | 0 | 6 |
| 0 | 0 | 0 | 0 |
После вычитания минимальных элементов получаем полностью редуцированную матрицу.
2. Методом проб и ошибок проводим поиск допустимого решения, для которого все назначения имеют нулевую стоимость.
Фиксируем нулевое значение в клетке (1, 1). Другие нули в строке 1 и столбце 1 вычеркиваем.
Фиксируем нулевое значение в клетке (2, 4). Другие нули в строке 2 и столбце 4 вычеркиваем.
Фиксируем нулевое значение в клетке (3, 2). Другие нули в строке 3 и столбце 2 вычеркиваем.
Фиксируем нулевое значение в клетке (4, 3). Другие нули в строке 4 и столбце 3 вычеркиваем.
В итоге получаем следующую матрицу:
| [0] | 6 | 5 | 1 |
| 7 | 5 | 4 | [0] |
| 3 | [0] | [-0-] | 4 |
| 9 | 3 | [0] | 6 |
Количество найденных нулей равно k = 4. В результате получаем эквивалентную матрицу Сэ:
| 0 | 6 | 5 | 1 |
| 7 | 5 | 4 | 0 |
| 3 | 0 | 0 | 4 |
| 9 | 3 | 0 | 6 |
4. Методом проб и ошибок определяем матрицу назначения Х, которая позволяет по аналогично расположенным элементам исходной матрицы (в квадратах) вычислить максимальное значение прибыли.
| [0] | 6 | 5 | 1 |
| 7 | 5 | 4 | [0] |
| 3 | [0] | [-0-] | 4 |
| 9 | 3 | [0] | 6 |
Cmax = 9 + 11 + 8 + 15 = 43
Таким образом, распределение продавцов по торговым точкам будет следующее:
1 продавец – торговая точка №1
2 продавец – торговая точка №4
3 продавец – торговая точка №2
4 продавец – торговая точка №3.
При таком назначении, максимальная эффективность составит 43.
Источник
Задача о назначениях онлайн
С помощю этого онлайн калькулятора можно решить задачу о назначениях (задачу о выборе) венгерским методом. Для решения задачи о назначениях задайте размерность матрицы, выберите из вариантов «максимальная прибыль» и «минимальные расходы». Затем введите данные в ячейки и нажимайте на кнопку «Вычислить». Теоретическую часть смотрите ниже.
Предупреждение
Задача о назначениях − теория
Математическая задача о назначениях или задача о выборе формулируется следующим образом. Требуется выбрать такую последовательность элементов  из следующей квадратной матрицы
из следующей квадратной матрицы

чтобы  достигала своего максимального значения, причем
достигала своего максимального значения, причем  при
при  . Другими словами, нужно выбрать из каждого столбца и каждой строки ровно по одному элементу так, чтобы их сумма была максимальной.
. Другими словами, нужно выбрать из каждого столбца и каждой строки ровно по одному элементу так, чтобы их сумма была максимальной.
Отметим, что если бы матрица C была устоена так, что максимальные элементы каждой строки лежали бы в разных столбцах, то решение задачи было бы элементарным, т.е. к качестве решения нужно было выбрать эти максимальные элементы. Однако обычно максимальные элементы нескольких строк(столбцов) расположены в одном и том же столбце (строке) и решение проблемы затрудняется.
При решении задачи о назначениях применяется венгерский метод, что существенно упрощает решение задачи.
Венгерский метод
Сделаем несколько определений.
1. Нулевые элементы  квадратной матрицы S будем называть независимыми нулями , если столбец и строка, в которых находится данный нулевой элемент не содержат другого нулевого элемента.
квадратной матрицы S будем называть независимыми нулями , если столбец и строка, в которых находится данный нулевой элемент не содержат другого нулевого элемента.
2. Две прямоугольные матрицы  и
и  порядка mxn называются эквивалентными, если
порядка mxn называются эквивалентными, если  ,
,  ,
,  .
.
Решение задачи имеет подголовительную и итерационную части.
Подготовительная часть. Для каждого столбца матрицы C найдем максимальный элемент и из этого элемента вычитаем каждый элемент данного столбца. (Если рассматривается задача на минимум, то находим минимальный элемент каждого столбца и из элементов данного столбца вычитаем этот минимальный элемент. Далее все по нижеизложенному алгоритму). В результате получим матрицу, в каждом столбце которой имеется нулевой элемент . Далее находим минимальный элемент каждой строки и из элементов данной строки вычитаем этот минимальный элемент. В результате получим матрицу, в каждой строке и в каждом столбце имеется по крайней мере один нулевой элемент.
Далее отмечаем звездочкой произвольный нуль в пероом столбце и просматриваем второй столбей и если в нем есть нули и в этой строке нет отмеченного нуля, то отмечаем данный нуль звездочкой. Аналогичным образом поступаем и с остальными столбцами. Отмеченные нули являются независимыми.
Этап 1. Если количество независимых нулей равно размерности матрицы, то задача решена и позиции отмеченных нулей является решением задачи о назначениях. Если же количество независимых нулей меньше n, то продолжаем процедуру. Выделяем столбцы матрицы C содержащие нули со звездочкой. Если среди невыделенных элементов матрицы нет нулевых, то переходим к этапу 3. Если обнаруживается невыделенный нуль, то есть два варианта:
Вариант 1. Строка, содержащая невыделенный нуль содержит также нуль со звездой. В этом случае ставим над найденным нулем знак °, выделяем строку, содержащую этот нуль, снимаем выделение из столбца, на пересечении которой с только что выделенной строкой находится нуль со звездой. Далее, если обнаруживается невыделенный нуль, переходим к этапу 1. Если невыделенных нулей нет, то переходим к этапу 3.
Вариант 2. Строка, содержащая невыделенный нуль не содержит нуль со звездой. В этом случае отмечаем этот нуль знаком ° и переходим к этапу 2.
Этап 2. Исходя из нуля со знаком °, в строке которой нет нуля со звездой (вариант 2) строим следующую цепочку элементов матрицы C: Исходный 0° − 0* (лежащий в одном столбце (если существует)) − 0° (лежащей в одной строке с предшествующим 0* и т.д. Цепочка имеет вид 0°−0*−0°−. и обязательно заканчивается 0°. Там, где 0°, заменяем на 0*, а на четных позициях уничтожаем знак * над нулями. Далее уничтожаем все ° над нулями и снимаем выделения из столбцов и строк. Число независимых нулей увеличился на единицу. Переходим к этапу 1.
Этап 3. К этому этапу переходим после завершения этапа 1, когда независимых нулей нет.
Среди невыделенных элементов находим минимальный q>0. Далее величину q вычитаем из всех элементов матрицы C расположенных на невыделенных строках, и прибавляем ко всем элементам на выделенных столбцах (можно и так: величину q вычитаем из всех невыделенных элементов матрицы C и прибавляем ко всем элементам, находящимся на пересечении выделенных строк и столбцов). В полученной матрице появятся невыделенные нули поэтому переходим к этапу 1.
Для рассмотрения численного примера задачи о назначениях (задачи выбора), введите в кальнуляторе в начале страницы элементы матрицы и нажмите на кнопу вычислить. Онлайн калькулятор выдаст подробное рашение задачи.
Источник
