Как найти оптимальное значение целевой функции

Ранее я описал, как принимать решения с учетом ограничивающих факторов. Цель таких решений – определить ассортимент продукции (производственный план), максимально увеличивающий прибыль компании. Решение заключалось в том, чтобы распределить ресурсы между продуктами согласно маржинальной прибыли, полученной на единицу ограниченных ресурсов, при соблюдении любых других ограничений, таких как максимальный или минимальный спрос на отдельные виды продукции. [1]

Если ограничивающий фактор один (например, дефицитный станок), решение может быть найдено с применением простых формул (см. ссылку в начале статьи). Если же ограничивающих факторов несколько, применяется метод линейного программирования.

Линейное программирование – это название, данное комбинации инструментов используемых в науке об управлении. Этот метод решает проблему распределения ограниченных ресурсов между конкурирующими видами деятельности с тем, чтобы максимизировать или минимизировать некоторые численные величины, такие как маржинальная прибыль или расходы. В бизнесе он может использоваться в таких областях как планирование производства для максимального увеличения прибыли, подбор комплектующих для минимизации затрат, выбор портфеля инвестиций для максимизации доходности, оптимизация перевозок товаров в целях сокращения расстояний, распределение персонала с целью максимально увеличить эффективность работы и составление графика работ в целях экономии времени.

Скачать заметку в формате Word, рисунки в формате Excel

Линейное программирование предусматривает построение математической модели рассматриваемой задачи. После чего решение может быть найдено графически (рассмотрено ниже), с использованием Excel (будет рассмотрено отдельно) или специализированных компьютерных программ. [2]

Пожалуй, построение математической модели – наиболее сложная часть линейного программирования, требующая перевода рассматриваемой задачи в систему переменных величин, уравнений и неравенств – процесс, в конечном итоге зависящий от навыков, опыта, способностей и интуиции составителя модели.

Рассмотрим пример построения математической модели линейного программирования

Николай Кузнецов управляет небольшим механическим заводом. В будущем месяце он планирует изготавливать два продукта (А и В), по которым удельная маржинальная прибыль оценивается в 2500 и 3500 руб., соответственно.

Изготовление обоих продуктов требует затрат на машинную обработку, сырье и труд (рис. 1). На изготовление каждой единицы продукта А отводится 3 часа машинной обработки, 16 единиц сырья и 6 единиц труда. Соответствующие требования к единице продукта В составляют 10, 4 и 6. Николай прогнозирует, что в следующем месяце он может предоставить 330 часов машинной обработки, 400 единиц сырья и 240 единиц труда. Технология производственного процесса такова, что не менее 12 единиц продукта В необходимо изготавливать в каждый конкретный месяц.

Рис. 1. Использование и предоставление ресурсов

Николай хочет построить модель с тем, чтобы определить количество единиц продуктов А и В, которые он доложен производить в следующем месяце для максимизации маржинальной прибыли.

Линейная модель может быть построена в четыре этапа.

Этап 1. Определение переменных

Существует целевая переменная (обозначим её Z), которую необходимо оптимизировать, то есть максимизировать или минимизировать (например, прибыль, выручка или расходы). Николай стремится максимизировать маржинальную прибыль, следовательно, целевая переменная:

Z =    суммарная маржинальная прибыль (в рублях), полученная в следующем месяце в результате производства продуктов А и В.

Существует ряд неизвестных искомых переменных (обозначим их х₁, х₂, х₃ и пр.), чьи значения необходимо определить для получения оптимальной величины целевой функции, которая, в нашем случае является суммарной маржинальной прибылью. Эта маржинальная прибыль зависит от количества произведенных продуктов А и В. Значения этих величин необходимо рассчитать, и поэтому они представляют собой искомые переменные в модели. Итак, обозначим:

х₁ = количество единиц продукта А, произведенных в следующем месяце.

х₂ = количество единиц продукта В, произведенных в следующем месяце.

Очень важно четко определить все переменные величины; особое внимание уделите единицам измерения и периоду времени, к которому относятся переменные.

Этап. 2. Построение целевой функции

Целевая функция – это линейное уравнение, которое должно быть или максимизировано или минимизировано. Оно содержит целевую переменную, выраженную с помощью искомых переменных, то есть Z выраженную через х₁, х₂… в виде линейного уравнения.

В нашем примере каждый изготовленный продукт А приносит 2500 руб. маржинальной прибыли, а при изготовлении х₁ единиц продукта А, маржинальная прибыль составит 2500 * х₁. Аналогично маржинальная прибыль от изготовления х₂ единиц продукта В составит 3500 * х₂. Таким образом, суммарная маржинальная прибыль, полученная в следующем месяце за счет производства х₁ единиц продукта А и х₂ единиц продукта В, то есть, целевая переменная Z составит:

Z = 2500 * х₁ + 3500 *х₂

Николай стремится максимизировать этот показатель. Таким образом, целевая функция в нашей модели:

Максимизировать Z = 2500 * х₁ + 3500 *х₂

Этап. 3. Определение ограничений

Ограничения – это система линейных уравнений и/или неравенств, которые ограничивают величины искомых переменных. Они математически отражают доступность ресурсов, технологические факторы, условия маркетинга и иные требования. Ограничения могут быть трех видов: «меньше или равно», «больше или равно», «строго равно».

В нашем примере для производства продуктов А и В необходимо время машинной обработки, сырье и труд, и доступность этих ресурсов ограничена. Объемы производства этих двух продуктов (то есть значения х₁ их₂) будут, таким образом, ограничены тем, что количество ресурсов, необходимых в производственном процессе, не может превышать имеющееся в наличии. Рассмотрим ситуацию со временем машинной обработки. Изготовление каждой единицы продукта А требует трех часов машинной обработки, и если изготовлено х₁, единиц, то будет потрачено З * х₁, часов этого ресурса. Изготовление каждой единицы продукта В требует 10 часов и, следовательно, если произведено х₂ продуктов, то потребуется 10 * х₂ часов. Таким образом, общий объем машинного времени, необходимого для производства х₁ единиц продукта А и х₂ единиц продукта В, составляет 3 * х₁ + 10 * х₂. Это общее значение машинного времени не может превышать 330 часов. Математически это записывается следующим образом:

3 * х₁ + 10 * х₂ ≤ 330

Аналогичные соображения применяются к сырью и труду, что позволяет записать еще два ограничения:

16 * х₁ + 4 * х₂ ≤ 400

6 * х₁ + 6 * х₂ ≤ 240

Наконец следует отметить, что существует условие, согласно которому должно быть изготовлено не менее 12 единиц продукта В:

х₂ ≥ 12

Этап 4. Запись условий неотрицательности

Искомые переменные не могут быть отрицательными числами, что необходимо записать в виде неравенств х₁ ≥ 0 и х₂ ≥ 0. В нашем примере второе условия является избыточным, так как выше было определено, что х₂ не может быть меньше 12.

Полная модель линейного программирования для производственной задачи Николая может быть записана в виде:

Максимизировать:    Z = 2500 * х₁ + 3500 *х₂

При условии, что:       3 * х₁ + 10 * х₂ ≤ 330

16 * х₁ + 4 * х₂ ≤ 400

6 * х₁ + 6 * х₂ ≤ 240

х₂ ≥ 12

х₁ ≥ 0

Рассмотрим графический метод решения задачи линейного программирования.

Этот метод подходит только для задач с двумя искомыми переменными. Модель, построенная выше, будет использована для демонстрации метода.

Оси на графике представляют собой две искомые переменные (рис. 2). Не имеет значения, какую переменную отложить вдоль, какой оси. Важно выбрать масштаб, который в конечном итоге позволит построить наглядную диаграмму. Поскольку обе переменные должны быть неотрицательными, рисуется только I-й квадрант.

Рис. 2. Оси графика линейного программирования

Рассмотрим, например, первое ограничение: 3 * х₁ + 10 * х₂ ≤ 330. Это неравенство описывает область, лежащую ниже прямой: 3 * х₁ + 10 * х₂ = 330. Эта прямая пересекает ось х₁ при значении х₂ = 0, то есть уравнение выглядит так: 3 * х₁ + 10 * 0 = 330, а его решение: х₁ = 330 / 3 = 110

Аналогично вычисляем точки пересечения с осями х₁ и х₂ для всех условий-ограничений:

Область допустимых значений	Граница допустимых значений	Пересечение с осью х1	Пересечение с осью х2
3 * х1 + 10 * х2 ≤ 330	3 * х1 + 10 * х2 = 330	х1 = 110; х2 = 0	х1 = 0; х2 = 33
16 * х1 + 4 * х2 ≤ 400	16 * х1 + 4 * х2 = 400	х1 = 25; х2 = 0	х1 = 0; х2 = 100
6 * х1 + 6 * х2 ≤ 240	6 * х1 + 6 * х2 = 240	х1 = 40; х2 = 0	х1 = 0; х2 = 40
х2 ≥ 12	х2 = 12	не пересекает; идет параллельно оси х1	х1 = 0; х2 = 12

Графически первое ограничение отражено на рис. 3.

Рис. 3. Построение области допустимых решений для первого ограничения

Любая точка в пределах выделенного треугольника или на его границах будет соответствовать этому ограничению. Такие точки называются допустимыми, а точки за пределами треугольника называются недопустимыми.

Аналогично отражаем на графике остальные ограничения (рис. 4). Значения х₁ и х₂ на или внутри заштрихованной области ABCDE будут соответствовать всем ограничениям модели. Такая область называется областью допустимых решений.

Рис. 4. Область допустимых решений для модели в целом

Теперь в области допустимых решений необходимо определить значения х₁ и х₂, которые максимизируют Z. Для этого в уравнении целевой функции:

Z = 2500 * х₁ + 3500 *х₂

разделим (или умножим) коэффициенты перед х₁ и х₂ на одно и тоже число, так чтобы получившиеся значения попали в диапазон, отражаемый на графике; в нашем случае такой диапазон – от 0 до 120; поэтому коэффициенты можно разделить на 100 (или 50):

Z = 25х₁ + 35х₂

затем присвоим Z значение равное произведению коэффициентов перед х₁ и х₂ (25 * 35 = 875):

875 = 25х₁ + 35х₂

и, наконец, найдем точки пересечения прямой с осями х₁ и х₂:

Уравнение целевой функции	Пересечение с осью х1	Пересечение с осью х2
875 = 25х1 + 35х2	х1 = 35; х2 = 0	х1 = 0; х2 = 25

Нанесем это целевое уравнение на график аналогично ограничениям (рис. 5):

Рис. 5. Нанесение целевой функции (черная пунктирная линия) на область допустимых решений

Значение Z постоянно на всем протяжении линии целевой функции. Чтобы найти значения х₁ и х₂, которые максимизируют Z, нужно параллельно переносить линию целевой функции к такой точке в границах области допустимых решений, которая расположена на максимальном удалении от исходной линии целевой функции вверх и вправо, то есть к точке С (рис. 6).

Рис. 6. Линия целевой функции достигла максимума в пределах области допустимых решений (в точке С)

Можно сделать вывод, что оптимальное решение будет находиться в одной из крайних точек области принятия решения. В какой именно, будет зависеть от угла наклона целевой функции и от того, какую задачу мы решаем: максимизации или минимизации. Таким образом, не обязательно чертить целевую функцию – все, что необходимо, это определить значения х₁ и х₂ в каждой из крайних точек путем считывания с диаграммы или путем решения соответствующей пары уравнений. Найденные значения х₁ и х₂ затем подставляются в целевую функцию для расчета соответствующей величины Z. Оптимальным решением является то, при котором получена максимальная величина Z при решении задачи максимизации, и минимальная – при решении задачи минимизации.

Определим, например значения х₁ и х₂ в точке С. Заметим, что точка С находится на пересечении линий: 3х₁ + 10х₂ = 330 и 6х₁ + 6х₂ = 240. Решение этой системы уравнений дает: х₁ = 10, х₂ = 30. Результаты расчета для всех вершин области допустимых решений приведены в таблице:

Точка	Значение х1	Значение х2	Z = 2500х1 + 3500х2
А	22	12	97 000
В	20	20	120 000
С	10	30	130 000
D	0	33	115 500
E	0	12	42 000

Таким образом, Николай Кузнецом должен запланировать на следующий месяц производство 10 изделий А и 30 изделий В, что позволит ему получить маржинальную прибыль в размере 130 тыс. руб.

Кратко суть графического метода решения задач линейного программирования можно изложить следующим образом:

1. Начертите на графике две оси, представляющие собою два параметра решения; нарисуйте только I-й квадрант.
2. Определите координаты точек пересечения всех граничных условий с осями, подставляя в уравнения граничных условий поочередно значения х₁ = 0 и х₂ = 0.
3. Нанести линии ограничений модели на график.
4. Определите на графике область (называемую допустимой областью принятия решения), которая соответствует всем ограничениям. Если такая область отсутствует, значит, модель не имеет решения.
5. Определите значения искомых переменных в крайних точках области принятия решения, и в каждом случае рассчитайте соответствующее значение целевой переменной Z.
6. Для задач максимизации решение – точка, в которой Z максимально, для задач минимизации, решение – точка, в которой Z минимально.

---

[1] Настоящая заметка написана по материалам CIMA.

[2] См., например, здесь.

Уровень сложности
Простой

Время на прочтение
11 мин

Количество просмотров 2.9K

Приветствую! Я, Ложкинс Алексей, консультант и разработчик оптимизационных решений и математических моделей для бизнеса. Это первая в цикле работ обучающая статья, часть личного образовательного проекта “Make optimization simple”. Цель проекта – продемонстрировать доступность технологий и показать на примерах, что моделировать можно без глубокого математического фундамента.

Из статьи вы узнаете об основных компонентах математической оптимизационной задачи на примере классической задачи о назначениях, в частности, распределение машин такси на заказы. Далее, я покажу, как реализовать программный прототип математической модели посредством Python и библиотеки PuLP, а также продемонстрирую, как получить оптимальное решение задачи всего в одной строке кода без реализации специальных алгоритмов.

Материал статьи предназначен

• для базового погружения в математическое моделирование и оптимизацию;

• для демонстрации доступности технологий и возможностей моделировать, решать оптимизационные задачи без порога входа и специальной подготовки (мат./тех. образования).

Математическая оптимизация

Математическая оптимизация – это мощный метод, используемый для поиска наилучшего решения задачи, отвечающего определенным критериям и удовлетворяющего набору ограничений. Она включает в себя четыре основных компонента:

1. Целевая функция – это математическое выражение, объект оптимизации. В зависимости от целей оптимизации выделяют два критерия: задача максимизации и задача минимизации целевой функции;

2. Ограничения – это условия, которые должны быть выполнены для того, чтобы решение было осуществимым. Они ограничивают возможные значения переменных и обычно выражаются в виде неравенств или равенств;

3. Решающие переменные – это неизвестные величины, которые мы хотим определить в результате решения оптимизационной задачи. Они используются для формулирования целевой функции и ограничений. Моделируют различные варианты выбора или действий, которые могут быть предприняты для достижения желаемого результата;

4. Метод оптимизации – это алгоритмы, используемые для нахождения оптимального решения задачи. Мы сконцентрируем наше внимание на задачах смешанного линейного программирования (MILP), для которых существуют стандартные методы их решения. Кроме того, есть упакованные программные пакеты с этими методами, что повышает доступность мат. моделирования.

Комбинация этих четырех компонентов – это то, что составляет задачу математической оптимизации. Тщательно сформулировав целевую функцию, переменные для принятия решения и ограничения, а также выбрав подходящий метод оптимизации, мы можем найти наилучшее решение для широкого спектра реальных проблем.

Постановка задачи

Рассмотрим типичную питерскую ситуацию в пятницу вечером. Иван, Михаил и Александр запланировали пойти в бар. Одновременно заказывают такси от своего дома до бара, используя один и тот же агрегатор такси одинакового класса (например, комфорт). Рядом оказываются свободными ровно три машины с разной удаленностью от потенциальных пассажиров. Кроме этого, действуют следующие вполне реалистичные условия: пассажир может ехать только на одной машине, одна машина может взять не более одного заказа (пассажира).

Задача: назначить клиентам машины таким образом, чтобы все клиенты добрались до бара на такси, каждая машина перевезла не более одного пассажира и общие затраты на перевозку пассажиров были минимальны.

Построение модели

Чтобы решить поставленную выше задачу, мы будем использовать линейное программирование. Оно представляет собой математических методов, используемых для оптимизации линейной целевой функции с учетом линейных ограничений. Линейное программирование имеет множество реальных применений, включая планирование производства, оптимизацию транспортировки и распределение ресурсов.

Построение программного прототипа линейной модели будем реализовывать посредством программного пакета PuLP, который предоставляет среду для инициализации самой математической модели и позволяет подключать сторонние пакеты (коммерческие или open source) для решения оптимизационных задач. Чтобы использовать PuLP для решения задачи с назначениями, нам сначала нужно будет установить библиотеку. Вы можете установить PuLP с помощью pip:

pip install pulp

Индексы и входные данные

Введем следующие обозначения:

C – список клиентов: Иван, Александр и Михаил;

T – список такси: желтое, зеленое, синее;

c ∈ C – индекс и множество клиентов, клиент c содержится во множестве C;

t ∈ T – индекс и множество такси, машина t содержится во множестве T.

Запишем эти множества в виде списков Python:

# Инициализируем множества клиентов и множество такси. Используем англоязычные названия
C = ["Ivan", "Aleksander", "Mikhail"]  # имена клиентов
T = ["yellow", "green", "blue"]  # цвета машин

Целевая функция рассматриваемой задачи – минимизация затрат. Разберемся в структуре затрат.

Общие затраты = постоянные затраты + переменные затраты.

Под постоянными затратами будем понимать затраты на перевозку пассажира от его местоположения до бара. Они не зависят от того, какая из трех машин будет выполнять заказ (уровень сервиса одинаковый). В свою очередь, переменные затраты – это затраты на подачу машины клиенту. В зависимости от клиента эти затраты могут отличаться: разное расстояние и разное прогнозное время в пути до клиента. Постоянные затраты не влияют на целевую функцию, т.к. они не зависят от назначения, поэтому будем рассматривать только переменные затраты. Ниже представлена матрица переменных затрат.

Для каждой комбинации клиента c (строка) и машины t (столбец) сопоставлены затраты e_ct в рублях. Воспользуемся словарем в Python для инициализации матрицы затрат, где по ключу (c, t) получим размер переменных затрат назначения.

# Матрица переменных затрат
E = {
    ("Ivan", "yellow"): 15,
    ("Ivan", "green"): 24,
    ("Ivan", "blue"): 21,
    ("Aleksander", "yellow"): 9,
    ("Aleksander", "green"): 21,
    ("Aleksander", "blue"): 12,
    ("Mikhail", "yellow"): 18,
    ("Mikhail", "green"): 12,
    ("Mikhail", "blue"): 15,
}

Инициализация модели

Импортируем библиотеку PuLP:

import pulp

Прежде чем создавать переменные и ограничения, необходимо инициализировать класс модели. В дальнейшем ограничения и целевая функция будут определяться в привязке к модели. В качестве аргументов передаем название модели “TaxiAssignmentProblem” и класс оптимизационной задачи, в нашем случае – минимизация затрат: pulp.LpMinimize. Модель может содержать только одну оптимизационную задачу.

# Инициализация модели
model = pulp.LpProblem("TaxiAssignmentProblem", pulp.LpMinimize)

Инициализация переменных

Модель инициализирована, теперь можем начать запись нашей модели. Сначала определим набор решающих переменных. Нам нужно выяснить, какую машину назначить какому клиенту. Определим для каждой возможной связки клиент-машина переменную, которая может принимать значение 1, если выбрана связка назначений, 0 – в противном случае. Таким образом, у нас есть 9 переменных для принятия решения.

Например: если переменная для связки Aleksander-green равна 1, следовательно, Александр поедет на зеленой машине. Если значение переменной равно 0, то Александр не поедет на зеленой машине.

Добавление переменных в модель pulp возможно через метод LpVariable, где в качестве аргументов передаем название переменной, нижнюю и верхнюю границы принимаемых значений (0 и 1 в нашем случае), тип переменной (в нашем случае – бинарная).

Комментарий: для переменных, которые могут принимать значения 0 или 1, в pulp выделен отдельный тип – бинарные переменные.

Переменные запишем в словарь, аналогичный словарю E. Назовем переменные x_ct, где c ∈ C – клиент, а t ∈ T – машина.

# Инициализация переменных
X = {}  # Словарь для хранения ссылок на переменные

for (client, car) in E:
  var_name = "x_" + client + "_" + car  # Название переменной
  X[client, car] = pulp.LpVariable(var_name, cat=pulp.LpBinary)

  # Эквивалентный способ задания переменных через целочисленный тип
  # X[client, car] = pulp.LpVariable(var_name, lowBound=0, upBound=1, cat="Integer")
  
# Задание переменных без цикла
# X = pulp.LpVariable.dicts("x", E.keys(), 0, 1, pulp.LpBinary)

Целевая функция

Целевая функция состоит в том, чтобы минимизировать переменные затраты. Для каждой переменной x_ct мы ставим в соответствие размер затрат e_ct, на который возрастут общие затраты, если x_ct = 1. Например, если желтая машина будет назначена Ивану x_Ivan,yellow = 1, то затраты вырастут на e_Ivan,yellow = 15 рублей. Это условие можно записать как произведение затрат на переменную: e_ct x_ct. 

Суммируем все возможные произведения e_ct x_ct, получим функцию общих затрат. В принятых нами обозначениях она будет иметь следующий вид: 

В более лаконичной форме с помощью символа суммы ∑ целевую функцию можно записать как 

Метод LpProblem.setObjective() добавляет целевую функцию в модель. В качестве аргументов передается сама целевая функция и “направленность” оптимизации (минимизация / максимизация). Для нашей задачи определим целевую функцию следующим образом:

# Построение целевой функции

# 1. Список произведений затрат на соответствующую переменную
lst_mult = [E[key] * var for key, var in X.items()]

# 2. Суммируем произведения
obj_expression = pulp.lpSum(lst_mult)  # Встроенный в pulp метод
# obj_expression = sum(lst_mult)  # Python сумма

# 3. Добавляем в модель
model.setObjective(obj_expression)

# Альтернативный способ инициализации целевой функции
# model += obj_expression

Ограничения

В нашей задаче два основных ограничения:

1. Все клиенты должны попасть в бар;

2. Одна машина не может перевозить более одного пассажира.

Оба этих ограничения можно записать в математическом виде и передать в модель. Для этого воспользуемся ранее введенными переменными.

Ограничение 1: Все клиенты должны попасть в бар

Рассмотрим клиента Ивана. В бар он должен попасть на одной из трех машин: желтой, зеленой или синей. С каждым вариантом назначения машины Ивану связана бинарная переменная: x_Ivan,yellow, x_Ivan,green и x_Ivan,blue. Условие можно переформулировать как: ровно одна машина должна быть назначена Ивану.

В случае Александра и Михаила строим аналогичные ограничения, но с учетом соответствующих им переменных:

Введенные ограничения можно записать в более лаконичной форме с использованием символа суммы ∑ и символа повторения для каждого элемента множества ∀ («Для любого…»).

Добавление ограничений в PuLP незамысловатое, используется сочетание символов +=: 

model += expression, expression_name

Ограничению можно привязать название или оставить поле пустым. Само выражение для нашего ограничения состоит из операции сложения переменных, тип ограничения ==, а значение правой части ограничения 1. 

# Ограничение: Все клиенты должны попасть в бар (Client Satisfaction Constraint)

for c in C:  # Создаем ограничение для каждого клиента
  # Название ограничения
  constr_name = f"{c}_sat_constr"  

  # Список возможных машин для клиента
  lst_vars = [X[c, t] for t in T]  

  # Добавление ограничений в модель 
  model += pulp.lpSum(lst_vars) == 1, constr_name 

Ограничение 2: Одна машина не может перевозить более одного пассажира.

Рассмотрим желтую машину. Она может взять Ивана, Александра, Михаила или никого. С каждым вариантом назначения желтой машины клиенту у нас связана бинарная переменная: x_Ivan,yellow, x_{Aleksander,yellow} и x_{Mikhail,yellow}. Ограничение запишется в следующем виде: 

Заметим, что данное ограничение позволяет всем переменным присвоить значений 0, что будет означать отсутствие назначений на желтую машину. 

Для остальных машин имеем аналогичные ограничения: 

Эти ограничения можно записать в более короткой форме с учетом ранее введенных обозначений: 

Процесс добавления ограничений “назначение машины не более чем на одного пассажира” не отличается от добавления в модель PuLP предыдущего ограничения:

# Ограничение: Одна машина не может перевозить более одного пассажира (Taxi Passengers Limitation Constraint)

for t in T:  # Создаем ограничение для каждой машины
  # Название ограничения
  constr_name = f"{t}_tpl_constr"  

  # Список возможных клиентов для машины t
  lst_vars = [X[c, t] for c in C]  

  # Добавление ограничений в модель 
  model += pulp.lpSum(lst_vars) <= 1, constr_name 

Поиск оптимального решения

Прежде чем переходить к решению оптимизационной задачи, посмотрим на полную математическую модель нашей задачи. Существует достаточно распространённый формат записи задач Линейного программирования в формат .lp, удобный для чтения пользователем. В PuLP для сохранения модели в формате .lp есть метод LpProblem.writeLP(), где в качестве аргументов передается название файла:

# Запись модели в файл
model.writeLP("TaxiAssignmentProblem.lp")

Файл можно открыть обычным блокнотом. Здесь можно увидеть целевую функцию, ограничения с привязкой к их названию и типы переменных.

* TaxiAssignmentProblem *
Minimize
OBJ: 12 x_Aleksander_blue + 21 x_Aleksander_green + 9 x_Aleksander_yellow
 + 21 x_Ivan_blue + 24 x_Ivan_green + 15 x_Ivan_yellow + 15 x_Mikhail_blue
 + 12 x_Mikhail_green + 18 x_Mikhail_yellow
Subject To
Aleksander_sat_constr: x_Aleksander_blue + x_Aleksander_green
 + x_Aleksander_yellow = 1
Ivan_sat_constr: x_Ivan_blue + x_Ivan_green + x_Ivan_yellow = 1
Mikhail_sat_constr: x_Mikhail_blue + x_Mikhail_green + x_Mikhail_yellow = 1
blue_tpl_constr: x_Aleksander_blue + x_Ivan_blue + x_Mikhail_blue <= 1
green_tpl_constr: x_Aleksander_green + x_Ivan_green + x_Mikhail_green <= 1
yellow_tpl_constr: x_Aleksander_yellow + x_Ivan_yellow + x_Mikhail_yellow <= 1
Binaries
x_Aleksander_blue
x_Aleksander_green
x_Aleksander_yellow
x_Ivan_blue
x_Ivan_green
x_Ivan_yellow
x_Mikhail_blue
x_Mikhail_green
x_Mikhail_yellow
End

Поиск оптимального решения в PuLP запускается с помощью метода LpProblem.solve():

# Поиск оптимального решения задачи
model.solve()

# Проверяем статус модели
print(pulp.LpStatus[model.status])

Теперь давайте извлечем оптимальное значение целевой функции, используя метод PuLP value(LpProblem.objective) и оптимальные значения переменных LpVariable.varValue.

# Значение целевой функции после решения задачи
obj_value = pulp.value(model.objective)
obj_value = int(obj_value)  # Преобразование в целочисленное значение

print(f"Минимальные переменные затраты для выполнения всех заказов = {obj_value} руб.")

# Извлечение значений переменных 
for (client, taxi), var in X.items():
  var_value =  var.varValue  # Извлечение значения переменной
  var_value = int(var_value)  # Преобразование в целочисленное значение

  if var_value > 0:  # Выводим оптимальные назначения машин клиентам
    print(f"- Клиенту {client} назначена машина {taxi}, затраты на подачу = {E[client, taxi]} руб.")

Минимальные переменные затраты для выполнения всех заказов = 39 руб.

• Клиенту Ivan назначена машина yellow, затраты на подачу = 15 руб.

• Клиенту Aleksander назначена машина blue, затраты на подачу = 12 руб.

• Клиенту Mikhail назначена машина green, затраты на подачу = 12 руб.

Предлагаю самостоятельно с помощью ручного перебора убедиться в том, что более оптимального решения при указанных ограничениях не получить.

Расширение задачи

Рассмотренная выше задача максимально упрощена для простого погружения в проблематику математического моделирования и возможностей решения задач оптимизации.

С целью закрепления материала предлагаю рассмотреть и попробовать добавить следующие ограничения:

1. Добавить четвертую машину в модель (например, “red”);

2. Добавить время ожидания в исходные данные для каждого назначения. Добавить в модель ограничение лимита ожидания для каждого клиента (сколько по времени клиент готов ждать);

3. Добавить параметр выручки за выполнение заказа. Скорректировать целевую функцию и изменить ограничение обязательного выполнения заказа на неравенство (Ограничение 1: Все клиенты должны попасть в бар);

4. Добавление нескольких клиентов в модель.

Заключение

Резюмирую содержание обучающего материала: построили математическую модель назначения машин агрегатора такси на заказы клиентов. Для этого сформировали список решающих переменных, целевую функцию минимизации затрат и набор из двух типов ограничений. Разработали программный прототип на базе Python пакета PuLP и решили оптимизационную задачу встроенным в PuLP решателем.

Ссылки

• Ссылка на Jupyter Notebook здесь;

• Документация Python библиотеки PuLP;

• Примеры мат.моделей для решения некоторых задач;

• Задача: Белки, Жиры и Углеводы – оптимизируем рацион питания; 

• Задача коммивояжёра с использованием разных пакетов (в том числе PuLP); 

• В основе структуры статьи лежит материал от сюда;

P.S. Направляйте оптимизационные задачи, которые хотелось бы увидеть в разборе.

P.S.S. Есть на примете статьи с моделями в PuLP или ORtools? Присылайте, дополню статью ссылками.

1. Для
   нахождения максимума целевой функции
   используйте функцию maximize, формат которой
   следующий
   maximize(<функция>,
   <система
   ограничений>,
   <опции>);

При
этом условие неотрицательности переменных
удобно указать опцией NONNEGATIVE.

>
optimum:=maximize(f,syst_ogr,NONNEGATIVE);

1. Используйте
   команду subs, которая позволяет подставить
   значения переменных x₁
   и
   x₂
   в функцию f.

>
fmax:=subs(x1=83/17,x2=19/17,f);

1. Примените
   функцию evalf для представления ответа
   в форме действительного числа с 4
   значащими цифрами.

>
fmax:=evalf(fmax,4);

Ознакомиться
с вариантом решения задачи ЛП без
пояснений можно в приложении.

Решение оптимизационных задач в специализированном пакете SimplexWin. Http://www.Simplexwin.Narod.Ru/

Данная программа
предназначена для решения задач линейного
программирования симплекс методом.

Задача.
Найти значения переменных x₁
и x₂,
при которых

при
ограничениях

Порядок
выполнения работы:

I. Оформление исходных данных.

1. Запустите
   программу SimplexWin
   и установите требуемый размер матрицы
   ограничений, выбрав в меню команду
   Настройки – Размер матрицы (рис. 13).

Рис.
13. Определение
размера матрицы.

1. Введите
   данные (рис. 14). Если задача вводится не
   в канонической форме, то дополнительные
   переменные и искусственные базисы (а
   также соответствующие им коэффициенты
   целевой функции) добавляются автоматически.

Рис.14.
Ввод данных.

II. Нахождение оптимального плана и оптимального значения целевой функции.

1. Нажмите
   кнопку Вычислить и получите форму
   Результаты (рис. 15).

Рис.
15. Форма
Результаты.

1. В
   форме Результаты нажмите кнопку
   Результат, которая позволяет произвести
   решение задачи в автоматическом режиме
   и отобразить на экране последнюю
   симплексную таблицу и результат (рис.
   16).

Рис.
16. Решение
задачи.

Решение
оптимизационных задач в Excel
[1]

Рассмотрим пример
нахождения для следующей задачи линейного
программирования.

Задача.
Найти значения переменных x₁
и x₂,
при которых

при
ограничениях

Порядок
выполнения работы:

I. Оформление исходных данных.

1. Создайте
   экранную форму для ввода условий задачи
   (переменных, целевой функции, ограничений)
   и введите в нее исходные данные
   (коэффициенты целевой функции,
   коэффициенты при переменных в
   ограничениях, правые части ограничений)
   (рис. 17).

Рис.
17. Экранная
форма задачи (курсор в ячейке D6).

Замечание:
В экранной форме на рис. 17 каждой
переменной и каждому коэффициенту
задачи поставлена в соответствие
конкретная ячейка в Excel.
Так, например, переменным задачи
соответствуют ячейки B3
(),
C3 (),коэффициентам
целевой функции соответствуют ячейки
B6
(),
C6
(),
правым частям ограничений соответствуют
ячейки F10
(),
F11 (),F12
()и т.д.

1. Введите
   зависимости из математической модели
   в экранную форму, т.е. введите формулу
   для расчета целевой функции и формулу
   для расчета значений левых частей
   ограничений.

Согласно
условию задачи значение целевой функции
определяется выражением
.
Используя обозначения соответствующих
ячеек вExcel,
формулу для расчета целевой функции
можно записать как сумму
произведений
каждой из ячеек, отведенных для значений
переменных задачи (B3,
C3),
на соответствующие ячейки, отведенные
для коэффициентов целевой функции (B6,
C6).

Для
того чтобы задать формулу зависимости
для целевой функции проделайте следующее:

– поставьте
курсор в ячейку D6;

– вызовите
окно Мастер
функций – шаг 1 из 2,
нажав кнопку
на стандартной панели инструментов;

– выберите
в окне Категория
категорию
Математические;

– в
окне Функция
выберите
функцию СУММПРОИЗВ;

– в
появившемся окне
СУММПРОИЗВ
в строку Массив
1 введите
выражение B$3:C$3,
а в строку Массив
2 – выражение
B6:С6;

– нажмите
кнопку OK.

Рис.
18. Ввод формулы
для расчета ЦФ в окне Мастер функций.

После
ввода ячеек в строки Массив
1 и Массив
2 в окне
СУММПРОИЗВ
появятся числовые значения введенных
массивов (рис. 18), а в экранной форме
появится текущее значение, вычисленное
по введенной формуле, то есть 0 (так как
в момент ввода формулы значения переменных
задачи нулевые) (рис. 19).

Замечание:
Символ $
перед
номером строки означает, что при
копировании этой формулы в другие места
листа Excel
номер строки 3 не изменится. Символ :
означает,
что в формуле использованы все ячейки,
расположенные между ячейками, указанными
слева и справа от двоеточия.

Левые
части ограничений задачи представляют
собой сумму
произведений
каждой из ячеек, отведенных для значений
переменных задачи (B3,
C3), на
соответствующую ячейку, отведенную для
коэффициентов конкретного ограничения
(B10,
C10 – 1
ограничение; B11,
C11 – 2
ограничение; B12,
C12 – 3
ограничение).

Формулы,
задающие левые части ограничений задачи,
отличаются друг от друга и от формулы
в целевой ячейке D6
только
номером строки во втором массиве. Этот
номер определяется той строкой, в которой
ограничение записано в экранной форме.
Поэтому для задания зависимостей для
левых частей ограничении достаточно
скопировать формулу из целевой ячейки
в ячейки левых частей ограничений.

Для
расчета значений левых частей ограничений
выполните следующее:

– поставьте
курсор в ячейку D6
и скопируйте в буфер содержимое ячейки
(клавишами Ctrl+C);

– поставьте
курсор поочередно в поля левой части
каждого из ограничений, то есть D10,
D11,
D12,
и вставляйте в эти поля содержимое
буфера (клавишами Ctrl+V)
(при этом номер ячеек во втором массиве
формулы будет меняться на номер той
строки, в которую была произведена
вставка из буфера).

После
ввода на экране в полях D10,
D11,
D12
появится 0
(нулевое значение) (рис. 19).

Рис.
19. Экранная
форма задачи после вода

всех
необходимых формул.

1. Проверьте
   правильность введения формул.

Для этого:

– произведите
поочередно двойное нажатие левой клавиши
мыши на ячейки с формулами, при этом на
экране рамкой будут выделяться ячейки,
используемые в формуле (рис. 20 и рис.
21).

Рис.
20. Проверка
правильности введения

формулы
в целевую ячейку D6.

Рис.
20. Проверка
правильности введения

формулы
в ячейку
D10 для левой
части ограничений.

1. Задайте
   целевую функцию и введите ограничения
   в окне Поиск
   решения (рис.
   21).

Для этого:

– поставьте
курсор в ячейку D6;

– вызовите
окно Поиск
решения,
выбрав на панели инструментов Данные
– Поиск решения;

– поставьте
курсор в поле Установить
целевую ячейку;

– введите
адрес целевой ячейки $D$6
или
сделайте одно нажатие левой клавишей
мыши на целевую ячейку в экранной форме,
что будет равносильно вводу адреса с
клавиатуры;

– укажите
направление оптимизации целевой функции,
щелкнув один раз левой клавишей мыши
по селекторной кнопке максимальному
значению;

– в
окне Поиск
решений в
поле Изменяя
ячейки введите
ячейки со значениями переменных
$B$3:$C$3,
выделив их в экранной форме, удерживая
левую кнопку мыши;

Рис.
21. Окно Поиск
решения.

– нажмите
кнопку Добавить;

– в
поле Ссылка
на ячейку введите
адрес ячейки левой части конкретного
ограничения, например, $D$10;

– в
соответствии с условием задачи выберите
в поле знака необходимый знак, например,
для 1 ограничения это знак
;

– в
поле Ограничение
введите
адрес ячейки правой части, рассматриваемого
ограничения, например $F$10;

– аналогичным
образом установите соотношения между
правыми и левыми частями других
ограничений ($D$11$F$11,
$D$12$F$12);

– подтвердите
ввод всех перечисленных условий нажатием
кнопки OK
(рис. 22 и рис.
23).

Рис.
22. Добавления
условия.

Замечание:
Если при вводе условия задачи возникает
необходимость в изменении или удалении
внесенных ограничений, то это можно
сделать на жав на кнопки Изменить
или Удалить.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Оптимальное значение – целевая функция

Cтраница 2

Из таблицы видно, что для сравнительно близких оптимальных значений целевой функции ( f ( z) ( при отклонениях порядка 1 %) количество изделий, подлежащих выпуску по этим оптимальным планам, по отдельным наименованиям колеблется в пределах нескольких сотен. Таким образом, эта задача является неустойчивой.
 [16]

В результате решения задачи линейного программирования находят оптимальное значение целевой функции ( желательное сочетание изделий – максимальный доход), а также соответствующие этому оптимальному решению значения переменных: основных х – типы изделий; дополнительных zt – резервы по ограниченным ресурсам; двойственных Уг – мера дефицитности ресурсов; дополнительных двойственных У – – какую продукцию целесообразно включить в оптимальный план.
 [17]

Если множество решений является непустым, то оптимальное значение целевой функции может быть либо конечным, либо неограниченно большим. В случае когда оптимальное значение целевой функции конечно, оно соответствует экстремальной точке.
 [18]

Поскольку пространство решений может быть неограниченным, оптимальное значение целевой функции может также оказаться бесконечно большим.
 [19]

Все ограничения удовлетворяются, если и только если оптимальное значение целевой функции выпуклой задачи равно нулю. В противном случае минимальное значение явля-ется неограниченным, и должен быть найден крайний луч, с помощью которого строится нарушенное ограничение.
 [20]

На любой итерации t известна нижняя оценка х оптимального значения целевой функции. Значение х можно выбрать точно так же. Кроме того, имеется основной список задач, в котором каждой задаче соответствует определенное частичное решение.
 [21]

Теперь можно найти то решение, которое соответствует оптимальному значению целевой функции.
 [22]

В начале любой итерации t известна верхняя оценка х оптимального значения целевой функции. Значение х определяется общепринятым способом. Кроме того, задан основной список задач, содержащий некоторое подмножество Xij 1, определяющее частичный цикл, и подмножество значений с – -, принятых в результате пересмотра равными оо. Для вычисления нижней оценки оптимального значения целевой функции, соответствующей циклу, который является дополнением частичного цикла, можно применить тот же метод, что и в алгоритме задания маршрутов. С другой стороны, можно определять оптимальное решение задачи о назначениях, включив в эту задачу коэффициенты с -, принадлежащие строкам и столбцам, не связанным с подмножеством xti 1, которые входят в частичный цикл.
 [23]

В таких случаях существует бесконечно много планов, отвечающих оптимальному значению целевой функции. В многомерном случае говорят, что гиперплоскость постоянной прибыли параллельна гиперплоскости – границе одного из ресурсов.
 [24]

Теорема 4.1. Последовательность Q ( Xh) сходится к оптимальному значению целевой функции детерминированной задачи, эквивалентной двухэтапной стохастической задаче линейного программирования. Последовательность лг / J содержит сходящуюся подпоследовательность. Каждая сходящаяся подпоследовательность из Xh сходится к оптимальному предварительному плану х двухэташюй стохастической задачи.
 [25]

Следует отметить, что очень часто в связи с ограничениями оптимальное значение целевой функции достигается не там, где ее поверхность имеет нулевой градиент. Нередко лучшее решение соответствует одной из границ области проектирования.
 [27]

В начале любой итерации t известна верхняя оценка х а оптимального значения целевой функции.
 [28]

В заключительной части настоящего раздела обсуждается вопрос о приближенных методах оценки оптимальных значений целевой функции при различных предположениях относительно структуры стохастической модели. В следующем разделе рассматривается другая формулировка двухшаговой стохастической задачи линейного программирования, допускающая переход к стандартной модели линейного программирования с сохранением размерности.
 [29]

Действительно, согласно ( VI5), значение двойственной функции всегда меньше оптимального значения целевой функции. Отсюда расчет двойственной функции при любых значениях множителей Лагранжа дает нижнюю оценку данного варианта ветвления.
 [30]

Страницы:  

   1

   2

   3

   4

Содержание:

Исследование различных процессов, в том числе и экономических, обычно начинается с их моделирования, т.е. отражения реального процесса через математические соотношения. При этом составляются уравнения или неравенства, которые связывают различные показатели (переменные) исследуемого процесса, образуя систему ограничений. В этих процессах выделяются такие переменные, меняя которые можно получить оптимальное значение основного показателя данной системы (прибыль, доход, затраты и т.д.). Соответствующие методы, позволяющие решать указанные задачи, объединяются под общим названием «математическое программирование» или математические методы исследования операций.

Математическое программирование включает в себя такие разделы математики, как линейное, нелинейное и динамическое программирование. Сюда же относят и стохастическое программирование, теорию игр, теорию массового обслуживания, теорию управления запасами и некоторые другие.

Математическое программирование – это раздел высшей математики, посвященный решению задач, связанных с нахождением экстремумов функций нескольких переменных, при наличии ограничений на переменные.

Методами математического программирования решаются задачи о распределении ресурсов, планировании выпуска продукции, ценообразования, транспортные задачи и т.д.

Построение математической модели экономической задачи включает следующие этапы:

1. выбор переменных задачи;
2. составление системы ограничений;
3. выбор целевой функции.

Переменными задачи называются величины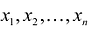

Система ограничений включает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий, например, положительности переменных и т.п.

Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи, и экстремум которой требуется найти.

Общая задача математического программирования формулируется следующим образом: найти экстремум целевой функции: 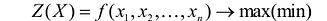и соответствующие ему переменные при условии, что эти переменные удовлетворяют системе ограничений:

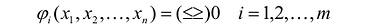
Если целевая функция и система ограничений линейны, то задача математического программирования называется задачей линейного программирования и в общем виде может быть записана следующим образом:

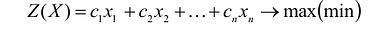
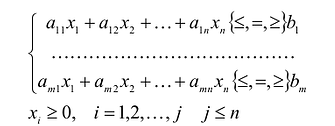
Данная запись означает следующее: найти экстремум целевой функции задачи и соответствующие ему переменные X = (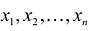). при условии, что эти переменные удовлетворяют системе ограничений и условиям неотрицательности.

Допустимым решением (планом) задачи линейного программирования называется любойX = (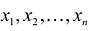). удовлетворяющий системе ограничений и условиям неотрицательности. Множество допустимых решений (планов) задачи образует область допустимых решений.

Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение задачи, при котором целевая функция достигает экстремума.

Задача линейного программирования

В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися. В случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической. Каноническая задача линейного программирования в координатной форме записи имеет вид:

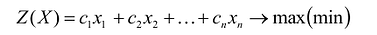
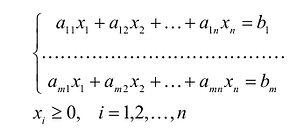
Используя знак суммирования эту задачу можно записать следующим образом:

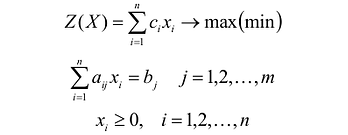
Каноническая задача линейного программирования в векторной форме имеет вид:

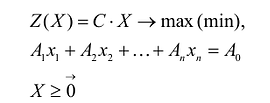
В данном случае введены векторы:

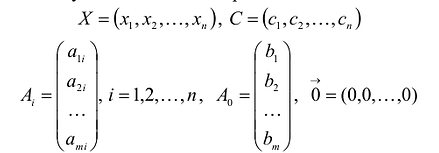
Здесь С – X – скалярное произведение векторов С и X.

Каноническая задача линейного программирования в матричной форме записи имеет вид:

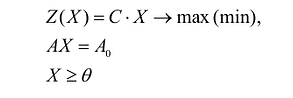
где:

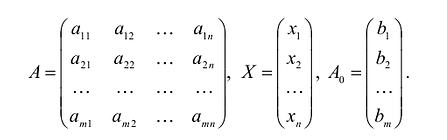
Здесь А – матрица коэффициентов системы уравнений, X -матрица-столбец переменных задачи; – матрица-столбец правых частей системы ограничений.

Нередко используются задачи линейного программирования, называемые симметричными, которые в матричной форме записи имеют вид:

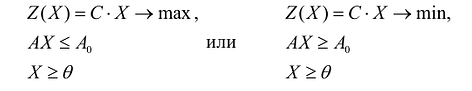
Приведение общей задачи линейного программирования к канонической форме

В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако, при составлении математических моделей экономических задач ограничения в основном формулируются системы неравенств, поэтому возникает необходимость перехода от системы неравенств к системе уравнений. Это может быть сделано следующим образом. К левой части линейного неравенства:

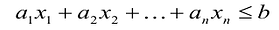прибавляется величина 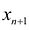такая, что переводит неравенство в равенство 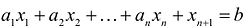, где: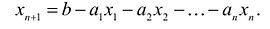

Неотрицательная переменная называется дополнительной переменной.

Основания для возможности такого преобразования дает следующая теорема.

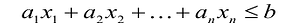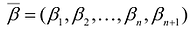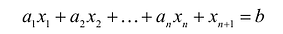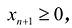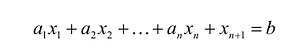Теорема. Каждому решению неравенства соответствует единственное решение уравнения: и неравенства и, наоборот, каждому решению уравнения: и неравенства соответствует единственное решение 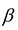неравенства: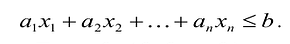

Доказательство. Пусть – решение неравенства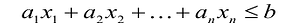. Тогда: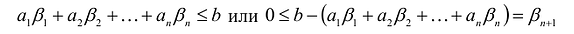

Если в уравнение 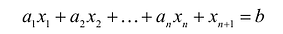вместо переменных подставить значения 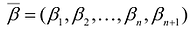, получится:

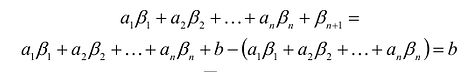
Таким образом, решение удовлетворяет уравнению: 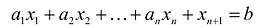и неравенству .

Доказана первая часть теоремы.

Пусть удовлетворяет уравнению 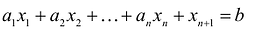и неравенству , т.е. 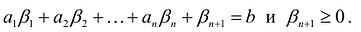. Отбрасывая в левой части равенства неотрицательную величину 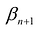, получим: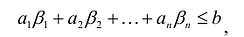

т.е. удовлетворяет неравенству: 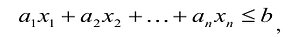что и требовалось доказать.

Если в левую часть неравенств системы ограничений вида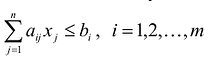

добавить переменную 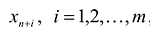, то получится система ограничений – уравнений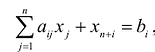 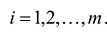В случае, если система неравенств-ограничений имеет вид 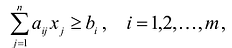, то из левой части неравенств-ограничений нужно вычесть соответствующую неотрицательную дополнительную переменную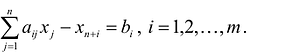

Полученная таким образом система уравнений-ограничений, вместе с условиями неотрицательности переменных, т.е. 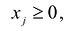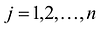и целевой функцией является канонической формой записи задачи линейного программирования.

Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому не влияют на ее значения.

В реальных практических задачах дополнительные неизвестные имеют определенный смысл. Например, если левая часть ограничений задачи отражает расход ресурсов на производство продукции в объемах 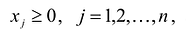, а правые части – наличие производственных ресурсов, то числовые значения дополнительных неизвестных 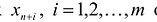и означают объем неиспользованных ресурсов i-го вида.

Иногда возникает также необходимость перейти в задаче от нахождения минимума к нахождению максимума или наоборот. Для этого достаточно изменить знаки всех коэффициентов целевой функции на противоположные, а в остальном задачу оставить без изменения. Оптимальные решения полученных таким образом задач на максимум и минимум совпадают, а значения целевых функций при оптимальных решениях отличаются только знаком.

Множества допустимых решений

Множество точек называется выпуклым, если оно вместе с любыми двумя своими точками содержит их произвольную выпуклую линейную комбинацию.

Выпуклой линейной комбинацией произвольных точек 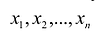Евклидова пространства 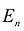называется сумма 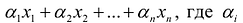– произвольные неотрицательные числа, сумма которых равна 1.

Геометрически это означает, что если множеству с любыми двумя его произвольными точками полностью принадлежит и отрезок, соединяющий эти точки, то оно будет выпуклым. Например, выпуклыми множествами являются прямолинейный отрезок, прямая, круг, шар, куб, полуплоскость, полупространство и др.

Точка множества называется граничной, если любая окрестность этой точки сколь угодно малого размера содержит точки, как принадлежащие множеству, так и не принадлежащие ему.

Граничные точки множества образуют его границу. Множество называется замкнутым, если оно содержит все свои граничные точки.

Ограниченным называется множество, если существует шар с радиусом конечной длины и центром в любой точке множества, содержащий полностью в себе данное множество. В противном случае множество будет неограниченным.

Пересечение двух или более выпуклых множеств будет выпуклым множеством, так как оно отвечает определению выпуклого множества.

Точка выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации двух других различных точек этого множества.

Так, угловые точки треугольника – его вершины, круга – точки окружности, ее ограничивающие, а прямая, полуплоскость, плоскость, полупространство, пространство не имеют угловых точек.

Выпуклое замкнутое ограниченное множество на плоскости, имеющее конечное число угловых точек, называется выпуклым многоугольником, а замкнутое выпуклое ограниченное множество в трехмерном пространстве, имеющее конечное число угловых точек, называется выпуклым многогранником.

Теорема. Любая тонка многоугольника является выпуклой линейной комбинацией его угловых точек.

Теорема. Область допустимых решений задачи линейного программирования является выпуклым множеством.

Уравнение целевой функции при фиксированных значениях самой функции является уравнением прямой линии (плоскости, гиперплоскости и т.д.). Прямая, уравнение которой получено из целевой функции при равенстве ее постоянной величине, называется линией уровня.

Линия уровня, имеющая общие точки с областью допустимых решений и расположенная так, что область допустимых решений находится целиком в одной из полуплоскостей, называется опорной прямой.

Теорема. Значения целевой функции в точках линии уровня увеличиваются, если линию уровня перемещать параллельно начальному положению в направлении нормали и убывают при перемещении в противоположном направлении.

Теорема. Целевая функция задачи линейного программирования достигает экстремума в угловой точке области допустимых решений; причем, если целевая функция достигает экстремума в нескольких угловых точках области допустимых решений, она также достигает экстремума в любой выпуклой комбинации этих точек.

Опорное решение задачи линейного программирования, его взаимосвязь с угловыми точками

Каноническая задача линейного программирования в векторной форме имеет вид:

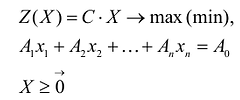
Положительным координатам допустимых решений ставятся в соответствие векторы условий. Эти системы векторов зависимы, так как число входящих в них векторов больше размерности векторов.

Базисным решением системы называется частное решение, в котором неосновные переменные имеют нулевые значения. Любая система уравнений имеет конечное число базисных решений, равное 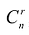, где n – число неизвестных, r- ранг системы векторов условий. Базисные решения, координаты которых удовлетворяют условию неотрицательности, являются опорными.

Опорным решением задачи линейного программирования называется такое допустимое решение , для которого векторы условий, соответствующие положительным координатам линейно независимы.

Число отличных от нуля координат опорного решения не может превосходить ранга r системы векторов условий (т.е. числа линейно независимых уравнений системы ограничений).

Если число отличных от нуля координат опорного решения равно m, то такое решение называется невырожденным, в противном случае, если число отличных от нуля координат опорного решения меньше т, такое решение называется вырожденным.

Базисом опорного решения называется базис системы векторов условий задачи, в состав которой входят векторы, соответствующие отличным от нуля координатам опорного решения.

Теорема. Любое опорное решение является угловой точкой области допустимых решений.

Теорема. Любая угловая точка области допустимых решений является опорным решением.

Пример:

Графический метод решения задачи линейной оптимизации рассмотрим на примере задачи производственного планирования при n = 2.

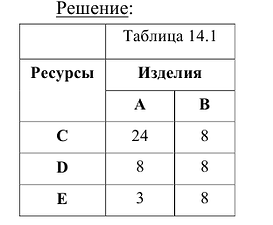
Предприятие изготавливает изделия двух видов А и В. Для производства изделий оно располагает сырьевыми ресурсами трех видов С, D и Е в объемах 600, 480 и 240 единиц соответственно. Нормы расхода ресурсов на единицу продукции каждого вида известны и представлены в табл. 14.1

Прибыль от реализации изделия А составляет 40 млн. руб., а изделия В – 50 млн.руб. Требуется найти объемы производства изделий А и В, обеспечивающие максимальную прибыль.

Построим математическую модель задачи, для чего обозначим 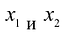– объемы производства изделий А и В соответственно.

Тогда прибыль предприятия от реализации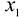 изделий А и 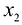изделий В составит:

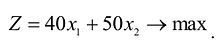
Ограничения по ресурсам будут иметь вид:

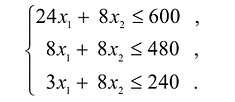
Естественно, объемы производства должны быть неотрицательными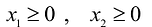

Решение сформулированной задами найдем, используя геометрическую интерпретацию. Определим сначала многоугольник решений, для чего систему ограничений неравенств запишем в виде уравнений и пронумеруем их:

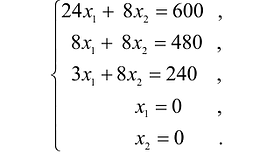
Каждое из записанных уравнений представляет собой прямую на плоскости, причем 4-я и 5-я прямые являются координатными осями.

Чтобы построить первую прямую, найдем точки ее пересечения с осями координат: 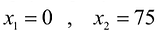а при .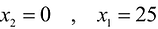

Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем точку O(0,0) подставив ее координаты в неравенство, видим, что оно удовлетворяется. Так как точка O(0,0) лежит левее первой прямой, то и полуплоскость будет находиться левее прямой

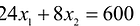. На рис 14 , расположение полуплоскости относительно первой прямой отмечено стрелками.

Аналогично построены 2-я и 3-я прямые и найдены полуплоскости, соответствующие 2-му и 3-му неравенству. Точки, удовлетворяющие ограничениям 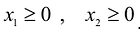, находятся в первом квадранте. Множество точек, удовлетворяющих всем ограничениям одновременно, является ОДР системы ограничений. Такой областью на графике (рис. 14.1) является многоугольник ОАВС.

Любая точка многоугольника решений удовлетворяет системе ограничений задачи и, следовательно, является ее решением. Это говорит о том, что эта задача линейной оптимизации имеет множество допустимых решений, т.е. моговариантпа. Нам же необходимо найти решение, обеспечивающее максимальную прибыль.

Чтобы найти эту точку, приравняем функцию к нулю и построим соответствующую ей прямую. Вектор-градиент прямой функции

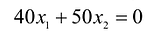имеет координаты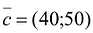

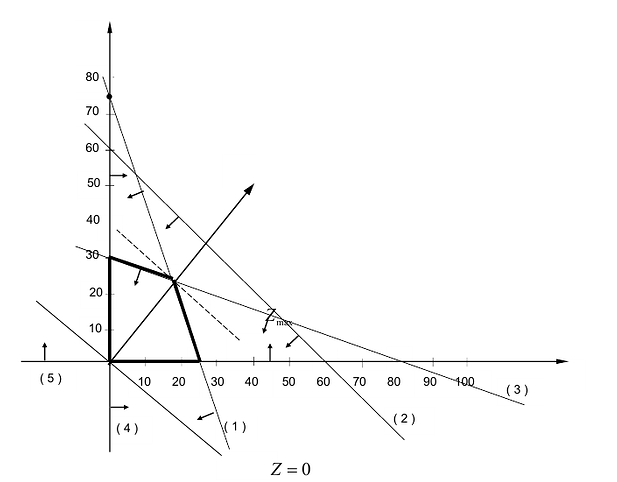
Рис. 14.1

Изобразим вектор на графике и построим прямую функции перпендикулярно вектору на рис. 14.1. Перемещая прямую функции параллельно самой себе в направлении вектора, видим, что последней точкой многоугольника решений, которую пересечет прямая функции, является угловая точка В. Следовательно, в точке В функция достигает максимального значения. Координаты точки В находим, решая систему уравнений, прямые которых пересекаются в данной точке.

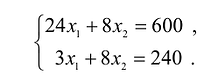
Решив эту систему, получаем, что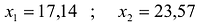

Следовательно, если предприятие изготовит изделия в найденных объемах, то получит максимальную прибыль, равную:

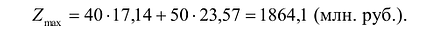
Алгоритм решения задачи линейного программирования графическим методом таков:

1. Строится область допустимых решений;
2. Строится вектор нормали к линии уровня с точкой приложении в начале координат;
3. Перпендикулярно вектору нормали проводится одна из линий уровня, проходящая через начало координат;
4. Линия уровня перемещается до положения опорной прямой. На этой прямой и будут находиться максимум или минимум функции.

В зависимости от вида области допустимых решений и целевой функции задача может иметь единственное решение, бесконечное множество решений или не иметь ни одного оптимального решения.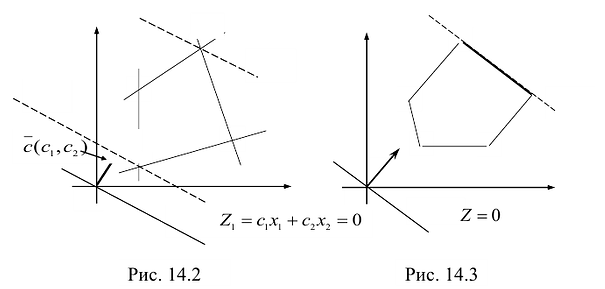

На рис. 14.3 показан случай, когда прямая функции параллельна отрезку АВ, принадлежащему ОДР. Максимум функции Z достигается в точке А и в точке В, а, следовательно, и в любой точке отрезка АВ, т.к. эти точки могут быть выражены в виде линейной комбинации угловых точек А и В.

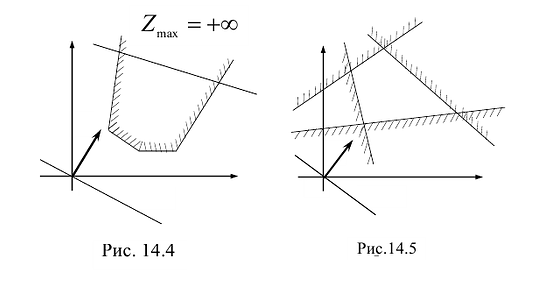
На рисунке 14.4 изображен случай, когда система ограничений образует неограниченное сверху множество. Функция Z в данном случае стремится к бесконечности, так как прямую функции можно передвигать в направлении вектора градиента как угодно далеко, а на рисунке 14.5 представлен случай несовместной системы ограничений.

Основные понятия симплексного метода решения задачи линейного программирования.

Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (или симплекс-метод), разработанный американским ученым Дж.Данцигом. Суть этого метода заключается в том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, но необязательно оптимальный (так называемое начальное опорное решение); оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций). Нахождение начального опорного решения и переход к следующему опорному решению проводятся на основе применения рассмотренного выше метода Жордана-Гаусса для системы линейных уравнений в канонической форме, в которой должна быть предварительно записана исходная задача линейного программирования; направление перехода от одного опорного решения к другому выбирается при этом на основе критерия оптимальности (целевой функции) исходной задачи.

Симплекс-метод основан на следующих свойствах задачи линейного программирования:

• Не существует локального экстремума, отличного от глобального. Другими словами, если экстремум есть, то он единственный.
• Множество всех планов задачи линейного программирования выпукло.
• Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранника решений (в его вершине). Если целевая функция принимает свое оптимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
• Каждой угловой точке многогранника решений отвечает опорный план ЗЛП.

Рассмотрим две разновидности симплексного метода: симплекс-метод с естественным базисом и симплекс-метод с искусственным базисом (или М-метод).

• Заказать решение задач по высшей математике

Симплекс-метод с естественным базисом

Для применения этого метода задача линейного программирования должна быть сформулирована в канонической форме, причем матрица системы уравнений должна содержать единичную подматрицу размерностью mхm. В этом случае очевиден начальный опорный план (неотрицательное базисное решение).

Для определенности предположим, что первые m векторов матрицы системы составляют единичную матрицу. Тогда очевиден первоначальный опорный план:

Проверка на оптимальность опорного плана проходит с помощью критерия оптимальности, переход к другому опорному плану — с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности.

Полученный опорный план снова проверяется на оптимальность и т.д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции.

Признак оптимальности заключается в следующих двух теоремах.

Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:

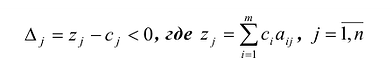
то можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:

1. если все координаты вектора, подлежащего вводу в базис, неположительны, то задача линейного программирования не имеет решения;
2. если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план.

Теорема 2. Если для всех векторов выполняется условие 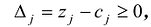то полученный план является оптимальным.

На основании признака оптимальности в базис вводится вектор Ак, давший минимальную отрицательную величину симплекс-разности: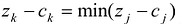

Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор 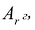, который дает минимальное положительное отношение:

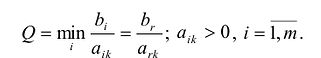
Строка 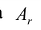называется направляющей, столбец 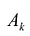и элемент 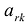— направляющими (последний называют также разрешающим элементом).

Элементы вводимой строки, соответствующей направляющей строке, в новой симплекс-таблице вычисляются по формулам:

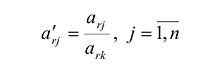
а элементы любой другой i-й строки пересчитываются по формулам:

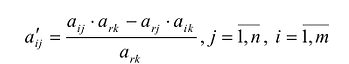
Значения базисных переменных нового опорного плана (показатели графы «план») рассчитываются по формулам:

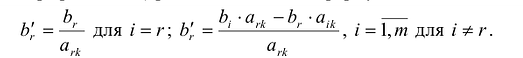
Если наименьшее значение Q достигается для нескольких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить следующий способ.

Вычисляются частные, полученные от деления всех элементов строк, давших одинаковое минимальное значение Q на свои направляющие элементы. Полученные частные сопоставляются по столбцам слева направо, при этом учитываются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответствующий строке, в которой раньше обнаружится меньшее частное.

Для использования приведенной выше процедуры симплекс -метода к минимизации линейной формы 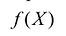следует искать максимум функции 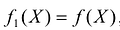затем полученный максимум взять с противоположным знаком. Это и будет искомый минимум исходной задачи линейного программирования.

Симплексный метод с искусственным базисом (М-метод)

Симплексный метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи линейного программирования, записанной в канонической форме.

М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной задачи линейного программирования таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае её максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М – достаточно большое положительное число.

В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки А, теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М – достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.

В процессе решения M-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М-задачи содержит искусственные векторы или М-задача неразрешима, то исходная задача также неразрешима.

Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.

Теория двойственности

Любой задаче линейного программирования можно сопоставить сопряженную или двойственную ей задачу. Причем, совместное исследование этих задач дает, как правило, значительно больше информации, чем исследование каждой из них в отдельности.

Любую задачу линейного программирования можно записать в виде:

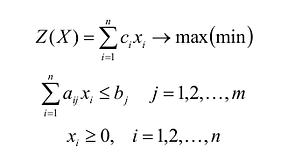
Первоначальная задача называется исходной или прямой.

Модель двойственной задачи имеет вид:

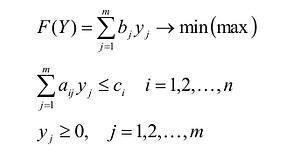
Переменные двойственной задачи 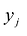называют объективно обусловленными оценками или двойственными оценками.

Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой. Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой.

Двойственная задача по отношению к исходной составляется согласно следующим правилам:

1. Целевая функция исходной задачи формулируется на максимум, а целевая функция двойственной задачи – на минимум, при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид <, а в задаче на минимум – вид
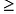
2. Матрица 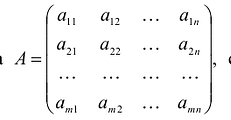, составленная из коэффициентов при неизвестных в системе ограничении исходной задачи, и аналогичная матрица 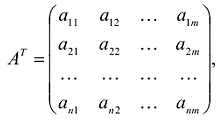, в двойственной задаче получаются друг из друга транспонированием;
3. Число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений в системе двойственной задачи – числу переменных в исходной задаче;
4. Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи – коэффициенты при неизвестных в целевой функции исходной задачи;
5. Каждому ограничению одной задачи соответствует переменная другой задачи: номер переменной совпадает с номером ограничения; при этом ограничению, записанному в виде неравенства <, соответствует переменная, связанная условием неотрицательности.

Если функциональное ограничение исходной задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, так и отрицательные значения.

Математические модели пары двойственных задач могут быть симметричными и несимметричными. В несимметричных двойственных задачах система ограничений исходной задачи задается в виде равенств, а двойственной – в виде неравенств, причем переменные в двойственной задаче могут быть и отрицательными. В симметричных двойственных задачах система ограничений как исходной, так и двойственной задачи задается в виде неравенств, причем на двойственные переменные налагается условие неотрицательности.

где:

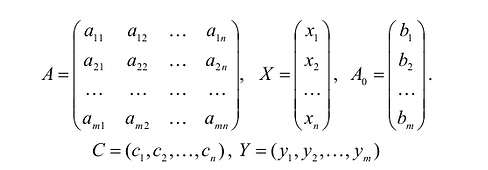
Рассмотрим пример, показывающий, как в реальной экономической ситуации появляются взаимно двойственные задачи линейного программирования.

На некотором предприятии после выполнения годового плана возник вопрос: как поступить с остатками сырья? Из оставшегося сырья можно наладить производство продукции и реализовать его или продать сырье.

Предположим, что имеется два вида сырья , остатки которого составляют соответственно 35 и 20 единиц. Из этого сырья можно наладить производство трех видов товаров:

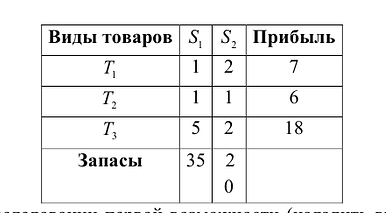
При исследовании первой возможности (наладить выпуск товаров ) возникает вопрос о плане выпуска, который задается тремя переменными 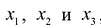, которые соответствуют количеству произведенного товара. Эти переменные должны удовлетворять условиям:

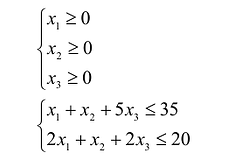
Прибыль, которую получит предприятие от реализации товара, составит:

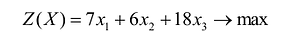
В интересах предприятия эту прибыль максимизировать.

Это прямая задача.

Объективно обусловленными оценками двойственной задачи 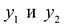будут цены, по которым целесообразно продавать излишки сырья, т.е. при продаже сырья по ценам ниже 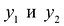предприятие будет терпеть убытки.

Справедливое требование со стороны продающего предприятия состоит в следующем: если взять сырье, идущее на производство единицы товара 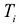то выручка от его продажи должна быть не меньше, чем прибыль от реализации готового изделия (в противном случае нет смысла продавать сырье – целесообразнее изготовить товар и получить прибыль от его реализации).

Это требование можно представить в виде системы неравенств: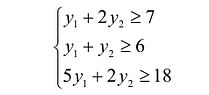

В левой части каждого неравенства предполагаемая выручка от продажи сырья, необходимого для производства единицы товара 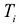а в правой – прибыль от реализации этой единицы товара.

Что касается покупателя, то он заинтересован в минимизации расходов на покупку сырья, т.е. величины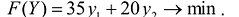

Теоремы двойственности

Теоремы двойственности позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач: можно либо найти оптимальное решение другой задачи, не решая ее, либо установить его отсутствие.

Возможны следующие случаи:

• обе задачи из пары двойственных имеют оптимальные решения;
• одна из задач не имеет решения ввиду неограниченности целевой функции, а другая – ввиду несовместности системы ограничений.

Первая теорема двойственности.

Для двойственных задач линейного программирования имеет место один из взаимоисключающих случаев:

1. В прямой и двойственной задачах имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают:
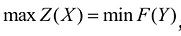
2. В прямой задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена сверху. При этом у двойственной задачи будет пустое допустимое множество.
3. В двойственной задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым;
4. Обе из рассматриваемых задач имеют пустые допустимые множества.

Вторая теорема двойственностн (теорема о дополняющей нежесткости):

Пусть 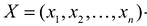– допустимое решение прямой задачи, а 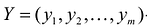допустимое решение двойственной задачи.

Для того, чтобы они были оптимальными решениями соответствующих взаимодвойственных задач, необходимо и достаточно, чтобы выполнялись следующие соотношения:

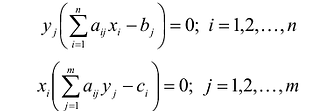
Эти условия устанавливают связь между оптимальными значениями прямой и двойственной задач и позволяют, зная решение одной из них, находить решение другой задачи.

Теорема об оценках:

Значения переменных 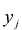в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов 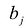системы ограничений – неравенств прямой задачи на величину :

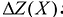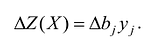
Диапазон изменения компонент вектора В, в котором сохраняется оптимальный базис, называется областью устойчивости оптимальных оценок.

Экономический смысл первой теоремы двойственности следующий. План производства X и набор ресурсов Y оказываются оптимальными тогда и только тогда, когда прибыль от реализации продукции, определенная при известных заранее ценах продукции 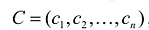, равна затратам на ресурсы по «внутренним» (определяемым только из решения задачи) ценам ресурсов 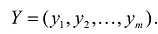Для всех других планов прибыль от продукции всегда меньше или равна стоимости затраченных ресурсов 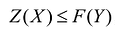, т.е. ценность выпущенной продукции не превосходит суммарной оценки затраченных ресурсов. Значит, величина Z(X)~ F(Y) характеризует производственные потери в зависимости от рассмотренной производственной программы и выбранных оценок ресурсов.