Хитрости »
14 Февраль 2017 25769 просмотров
Как быстро подобрать оптимальный вариант решения
Практически в любой компании в определенные периоды могут “высвобождаться” из оборота временно свободные денежные средства(ВСДС). Оставлять эти деньги просто так на счетах компании весьма нецелесообразно. Деньги должны делать деньги. Конечно, вложение денег в банковские депозиты может показаться не самым лучшим вариантом для инвестиций, но все же это хоть какой-то доход, который если и не будет колоссальным, то хотя бы частично покроет инфляционные потери.
И самое сложное это выбрать банк, программу депозита и срок для вложений таким образом, чтобы получить максимальную выгоду. Сделать это поможет один из самых мощных, но в тоже время малоиспользуемых инструментов Excel – надстройка Поиск решения(Solver).
Чтобы пошагово выполнять дальнейшие действия, описанные в статье рекомендую сразу скачать файл с моделью для Поиска решения:
Модель_расчета_ВСДС.xls (44,5 KiB, 1 471 скачиваний)
Надстройка Поиск решения хоть и устанавливается автоматически вместе с Excel(начиная с версий 2007 и выше), но по умолчанию отключена. Чтобы включить надстройку необходимо перейти в Файл(File) –Параметры(Options). В появившемся диалоговом окне выбрать слева пункт Надстройки(Add-ins). Далее справа внизу в выпадающем списке Управление выбрать –Надстройки Excel(Excel Add-ins) и нажать Перейти(Go):

В окне Надстройки(Add-ins) устанавливаем галочку напротив пункта Поиск решения(Solver), жмем ОК.

Поиск решения теперь будет доступен с вкладки Данные(Data) -группа Анализ(Analize):

Исходные данные
Для начала нам потребуется определить сумму временно свободных денежных средств и сроки, на которые мы хотим эти средства разместить в банке. Далее конечно же потребуется выбрать несколько банков (или конкретные предложения отдельного банка) с различными процентами годовых за размещение ДС. Но так же придется учесть и реалии: не стоит все средства размещать исключительно в одном банке и поэтому надо для банков/предложений определить лимит ДС, который нельзя превышать.
Т.е. наши исходные данные выглядят примерно так:
- период размещения ДС на депозите(скажем 14 дней, 28 дней, 62 дня и 91 день)
- сумма ДС, доступная на каждый период размещения
- процент за размещение ДС на каждый период для каждого типа размещения(срочный депозит, до востребования, овернайт и т.д.) или банка
- лимит на размещение средств по каждому типу депозита или для каждого банка(лимит определяется самой компанией)
Как работает Поиск решения
Поиск решения хорош тем, что он может быть применен практически к любой задаче. Что он делает? Он на основании заданных условий и ограничений перебирает все возможные варианты, которые подходят под условия и не выходят за рамки заданных ограничений, если они есть. И из всех подобранных вариантов выбирает самый оптимальный. В нашем случае будем подбирать наиболее выгодный для нас вариант размещения ВСДС.
А что считать наиболее выгодным? Конечно то, что принесет наибольший доход. При этом наша цель не просто выбрать депозит с самым большим процентом (это было бы слишком просто и для этого не нужен Поиск решения), а может даже совместить несколько вариантов размещения ВСДС на разных депозитах с разными ставками и разными периодами. Ведь для различных сумм или сроков и ставки могут быть разными.
И теперь останется определить какие у нас могут быть ограничения. По сути их два основных:
- Непосредственно сумма ВСДС – мы не должны при расчете максимального дохода выходить за рамки общей суммы доступных ВСДС
- Лимит по депозиту для размещения – как упоминалось выше, могут быть установлены лимиты на размещение средств в том или ином банке на усмотрение компании. Конечно, любой банк заинтересован в большей сумме, но не стоит рисковать и вкладывать всю сумму в один банк
Исходные данные определены, ограничения тоже. Осталось записать все это в удобную таблицу(приложена к статье), в которой при необходимости сможем изменять эти исходные данные и ограничения:

Для большей наглядности блоки таблицы разделены цветами:
- Синий и голубой – заполняемые вручную данные: суммы ВСДС, сроки ВСДС, лимиты размещения ВСДС в банках, процент по каждому банку/размещению
- Зеленый – расчетные поля. Их не надо изменять вручную
- Красный – поля, заполняемые автоматически Поиском решения или формулами. Их не надо изменять вручную
- Так же серый шрифт – это “служебные” ячейки, которые не влияют на расчеты непосредственно в таблице, но которые потребуются нам для корректной работы Поиска решения для учета ограничений
После заполнения таблицы исходными данными можно приступать к определению максимального выгодного вложения ВСДС.
Переходим на вкладку Данные(Data) -группа Анализ(Analize) –Поиск решения(Solver). В появившемся окне указываем следующие данные:

- Оптимизировать целевую функцию(Set Objective) – указываем ячейку H18, в которой у нас подводится сумма общего дохода от вложений
- До(To) – выбираем Максимум(Max), т.к. нам нужен максимально возможный доход
- Изменяя ячейки переменных(By Changing Variable Cells) – указываем H9:K14. В эти ячейки Поиск решения будет подставлять суммы к размещению и вычисляя от этого возможный доход. Собственно, заполненные здесь данные нам и нужны в итоге
- В соответствии с ограничениями(Subject to the Constraints) – здесь мы сами добавляем ограничения, которые необходимо учитывать при расчете дохода. Нам потребуется добавить два ограничения(на скрине выше они уже добавлены, но в любом случае необходимо знать как их создавать). Нажимаем справа кнопку Добавить(Add), появится окно добавления ограничения:

В данном случае я хочу добавить ограничение, что суммы в ячейках с лимитом размещения в банке должны быть больше или равны общей сумме размещенных ВСДС. Эта сумма у нас подводится в ячейках L9:L14. Таким образом нам в левой части надо выбрать ячейки с суммами заданных лимитов (C9:C14), а в правой суммы всех вложений – L9:L14. В выпадающем списке между двумя этими полями можно выбрать тип сравнения. В нашем случае ячейки слева (лимиты ДС) должны быть больше или равны(>=) общей сумме вложений по данному типу – ячейки справа.
Аналогично добавляем второе ограничение – суммы доступных ВСДС не должны превышать суммы, которые Поиск решения предложит разместить. Доступные суммы у нас указаны в ячейках D7:G7, а общие суммы предложенных к размещению Поиском решения – в ячейках H16:K16(в этих ячейках записаны формулы, суммирующие данные сумм по каждому периоду в ячейках H9:K14) - Так же лучше установить галочку Сделать переменные без ограничений неотрицательными(Make Unconstrained Variables Non-Negative), чтобы Поиск решения не стал подбирать отрицательные суммы для выполнения условий
В рассматриваемой задаче это маловероятно, но при использовании Поиска решения в других задачах этому пункту советую уделять особое внимание, т.к. иногда оптимальным решением для достижения заданного результата с точки зрения Поиска решения будет добавление отрицательного значения среди заполняемых ячеек
Нажимаем Найти решение(Solve). Если все условия заданы правильно и ограничения выполнимы, то Поиск решения заполнит ячейки суммами и выдаст сообщение о том, что решение найдено и предложит сохранить найденные значения или восстановить предыдущие. В нашем случае надо оставить пункт Сохранить найденное решение(Keep Solver Solution) и нажать Ок.

После этого мы сможем более детально изучить предложенное решение:

При необходимости изменить какие-то исходные данные и запустить поиск решения заново. Все ранее указанные ограничения и условия сохраняются и создавать их заново не придется.
В приложенном к статье файле все ограничения и условия уже созданы и для их просмотра и правки достаточно просто запустить Поиск решения
Осталось понять Как работает вся эта таблица в Поиске решения
В блоке Доход в зависимости от срока размещения, руб(M9:P14) записаны формулы, которые определяют сумму дохода в зависимости от вложенной суммы и срока размещения. При этом рассчитываются они из сумм, записанных в ячейках красного блока (Суммы к размещению на соответствующие сроки – H9:K14) и от сроков, указанных в исходных данных(D8:G8). В ячейке Итого доходность(H18) подводится сумма этих ячеек. Т.е. мы определяем общий доход от вложений. Все, что остается делать Поиску решения – это изменять значения ячеек Суммы к размещению на соответствующие сроки (H9:K14) до тех пор, пока сумма всех доходов (Итого доходность – H18) не достигнет максимального значения из всех возможных вариантов при всех существующих ограничениях. Суммы в ячейках H9:K14 и будут являться оптимальным решением.
При этом если мы захотим исключить какой-либо банк/тип депозита из просчета, достаточно будет установить в ячейках C7:C14 для этого типа значение 0. Тогда он не будет учитываться для размещения Поиском решения и не надо будет удалять/добавлять строки и переопределять ограничения.
Проверка результатов
Надстройка Поиск решения реализована при помощи весьма сложных алгоритмов и, пожалуй, является самой непредсказуемой надстройкой в Excel. Поэтому рекомендуется тщательно перепроверять результаты вручную, прежде чем полностью на них положиться. Сверяйте полученные результаты, чтобы убедиться, что ограничения не нарушены и главное, что результат отвечает ожиданиям (хотя бы примерно).
Так же следует учитывать, что надстройка может при одинаковых условиях и исходных данных выдавать различные результаты при многократном запуске. Это так же обусловлено сложностью заложенных алгоритмов. Т.е. теоретически, запустив Поиск решения пять раз есть вероятность, что все пять раз решение будет разным. Хотя в большинстве случаев я наблюдал ситуации, когда при одинаковых исходных данных решение было одинаковым.
Скачать пример:
 Модель_расчета_ВСДС.xls (44,5 KiB, 1 471 скачиваний)
Модель_расчета_ВСДС.xls (44,5 KiB, 1 471 скачиваний)
Подбор под сумму через Поиск решения
И еще один пример применения Поиска решения. Предположим, что у нас есть таблица с начислениями НДС за первый квартал. И есть некая итоговая сумма, которая должна быть отчислена за первый квартал. Проблема в том, что не все строки из таблицы были использованы для отчисления общего налога за первый квартал. Задача отобрать из всех сумм только те, которые при сложении дадут именно нужную итоговую сумму отчислений. Данный прием я решил не описывать текстом, а записать видео для большей наглядности:
Скачать файл из видео:
 Подбор под сумму.xls (60,5 KiB, 880 скачиваний)
Подбор под сумму.xls (60,5 KiB, 880 скачиваний)
Так же см.:
План-фактный анализ в Excel при помощи Power Query
Автообновляемая сводная таблица
Статья помогла? Поделись ссылкой с друзьями!
![]() Видеоуроки
Видеоуроки
Поиск по меткам
Access
apple watch
Multex
Power Query и Power BI
VBA управление кодами
Бесплатные надстройки
Дата и время
Записки
ИП
Надстройки
Печать
Политика Конфиденциальности
Почта
Программы
Работа с приложениями
Разработка приложений
Росстат
Тренинги и вебинары
Финансовые
Форматирование
Функции Excel
акции MulTEx
ссылки
статистика
“Поиск решения” — это надстройка для Microsoft Excel, которую можно использовать для анализ “что если”. С ее помощью можно найти оптимальное значение (максимум или минимум) формула, содержащейся в одной ячейке, называемой целевой, с учетом ограничений на значения в других ячейках с формулами на листе. Надстройка “Поиск решения” работает с группой ячеек, называемых ячейками переменных решения или просто ячейками переменных, которые используются при расчете формул в целевых ячейках и ячейках ограничения. Надстройка “Поиск решения” изменяет значения в ячейках переменных решения согласно пределам ячеек ограничения и выводит нужный результат в целевой ячейке.
Проще говоря, с помощью надстройки “Поиск решения” можно определить максимальное или минимальное значение одной ячейки, изменяя другие ячейки. Например, вы можете изменить планируемый бюджет на рекламу и посмотреть, как изменится планируемая сумма прибыли.
Примечание: В версиях надстройки “Поиск решения”, выпущенных до Excel 2007, ячейки переменных решения назывались изменяемыми или регулируемыми. В Excel 2010 надстройка “Поиск решения” была значительно улучшена, так что работа с ней в Excel 2007 будет несколько отличаться.
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка “Поиск решения” может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка F5), пока общая прибыль (целевая ячейка F7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке F7, =СУММ (Q1 Прибыль:Q2 Прибыль).
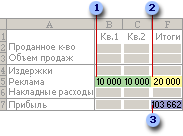
1. Ячейки переменных
2. Ячейка с ограничениями
3. Целевая ячейка
После выполнения процедуры получены следующие значения.

-
На вкладке Данные в группе Анализ нажмите кнопку Поиск решения.
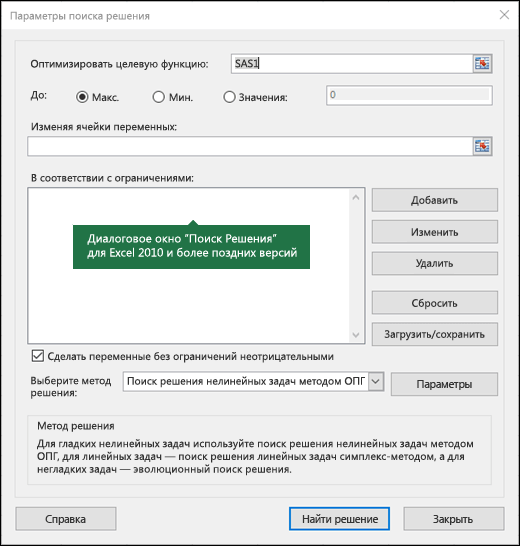
-
В поле Оптимизировать целевую функцию введите ссылка на ячейку или имя целевой ячейки. Целевая ячейка должна содержать формулу.
-
Выполните одно из следующих действий.
-
Чтобы значение целевой ячейки было максимальным из возможных, установите переключатель в положение Макс.
-
Чтобы значение целевой ячейки было минимальным из возможных, установите переключатель в положение Мин.
-
Чтобы задать для целевой ячейки конкретное значение, установите переключатель в положение Значение и введите в поле нужное число.
-
В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми. Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
-
-
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить. Для этого выполните указанные ниже действия.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
-
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
-
Щелкните связь (<=, =, >=, int,binили dif), которая требуется между ячейкой, на которую ссылается ссылка, и ограничением. Если щелкнуть int, в поле Ограничение появится integer. Если щелкнуть бин,в поле Ограничение появится двоичное поле. Если нажать кнопку dif,в поле Ограничение появится ссылкаalldifferent.
-
Если в поле Ограничение было выбрано отношение <=, = или >=, введите число, ссылку на ячейку (или имя ячейки) или формулу.
-
Выполните одно из указанных ниже действий.
-
Чтобы принять данное ограничение и добавить другое, нажмите кнопку Добавить.
-
Чтобы принять ограничение и вернуться в диалоговое окно Параметрырешения, нажмите кнопку ОК.
Примечание Отношения int,binи dif можно применять только в ограничениях для ячеек переменных решения.Чтобы изменить или удалить существующее ограничение, выполните указанные ниже действия.
-
-
В диалоговом окне Параметры поиска решения щелкните ограничение, которое требуется изменить или удалить.
-
Нажмите кнопку Изменить и внесите изменения либо нажмите кнопку Удалить.
-
-
Нажмите кнопку Найти решение и выполните одно из указанных ниже действий.
-
Чтобы сохранить значения решения на листе, в диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
-
Чтобы восстановить исходные значения перед нажатием кнопки Найти решение, выберите вариант Восстановить исходные значения.
-
Вы можете прервать поиск решения, нажав клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных решения.
-
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, будут доступны только некоторые отчеты или они вообще не будут доступны.
-
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.
-
-
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
-
Чтобы просмотреть значения всех найденных решений, в диалоговом окне Параметры установите флажок Показывать результаты итераций и нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
-
В диалоговом окне Показать предварительное решение выполните одно из указанных ниже действий.
-
Чтобы остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения, нажмите кнопку Стоп.
-
Чтобы продолжить процесс поиска решения и просмотреть следующий вариант решения, нажмите кнопку Продолжить.
-
-
В диалоговом окне Параметры поиска решения нажмите кнопку Параметры.
-
В диалоговом окне на вкладках Все методы, Поиск решения нелинейных задач методом ОПГ и Эволюционный поиск решения выберите или введите значения нужных параметров.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Загрузить/сохранить.
-
Введите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.
При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.
Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки “Поиск решения”, и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить или сохранить для сохранения задач по отдельности.
В диалоговом окне Параметры поиска решения можно выбрать любой из указанных ниже алгоритмов или методов поиск решения.
-
Нелинейный метод обобщенного понижающего градиента (ОПГ). Используется для гладких нелинейных задач.
-
Симплекс-метод. Используется для линейных задач.
-
Эволюционный метод Используется для негладких задач.
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка “Поиск решения” может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка D5), пока общая прибыль (целевая ячейка D7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке D7, =СУММ (Q1 Прибыль:Q2 Прибыль).
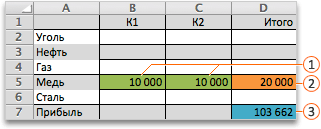
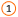 переменных
переменных
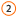 с ограничениями
с ограничениями
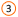 цель
цель
В результате выполнения получены следующие значения:

-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.

В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.

-
В разделе Оптимизировать целевую функцию, введите ссылка на ячейку или имя целевой ячейки.
Примечание: Целевая ячейка должна содержать формулу.
-
Выполните одно из следующих действий.
Задача
Необходимые действия
Сделать так, чтобы значение целевой ячейки было максимальным из возможных
Выберите значение Макс.
Сделать так, чтобы значение целевой ячейки было минимальным из возможных
Выберите значение Мин.
Сделать так, чтобы целевая ячейка имела определенное значение
Щелкните Значение, а затем введите нужное значение в поле.
-
В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми.
Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
-
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить.
Для этого выполните следующие действия:
-
В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
-
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
-
Во всплывающем меню <= задайте требуемое отношение между целевой ячейкой и ограничением. Если вы выбрали <=, =, или >= в поле Ограничение, введите число, имя ячейки, ссылку на нее или формулу.
Примечание: Отношения int, бин и раз можно использовать только в ограничениях для ячеек, в которых находятся переменные решения.
-
Выполните одно из указанных ниже действий.
Задача
Необходимые действия
Принять ограничение и добавить другое
Нажмите кнопку Добавить.
Принять ограничение и вернуться в диалоговое окно Параметры поиска решения
Нажмите кнопку ОК.
-
-
Нажмите кнопку Найти решение и выполните одно из следующих действий:
Задача
Необходимые действия
Сохранить значения решения на листе
В диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
Восстановить исходные значения
Щелкните Восстановить исходные значения.
Примечания:
-
Чтобы прервать поиск решения, нажмите клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных.
-
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, отчет не будет доступен.
-
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.

В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.

-
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
-
Чтобы просмотреть значения всех предварительных решений, установите флажок Показывать результаты итераций и нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
-
В диалоговом окне Показать предварительное решение выполните одно из следующих действий:
Задача
Необходимые действия
Остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения
Нажмите кнопку Стоп.
Продолжить поиск и просмотреть следующее предварительное решение
Нажмите кнопку Продолжить.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.

В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.

-
Нажмите кнопку Параметры, а затем в диалоговом окне Параметры или Поиск решения выберите один или несколько из следующих вариантов:
Задача
Необходимые действия
Настроить время решения и число итераций
На вкладке Все методы в разделе Пределы решения в поле Максимальное время (в секундах) введите количество секунд, в течение которых можно будет искать решение. Затем в поле Итерации укажите максимальное количество итераций, которое вы хотите разрешить.
Примечание: Если будет достигнуто максимальное время поиска решения или количество итераций, а решение еще не будет найдено, средство “Поиск решения” выведет диалоговое окно Показать предварительное решение.
Задать точность
На вкладке Все методы введите в поле Точность ограничения нужное значение погрешности. Чем меньше число, тем выше точность.
Задать степень сходимости
На вкладке Поиск решения нелинейных задач методом ОПГ или Эволюционный поиск решения в поле Сходимость укажите, насколько должны отличаться результаты последних пяти итераций, чтобы средство прекратило поиск решения. Чем меньше число, тем меньше должно быть изменение.
-
Нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение или Закрыть.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.

В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.

-
Щелкните Загрузить/сохранить, укажите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.
При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.
Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки “Поиск решения”, и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить/сохранить для сохранения задач по отдельности.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.

В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.

-
Во всплывающем меню Выберите метод решения выберите одно из следующих значений:
|
Метод решения |
Описание |
|---|---|
|
Нелинейный метод обобщенного понижающего градиента (ОПГ) |
Используется по умолчанию для моделей со всеми функциями Excel, кроме ЕСЛИ, ВЫБОР, ПРОСМОТР и другие ступенчатые функции. |
|
Поиск решения линейных задач симплекс-методом |
Используйте этот метод для задач линейного программирования. В формулах модели, которые зависят от ячеек переменных, должны использоваться функции СУММ, СУММПРОИЗВ, +, – и *. |
|
Эволюционный поиск решения |
Этот метод, основанный на генетических алгоритмах, лучше всего подходит в том случае, если в модели используются функции ЕСЛИ, ВЫБОР и ПРОСМОТР с аргументами, которые зависят от ячеек переменных. |
Примечание: Авторские права на части программного кода надстройки “Поиск решения” версий 1990–2010 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.
Поскольку надстройки не поддерживаются в Excel в Интернете, вы не сможете использовать надстройку “Поиск решения” для анализа данных “что если”, чтобы найти оптимальные решения.
Если у вас есть Excel, вы можете нажать кнопку Открыть в Excel, чтобы открыть книгу для использования надстройки “Поиск решения”.
Дополнительная справка по надстройке “Поиск решения”
За дополнительной справкой по надстройке “Поиск решения” обращайтесь по этим адресам:
Frontline Systems, Inc.
P.O. Box 4288
Incline Village, NV 89450-4288
(775) 831-0300
Веб-сайт: http://www.solver.com
Электронная почта: info@solver.com
“Решение” на www.solver.com.
Авторские права на части программного кода надстройки “Поиск решения” версий 1990-2009 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Использование “Решения” для бюджетов с использованием средств на счете вех
Использование “Решение” для определения оптимального сочетания продуктов
Введение в анализ гипотетических вариантов
Полные сведения о формулах в Excel
Рекомендации, позволяющие избежать появления неработающих формул
Обнаружение ошибок в формулах
Сочетания клавиш в Excel
Функции Excel (по алфавиту)
Функции Excel (по категориям)
«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил. Рассказываем, как освоить функцию поиска решений.
Основные параметры поиска решений
Найти решение задачи можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый и покажет максимально точное решение, если знать, как использовать функцию.
Итак, мы решаем задачу с помощью поиска решений в Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. К поиску решения вернемся чуть позже, а сейчас разберемся, что входит в каждый из этих типов:
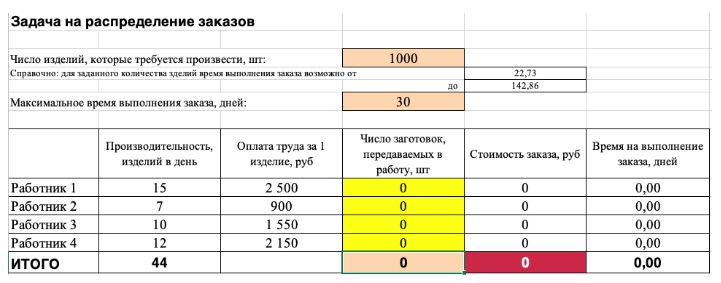
Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).
Изменяемые ячейки — переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон. При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения.
Целевая функция — результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.
Ограничения — условия, которые необходимо учесть при оптимизации функции, называющейся целевой. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.
Пример использования поиска решений
Теперь перейдем к самой функции.
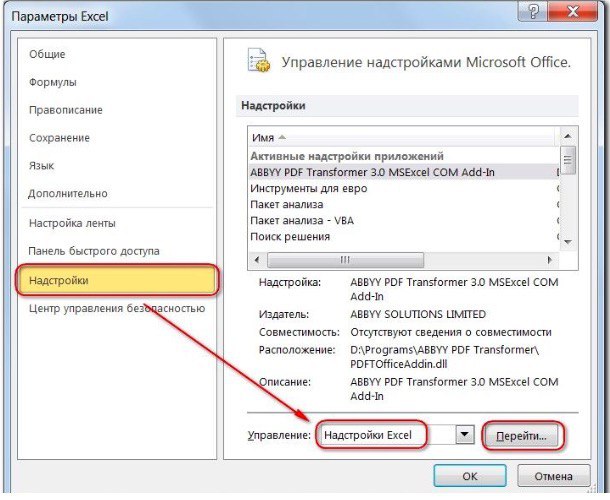
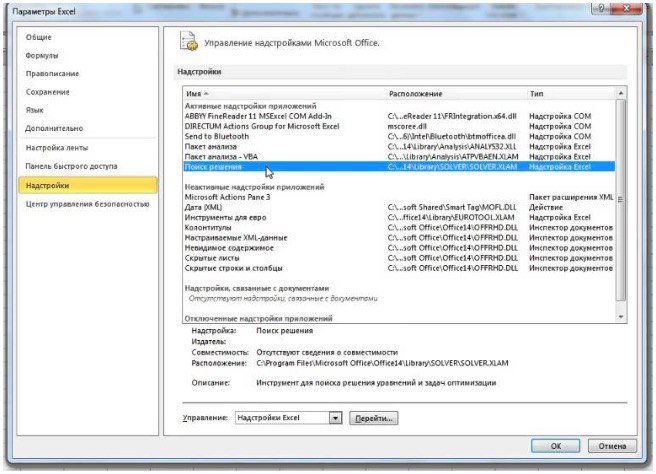
1) Чтобы включить «Поиск решений», выполните следующие шаги:
- нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
- в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
- в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.
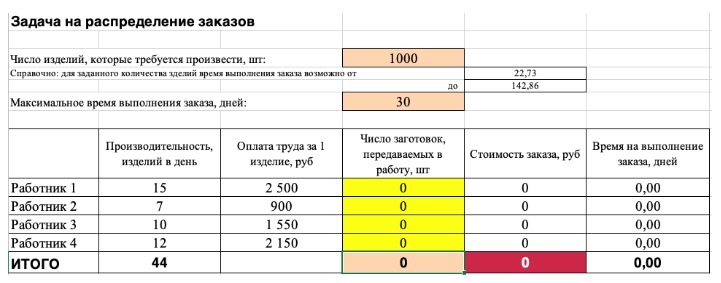
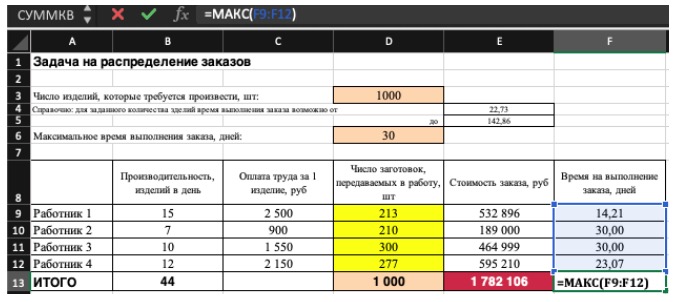
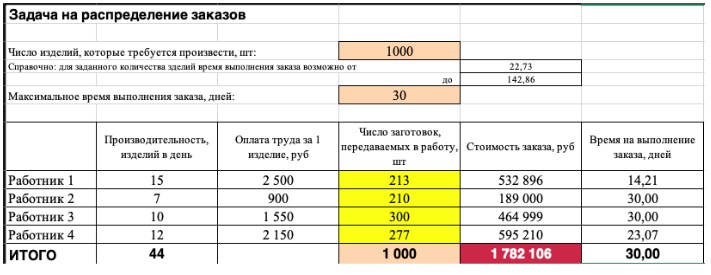
2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым – изменяемые ячейки.
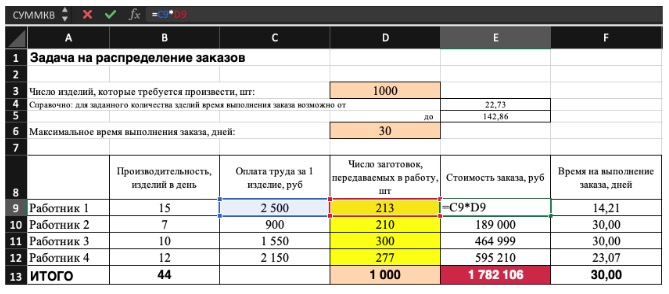
Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».
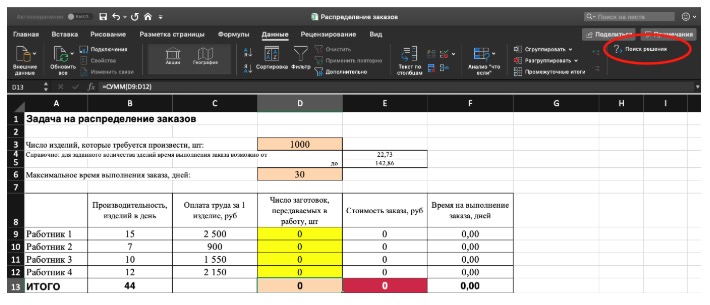
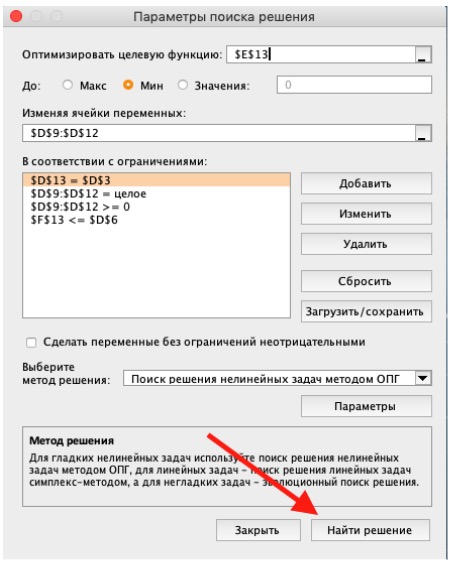
3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).
4) Заполните параметры «Поиска решений» и нажмите «Найти решение».
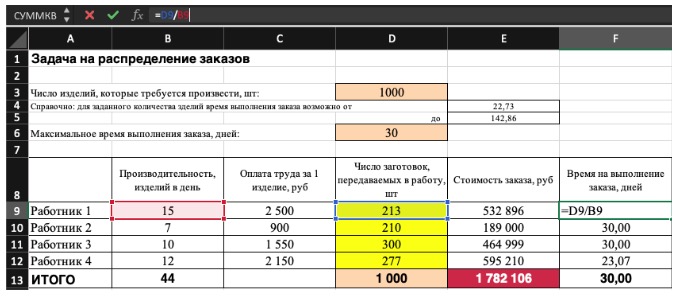
Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.
В нашем примере следующие ограничения:
- общее количество изделий 1000 штук ($D$13 = $D$3);
- число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
- количество дней меньше либо равно 30 ($F$9:$F$12 < = $D$6, либо как в примере в ячейке F13 задать функцию МАКС(F9:F12) и поставить ограничение $F$13 < = $D$6).
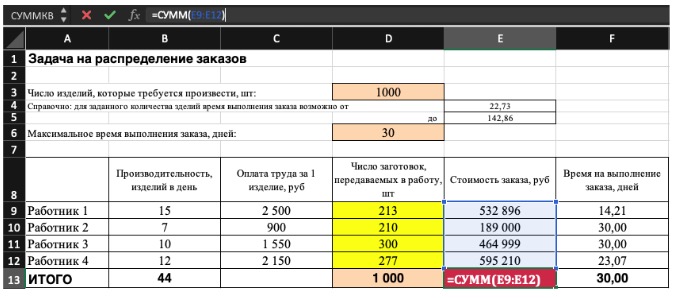
5) В конце проверьте полученные данные на соответствие заданному целевому значению. Если что-то не сходится — нужно пересмотреть исходные данные, введенные формулы и ограничения.
Хотите научиться решать задачи в Excel, как это делают в компаниях-лидерах? Приходите на наш онлайн-курс, на котором вы освоите этот инструмент на уровне профи. Вашими преподавателями будут эксперты-практики, а после обучения вы сможете дополнить резюме весомой строчкой. Регистрируйтесь!
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
- Подбор параметров («Данные» – «Работа с данными» – «Анализ «что-если»» – «Подбор параметра») – находит значения, которые обеспечат нужный результат.
- Поиск решения (надстройка Microsoft Excel; «Данные» – «Анализ») – рассчитывает оптимальную величину, учитывая переменные и ограничения. Перейдите по ссылке и узнайте как подключить настройку «Поиск решения».
- Диспетчер сценариев («Данные» – «Работа с данными» – «Анализ «что-если»» – «Диспетчер сценариев») – анализирует несколько вариантов исходных значений, создает и оценивает наборы сценариев.
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» – 250 рублей. «3» – 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.
Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter – это обязательное условие для ввода массивов.

Скачать примеры
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
Лабораторная
работа Часть 1. Подбор параметра
Создайте таблицу
(цена и объем выбрать можете произвольно), а остальные столбцы рассчитайте по
формулам:
|
Курс |
55 |
|||
|
Наименование |
Цена в $ |
Объем заказа |
Сумма в $ |
Сумма в руб. |
|
оргтехника |
||||
|
ПК |
89 |
6 |
534 |
29 370,00 ₽ |
|
Ноутбуки |
69 |
10 |
690 |
37 950,00 ₽ |
|
Принтеры |
57 |
13 |
741 |
40 755,00 ₽ |
|
Ксероксы |
83 |
5 |
415 |
22 825,00 ₽ |
|
сканеры |
77 |
9 |
693 |
38 115,00 ₽ |
|
ИТОГО |
375 |
43 |
3073 |
169 015,00 ₽ |
Эта
таблица, в которой объемы заказов являются желаемыми. Видно, что итоговая сумма
169015,00 руб. Допустим у нас ограниченный бюджет на закупку оргтехники в
размере 150 000 руб. Возникает вопрос в том, что объем заказа нужно
сокращать.
Например, мы считаем
что для нас допустимым является уменьшить число принтеров. Чтобы автоматически
найти до какого количества можно сократить число принтеров, воспользуемся
«подбором» параметра.
Выделите ячейку с
объемом принтеров. Найдите функцию «подбор параметра» на вкладке «данные». Если
его нет, то через кнопку «Офис» и «параметры эксель» найдите эту функцию и
добавьте ее:

Далее запустив данную функцию увидите окно:

В котором нужно указать ячейку где
рассчитывается стоимость всего заказа. В поле «значение» установите значение
равное 150 000 (это помним ограничение по бюджету). Изменяемой ячейкой
естественно должна быть ячейка в которой указывает объем заказыаемых принтеров.
Нажмите Ок.
В итоге:

Видим, что число заказываемых принтеров 6.9,
следовательно не более 6 целых принтеров мы можем заказать , чтобы уложиться в
бюджет.
Задания. Теперь выполните подбор параметра для «курса валюты» при котором бы все
заявленные объемы могли быть приобретены в рамках данного бюджета в
150 000 руб. Также выполните подбор параметра для ячейки «цена ПК» при
которой можно было бы уложиться в указанный бюджет в размере 145 000 руб,
не изменяя исходных объемов заказа.
Часть
2. Расчет оптимальных значений (поиск оптимальных значений).
Необходимо решить задачу оптимизации. Возьмем
задачу линейного программирования, в которой есть целевая функция (критерий) Z, и три ограничения.
Условие
задачи: Завод производит два вида продукции:
велосипеды и мотоциклы. При этом цех по сборке велосипедов имеет мощность 100
тыс. штук в год, цех по сборке мотоциклов – 30 тыс. Одна группа механических
цехов завода может производить либо детали для 120 тыс. велосипедов, либо
детали для 40 тыс. мотоциклов, либо другую комбинацию деталей, ограниченную
этими данными. Другая группа механических цехов может выпускать детали либо для
80 тыс. велосипедов, либо для 60 тыс. мотоциклов, либо любую допустимую их
комбинацию. В результате реализации каждой тысячи велосипедов завод получает
прибыль в 2 тыс. рублей, а каждой тысячи мотоциклов – 3 тыс. рублей.
Математический
вид задачи:
![]() ,
,

![]() .
.
В
качестве переменных задачи естественно взять количества велосипедов и
мотоциклов, выпускаемых заводом в год (в тыс. штук): ![]() и
и ![]() .
.
В
екселе решение задачи будет выглядеть так:

В
итоге необходимо решить данную задачу средствами ексель. Воспользуемся
«надстройкой» называемой «поиск решения». «Поиск решения» должна быть во
вкладке «данные». Если ее нет. Установите ее, через кнопку «офис»-«параметры Ексель»-«надстройки». Здесь поиск решения будет
отображаться среди неактивных настроек:

Выберите ее и нажмите «перейти». Получим:

Выбираем «поиск решения». Ставим галочку и
нажимаем ОК. Далее происходит установка этой надстройки. Подождите.
Затем на вкладке данные появится возможность
вызвать данную функцию:

Запустите ее. Видим:

Здесь укажите тип задачи (максимизация или
минимизация) в нашем случае – максимизация примбыли, а в целевой ячейке,
укажите ячейку в которой рассчитывается целевая функция Z.
Это в нашем примере ячейка D1. В ней должна быть формула
для расчета целевой функции (обратите внимание, что она соответствует
математической записи задачи):
![]()
Где B4 и В5 это ячейки
для значений переменных х1 и х2:

Эти две ячейки (B4 и В5)
нужно указать здесь:
![]()
Далее в поле «Ограничение» указываем ячейки в
которых рассчитываются ограничения:

Формулы для ячеек с ограничениями:

Т.е. при добавлении ограничения, видим:

Где указыается ячейка для ограничения и
значение (число) чем значение ограничивается, в нашем случае 1 (см.
математическую запись задачи).
После того, как все ограничения введены
получим решения нажав «выполнить»
Видим:

Максимум прибыли равно 163.333. При этом нужно
выпускать 66.6 велосипедов, и 10 мотоциклов.
Решить задачи самостоятельно в ексель:
1. ![]() ,
,  ,
, ![]()
Ответ: ![]()
2. ![]() ,
,  ,
, ![]()
Ответ: ![]()
3. ![]() ,
,  ,
, ![]()
Ответ: ![]()
4. ![]() ,
,  ,
, ![]() .
.
5. ![]() ,
,  ,
,
