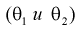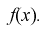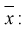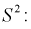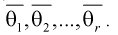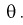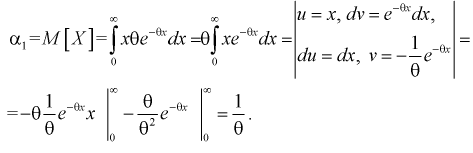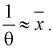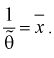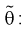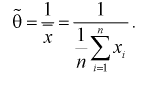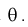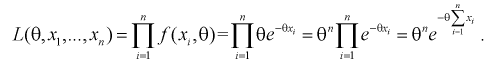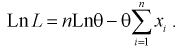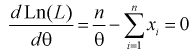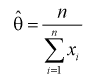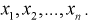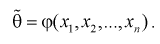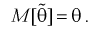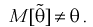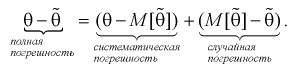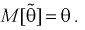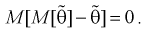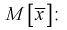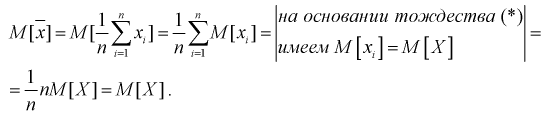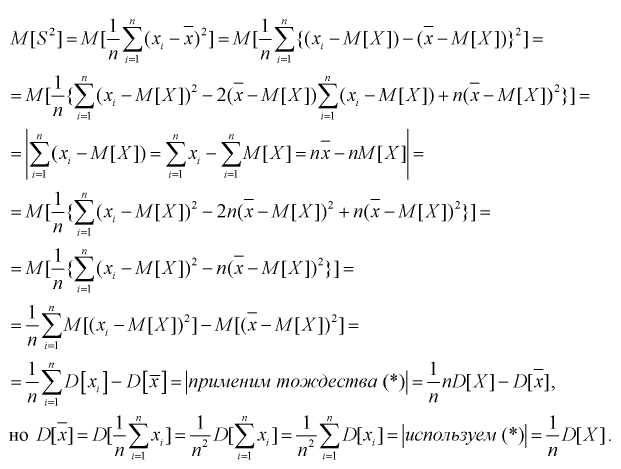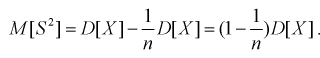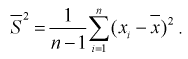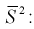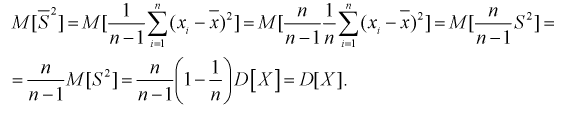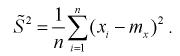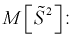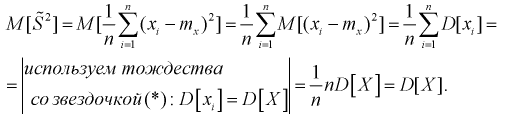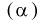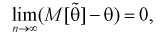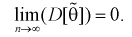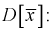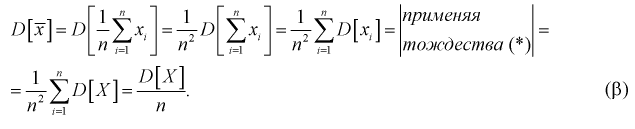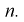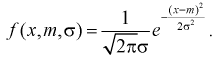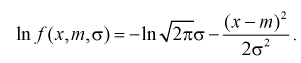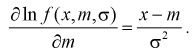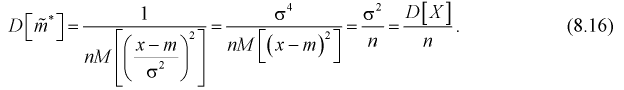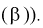Достаточные статистики и оптимальные оценки.
Если для любой оценки
из
класса
,
для любого
,
то оценку Т* называют оценкой с
равномерно минимальной дисперсией.
Такая оценка
называется оптимальной
оценкой.
Итак, T*
– оптимальная оценка для параметрической
функции
,
если
,
,
.
Статистика
называется
достаточной
для
параметрического семейства распределений
P=(или
достаточной для параметра
),
если условный закон распределения
выборки при условии, что статистика
T(X)
приняла некоторое фиксированное значение
t,
не зависит от параметра
.
Теорема
Рао-Блекуэлла-Колмогорова: Оптимальная
оценка, если она существует, является
функцией от достаточной статистики.
Теорема:
Если существует полная достаточная
статистика, то всякая функция от неё
является оптимальной оценкой своего
математического ожидания.
То есть оптимальная
оценка однозначно определяется уравнением
,
где Т – полная достаточная статистика,
H(T)
– произвольная функция от Т.
Функция
,
рассматриваемая при фиксированной
реализации выборки
как
функция от
,
называется функцией
правдоподобия.
Критерий
факторизации.
Для того, чтобы
статистика была достаточной для
параметрического семейства распределений
P,
необходимо и достаточно, чтобы функция
правдоподобия выборки
в
нём допускала следующее представление:
Где множитель h(x)
от
не зависит, а функция g(.)
от реализации выборки
зависит
через функцию T(x).
Если
при
возрастании θ, то в этом случае существует
одномерная достаточная статистика
Аналогично, если
при
возрастании θ, то одномерная достаточная
статистика существует и имеет вид
Этими двумя случаями
исчерпываются ситуации, когда в модели
существует одномерная достаточная
статистика.
Для модели
достаточной
статистикой является
,
а для моделей
и
минимальной
достаточной статистикой является T.
Оценка методом моменов .
Пусть неизвестный
параметр распределения наблюдаемой
случайной величины
векторный:
и у случайной величины
существует
конечный r-ый
момент:
Оценкой неизвестного
параметра
,
полученной методом моментов (ОММ),
называется вектор
,
где
есть решение системы
уравнений:
Теоретические
моменты, являющиеся функциями от
неизвестных параметров
,
приравниваются к
их статистическим аналогам – выборочным
моментам. Полученная система – это
система r
уравнений с r
переменными. Если решения системы
уравнений нет, оценки по методу моментов
не существует. Если имеется несколько
решений, то существует несколько таких
оценок. Если система уравнений имеет
единственное решение, то оценка по
методу моментов является состоятельной
оценкой параметра
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Виктория123 писал(а):
… чтобы доказать полноту, надо поссчитать мат.ожидание от какой то функции 


Да.
Пусть оптимальной оценкой
называется несмещенная оценка с равномерно минимальной дисперсией. В зависимости от программы, возможно несколько способов построения оптимальной оценки 
0. Угадать и проверить по определению.
1. Воспользоваться теоремой о том, что функция от полной достаточной статистики является оптимальной оценкой своего ожидания.
2. Воспользоваться критерием Бхаттачария.
Идя первым путем, Вы доказали достаточность. Для доказательства полноты, попробуйте воспользоваться его определением (приведите свое определение; используемое мною может отличаться от принятого у Вас в курсе). После этого, попробуйте подобрать функцию этой статистики, математическое ожидание которой равно, возможно с точностью до постоянного коэффициента, 
Добавлено
Виктория123 писал(а):
В семействе биномиальных распределений 
) оценку для параметрической функции
[Выделение цветом – GAA
]
Иногда, оптимальной
(в [1], и ряде других книг, принят термин эффективная
) называют несмещенную
оценку с равномерно минимальной дисперсией. Именно о построении такой оценки я писал выше.
[1] Боровков А.А. Математическая статистика. Оценка параметров, проверка гипотез. — М.: Наука, 1984.
14.4.1. Оптимальная оценка по критерию максимума апостериорной плотности.
Предположим теперь, что однородная независимая выборка 






где

Так как логарифм — монотонная функция, то точки экстремумов функции 



Если функция 



при условии

Для независимой выборки из (14.72) следует

Оценка максимальной апостериорной плотности вероятности состоятельная и асимптотическая эффективная. Распределение ее при 


Если априорное распределение случайного параметра 

и, следовательно, при этом оценка максимальной апостериорной плотности совпадает с оценкой максимального правдоподобия.
14.4.2. Байесовские оценки.
Предположим, что наряду с априорными данными, указанными в п. 14.4.1, задана также функция потерь 


Минимизация функционала (14.74) представляет задачу вариационного исчисления, Функционал 


Выбор функции потерь в известной мере субъективен и зависит от конкретной задачи оценивания параметра. Наиболее часто используются функции потерь, которые представляют четные функции ошибки 
Далее рассматриваются байесовские ошибки при функциях потерь указанного вида.
14.4.3. Простая функция потерь.
Рассмотрим функцию потерь, которая равна постоянной с для всех значений ошибок и дает бесконечный «выигрыш» при точном оценивании

Функция потерь (14.76) называется простой.
Подставляя (14.76) в (14.74), получаем

Из (14.77) следует, что байесовская оценка при простой функции потерь совпадает с оценкой максимальной апостериорной плотности вероятности оцениваемого параметра.
14.4.4. Квадратичная функция потерь.
При квадратичной функции потерь

апостериорный риск

Подставляя (14.79) в (14.75) и разрешая уравнение относительно функции 

или

Функцию правдоподобия 

где 
Из (14.80) следует, что байесовская оценка при квадратичной функции потерь представляет условное среднее значение оцениваемого параметра 


Условное среднее (14.80) является несмещенной оценкой параметра

и, следовательно, [см. (14.79)]

В отличие от простой функции потерь, для которой байесовская оценка определяется локальными свойствами апостериорной плотности вероятности оцениваемого параметра 

14.4.5. Функция потерь, равная модулю ошибки.
Для функции потерь

апостериорный риск

откуда согласно условию (14.75)

или

Из (14.84) следует, что байесовская оценка при функции потерь, равной модулю ошибки, совпадает с условной медианой оцениваемого параметра 

Если апостериорная плотность вероятности оцениваемого параметра унимодальна и симметрична относительно моды, то медиана и среднее значение этого распределения совпадают и равны его моде. В этом случае байесовские оценки при функции потерь, равной модулю ошибки, и при квадратичной функции потерь одинаковы и совпадают с оценкой максимальной апостериорной плотности вероятности.
14.4.6. Прямоугольная функция потерь.
Для функции потерь

апостериорный риск

откуда из (14.75) получаем следующее трансцендентное уравнение для определения байесовской оценки при прямоугольной функции потерь:

Если апостериорная плотность вероятности оцениваемого параметра унимодальна и симметрична относительно моды, то единственным решением уравнения (14.86) является такая оценка 
14.4.7. Симметричная функция потерь.
Рассмотрим произвольную функцию потерь, четную относительно ошибки и неубывающую при увеличении модуля ошибки

Все указанные в п.п. 14.4.3-14.4.6 функции потерь являются функциями такого вида. Предположим, что апостериорная плотность вероятности параметра 




Запишем уравнение (14.75)

Так как 


Поэтому величина 



потому что при выполнении равенства (14.89) подынтегральная функция становится нечетной функцией относительно новой переменной интегрирования 
Сравнивая (14.89) с (14.80), приходим к выводу, что байесовская оценка при квадратичной функции потерь является также байесовской оценкой при симметричной функции потерь для целого класса апостериорных плотностей оцениваемого параметра, удовлетворяющих условиям унимодальности и симметричности относительно моды.
14.4.8. Байесовские оценки векторного параметра.
Предположим, что однородная независимая выборка 







Апостериорный риск 



определяет необходимое условие экстремума этого функционала. Для простой функции потерь

апостериорный риск

При этом из (14.92) следует, что байесовская оценка векторного параметра 


Для квадратичной функции потерь

байесовские оценки компонент векторного параметра 

From Wikipedia, the free encyclopedia
In applied statistics, optimal estimation is a regularized matrix inverse method based on Bayes’ theorem.
It is used very commonly in the geosciences, particularly for atmospheric sounding.
A matrix inverse problem looks like this:
The essential concept is to transform the matrix, A, into a conditional probability and the variables, 

Derivation[edit]
Typically, one expects the statistics of most measurements to be Gaussian. So for example for 
where m and n are the numbers of elements in 





Here 



The nice thing about the Gaussian distributions is that only two parameters are needed to describe them and so the whole problem can be converted once again to matrices. Assuming that 






Because we are using Gaussians, the expected value is equivalent to the maximum likely value, and so this is also a form of maximum likelihood estimation.
Typically with optimal estimation, in addition to the vector of retrieved quantities, one extra matrix is returned along with the covariance matrix. This is sometimes called the resolution matrix or the averaging kernel and is calculated as follows:
This tells us, for a given element of the retrieved vector, how much of the other elements of the vector are mixed in. In the case of a retrieval of profile information, it typical indicates the altitude resolution for a given altitude. For instance if the resolution vectors for all the altitudes contain non-zero elements (to a numerical tolerance) in their four nearest neighbours, then the altitude resolution is only one fourth that of the actual grid size.
References[edit]
- Clive D. Rodgers (1976). “Retrieval of Atmospheric Temperature and Composition From Remote Measurements of Thermal Radiation”. Reviews of Geophysics and Space Physics. 14 (4): 609. doi:10.1029/RG014i004p00609.
- Clive D. Rodgers (2000). Inverse Methods for Atmospheric Sounding: Theory and Practice. World Scientific.
- Clive D. Rodgers (2002). “Atmospheric Remote Sensing: The Inverse Problem”. Proceedings of the Fourth Oxford/RAL Spring School in Quantitative Earth Observation. University of Oxford.
Содержание:
Оценки и методы их получения:
Приближенные значения параметров, входящих в законы распределения, определяемые каким-либо способом по выборкам, называются оценками или статистиками. Оценки бывают точечными и интервальными. Точечные оценки представляются одним числом, интервальные – двумя числами
Метод моментов
Пусть генеральная случайная величина X имеет плотность распределения
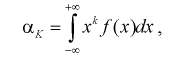
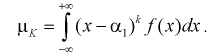
По выборке 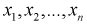
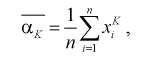
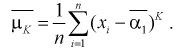
Метод моментов состоит в том, что генеральные моменты (8.1, 8.2), в которые входят оцениваемые параметры, приблизительно приравниваются к соответствующим выборочным моментам (8.3), (8.4). Составляется система уравнений:
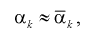
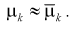
Решая систему (8.5), (8.6), находим оцениваемые параметры.
Особо важную роль играет 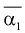
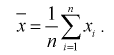
Следующим по важности выборочным моментом является выборочный центральный момент 2-го порядка 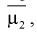
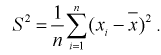
Наиболее часто используются две формулы метода моментов.
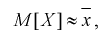
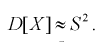
Сформулируем метод моментов в общем виде.
Пусть 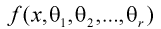
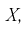
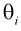
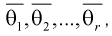
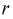
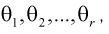
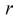
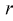
Пример:
Пусть генеральная случайная величина X имеет показательный закон распределения с плотностью 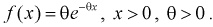
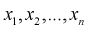
1. Определяем 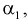
2. По (8.3) или (8.7) находим выборочный начальный момент 1-го порядка или 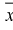
3. Заменяя в п. 2 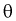
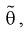
4. Откуда определим оценку параметра
Метод наибольшего правдоподобия
Этот метод предложен математиком Фишером в 1912 г.
Пусть 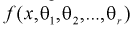
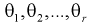
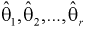
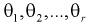
Для непрерывной случайной величины
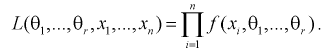
Для дискретной случайной величины
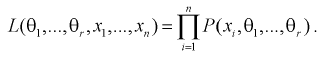
Здесь 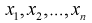
Априорные выборочные значения 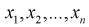
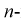
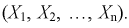
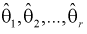
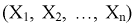
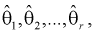
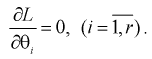
Так как функция и ее логарифм достигают экстремума в одной точке, то часто для упрощения решения задачи используют логарифмическую функцию правдоподобия. В случае логарифмической функции правдоподобия составляется система следующих уравнений:
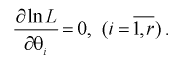
Пример:
Пусть генеральная случайная величина X имеет показательный закон распределения с плотностью 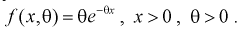
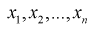
1. Так как нам необходимо оценить один параметр 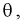
2. Составим логарифмическую функцию правдоподобия:
3. Для определения максимума логарифмической функции правдоподобия составляем и решаем следующее уравнение:
Откуда оценка 0 параметра 0 определяется так:
При сравнение это выражение с оценкой 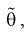
Свойства оценок
Пусть 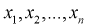
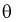
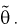
Так как любая выборка типа 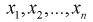
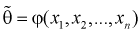
1. Оценка 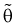
В противном случае оценка называется смещенной.
Полную погрешность 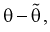
Таким образом, если оценка несмещенная, то систематическая погрешность равна нулю, т. е.
Наиболее опасна систематическая ошибка, если она заранее неизвестна или среднее квадратичное отклонение не очень большое. Среднее значение случайной ошибки
Мы уже отмечали, что 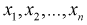
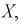
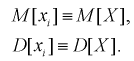
Проверим смещенность оценки математического ожидания выборочной средней 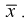
Обозначим 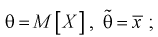
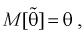
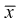
Проверим смещенность оценки дисперсии выборочной дисперсией 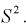
То есть дисперсия выборочной средней в 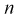
Обозначим 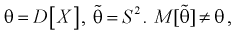
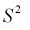
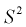
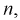
При решении практических задач часто используется несмещенная оценка дисперсии – это модифицированная выборочная дисперсия:
Найдем математическое ожидание от
Обозначим 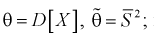
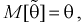
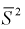
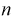
Найдем
Обозначим 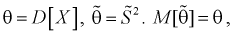
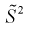
2. Оценка 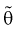
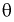
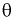
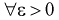
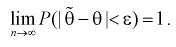
Условие 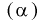
а)
б)
Как видим, оценка 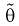
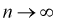
Пример:
Проверим состоятельность оценки математического ожидания выборочной средней 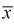
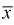
Видим, что при 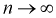
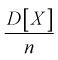
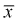
3. Несмещенная оценка 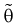
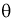
Для определения наименьшей дисперсии эффективной оценки 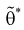
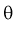
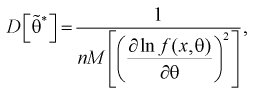
где 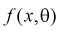
Отметим, если оценка 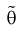
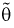
Пример:
Задана нормальная случайная величина 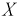
Проверим эффективность оценки математического ожидания выборочной средней 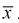
Найдем дисперсию эффективной оценки параметра 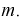
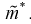
Найдем производную:
Подставим полученное выражение в (8.15):
Ранее мы показали, что такую же дисперсию имеет 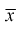
Видим, что правые части формул (8.16) и 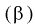
Отметим, что оценки, полученные методом наибольшего правдоподобия, являются состоятельными. Если существуют эффективная оценка, то метод наибольшего правдоподобия позволяет найти ее, но не всегда оценки, полученные этим методом, являются несмещенными.
- Теория статистической проверки гипотез
- Линейный регрессионный анализ
- Вариационный ряд
- Законы распределения случайных величин
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Статистическая проверка гипотез
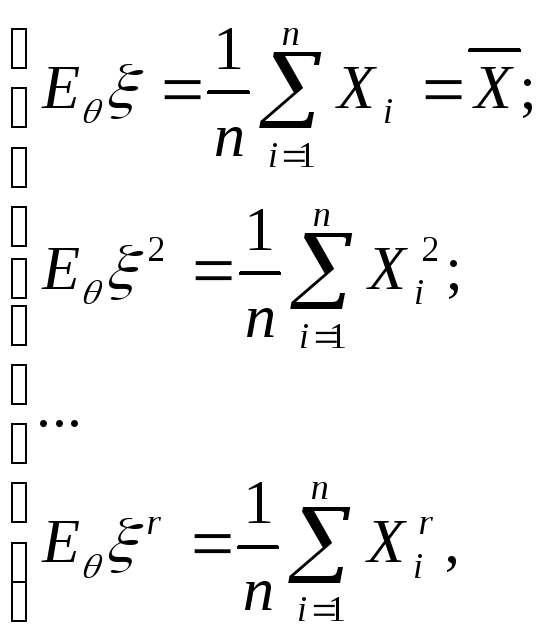


![P(vec y|vec x) = frac {1} {(2 pi)^{m n/2} | boldsymbol{S_y}|}
exp left [ -frac{1}{2} (boldsymbol{A} vec{x} - vec{y})^T
boldsymbol {S_y}^{-1}
(boldsymbol{A} vec{x} - vec{y}) right ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2f191f37ccb7c58571658ce7baa6aa772b8d300)
![P(vec x) = frac {1} {(2 pi)^{m/2} | boldsymbol {S_{x_a}}|}
exp left [-frac {1}{2} (vec{x}-widehat{x_a})^T
boldsymbol {S_{x_a}}^{-1} (vec{x}-widehat{x_a}) right ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b771725bb9ca3d58a99621e5561eef14d9bfbe99)
![P(vec x|vec y) = frac {1} {(2 pi)^{m n/2} | boldsymbol {S_x} |}
exp left [ -frac{1}{2} (vec{x} - widehat{x}) ^T
boldsymbol {S_x}^{-1} (vec{x} - widehat{x}) right ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51116a3995d5c9920e45ccdabae128f8c9c6e67a)