Как найти оптимальную стратегию в смешанных стратегиях

1. Понятие о частоте
применения разных стратегий.

2. Матричный метод
определения оптимальных смешанных
стратегий и цены игры для игр 2х2.

3. Графический
метод решения игр 2хm
и 3хm.

1.
Итак, на прошлой лекции мы выяснили, что
большинство игр с нулевой суммой не
поддается простому и красивому решению
в чистых стратегиях. Конечно, путем
исключения доминируемых и дублирующих
стратегий иногда удается существенно
уменьшить матрицу игры. И если удалось
ее свести к одной строке или одному
столбцу – игра решена в чистых стратегиях
даже без принципа минимакса и нахождения
седловой точки. Но чаще приходится
признать, что ни одна из чистых стратегий
не является оптимальной. Выход из этой
казалось бы тупиковой ситуации тем не
менее существует – надо чередовать
стратегии в определенной пропорции.
Поэтому решением игры в этом случае
является как раз такая пропорция.
Например, если у игрока 3 чистых стратегии
и мы после определенных расчетов говорим
– ему надо использовать эти стратегии
в пропорции 5:1:4. В принципе, здесь могут
стоять любые натуральные числа или даже
ноль. В последнем случае говорят, что
соответствующая стратегия не используется
в смеси стратегий и является неактивной.
Те же, которые используются, называют
активными
стратегиями.
А само поведение игрока, связанное с
чередованием его стратегий, называют
смешанной
стратегией.
Основная
теорема теории игр
(она же теорема Неймана или теорема о
минимаксе) гласит: любая
парная игра с нулевой суммой имеет
решение в чистых или смешанных стратегиях.
Это решение определяет оптимальные
минимаксные стратегии игроков и цену
игры. Использование любой другой
стратегии в среднем менее выгодно
каждому из игроков. Цена игры всегда
находится между нижней и верхней ценой
матрицы игры. Решение в чистых стратегиях
– это просто частный случай решения в
смешанных стратегиях (когда в смеси
активна лишь одна стратегия).

Если
смешанная стратегия выражена в виде
пропорции, то стоящие в ней числа называют
относительными частотами применения
стратегий. Существует и другой способ
задания смешанной стратегии – через
вероятности реализации чистых стратегий.
Их легко рассчитать по известным
относительным частотам. Пусть например
задана смесь четырех стратегий в виде
пропорции N₁:
N₂:
N₃:
N₄.
Тогда вероятность реализации первой
стратегии равна:

р₁
= N₁/(
N₁+
N₂+
N₃+
N₄)

Аналогично
рассчитываются и остальные 3 вероятности
р₂,
р₃,
р₄.
Естественно, что сумма всех вероятностей
в этом случае равна 1. На самом деле мы
довольно часто сталкиваемся с такого
рода понятиями. Например, при игре в
русскую рулетку, когда в 6-зарядный
барабан револьвера вставляется один
патрон и выстрел производится после
вращения барабана – реализуется смесь
двух стратегий (убить – не убить) с
относительными частотами 1:5, а вероятность
рокового выстрела – 1/6. Или когда в годы
репрессий давали разнарядку типа
«каждого десятого» – это тоже смешанная
стратегия с частотами 1:9.

Если
действия по реализации стратегий
производятся многократно, то вполне
достаточно буквального использования
относительных частот. Например, если
работнику консульского отдела
рекомендована смесь 2-х стратегий (выдать
– не выдать визу) с частотами 2:3, то он
может первым двум посетителям оформить
визу, следующим 3-м – отказать и т.д. Но
при этом он рискует тем, что посетители
его «просчитают» и будут заранее знать
кому он не откажет. Поэтому в теории игр
обычно используется другой способ,
который в принципе исключает возможность
знать следующий ход. Он основан на
вероятностном подходе и связан с
использованием датчика
случайных чисел.
Такие датчики есть во многих компьютерных
программах, хотя на практике чаще
используют подручные средства типа
бросания монетки или игральной кости.
Например, при частотах 1:2 надо при каждом
ходе бросать кубик и применять первую
стратегию, когда выпадет 1 или 2, а в
остальных случаях – использовать вторую
стратегию. Любые вычислительные методы,
использующие датчик случайных чисел,
принято называть методами
Монте-Карло.
Заметим, что по
методу Монте-Карло
можно реализовать смешанную стратегию
даже в одноходовой игре, которыми обычно
и являются игры, представленные в
нормальной форме. Осталось понять, как
найти оптимальную смесь стратегий.

2.Итак,
допустим, что проверка на наличие
седловой точки в игровой матрице дала
отрицательный результат. Тогда выполняется
процедура выбраковки доминируемых и
дублирующих стратегий. Если при этом
получилась матрица 2х2, то можно вздохнуть
спокойно – решение в смешанных стратегиях
удастся найти сравнительно просто. В
противном случае элементарного решения
нет, придется потрудится. Причем объем
вычислений резко увеличивается для
матриц большой размерности и в этом
случае используют приближенные методы
решения игр. Отчасти поэтому в литературе
обычно рассматриваются именно игры
2х2.

Пример
10. Игра «наступление и оборона»

Обороняющая
сторона защищает 2 объекта, причем один
из них в 3 раза важнее другого. Сил
достаточно только на охрану одного из
объектов, причем при нападении на
охраняемый объект побеждает оборона.
У нападения тоже сил достаточно только
для атаки одного объекта. Спрашивается
– какой из объектов надо охранять и на
какой надо нападать. Это типичная парная
игра 2х2. Первая стратегия обороны –
защитить важный объект, вторая – защитить
не важный. Аналогично и у нападения –

Первая
стратегия напасть на важный объект и
вторая – на второстепенный. С учетом
важности объектов получаем матрицу
игры (первый игрок – оборона):

Элементы
матрицы равны суммарной важности
уцелевших после нападения объектов.

Ищем
минимаксные стратегии и седловую точку.

4 3 | 3*

1
4 | 1

_____

4
4

*
*

Как
видим, седловой точки нет, хотя у второго
игрока даже 2 минимаксные стратегии.
Нижняя цена игры равна 3, верхняя – 4.
Чтобы найти решение в смешанных
стратегиях, в случае произвольной
матрицы 2х2 надо просто вычесть второй
столбец матрицы из первого. Отношение
двух полученных разностей (независимо
от их знаков) равно оптимальному
соотношению применения первым игроком
второй и первой стратегий. Аналогично
потом вычитают вторую строку исходной
матрицы из первой, отношение полученных
разностей задает оптимальное отношение
частоты применения вторым игроком его
второй и первой стратегий. Обратим
внимание – отношение первой разности
ко второй равно в обоих случаях отношению
частот именно второй и первой стратегий
(а не наоборот) в оптимальной смеси. В
данном случае получаем разность столбцов
вида:

1

-3

Поэтому
обороне надо использовать стратегии с
частотами 3:1, то есть в 3 раза чаще охранять
важный объект. Разность строк дает: (3
-1), значит у нападения относительные
частоты применения чистых стратегий
1:3. Нападать получается чаще надо на
менее важный объект.

Пример
11

Матрица
игры имеет вид:

Седловой
точки тоже нет. Вычитание столбцов дает
(4, -9). Поэтому первый игрок должен
применять свои первую и вторую стратегии
в пропорции 9:4. Разность строк дает (5,
-8), то есть второй игрок применяет свои
стратегии с частотой 8:5.

Этот
метод строго выводится из условия
неизменности средней цены игры в случае
применения первым игроком оптимальной
смеси стратегий, а вторым – чистой 1-й и
2-й стратегий. Независимость выигрыша
первого игрока при его оптимальной игре
от выбора той или иной смеси активных
стратегий вторым игроком следует из
теоремы об активных стратегиях. Это
обстоятельство позволяет кстати
рассчитать и цену игры – достаточно от
частот перейти к вероятностям стратегий
и воспользоваться формулой:

ν
= р₁а₁₁
+ р₂а₂₁

Здесь
а₁₁
и а₂₁
– элементы первого столбца матрицы
игры. С таким же успехом можно использовать
и элементы второго столбца – результат
будет тот же. В примере 1 р₁
= ¾ и р₂
= ¼, поэтому:

ν
= 0.75*4 + 0.25*1 = 3,25.

Повтор
с использованием второго столбца дает
тот же результат:

ν
= 0.75*3 + 0.25*4 = 3,25.

Заметим,
что это число действительно находится
между верхней и нижней ценой игры.

3.
Существует и другой – графический метод
решения игр, который применим не только
к играм 2х2, но и к играм, в которых у
второго игрока число стратегий m
> 2 (их называют играми 2хm). Метод состоит
в построении графиков зависимости
выигрыша от пропорции, в которой смешаны
2 стратегии первого игрока. Рассмотрим
матрицу игры а_ij
размерности 2хm. Пусть у первого игрока
доля (вероятность) первой стратегии в
смеси равна х, тогда доля второй (1-х).
Если второй игрок использует чистую
первую стратегию, то выигрыш первого
составит:

х*а₁₁
+ (1-х)*а₂₁
= а₂₁
+ (а₁₁
– а₂₁)х

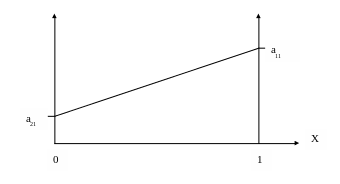
На
графике этой функции соответствует
прямая, у которой ордината равна а₂₁

при
х=0 и а₁₁
при х=1:

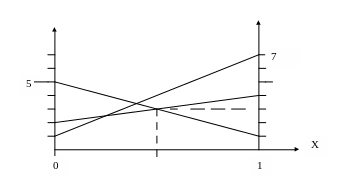
Если
у второго игрока 3 стратегии (m = 3), то на
таком графике будет 3 линии. Каждая из
них строится аналогично – на левой оси
откладывается значение a2j , а на правой
a1j. Например, при матрице:

слева
откладываются 2, 1, 5, а справа 4, 7, 1, после
чего соответствующие точки на обеих
осях соединяются (см.рис.).

Другими
словами – слева откладывают числа со
второй строки матрицы, справа – с первой.
Ясно, что противник выберет такие
стратегии, чтобы ваш выигрыш был меньше.
На графике этому соответствует нижняя
ломаная линия из трех отрезков. А вы
выберете на ней максимум (откуда опущен
пунктир на ось). Абсцисса этой точки
соответствует оптимальной доли первой
стратегии х для первого игрока, а ее
ордината равна цене игры. Оптимальная
смесь стратегий второго игрока
определяется потом путем дополнительных
расчетов, хотя сразу можно сказать, что
противнику следует использовать только
те стратегии, линии которых проходят
через выделенную точку (первая и третья
в данном случае). Поэтому можно просто
вычеркнуть второй столбец из матрицы
и для оставшейся матрицы 2х2 найти
решение.

Игры
3хm (у первого игрока 3 стратегии) решаются
аналогично в трехмерном пространстве.
При этом каждой чистой стратегии второго
игрока теперь соответствует не прямая,
а плоскость. Эти плоскости образуют
конструкцию типа крыши и надо сначала
выделить самую нижнюю «крышу», а потом
найти координаты ее верхней точки.

Приближенно
можно решить любую матричную игру,
используя средство «Поиск решения» в
меню «Сервис» программы EXCEL. Пусть у
первого игрока n стратегий, а у второго
m. Надо найти оптимальные доли стратегий
р_i
в их смеси для первого игрока. Обозначим
цену игры ν, тогда при использовании
противником любой из его m стратегий
выигрыш первого игрока будет не меньше
ν. Выразив этот выигрыш через р_i
и элементы матрицы игры, получим
соответствующие m неравенств вида:

a_1j
p₁
+ a_2j
p₂
+ … + a_nj
p_n
≥ ν

Если
обе части разделить на ν и обозначить
х_j
= p_j/ν,
то неравенства преобразуются к виду:

a_1j
х₁
+ a_2j
х₂
+ … + a_nj
х_n
≥ 1 ( 1 )

Кроме
того должно выполняться условие на
сумму всех долей:

p₁
+ p₂
+ … + p_n
= 1,

которое
для переменных х имеет вид:

х₁
+ х₂
+ … + х_n
= 1/ν . ( 2 )

Так
как первый игрок стремится повысить
цену игры, последнюю сумму можно
рассматривать как функцию цели и решать
задачу по нахождению оптимальных
значений переменных х_j,
на которые наложено ограничение (1). С
этой целью на рабочем листе EXCEL для
каждой переменной х_j,
заводим по ячейке и записываем туда
некоторые начальные значения,
соответствующие ограничениям (1).
Например, это могут быть просто нули и
единицы. После этого в одной из ячеек
задаем х₁
+ х₂
+ … + х_n
и указываем имя этой ячейки в меню
«Поиск решения» на месте функции цели.
Указываем также поиск минимума функции.
Потом задаем платежную матрицу опять
же на рабочем листе и через имена
соответствующих ячеек выражаем
ограничения на значения х. Для этого
заводим ячейки на рабочем листе для
вычисления левых частей неравенств
(1), после чего в «Поиске решения» указываем
в левой части имена этих ячеек, потом
знак ≥, потом в правой части 1. Указывается
также ограничение на знак величин х_j
≥ 0, при этом опять в левой части
указывается только имя ячейки,
соответствующей х_j.
Далее дается команда «Найти» и в ячейках
для х_j
появляются оптимальные значения. Их
сумма позволяет найти цену игры, пользуясь
(2), после чего находятся и сами оптимальные
доли стратегий в смеси р_j
= х_j
* ν. Аналогично находится оптимальная
смесь стратегий второго игрока, только
теперь потребуется максимизировать
функцию цели.

Вопросы:

1. Как
   достигается смешивание стратегий в
   одноходовой игре?

2. В
   чем состоит основная теорема теории
   игр?

3. Как
   зависит выигрыш игрока, избравшего
   оптимальную смешанную стратегию, от
   использования активных стратегий
   вторым игроком (теорема об активных
   стратегиях)?

4. Что
   надо проверить до того как приступить
   к решению игры в смешанных стратегиях?

5. Какие
   игры решаются в смешанных стратегиях
   точно, а какие – приближенно?

6. Определение
   выигрыша при заданной смешанной
   стратегии у одного игрока и чистой
   стратегии – у другого.

7. Определение
   выигрыша при заданных смешанных
   стратегиях обоих игроков, в том числе
   в биматричной игре.

8. Решение
   игры 2х2 (определение ее цены и оптимальной
   смеси стратегий первого игрока).

9. Решение
   игры 2хm графическим методом (определение
   цены игры, оптимальной смеси стратегий
   1-го игрока и активных стратегий 2-го
   игрока).

10. Приближенное
    решение игры с произвольной прямоугольной
    платежной матрицей (определение цены
    игры и оптимальной смеси стратегий
    1-го игрока).

Литература:

Учебные пособия
и монографии:

1. Вильямс
   Дж.Д. Совершенный стратег или букварь
   по теории стратегических игр: Пер. с
   англ. – М.: Советское радио, 1960. – 269 с.

2. Данилов
   В. Лекции по теории игр: Конспект лекций.
   – М.: Российская экономическая школа,
   2002. – 140 с.

3. Льюис
   Р.Д., Райфа Х. Игры и решения: Пер. с англ.
   – М.: Издательство иностранной литературы,
   1961. – 642 с.

4. Матвеев
   В.А. Конечные бескоалиционные игры и
   равновесия: Учебное пособие. Псков,
   2005. – 176 с.

5. Печерский
   С.Л., Беляева А.А. Теория игр для
   экономистов: Вводный курс: Учебное
   пособие. – СПб.: Изд-во европейского
   университета в Санкт-Петербурге, 2001. –
   253 с.

6. Augenstein
   Bruno W. A brief history of RAND’s Mathematics Department and Some
   of Its Accomplishments. Rand
   Corporation, 1993.

7. Brams
   Steven J. Game Theory and Politics. Dover Publications, 2004.

8. Dixit
   A., Skeath S. Games of Strategy. W.W.Norton & Company, 1999.

9. Dresher
   M. Games of Strategy. Theory and Application. Prentice-Hall, Inc.,
   1961.

10. Robinson
    Thomas W. Game Theory and Politics: Recent Soviet Views. Rand
    Corporation, 1970.

Статьи в
периодических изданиях:

1. Allan
   P., Dupont C. International Relations Theory and Game Theory:
   Baroque Modeling Choices and Empirical Robustness. International
   Political Science Review
   (1999), Vol. 20, No. 1, pp.23–47.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Если матричная игра содержит седловую точку, то ее решение находится по принципу минимакса. Если же платежная матрица не имеет седловых точек, то применение минимаксных стратегий каждым из игроков показывает, что игрок I обеспечит себе выигрыш не меньше a, а игрок II обеспечит себе проигрыш не больше b. Так как a < b, то игрок I стремится увеличить выигрыш, а игрок II уменьшить проигрыш. Если информация о действиях противной стороны будет отсутствовать, то игроки будут многократно применять чистые стратегии случайным образом с определенной вероятностью. Такая стратегия в теории игр называется смешанной стратегией. Смешанная стратегия игрока — это полный набор его чистых стратегий при многократном повторении игры в одних и тех же условиях с заданными вероятностями. Для применения смешанных стратегий должны быть следующие условия:

1) в игре отсутствует седловая точка;

2) игроками используется случайная смесь чистых стратегий с соответствующими вероятностями;

3) игра многократно повторяется в одних и тех же условиях;

4) при каждом из ходов один игрок не информирован о выборе стратегии другим игроком;

5) допускается осреднение результатов игр.

Основная теорема теории игр Дж. фон Неймана: Любая парная конечная игра с нулевой суммой имеет, по крайней мере, одно решение, возможно среди смешанных стратегий.

Отсюда следует, что каждая конечная игра имеет цену, которую обозначим через g, средний выигрыш, приходящийся на одну партию, удовлетворяющий условию a £ g £ b. Каждый игрок при многократном повторении игры, придерживаясь смешанных стратегий, получает более выгодный для себя результат. Оптимальное решение игры в смешанных стратегиях обладает следующим свойством: каждый из игроков не заинтересован в отходе от своей оптимальной смешанной стратегии, если его противник применяет оптимальную смешанную стратегию, так как это ему невыгодно.

Чистые стратегии игроков в их оптимальных смешанных стратегиях называются Активными.

Теорема об активных стратегиях. Применение оптимальной смешанной стратегии обеспечивает игроку максимальный средний выигрыш (или минимальный средний проигрыш), равный цене игры G, независимо от того, какие действия предпринимает другой игрок, если только он не выходит за пределы своих активных стратегий.

Смешанные стратегии игроков S1 и S2 обозначим соответственно A1 , A2 , … Am и B1 , B2 , B3 … Bn, а вероятности их использования через pA = (p1, p2, …, pm) и qB = (q1, q2, …, qn), где pi ³ 0, qj ³ 0, при этом .

Тогда смешанная стратегия игрока I — SI, состоящая из стратегий A1, A2, …, Am, имеет вид:

.

Соответственно для игрока II:

.

Зная матрицу А для игрока I можно определить средний выигрыш (математическое ожидание) :

,

Игрок I, применяя свои смешанные стратегии, стремится увеличить свой средний выигрыш, достигая

.

Игрок II добивается:

.

Обозначим через и векторы, соответствующие оптимальным смешанным стратегиям игроков I и II, при которых выполняется равенство:

.

При этом выполняется условие:

Решить игру — это означает найти цену игры и оптимальные стратегии.

Рассмотрим наиболее простой случай конечной игры 2 ´ 2 без седловой точки с матрицами:

,

С платежной матрицей

.

Требуется найти оптимальные смешанные стратегии игроков , и цену игры g.

Каковы бы ни были действия противника, выигрыш будет равен цене игры g. Это означает, что если игрок I придерживается своей оптимальной стратегии , то игроку II нет смысла отступать от своей оптимальной стратегии .

В игре 2 ´ 2, не имеющей седловой точки, обе стратегии являются активными.

Для игрока I имеем систему уравнений:

Для игрока II аналогично:

Если g ¹ 0 и игроки имеют только смешанные оптимальные стратегии, то определитель матрицы не равен нулю, следовательно, эти системы имеют единственное решение.

Решая систему уравнений (10) и (11) находим оптимальные ешения, и g:

Пример: Дана платежная матрица:

Найти решение.

Решение. Так как a = 3, b = 5, то a ¹ b, то и матрица игра не имеет седловой точки. Следовательно, решение ищем в смешанных стратегиях. Запишем системы уравнений:

Для игрока I:

Для игрока II:

Решив эти системы находим:

Следовательно оптимальные стратегии игроков имеют вид:

,

Время на прочтение
18 мин

Количество просмотров 29K

Теория игр — математическая дисциплина, рассматривающая моделирование действий игроков, которые имеют цель, заключающуюся в выбор оптимальных стратегий поведения в условиях конфликта. На Хабре эта тема уже освещалась, но сегодня мы поговорим о некоторых ее аспектах подробнее и рассмотрим примеры на Kotlin.

Так вот, стратегия – это совокупность правил, определяющих выбор варианта действий при каждом личном ходе в зависимости от сложившейся ситуации. Оптимальная стратегия игрока – стратегия, обеспечивающая наилучшее положение в данной игре, т.е. максимальный выигрыш. Если игра повторяется неоднократно и содержит, кроме личных, случайные ходы, то оптимальная стратегия обеспечивает максимальный средний выигрыш.

Задача теории игр – выявление оптимальных стратегий игроков. Основное предположение, исходя из которого находятся оптимальные стратегии, заключается в том, что противник (или противники) не менее разумен, чем сам игрок, и делает все для того, чтобы добиться своей цели. Расчет на разумного противника – лишь одна из потенциальных позиций в конфликте, но в теории игр именно она кладется в основу.

Существуют игры с природой в которых есть только один участник, максимизирующий свою прибыль. Игры с природой – математические модели, в которых выбор решения зависит об объективной действительности. Например, покупательский спрос, состояние природы и т.д. «Природа» – это обобщенное понятие не преследующего собственных целей противника. В таком случае для выбора оптимальной стратегии используется несколько критериев.
Различают два вида задач в играх с природой:

1. задача о принятии решений в условиях риска, когда известны вероятности, с которыми природа принимает каждое из возможных состояний;
2. задачи о принятии решений в условиях неопределенности, когда нет возможности получить информацию о вероятностях появления состояний природы.

Кратко об этих критериях рассказано здесь.

Сейчас мы рассмотрим критерии принятия решений в чистых стратегиях, а в конце статьи решим игру в смешанных стратегиях аналитическим методом.

Постановка задачи

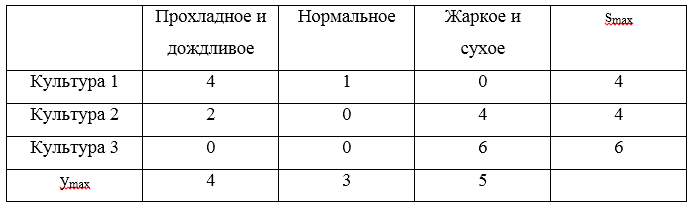
Все критерии принятия решений мы разберем на сквозном примере. Задача такова: фермеру необходимо определить, в каких пропорциях засеять свое поле тремя культурами, если урожайность этих культур, а, значит, и прибыль, зависят от того, каким будет лето: прохладным и дождливым, нормальным, или жарким и сухим. Фермер подсчитал чистую прибыль с 1 гектара от разных культур в зависимости от погоды. Игра определяется следующей матрицей:

Далее эту матрицу будем представлять в виде стратегий:

Искомую оптимальную стратегию обозначим

. Решать игру будем с помощью критериев Вальда, оптимизма, пессимизма, Сэвиджа и Гурвица в условиях неопределенности и критериев Байеса и Лапласа в условиях риска.

Как и говорилось выше примеры будут на Kotlin. Замечу, что вообще-то существуют такие решения как Gambit (написан на С), Axelrod и PyNFG (написанные на Python), но мы будем ехать на своем собственном велосипеде, собранном на коленке, просто ради того, чтобы немного потыкать стильный, модный и молодежный язык программирования.

Чтобы программно реализовать решение игры заведем несколько классов. Сначала нам понадобится класс, позволяющий описать строку или столбец игровой матрицы. Класс крайне простой и содержит список возможных значений (альтернатив или состояний природы) и соответствующего им имени. Поле key будем использовать для идентификации, а также при сравнении, а сравнение понадобится при реализации доминирования.

import java.text.DecimalFormat
import java.text.NumberFormat

open class GameVector(name: String, values: List<Double>, key: Int = -1) : Comparable<GameVector> {

    val name: String
    val values: List<Double>
    val key: Int

    private val formatter:NumberFormat = DecimalFormat("#0.00")

    init {
        this.name = name;
        this.values = values;
        this.key = key;
    }

    public fun max(): Double? {
        return values.max();
    }

    public fun min(): Double? {
        return values.min();
    }

    override fun toString(): String{
        return name + ": " + values
                .map { v -> formatter.format(v) }
                .reduce( {f1: String, f2: String -> "$f1   $f2"})
    }

    override fun compareTo(other: GameVector): Int {
        var compare = 0
        if (this.key == other.key){
            return compare
        }
        var great = true
        for (i in 0..this.values.lastIndex){
            great = great && this.values[i] >= other.values[i]
        }
        if (great){
            compare = 1
        }else{
            var less = true
            for (i in 0..this.values.lastIndex){
                less = less && this.values[i] <= other.values[i]
            }
            if (less){
                compare = -1
            }
        }
        return compare
    }
}

Игровая матрица содержит информацию об альтернативах и состояниях природы. Кроме того в ней реализованы некоторые методы, например нахождение доминирующего множества и чистой цены игры.

open class GameMatrix(matrix: List<List<Double>>, alternativeNames: List<String>, natureStateNames: List<String>) {
    val matrix: List<List<Double>>
    val alternativeNames: List<String>
    val natureStateNames: List<String>

    val alternatives: List<GameVector>
    val natureStates: List<GameVector>

    init {
        this.matrix = matrix;
        this.alternativeNames = alternativeNames
        this.natureStateNames = natureStateNames

        var alts: MutableList<GameVector> = mutableListOf()
        for (i in 0..matrix.lastIndex) {
            val currAlternative = alternativeNames[i]
            val gameVector = GameVector(currAlternative, matrix[i], i)
            alts.add(gameVector)
        }
        alternatives = alts.toList()

        var nss: MutableList<GameVector> = mutableListOf()
        val lastIndex = matrix[0].lastIndex // нет провеврки на равенство длин всех строк, считаем что они равны
        for (j in 0..lastIndex) {
            val currState = natureStateNames[j]
            var states: MutableList<Double> = mutableListOf()
            for (i in 0..matrix.lastIndex) {
                states.add(matrix[i][j])
            }
            val gameVector = GameVector(currState, states.toList(), j)
            nss.add(gameVector)
        }
        natureStates = nss.toList()
    }

    open fun change (i : Int, j : Int, value : Double) : GameMatrix{
        var mml = this.matrix.toMutableList()

        var rowi = mml[i].toMutableList()
        rowi.set(j, value)

        mml.set(i, rowi)

        return GameMatrix(mml.toList(), alternativeNames, natureStateNames)
    }

    open fun changeAlternativeName (i : Int, value : String) : GameMatrix{
        var list = alternativeNames.toMutableList()
        list.set(i, value)

        return GameMatrix(matrix, list.toList(), natureStateNames)
    }

    open fun changeNatureStateName (j : Int, value : String) : GameMatrix{
        var list = natureStateNames.toMutableList()
        list.set(j, value)

        return GameMatrix(matrix, alternativeNames, list.toList())
    }

    fun size() : Pair<Int, Int>{
        return Pair(alternatives.size, natureStates.size)
    }

    override fun toString(): String {
        return "Состояния природы:n" +
            natureStateNames.reduce { n1: String, n2: String -> "$n1;n$n2" } +
            "nМатрица игры:n" +
            alternatives
                .map { a: GameVector -> a.toString() }
                .reduce { a1: String, a2: String -> "$a1;n$a2" }
    }

    protected fun dominateSet(gvl: List<GameVector>, list: MutableList<String>, dvv: Int) : MutableSet<GameVector>{
        var dSet: MutableSet<GameVector> = mutableSetOf()
        for (gv in gvl){
            for (gvv in gvl){
                if (!dSet.contains(gv) && !dSet.contains(gvv)) {
                    if (gv.compareTo(gvv) == dvv) {
                        dSet.add(gv)
                        list.add("[$gvv] доминирует [$gv]")
                    }
                }
            }
        }
        return dSet
    }

    open fun newMatrix(dCol: MutableSet<GameVector>, dRow: MutableSet<GameVector>)
                            : GameMatrix{
        var result: MutableList<MutableList<Double>> = mutableListOf()
        var ralternativeNames: MutableList<String> = mutableListOf()
        var rnatureStateNames: MutableList<String> = mutableListOf()

        val dIndex =  dCol.map { c -> c.key }.toList()

        for (i in 0 .. natureStateNames.lastIndex){
            if (!dIndex.contains(i)){
                rnatureStateNames.add(natureStateNames[i])
            }
        }

        for (gv in this.alternatives){
            if (!dRow.contains(gv)){
                var nr: MutableList<Double> = mutableListOf()
                for (i in 0 .. gv.values.lastIndex){
                    if (!dIndex.contains(i)){
                        nr.add(gv.values[i])
                    }
                }
                result.add(nr)
                ralternativeNames.add(gv.name)
            }
        }

        val rlist = result.map { r -> r.toList() }.toList()
        return GameMatrix(rlist, ralternativeNames.toList(), rnatureStateNames.toList())
    }

    fun dominateMatrix(): Pair<GameMatrix, List<String>>{
        var list: MutableList<String> = mutableListOf()

        var dCol: MutableSet<GameVector> = dominateSet(this.natureStates, list, 1)
        var dRow: MutableSet<GameVector> = dominateSet(this.alternatives, list, -1)

        val newMatrix = newMatrix(dCol, dRow)

        var ddgm = Pair(newMatrix, list.toList())

        val ret = iterate(ddgm, list)
        return ret;
    }

    protected fun iterate(ddgm: Pair<GameMatrix, List<String>>, list: MutableList<String>)
            : Pair<GameMatrix, List<String>>{
        var dgm = this
        var lddgm = ddgm

        while (dgm.size() != lddgm.first.size()){
            dgm = lddgm.first
            list.addAll(lddgm.second)
            lddgm = dgm.dominateMatrix()
        }

        return Pair(dgm,list.toList().distinct())
    }


    fun minClearPrice(): Double{
        val map: List<Double> = this.alternatives.map { a -> a?.min() ?: 0.0 }
        return map?.max() ?: 0.0
    }

    fun maxClearPrice(): Double{
        val map: List<Double> = this.natureStates.map { a -> a?.max() ?: 0.0 }
        return map?.min() ?: 0.0
    }

    fun existsClearStrategy() : Boolean{
        return minClearPrice() >= maxClearPrice()
    }
}

Опишем интерфейс, соответствующий критерию

interface ICriteria {
    fun optimum(): List<GameVector>
}

Принятие решений в условиях неопределенности

Принятие решений в условиях неопределённости предполагает, что игроку не противостоит разумный противник.

Критерий Вальда

В критерии Вальда максимизируется наихудший из возможных результатов:

Использование критерия страхует от наихудшего результата, но цена такой стратегии – потеря возможности получить наилучший из возможных результатов.

Рассмотрим пример. Для стратегий

найдем минимумы и получим следующую тройку

. Максимумом для указанной тройки будет являться значение 1, следовательно, по критерию Вальда выигрышной стратегией является стратегия

, соответствующая посадке Культуры 2.

Программная реализация критерия Вальда незатейлива:

class WaldCriteria(gameMatrix : GameMatrix) : ICriteria {

    val gameMatrix: GameMatrix

    init{
        this.gameMatrix = gameMatrix
    }

    override fun optimum(): List<GameVector> {
        val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) }
        val max =  mins.maxWith( Comparator { o1, o2 ->  o1.second!!.compareTo(o2.second!!)})
        return mins
                .filter { m -> m.second == max!!.second }
                .map { m -> m.first }
    }
}

Для большей понятности в первый раз покажу, как решение выглядело бы в виде теста:

private fun matrix(): GameMatrix {
        val alternativeNames: List<String> = listOf("Культура 1", "Культура 2", "Культура 3")
        val natureStateNames: List<String> = listOf("Прохладное и дождливое", "Нормальное", "Жаркое и сухое")
        val matrix: List<List<Double>> = listOf(
                listOf(0.0, 2.0, 5.0),
                listOf(2.0, 3.0, 1.0),
                listOf(4.0, 3.0, -1.0)
        )
        val gm = GameMatrix(matrix, alternativeNames, natureStateNames)
        return gm;
    }
}
private fun testCriteria(gameMatrix: GameMatrix, criteria: ICriteria, name: String){
        println(gameMatrix.toString())
        val optimum = criteria.optimum()
        println("$name. Оптимальная стратегия: ")
        optimum.forEach { o -> println(o.toString()) }
    }
@Test
    fun testWaldCriteria() {
        val matrix = matrix();
        val criteria = WaldCriteria(matrix)
        testCriteria(matrix, criteria, "Критерий Вальда")
    }

Нетрудно догадаться, что для других критериев отличие будет только в создании объекта criteria.

Критерий оптимизма

При использовании критерия оптимиста игрок выбирает решение, дающее лучший результат, при этом оптимист предполагает, что условия игры будут для него наиболее благоприятными:

Стратегия оптимиста может привести к отрицательным последствиям, когда максимальное предложение совпадает с минимальным спросом – фирма может получить убытки при списании нереализованной продукции. В тоже время стратегия оптимиста имеет определённый смысл, например, не нужно заботиться о неудовлетворённых покупателях, поскольку любой возможный спрос всегда удовлетворяется, поэтому нет нужды поддерживать расположения покупателей. Если реализуется максимальный спрос, то стратегия оптимиста позволяет получить максимальную полезность в то время, как другие стратегии приведут к недополученной прибыли. Это даёт определённые конкурентные преимущества.

Рассмотрим пример. Для стратегий

найдем найдем максимум и получим следующую тройку

. Максимумом для указанной тройки будет являться значение 5, следовательно, по критерию оптимизма выигрышной стратегией является стратегия

, соответствующая посадке Культуры 1.

Реализация критерия оптимизма почти не отличается от критерия Вальда:

class WaldCriteria(gameMatrix : GameMatrix) : ICriteria {

    val gameMatrix: GameMatrix

    init{
        this.gameMatrix = gameMatrix
    }

    override fun optimum(): List<GameVector> {
        val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) }
        val max =  mins.maxWith( Comparator { o1, o2 ->  o1.second!!.compareTo(o2.second!!)})
        return mins
                .filter { m -> m.second == max!!.second }
                .map { m -> m.first }
    }
}

Критерий пессимизма

Данный критерий предназначен для выбора наименьшего элемента игровой матрицы из ее минимально возможных элементов:

Критерий пессимизма предполагает, что развитие событий будет неблагоприятным для лица, принимающего решение. При использовании этого критерия лицо принимающее решение ориентируется на возможную потерю контроля над ситуацией, поэтому, старается исключить потенциальные риски выбирая вариант с минимальной доходностью.

Рассмотрим пример. Для стратегий

найдем найдем минимум и получим следующую тройку

. Минимумом для указанной тройки будет являться значение -1, следовательно, по критерию пессимизма выигрышной стратегией является стратегия

, соответствующая посадке Культуры 3.

После знакомства с критериями Вальда и оптимизма то, как будет выглядеть класс критерия пессимизма, думаю, легко догадаться:

class PessimismCriteria(gameMatrix : GameMatrix) : ICriteria {

    val gameMatrix: GameMatrix

    init{
        this.gameMatrix = gameMatrix
    }

    override fun optimum(): List<GameVector> {
        val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) }
        val min =  mins.minWith( Comparator { o1, o2 ->  o1.second!!.compareTo(o2.second!!)})
        return mins
                .filter { m -> m.second == min!!.second }
                .map { m -> m.first }
    }
}

Критерий Сэвиджа

Критерий Сэвиджа (критерий сожалеющего пессимиста) предполагает минимизацию наибольшей потерянной прибыли, иными словами минимизируется наибольшее сожаление по потерянной прибыли:

В данном случае S — это матрица сожалений.

Оптимальное решение по критерию Сэвиджа должно давать наименьшее сожаление из найденных на предыдущем шаге решения сожалений. Решение, соответствующее найденной полезности, будет оптимальным.

К особенностям полученного решения относятся гарантированное отсутствие самых больших разочарований и гарантированное снижение максимальных возможных выигрышей других игроков.

Рассмотрим пример. Для стратегий

составим матрицу сожалений:

Тройка максимальных сожалений

. Минимальным значением из указанных рисков будет являться значение 4, которое соответствует стратегиям

и

.

Запрограммировать критерий Сэвиджа немного сложнее:

class SavageCriteria(gameMatrix: GameMatrix) : ICriteria {

    val gameMatrix: GameMatrix

    init {
        this.gameMatrix = gameMatrix
    }

    fun GameMatrix.risk(): List<Pair<GameVector, Double?>> {
        val maxStates = this.natureStates.map { n -> Pair(n, n.values.max()) }
                .map { n -> n.first.key to n.second }.toMap()

        var am: MutableList<Pair<GameVector, List<Double>>> = mutableListOf()
        for (a in this.alternatives) {
            var v: MutableList<Double> = mutableListOf()
            for (i in 0..a.values.lastIndex) {
                val mn = maxStates.get(i)
                v.add(mn!! - a.values[i])
            }
            am.add(Pair(a, v.toList()))
        }
        return am.map { m -> Pair(m.first, m.second.max()) }
    }

    override fun optimum(): List<GameVector> {
        val risk = gameMatrix.risk()
        val minRisk = risk.minWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) })
        return risk
                .filter { r -> r.second == minRisk!!.second }
                .map { m -> m.first }
    }
}

Критерий Гурвица

Критерий Гурвица является регулируемым компромиссом между крайним пессимизмом и полным оптимизмом:

A(0) — стратегия крайнего пессимиста, A(k) — стратегия полного оптимиста,

— задаваемое значение весового коэффициента:

;

— крайний пессимизм,

— полный оптимизм.

При небольшом числе дискретных стратегий, задавая желаемое значение весового коэффициента

, а затем округлять получаемый результат до ближайшего возможного значения с учётом выполненной дискретизации.

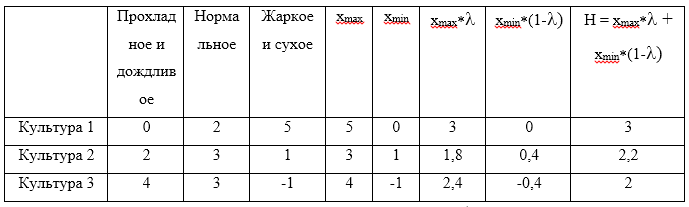
Рассмотрим пример. Для стратегий

. Примем, что коэффициент оптимизма

. Теперь составим таблицу:

Максимальным значением из рассчитанных H будет являться значение 3, которое соответствует стратегии

.

Реализация критерия Гурвица уже более объемная:

class HurwitzCriteria(gameMatrix: GameMatrix, optimisticKoef: Double) : ICriteria {

    val gameMatrix: GameMatrix
    val optimisticKoef: Double

    init {
        this.gameMatrix = gameMatrix
        this.optimisticKoef = optimisticKoef
    }

    inner class HurwitzParam(xmax: Double, xmin: Double, optXmax: Double){
        val xmax: Double
        val xmin: Double
        val optXmax: Double

        val value: Double

        init{
            this.xmax = xmax
            this.xmin = xmin
            this.optXmax = optXmax
            value = xmax * optXmax + xmin * (1 - optXmax)
        }

    }

    fun GameMatrix.getHurwitzParams(): List<Pair<GameVector, HurwitzParam>> {
        return this.alternatives.map { a -> Pair(a, HurwitzParam(a.max()!!, a.min()!!, optimisticKoef)) }
    }

    override fun optimum(): List<GameVector> {
        val hpar = gameMatrix.getHurwitzParams()
        val maxHurw = hpar.maxWith(Comparator { o1, o2 -> o1.second.value.compareTo(o2.second.value) })
        return hpar
                .filter { r -> r.second == maxHurw!!.second }
                .map { m -> m.first }
    }
}

Принятие решений в условиях риска

Методы принятия решений могут полагаться на критерии принятия решений в условиях риска при соблюдении следующих условий:

• отсутствия достоверной информации о возможных последствиях;
• наличия вероятностных распределений;
• знания вероятности наступления исходов или последствий для каждого решения.

Если решение принимается в условиях риска, то стоимости альтернативных решений описываются вероятностными распределениями. В связи с этим принимаемое решение основывается на использовании критерия ожидаемого значения, в соответствии с которым альтернативные решения сравниваются с точки зрения максимизации ожидаемой прибыли или минимизации ожидаемых затрат.

Критерий ожидаемого значения может быть сведен либо к максимизации ожидаемой (средней) прибыли, либо к минимизации ожидаемых затрат. В данном случае предполагается, что связанная с каждым альтернативным решением прибыль (затраты) является случайной величиной.

Постановка таких задач как правило такова: человек выбирает какие-либо действия в ситуации, где на результат действия влияют случайные события. Но игрок имеет некоторые знания о вероятностях этих событий и может рассчитать наиболее выгодную совокупность и очередность своих действий.

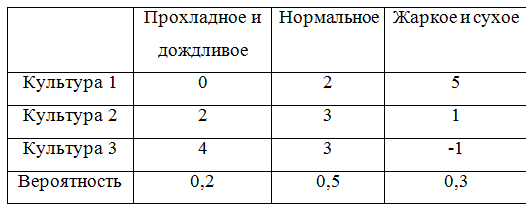
Чтобы можно было и дальше приводить примеры, дополним игровую матрицу вероятностями:

Для того, чтобы учесть вероятности придется немного переделать класс, описывающий игровую матрицу. Получилось, по правде говоря, не очень-то изящно, ну да ладно.

open class ProbabilityGameMatrix(matrix: List<List<Double>>, alternativeNames: List<String>,
                                 natureStateNames: List<String>, probabilities: List<Double>) :
        GameMatrix(matrix, alternativeNames, natureStateNames) {
    val probabilities: List<Double>

    init {
        this.probabilities = probabilities;
    }

    override fun change (i : Int, j : Int, value : Double) : GameMatrix{
        val cm = super.change(i, j, value)
        return ProbabilityGameMatrix(cm.matrix, cm.alternativeNames, cm.natureStateNames, probabilities)
    }

    override fun changeAlternativeName (i : Int, value : String) : GameMatrix{
        val cm = super.changeAlternativeName(i, value)
        return ProbabilityGameMatrix(cm.matrix, cm.alternativeNames, cm.natureStateNames, probabilities)
    }

    override fun changeNatureStateName (j : Int, value : String) : GameMatrix{
        val cm = super.changeNatureStateName(j, value)
        return ProbabilityGameMatrix(cm.matrix, cm.alternativeNames, cm.natureStateNames, probabilities)
    }

    fun changeProbability (j : Int, value : Double) : GameMatrix{
        var list = probabilities.toMutableList()
        list.set(j, value)

        return ProbabilityGameMatrix(matrix, alternativeNames, natureStateNames, list.toList())
    }

    override fun toString(): String {
        var s = ""
        val formatter: NumberFormat = DecimalFormat("#0.00")
        for (i in 0 .. natureStateNames.lastIndex){
            s += natureStateNames[i] + " = " + formatter.format(probabilities[i]) + "n"
        }
        return "Состояния природы:n" +
                s +
                "Матрица игры:n" +
                alternatives
                        .map { a: GameVector -> a.toString() }
                        .reduce { a1: String, a2: String -> "$a1;n$a2" }
    }

    override fun newMatrix(dCol: MutableSet<GameVector>, dRow: MutableSet<GameVector>)
            : GameMatrix{
        var result: MutableList<MutableList<Double>> = mutableListOf()
        var ralternativeNames: MutableList<String> = mutableListOf()
        var rnatureStateNames: MutableList<String> = mutableListOf()
        var rprobailities: MutableList<Double> = mutableListOf()

        val dIndex =  dCol.map { c -> c.key }.toList()

        for (i in 0 .. natureStateNames.lastIndex){
            if (!dIndex.contains(i)){
                rnatureStateNames.add(natureStateNames[i])
            }
        }

        for (i in 0 .. probabilities.lastIndex){
            if (!dIndex.contains(i)){
                rprobailities.add(probabilities[i])
            }
        }

        for (gv in this.alternatives){
            if (!dRow.contains(gv)){
                var nr: MutableList<Double> = mutableListOf()
                for (i in 0 .. gv.values.lastIndex){
                    if (!dIndex.contains(i)){
                        nr.add(gv.values[i])
                    }
                }
                result.add(nr)
                ralternativeNames.add(gv.name)
            }
        }

        val rlist = result.map { r -> r.toList() }.toList()
        return ProbabilityGameMatrix(rlist, ralternativeNames.toList(), rnatureStateNames.toList(),
                rprobailities.toList())
    }

}
}

Критерий Байеса

Критерий Байеса (критерий математического ожидания) используется в задачах принятия решения в условиях риска в качестве оценки стратегии

выступает математическое ожидание соответствующей ей случайной величины. В соответствии с этим правилом оптимальная стратегия игрока

находится из условия:

Иными словами, показателем неэффективности стратегии

по критерию Байеса относительно рисков является среднее значение (математическое ожидание ожидание) рисков i-й строки матрицы

, вероятности которых, совпадают с вероятностями природы. Тогда оптимальной среди чистых стратегий по критерию Байеса относительно рисков является стратегия

, обладающая минимальной неэффективностью то есть минимальным средним риском. Критерий Байеса эквивалентен относительно выигрышей и относительно рисков, т.е. если стратегия

является оптимальной по критерию Байеса относительно выигрышей, то она является оптимальной и по критерию Байеса относительно рисков, и наоборот.

Перейдем к примеру и рассчитаем математические ожидания:

Максимальным математическим ожиданием является

, следовательно, выигрышной стратегией является стратегия

.

Программная реализация критерия Байеса:

class BayesCriteria(gameMatrix: ProbabilityGameMatrix) : ICriteria {

    val gameMatrix: ProbabilityGameMatrix

    init {
        this.gameMatrix = gameMatrix
    }

    fun ProbabilityGameMatrix.bayesProbability(): List<Pair<GameVector, Double?>> {
        var am: MutableList<Pair<GameVector, Double>> = mutableListOf()
        for (a in this.alternatives) {
            var alprob: Double = 0.0
            for (i in 0..a.values.lastIndex) {
                alprob += a.values[i] * this.probabilities[i]
            }
            am.add(Pair(a, alprob))
        }
        return am.toList();
    }

    override fun optimum(): List<GameVector> {
        val risk = gameMatrix.bayesProbability()
        val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) })
        return risk
                .filter { r -> r.second == maxBayes!!.second }
                .map { m -> m.first }
    }
}

Критерий Лапласа

Критерий Лапласа представляет упрощенную максимизацию математического ожидания полезности, когда справедливо предположение о равной вероятности уровней спроса, что избавляет от необходимости сбора реальной статистики.

В общем случае при использовании критерия Лапласа матрица ожидаемых полезностей и оптимальный критерий определяются следующим образом:

Рассмотрим пример принятия решений по критерию Лапласа. Рассчитаем среднеарифметическое для каждой стратегии:

Таким образом, выигрышной стратегией является стратегия

.

Программная реализация критерия Лапласа:

class LaplaceCriteria(gameMatrix: GameMatrix) : ICriteria {

    val gameMatrix: GameMatrix

    init {
        this.gameMatrix = gameMatrix
    }

    fun GameMatrix.arithemicMean(): List<Pair<GameVector, Double>> {
        return this.alternatives.map { m -> Pair(m, m.values.average()) }
    }

    override fun optimum(): List<GameVector> {
        val risk = gameMatrix.arithemicMean()
        val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second.compareTo(o2.second) })
        return risk
                .filter { r -> r.second == maxBayes!!.second }
                .map { m -> m.first }
    }
}

Смешанные стратегии. Аналитический метод

Аналитический метод позволяет решить игру в смешанных стратегиях. Для того, чтобы сформулировать алгоритм нахождения решения игры аналитическим методом, рассмотрим некоторые дополнительные понятия.

Стратегия

доминирует стратегию

, если все

. Иными словами, если в некоторой строке платёжной матрицы все элементы больше или равны соответствующим элементам другой строки, то первая строка доминирует вторую и называется доминант-строкой. А также если в некотором столбце платёжной матрицы все элементы меньше или равны соответствующим элементам другого столбца, то первый столбец доминирует второй и называется доминант-столбцом.

Нижней ценой игры называется

.
Верхней ценой игры называется

.

Теперь можно сформулировать алгоритм решения игры аналитическим методом:

1. Вычислить нижнюю и верхнюю цены игры. Если , то записать ответ в чистых стратегиях, если нет — продолжаем решение дальше
2. Удалить доминирующие строки доминирующие столбцы. Их может быть несколько. На их место в оптимальной стратегии соответствующие компоненты будут равны 0
3. Решить матричную игру методом линейного программирования.

Для того, чтобы привести пример необходимо привести класс, описывающий решение

class Solve(gamePriceObr: Double, solutions: List<Double>, names: List<String>) {

    val gamePrice: Double
    val gamePriceObr: Double
    val solutions: List<Double>
    val names: List<String>

    private val formatter: NumberFormat = DecimalFormat("#0.00")

    init{
        this.gamePrice =  1 / gamePriceObr
        this.gamePriceObr = gamePriceObr;
        this.solutions = solutions
        this.names = names
    }

    override fun toString(): String{
        var s =  "Цена игры: " + formatter.format(gamePrice) + "n"
        for (i in 0..solutions.lastIndex){
            s += "$i) " + names[i] + " = " + formatter.format(solutions[i] / gamePriceObr) + "n"
        }
        return s
    }

    fun itersect(matrix: GameMatrix): String{
        var s =  "Цена игры: " + formatter.format(gamePrice) + "n"
        for (j in 0..matrix.alternativeNames.lastIndex) {
            var f = false
            val a = matrix.alternativeNames[j]
            for (i in 0..solutions.lastIndex) {
                if (a.equals(names[i])) {
                    s += "$j) " + names[i] + " = " + formatter.format(solutions[i] / gamePriceObr) + "n"
                    f = true
                    break
                }
            }
            if (!f){
                s += "$j) " + a + "  = 0n"
            }
        }
        return s
    }
}

И класс, выполняющий решение симплекс-методом. Поскольку в математике я не разбираюсь, то воспользовался готовой реализацией из Apache Commons Math

open class Solver (gameMatrix: GameMatrix) {

    val gameMatrix: GameMatrix

    init{
        this.gameMatrix = gameMatrix
    }

    fun solve(): Solve{
        val goalf: List<Double> = gameMatrix.alternatives.map { a -> 1.0 }
        val f = LinearObjectiveFunction(goalf.toDoubleArray(), 0.0)

        val constraints = ArrayList<LinearConstraint>()
        for (alt in gameMatrix.alternatives){
            constraints.add(LinearConstraint(alt.values.toDoubleArray(), Relationship.LEQ,  1.0))

        }

        val solution = SimplexSolver().optimize(f, LinearConstraintSet(constraints), GoalType.MAXIMIZE,
                NonNegativeConstraint(true))

        val sl: List<Double> = solution.getPoint().toList()
        val solve = Solve(solution.getValue(), sl, gameMatrix.alternativeNames)

        return solve
    }
}

Теперь выполним решение аналитическим методом. Для наглядности возьмем другую игровую матрицу:

В этой матрице есть доминирующее множество:
begin{pmatrix} 2& 4\ 6& 2end{pmatrix}

val alternativeNames: List<String> = listOf("Культура 1", "Культура 2", "Культура 3")
val natureStateNames: List<String> = 
    listOf("Прохладное и дождливое", "Нормальное", "Жаркое и сухое", "Ветреное")
val matrix: List<List<Double>> = listOf(
     listOf(2.0, 4.0, 8.0, 5.0),
     listOf(6.0, 2.0, 4.0, 6.0),
     listOf(3.0, 2.0, 5.0, 4.0)
)
val gm = GameMatrix(matrix, alternativeNames, natureStateNames)
val (dgm, list) = gm.dominateMatrix()
println(dgm.toString())
println(list.reduce({s1, s2 -> s1 + "n" + s2}))
println()
val s: Solver = Solver(dgm)
val solve = s.solve()
println(solve)

Решение игры

при цене игры равной 3,33

Вместо заключения

Надеюсь, эта статья будет полезна тем, кому необходимо в первом приближении с решением игр с природой. Вместо выводов ссылка на GitHub.

Буду благодарен за конструктивную обратную связь!

Теория игр. Матричные игры. Онлайн калькулятор

С помощю этого онлайн калькулятора можно решить задачу теории игр. Для решения задачи теории игр задайте количество строк и количество столбцов матрицы. Затем введите данные в ячейки и нажимайте на кнопку “Вычислить”. Теоретическую часть смотрите ниже.

Теория игр − теоретическая часть

Бывают ситуации, в которых сталкиваются интересы двух и более сторон. При этом эффективность принимаемого решения одной стороны зависит от действий другой стороны. Такие ситуации называются конфликтными. Конфликтная ситуация называется антагонистической, если увеличение выигрыша одной стороны на определенную величину приводит к уменьшению выигрыша другой стороны на такую же величину. Математическая модель таких ситуаций описывается матричной игрой. Участники игры (т.е. лица, принимающие решение) называются игроками. Принятие игроком того или иного решения в процессе игры и его реализация называется ходом. Ходы могут быть личными (т.е. сознательными) и случайными. Стратегия игрока − осознанный выбор одного из множества вариантов его действий. Стратегия называется чистой, если выбор игрока неизменен от партии к партии. У первого игрока есть m чистых стратегий, а у второго игрока n чистых стратегий. Если множество стратегий игроков конечный, то игра называется конечной, а если хотя бы у одного игрока множество стратегий бесконечно, то игра называется бесконечной. Стратегия игрока называется оптимальной, если она обеспечивает данному игроку (при многократном повторении) максимально возможный средний выигрыш или минимально возможный средний проигрыш.

Игры, в которых учавствуют 2 игрока, называются парными, а игры с большим числом участников − множественными. Если в парной игре выигрыш одной стороны точностью совпадает с проигрышем другой стороны, то игра называется игрой с нулевой суммой.

В зависимости от вида функций выигрышей, игры бывают матричные, биматричные, непрерывные, выпуклые и др.

Рассмотрим матричную игру двух участников с нулевой суммой и конечным числом возможных ходов.

Решение матричной игры в чистых стратегиях

Пусть игроки A и B распологают конечным числом возможных действий (чистых стратегий). Обозначим их через и , соответственно. Игрок A может выбрать чистую стратегию . В ответ на этот выбор, игрок B может выбрать чистую стратегию . Выбор стратегии первого игрока и ответный выбор стратегии игрока B единственным образом определяет результат a_ij выигрыш игрока A или проигрыш игрока B.

Таким образом игра с нулевой суммой однозначно определяется матрицей

которая называется платежной матрицей или матрицей выигрышей. Строки матрицы (1) определяют стратегии первого игрока (), а столбцы соответствуют стратегиям второго игрока ().

Игра проходит партиями. Партия начинается с первого игрока. Он выбирает некоторую строку i матрицы. В ответ на это второй игрок выбирает некоторый столбец j. На этом заканчивается партия и второй игрок платит первому сумму a_ij, если a_ij>0 или первый игрок платит сумму a_ij второму игроку, если a_ij<0. Цель каждого игрока − выиграть как можно большую (или проиграть как можно меньшую) сумму в результате большого числа партий.

Чтобы определить наилучшие стратегии игроков, мы предполагаем, что участники разумны, т.е. делают все, чтобы добится наилучшего результата для себя. Методом логических рассуждений найдем наилучшую стратегию игрока A. Для этого проанализируем по шагам все его стратегии. Выбирая стратегию A_i (строка i) игрок A должен рассчитывать, что игрок B должен ответить такой стратегией B_j (столбец j), чтобы выигрыш первого игрока был бы минимальным. Поэтому найдем для каждой строки минимальное число:

Зная для каждой строки число α_i (i=1,2,…m) игрок A должен выбрать ту стратегию, при котором его выигрыш будет максимальным:

Величина α называется минимальным гарантированным выигрышем, к которому может достигнуть игрок A, при любых стратегиях игрока B. α называется нижней ценой игры или максимином.

Рассмотрим, теперь, игру со стороны игрока B. Игрок B заинтересован уменьшить свой проигрыш (или минимизировать выигрыш игрока A. Поэтому для каждого столбца он оценивает свой максимальный проигрыш в связи с тем, какую стратегию i выберет игрок A:

Зная для каждого столбца число β_j (j=1,2,…n), игрок B должен выбирать ту стратегию, при котором его проигрыш будет минимальным:

Величину β называют верхней ценой игры или максимином, к которому может достигнуть игрок A, при любых стратегиях игрока B. α называется нижней ценой игры или максимином. Она показывает максимальный проигрыш, которого может достигать игрок B при любых стратегиях игрока A.

Теорема 1. В матричной игре нижняя цена игры не превосходит верхней цены, т.е. α ≤ β.

Действительно:

Если для чистых стратегий A_k и B_l игроков A и B имеет место равенство α = β, то пару чистых стратегий (A_k,B_l) называют седловой точкой матричной игры а γ=α = β чистой ценой игры. Элемент a_kl называют седловым элементом платежной матрицы.

Заметим, что отклонение игрока A от максимальной стратегии A_k ведет к уменьшению его выигрыша, а отклонение игрока B от минимальной стратегии B_l ведет к увеличению его проигрыша. Поэтому A_k и B_l являются оптимальными чистыми стратегиями игроков A и B, соответственно.

Тройку (A_k, B_l, γ) называют решением матричной игры. Если игра имеет седловую точку, то говорят, что она решается в чистых стратегиях.

Решение матричной игры в смешанных стратегиях

Если матричная игра не имеет седловой точки, то α ≠ β, и, Теорему 1, получим: α < β. Получается, что применение минимаксных стратегий приводит к тому, что выигрыш игрока A не больше α, а проигрыш игрока B не больше β. В этом случае решение матричных игр находят в смешанных стратегиях.

Смешанной стратегией игрока A называется вектор , где

p_i− вероятность, с которой игрок A выбирает свою чистую стратегию A_i.

Смешанной стратегией игрока B называется вектор , где

q_j− вероятность, с которой игрок B выбирает свою чистую стратегию B_j.

Замемим, что чистые стратегии являются частным случаем смешанных стратегий. Если, например игрок A выбрал чистую стратегию A₃, то это означает, что вероятность ее выбора равна 1, т.е. . Средняя величина выигрыша игрока A (или проигрыша игрока B) определяется по формуле математического ожидания:

Функция M(p,q) называется платежной функцией матричной игры с матрицей. Смешанные стратегии p^* и q^* называются оптимальными, если они образуют седловую точку для платежной функции M(p,q), т.е.

Значение платежной функции при оптимальных смешанных стратегиях p^* и q^* называют ценой игры:

Теорема 2 (Основная теорема теории матричных игр). В любой матричной игре у игроков есть оптимальные смешанные стратегии.

Доказательство. Пусть игра имеет платежную матрицу

где все элементы положительны.

Пусть и − смешанные стратегии игроков A и B , соотвестстенно.

Математическое ожидание выигрыша игрока A равна:

При любом выборе игроками своих смешанных стратегий p и q, математическое ожидание будет положительным, так как все элементы a_ij платежной матрицы положительны, p_i неотрицательные числа и среди них есть хотя бы одно положительное число, q_j неотрицательные числа и среди них есть хотя бы одно положительное число.

Нижняя цена игры

так как a_ij >0, i=1,2,…m, j=1,2,…n. Поскольку α>0 и γ не может быть меньше нижней цены игры, то γ ≥ α, а так как α>0, то γ >0.

Пусть игрок A выбирает такую стратегию p, что математическое ожидание его выигрыша независимо от того, какую стратегию выбирает игрок B было не меньше некоторой величины γ:

где p_i >0, i=1,2,…m, . Каждая строка в системе линейных неравенств (3) соотвесттвует определенной стратегии игрока B.

Преобразуем систему нерравенств (3), введя новые обозначения:

Разделим все неравенства системы (3) на положительное число γ. Тогда имеем:

y_i >0, i=1,2,…m.

При этом

Цель игрока A − максимизировать свой гарантированный выигрыш γ или минимизировать величину

Таким образом, приходим к следующей задаче линейного программирования:

Сделав аналогичные рассуждения с позиции игрока B, получим следующую задачу линейного программирования:

Покажем, что задачи линейного программирования (4) и (5) имеют допустимые решения. Так как a_ij >0, то можно подобрать достаточно большие положительные числа y_i, i=1,2,…m так, чтобы выполнялись неравенства (4b). Значит задача линейного программирования (4) имеет допустимое решение.

Допустимое решение задачи линейного программирования (5) является нулевой вектор. Таким образом, пары двойственных задач линейного программирования (4) и (5) имеют допустимые решения. Тогда, согласно теории двойственных задач линейного программирования, обе эти задачи имеют оптимальные планы , , при этом оптимальные значения целевых функций данных задач равны:

Цена игры равна:

Найдем оптимальные смешанные стратегии игроков:

Тогда

Пара образует седловую точку данной матричной игры в смешанных стратегиях.

Если в матрице есть отрицательные элементы или нули, то можно сделать матрицу положительным, добавив к каждому элементу матрицы достаточно большое положительное число r. Тогда получим следующую матрицу A’(a_ij+r).

Математическое ожидание выигрыша игрока A с платежной матрицей A(a_ij):

Математическое ожидание игрока A с платежной матрицей A’(a_ij+r):

Тогда

Игра с платежной матрицей A’ имеет седловую точку в смешанных стратегиях:

Следовательно, игра с платежной матрицей A также имеет седловую точку в смешанных стратегиях а цена игры с платежной матрицей A равна:

Для рассмотрения численного примера матричной игры, введите в калькуляторе в начале страницы элементы матрицы и нажмите на кнопку вычислить. Онлайн калькулятор выдаст подробное рашение задачи.