Как найти оптимальные условия - Сайт, где вы сможете решить свои вопросы

Поиск оптимальных условий

ЗАДАНИЕ

на курсовое проектирование

по дисциплине “Планирование и организация экспериментов”

Задача проекта: организовать “экспериментальные” исследования
некоторого объекта с целью поиска минимального значения выходной величины Y. Объект имеет входные управляющие
воздействия X1, X2, X3, …,
Xn.

X2
Объект исследования Y

Имеются заданные начальные условия. Необходимо проводя экстремальные
“эксперименты” на программном эмуляторе объекта получить такие режимы
его работы, при которых достигается минимальное значение величины Y. При этом следует построить и
обосновать стратегию “экспериментальных” работ, выбрать и обосновать
применяемые методы (2 различных). В записке к проекту привести обоснование и
описание стратегии организации экспериментальных работ, используемых методов,
“экспериментальные” результаты (т.е. полученные путем расчетов по
программному имитатору объекта) включая промежуточные, результаты их
статистической обработки, принимаемые в процессе экспериментирования решения,
их обоснования, полученные оптимальные результаты X1*, X2*, X3*, …, Xn*, Y*.

Обосновать полученное решение с точки зрения: локальный найден минимум
или глобальный?

Необходимо подобрать реальный процесс, для которого могла бы быть поставлена
аналогичная содержательная задача, и описать его с обоснованием постановки
задачи.

Содержание

Введение

. Обоснование и описание методов оптимизации

1.1 Метод Гаусса-Зайделя

1.2 Метод Наказания случайностью

2. Проведение экспериментов

2.1 Метод Гаусса-Зайделя

.2 Метод наказания случайностью

3. Подбор реального процесса

. Список используемой литературы

Введение

Основной целью решения различного рода исследовательских проблем
управления, проектирования и планирования является исследование объектов,
прогнозирование их поведения, поиск наилучших условий функционирования.
Оптимизацией называют процесс выбора наилучшего варианта из всех возможных.
Постановка задачи оптимизации предполагает наличие объекта оптимизации. Объект
оптимизации должен обладать определенными степенями свободы – управляющими
воздействиями, которые позволяют применять его состояние в соответствие с теми
или иными требованиями.

В процессе решения задачи оптимизации обычно необходимо найти оптимальные
значения некоторых параметров, при которых выходная величина имеет минимум (или
максимум). В общем случае задача оптимизации записывается следующим образом:

R( …)→ (1)

–
критерий оптимальности

Решением
этой задачи называется такой (,…), при
котором R()=(), R()≥R(x)
для любого x.

Методы
оптимизации – поиска экстремума функции (в практических задачах – критериев
оптимальности) при наличии ограничений или без ограничений очень широко
используются на практике. Количественная оценка оптимизируемого качества
объекта обычно называется критерием оптимальности. Критерий оптимизации y
обычно задается. Этот критерий должен удовлетворять следующим основным
требованиям: 1) экстремум величины R должен характеризовать
наилучшее состояние объекта в выбранном смысле; 2) Критерий должен выражаться
количественно. Если критерий не выражается количественно, то можно ввести
рейтинговые, бальные, экспертные оценки, которые количественно выражают лучшее
или худшее; 3) По возможности критерий оптимальности должен выражаться одним
числом, хотя на практике часто его выражают совокупностью чисел, т.е. разными
частными критериями.

Решение
задачи оптимизации осуществляют с помощью экспериментального поиска. Для этого
сначала осуществляют изучение характера поверхности отклика в районе
первоначально выбранной точки факторного пространства (с помощью специально
спланированных «пробных» опытов). Затем совершают «рабочее» движение в сторону
экстремума, причем направление движения определяют по результатам пробных
опытов. Такое движение может осуществляться путем ряда этапов, которые могут
объединяться в «циклы».

После
выхода в район экстремума оптимальную точку можно уточнить одним из двух
способов: 1) постановкой дополнительных, особым образом спланированных опытов;
2) получением математической модели второго или более высокого порядка и
последующим решением системы уравнений.

В
настоящее время существует достаточно большое количество численных методов
оптимизации (поиска экстремума функции, критерия оптимальности),
классифицируемых по размерности решаемой задачи, способу формирования шага,
наличию ограничений.

1.
Обоснование и описание методов оптимизации

Существует достаточно большое количество численных методов оптимизации.
Рассмотрим два метода поисковой оптимизации: «Метод Гауса-Зайделя» и «Метод
наказанием случайностью». Первый метод относится к многомерной безградиентной
оптимизации, а второй метод аналог метода наискорейшего спуска. Эти методы
различаются способами постановки пробных опытов и определения направления
движения к экстремуму, а также способами организации самого рабочего движения к
экстремуму.

Задача надежности отыскания экстремума усложняется, если на объект
воздействуют случайные помехи έ. Для повышения надежности результатов
применяют специальные методы, например в каждой запланированной точке
факторного пространства выполняют по нескольку параллельных опытов. Кроме того,
разные поисковые методы в равных условиях обладают различной
помехоустойчивостью.

1.1 Метод Гаусса-Зайделя

Метод сводится к поиску экстремума поочередно по каждой переменной
отдельно. Алгоритм выражается формулой: xj+1= xj+f(R (xj)).

Пусть имеется некоторая начальная точка x0 и R(x1,x2). Сначала будем искать по первой переменной x1, при этом фиксируя значение
остальных переменных и начинаем менять x1. Смотрим результат. Найденную точку с наилучшим значением
по первой переменной фиксируем и начинаем менять вторую переменную x2. Найденная наилучшая точка x1 завершает первый цикл.
Последовательный поиск экстремума по каждой переменной не приводит нас в общем
случае, к экстремуму функции, поэтому после завершения первого цикла наступает
второй, третий и т. д. Точность нахождения экстремума зависит от величины шага
по переменной. Его выбирают так, чтобы:

– уверенно почувствовать изменение функции при наличии помех;

общее число экстремумов не слишком большое;

далеко не проскакивать оптимум по направлению.

Основная особенность рассматриваемого метода – отсутствие вычисления
градиента критерия оптимальности. Ряд методов прямого поиска базируется на
последовательном применении одномерного поиска по переменным или по другим
задаваемым направлениям, что облегчает их алгоритмизацию и применение.

Метод обладает низкой эффективностью в овражных функциях, может
застревать в «ловушках», особенно при сравнительно больших шагах h при поиске оптимума по каждой
переменной, очень чувствителен и к выбору системы координат. Метод прост в
реализации. На эффективность метода влияет порядок чередования переменных.

Достоинства метода:

• очевидная простота стратегии и наглядность;

• высокая помехозащищенность в смысле выбора направления движения.

Недостатки метода:

• при большом числе влияющих n факторов путь к главному экстремуму оказывается обычно долгим;

• в условиях крупного промышленного производства оказывается трудным
застабилизировать n-1 факторов на
длительное время;

• если поверхность отклика имеет сложную форму (узкие гребни, овраги и
т.п.), то использование метода может привести к ложному ответу на вопрос о
месте расположения экстремума;

• метод не дает информации о взаимодействиях факторов.

Условием окончания поиска является малость изменения критерия
оптимальности за один цикл или невозможность улучшения критерия оптимальности
ни по одной из переменных.

.2 Метод с наказанием случайностью

Метод
является аналогом метода наискорейшего спуска, только направление локального
поиска не градиентное, а случайное. Метод относится к методам многомерной
случайной оптимизации, где величина шага при
построении улучшающей последовательности формируется
случайным образом. Поэтому в одной и той же ситуации шаг может быть различен в отличие от регулярных методов.

Суть
метода заключается в следующем: из текущей точки делают случайные шаги до тех
пор, пока не будет найдена точка с лучшим значением критерия оптимальности.
Затем в этом направлении регулярным методом одномерного поиска ищут оптимум. В
точке оптимума по направлению опять случайным образом ищут новое направление и
т.д.

Достоинства
метода:

· очевидная простота;

· выбор случайного вектора для выполнения пробного опыта не
зависит от случайных помех и формы поверхности отклика;

· позволяет находить глобальный экстремум;

· эффективен в задачах высокой размерности и вдали от оптимума,
позволяет в среднем быстрее выходить в район оптимума.

Недостатки метода:

· в общем случае направление рабочих шагов не является оптимальным;

· малая эффективность в условиях пологих поверхностей отклика.

Поиск
заканчивают, когда за заданное число попыток не
удается найти точку с лучшим значением критерия оптимальности, чем имеющаяся
текущая.

2.
Проведение экспериментов

2.1 Метод Гаусса – Зайделя

В связи с тем, что на рассматриваемый нами объект действуют случайные
помехи (процесс стохастический), будем дублировать в каждой запланированной
точке эксперимент.

В начальной точке (2; -2; 1; 3; 1) проведем двадцать экспериментов и
найдем дисперсию и среднее квадратическое отклонение единичного результата.

У1	У2	У3	У4	У5	Уср
21,614	21,071	17,271	21,886	17,814	19,6464
У6	У7	У8	У9	У10
19,986	20,529	18,629	19,443	17,000
У11	У12	У13	У14	У15
20,800	17,000	20,257	18,900	17,000
У16	У17	У18	У19	У20
20,257	22,157	18,357	20,800	22,157

;

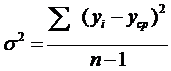где
2 – дисперсия;

– среднее
квадратическое отклонение;число экспериментов.

σ2 =3,217

σ=1,794

Зададимся
числом дублей при одних и тех же параметрах xi. Пусть число
повторений в процессе проведения эксперимента равно пяти. Тогда найдем среднее
квадратическое отклонение для числа экспериментов m=5.

1,794/5=0,359

Отсюда
получим

Следовательно,
изменение выходной величины уiср должно быть

больше
при различных значениях параметров хi,
т.е.

где
Yi -среднее
значение критерия оптимальности i-ого цикла;

Yi+1 -среднее
значение критерия оптимальности (i+1) цикла.

Учитываем
что, хi может изменяться в пределах [-5;5]

Из
начальной точки с координатами (2; -2; 1; 3; 1) с Уср=19,6464 ищем минимум
критерия поочередно по всем переменным. Используем прием последовательного
сканирования, т.е. “шагаем” до первого лучшего значения критерия, применяя
алгоритм х1i+1=хi1h, где h –
шаг. Знак «+» или «-» выбирается в зависимости от направления изменения
критерия: нужно взять такой знак, при котором критерий уменьшается.

Необходимо выбрать шаг: класс точности промышленного прибора равного
0,5%, при изменении x в интервале
[-5:5] получаем:

hmin=
(10∙0,5)/100 = 0,05,

где hmin -минимальный шаг изменения x, который мы можем контролировать.

Соответственно шаг h
должен быть больше hmin=0,05. Возьмем
в первом цикле нашего поиска h=1.
Условием окончания поиска будет являться малость изменения критерия
оптимальности за один цикл:

>1,077,

где
Yi -среднее
значение критерия оптимальности i-ого цикла;

Yi+1 -среднее
значение критерия оптимальности (i+1) цикла.

Так
же условием окончания может быть невозможность улучшения критерия оптимальности
ни по одной из переменных.

Таблица
1 – Цикл первый, h=1

X1	X2	X3	X4	X5	У1	У2	У3	У4	У5	Уср
2	-2	1	3	1						19,6460
3					23,629	26,614	24,986	22,000	22,543	23,9544
1					17,800	16,986	18,343	15,900	18,343	17,4744	Улучшение
0					14,900	15,986	14,629	13,543	13,271	14,4658
-1					19,157	16,714	18,343	19,157	16,171	17,9084	Ухудшение
0	-3				16,171	17,529	15,900	16,714	14,543	16,1714
	-1				12,543	12,814	13,900	14,443	16,886	14,1172	Улучшение
	0				12,900	12,900	11,000	15,343	14,529	13,3344
	1				13,800	12,714	10,000	12,443	15,157	12,8228
	2				14,157	11,714	11,171	9,543	13,614	12,0398
	3				10,443	10,986	10,714	12,614	10,443	11,0400
	4				9,714	11,886	12,157	7,271	9,986	10,2028
	5				6,000	7,900	6,543	9,257	7,629	7,4658	Предел Х2
0	5	0			-11,743	-9,843	-9,843	-13,914	-10,657	-11,2000	Улучшение
		2			33,071	33,071	33,343	29,271	33,343	32,4198
		-1			-33,729	-34,000	-28,843	-29,929	-31,286	-31,5574
		-2			-51,000	-49,914	-48,014	-46,657	-48,557	-48,8284	Улучшение
		-3			-61,657	-63,557	-61,114	-65,729	-65,729	-63,5572
		-4			-74,657	-78,729	-74,386	-74,386	-74,929	-75,4174
		-5			-85,929	-88,371	-87,557	-87,829	-88,914	-87,7200	Предел Х3
0	5	-5	2		-91,743	-90,657	-91,743	-93,643	-92,014	-91,9600	Улучшение
			4		-78,929	-81,914	-81,100	-78,657	-78,114	-79,7428
			1		-95,557	-94,200	-94,200	-97,186	-95,829	-95,3944	Улучшение
			0		-96,557	-98,457	-94,657	-93,843	-94,929	-95,6886	Улучшение
			-1		-93,386	-98,000	-92,843	-92,843	-97,729	-94,9602	Ухудшение
			-2		-89,843	-92,286	-93,100	-92,286	-92,829	-92,0688	Ухудшение
0	5	-5	0	0	-98,371	-97,286	-99,729	-94,843	-97,9916	Улучшение
				2	-91,929	-96,000	-91,929	-95,729	-91,929	-93,5032	Ухудшение
				-1	-95,743	-94,657	-94,929	-94,929	-94,929	-95,0374	Ухудшение
				-2	-92,200	-93,286	-94,914	-94,643	-95,729	-94,1544	Ухудшение

На данном этапе цикл 1 при шаге h=1 заканчивается. Лучшая точка имеет координаты (0;5;-5;0;0), значение
критерия уср= -97,9916. Следующий цикл заключается опять в поиске минимума
функции по переменной x1,
затем по x2 и далее по x3, x4 и x5.

На следующем этапе уменьшаем шаг h до 0,5

Таблица 2 – Цикл второй, h=0,5

X1	X2	X3	X4	X5	У1	У2	У3	У4	У5	Уср
0	5	-5	0	0	-98,371	-99,729	-97,286	-99,729	-94,843	-97,9916
-0,5					-96,493	-95,679	-96,221	-95,407	-97,85	-96,3300
0,5					-98,664	-95,136	-99,207	-94,864	-98,664	-97,3070
0	4,5				-69,114	-71,557	-69,114	-70,2	-73,186	-70,6342
0	5	-4,5			-90,407	-94,479	-90,136	-93,121	-89,864	-91,6014
0	5	-5	-0,5		-96,493	-94,593	-98,121	-98,664	-98,936	-97,3614
			0,5		-94,593	-95,136	-96,221	-98,121	-97,036	-96,2214
0	5	-5	0	-0,5	-95,95	-96,764	-97,579	-98,121	-98,664	-97,4156
				0,5	-95,407	-95,136	-95,95	-96,221	-97,307	-96,0042

Т.к. улучшений не наблюдается, для уточнения найденного критерия
оптимальности уменьшим шаг h до
0,1.

Таблица 3 – Цикл третий, h=0,1

X1	X2	X3	X4	X5	У1	У2	У3	У4	У5	Уср
0	5	-5	0	0	-98,371	-99,729	-97,286	-99,729	-94,843	-97,9916
0,1					-96,733	-99,719	-95,376	-97,547	-94,833	-96,8416
-0,1					-98,090	-96,190	-99,719	-94,833	-97,819	-97,3302
0	4,9				-93,203	-92,660	-93,746	-93,746	-89,946	-92,6602
0	5	-4,9			-97,633	-98,176	-98,719	-98,990	-96,276	-97,9588
0	5	-5	0,1		-99,990	-96,733	-97,547	-99,447	-98,633	-98,4700	Улучшение
			-0,1		-99,719	-96,190	-96,733	-99,176	-99,176	-98,1988
			0,2		-99,689	-99,417	-96,160	-99,417	-98,874	-98,7114	Улучшение
			0,3		-99,910	-99,096	-99,096	-99,639	-95,839	-98,7160	Улучшение
			0,4		-99,026	-99,840	-97,397	-97,126	-95,497	-97,7772	Ухудшение
0	5	-5	0,3	0,1	-98,271	-97,457	-95,829	-95,557	-99,357	-97,2942
				-0,1	-94,743	-94,743	-98,543	-96,643	-99,086	-96,7516

На данном этапе цикл 3 при шаге h=0,1 заканчивается. Лучшая точка имеет координаты (0;5;-5;0,3;0),
значение критерия уср= – 98,7160.

=|-97,9916-(-98,7160)|=0,7244
< 1,077

Так
как улучшений не наблюдается ни по одной из переменных, то на этом этапе можно
считать, что поиск завершен.

Таким
образом, получили точку (0;5;-5;0,3;0), которая является решением поставленной
задачи, с критерием оптимальности уср= – 98,716.

Чтобы
определить, является ли найденный экстремум глобальным или локальным, возьмем
новую начальную точку (-2; 2;-1;-3;-1) и проведем заново весь поиск.

У1	У2	У3	У4	У5	Уср
11,714	9,814	9,814	13,343	9,543
У6	У7	У8	У9	У10
13,071	12,529	10,629	12,800	10,357
У11	У12	У13	У14	У15	9,4800
12,257	13,886	12,529	12,800	13,071
У16	У17	У18	У19	У20
11,171	10,900	13,071	13,886	9,814

σ2=1,893

σ=1,376

Среднее квадратическое отклонение для числа экспериментов m=5:

1,376/5=0,275

Из
новой начальной точки (-2;2;-1;-3;-1) с уcр=9,4800 ищем
минимум критерия оптимальности по переменной х1, х2, х3, х4 и потом х5.

Таблица
4 – Цикл первый, h=1

X1	X2	X3	X4	X5	У1	У2	У3	У4	У5	Уср
-2	2	-1	-3	-1						9,4800
-3					18,886	14,271	15,900	15,629	16,714	16,2800
-1					6,000	10,614	9,529	9,800	7,086	8,6058	Улучшение
0					8,257	7,714	7,443	5,814	5,271	6,8999
1					6,814	7,629	6,814	10,071	6,000	7,4656	Ухудшение
0	1				13,529	10,543	14,071	14,614	13,257	13,2028
	3				-1,014	0,343	-1,829	-1,014	0,343	Улучшение
	4				-16,457	-12,386	-14,557	-14,829	-15,100	-14,6658
	5				-34,000	-29,929	-33,186	-33,729	-29,114	-31,9916	Предел Х2
0	5	-2			-47,471	-48,014	-50,729	-49,914	-50,729	-49,3714	Улучшение
		0			-10,386	-12,829	-15,000	-12,014	-9,843	-12,0144
		-3			-65,729	-64,371	-61,114	-63,286	-62,471	-63,3942	Улучшение
		-4			-76,014	-76,829	-79,000	-77,100	-73,843	-76,5572	Улучшение
		-5			-87,557	-87,286	-85,114	-88,371	-88,371	-87,3398	Предел Х3
0	5	-5	-4		-81,371	-77,843	-80,829	-82,186	-82,729	-80,9916
			-2		-92,286	-92,829	-93,100	-93,914	-92,829	-92,9916	Улучшение
			-1		-95,286	-98,000	-94,471	-92,843	-96,100	-95,3400
			0		-97,371	-96,286	-94,657	-97,643	-95,743	-96,3400
			1		-93,386	-94,471	-93,114	-96,100	-93,929	-94,2000	Ухудшение
0	5	-5	0	-2	-91,929	-95,729	-93,557	-93,286	-93,557	-93,6116
				0	-98,914	-97,557	-96,743	-94,843	-95,929	-96,7972	Улучшение
				1	-95,200	-95,471	-96,557	-97,100	-94,114	-95,6884	Ухудшение

На данном этапе цикл 1 при шаге h=1 заканчивается. Лучшая точка имеет координаты (0;5;-5;0;0), значение
критерия уср= -96,7972

Таблица 5 – Цикл второй, h=0,5

X1	X2	X3	X4	X5	У1	У2	У3	У4	У5	Уср
0	5	-5	0	0						-96,7972
-0,5					-94,864	-98,936	-97,036	-94,593	-95,950	-96,2758
0,5					-99,479	-97,036	-97,579	-95,679	-98,121	-97,5788	Улучшение
1					-94,929	-94,386	-96,286	-94,657	-96,014	-95,2544	Ухудшение
0,5	4,5				-73,750	-72,393	-71,850	-69,136	-73,207	-72,0672	Ухудшение
0,5	5	-4,5			-89,886	-92,871	-93,686	-90,492	-89,886	-91,3642	Ухудшение
0,5	5	-5	-0,5		-95,429	-98,957	-98,143	-97,871	-95,700	-97,2200	Ухудшение
			0,5		-96,514	-99,229	-96,514	-98,143	-98,957	-97,8714	Улучшение
			1		-95,674	-93,864	-97,936	-94,679	-98,750	-96,1986	Ухудшение
0,5	5	-5	0,5	-0,5	-98,707	-94,636	-98,164	-95,721	-99,250	-97,2956
				0,5	-94,364	-94,093	-95,993	-98,436	-94,093	-95,3958

На данном этапе цикл 2 при шаге h=0,5 заканчивается. Лучшая точка имеет координаты (0,5;5;-5;0,5;0),
значение критерия уср= -97,8714

поиск оптимизация эффективность
гидрогенизационный

=|-96,7972-(-97,8714)|=1,0742
> 0,825

Проверим
на следующем этапе с меньшим шагом не является ли полученная точка искомым
экстремумом. Уменьшим шаг h до 0,1.

Таблица
6 – Цикл третий, h=0,1

X1	X2	X3	X4	X5	У1	У2	У3	У4	У5	Уср
0,5	5	-5	0,5	0						-97,8714
0,4					-94,976	-97,419	-98,233	-97,690	-95,519	-96,7674
0,6					-96,947	-98,847	-96,404	-96,947	-97,219	-97,2728
0,5	4,9				-93,246	-92,160	-89,174	-89,989	-88,903	-90,6944
0,5	5	-4,9			-93,604	-97,676	-98,490	-94,961	-97,947	-96,5356
0,5	5	-5	0,4		-97,147	-98,776	-97,147	-98,233	-96,876	-97,6358
			0,6		-96,133	-97,490	-98,033	-98,576	-99,119	-97,8702
0,5	5	-5	0,5	-0,1	-97,319	-94,604	-98,133	-97,861	96,233	-58,3368
				0,1	-95,690	-98,676	-95,961	-97,861	-98,404	-97,3184

Т.к. улучшений не наблюдается, для уточнения найденного критерия
оптимальности уменьшим шаг h до hmin=0,05

Таблица 7 – Цикл четвертый, h=0,05

X1	X2	X3	X4	X5	У1	У2	У3	У4	У5	Уср
0,5	5	-5	0,5	0						-97,8714
0,45					-98,733	-94,390	-95,748	-96,019	-95,748	-96,1276
0,55					-95,919	-96,733	-96,190	-97,547	-97,547
0,5	4,95				-92,151	-95,679	-92,965	-94,322	-91,879	-93,3992
0,5	5	-4,95			-94,926	-97,369	-96,012	-97,640	-97,912	-96,7718
0,5	5	-5	0,45		-99,005	-94,933	-99,276	-97,647	-97,105	-97,5932
			0,55		-98,090	-98,905	-97,005	-98,090	-96,733	-97,7646
0,5	5	-5	0,5	-0,05	-98,412	-98,683	-96,783	-98,412	-94,340	-97,3260
				0,05	-95,155	-97,326	-99,498	-95,426	-97,055	-96,8920

Так как улучшений не наблюдается ни по одной из переменных, то на этом
этапе можно считать, что поиск завершен.

Таким образом, получили точку (0,5;5;-5;0,5;0), которая является решением
поставленной задачи, с критерием оптимальности уср= -97,8714.

После проведения поисков методом Гаусса-Зайделя из двух различных
начальных точек получили, что исследуемая функция является многоэкстремальной,
имеет несколько минимумов. По методу Гаусса-Зайделя, первый минимум находится в
точке (0;5;-5;0,3;0) со значением критерия уср= – 98,716, второй – в точке
(0,5;5;-5;0,5;0) с уср= -97,8714. Следовательно, можно сделать вывод о том, что
найденный минимум локальный.

.2 Метод с «наказанием
случайностью»

Из начальной точки (2;-2;1;3;1) с Уср=19,6464 ищем минимум критерия
оптимальности. Зададим число изменений Х = 30.

Поиск первой точки. Шаги для первой точки:

εiн= εi √ε
12+ε22+ε32 +ε42+ε52

εi=ε iн-0.5

xi+1=xi+h*ε, xi+1=xi+∆x

1) ε1=0,3561; ε2=0,7003; ε3=0,0525; ε4=0,5933; ε5=0,8041

ε1н = =
0,28

ε2н= =
0,55

ε3н= =
0,04

ε4н= = 0,47

ε5н= = 0,63

ε1 = 0,28-0,5= -0,22

ε2 =0,55-0,5=0,05

ε3=0,04-0,5= -0,46

ε4 =0,47-0,5= -0,03

ε5 =0,63-0,5=0,13

∆x1 = -0,22*2= -0,4

∆x2 =0,05*2=0,1

∆x3 = -0,46*2= -0,9

∆x4 = -0,03*2= -0,1

∆x5 =0,13*2=0,3

Первый
шаг (-0,4; 0,1; -0,9; -0,1; 0,3)

2) ε1=0,1855; ε2=0,0180; ε3=0,7538; ε4=0,2895; ε5=0,4584

ε1н = =
0,20

ε2н= =
0,02

ε3н= =
0,80

ε4н= = 0,31

ε5н= = 0,48

ε1 = 0,20-0,5= -0,30

ε2 =0,02-0,5= -0,48

ε3=0,80-0,5= 0,30

ε4 =0,31-0,5= -0,19

ε5 =0,48-0,5= -0,02

∆x1 =
-0,30*3= -0,9

∆x2 =
-0,48*3= -1,4

∆x3 =
0,30*3= 0,9

∆x4 =
-0,19*3= -0,6

∆x5 =
-0,02*3= -0,1

Второй
шаг (-0,9; -1,4; 0,9; -0,6; -0,1)

3) ε1=0,1673; ε2=0,2984; ε3=0,0333; ε4=0,7109; ε5=0,6263

ε1н = =
0,17

ε2н= =
0,30

ε3н= =
0,03

ε4н= = 0,71

ε5н= = 0,62

ε1 = 0,17-0,5= -0,33

ε2 =0,30-0,5= -0,20

ε3=0,03-0,5= -0,47

ε4 =0,71-0,5= 0,21

ε5 =0,62-0,5= 0,12

∆x1 =
-0,33*0,7= -0,2

∆x2 =
-0,20*0,7= -0,1

∆x3 =
-0,47*0,7= -0,3

∆x4 =
0,21*0,7= 0,1

∆x5 =
0,12*0,7= 0,1

Третий
шаг (-0,2; -0,1; -0,3; 0,1; 0,1)

4) Так как для двух переменных Х2 и Х3 достигнут максимум, то их
менять не будем.

ε1=0,6670; ε4=0,1659; ε5=0,0788

ε1н = = 0,96

ε4н= = 0,24

ε5н= = 0,11

ε1 = 0,96-0,5= 0,46

ε4 =0,24-0,5= -0,26

ε5 =0,11-0,5= -0,39

∆x1 =
0,46*0,5= 0,2

∆x4 =
-0,26*0,5= -0,1

∆x5 =
-0,39*0,5= -0,2

Четвертый
шаг (0,2; 0; 0; -0,1; -0,2)

№	Х1	Х2	Х3	Х4	Х5	У1	У2	У3	У4	У5	Уср	Комментарии
1	2	-2	1	3	1						19,6464
2	1,6	-1,9	0,1	2,9	1,3	11,782	14,768	14,497	9,611	13,140	12,7596	Шаги (-0,4; 0,1; -0,9; -0,1; 0,3) Улучшение
3	1,2	-1,8	-0,8	2,8	1,6	7,922	6,022	9,551	8,737	7,108	7,8680
4	0,8	-1,7	-1,7	2,7	1,9	4,823	5,366	8,623	4,008	6,451	5,8541
5	0,4	-1,6	-2,6	2,6	2,2	5,144	9,487	7,315	5,144	7,044	6,8269	Ухудшение
6	-0,1	-3,1	-0,8	2,1	1,8	-9,849	-7,135	-11,478	-6,864	-10,392	-9,1436	Шаги (-0,9; -1,4; 0,9; -0,6; -0,1) Улучшение
7	-1	-4,5	0,1	1,5	1,7	-8,911	-9,182	-7,011	-11,625	-6,468	-8,6393	Ухудшение
8	-0,3	-3,2	-1,1	2,2	1,9	-12,831	-10,117	-14,731	-13,374	-10,931	-12,3968	Шаги (-0,2; -0,1; -0,3; 0,1; 0,1) Улучшение
9	-0,5	-3,3	-1,4	2,3	2	-15,456	-15,999	-14,642	-17,085	-14,099	-15,4562
10	-0,7	-3,4	-1,7	2,4	2,1	-18,285	-20,456	-21,542	-19,642	-21,542	-20,2934
11	-0,9	-3,5	-2	2,5	2,2	-26,764	-25,950	-23,507	-25,679	-24,050	-25,1900
12	-1,1	-3,6	-2,3	2,6	2,3	-32,498	-31,955	-28,698	-30,055	-31,955	-31,0322
13	-1,3	-3,7	-2,6	2,7	2,4	-37,404	-33,061	-32,247	-36,861	-32,790	-34,4726
14	-1,5	-3,8	-2,9	2,8	2,5	-37,700	-39,057	-37,429	-40,686	-42,315	-39,4374
15	-1,7	-3,9	-3,2	2,9	2,6	-44,262	-45,076	-43,719	-46,976	-46,162	-45,2390
16	-1,9	-4	-3,5	3	2,7	-50,321	-51,407	-50,050	-53,579	-50,050	-51,0814
17	-2,1	-4,1	-3,8	3,1	2,8	-59,425	-58,611	-58,068	-57,254	-59,697	-58,6110
18	-2,3	-4,2	-4,1	3,2	2,9	-64,263	-64,534	-65,077	-63,177	-63,9912
19	-2,5	-4,3	-4,4	3,3	3	-71,366	-70,552	-72,180	-68,923	-72,995	-71,2032
20	-2,7	-4,4	-4,7	3,4	3,1	-78,853	-79,668	-78,853	-77,768	-75,596	-78,1476
21	-2,9	-4,5	-5	3,5	3,2	-87,014	-84,571	-84,029	-85,386	-85,657	-85,3314	Х3 не меняем и шагаем дальше
22	-3,1	-4,6	-5	3,6	3,3	-91,500	-88,514	-88,243	-90,143	-89,057	-89,4914
23	-3,3	-4,7	-5	3,7	3,4	-90,286	-94,900	-90,286	-90,557	-93,271	-91,8600
24	-3,5	-4,8	-5	3,8	3,5	-95,586	-97,214	-93,414	-97,486	-93,686	-95,4772
25	-3,7	-4,9	-5	3,9	3,6	-96,814	-97,086	-99,800	-98,986	-100,890	-98,7152
26	-3,9	-5	-5	4	3,7	-102,390	-103,200	-100,760	-103,200	-102,110	-102,3320	Х2 не меняем и шагаем дальше
27	-4,1	-5	-5	4,1	3,8	-100,580	-98,140	-101,400	-97,054	-101,400	-99,7148	Ухудшение
28	-3,7	-5	-5	3,9	3,5	-106,140	-103,690	-108,310	-104,780	-107,220	-106,0280	Шаги (-0,2; 0; 0; 0,1; 0,1) Улучшение
29	-3,5	-5	-5	3,8	3,3	-112,420	-109,430	-107,810	-109,980	-110,520	-110,0320
30	-3,3	-5	-5	3,7	3,1	-113,100	-113,640	-110,920	-111,470	-110,920	-112,0100

На данном этапе эксперимент может быть завершен, поскольку произвели 30
изменений Х. Получили точку (-3,3; -5; -5; 3,7; 3,1) с критерием оптимальности
Уср= -112,0100

Чтобы определить, является ли найденный экстремум глобальным или
локальным, возьмем новую начальную точку (-2;2;-1;-3;-1) с Уср = 9,4800 и
проведем заново весь поиск.

Поиск второй точки. Шаги для второй точки:

1) ε1=0,7569; ε2=0,4276; ε3=0,1191; ε4=0,4764; ε5=0,2731

ε1н = =
0,73

ε2н= =
0,41

ε3н= =
0,12

ε4н= = 0,46

ε5н= = 0,26

ε1 = 0,73-0,5= 0,23

ε2 =0,41-0,5= -0,09

ε3=0,12-0,5= -0,38

ε4 =0,46-0,5= -0,04

ε5 =0,26-0,5= -0,24

∆x1 =
0,23*3= 0,7

∆x2 =
-0,09*3= -0,3

∆x3 =
-0,38*3= -1,2

∆x4 =
-0,04*3= -0,1

∆x5 =
-0,24*3= -0,7

Первый
шаг ( 0,7; -0,3; -1,2; -0,1; -0,7)

2) ε1=0,3199; ε2=0,4557; ε3=0,1747; ε4=0,2722; ε5=0,9290

ε1н = =
0,28

ε2н= =
0,40

ε3н= =
0,15

ε4н= = 0,24

ε5н= = 0,82

ε1 = 0,28-0,5= -0,22

ε2 =0,40-0,5= -0,10

ε3=0,15-0,5= -0,35

ε4 =0,24-0,5= -0,26

ε5 =0,82-0,5= 0,32

∆x1 =
-0,22*0,9= -0,2

∆x2 =
-0,10*0,9= -0,1

∆x3 =
-0,35*0,9= -0,3

∆x4 =
-0,26*0,9= -0,2

∆x5 =
0,32*0,9= 0,3

Второй
шаг (-0,2; -0,1; -0,3; -0,2; 0,3)

3) ε1=0,9250; ε2=0,0052; ε3=0,8863; ε4=0,9696; ε5=0,0031

ε1н = = 0,58

ε2н= = 0,003

ε3н= = 0,55

ε4н= = 0,60

ε5н= = 0,002

ε1 = 0,58-0,5= 0,08

ε2 =0,003-0,5= -0,50

ε3=0,55-0,5= 0,05

ε4 =0,60-0,5= 0,10

ε5 =0,002-0,5= -0,50

∆x1 =
0,08*2= 0,2

∆x2 =
-0,50*2= -1

∆x3 =
0,05*2= 0,1

∆x4 =
0,10*2= 0,2

∆x5 =
-0,50*2= -1

Третий
шаг (0,2; -1; 0,1; 0,2; -1)

4) Так как
для переменной Х2 достигнут максимум, то ее менять не будем.

ε1=0,5257; ε3=0,1962; ε4=0,8640; ε5=0,0118

ε1н = = 0,51

ε3н= = 0,19

ε4н= = 0,84

ε5н= = 0,01

ε1 = 0,51-0,5= 0,01

ε3=0,19-0,5= -0,31

ε4 =0,84-0,5= 0,34

ε5 =0,01-0,5= -0,49

∆x1 =
0,01*5= 0,05

∆x3 =
-0,31*5= -1,5

∆x4 =
0,34*5= 1,7

∆x5 =
-0,49*5= -2,4

Четвертый
шаг (0,05; 0; -1,5; 1,7; -2,4)

5) Так как
для переменной Х5 достигнут максимум, то ее менять не будем.

ε1=0,7386; ε3=0,5429; ε4=0,9185

ε1н = = 0,42

ε3н= = 0,57

ε4н= = 0,71

ε1=0,42-0,5= -0,08

ε3 = 0,57-0,5= 0,07

ε4 =0,71-0,5= 0,21

∆x1 =
-0,08*2= -0,2

∆x3 =
0,07*2= 0,1

∆x4 =
0,71*2= 0,4

Пятый
шаг (-0,2; 0; 0,1; 0,4; 0)

6) Так как
для переменной Х3 достигнут максимум, то ее менять не будем.

ε1= 0,1859; ε4=0,3008

ε1н = = 0,53

ε4н= = 0,85

ε1=0,53-0,5= 0,03

ε4 =0,85-0,5= 0,35

∆x1 =
0,03*2= 0,05

∆x4 =
0,35*2= 0,7

Шестой
шаг (0,05; 0; 0; 0,7; 0)

7) ε1= 0,9828; ε4=0,8732

ε1н = = 0,75

ε4н= = 0,66

ε1=0,75-0,5= 0,25

ε4 =0,66-0,5= 0,16

∆x1 =
0,25*3= 0,7

∆x4 =
0,16*3= 0,5

Седьмой
шаг (0,7;0; 0; 0,5; 0)

8) ε1= 0,2633; ε4=0,4838

ε1н = = 0,48

ε4н= = 0,88

ε1=0,48-0,5= -0,02

ε4 =0,88-0,5= 0,38

∆x1 =
-0,02*5= -0,1

∆x4 =
0,38*5= 1,9

Восьмой
шаг (-0,1;0; 0; 1,9; 0)

№	Х1	Х2	Х3	Х4	Х5	У1	У2	У3	У4	У5	Уср	Комментарии
1	-2	2	-1	-3	-1						9,4800
2	-1,3	1,7	-2,2	-3,1	-1,7	14,336	17,051	15,693	18,679	16,236	16,3990	Шаги ( 0,7; -0,3; -1,2; -0,1; -0,7) Ухудшение. Шагаем в противоположную сторону.
3	-2,7	2,3	0,2	-2,9	-0,3	12,495	11,138	16,295	14,667	12,767	13,4724	Ухудшение
4	-2,2	1,9	-1,3	-3,2	-0,7	13,598	12,241	11,427	14,684	15,770	13,5440	Шаги (-0,2; -0,1; -0,3; -0,2; 0,3) Ухудшение. Шагаем в противоположную сторону.
5	-1,8	2,1	-0,7	-2,8	-1,3	8,590	7,776	9,947	11,304	8,862	9,2958	Улучшение
6	-1,6	2,2	-0,4	-2,6	-1,6	10,212	11,301	6,958	8,858	6,958	8,8575
7	-1,4	2,3	-0,1	-2,4	-1,9	10,094	9,551	9,008	7,108	8,8453
8	-1,2	2,4	0,2	-2,2	-2,2	9,872	6,615	7,429	10,958	8,515	8,6778
9	-1	2,5	0,5	-2	-2,5	10,382	7,668	10,111	12,282	9,296	9,9479	Ухудшение
10	-1	1,4	0,3	-2	-3,2	17,067	17,609	18,424	16,524	18,695	17,6638	Шаги (0,2; -1; 0,1; 0,2; -1) Ухудшение. Шагаем в противоположную сторону.
11	-1,4	3,4	0,1	-2,4	-1,2	0,055	3,583	0,055	1,683	3,312	1,7374	Улучшение
12	-1,6	4,4	0	-2,6	-0,2	-8,643	-5,657	-9,729	-6,471	-7,557	-7,6114	Шаг для Х2 делаем на границу
13	-1,8	5	-0,1	-2,8	0,8	-12,827	-11,470	-13,913	-15,270	-10,927	-12,8814	Х2 не меняем, и идем вдоль границы
14	-2	5	-0,2	-3	1,8	-11,634	-8,106	-9,191	-12,177	-11,906	-10,6028	Ухудшение
15	-1,75	5	-1,6	-1,1	-1,6	-47,608	-44,350	-42,450	-46,250	-47,608	-45,6532	Шаг (0,05; 0; -1,5; 1,7; -2,4) Улучшение
16	-1,7	5	-3,1	0,6	-4	-54,611	-55,969	-56,511	-52,983	-54,883	-54,9914
17	-1,65	5	-4,6	2,3	-5	-61,199	-60,656	-58,485	-59,299	-60,928	-60,1134	Шаг для Х5 делаем на границу
18	-1,6	5	-5	4	-5	-53,454	-52,911	-51,826	-52,369	-53,183	-52,7486	Ухудшение
19	-1,85	5	-4,5	2,7	-5	-57,952	-55,780	-56,595	-54,965	-55,509	-56,1602	Шаги (-0,2; 0; 0,1; 0,4; 0) Ухудшение. Шагаем в противоположную сторону.
20	-1,45	5	-4,7	1,9	-5	-61,855	-63,483	-63,212	-61,855	-61,040	-62,2890	Улучшение
21	-1,25	5	-4,8	1,5	-5	-68,605	-66,162	-68,333	-65,619	-66,976	-67,1390
22	-1,05	5	-4,9	1,1	-5	-68,692	-70,320	-70,863	-70,049	-71,678	-70,3204
23	-0,85	5	-5	0,7	-5	-73,787	-71,073	-72,159	-73,245	-69,173	-71,8874	Х3 не меняем, и идем вдоль границы
24	-0,65	5	-5	0,3	-5	-74,487	-71,502	-69,873	-74,487	-73,130	-72,6958
25	-0,45	5	-5	-0,1	-5	-73,430	-69,902	-70,173	-73,702	-72,616	-71,9646	Ухудшение
26	-0,6	5	-5	0,6	-5	-72,380	-69,666	-74,280	-72,651	-73,737	-72,5428	Шаги (0,05; 0; 0; 0,7; 0) Ухудшение. Шагаем в противоположную сторону.
27	-0,7	5	-5	-0,1	-5	-70,700	-74,500	-71,514	-70,157	-72,600	-71,8942	Ухудшение
28	0,05	5	-5	0,8	-5	-71,372	-72,186	-71,100	-69,472	-71,372	-71,1004	Шаги (0,7; 0; 0; 0,5; 0) Ухудшение. Шагаем в противоположную сторону.
29	-1,35	5	-5	-0,2	-5	-70,152	-69,880	-70,695	-71,237	-67,980	-69,9888	Ухудшение
30	-0,55	5	-5	2,2	-5	-68,229	-66,058	-67,686	-66,872	-64,700	-66,7090	Шаги (-0,1; 0; 0; 1,9; 0) Ухудшение.

На данном этапе эксперимент может быть завершен, поскольку произвели 30
изменений Х. Получили точку (-0,65; -5; -5; 0,3; -5) с критерием оптимальности
Уср= -72,6958. После проведения экспериментов двумя разными методами мы
получаем разные результаты, а это означает, что найденный минимум является
локальным.

3.Подбор реального процесса

Необходимо подобрать процесс с пятью влияющими выходными переменными.

Крекинг – переработка нефти и её фракций для получения главным образом
моторных топлив, а также химического сырья, протекающая с распадом тяжёлых
углеводородов. Бензин – самый важный продукт переработки нефти. Крекинг-процесс
позволяет увеличить выход бензина из сырой нефти. Но в процессе крекинга
образуется кокс, который снижает количество выхода крекинг-бензина. Для
устранения коксообразования при крекинге необходим ввод водорода, восполняющего
убыль из-за разложения легких продуктов, богатых водородом. Поэтому логическим
продолжением обычного крекинга является крекинг в присутствии водорода.
Промышленные процессы такого типа именуются гидрогенизационными. Гидрогенизация
есть совокупность реакций присоединения водорода, протекающих под влиянием
катализаторов в соответствующих условиях.

За критерий оптимальности примем количество образующегося кокса.

К основным параметрам гидрогенизационных процессов, относятся давление,
объемная скорость подачи сырья, количество циркулирующего водородсодержащего
газа и содержание в нем водорода, температура.

Давление в гидрогенизационных процессах следует рассматривать комплексно
– учитывать общее давление в системе и парциальное давление водорода в
циркулирующем газе. С повышением парциального давления водорода увеличивается
скорость гидрирования и достигается более полное удаление серы, азота,
кислорода и металлов, а также насыщение непредельных углеводородов; на
катализаторах, вызывающих деструкцию (гидрокрекинг), снижается содержание
ароматических углеводородов и асфальтенов и уменьшается закоксованность
катализаторов, что увеличивает срок их службы. Целесообразно также поддерживать
содержание водорода в циркулирующем газе на максимально возможном уровне.
Процесс гидроочистки лучше вести при повышенном парциальном давлении водорода –
в циркулирующем газе должно быть 75-90 объемн.% Н2 (во всяком случае, не менее
60 объемн,%). Снижение давления в реакторах гидроочистки с 40-50 до 28-30 ат
позволит сократить расход водорода на установке на 30% без ухудшения качества
очистки.

Объемная скорость подачи сырья может сильно влиять на результаты
гидрогенизации. Повышение скорости ведет к снижению интенсивности реакций,
вследствие этого снижаются расход водорода и коксообразование. Чем легче
продукт, подвергаемый гидрированию, тем более высокую объемную скорость можно
поддерживать в процессе. Обычно объемную скорость поддерживают на уровне 0,5-7
ч-1. При переработке продуктов, полученных из вторичных процессов, объемную
скорость приходится снижать по сравнению со скоростью переработки продуктов
такого же фракционного состава, но полученных при первичной переработке нефти.
Важное значение имеет и содержание серы в перерабатываемом сырье: чем оно выше,
тем ниже должна быть объемная скорость, так как скорость гидрирования
органических сернистых соединений выше, чем для других соединений (за
исключением кислородсодержащих). Выбор объемной скорости в значительной степени
зависит от природы и фракционного состава сырья, а также от технологии его
получения (первичная перегонка или вторичные процессы). При переработке того
или иного сырья необходимо выдерживать объемные скорости, соответствующие
данному сырью. Если на установку направляется новый вид сырья, приходится
менять объемную скорость; при этом меняется производительность установки и
другие параметры технологического режима. Если новое сырье, по сравнению с
ранее перерабатываемым, позволяет повысить объемную скорость,
производительность установки будет повышаться. При неизменных температурах,
объемной скорости и общем давлении соотношение циркулирующего
водородсодержащего газа и сырья влияет на долю испаряющегося сырья, парциальное
давление водорода и продолжительность контакта с катализатором.

Кратность циркуляции водородсодержащего газа. Соотношение между объемом
водородсодержащего газа при 0˚С и 0,1 МПа и объемом сырья при 20˚С,
поступающих в реактор, называется кратностью подачи (или кратностью циркуляции)
водородсодержащего газа. При стехиометрических соотношениях водород/сырье
реакции гидрирования сернистых соединений могут протекать практически нацело,
но скорость их будет очень мала из-за низкого парциального давления водорода.
Поэтому процесс проводят при избытке водорода. Количество подаваемого
циркулирующего водородсодержащего газа (в нормальных метрах кубических, нм )
приходящегося на 1 м жидкого сырья, называется кратностью циркуляции. Кратность
циркуляции ВСГ при гидроочистке бензиновых фракций не должна быть ниже 90 нм /м
сырья.

Концентрация водорода в циркулирующем водородсодержащем газе влияет на
необходимую кратность ВСГ к сырью и парциальное давление водорода в реакторе.
Оптимальной считается 70 %, в зависимости от состава сырья, содержания кокса и
хлора на катализаторе риформинга.

Температура. С повышением температуры жесткость процесса возрастает, что
приводит к снижению содержания серы, азота, кислорода и металлов в продуктах
гидрогенизации. По мере повышения температуры расход водорода увеличивается, а
затем может несколько снизиться, так как могут начаться реакции дегидрирования.
Однако до этого момента расход водорода возрастает весьма быстро при увеличении
температуры. Поэтому рекомендуется поддерживать температуру процесса возможно
более низкой, естественно, если это не отражается на качестве получаемых
продуктов. При этом надо стремиться еще и к тому, чтобы свести к минимуму
скорость отравления катализатора. При гидроочистке температуру поддерживают в
пределах 260-415 °С.

4. Список используемой литературы

1. Планирование эксперимента в
исследовании технологических процессов. Под ред. Лецкого Э.К. – М.: Мир, 1977.
– 572 с.

2. Статистические методы в инженерных
исследованиях. Под ред. Круга Г.К. – М.: Высшая школа, 1985. – 216 с.

3. Ахназарова С.Л., Кафаров В.В.
Оптимизация эксперимента в химии и химической технологии. – М.: Высшая школа,
1978. – 320 с.

4. Адлер Ю.П., Маркова Е.В., Грановский
Ю.В. Планирование эксперимента при поиске оптимальных условий. – М.: Наука, 1976.
– 280 с.

Источник

АКАДЕМИЯ НАУК СССР

НАУЧНЫЙ СОВЕТ ПО КОМПЛЕКСНОЙ ПРОБЛЕМЕ «КИБЕРНЕТИКА»

Секция «Математическая теория эксперимента»

УДК 519.24.001.5 : 62-50

Планирование эксперимента — новая научная дисциплина. Она применяется для решения широкого круга задач: построе ния интерполяционных моделей, изучения кинетики и ме ханизма явлений, оптимизации процессов и др. Наибольшее практическое значение имеет оптимизация процессов (плани рование экстремальных экспериментов). Этому направлению и посвящена монография. Она представляет собой вводный курс по планированию эксперимента при поиске оптималь ных условий.

Рассчитана на научных и инженерно-технических работников.

А	30501—013	© Издательство «Наука», 1976 г.
	055(02)—76 726-76

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ

Эта книга вышла из печати первым изданием в 1971 г. За про шедшее время авторам пришлось выслушать и прочесть большое число мнений о книге, высказанных читателями. Одновременно накапливался опыт использования книги в качестве учебного пособия или даже учебника (в Московском институте повышения квалификации Министерства химической промышленности СССР)

по курсу планирования эксперимента. Все мнения сводились к тому, что книгу следует переиздать, внеся многие исправления. Читатели высказывали самые различные суждения о’дополнениях, вплоть до включения в книгу планов второго порядка, отсеиваю щего эксперимента, априорного ранжирования и т. д. С одной стороны, включение в книгу подобного материала сделало бы ее весьма громоздкой, да и материал заслуживает, на наш взгляд, отдельного подробного рассмотрения, с другой стороны, некоторое расширение книги казалось целесообразным. В результате обсуж дений, колебаний и компромиссов родилась следующая структура второго издания.

Прежде всего возникла мысль дополнить вторую главу мате риалом по обобщенному критерию оптимизации, получившему в последнее время широкое распространение. Попытка подробно это изложить привела к появлению новой самостоятельной главы.

Желание дополнить изложение регрессионного анализа рас смотрением более сложных случаев (неравномерное дублирование опытов, критерии оптимальности планов й т. д.) привело нас к необходимости обратиться к матричному аппарату. Тем более, что он получает все более широкое распространение не только в теоретических, но и в прикладных публикациях. Так воз никла довольно большая глава по матричному аппарату рег рессии.

Хотя в тексте первого издания каждое существенное высказы вание авторы стремились систематически иллюстрировать приме

рами, последние оказались разрозненными, отрывочными и было много предложений о построении сквозного примера, чтобы можно было бы проследить все операции подряд от начала до конца. Учитывая это, мы построили такой пример.

Чтобы связать книгу со всей концепцией математической теории эксперимента, было решено написать главу по классифи кации планов (в ее написании принимал участие А. Н. Лисенков).

Особо отметим одно из наших решений — отказ от програм мированного способа изложения материала. Для этого, соб ственно, не было особых оснований в отзывах читателей, хотя некоторых читателей такая форма изложения раздражала и мешала чтению. Но не они определилй наше решение. Авторам казалось интересным проведение своеобразного педагогического эксперимента по обучению планированию с помощью как про граммированных, так и обычных учебников. Для этого надо иметь один и тот же материал, изложенный двумя способами: с программированием и без него. Разумеется, такой подход не является отказом от принципов программированного обучения.

Таким образом, в новом издании осуществлены значительные изменения объема и структуры материала без существенных выхо дов за рамки тематики, определенной первым изданием.

При подготовке этого издания нами учтены критические заме чания и пожелания многих читателей. Особенно авторы благо дарны Г. В. Лейбу, А. И. Смирнову, А. А. Сухову.

Авторы будут признательны за отзывы, предложения, замеча ния, которые можно направлять по адресу: 117333, Москва, ул. Вавилова, д. 40. Научный совет по комплексной проблеме «Кибернетика» при Президиуме АН СССР, секция «Математиче ская теория эксперимента».

ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ

Перед вами книга, посвященная одному из методов планиро вания эксперимента — методу Бокса — Уилсона. Ее задача — дать по возможности простое введение в предмет, рассчитанное на людей с высшим техническим образованием, а также студентов. Такая постановка задачи заставила отказаться от рассмотрения многих современных методов планирования эксперимента и огра ничиться подробным изложением одного метода.

Метод Бокса — Уилсона, пожалуй, простейший из методов планирования эксперимента. Однако его успешное применение зависит от решения многих вопросов, связанных с принятием неформализованных решений при выборе параметра оптимизации, факторов, плана экспериментов и при интерпретации резуль татов.

В книге сделана попытка на многих примерах рассмотреть эти вопросы, обычно не освещаемые в литературе. Примеры заим ствованы главным образом из собственных работ авторов. Это сделано не Дотому, что в литературе не было лучших. Просто для детального рассмотрения требуется слишком много информации, обычно отсутствующей в публикациях.

При изложении материала были использованы элементы про граммированного обучения — «метод многовариантного ответа». Это сравнительно новый метод изложения, хотя тенденция к его распро странению очевидна. Его цель — активизировать усвоение материала, выработать необходимые навыки.

Для эффективной проработки материала, изложенного в такой форме, вообще говоря, требуется специальный набор текста, когда значительная часть страницы остается пустой. К сожалению, по добное расточительство в настоящее время невозможно, и в дан ном издании пришлось прибегнуть к паллиативу: текст набран подряд, но порции информации пронумерованы.

Несколько слов о стиле. В книге сделана попытка вести изло жение в манере, близкой к разговорному языку. Это не долж но ввести читателя в заблуждение: какова бы ни была форма, для овладения предметом требуется серьезный систематический

ТРУД.

Книгу в рукописи прочло много людей, чьи доброжелатель ные отзывы и товарищеская критика постоянно поддерживали авторов, которые выражают им свою признательность. Особенно благодарны авторы А. И. Бергу, В. Г. Горскому, И. А. Гришкану, А. Н. Захарову, Ю. Л. Клокову, Ю. П. Назаренко, В. В. Налимову, Е. Л. Мамутову, Э. М. Менчеру.

ЦЕЛИ КНИГИ

Прежде чем вы начнете знакомство с планированием экспери мента, мы хотим познакомить вас с целями, которые преследовали авторы, приступая к написанию этой книги. Некоторые термины могут показаться вам незнакомыми, но это не должно вас смущать: далее они будут определены. Нам кажется, что такое начало позволит вам уяснить общую структуру книги, а также поможет проконтролировать себя после ее изучения.

Мы стремились, чтобы читатель, проработав эту книгу, усвоил, какая информация нужна для построения факторного экспери мента при оптимизации различных процессов. Получив эту инфор мацию, он сможет выбрать нужный план опытов, построить мате матическое описание процесса в области экспериментирования и провести статистический анализ, выбрать наикратчайший путь к оптимуму и осуществить движение до этому пути.

Авторы хотели бы, чтобы читатель, усвоив изложенный мате риал, смог:

применить методы планирования эксперимента при оптимиза ции многофакторных процессов;

дать определение параметру оптимизации; дать определение факторам, определяющим процесс; дать определение поверхности отклика; дать определение матрице планирования;

дать определение условиям ортогональности и ротатабельности;

дать определение полному факторному эксперименту 2к и дробным репликам от него;

дать определение уравнению регрессии; дать определение основным эффектам и эффектам взаимодей

ствия; дать определение кратчайшему пути к оптимуму;

выбрать параметр оптимизации; выбрать уровни факторов и интервалы их варьирования;

построить полный факторный эксперимент 2к и дробные реп лики от него;

получить уравнение регрессии; произвести статистический анализ уравнения регрессии;

произвести содержательную (например, физико-химическую) интерпретацию уравнения регрессии;

найти и реализовать кратчайший путь к оптимуму.

Мы стремились, чтобы читатель получил навыки, необходимые экспериментатору для принятия решений на основе использования методов планирования эксперимента в простейших случаях.

Получив эти навыки, читатель сможет:

выбрать область, в которой имеет смысл планировать экспери мент;

использовать имеющиеся данные при составлении плана экспе римента;

принять решение о необходимых действиях после получения и статистического анализа уравнения регрессии.

ОГРАНИЧЕНИЯ

Читатель не должен питать иллюзий относительно того, с чем ему предстоит познакомиться на следующих страницах.

Мы будем предполагать, что изучаемый процесс физически осу ществлен, и перед исследователем стоит задача его оптимизации.

Из многих возможных путей поиска оптимальных условий мы рассмотрим лишь один, который получил название метода Бокса — Уилсона или метода крутого восхождения.

Этот метод позволяет получать статические математическйе модели процессов, используя факторное” планирование, регрес сионный анализ и движение по градиенту.

Кроме того, мы будем предполагать, что: множество’’’ определяющих факторов задано, каждый из факторов управляем, результаты опытов воспроизводятся,

опыты равноценны, т. е. различием в стоимости можно пре небречь,

решается задача поиска оптимальных условий (или в некоторых случаях интерполяции),

математическая модель процесса заранее не известна.

Мы будем рассматривать задачи с числом факторов от двух до пятнадцати. (Но кое-что пригодится и при большем числе факторов.)

Некоторые менее существенные ограничения будут приве дены в тексте.

Конечно, столь ограниченная задача является частной, и вам может показаться, что на ее изучение не стоит тратить времени. Мы можем возразить так: это частная, но достаточно широко рас

пространенная на практике задача;	ее изучение служит осно
вой для понимания более сложных	задач.
Что&ы достигнуть вершин, надо		начать движение.

ВВЕДЕНИЕ

Некоторые люди, считая ошибочными все пра вила и наставления, глубоко убеждены в том, что величественное вложено в нас природой, а не постигается в обучении. . что способности чах нут и теряют свою естественность при соприкос новении с иссушающими природу учеными на ставлениями.

Греческий аноним. I в. н. э. О возвышенном

Мысль о том, что эксперимент можно планировать, восходит к глубокой древности. Наш далекий предок, убедившийся, что острым камнем можно убить-даже мамонта, несомненно выдвигал гипотезы, которые после целенаправленной экспериментальной проверки привели к созданию копья, дротика, а затем и лука со стрелами.

Он, однако, не пользовался статистическими методами, по этому остается непонятным, как он , вообще выжил и обеспечил тем самым наше существование.

Только в начале нашего века люди, наконец, поняли, что дальше дело так не пойдет, и придумали статистические методы планирования эксперимента. Честь открытия этой идеи принад лежит английскому статистику Рональду Фишеру (конец двад цатых годов), который впервые показал целесообразность одно временного варьирования всеми факторами в противовес широко распространенному однофакторному эксперименту [1] *. Понадо билось еще несколько десятилетий, чтобы в начале пятидесятых годов появилось новое направление в планировании экспери мента, связанное с оптимизацией процессов, — планирование экстремального эксперимента. Первая работа в этой области была опубликована в 1951 г. Боксом и Уилсоном в Англии [2]. Идея метода Бокса — Уилсона крайне проста. Экспериментатору пред лагается ставить последовательные небольшие серии опытов, в каждой из которых одновременно варьируются по определенным правилам все факторы. Серии организуются таким образом, чтобы после математической обработки предыдущей можно было выбрать условия проведения (т. е. спланировать) следующую серию. Так последовательно, шаг за шагом, достигается область оптимума.

Применение планирования эксперимента делает поведение экспериментатора целенаправленным и организованным, суще ственно способствует повышению производительности его труда и надежности полученных результатов. Важным достоинством

* Ссылки на литературу читатель найдет после каждой главы.

Источник

Математические методы оптимизации можно эффективно применять лишь при наличии математического описания оптимизируемого объекта. Если же математическое описание, достаточно точное в качественном и количественном отношении, отсутствует, то единственная возможность оптимизации заключается в исследовании реального объекта, для чего его оборудуют необходимыми измерительными средствами и проводят достаточно большое число экспериментов. Однако такой подход к отысканию оптимальных условий осуществления процесса обладает рядом принципиальных недостатков, к числу которых относится прежде всего сложность изменения аппаратурного оформления. Кроме того, не всегда удается оборудовать объект нужными измерительными средствами без значительного изменения нормального режима его работы. Наконец, достигаемые при оптимизации действующего объекта результаты носят обычно частный характер и почти не поддаются обобщению, что затрудняет накопление опыта, получаемого при оптимизации даже аналогичных производств. [c.40]

Применение метода наискорейшего спуска (подъема) в экспериментальных исследованиях для определения оптимальных условий осуществления процесса рассмотрено в главе I. Определение экстремума функции многих переменных, когда эта функция находится не в результате эксперимента, а при расчете по математическому описанию, рассмотрим на примере расчета констант скоростей по результатам эксперимента. [c.219]

Оптимальные условия осуществления процесса [c.82]

При помощи номограмм У1-2 и У1-3 можно быстро рассчитывать различные варианты реакторов и тем самым находить оптимальные условия осуществления процесса. Возможно также и аналитическое решение указанной задачи, которое в ряде случаев оказывается не более длительным, чем решение с применением графического метода. Поэтому в рассмотренном примере номограммы были использованы только для иллюстрации применения графического метода. [c.140]

Следующий пример показывает, как найти оптимальные условия осуществления процесса при помощи аналитического метода. [c.140]

Если й 1< а, т. е. порядок основной реакции меньше, чем порядок побочной реакции, то для преимущественного образования продукта Я нужно проводить процесс при низкой концентрации вещества А. Однако в этих условиях необходим реактор большого объема, т. е. требование получения продукта с минимальным количеством побочного вещества 5 и требование минимизации объема реактора являются в данном случае взаимно исключающими. Оптимальные условия осуществления процесса можно найти сопоставлением затрат на. очистку конечной смеси от побочного продукта 5 и затрат на приобретение и обслуживание реактора относительно большой емкости. [c.166]

Термодинамическим анализом модельной системы, содержащей метан, этан и водяной пар, определены возможность и оптимальные условия осуществления процесса паровой очистки природного газа от гомологов метана [13]. [c.111]

Всякий технологический адсорбционный процесс, независимо от того, по какой схеме он осуществляется — периодической или непрерывной, включает ряд обязательных стадий, в первую очередь стадий адсорбции и десорбции. Только комплексное рассмотрение равновесных и кинетических закономерностей адсорб-ционно-десорбционного цикла и вспомогательных стадий (охлаждение, сушка и т. д.) позволяет выявить оптимальные условия осуществления процесса в целом для рассматриваемой системы адсорбент—адсорбат и рекомендовать обоснованную методику инженерного расчета процесса. [c.503]

В итоге изучения взаимодействия ряда органических веществ природных и сточных вод окислителями (хлором, озоном и другими) определены оптимальные условия осуществления процессов их обесцвечивания, дезодорации и обеззараживания, а также установлены конечные продукты реакций, образующиеся в различных условиях, что позволило дать санитарно-гигиеническое обоснование использования окислительных процессов в технологии водоподготовки. Создана соответствующая аппаратура для использования на практике перечисленных процессов и разработаны измерительные приборы для контроля за их протеканием. [c.526]

Основные успехи в области получения высокочистых веществ химическим осаждением из газовой фазы достигнуты главным образом в результате эмпирического подбора оптимальных условий, основанного на экспериментальном определении влияния различных факторов на качество получаемых веществ. Несмотря на то, что в настоящее время накоплен большой материал, позволяющий оценить влияние таких факторов, как температура, состав газовой фазы, качество подложки, скорость и направление потока газов по отношению к реакционной поверхности, тем не менее для каждого конкретного случая необходимо подбирать оптимальные условия осуществления процесса исходя из самых общих, в основном, термодинамических положений и результатов экспериментального изучения кинетики химических реакций, лежащих в основе процесса. [c.104]

Зависимость безразмерной скорости активации от степени использования света вместе с зависимостью безразмерного квантового выхода от величины ф позволяют выбирать в каждом конкретном случае оптимальные условия осуществления процесса. [c.441]

Этапами математического моделирования являются 1) создание математического описания процесса на основе экспериментального изучения кинетики, массо- и теплопередачи, процессов перемешивания 2) разработка алгоритмов расчета процесса и программ для электронновычислительных машин (ЭВМ) 3) расчетное определение неизвестных коэффициентов (параметров) математического описания исследование устойчивости решения, параметрической чувствительности 4) расчетное исследование на ЭВМ изменения концентраций компонентов, температуры и давления процесса 5) расчетное определение оптимальных условий осуществления процесса. [c.266]

Пробные опыты, проведенные при ранее найденных оптимальных условиях, дали сниженное содержание оксалата иатрия в готовом продукте. Предположив, что при переходе к барабанному реактору оптимальные условия осуществления процесса изменятся, авторы поставили опыты, выявляющие новые условия работы. [c.257]

Как всякий гетерогенный процесс, растворение металлов в растворах электролитов включает в себя помимо стадии электрохимического растворения стадию массопереноса (отвод продукта анодного растворения от поверхности металла и перенос частиц, участвующих в катодных реакциях, в глубь раствора), осуществляемую конвективной диффузией. Суммарная скорость процесса растворения, определяемая как масса вещества, покидающая твердую фазу в единицу времени с единицы поверхности, лимитируется наиболее замедленной из этих стадий. Вопрос о лимитирующей стадии является важным в практическом отнощении и позволяет получить информацию, необходимую для выбора наиболее оптимальных условий осуществления процесса. [c.39]

К числу физико-химических диаграмм состав — свойство относятся и диаграммы фазовых превращений. Особенно часто пользуются этими диаграммами для решения вопросов, связанных с важнейшими операциями солевой технологии — с растворением и кристаллизацией солей из водных растворов. Выбор рациональных методов переработки сложных солевых систем (в частности, нри производстве удобрений), оптимальных условий осуществления процессов, состава исходных растворов и определение выхода продуктов значительно облегчаются при использовании равновесных диаграмм растворимости солей. Анализ этих диаграмм позволяет установить и закономерности образования природных солевых залежей, а в некоторых случаях предвидеть не только их состав, но и условия залегания. [c.67]

В ходе лабораторных исследований, которые обычно проводятся в идеализированных условиях (изотермический режим, кинетическая область, отсутствие примесей, низкие глубины превращения и небольшая продолжительность) выясняется механизм элементарных стадий, их последовательность и взаимосвязь и создается кинетическая модель, являющаяся основой математического описания и управления процессом. Этот этап разработки процесса обычно завершается выбором оптимальных условий осуществления процесса и выдачей первичного варианта регламента. [c.361]

В ходе проектирования и освоения непрерывного метода экстракции сланцевых фенолов в связи со склонностью продуктов к эмульгированию возникла необходимость разработки наиболее совершенных конструкций экстракционных аппаратов и определения оптимальных условий осуществления процесса. Это потребовало исследования механизма массопередачи из единичных капель. [c.174]

При определении оптимальных условий осуществления процессов тонкой каталитической очистки газов в некоторых случаях необходимо учитывать возможность изменения каталитических свойств контактов под воздействием компонентов реакционной смеси. Так, в работах Г. К. Борескова с сотрудниками по исследованию каталитической активности металлов в отношении реакции взаимодействия водорода с кислородом 2—5] установлено, что в случае непористого никелевого контакта при увеличении концентрации кислорода выше 0,1% при 180° С резко снижается активность и изменяется порядок реакции по кислороду от первого к нулевому, причем, чем ниже температура, тем при меньших концентрациях кислорода наступает этот критический переход. В случае же пористого катализатора критический переход не наступает даже при концентрациях кислорода до 2—2,5% и температурах выше 40° С. Это обусловлено тем, что контактный процесс в таких условиях протекает в области внешней диффузии. [c.124]

Для описания массообменных процессов можно применить не только коэффициент массопередачи, но и другой не менее важный показатель — коэффициент полезного действия (1 . п. д.) аппарата. Каждый из этих способов может дать необходимые данные для суждения об эффективности работы пенного аппарата и для его расчета. Выбор оптимальных условий осуществления процесса массопередачи должен быть основан на совместном анализе этих двух показателей. [c.73]

Основной принцип матеиатического моделирования состоит в том, что реальный процесс, представляющий собой слолшую сово -купность элементарных актов и явлений разнородной природы, исследуется не во всей его слозшости, а по отдельным составляющим уровням, инвариантным к масштабу осуществления процесса в целом. Полученная в результате этих исследований информация представляется в виде математических зависимостей, которые вместе с граничными и начальными условиями, характеризующими конкретную физическую обстановку, являются знаковой моделью про -цесса, его математическим описанием. Исследование математического описания (для чего зачастую приходится использовать вычислительную технику) позволяет найти оптимальные условия осуществления процесса, исследовать устойчивость и параметрическую чувствительность оптимальных режимов на основе чего можно обоснованно сформулировать требования к системе автоматического управления. [c.57]

Многообразие химических процессов обусловливает собой разхюобра-зие конструкций химических реакторов. Химический реактор является тем элементом технологической схемы, от совершенства которого зависит возможность осуществления в промышленных условиях всего производства. Общая теория химических реакторов за последние годы получила значительное развитие в результате применения метода математического моделирования химических процессов для решения задачи масштабного перехода от результатов лабораторных экспериментов к промышленным условиям. Успехи в области изучения химической кинетики, исследование явлений переноса тепла и вещества, сопутствующих химическим реакциям, и применение метода математического моделирования позволяют теперь более строго подходить к расчету промышленных реакторов, создавать новые эффективные конструкции реакторов большой единичной мощности и определять оптимальные условия осуществления процессов. [c.65]

Имеющиеся данные по равновесию в системе СаО—SO3— —Р2О5—Н2О [1, 2] и в системе СаО—Р2О5—Н2О [3—9] позволяют установить характер образующихся продуктов и с достаточной полнотой оценить выход кристаллизующихся веществ [10, 11] в зависимости от температуры и концентрации взаимодействующих реагентов. Однако для выбора оптимальных условий осуществления процесса и разработки рациональных способов кислотного разложения фосфатов необходимо также знание закономерностей, характеризующих скорость растворения фосфатов и кристаллизации образующихся твердых фаз. [c.9]

В результате изучения взаимодействия органических веществ природных вод с окислителями (хлором, озоном и другими) были определены оптимальные условия осуществления процессов обесцвечивания и дезодорации питьевых вод, а также установлены конечные продукты реакций, образующиеся в различных условиях. Это позволило дать санитарно-гигиеническое обоснование использования окислительных процессов при подготовке хо-зяйственно-питьевых вод высокого качества. [c.460]

Таким образом, расчеты термодинамического равновесия реакций диспропорционирования олефинов дают результаты, согла-суюшиеся с экспериментальными данными, и служат эффективным средством прогнозирования оптимальных условий осуществления процесса. [c.135]

Источник

Аннотация: Цель работы: изучить методику планирования активного эксперимента при поиске экстремума функции отклика как функции двух переменных — факторов. Среда программирования — MATLAB.

Теоретическая часть

Одной из центральных задач планирования эксперимента является задача поиска экстремума функции отклика [1] — например, при оптимизации производственных и других процессов.

Поиск экстремума функции отклика происходит путем исследования поверхности отклика. Это исследование осуществляется посредством измерения поверхности отклика в различных точках факторного пространства. Возникает вопрос: какой должна быть стратегия планирования эксперимента, чтобы число опытов (измерений), необходимое для нахождения экстремума или близких к нему значений, было как можно меньше?

Воспользоваться с этой целью непосредственно известными методами поиска экстремума функции многих переменных невозможно, поскольку “измерение” функции отклика в каждой точке факторного пространства происходит с ошибкой. Однако эти методы составляют основу методов поиска экстремума функции отклика.

При решении задач планирования эксперимента наибольшее распространение получили алгоритмы поиска, использующие градиентные методы. Их особенность состоит в том, что движение при поиске происходит в направлении не самого градиента, который неизвестен, а его оценки. Если функция отклика априорно выражается зависимостью 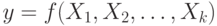$y = f(X_{1}, X_{2}, … , X_{k})$ , то оценка градиента 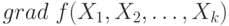$gradmbox{ }f(X_{1}, X_{2}, … , X_{k})$ в точке факторного пространства при этом находится по результатам измерений, проводимым в ее окрестности. Из класса градиентных методов практическое применение получил метод, разработанный Боксом и Уильсоном. В нем используется метод крутого восхождения в сочетании с последовательно планируемым факторным экспериментом для нахождения оценки градиента [1]. В общем виде метод Бокса и Уильсона состоит в следующем:

построение факторного эксперимента в окрестности некоторой точки;
вычисление оценки градиента в этой точке по результатам эксперимента;
крутое восхождение в направлении оценки градиента;
нахождение оценки максимума (минимума) функции отклика по этому направлению;
анализ оценки максимума функции отклика и принятие решения о дальнейшем восхождении.

1. Оценивание градиента

Рассмотрим оценивание градиента функции отклика, когда факторы имеют два уровня. Пусть функция отклика

(
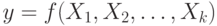10.1)

определена в области .

Используем произвольную точку факторного пространства 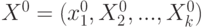как центр плана. Верхний 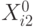$X_{i2}^0$ и нижний 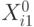$X_{i1}^0$ уровни выбираем симметричными относительно центра плана, чтобы перейти к кодированным переменным (факторам):

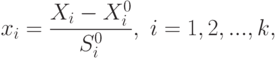
$x_i=frac{X_i-X_i^0}{S_i^0},mbox{ }i=1,2,...,k,$

где 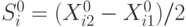$S_i^0=(X_{i2}^0-X_{i1}^0)/2$ — интервал варьирования.

Тогда функцию отклика (10.1) можно выразить через кодированные переменные:

(
10.2)

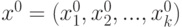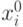
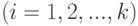Под задачей оценивания градиента теперь понимается определение оценки градиента функции отклика (10.2) в точке , где x_i^0 , т. е. в нулевой точке кодированных переменных. Принимаем, что в окрестности точки 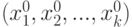функция отклика (10.2) допускает разложение по формуле Тейлора вида

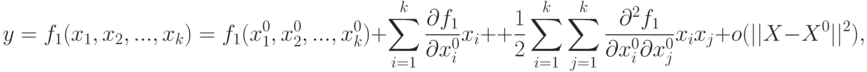$y=f_1(x_1,x_2,...,x_k)=f_1(x_1^0,x_2^0,...,x_k^0)+sumlimits_{i=1}^{k}frac{partial f_1}{partial x_i^0}x_i+\ +frac{1}{2}sumlimits_{i=1}^{k}sumlimits_{j=1}^{k}frac{partial^2 f_1}{partial x_i^0partial x_j^0}x_ix_j+ o(|| X-X^0||^2),$

(
10.3)

где $limlimits_{xto x^0} o(|| X-X^0||^2)=0$ .

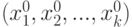Как известно [10], вектор-градиент функции в заданной точке есть

$gradmbox{ }f_1(x_1^0,x_2^0,...,x_k^0)= left( begin{array}{c} frac{partial f_1}{partial x_1^0} \ frac{partial f_1}{partial x_2^0}\ vdots\ frac{partial f_1}{partial x_k^0} end{array} right) = left( frac{partial f_1}{partial x_i^0}, frac{partial f_1}{partial x_i^0}, ..., frac{partial f_1}{partial x_i^0} right)^T.$

(
10.4)

Частные производные в (10.3) и в (10.4) рассчитываются в заданных точках и, таким образом, они представляют собой числовые значения.

Используем обозначения

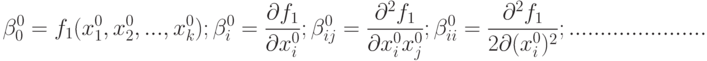$beta_0^0=f_1(x_1^0,x_2^0,...,x_k^0);\ beta_i^0=frac{partial f_1}{partial x_i^0};\ beta_{ij}^0=frac{partial^2 f_1}{partial x_i^0x_j^0};\ beta_{ii}^0=frac{partial^2 f_1}{2partial (x_i^0)^2};\ ......................$

(
10.5)

С учетом введенных обозначений (10.5) можно записать, что функция отклика будет определяться в следующем виде:

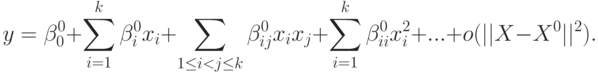$y=beta_0^0+ sumlimits_{i=1}^{k}beta_i^0x_i+ sumlimits_{1le i<jle k}^{}beta_{ij}^0x_ix_j+ sumlimits_{i=1}^{k}beta_{ii}^0x_i^2+...+o(|| X-X^0||^2).$

(
10.6)

Отметим также, что

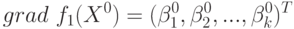
$gradmbox{ }f_1(X^0)=(beta_1^0,beta_2^0,...,beta_k^0)^T$

Разложение (10.6) можно рассматривать как многофакторное уравнение регрессии, линейное относительно своих коэффициентов.

Таким образом, для оценки градиента — оценки коэффициентов уравнения регрессии 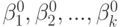можно использовать метод наименьших квадратов, с помощью которого возможно определить все коэффициенты аппроксимации поверхности отклика и затем выделить оценки коэффициентов 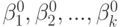, оценку градиента. Вид аппроксимации, количество слагаемых в разложении (10.6) задает исследователь по своим априорным сведениям.

2. Метод Бокса и Уильсона

Пусть функция отклика относительно кодированных переменных имеет вид

(
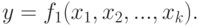10.7)

Для функции отклика (10.7) может быть найдена оценка градиента в точке .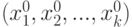

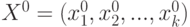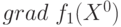Для поиска максимума функции отклика делается некоторый шаг (первый шаг) из точки в направлении оценки градиента $gradmbox{ }f_1(X^0)$ :

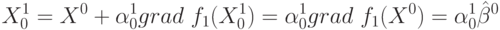$X_0^1=X^0+alpha_0^1 gradmbox{ }f_1(X^1_0)=alpha_0^1 gradmbox{ }f_1(X^0)=alpha_0^1 hatbeta^0$

(
10.8)

где:

— скаляр, параметр шага ;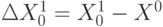

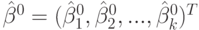— оценка градиента на предыдущем шаге;

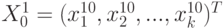$X^1_0=(x_1^{10},x_2^{10},...,x_k^{10})^T$ — новая точка факторного пространства.

Векторная запись (10.8) в координатной форме имеет вид

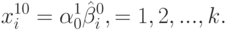$x_i^{10}=alpha_0^1 hatbeta_i^0,qquadi=1,2,...,k.$

(
10.9)

Переход от кодированных переменных $x_i^{10}$ к натуральным переменным $X_i^{10}$ осуществляется по формуле

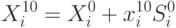$X_i^{10}=X_i^{0}+x_i^{10}S_i^{0}$

(
10.10)

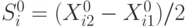где $S_i^{0}=(X_{i2}^{0}-X_{i1}^{0})/2$ .

В точке кодированных переменных (факторов) 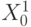$X_{0}^{1}$ следует произвести наблюдения функции отклика 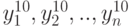$y_1^{10},y_2^{10},..,y_n^{10}$ и найти ее оценку:

$hat y_0^1=frac{1}{n}sumlimits_{u=1}^{n}y_u^{10}.$

(
10.11)

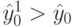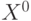Оценка функции отклика (10.11) есть результат измерений, которые производятся в реальных условиях с ошибками. Так как задача заключается в определении максимума функции отклика, естественно предположить, что оценка (10.11) значимо больше оценки в начальной точке, т. е. , где hat y_0 — оценка функции отклика в точке факторного пространства X^0 . Тогда можно сделать следующий шаг в направлении градиента (его оценки) 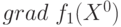$gradmbox{ }f_1(X^0)$ . Записывая (10.8) для -го шага, будем иметь точку факторного пространства, полученную в направлении оценки градиента, т. е.

(
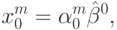10.12)

где $alpha_0^m >alpha_0^{m-1}>...>alpha_0^1$ .

Для каждого шага рассчитывается оценка функции отклика для всех точек плана. Например, для двухфакторного полного эксперимента потребуется четыре измерения функции отклика. для трехфакторного эксперимента — восемь измерений и т. д.

В направлении градиента производится средняя оценка функции отклика для значений $alpha_0^m >alpha_0^{m-1}>...>alpha_0^1$ параметров шага. Как только будет найдена максимальная оценка функции отклика, то ее и принимают за оценку максимума функции отклика при движении в направлении оценки градиента [1]. Определение максимума функции отклика осуществляется простым перебором и сравнением, что, однако, приводит к увеличению затрат на проведение эксперимента.

После определения максимума оценки функции отклика производится переход к системе координат натуральных факторов (переход от кодированных к натуральным). Относительно точки, в которой найдена оценка максимума функции отклика, строится новый факторный план со своими интервалами варьирования факторов. Снова вводятся кодированные переменные и производится расчет параметров линейной модели — коэффициентов уравнения регрессии. Определяются оценки составляющих градиента в новой точке планирования. Далее делаются шаги в направлении градиента, чтобы найти оценку максимума функции отклика.

Таким образом, организуется крутое восхождение к экстремуму функции отклика. В этом состоит схематичное изложение метода Бокса и Уильсона. Следует иметь в виду, что аналитический вид функции отклика, как правило, неизвестен.

В заключение следует отметить, что при планировании основная задача состоит в повышении эффективности эксперимента. Если эксперимент в реальных условиях является дорогостоящим, то поиск часто заканчивают при получении удовлетворительных для исследователя значений функции отклика без достижения области экстремума. Достижение области экстремума в этом случае по экономическим соображениям может оказаться нецелесообразным.

Источник

Поиск оптимальных условий

Введение

Теоретическая часть

1. Оценивание градиента

2. Метод Бокса и Уильсона

Вам также может понравиться

Как найти площадь в задаче по математике

Как найти волка среди овец

Как найти человека если компьютер не нашел

Добавить комментарий Отменить ответ