Как найти оптимум на графике

Как найти оптимум на графике

Общая полезность

Общая полезность – удовлетворение, которое получают от потребления определенного набора товара или услуги.

Предельная полезность – это прирост общей полезности товарного набора при увеличении объема потребления данного товара на единицу.

Mu = (Tu1 – Tu0)/(Q1 – Q0)

Производная по количеству Q

Mu = dTu/dQ
Как найти производную.

Например, TU = x*y. Mux = d(x*y)/dx = y; Muy = d(x*y)/dy = x

Например, TU = 10x2 + 2x + 2. Mux = d(10x2 + 2x + 2)/dx = 20x + 2

Функция полезности – функция, показывающая убывание полезности блага с ростом его количества:

Tu = f(Qi)

Условия равновесия потребителя

Условия равновесия потребителя можно выразить формулой:Mux / Muy = Px / Pyгде Px и Py – цены на товары X и Y.

Точка касания кривой безразличия с бюджетной линией означает равновесие потребителя.

Пример задачи на нахождение оптимального набора покупок

Пример задачи на нахождение оптимального набора товаров при заданной функции полезности

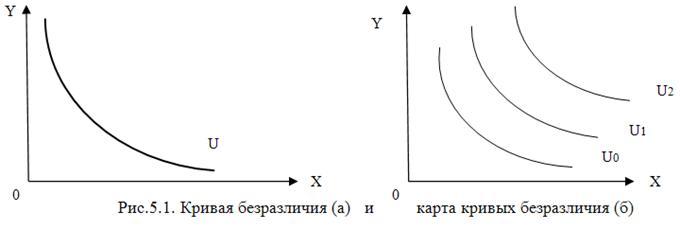
Кривая безразличия

Кривая безразличия – это множество точек на кривой, которые показывают различные комбинации двух экономических благ, имеющих одинаковую полезность для потребителя.

Предельная норма замещения (marginal rate of substitution – MRS) – количество, на которое потребление одного из двух благ должно быть увеличено (или уменьшено), чтобы полностью компенсировать потребителю уменьшение (или увеличение) потребления другого блага на одну дополнительную единицу:

MRSxy = ΔY / ΔXΔY = Y1 – Y0ΔX = X1 – X0илиMRSxy = Mux / Muy

Точка касания кривой безразличия с бюджетной линией означает оптимальный набор товаров потребителя.

Бюджетная линия

Бюджетная линия представляет собой прямую линию с отрицательным наклоном, графически отображающую множество наборов из двух товаров, требующих одинаковых затрат на их потребление. Она показывает, какие потребительские наборы можно приобрести за данную сумму денег.I = PxX + PyYгде I – доход потребителя;
Px – цена блага Х;
Py – цена блага Y;
X,Y – составляют соответственно купленные количества благ.

Пример. Функция полезности U(xy)=xy. Доход потребителя равен 80 ден. ед. Цены товаров x и y соответственно равны Px=2 руб. и Py=4 руб. Найдите равновесный набор.

Решение: Из условия равновесия потребителя: Mux / Muy = Px / Py получаем: Mux = d(x*y)/dx = y; Muy = d(x*y)/dy = x

Тогда: y / x = 2 / 4 = 1/2 или y = 1/2x

Для наших данных уравнение бюджетной линии запишем как: 80 = 2x + 4y = 2x + 4*1/2x = 4x

Откуда: x = 20 ед., y = 1/2*20 = 10 ед.

Ответ: потребитель приобретет 20 ед. товара x и 10 ед. товара y.

Пример решения определения оптимума потребителя

Потребитель тратит 600 рублей в месяц на приобретение двух товаров. Цена товара Х – 20 рублей, а товара Y – 10 рублей. Задана функция полезности потребителя U = ХY. Составить уравнение бюджетной линии. Найти предельную норму замещения. Определить оптимум потребителя. Представить графически. Если цена товара Х уменьшится на 5 руб., на сколько единиц изменится объем спроса данного товара всего?|Уравнение бюджетной линии:I = PxX + PyY 600 = 20X + 10Y

Предельная полезность товаров:

Mux = dU/dx = d(xy)/dx = yMuy = dU/dy = d(xy)/dy = x

Оптимум потребителя достигается при равенстве:

Mux / Muy = Px / PyMux / Muy = 20 / 10 = 2

Предельная норма замещения

MRSxy = Mux / Muy = 2

Выразим y через x.

Mux / Muy = y / x = 2y = 2x

Подставим в уравнение бюджетной линии:

600 = 20x + 10*2x = 20x + 20xоткуда X = 15; Y = 2x = 30

Точка касания кривой безразличия с бюджетной линией означает оптимальный набор товаров потребителя.

Точка касания кривой безразличия

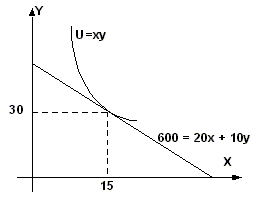
Проверка: 20 х 15 + 10 х 30 = 300 + 300 = 600.

При уменьшении цены товара X на 5 руб.
Px = 20 – 5 = 15
Найдем новый оптимум потребителя.

600 = 15X + 10Y = 15X + 20X = 35Xоткуда x = 17.14; y = 2x = 34.29
Спрос на товар Х увеличился на 2.14 (17.14 – 15)

Проверка: 15 х 17.14 + 10 х 34.29 = 257.1 + 342.9 = 600.

Пример нахождения цен товаров при оптимальном выборе покупателя

Утилитарное решение и решение, оптимальное по Нэшу

Определить утилитарное решение и решение, оптимальное по Нэшу, если функции полезности агентов равны u1 = х1 + 3, u2= 3х2 – 2 при х1 + x2 = 3 . Проверить независимость от масштаба для указанных ПКБ, если функция полезности первого агента была уменьшена в три раза.

Решение. Определим эгалитарное решение, для этого должно выполняться условие u1 = u2 или x1 + 3 = 3x2 – 2. Учитывая, что x2 = 3- x1, получаем x2 = 2, тогда x1 = 1. Вектор полезностей (4,4).

Утилитарное решение находим, максимизируя сумму полезностей агентов: x1 + 3 + 3x2 – 2 → max, подставив x1 вместо x2, получаем 4x2 + 1 → max. Рассматриваемая функция возрастает от x1 и достигает своего максимума при x1 = 3, тогда x2 = 0. Здесь вектор полезностей (1,1).

Независимость от масштаба

Определим эгалитарное решение, для этого должно выполняться условие u1 = u2 или x1/3 + 1 = 3x2 – 2. Учитывая, что x2 = 3- x1, получаем 10/3 x1 – 6 = 0, тогда x1 = 9/5, то x2 = 6/5. Вектор полезностей (8/5,8/5).

Множество допустимых распределений пары продуктов на неотрицательные количества определяется так:x1,x2 0, x1 + x1 = a, x2 = b.

Максимизируя ФКП Нэша, мы выбираем эффективное распределение. Оптимальное распределение определяется как решение задачи:

Максимизия ФКП Нэша

Утилитарное решение

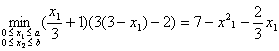
Минимум достигается x1 = 2,17; x2 = 0,83.

Видим, что соблюдается условия:
а) 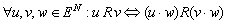эгалитарное решение,
б) 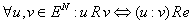оптимальное решение по Нэшу

Источник

 Теорема 1. Необходимые условия того, что х* является точкой Локального минимума (максимума) дважды дифференцируемой функции F на открытом интервале (A,B), выражаются следующими соотношениями:

Эти условия необходимы, но не достаточны для того, чтобы точка Х* была точкой локального минимума (максимума).

Определение. Стационарной точкой называется точка х*, в которой

,

Если стационарная точка не соответствует локальному оптимуму (минимуму или максимуму), то она является Точкой перегиба или седловой точкой.

Теорема 2. Пусть в точке х* первые (N-1) производные функции обращаются в нуль, а производная порядка N отлична от нуля. Тогда:

1)  если N – нечетное, то х* – точка перегиба;

2)  если N – четное, то х* – точка локального оптимума.

Кроме того,

A)   если эта производная положительная, то х* – точка локального минимума;

Б)  если эта производная отрицательная, то х* – точка локального максимума.

Замечание. Выше предполагалось, что рассматриваемая функция дифференцируема или, что её первая производная существует и непрерывна. Однако если функция не является дифференцируемой, во всех точках области определения, то даже необходимое условие наличия оптимума, позволяющее идентифицировать стационарные точки, может не выполняться в точке оптимума.

Пример 8.

Рассмотрим функцию

 Эта функция непрерывна во всех точках действительной оси, но недифференцируема при Х=2. Функция достигает максимума в точке Х=2, которая не является стационарной в соответствии с данным выше определением. Это подтверждает тот факт, что Теорема 1 является необходимым, но не достаточным условием оптимума.

Пример 9. Найти и идентифицировать оптимумы функции

Решение. Найдем первую производную функции:

Найдем стационарные точки. Для этого решим уравнение  Следовательно,  получили единственную стационарную точку Х=0. Найдем вторую производную  

Для идентификации точки оптимума, вычислим значение второй производной в стационарной точке.

Х

F(X)

0

-8

2

Значит, Х=0 – точка  минимума.

Пример 10. Найти и идентифицировать оптимумы функции

Решение. Сначала найдем первую производную функции:

.

Найдем стационарные точки. Для этого решим уравнение:

Следовательно, стационарные точки:  

Найдем вторую производную

Для идентификации точек оптимума, вычислим значение второй производной в стационарных точках.

X

F(x)

0

36

0

1

27.5

60

2

44

-120

3

5.5

540

 Значит, Х=1 х=3 – точки локальных минимумов, Х=2 – точка локального максимума.

Чтобы идентифицировать точку Х=0, найдем и вычислим третью производную:

Так как  и N=3 – нечетное, то (по теореме 2) Х*=0 – точка перегиба.

 Вопросы к главе 3

1.  Приведите определение функции.

2. Что такое область определения и область допустимых значений функции?

3. Какие существуют способы задания функции? Приведите конкретные примеры каждого способа.

4.  Дайте определения возрастания и убывания функции. Приведите примеры возрастающей и убывающей функций.

5.  Как проверить, является ли функция возрастающей или убывающей?

1. Приведите пример функции, описывающей зависимость предложения от цены. Постройте ее график.

2. Что такое точка перегиба и как её идентифицировать?

3.  Как проверить, является ли функция выпуклой или вогнутой?

4.  В чем состоит свойство унимодальности функций?

5.  Пусть данная точка удовлетворяет достаточным условиям существования локального минимума. Как установить, является ли этот минимум глобальным?

6.  Приведите алгоритм определения глобального оптимума.

< Предыдущая   Следующая >
Источник

Рентабельность и нахождение оптимума фирмы по графику

Данные об издержках совершенно конкурентной фирмы представлены графически:

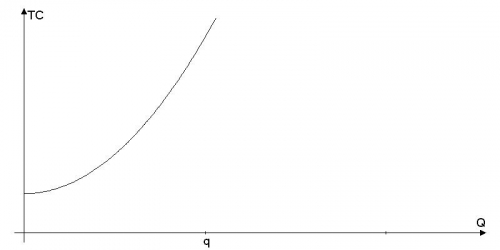
Такая функция издержек, к сожалению, не позволяет фирме получать положительную экономическую прибыль в краткосрочном периоде. При текущем выпуске $(Q = q)$ рентабельность фирмы составляет $(-50%)$.

  1. Найдите с помощью графика объем выпуска, минимизирующий убытки фирмы.
  2. Стоит ли фирме оставаться в отрасли в краткосрочном периоде?

Решение и ответ

  1. Восстановим график $TR$. Для совершенно конкурентной фирмы это прямая, выходящая из начала координат, так как цена постоянна. Для получения второй точки используем тот факт, что $pi (q) = – 0,5 cdot TC(q) Rightarrow TR(q) = 0,5 cdot TC(q)$: находим по графику $TC(q)$ и делим полученный отрезок пополам. В точке оптимального выпуска $P = MC$: наклоны графиков $TR$ и $TC$ должны совпадать. Значит, касательная, проведенная в точке оптимума к графику $TC$, должна быть параллельна графику $TR$. Исходя из этого и определяем точку оптимума (см. рис.).
  2. Как видно из графика, минимальные убытки фирмы $left( {TC(Q^* ) – TR(Q^* )} right)$ меньше, чем $FC = TC(0)$. Поэтому фирме стоит оставаться в отрасли.

 

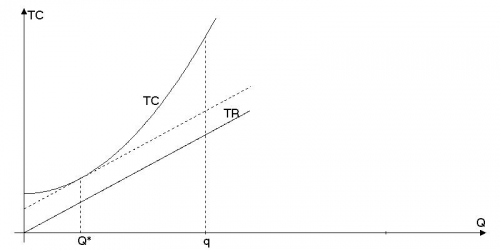
Ответ: 

1) см. рис. 2) да, стоит.

Источник

Оптимум функции

Содержание:

  1. Определение функции многих переменных.

Определение функции многих переменных.

Некоторые конкретные функции многих переменных хорошо знакомы, приведем несколько простых примеров:

Примеры:

а) объем прямоугольного параллелепипеда Оптимум функции — его длина, ширина и высота, т.е. объем прямоугольного параллелепипеда есть функция трех его измерений;

б) по формуле Герона площадь треугольника Оптимум функции, где а, Ь, с — длины трех его сторон, Оптимум функции — полупериметр, т.е. площадь треугольника есть функция трех аргументов — длин трех его сторон;

в) сила гравитационного притяжения между двумя телами Оптимум функции, где Оптимум функции — массы тел, R — расстояние между ними и Оптимум функции — гравитационная постоянная.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Все это — примеры функций трех независимых аргументов или временных. Независимыми аргументы называются потому, что значение, принятое одним из них, не определяет значений, которые могут принять другие аргументы.

Общее понятие функции было рассмотрено в п. 1 раздела 4.2 Части 1. Кратко повторим основное.

Пусть даны два множества Оптимум функции. Пусть каким-то способом Оптимум функции каждому элементу х множества X поставлен в соответствие один элемент Оптимум функции Тогда соответствие Оптимум функции называется функцией с областью определения Оптимум функции и областью значений Оптимум функции При этом х называется независимым переменным, или аргументом функции, а Оптимум функции— значением функции, или зависимым переменным.

Множество пар Оптимум функции называется графиком функции/ Определим теперь, что такое функция многих переменных. Ссьма часто элементы области определения функции сами могут иметь сложную структуру. Пусть имеется несколько множеств Оптимум функции

Возможно вам будут полезны данные страницы:

Примеры (функций многих переменных):

а) предприятие производит п видов продукции, которые реализует по ценам Оптимум функции; при объемах реализации Оптимум функциивыручка Оптимум функции Оптимум функции

о) определитель Оптимум функции квадратной матрицы размера 2 есть функция всех четырех элементов этой матрицы; пусть Оптимум функции тогда Оптимум функции

в) квартирная плата зависит от метража жилой или всей площади, от числа жильцов, от тарифов на электричество, газ, воду холодную и горячую, от льгот, которые имеют жильцы, но если для двух квартир в доме все эти показатели одинаковы, то и плата одна и та же; значит, размер квартирной платы есть функция от этих показателей;

г) налог, который должна заплатить фирма, рассчитывается по специальной методике, но если у двух фирм показатели одинаковы, то и налогдолжен быть одинаковым; значит, величина налога есть функция от этих показателей.

Оптимум функции

Оптимум функции

Лекции:

  • Метод неопределенных коэффициентов. Первая производная
  • Производные высших порядков
  • Логарифмы: примеры и решения
  • Производная и дифференциал
  • Правило Лопиталя: пример решения
  • Метод Жордана Гаусса
  • Некоторые простые неявные функции
  • Рациональные числа
  • Предел числовой последовательности
  • Пересекающиеся прямые

Источник

ПРЕДПОЧТЕНИЯ –
один из факторов, воздействующих на
выбор конкретных благ отдельными
потребителями.

Благо в теории
потребления
– любой объект потребления, доставляющий
определенное удовлетворение потребителю.

Набор благ
– совокупность конкретных видов благ
в определенных объемах, потребляемых
в данный период.

При выборе благ с
целью их покупки потребитель исходит
из достижения наибольшей выгоды при
имеющихся возможностях, которая
представляет собой меру удовлетворения
потребностей индивида, т. е. полезность.
Покупатель при выборе приобретаемых
благ обладает определенными индивидуальными
предпочтениями, но он ограничен в
удовлетворении своих предпочтений
бюджетным ограничением.

Полезность –
благо U
(ютиль) это способ эконом благ удовлетворяющ.
1 или несколько чел потребностей.

Функция полезности
– это
соотношение между объемами потребляемых
благ и уровнем полезности, достигаемым
при этом потребителем, т. е. показывает
предпочтения потребителя.

Порядковая
(это последовательность для данного
набора в котором распространены группы
набора) и количественная
функции
(оценка разности в уравнении благосостояния
каждого набора. Эта функция позволяет
определить не только общую, но и предельную
полезность блага).

ПОЛЕЗНОСТЬ
выражает
меру удовлетворения, которое получает
субъект от потребления блага или
выполнения какого-либо действия.

Полезность имеет
свойство порядковой измеримости, когда
альтернативы могут быть ранжированы,
но не имеет свойства количественной
измеримости.

Различают общую
и предельную полезность.

Общая (совокупная)
полезность
(ТU)–
это удовлетворение, которое получают
потребители от потребления конкретного
набора благ.

Предельная
полезность
(MU)
– это приращение степени полезности
при потреблении или использовании
дополнительной единицы блага за
определенный период времени. Предельной
полезностью называют полезность, равную
приращению, увеличению общей полезности
вследствие покупки дополнительной
единицы данного блага.

MU=
TU/
Q

11. Бюджетное ограничение и кривые безразличия. Кривая Энгеля.

Кривая
безразличия показывает
различные комбинации 2-х экономических
благ, имеющих одинаковую полезность
для потребителя. На рис.5.1(а) показана
кривая безразличия (U). По осям откладывается
количество блага Х и блага Y, между
которыми делает выбор потребитель.

Множество кривых
безразличия называется картой кривых
безразличия (рис.5.1б). Чем правее и выше
расположена кривая безразличия, тем
больше удовлетворения приносят
представленные ею комбинации благ.
Кривые безразличия имеют отрицательный
наклон, выпуклы относительно начала
координат и никогда не пересекаются
друг с другом. Поэтому через любую точку
можно провести лишь 1 кривую.

Зона замещения
(субституции) –
участок кривой безразличия, в котором
возможна эффективная замена одного
блага другим.

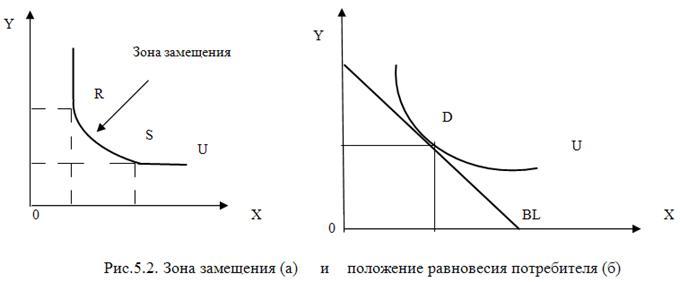На
кривой безразличия зона замещения
обозначена отрезком RS (рис.5.2а). Взаимная
замена благ Х и Y имеет смысл только в
пределах отрезка RS. Вне отрезка замена
исключается. Два блага выступают как
независимые друг от друга.

Бюджетное
ограничение (линия цен, прямая
расходов) показывает,
какие потребительские наборы можно
приобрести за данную сумму денег.
Если
I – доход потребителя, Рх – цена блага
Х, Рy – цена блага Y, а Х и Y составляют
купленные кол-ва благ, то уравнение
бюджетного ограничения можно записать
следующим образом:

I = Рх Х + Рy Y.

При Х=0, Y= I/Рy ,
т.е. весь доход потребителя расходуется
на благо Y. При Y= 0, Х = I/Рх, т.е. мы находим
кол-во блага Х, которое потребитель
может купить по цене Рх. Точка касания
кривой безразличия с бюджетным
ограничением (точка D) означает положение
равновесия потребителя (рис.5.2б).
Кривые
Энгеля –
иллюстрируют зависимость между объемом
потребления благ (C)
и доходом потребителя (I)
при неизменных ценах и предпочтениях.
Названа в честь немецкого статистика
Эрнста Энгеля, занимавшегося анализом
влияния изменения дохода на структуру
потребительских расходов.
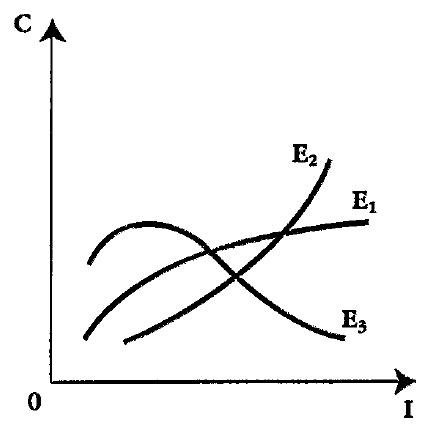На
оси абсцисс откладывается уровень
дохода потребителя, а на оси ординат —
расходы на потребление данного блага.
На графике показан примерный вид кривых
Энгеля:

E1 —
кривая для нормальных товаров;
E2 —
кривая для предметов роскоши;
E3 —
кривая для низкокачественных товаров.

12. Норма замещения
и предельная норма замещения. Оптимум
потребителя.
Предельная
норма замещения
– кол-во на которое потребитель 1блага
должно увеличив (уменьш.), чтобы
компенсировать потребителю уменьш.
(ув.) потреб. другого блага на 1доп. или
пред. ед.полезности.

Итак, кривые
безразличия показывают возможности
замены одного товара другим, а бюджетные
линии – то, что могут себе позволить
потребители. Какой товарный набор
выберет потребитель?

Первый критерий
– тот набор, который находится на
наиболее удаленной от начала координат
кривой безразличия, чтобы получить
больше полезности.

Второй критерий
– доход и цены, т. е. потребитель не может
выйти за пределы бюджетной линии.

Оптимум потребителя
предполагает сочетание обоих критериев.

Чтобы найти оптимум
потребителя на графике, необходимо
бюджетную линию наложить на карту
безразличия.

Оптимум потребителя
характеризует точка касания бюджетной
линии и кривой безразличия – точка е.
Любое отклонение от нее либо снижает
уровень потребления (точки а, в), либо
недоступно по средствам (точки d, c).

В точке е вариант
относительно самый дешевый и в рамках
дохода дает наибольшую полезность для
потребителя. Таким образом, точка е
характеризует положение равновесия
потребителя.

В точке оптимума
выполняется равенство:

Оно показывает,
что соотношение, в котором потребитель
при данных ценах способен замещать один
товар другим, равно соотношению, в
котором потребитель согласен на такую
замену без изменения уровня полезности.

13.Производство
экономических благ. Закон убывающей
предельной производительности.
Производство
– это деятельность по исполнению
факторов производства с целью достижения
наилучшего результата.

Закон убывающей
предельной производительности, как и
другие законы, действует в виде общей
тенденции и проявляется только при
неизменности применяемой технологии
и в короткий отрезок времени.

Для того чтобы
проиллюстрировать действие закона
убывающей предельной производительности,
следует ввести понятия:

общий продукт:
производство продукта с помощью ряда
факторов, один из которых является
переменным, а остальные – постоянными;

средний продукт:
результат деления общего продукта на
величину переменного фактора;

предельный продукт:
приращение общего продукта за счет
приращения переменного фактора.

Если переменный
фактор будет приращиваться непрерывно
бесконечно малыми величинами, то его
производительность будет выражаться
в динамике предельного продукта, и мы
сможем отследить ее на графике.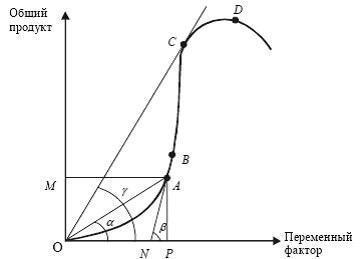

14. Правила
минимизации издержек и максимизации
прибыли.

где: MR –
предельный доход P–
цена L–
труд k –
капитал.

При MC
> MR –
прирост выпуска продукции становится
неэффективным. 
При MC
< MR –
фирма увеличивает спрос на факторы
производства до тех пор, пока доход от
их предельного продукта не уравновесится
с ценой каждого из применяемых факторов.
 

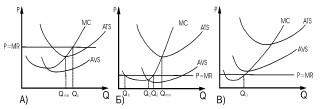
Оптимизация объема
производства в условиях максимизации
прибыли А), минимизации убытков Б), и
прекращения производства В).

В условиях
совершенной конкуренции максимизация
прибыли (минимизация убытков) достигается
при объеме производства, соответствующем
точке равенства цены и предельных
издержек.

Рис. показывает,
как происходит выбор в условиях
максимизации прибыли. Максимизирующая
прибыль предприятия устанавливает
объем своего производства на уровне
Qo, соответствующем точке пересечения
кривых MR и MC. На рисунке она обозначена
точкой О.

Правило наименьших
издержек –
условие, согласно которому издержки
минимизируются в том случае, когда
последний доллар , затраченный на каждый
ресурс , дает одинаковую отдачу –
одинаковый предельный продукт МР. Данное
правило аналогично правилу максимизации
полезности для потребителя.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Добавить комментарий