Общая полезность
Общая полезность – удовлетворение, которое получают от потребления определенного набора товара или услуги.
Предельная полезность – это прирост общей полезности товарного набора при увеличении объема потребления данного товара на единицу.
Mu = (Tu1 – Tu0)/(Q1 – Q0)
Производная по количеству Q
Mu = dTu/dQ
Как найти производную.
Например, TU = x*y. Mux = d(x*y)/dx = y; Muy = d(x*y)/dy = x
Например, TU = 10x2 + 2x + 2. Mux = d(10x2 + 2x + 2)/dx = 20x + 2
Функция полезности – функция, показывающая убывание полезности блага с ростом его количества:
Tu = f(Qi)
Условия равновесия потребителя
Условия равновесия потребителя можно выразить формулой:Mux / Muy = Px / Pyгде Px и Py – цены на товары X и Y.
Точка касания кривой безразличия с бюджетной линией означает равновесие потребителя.
Пример задачи на нахождение оптимального набора покупок
Пример задачи на нахождение оптимального набора товаров при заданной функции полезности
Кривая безразличия
Кривая безразличия – это множество точек на кривой, которые показывают различные комбинации двух экономических благ, имеющих одинаковую полезность для потребителя.
Предельная норма замещения (marginal rate of substitution – MRS) – количество, на которое потребление одного из двух благ должно быть увеличено (или уменьшено), чтобы полностью компенсировать потребителю уменьшение (или увеличение) потребления другого блага на одну дополнительную единицу:
MRSxy = ΔY / ΔXΔY = Y1 – Y0ΔX = X1 – X0илиMRSxy = Mux / Muy
Точка касания кривой безразличия с бюджетной линией означает оптимальный набор товаров потребителя.
Бюджетная линия
Бюджетная линия представляет собой прямую линию с отрицательным наклоном, графически отображающую множество наборов из двух товаров, требующих одинаковых затрат на их потребление. Она показывает, какие потребительские наборы можно приобрести за данную сумму денег.I = PxX + PyYгде I – доход потребителя;
Px – цена блага Х;
Py – цена блага Y;
X,Y – составляют соответственно купленные количества благ.
Пример. Функция полезности U(xy)=xy. Доход потребителя равен 80 ден. ед. Цены товаров x и y соответственно равны Px=2 руб. и Py=4 руб. Найдите равновесный набор.
Решение: Из условия равновесия потребителя: Mux / Muy = Px / Py получаем: Mux = d(x*y)/dx = y; Muy = d(x*y)/dy = x
Тогда: y / x = 2 / 4 = 1/2 или y = 1/2x
Для наших данных уравнение бюджетной линии запишем как: 80 = 2x + 4y = 2x + 4*1/2x = 4x
Откуда: x = 20 ед., y = 1/2*20 = 10 ед.
Ответ: потребитель приобретет 20 ед. товара x и 10 ед. товара y.
Пример решения определения оптимума потребителя
Потребитель тратит 600 рублей в месяц на приобретение двух товаров. Цена товара Х – 20 рублей, а товара Y – 10 рублей. Задана функция полезности потребителя U = ХY. Составить уравнение бюджетной линии. Найти предельную норму замещения. Определить оптимум потребителя. Представить графически. Если цена товара Х уменьшится на 5 руб., на сколько единиц изменится объем спроса данного товара всего?|Уравнение бюджетной линии:I = PxX + PyY 600 = 20X + 10Y
Предельная полезность товаров:
Mux = dU/dx = d(xy)/dx = yMuy = dU/dy = d(xy)/dy = x
Оптимум потребителя достигается при равенстве:
Mux / Muy = Px / PyMux / Muy = 20 / 10 = 2
Предельная норма замещения
MRSxy = Mux / Muy = 2
Выразим y через x.
Mux / Muy = y / x = 2y = 2x
Подставим в уравнение бюджетной линии:
600 = 20x + 10*2x = 20x + 20xоткуда X = 15; Y = 2x = 30
Точка касания кривой безразличия с бюджетной линией означает оптимальный набор товаров потребителя.
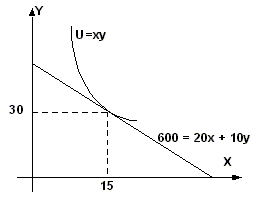
Проверка: 20 х 15 + 10 х 30 = 300 + 300 = 600.
При уменьшении цены товара X на 5 руб.
Px = 20 – 5 = 15
Найдем новый оптимум потребителя.
600 = 15X + 10Y = 15X + 20X = 35Xоткуда x = 17.14; y = 2x = 34.29
Спрос на товар Х увеличился на 2.14 (17.14 – 15)
Проверка: 15 х 17.14 + 10 х 34.29 = 257.1 + 342.9 = 600.
Пример нахождения цен товаров при оптимальном выборе покупателя
Утилитарное решение и решение, оптимальное по Нэшу
Определить утилитарное решение и решение, оптимальное по Нэшу, если функции полезности агентов равны u1 = х1 + 3, u2= 3х2 – 2 при х1 + x2 = 3 . Проверить независимость от масштаба для указанных ПКБ, если функция полезности первого агента была уменьшена в три раза.
Решение. Определим эгалитарное решение, для этого должно выполняться условие u1 = u2 или x1 + 3 = 3x2 – 2. Учитывая, что x2 = 3- x1, получаем x2 = 2, тогда x1 = 1. Вектор полезностей (4,4).
Утилитарное решение находим, максимизируя сумму полезностей агентов: x1 + 3 + 3x2 – 2 → max, подставив x1 вместо x2, получаем 4x2 + 1 → max. Рассматриваемая функция возрастает от x1 и достигает своего максимума при x1 = 3, тогда x2 = 0. Здесь вектор полезностей (1,1).
Независимость от масштаба
Определим эгалитарное решение, для этого должно выполняться условие u1 = u2 или x1/3 + 1 = 3x2 – 2. Учитывая, что x2 = 3- x1, получаем 10/3 x1 – 6 = 0, тогда x1 = 9/5, то x2 = 6/5. Вектор полезностей (8/5,8/5).
Множество допустимых распределений пары продуктов на неотрицательные количества определяется так:x1,x2 0, x1 + x1 = a, x2 = b.
Максимизируя ФКП Нэша, мы выбираем эффективное распределение. Оптимальное распределение определяется как решение задачи:
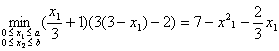
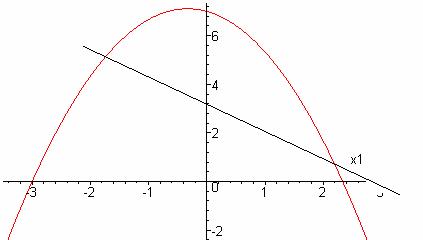
Минимум достигается x1 = 2,17; x2 = 0,83.
Видим, что соблюдается условия:
а) 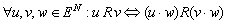 ,
,
б) 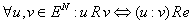
Кривые
безразличия и их свойства. Предельная
норма замещения.
-
П
 олезность
олезность
и доход. -
Условия
оптимума потребителя при порядковом
способе исчисления полезности. -
Эффект
замещения и эффект дохода.
1. Кривые безразличия и их свойства. Предельная норма замещения.
Пример.
Пусть есть два товара (обозначим их как
F
– food
и C
– clothes),
тогда U(F,C)
– функция полезности двух товаров,
показывающая степень удовлетворенности
от потребления этих товаров. Допущение:
U(F,C)
= FC,
что верно далеко не всегда. На основании
нижеследующей таб- лицы составим график,
называемый картой
безразличия
(рис. 12).
Кривая
безразличия –
линия равной полезности наборов товаров.
Карта
безразличия
– совокупность кривых безразличия,
каждая из которых соответствует своему
уровню полезности набора товаров.
Рис. 12. Карта
безразличия.

|
точка |
F |
C |
U(F,C) |
|
A |
5 |
5 |
25 |
|
B |
10 |
2,5 |
25 |
|
C |
2,5 |
10 |
25 |
Свойства
кривых безразличия:
-
Кривые
безразличия имеют отрицательный наклон. -
Две
кривые безразличия ни- когда не
пересекаются. -
Кривая
безразличия может быть проведена через
лю-бую точку В
в пространстве товаров. -
Предельная
норма замещения (замены) одного товара
другим уменьшается при движении вдоль
кривой безразличия. -
Кривые
безразличия выпуклы по отношению к
началу координат.
Норма
замены
– показывает, от какого количества
товара Y
мы отказываем- ся, чтобы получить
дополнительное количество единиц товара
Х
(обозначе- ние – RS
от англ. rate
of
substitution):
![]()
Предельная
норма замены
(обозначение – MRS
от англ. marginal
rate
of
substitution):
![]()
Норма
замены товара Х
товаром Y
– такое количество товара, которое
потребитель готов уступить в обмен на
увеличение другого товара на 1 с тем,
чтобы общий уровень удовлетворения
остался прежним. Величина MRS
соот- ветствует коэффициенту угла
наклона касательной к кривой безразличия
в данной точке.
Пример.
В качестве иллюстрации вышеприведенного
определения рас- смотрим следующую
таблицу:

|
Y |
16 |
8 |
5 |
3 |
|
X |
1 |
2 |
3 |
4 |
![]()
![]()
![]()
![]()
Рис.
13. Кривая
безразличия и MRS.
О тсюда
тсюда
видно, что при движении вниз по кривой
безразличия значениеMRS
уменьшается. Крайние случаи безразличия:
-
Эта
ситуация соответствует совершен-ной
взаимозаменяемости товаров. В данном
случае MRS
не изменяется.

-
Эта
ситуация соответствует взаимодополняемости
товаров (например, левый и правый
ботинки). В этом случае MRS
равно 0.

Ситуация,
когда товар Х
слишком дорогой:
![]()

-
Ситуация,
когда товар Y
слишком дорогой:
![]()
2. Полезность и доход. Условия оптимума потребителя при порядковом способе исчисления полезности.
Бюджетная
линия
– все сочетания товаров Х
и Y,
при которых общая сумма затрат равна
доходу. Для каждой бюджетной кривой
можно найти опи- сывающее ее уравнение.
Пример.
Вернемся к предыдущему примеру с едой
и одеждой. Введем стоимость наших
товаров: PF
= 1 у.е., PC
= 2 у.е. Составим таблицу:
|
Наборы |
F |
C |
Расходы |
|
A |
0 |
20 |
40 |
|
B |
10 |
15 |
40 |
|
C |
20 |
10 |
40 |
|
D |
30 |
5 |
40 |
|
E |
40 |
0 |
40 |
В
нашем случае бюджетная линия (ее
уравнение: F
+
2C
=
40)
будет
выглядеть так:

Рис.
14. Бюджетная
линия.
В
общем же случае уравнение бюджетной
линии записывается в виде
![]()
Для
удобства построения графика выразим
отсюда Y:
![]()
Задача.
Имеется
два продукта: Х
– “Пепси-Кола”, Y
–
лимонад.
Цена лимонада PY
= 12 у.е. Требуется найти: цену “Пепси-Колы”
PХ,
доход
потребителя
М
и уравнение бюджетной линии.
Р ешение
ешение
проведем в несколько шагов.
Шаг
1.
Определяем
доход:
![]() у.е.
у.е.
Шаг
2.
Находим
цену “Пепси-Колы”:
![]() у.е.
у.е.
Шаг
3.
Найдем
уравнение бюджетной линии:
![]()
Оптимум
потребителя
– наиболее эффективное использование
денежных средств или покупка товаров,
обладающих наибольшей полезностью. На
рис. 15 точка касания A
кривой безразличия и бюджетной линии
и есть точка оптимума потребителя.
 В
В
этой точке потребитель расходует весь
свой доход, максимально удовлетворяя
при этом все свои потребности. У кривыхI0
и I2
точек оптимума нет, а полезность наборов
В
и С
меньше полезности набора А.
Условие
потребительского оптимума при порядковом
способе измерения полезности записывается
в виде формулы
![]()
где
отношение
![]() показывает угол наклона бюджетной
показывает угол наклона бюджетной
линии.
Положение
бюджетной линии может меняться под
воздействием ряда факторов:
Рис.
15. Точка
потребительского оптимума.
-
Изменение
дохода. Цена –
потребление


2. Изменение
цен на товары. Доход – потребление
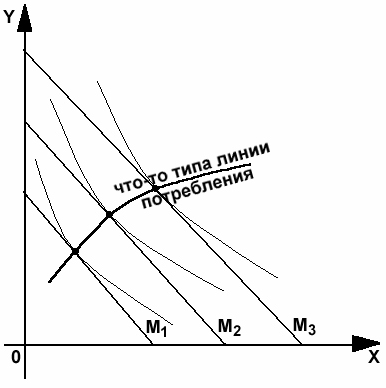

При
увеличении дохода мы начинаем больше
потреблять, однако, через не- которое
время наступает момент насыщения.
Соседние файлы в папке Лекции ЦИК
- #
17.04.2013100 б15Readme.txt
- #
- #
17.04.20132.04 Mб8Цены и конкуренциdoc
Оптимум потребителя
Задача №61. Расчёт оптимального объёма потребления двух благ
В таблице представлены следующие данные о предельной полезности двух благ.
| Количество, кг | Конфеты | Виноград |
|---|---|---|
| 1 | 60 | 150 |
| 2 | 40 | 120 |
| 3 | 20 | 90 |
Цена 1 кг конфет 80 ден. ед., а цена 1 кг винограда 160 ден. ед.
Бюджет потребителя составляет 400 ден. ед.
Определить оптимальный объём потребления конфет и винограда.
Решение
Задача №64. Расчёт оптимального объёма потребления
У Оксаны есть 30 рублей. Она хочет купить шоколадки «Шок» ценой 3 р. Полезность от этой покупки она оценивает функцией:
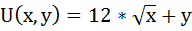
х – приобретённое количество шоколадок,
y – оставшаяся часть дохода.
Сколько купит шоколадок «Шок» рациональная Оксана?
Решение

ВНД, ВРП, ВНС

Счёт использования располагаемого дохода

Счёт производства





Рыночное рановесие

Рыночное равновесие

Рыночное равновесие

Эластичность

Задача №68. Расчёт оптимального набора потребителя
Потребитель свой располагаемый доход в размере 90 руб. тратит на приобретение кефира и картофеля.
Стоимость продуктов питания:
Ркеф = 15 руб. за 1 л.
Ркар= 3 руб. за 1 кг.
Предпочтения потребителя описываются следующей функцией полезности:
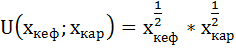
Насколько изменится оптимальный набор потребителя, если его предпочтения станут описываться функцией полезности вида:
1) 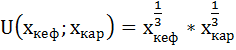
2) 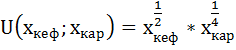
Решение
Задача №69. Расчёт оптимального объёма потребления
Маша тратит 140 р. в месяц на персики и клубнику.
а) Общая полезность персиков независимо от количества клубники оценивается в:
TU(x) = 30x – 2x2,
где
х – количество килограммов персиков в месяц.
Общая полезность клубники также не зависит от наличия персиков и составляет:
TU(y) = 20y – y2,
где
у – количество килограммов клубники.
Цена персиков – 10 р. за килограмм, а клубники – 20 р.
Сколько купит клубники рациональная Маша?
б) Предположим, что изменились условия в том, что касается полезности клубники:
TU(y) = 20y – ху.
в) Что будет, если общая полезность задаётся формулой:
TU(x,y) = 20y*30x – xy ?
Решение
Задача №84. Расчёт оптимального объёма потребления
Студент приобретает кофе и пирожки. Цена чашки кофе $2, пирожка $3. При этом он располагает бюджетом в размере $23. Известны предпочтения студента в виде общей полезности:
| Количество | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| TU кофе, ютилей | 20 | 36 | 50 | 62 | 72 | 80 | 86 |
| TU пирожков, ютилей | 36 | 66 | 93 | 117 | 135 | 144 | 150 |
Как потратить максимум бюджета так, чтобы купить набор этих двух благ с наибольшей полезностью? Сколько она составит?
Решение






ВВП



Индексы

Регрессия

Эластичность

Какими свойствами должен обладать набор товаров, с точки зрения инструментария кривых безразличия и бюджетных линий, который стремится выбрать потребитель и при данном соотношении цен и заданном бюджете?
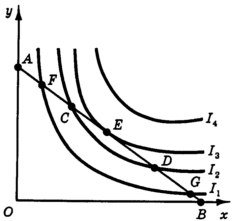
Напомним, что рациональный потребитель стремится к максимизации общей полезности.
На графике множество доступных нашему потребителю товарных наборов отображается треугольником ОАВ. Наборы товаров лежащие правее линии АВ потребителю не доступны.
Представим себе, что точка потребительского выбора в доступном множестве лежит ниже бюджетной линии АВ. Это означает, что некоторая часть потребительского дохода осталась неизрасходованной, а значит некоторый «объем» полезности остался недополученным.
Это означает, что точка оптимального потребительского выбора обязательно должна лежать на бюджетной линии АВ.
Какая же из точек на бюджетной линии соответствует оптимальному, с точки зрения потребителя, набору товаров? Рассмотрим точку F. Точка F лежит на пересечении бюджетной линии АВ и кривой безразличия I1. Очевидно, что точка F (и G) не являются наиболее предпочтительными для потребителя, поскольку при движении вниз по бюджетной линии от точки F и вверх по бюджетной линии от точки G потребитель переходит на более высоко расположенные кривые безразличия и, следовательно, на более высокий уровень полезности.
Очевидно, что если некоторая кривая безразличия пересекает бюджетную линию в двух точках, то все точки бюджетной линии между ними будут более предпочтительны для потребителя. И лишь в том только случае, если кривая безразличия имеет одну и только одну общую точку с бюджетной линией (точка Е), эта точка соответствует наиболее предпочтительному для потребителя набору товаров из всего множества доступных этому потребителю наборов.
Точка Е называется точкой потребительского оптимума, поскольку расположена на наиболее высоко лежащей из доступных потребителю кривых безразличия, т.е. соответствует наиболее высокому уровню удовлетворения при данных доходе потребителя и ценах товаров.
Формализуем найденное условие оптимума потребителя
Как известно, наклоны двух линий в точке их касания равны. Следовательно, в точке Е наклон бюджетной линии равен наклону кривой безразличия.
MRS = PX/PY или
MUx/MUy = PX/PY или
MUx/Px=MUy/Py
Добавив к этой формуле уравнение бюджетной линии (I = Y*Py+X*Px), мы получаем систему из двух уравнений, позволяющую найти оптимум потребителя при заданном бюджете.

|
|

|
|||
|
|||||
|
–
|




