Как найти орбитальную скорость астероида

Скорость астероида и движение самых крупных из них

Сегодня мы поговорим про скорость астероида, точнее его перемещения по бескрайним просторам нашей Вселенной. Как известно, эти твёрдые небесные тела движутся вокруг Солнца по своей определённой орбите, так же как и планеты. Но у каждого особый характер передвижения.

Что такое скорость?

По сути, это расстояние, пройденное объектом за единицу времени. Обычно, чтобы узнать скоростное значение, необходимо пройденное расстояние разделить на время, затраченное на преодоление этого расстояния.
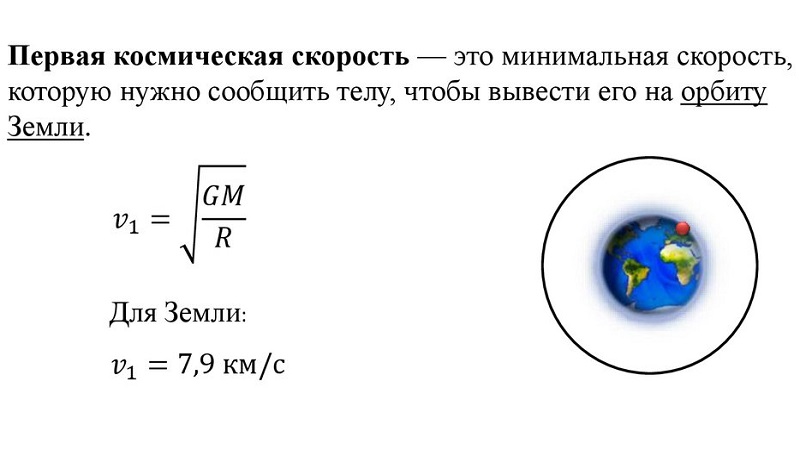
Правда, в физике и астрономии бывают разные виды этой величины. Например, выделяют первую космическую или круговую скорость. Это наименьшая горизонтальная скорость для заданной высоты над поверхностью планеты, которую нужно придать объекту, чтобы он смог двигаться по круговой орбите вокруг планеты.
Стоит отметить, такой темп для ближайшей земной орбиты равен 7,91 км/с. Вообще, учёные смогли найти круговую скорость практически каждого известного астероида.

Движение большинства астероидов

В космическом пространстве астероид летит со средней скоростью, которая составляет примерно 20 км/с. В среднем, период обращения вокруг Солнца занимает 3-9 лет.

Конечно, динамика движения отдельных астероидов различается. Однако она всегда выше второй космической скорости (11,2 км/с). При таких значениях космическое тело может пересиливать гравитационное притяжение планет.

Помимо этого, астероиды вращаются вокруг своей оси. Чаще всего на один полный оборот затрачивается около 7 часов. В сравнении с планетным это вращение небыстрое. Ведь астероидные объекты намного меньше планет. Собственно, поэтому сам оборот занимает меньше времени.

Самые большие астероиды и их скорость движения

Давайте рассмотрим как движутся некоторые крупные астероиды.
Прежде всего, нужно отметить астероид, а вернее карликовую планету, Церера. Она летит по орбите со скоростью 17,882 км/с и обращается вокруг Солнца примерно за 4,6 лет.

Хотя орбитальная скорость крупнейшего астероида Веста 19,346 км/с. При этом период обращения вокруг главной звезды составляет 3,628 лет.

А вот другой крупный астероид Паллада летит в темпе 17,645 км/с. Её полный оборот относительно Солнца практически соответствует Церере: он равен 4,618 годам.

Гигея перемещается со средней скоростью 16,753 км/с, а на один цикл вращения по окружности Солнца ей требуется 5,562 лет.

В то же время, астероид Европа обладает чуть большим показателем: 16,876 км/с. Соответственно, период обращения занимает немного меньше времени — 5,451 год.

Также определили среднюю скорость Гектора 13,012 км/с, который обращается вокруг Солнца за 11,989 лет.
Разумеется, здесь указан характер движения лишь самых известных астероидных тел. Вообще, их открыто около 300 тысяч. Но мы не будем перечислять все.

• 
• 
• 

Как уже было сказано, скоростные показатели превышают вторую космическую скорость и обладают необходимым темпом для удержания на планетных орбитах. По предположению учёных, могут быть не обнаруженные объекты, которые проворно и быстро проносятся по Вселенной (на огромных скоростях).

В любом случае, астероиды резво путешествуют в космосе. Наверное, поэтому они часто сталкиваются друг с другом, а также с другими небесными телами.

Оценка статьи:

(пока оценок нет)

Загрузка…

V is a measurement of visual magnitude, not velocity. Judging from the ephemeris data, it looks like you obtained information as the object was getting closer to earth. That would explain why the “v” was getting smaller. Smaller numbers in magnitude record brighter objects. Venus, for example is a “negative” number, while very distant, and dim objects have higher magnitude numbers.

I do not not know how to do this – however if your math is strong – then calculate the difference in RA (right ascension) and calculate the difference in declination (decl). These are the coordinates for 2011 CQ1.

Calculate the distance between each point. Record the time difference, as well, for each point calculated.

You can now determine the angular distance in arc seconds, or arc minutes.

As for velocity, in meters/second, or miles/hour – I’ve yet stumbled upon a clear cut example of how to do this.

Although, having imaged some known asteroids – and NASA has reported their diameter in kilometers – I have noted the time difference between frames – and measured the distance traveled in “asteroid” units (hehe).

Asteroid 1362 Griqua, for example, measures 28 km across. For arguments sake, it took 765 seconds to transverse 3.266 Griqua units. Which is 430 km/hr

In a separate measurement, I have recorded 26.13 “pixels” from one asteroid location, to the “last”, over 765 seconds. Griqua is 8 pixels across, in my image. 26.13 / 8 = 3.266 Griqua units.

28 km * 3.266 = 91.5 km
91.5 km / 765 seconds = 430 km/hr

There was a jump in imaging between my first and second frame resulting in:

1,445 seconds elapsed between a distance of 48.88 pixel distance (center to center).

48.88 / 8 = 6.11 Griqua units.
6.11 * 28km = 171 km
171 km / 1,445 s = 426 km / hr

Cheers!

P.S. – way beyond my ability – if I were to re-image this minor planet as it passed by Jupiter, and observed its perturbations – one could derive its mass. Just a thought.

PPS – disappointing as it may seem – 430 km / hr is way too slow for this asteroid. For instance, the earth velocity is 30 km/s which is 108,000 km / hr, and a German orbital velocity study of Griqua was 16.49 km/s which is 59,364 km / hr.

The earth was moving “away” from Griqua (as Griqua was moving towards the earth during my measurement. If there is a difference in velocity of 108,000 – 59,364 = of around 50,000 km / hr makes a measurement of 430 km off by two decimal places.

Too much error in fact to disregard the answer as being close.

I will be looking at the field of view (FOV) of the telescope. And most likely the “size” of the asteroid was dilated and blurry, and needs to be “sharpened”. If the visual was made smaller, the inherent velocity calculation would yield a much higher number. If this worlds out to 100x more, is unlikely, however.

A month later I decided to use actual mathematical calculations, and have verified them to be “precise”.

Here ya go:
So that I do not get lost in the labyrinth of my own observations, I am noting here that Skynet 1362 Griqua observation # is 2335994, and the ID and location of image 0 and image 7 are:
ID: 19892011 RA/DEC: 00:27:52.198 / -24:59:39.468
ID 19892018 RA/DEC: 00:27:54.559 / -24:59:11.705

Both imaged on Prompt-5 telescope employing a Lum filter, and 4 seconds exposure.

The Universal Time (UT) stamp on my first image (image 0) is 01:30:06.154, and on my last (image 7) is 02:06:53.926. Whew! That was a mouthful !

We convert the hours, and minutes to seconds to make the math easier, multiplying minutes by 60 and hours by 3600.

01:30:06.154 = 5,406.154 s
02:06:53.926 = 7,613.926 s

Now take the difference, which will result in the time that passed between observations of image (0) and image (7) at the telescope: 7,613.926 – 5,406.154 = 2,207.772 s

The time elapsed was 2,207.772 seconds !

That was some pretty basic arithmetic. Now we have to delve a little deeper into the frugal realm of Pythagorus.

c (squared) = a(squared) + b(squared)

Or if you will permit me to flaunt my limited mathematical prowess:

c = the square root of ( (aa) + (bb) )

Hurray for right ascension and declination. They are the known coordinates of where we looked into the night sky. They happen to have a happy relationship as right angles to each other.

If you would, “one goes up” while “the other goes down”. No? How about, “right ascension or RA” is like horizontal direction, and “declination or DEC” is our vertical direction?

Still no?,…ummm..ok – my bad – I’ll try again – RA and DEC are two legs of a right triangle and we are going to solve for the hypotenuse. Yup, sorry. You asked teacher back in high school, “what am I going to do with geometry?” – well, here it is, my fellow budding amateur.

Take the DEC values, from above, and convert the coordinates to arc seconds. Multiply the minutes by 60 and the degrees by 3600. Sounds familiar, doesn’t it?

24:59:39.469 = 89,979.469 arc seconds
24:59:11.705 = 89,951.705 arc seconds

Now take the difference to find the change in DEC for our images:
89,979.469 – 89,951.705 = 27.764 arc sec

Take the RA values, from above, and convert the coordinates to arc seconds. Again, multiply the minutes by 60 and the hours by 3600.

00:27:54.559 = 1,674.559 seconds
00:27:52.198 = 1,672.198 seconds

Now, take the difference to find the change in RA for our images:
1674.559 – 1,672.198 = 2.361 sec

Our noteworthy author points out that our RA system is a grid of bent lines from earth bound pole to pole. And that the closer to the poles, the less space between the lines. And the closer to the equator, the more space between the lines. This curvature issue is solved by introducing the cosine into our math.

Another way to look at this, is that the circles that circumscribe the earth, as we vary the latitude, get smaller and smaller as we work our way to either North or South pole. That is what the cosine is there for.

First convert the DEC to degrees by dividing the arc seconds by 3600:
27.764 / 3600 = 0.00771222 degrees

change in RA(adjusted) = RA in seconds X 15 X cosine(DEC in degrees)

[note: the declination in degrees is NOT the difference, it is the actual DEC rounded off to the nearest degree]

= 2.361 X 15 X cosine(-25)

= 2.361 X 15 X cosine (-25)
= 2.361 X 15 X (0.906307787037)
= 32.096890277915355

Back to old Pythagorus:

take the square root of:
(32.096890277915355 * 32.096890277915355 + (27.764 * 27.764)

(1030.210365512537234729) + (770.8396960) = 1801.050061512537234729
…
= 42.438780160515184566614 arc seconds

Calculating the angular velocity of asteroid Griqua on December 27, 2017 is:

=42.438780160515184566614 / 2207.772 seconds
= 0.019222446955806661451732 arc seconds / second

( yes-sir-ree Bob! that be “arc seconds” per “second” ! )

Now onto the clear blue waters of Tangential Velocity of my beloved Griqua.

We need to know its angular velocity (already calculated as above), and its distance. Since I have no parallax data to provide us with (which would be used to calculate distance to the asteroid) we will peer into one of NASA’s databases to find our distance, on the evening of December 27, 2017, and use the starting time of observation for our starting point in time. However, as we look into a National solution, we find none. So we expand our search to include those found across the pond.

Plugging in our date time group, for our first and last observation into the ephemerides generator, located at the AstDyS-2 sponsored by ESA, and being observant to enter the telescopes’ location at Cerro Tololo, observatory code: 807, I get a delta (distance to asteroid from Earth) that varies from 1.9204 astronomical units (AU) to 1.9206 AU. Let’s use 1.9205, shall we? (our Sidereal Times editor will provide a link to ephemerides data, here).

Using a Google provided calculator, we convert 1.9205 AU, found here:
https://www.calculateme.com/Astronomy/AstronomicalUnits/ToKilometers.htm

1.9205 Astronomical Units =
287,302,710.67935 Kilometers

Tangential Velocity = (Angular velocity X distance) / 206,265
Vt = (0.019222446955806661451732 X 287302710) / 206,265

Vt = 26.775 km/s

Космос представляет собой пространство наполненное энергией. Силы природы заставляют, хаотично существующую материю группироваться. Образуются объекты с определенной формой и структурой. В солнечной системе давно сформированы планеты, их спутники, но этот процесс не заканчивается. Огромное количество вещества: пыль, газ, лёд, камень и метал, наполняют космос. Эти объекты имеют классификацию.

Тело размером не более десятка метров называют метеороидом более крупное тело можно считать астероидом. Метеор это сгорающий в атмосфере объект, упав на поверхность, становится метеоритом.

В солнечной системе, открыты сотни тысяч астероидов. Некоторые достигают более 500 километров в диаметре. Массивы больших размеров принимают шарообразную форму и начинают классифицироваться учеными как карликовые планеты. Скорость астероидов ограничена присутствием в солнечной системе, они вращаются вокруг солнца. Паллада — на данный момент считается самым крупным астероидом, 582×556×500 км. Имеет среднюю скорость 17 километров в секунду, развиваемая астероидами скорость не превышает это значение более чем в два три раза. Названием астероидам служит дата их открытия (1959 LM, 1997 VG). После изучения, вычисления орбиты объект может получить собственное имя.

Небесные тела неизбежно сталкиваются друг с другом. Луна сохранила результат миллионов и миллионов лет взаимодействия. На земле огромные кратеры говорят о том, что когда-то, происходили глобальные разрушения. Люди всегда стремятся к контролю, все потенциальные угрозы должны иметь методы, технологии к их устранению. Очевидный вариант с применением ядерного оружия малоэффективен. Большая часть энергии взрыва попросту рассеивается в пространстве. Крайне важно как можно раньше обнаружить опасную глыбу, что не всегда получается. Хорошо то, что чем больше тело, тем легче его обнаружить.

В атмосферу каждый день влетают тонны космической пыли, ночью можно наблюдать, как небольшие метеорные тела сгорают, так называемыми «падающими звёздами». Каждый год метеороиды размером до нескольких метров попадают в воздушное пространство нашей планеты. Метеорит может входить в атмосферу со скоростью 100 000 км/ч. На высоте нескольких десятков километров скорость резко падает. Вообще сведения о скорости метеоритов размыты. Приводят пределы от 11 до 72 километров в секунду для метеоритов солнечной системы, залетные извне развивают на порядок большую скорость.

15 февраля 2013 года в Челябинской области упал метеорит. Предположительно его диаметр был от 10 до 20 метров. Скорость метеорита точно не определена. Яркое свечение болида наблюдалось за сотни километров от эпицентра. Болид взорвался на большой высоте. В видеоролике запечатлен момент вспышки, через 2 мин. 22 сек. приходит ударная волна.

Метеориты делят на каменные и железные. Состав всегда включает в себя смесь элементов с разнообразными пропорционными соотношениями. Структура может быть неоднородной с вкраплениями. Металлический сплав железных метеоритов отличного качества, подходит для изготовления всяких изделий.

» Планеты и их осколки » Какова скорость астероида?

С какой скоростью движутся небесные тела? Этот вопрос интересует многих. Нетрудно узнать, как быстро перемещаются автомобиль или ракета. Но вот с какой скоростью движутся астероиды, кометы и метеориты –выяснить гораздо сложнее. Но учёные всё же смогли ответить на этот вопрос.

Для начала нужно разобраться, что представляют собой эти небесные объекты. Начнём с астероидов. Это твёрдые тела, они так же, как и планеты, движутся вокруг Солнца по своим орбитам. Может возникнуть вопрос: чем же тогда астероиды отличаются от планет? Размерами. Эти небесные тела гораздо меньше, чем планеты. Величина астероидов может составлять от нескольких десятков до тысячи километров.

Сегодня нам известно около 20 тысяч этих космических объектов, 10 тысяч из них зарегистрированы, им присвоены определённые номера и собственные имена, например, Икар, 1950 DA. Движутся эти космические тела со скоростью примерно 20 км/сек и при столкновении уничтожают друг друга.

Кометы
Если говорить о кометах, то нужно для начала определить, какие небесные тела называют кометами. Итак, комета – это космический объект, состоящий из ядра и хвоста. Ядро состоит из замороженных газов, пыли и твёрдых вкраплений.
Когда комета подлетает близко к Солнцу или к другой звезде, она притягивает энергию этой звезды и начинает светиться. При этом у неё появляется хвост, размеры которого могут быть такими же, как расстояние от Земли до Солнца. В хвосте кометы содержатся ионизированные молекулы угарного газа. Средняя скорость движения комет составляет 20 км/с .

Метеориты
Что же касается метеоритов, то их размер гораздо меньше, чем размер астероидов, но больше размеров молекулы. Метеорит – это часть метеороида, которая достигает земной поверхности. При этом часть метеорита сгорает, «стирается» при попадании в атмосферу Земли. Метеориты бывают трёх видов: железоникелевые, железокаменные и каменные. Обычно эти космические объекты движутся со скоростью около 50 км/сек . Метеориты находят в пустынях, там их легче всего обнаружить.

Содержание статьи

• С какой скоростью метеорит падает на землю
• Почему звезды падают
• Где и когда можно наблюдать звездопад

Любое небесное тело, превышающее по размерам космическую пыль, но уступающее астероиду, называют метеороидом. Попавший в земную атмосферу метеороид именуется метеором, а упавший на земную поверхность – метеоритом.

Скорость движения в космосе

Скорость метеороидных тел, движущихся в космическом пространстве, может быть различной, но в любом случае она превышает вторую космическую скорость, равную 11,2 км/с. Такая скорость позволяет телу преодолевать гравитационное притяжение планеты, но она присуща лишь тем метеорным телам, которые родились в Солнечной системе. Для метеороидов, которые прилетают извне, характерны и более высокие скорости.

Минимальная скорость метеорного тела при встрече с планетой Земля определяется тем, как соотносятся направления движения обоих тел. Минимальная сопоставима со скоростью движения Земли по орбите – около 30 км/с. Это относится к тем метеороидам, которые движутся в том де направлении, что и Земля, как бы догоняя ее. Таких метеорных тел большинство, ведь метеороиды возникли из того же вращающегося протопланетного облака, что и Земля, следовательно, должны двигаться в том же направлении.

Если метеороид движется навстречу Земле, то его скорость прибавляется к орбитальной и потому оказывается более высокой. Скорость тел из метеорного потока под названием Персеиды, через который Земля каждый год проходит в августе, равна 61 км/с, а метеороиды из потока Леонид, с которым планета встречается между 14 и 21 ноября, имеют скорость 71 км/с.

Наибольшая скорость характерна для фрагментов комет, она превышает третью космическую – такую, которая позволяет телу покинуть пределы Солнечной системы – 16,5 км/с, к которой нужно прибавить и орбитальную скорость, и сделать поправки на направление движения относительно Земли.

Метеорное тело в земной атмосфере

В верхних слоях атмосферы воздух почти не препятствует движению метеора – он здесь слишком разрежен, расстояние между молекулами газа может превышать размеры среднего метеорного тела. Но в более плотных слоях атмосферы на метеор начинает воздействовать сила трения, и движение его замедляется. На высоте 10-20 км от земной поверхности тело попадает в область задержки, теряя космическую скорость и как бы зависая в воздухе.

В дальнейшем сопротивление атмосферного воздуха уравновешивается земной силой тяжести, и метеор падает на поверхность Земли подобно любому другому телу. Скорость его при этом достигает 50-150 км/с, в зависимости от массы.

Не всякий метеор достигает земной поверхности, становясь метеоритом, многие сгорают в атмосфере. Отличить метеорит об обычного камня можно по оплавленной поверхности.

В этой статье мы рассмотрим задачи, связанные с определением различных скоростей тел. При этом, в том числе, будем пользоваться понятием истинная аномалия. Это всего лишь угол между радиус-вектором тела и направлением на перицентр орбиты. То есть, если тело находится в перицентре, то истинная аномалия – ноль градусов, а если в апоцентре – то . По тому, на сколько отличается скорость тела от вычисленной для него параболической или круговой скорости, можно судить о форме орбиты: если скорость меньше параболической, но приближается к ней по значению, форма орбиты – сильно вытянутый эллипс с большим эксцентриситетом. Если скорость достаточно близка к круговой – то и форма орбиты почти круговая или с очень небольшим эксцентриситетом.

В частном случае задачи двух тел рассматривается движение тела меньшей массы относительно тела большей массы , принимаемого за неподвижное и называемого центральным телом.

Линейная скорость движущегося тела относительно центрального   определяется   интегралом   энергии

где , — большая полуось орбиты тела меньшей массы, — радиус-вектор того же тела, — гравитационная постоянная.

Если масса движущегося тела пренебрежимо мала в сравнении с массой центрального тела, то задача двух тел называется ограниченной и тогда .

Согласно интегралу энергии, чтобы тело меньшей массы обращалось вокруг центрального тела по круговой орбите (эксцентриситет ) радиусом , оно должно на этом расстоянии иметь скорость

называемую круговой скоростью. Как средняя скорость движения тела, она может быть также подсчитана по периоду обращения и большой полуоси орбиты тела:

Если движущееся тело на расстоянии от центрального тела имеет скорость

то орбитой будет парабола (, ). Поэтому скорость называется параболической.

Если , то движущееся тело пройдет мимо центрального тела по гиперболе ().

В каждой точке орбиты с радиус-вектором скорость тела

Точка эллиптической орбиты, ближайшая к центральному телу, называется перицентром, а наиболее удаленная от него—апоцентром. Эти точки получают конкретные наименования но названию центрального тела, например, для Земли – апогей и перигей, для Луны – апоселений и периселений.

В перицентре, при , тело-спутник обладает наибольшей скоростью

а в апоцентре, при , — наименьшей   скоростью

Скорость небесных тел всегда выражается в км/с, а расстояния могут быть заданы в астрономических единицах, километрах или радиусах центрального тела. Поэтому в формулы необходимо подставлять значения расстояний в одинаковых единицах измерения.

В поле тяготения Солнца, на произвольном от него расстоянии , выраженном в астрономических единицах (а. е.), круговая скорость (км/с)

Если расстояния заданы в километрах, а масса центрального тела выражена в массах Земли, то круговая скорость (км/с)

Наконец, при измерении масс в массах Земли и расстояний в радиусах Земли круговая скорость (км/с)

Средняя или круговая скорость тела, обращающегося вокруг центрального тела по эллиптической орбите с большой полуосью , вычисляется по тем же формулам с подстановкой в них .

Подстановка в последние формулы ( – радиус небесного тела) дает значение круговой скорости  у поверхности этого тела, называемой в космонавтике первой космической скоростью. Вторая космическая скорость . Очевидно, что

где отсчитывается от центра небесного тела и выражается в его радиусах.

Третий обобщенный закон Кеплера

применим к любым системам тел с массами и , обращающихся с периодами и вокруг своих центральных тел (с массами и ) по эллиптическим орбитам, большие полуоси которых соответственно равны и .

Массы планет и их спутников выражаются обычно в массах Земли (реже – в массах Солнца, в тоннах и килограммах), большие полуоси орбит – в астрономических единицах или в километрах, а периоды обращения- в годах и сутках, а иногда – в часах и минутах.

При вычислениях по формуле закона Кеплера выбор системы единиц не имеет значения, лишь бы однородные величины были выражены в одинаковых единицах. Если же этот закон используется в виде

то решение задач проводится обязательно в определенной системе единиц, так как в разных системах численное значение гравитационной постоянной различно.

Если периоды обращения заданы в земных средних сутках, расстояния – в километрах и массы тел – в массах Земли, то третий закон Кеплера имеет вид

Задача 1.

Чему равна круговая и параболическая скорость относительно Солнца на средних расстояниях Венеры (0,723 а. е.), Земли (1,00 а. е.), Юпитера (5,20 а. е.) и Плутона (39,5 а. е.)? По общим результатам найти и объяснить найденную закономерность. Расстояния планет от Солнца указаны в скобках.

Для Венеры

Для Земли

Для Юпитера

Для Плутона

Ответ: для Венеры круговая скорость равна 35,02 км/с, параболическая – 49,5 км/с; для Земли круговая 29,78 км/с, параболическая 42,11 км/с; для Юпитера круговая 13,06 км/с, параболическая 18,47 км/с; для Плутона круговая 4,74 км/с, параболическая 6,70 км/с. С удалением от Солнца скорость падает.

Задача 2.

Вычислить скорость малых планет Ахиллеса и Гектора в перигелии и афелии, если их круговая скорость близка к 13,1 км/с, а эксцентриситеты орбит соответственно равны 0,148 и 0,024. Примерно на каком среднем гелиоцентрическом расстоянии находятся эти планеты?

Скорость в перигелии можно вычислить по формуле:

Для Ахиллеса

Для Гектора

Скорость в афелии можно вычислить по формуле

Для Ахиллеса

Для Гектора

Так как

То среднее гелиоцентрическое расстояние равно

Ответ: для Ахиллеса скорость в перигелии 15,2 км/с, в афелии 11,2 км/с. Для Гектора скорость в перигелии 13,41 км/с, в афелии 12,7 км/с. Среднее гелиоцентрическое расстояние 5,48 а.е.

Задача 3.

Большая полуось и эксцентриситет opбиты Меркурия равны 0,387 а. е. и 0,206, а орбиты Марса — 1,524 а. е. и 0,093. Найти среднюю скорость этих планет, их скорость в перигелии и в афелии.

Рассчитаем перигельное и афелийное расстояния для Меркурия:

Определим круговую скорость:

Определяем скорость в перигелии:

И скорость в афелии:

Теперь все то же проделаем для Марса:

Рассчитаем перигельное и афелийное расстояния:

Определим круговую скорость:

Определяем скорость в перигелии:

И скорость в афелии:

Ответ: для Меркурия км/с, км/с, км/с; для Марса км/c, км/с, км/c.

Задача 4.

Считая орбиты планет круговыми и лежащими в плоскости эклиптики, найти лучевую скорость Меркурия, Венеры и Марса во время их основных конфигураций. Необходимые для решения данные заимствовать из задач 1 и 3. (Лучевой скоростью называется проекция пространственной скорости на луч зрения наблюдателя, т. е. в данном случае на направление от Земли к планете.)

Для Венеры и Меркурия основной конфигурацией будет нижнее соединение, так как это внутренние планеты. Также можно рассмотреть восточную и западную элонгации. Для Марса, который является внешней планетой, можно рассмотреть противостояние и обе квадратуры, восточную и западную.

Лучевая скорость во всех случаях, когда планеты расположены радиально, равна нулю: это соединения и противостояния. При элонгациях лучевую скорость можно найти как разность круговой скорости планеты и проекции скорости земли на линию, соединяющую планеты. Это хорошо поясняет рисунок ниже.

Для Венеры круговая скорость– 35,02 км/c, для Меркурия – 47,87 км/с.

Определим косинус угла для Меркурия:

Определим косинус угла для Венеры:

Проекция скорости земли на линию, соединяющую планеты, будет равна

Определяем проекцию скорости Земли на линию, соединяющую планеты, для Меркурия:

Для Венеры:

Таким образом, лучевая скорость Меркурия в элонгациях

Лучевая скорость Венеры в элонгациях:

Примерно так же обстоит дело с квадратурами. Чтобы определить скорость планеты в квадратурах – а она будет одинакова и для западной, и для восточной квадратуры, надо найти проекцию круговой скорости планеты на линию, соединяющую обе планеты.

Определим для этого из треугольника расстояний между планетами и Солнцем:

Тогда проекция скорости Марса равна

Таким образом, лучевая скорость Марса в квадратурах

Ответ: лучевые скорости внутренних планет в соединениях равны 0, в элонгациях для Меркурия – 20,41 км/с, для Венеры – 14,45 км/с . Для внешних планет лучевые скорости в противостояниях равны 0, в квадратуре для Марса лучевая скорость равна 13,97 км/с.

Задача 5.

Вычислить скорость астероидов Лидии и Адониса на их среднем, перигельном и афелийном расстояниях, а также круговую и параболическую скорость на этих расстояниях. Большая полуось и эксцентриситет орбиты первого астероида равны 2,73 а. е. и 0,078, а второго— 1,97 а. е. и 0,778.

Сначала сделаем расчет для Лидии, а затем повторим все действия для Адониса.

Рассчитываем круговую скорость:

Перигельное расстояние:

Рассчитываем афелийное расстояние:

Скорость в перигелии:

И скорость в афелии:

Круговая скорость Лидии на среднем гелиоцентрическом расстоянии км/с, параболическая скорость на этом расстоянии км/с.

На перигельном расстоянии круговая скорость астероида

Параболическая скорость:

На афелийном расстоянии круговая скорость астероида

Параболическая скорость:

Повторим все действия для Адониса.

Рассчитываем круговую скорость:

Перигельное расстояние:

Рассчитываем афелийное расстояние:

Скорость в перигелии:

И скорость в афелии:

Круговая скорость Адониса на среднем гелиоцентрическом расстоянии км/с, параболическая скорость на этом расстоянии км/с.

На перигельном расстоянии круговая скорость астероида

Параболическая скорость:

На афелийном расстоянии круговая скорость астероида

Параболическая скорость:

Ответ: Лидия: круговая скорость 18,02 км/с, в перигелии 19,27 км/с, в афелии 16,85 км/c, круговая скорость на среднем расстоянии 18,02 км/с, в перигелии 18,57 км/с, в афелии 17,36 км/с, параболическая скорость на среднем расстоянии 25,38 км/с, в перигелии 26,2 км/с, в афелии 24,49 км/с.

Адонис:  круговая скорость 21,21 км/с, в перигелии 60,51 км/с, в афелии 7,43 км/c, круговая скорость на среднем расстоянии 21,21 км/с, в перигелии 45,4 км/с, в афелии 15,92 км/с, параболическая скорость на среднем расстоянии 29,9 км/с, в перигелии 64,03 км/с, в афелии 22,44 км/с.

Задача 6.

На каких гелиоцентрических расстояниях скорость Меркурия равна 56,1 км/с и 41,7 км/с? Большая полуось орбиты планеты 0,387 а. е.

Сначала определим круговую скорость на среднем гелиоцентрическом расстоянии:

Теперь воспользуемся формулой

Из нее следует, что

Теперь подставим в нее числовые значения скоростей и определим оба расстояния:

Ответ: а.е., а.е.

Задача 7.

С какой скоростью относительно Солнца проходил Марс в эпоху великого противостояния при геоцентрическом расстоянии в км? Сопоставить эту скорость с круговой и параболической скоростью на том же расстоянии от Солнца. Большая полуось орбиты Марса равна 1,524 а. е.

Рассчитываем круговую скорость:

Рассчитаем скорость прохождения:

Переведем расстояние между Землей и Марсом в астрономические единицы: а.е. Таким образом, расстояние от Солнца до Марса в этот момент а.е.

Определим круговую скорость на этом расстоянии

Определим параболическую скорость:

Ответ: скорость прохождения Марса 26,46 км/с. Это больше круговой скорости (25,3 км/с) и меньше параболической (35,74 км/с).

Задача 8.

Решить предыдущую задачу для астероида Эрота, если он в эпоху великого противостояния проходил свой перигелий 23 января 1975 г. на расстоянии км от Земли. Период обращения Эрота вокруг Солнца равен 1,76 года.

Так как сказано, что астероид находился в противостоянии, то его гелиоцентрическое расстояние, очевидно, больше, чем у Земли.

Переведем расстояние между Землей и астероидом в астрономические единицы: а.е. Таким образом, расстояние от Солнца до астероида в этот момент а.е.

Определим большую полуось орбиты по закону Кеплера:

Определим круговую скорость на этом расстоянии

Рассчитаем скорость прохождения:

На перигельном расстоянии круговая скорость астероида

Определим параболическую скорость:

Ответ: скорость прохождения 30,55 км/с, круговая скорость 27,75 км/c, параболическая 39,1 км/с.

Задача 9.

На каком расстоянии от Солнца прошла комета, если ее скорость на этом расстоянии равнялась 65 км/с и комета двигалась по параболической орбите?

Зная параболическую скорость, определим круговую на этом расстоянии:

Откуда расстояние прохождения

Ответ: 0,417 а.е.

Задача 10.

Комета 1931 IV прошла свой перигелий на расстоянии 0,07 а. е. от Солнца со скоростью 160 км/с, а комета 1945 II —на расстоянии 1,24 а. е. со скоростью 36,5 км/с. Определить род орбит, по которым двигались эти кометы и установить, вернутся ли они к Солнцу и когда именно.

Комета 1931 IV:

На перигельном расстоянии круговая скорость кометы

Определим параболическую скорость:

Так как параболическая скорость меньше той, которую имела комета, то траектория – парабола и комета более к Солнцу не вернется.

Комета 1945 II:

На перигельном расстоянии круговая скорость кометы

Определим параболическую скорость:

Так как скорость кометы меньше, чем параболическая, то траектория – эллипс. Определим большую полуось с помощью формулы:

Откуда

Зная большую полуось, определим период обращения по закону Кеплера:

Ответ: первая комета имеет параболическую траекторию и не вернется к Солнцу, вторая вернется через 27 лет, траектория – эллипс.

Задача 11.

Синодический период обращения астероида Колхиды равен 1,298 года, а его скорость в перигелии — 20,48 км/с. Чему равны сидерический период обращения астероида, большая полуось и эксцентриситет его орбиты, перигельное и афелийное расстояния, а также скорость на среднем гелиоцентрическом расстоянии и в афелии?

По формуле

Определим сидерический период :

Теперь можно найти большую полуось орбиты, а.е.:

Круговую скорость найдем, зная большую полуось:

Скорость в перигелии дает возможность найти перигельное расстояние:

Из этой формулы следует, что

Тогда можно определить эксцентриситет:

Далее можно найти афелийное расстояние:

Скорость в афелии:

Ответ: сидерический период –  4,356 года, большая полуось – 2,667 а.е., эксцентриситет – 0,116, перигелий – 2,358 а.е., афелий – 2,976 а.е., скорость на среднем расстоянии км/с, скорость в афелии 16,22 км/c.

Задача 12.

Эксцентриситет орбиты астероида Узбекистании равен 0,092, а его скорость в афелии— 15,21 км/с. Найти большую полуось орбиты астероида, его звездный и синодический периоды обращения, скорость в перигелии и при истинной аномалии в и.

По скорости в афелии и эксцентриситету найдем круговую скорость на среднем расстоянии:

Теперь найдем большую полуось:

Синодический период

Звездный период:

Или 443 дня.

Перигельное расстояние:

Скорость в перигелии

Для определения скоростей в точках с указанными истинными аномалиями найдем расстояния до этих точек:

При :

При :

При :

Определяем скорости: