Как найти орбитальный магнитный момент электрона

Как найти орбитальный магнитный момент электрона

From Wikipedia, the free encyclopedia

In atomic physics, the electron magnetic moment, or more specifically the electron magnetic dipole moment, is the magnetic moment of an electron resulting from its intrinsic properties of spin and electric charge. The value of the electron magnetic moment (symbol μe) is −9.2847647043(28)×10−24 J⋅T−1.[1] In units of the Bohr magneton (μB) it is −1.00115965218128(18) μB,[2] a value that was measured with a relative accuracy of 1.7×10−13.[2]

Magnetic moment of an electron[edit]

The electron is a charged particle with charge −e, where e is the unit of elementary charge. Its angular momentum comes from two types of rotation: spin and orbital motion. From classical electrodynamics, a rotating distribution of electric charge produces a magnetic dipole, so that it behaves like a tiny bar magnet. One consequence is that an external magnetic field exerts a torque on the electron magnetic moment that depends on the orientation of this dipole with respect to the field.

If the electron is visualized as a classical rigid body in which the mass and charge have identical distribution and motion that is rotating about an axis with angular momentum L, its magnetic dipole moment μ is given by:

{displaystyle {boldsymbol {mu }}={frac {-e}{2m_{text{e}}}},mathbf {L} ,,}

where me is the electron rest mass. The angular momentum L in this equation may be the spin angular momentum, the orbital angular momentum, or the total angular momentum. The ratio between the true spin magnetic moment and that predicted by this model is a dimensionless factor ge, known as the electron g-factor:

{displaystyle {boldsymbol {mu }}=g_{text{e}},{frac {(-e)}{~2m_{text{e}}~}},mathbf {L} ,.}

It is usual to express the magnetic moment in terms of the reduced Planck constant ħ and the Bohr magneton μB:

{displaystyle {boldsymbol {mu }}=-g_{text{e}},mu _{text{B}},{frac {mathbf {L} }{hbar }},.}

Since the magnetic moment is quantized in units of μB, correspondingly the angular momentum is quantized in units of ħ.

Formal definition[edit]

Classical notions such as the center of charge and mass are, however, hard to make precise for a quantum elementary particle. In practice the definition used by experimentalists comes from the form factors {displaystyle F_{i}(q^{2})}
appearing in the matrix element
{displaystyle langle p_{f}|j^{mu }|p_{i}rangle ={bar {u}}(p_{f})left{F_{1}(q^{2})gamma ^{mu }+{frac {~isigma ^{mu nu }~}{~2,m_{rm {e}}~}}q_{nu }F_{2}(q^{2})+iepsilon ^{mu nu rho sigma }sigma _{rho sigma }q_{nu }F_{3}(q^{2})+{frac {1}{~2,m_{rm {e}}~}}left(q^{mu }-{frac {q^{2}}{2m}}gamma ^{mu }right)gamma _{5}F_{4}(q^{2})right}u(p_{i})}

of the electromagnetic current operator between two on-shell states. Here {displaystyle u(p_{i})} and {displaystyle {bar {u}}(p_{f})} are 4-spinor solution of the Dirac equation normalized so that {displaystyle {bar {u}}u=2m_{rm {e}}}, and {displaystyle q^{mu }=p_{f}^{mu }-p_{i}^{mu }} is the momentum transfer from the current to the electron. The {displaystyle q^{2}=0} form factor {displaystyle F_{1}(0)=-e} is the electron’s charge, {displaystyle mu =[,F_{1}(0)+F_{2}(0),]/[,2,m_{rm {e}},]} is its static magnetic dipole moment, and {displaystyle -F_{3}(0)/[,2,m_{rm {e}},]} provides the formal definion of the electron’s electric dipole moment. The remaining form factor {displaystyle F_{4}(q^{2})} would, if non zero, be the anapole moment.

Spin magnetic dipole moment[edit]

The spin magnetic moment is intrinsic for an electron.[3] It is

{displaystyle {boldsymbol {mu }}_{text{s}}=-g_{rm {s}},mu _{text{B}},{frac {~mathbf {S} ~}{hbar }},.}

Here S is the electron spin angular momentum. The spin g-factor is approximately two: {displaystyle g_{rm {s}}approx 2}. The magnetic moment of an electron is approximately twice what it should be in classical mechanics. The factor of two implies that the electron appears to be twice as effective in producing a magnetic moment as the corresponding classical charged body.

The spin magnetic dipole moment is approximately one μB because {displaystyle g_{rm {s}}approx 2} and the electron is a spin-1⁄2 particle (S = ħ⁄2):

The z component of the electron magnetic moment is

{displaystyle ({boldsymbol {mu }}_{text{s}})_{z}=-g_{text{s}},mu _{text{B}},m_{text{s}},,}

where ms is the spin quantum number. Note that μ is a negative constant multiplied by the spin, so the magnetic moment is antiparallel to the spin angular momentum.

The spin g-factor gs = 2 comes from the Dirac equation, a fundamental equation connecting the electron’s spin with its electromagnetic properties. Reduction of the Dirac equation for an electron in a magnetic field to its non-relativistic limit yields the Schrödinger equation with a correction term, which takes account of the interaction of the electron’s intrinsic magnetic moment with the magnetic field giving the correct energy.

For the electron spin, the most accurate value for the spin g-factor has been experimentally determined to have the value

−2.00231930436256(35).[4]

Note that this differs only marginally from the value from the Dirac equation. The small correction is known as the anomalous magnetic dipole moment of the electron; it arises from the electron’s interaction with virtual photons in quantum electrodynamics. A triumph of the quantum electrodynamics theory is the accurate prediction of the electron g-factor. The CODATA value for the electron magnetic moment is

−9.2847647043(28)×10−24 J⋅T−1.[1]

Orbital magnetic dipole moment[edit]

The revolution of an electron around an axis through another object, such as the nucleus, gives rise to the orbital magnetic dipole moment. Suppose that the angular momentum for the orbital motion is L. Then the orbital magnetic dipole moment is
{displaystyle {boldsymbol {mu }}_{L}=-g_{text{L}},mu _{text{B}},{frac {~mathbf {L} ~}{hbar }},.}

Here gL is the electron orbital g-factor and μB is the Bohr magneton. The value of gL is exactly equal to one, by a quantum-mechanical argument analogous to the derivation of the classical gyromagnetic ratio.

Total magnetic dipole moment[edit]

The total magnetic dipole moment resulting from both spin and orbital angular momenta of an electron is related to the total angular momentum J by a similar equation:
{displaystyle {boldsymbol {mu }}_{text{J}}=-g_{text{J}},mu _{text{B}},{frac {~mathbf {J} ~}{hbar }},.}

The g-factor gJ is known as the Landé g-factor, which can be related to gL and gS by quantum mechanics. See Landé g-factor for details.

Example: hydrogen atom[edit]

For a hydrogen atom, an electron occupying the atomic orbital Ψn,ℓ,m , the magnetic dipole moment is given by

{displaystyle mu _{text{L}}=-g_{text{L}}{frac {mu _{text{B}}}{hbar }}langle Psi _{n,ell ,m}|L|Psi _{n,ell ,m}rangle =-mu _{text{B}}{sqrt {ell (ell +1)}}.}

Here L is the orbital angular momentum, n, ℓ, and m are the principal, azimuthal, and magnetic quantum numbers respectively.
The z component of the orbital magnetic dipole moment for an electron with a magnetic quantum number mℓ is given by

{displaystyle ({boldsymbol {mu }}_{text{L}})_{z}=-mu _{text{B}}m_{ell }.}

History[edit]

The electron magnetic moment is intrinsically connected to electron spin and was first hypothesized during the early models of the atom in the early twentieth century. The first to introduce the idea of electron spin was Arthur Compton in his 1921 paper on investigations of ferromagnetic substances with X-rays.[5][6] In Compton’s article, he wrote: “Perhaps the most natural, and certainly the most generally accepted view of the nature of the elementary magnet, is that the revolution of electrons in orbits within the atom give to the atom as a whole the properties of a tiny permanent magnet.”[5]: 146  That same year Otto Stern proposed an experiment carried out later called the Stern–Gerlach experiment in which silver atoms in a magnetic field were deflected in opposite directions of distribution. This pre-1925 period marked the old quantum theory built upon the Bohr-Sommerfeld model of the atom with its classical elliptical electron orbits. During the period between 1916 and 1925, much progress was being made concerning the arrangement of electrons in the periodic table. In order to explain the Zeeman effect in the Bohr atom, Sommerfeld proposed that electrons would be based on three ‘quantum numbers’, n, k, and m, that described the size of the orbit, the shape of the orbit, and the direction in which the orbit was pointing.[7] Irving Langmuir had explained in his 1919 paper regarding electrons in their shells, “Rydberg has pointed out that these numbers are obtained from the series {displaystyle N=2(1+2^{2}+2^{2}+3^{2}+3^{2}+4^{2})}. The factor two suggests a fundamental two-fold symmetry for all stable atoms.”[8] This 2n^{2} configuration was adopted by Edmund Stoner, in October 1924 in his paper ‘The Distribution of Electrons Among Atomic Levels’ published in the Philosophical Magazine. Wolfgang Pauli hypothesized that this required a fourth quantum number with a two-valuedness.[9]

Electron spin in the Pauli and Dirac theories[edit]

Starting from here the charge of the electron is e < 0 . The necessity of introducing half-integral spin goes back experimentally to the results of the Stern–Gerlach experiment. A beam of atoms is run through a strong non-uniform magnetic field, which then splits into N parts depending on the intrinsic angular momentum of the atoms. It was found that for silver atoms, the beam was split in two—the ground state therefore could not be integral, because even if the intrinsic angular momentum of the atoms were as small as possible, 1, the beam would be split into 3 parts, corresponding to atoms with Lz = −1, 0, and +1. The conclusion is that silver atoms have net intrinsic angular momentum of 1⁄2. Pauli set up a theory which explained this splitting by introducing a two-component wave function and a corresponding correction term in the Hamiltonian, representing a semi-classical coupling of this wave function to an applied magnetic field, as so:

H={frac {1}{2m}}left[{boldsymbol {sigma }}cdot left(mathbf {p} -{frac {e}{c}}mathbf {A} right)right]^{2}+ephi .

Here A is the magnetic vector potential and ϕ the electric potential, both representing the electromagnetic field, and σ = (σx, σy, σz) are the Pauli matrices. On squaring out the first term, a residual interaction with the magnetic field is found, along with the usual classical Hamiltonian of a charged particle interacting with an applied field:

H={frac {1}{2m}}left(mathbf {p} -{frac {e}{c}}mathbf {A} right)^{2}+ephi -{frac {ehbar }{2mc}}{boldsymbol {sigma }}cdot mathbf {B} .

This Hamiltonian is now a 2 × 2 matrix, so the Schrödinger equation based on it must use a two-component wave function. Pauli had introduced the 2 × 2 sigma matrices as pure phenomenology — Dirac now had a theoretical argument that implied that spin was somehow the consequence of incorporating relativity into quantum mechanics. On introducing the external electromagnetic 4-potential into the Dirac equation in a similar way, known as minimal coupling, it takes the form (in natural units ħ = c = 1)

left[-igamma ^{mu }left(partial _{mu }+ieA_{mu }right)+mright]psi =0,

where scriptstyle gamma ^{mu } are the gamma matrices (known as Dirac matrices) and i is the imaginary unit. A second application of the Dirac operator will now reproduce the Pauli term exactly as before, because the spatial Dirac matrices multiplied by i, have the same squaring and commutation properties as the Pauli matrices. What is more, the value of the gyromagnetic ratio of the electron, standing in front of Pauli’s new term, is explained from first principles. This was a major achievement of the Dirac equation and gave physicists great faith in its overall correctness. The Pauli theory may be seen as the low energy limit of the Dirac theory in the following manner. First the equation is written in the form of coupled equations for 2-spinors with the units restored:

{begin{pmatrix}(mc^{2}-E+ephi )&csigma cdot left(mathbf {p} -{frac {e}{c}}mathbf {A} right)\-c{boldsymbol {sigma }}cdot left(mathbf {p} -{frac {e}{c}}mathbf {A} right)&left(mc^{2}+E-ephi right)end{pmatrix}}{begin{pmatrix}psi _{+}\psi _{-}end{pmatrix}}={begin{pmatrix}0\0end{pmatrix}}.

so

{begin{aligned}(E-ephi )psi _{+}-c{boldsymbol {sigma }}cdot left(mathbf {p} -{frac {e}{c}}mathbf {A} right)psi _{-}&=mc^{2}psi _{+}\-(E-ephi )psi _{-}+c{boldsymbol {sigma }}cdot left(mathbf {p} -{frac {e}{c}}mathbf {A} right)psi _{+}&=mc^{2}psi _{-}end{aligned}}

Assuming the field is weak and the motion of the electron non-relativistic, we have the total energy of the electron approximately equal to its rest energy, and the momentum reducing to the classical value,

{begin{aligned}E-ephi &approx mc^{2}\p&approx mvend{aligned}}

and so the second equation may be written

psi _{-}approx {frac {1}{2mc}}{boldsymbol {sigma }}cdot left(mathbf {p} -{frac {e}{c}}mathbf {A} right)psi _{+}

which is of order v⁄c – thus at typical energies and velocities, the bottom components of the Dirac spinor in the standard representation are much suppressed in comparison to the top components. Substituting this expression into the first equation gives after some rearrangement

left(E-mc^{2}right)psi _{+}={frac {1}{2m}}left[{boldsymbol {sigma }}cdot left(mathbf {p} -{frac {e}{c}}mathbf {A} right)right]^{2}psi _{+}+ephi psi _{+}

The operator on the left represents the particle energy reduced by its rest energy, which is just the classical energy, so we recover Pauli’s theory if we identify his 2-spinor with the top components of the Dirac spinor in the non-relativistic approximation. A further approximation gives the Schrödinger equation as the limit of the Pauli theory. Thus the Schrödinger equation may be seen as the far non-relativistic approximation of the Dirac equation when one may neglect spin and work only at low energies and velocities. This also was a great triumph for the new equation, as it traced the mysterious i that appears in it, and the necessity of a complex wave function, back to the geometry of space-time through the Dirac algebra. It also highlights why the Schrödinger equation, although superficially in the form of a diffusion equation, actually represents the propagation of waves.

It should be strongly emphasized that this separation of the Dirac spinor into large and small components depends explicitly on a low-energy approximation. The entire Dirac spinor represents an irreducible whole, and the components we have just neglected to arrive at the Pauli theory will bring in new phenomena in the relativistic regime – antimatter and the idea of creation and annihilation of particles.

In a general case (if a certain linear function of electromagnetic field does not vanish identically), three out of four components of the spinor function in the Dirac equation can be algebraically eliminated, yielding an equivalent fourth-order partial differential equation for just one component. Furthermore, this remaining component can be made real by a gauge transform.[10]

Measurement[edit]

The existence of the anomalous magnetic moment of the electron has been detected experimentally by magnetic resonance method. This allows the determination of hyperfine splitting of electron shell energy levels in atoms of protium and deuterium using the measured resonance frequency for several transitions.[11][12]

The magnetic moment of the electron has been measured using a one-electron quantum cyclotron and quantum nondemolition spectroscopy. The spin frequency of the electron is determined by the g-factor.

{displaystyle nu _{s}={frac {g}{2}}nu _{c}}
{displaystyle {frac {g}{2}}={frac {{bar {nu }}_{c}+{bar {nu }}_{a}}{{bar {nu }}_{c}}}}

See also[edit]

  • Spin (physics)
  • Electron precipitation
  • Bohr magneton
  • Nuclear magnetic moment
  • Nucleon magnetic moment
  • Anomalous magnetic dipole moment
  • Electron electric dipole moment
  • Fine structure
  • Hyperfine structure

References[edit]

  1. ^ a b “2018 CODATA Value: electron magnetic moment”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2022-09-10.
  2. ^ a b “2018 CODATA Value: electron magnetic moment to Bohr magneton ratio”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2022-09-10.
  3. ^ Mahajan, A.; Rangwala, A. (1989). Electricity and Magnetism. p. 419. ISBN 9780074602256.
  4. ^ “2018 CODATA Value: electron g factor”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2020-03-13.
  5. ^ a b Compton, Arthur H. (August 1921). “The Magnetic Electron”. Journal of the Franklin Institute. 192 (2): 145–155. doi:10.1016/S0016-0032(21)90917-7.
  6. ^ Charles P. Enz, Heisenberg’s applications of quantum mechanics (1926-33) or the settling of the new land*), Department de Physique Théorique Université de Genève, 1211 Genève 4, Switzerland (10. I. 1983)
  7. ^ Manjit Kumar, Quantum: Einstein, Bohr and the Great Debate About the Nature of Reality, 2008.
  8. ^ Langmuir, Irving. (1919). The arrangement of electrons in atoms and molecules. https://doi.org/10.1016/s0016-0032(19)91097-0
  9. ^ Wolfgang Pauli. Exclusion principle and quantum mechanics. Online available via ⟨http://nobelprize.org⟩[permanent dead link]. Nobel Lecture delivered on December 13th 1946 for the 1945 Nobel Prize in Physics.
  10. ^ Akhmeteli, Andrey (2011). “One real function instead of the Dirac spinor function”. Journal of Mathematical Physics. 52 (8): 082303. arXiv:1008.4828. Bibcode:2011JMP….52h2303A. doi:10.1063/1.3624336. S2CID 119331138. Archived from the original on 18 July 2012. Retrieved 26 April 2012.
  11. ^ Foley, H.M.; Kusch, Polykarp (15 February 1948). “Intrinsic moment of the electron”. Physical Review. 73 (4): 412. doi:10.1103/PhysRev.73.412. Archived from the original on 8 March 2021. Retrieved 2 April 2015.
  12. ^ Kusch, Polykarp; Foley, H.M. (1 August 1948). “The magnetic moment of the electron”. Physical Review. 74 (3): 207–11. Bibcode:1948PhRv…74..250K. doi:10.1103/PhysRev.74.250. PMID 17820251. Archived from the original on 22 April 2021. Retrieved 2 April 2015.

Bibliography[edit]

  • Sergei Vonsovsky (1975). Magnetism of Elementary Particles. Mir Publishers.
  • Sin-Itiro Tomonaga (1997). The Story of Spin. University of Chicago Press.
Источник

Всякий
атом представляет собой динамическую
систему, состоящую из ядра и электронного
облака. Каждый электрон обладает
определенным спиновым магнитным моментом
Рсп,
кроме того, движение электрона по
некоторой замкнутой орбите внутри атома
создает так называемый орбитальный
магнитный момент Рорб
. Следовательно, полный магнитный момент
атома Рат
будет представлять геометрическую
сумму орбитальных и спиновых магнитных
моментов электронов, принадлежащих
данному атому

,

где
z
– число электронов в атоме.

Рассмотрим процессы
в атомах, молекулах и кристаллах, которые
определяют принадлежность данного
вещества к одному из пяти видов магнетиков.
Для этого выясним сначала соотношение
между магнитным и механическим моментами
электрона.

Электрон,
вращающийся вокруг ядра с частотой ,
по своему магнитному действию эквивалентен
круговому току. Магнитный момент этого
тока и есть орбитальный магнитный момент
электрона, модуль которого равен:

,

где

–
сила тока,–
частота вращения,S
– площадь орбиты электрона.

Если
электрон движется по часовой стрелке,
то ток направлен против часовой стрелки
и вектор
в соответствии с правилом правого винта
направлен перпендикулярно плоскости
орбиты электрона (см. рисунок 9.1).

С
другой стороны, движущийся по орбите
электрон обладает механическим моментом
импульса, модуль которого равен:

,

где

,
а.
Вектор,
направление которого также подчиняется
правилу правого винта, называется
орбитальным механическим моментом
электрона.

Векторы


и
жестко
связаны и всегда противоположны (см.
рисунок 9.1) (так как направление тока
противоположно направлению движения
электрона), поэтому поворот одного из
векторов обязательно сопровождается
таким же поворотом другого вектора.

Отношение
магнитного момента к механическому
называется гиромагнитным
отношением орбитальных моментов:

В
полученную формулу не входит номер
орбиты электрона п.
Следовательно,
орбитальное гиромагнитное отношение
одинаково для любой электронной орбиты.
Формула
выведена для круговой орбиты электрона,
но можно доказать, что она справедлива
и для любой эллиптической орбиты.

Экспериментальное
определение гиромагнитного отношения
было проведено в опытах Эйнштейна и де
Гааза, которые наблюдали поворот свободно
подвешенного на тончайшей кварцевой
нити железного стержня при его
намагничивании во внешнем магнитном
поле. Значение гиромагнитного отношения,
найденное в этих опытах, оказалось
равным
,
т. е. в два раза больше, чем определенное
ранее.

Д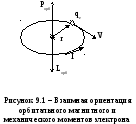ля
объяснения этого результата было
предположено, а впоследствии доказано,
что кроме орбитальных моментов электрон
обладает собственным механическим
моментом импульса,
называемый спином. Спину электрона
соответствует спиновой магнитный момент.

Величина
спинового орбитального момента в два
раза больше орбитального:

.

Важнейшей
особенностью спина электрона является
то, что в магнитном поле спин может быть
ориентирован только двумя способами:
либо параллельно напряженности поля,
либо антипараллельно.

Источник

Электрон в атоме
движется вокруг ядра. В классической
физике движению точки по окружности
соответствует момент импульса L=mvr, где
m – масса частицы, v – её скорость, r
– радиус траектории. В квантовой
механике эта формула неприменима, так как
неопределенны одновременно радиус и
скорость (см. “Соотношение неопределенностей”). Но сама величина
момента импульса существует. Как его
определить? Из квантово-механической
теории атома водорода следует, что модуль
момента импульса электрона может
принимать следующие дискретные
значения:

(40)

где l – так называемое орбитальное
квантовое число, l = 0, 1, 2, … n–1.
Таким образом, момент импульса электрона,
как и энергия, квантуется, т.е.
принимает дискретные значения.
Заметим, что при больших значениях
квантового числа l (l >>1)
уравнение (40) примет вид .
Это не что иное, как один из постулатов Н.
Бора.

Из квантово-механической
теории атома водорода следует еще один
важный вывод: проекция момента импульса
электрона на какое-либо заданное
направление в пространстве z (например,
на направление силовых линий магнитного
или электрического поля) также квантуется
по правилу:

(41)

где m = 0, ± 1, ± 2, …± l –
так называемое магнитное квантовое
число.

Электрон,
движущийся вокруг ядра, представляет
собой элементарный круговой
электрический ток. Такому току
соответствует магнитный момент pm
. Очевидно, что он
пропорционален механическому моменту
импульса L. Отношение магнитного
момента pm электрона к
механическому моменту импульса L
называется гиромагнитным отношением.
Для электрона в атоме водорода

(42)

(знак минус показывает, что
вектора магнитного и механического
моментов направлены в противоположные
стороны). Отсюда можно найти так
называемый орбитальный магнитный
момент электрона:

(43)

Эта величина,как
видим, также квантуется.

В формуле (43)
величина
является константой. Обозначим её mв

и назовем магнетоном Бора. Магнетон
Бора служит естественной единицей
магнитного момента электрона, так как
значения магнитного момента кратны
величине mв
:

(44)
Источник
  • Физика
  • Математика

Орбитальный магнитный момент

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng! 
Занимаюсь там сам – очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА

Орбитальный магнитный момент — Электрон двигающийся со скоростью v по орбите радиуса г через площадку, расположенную в любом месте на пути электрона, переносится в единицу времени заряд ev, где е — заряд электрона, a v — число оборотов в секунду

LARGE p_m=IS=e upsilon pi r^2

Произведение 2Пrv дает скорость движения электрона v, поэтому можно написать, что

LARGE p_m=frac{eupsilon r}{2}

Орбитальный магнитный момент

Тут мы использовали :

p_m — Орбитальный магнитный момент

upsilon — Число оборотов в секунду.

e — Заряд электрона

r — Радиус орбиты

Сайт «Все формулы» работает на WordPress

Источник

Различные среды при рассмотрении их магнитных свойств называют магнетиками.

Все вещества в той или иной мере взаимодействуют с магнитным полем. У некоторых материалов магнитные свойства сохраняются и в отсутствие внешнего магнитного поля. Намагничивание материалов происходит за счет токов, циркулирующих внутри атомов – вращения электронов и движения их в атоме. Поэтому намагничивание вещества следует описывать при помощи реальных атомных токов, называемых амперовскими токами.

В отсутствие внешнего магнитного поля магнитные моменты атомов вещества ориентированы обычно беспорядочно, так что создаваемые ими магнитные поля компенсируют друг друга. При наложении внешнего магнитного поля атомы стремятся сориентироваться своими магнитными моментами по направлению внешнего магнитного поля, и тогда компенсация магнитных моментов нарушается, тело приобретает магнитные свойства – намагничивается. Большинство тел намагничивается очень слабо и величина индукции магнитного поля B в таких веществах мало отличается от величины индукции магнитного поля в вакууме . Если магнитное поле слабо усиливается в веществе, то такое вещество называется парамагнетиком:

( , , , , , , Li, Na);

если ослабевает, то это диамагнетик:

(Bi, Cu, Ag, Au и др.).

Но есть вещества, обладающие сильными магнитными свойствами. Такие вещества называются ферромагнетиками:

(Fe, Co, Ni и пр.).

Эти вещества способны сохранять магнитные свойства и в отсутствие внешнего магнитного поля, представляя собой постоянные магниты.

Все тела при внесении их во внешнее магнитное поле намагничиваются в той или иной степени, т.е. создают собственное магнитное поле, которое накладывается на внешнее магнитное поле.

Магнитные свойства вещества определяются магнитными свойствами электронов и атомов.

Магнетики состоят из атомов, которые, в свою очередь, состоят из положительных ядер и, условно говоря, вращающихся вокруг них электронов.

Электрон, движущийся по орбите в атоме эквивалентен замкнутому контуру с орбитальным током:

где е – заряд электрона, ν – частота его вращения по орбите:

.

Орбитальному току соответствует орбитальный магнитный момент электрона

где S – площадь орбиты, – единичный вектор нормали к S, – скорость электрона. На рисунке 6.1 показано направление орбитального магнитного момента электрона.

Электрон, движущийся по орбите, имеет орбитальный момент импульса , который направлен противоположно по отношению к и связан с ним соотношением

Здесь коэффициент пропорциональности γ называется гиромагнитным отношением орбитальных моментов и равен:

где m – масса электрона.

Кроме того, электрон обладает собственным моментом импульса , который называется спином электрона

где , – постоянная Планка

Спину электрона соответствует спиновый магнитный момент электрона , направленный в противоположную сторону:

Величину называют гиромагнитным отношением спиновых моментов

Проекция спинового магнитного момента электрона на направление вектора индукции магнитного поля может принимать только одно из следующих двух значений:

где – квантовый магнитный момент электрона – магнетон Бора.

Орбитальным магнитным моментом атома называется геометрическая сумма орбитальных магнитных моментов всех электронов атома

где Z – число всех электронов в атоме – порядковый номер элемента в периодической системе Менделеева.

Орбитальным моментом импульса L атома называется геометрическая сумма моментов импульса всех электронов атома:

Более подробно вышеназванные характеристики мы обсудим в разделе «Атомная и ядерная физика».

Магнитные моменты электрона – орбитальный и спиновой. Орбитальное магнитомеханическое отношение для электрона.

Магнитное поле ядра значительно меньше магнитного поля электронов, поэтому при рассмотрении многих вопросов его можно не учитывать. Будем рассматривать движение электрона в атоме как равномерное вращение вокруг ядра с некоторой скоростью v., что можно уподобить круговому току и применить к нему используемые в этом случае характеристики.

Магнитный момент контура с током.Пусть по контуру с площадью течет ток I. Величина Pm = I • S называется магнитным моментом контура с током. Магнитный момент контура с током — это вектор, который направлен перпендикулярно плоскости контура и связан с направлением тока правилом правого буравчика (рис 33.1).

Индукция контура с током прямо пропорциональна величине магнитного момента контура. Единицей магнитного момента является ампер на квадратный метр (А×м 2 ) в “СИ”.

Магнитный момент является характеристикой не только контура с током, но и многих элементарных частиц (протонов, нейтронов, электронов и др.), ядер, атомов и молекул, определяя их поведение в магнитном поле.

Магнетон – единица магнитного момента, применяемая в атомной и ядерной физике. При измерении магнитных моментов электронов, атомов и молекул пользуются магнетоном Бора:

9,27× 10 -24 А×м 2 (Дж/Тл),

где “е” – заряд электрона, h – постоянная Планка, me – масса электрона.

При измерении магнитных моментов нуклонов (протонов и нейтронов) и атомных ядер пользуются ядерным магнетоном:

5,05× 10 -27 А×м 2 (Дж/Тл),

Орбитальный магнитный момент электрона. Используя аналогию с контуром, вычислим магнитный момент, соответствующий орбитальному движению электрона (рорбm). Сила тока, соответствующая вращению электрона по круговой орбите, определяется формулой I = е/Т, где е — заряд электрона, Т – период его обращения. Так как период Т = 2πr/v (r — радиус орбиты, v — скорость электрона), то сила тока равна I = ev/2πr . Площадь контура — это площадь круга S = πr 2 .Теперь можно рассчитать орбитальный магнитный момент электрона:

Орбитальный момент импульса электрона. В физических экспериментах обычно измеряют не сам орбитальный магнитный момент, а его отношение к другой характеристике орбитального движения — моменту импульса. Моментом импульса материальной точки относительно оси называют величину, равную произведению импульса точки на расстояние ее до оси вращения. В соответствии с этим момент импульса электрона, вращающегося по круговой орбите, выражается следующей формулой: Lорб = mvr, где m – масса электрона.

Направления векторов Lop6 и рорбm показаны на рис. 33.2.

Поскольку электрон — отрицательная частица, то его вращению по часовой стрелке соответствует «ток», текущий против часовой стрелки.

Орбитальное магнитомеханическое отношение для электрона.Можно вычислить упомянутое выше отношение магнитного момента к моменту импульса для орбитального движения электрона. Это отношение называют магнитомеханическим отношением Gop6 :

Мы видим, что это отношение является постоянной величиной, то есть магнитный момент и момент импульса жестко связаны друг с другом.

Спин. Спиновый магнитный момент электрона. Обнаружилось, что электрон, помимо орбитального момента импульса, обладает и собственным моментом импульса, который называется спином. Первоначально это связывали с вращением электрона вокруг собственной оси (отсюда и название спин — волчок). Позже выяснилось, что эта наглядная аналогия является очень грубой. Поэтому физики от нее отказались и считают спин неотъемлемой характеристикой элементарных частиц, присущей их природе. Спин обозначают Lcn (формулу для расчета спина мы не рассматриваем). Со спином электрона (и других частиц) связан еще один магнитный момент, который называется спиновым магнитным моментом (рcn). Таким образом, полный магнитный момент электрона складывается из двух частей: орбитальной (р op6) и спиновой (рcn). Для электрона отношение собственного магнитного момента к собственному моменту импульса (спину) вдвое больше, чем для орбитального движения:

Это отношение называют спиновым магнитомеханическим отношением.

Множитель Ланде (gr-фактор).Формулы можно записать в обобщенном виде:P/L= g(e/2m). Коэффициент g называют множителем Ланде. Для орбитального движения электрона он равен 1 (goрб = 1), для спина электрона он равен 2 (gcn = 2). Специальные физические эксперименты позволяют определять магнитомеханические отношения для конкретных веществ и на основании этого делать выводы о роли орбитальных или спиновых магнитных моментов в процессах намагничивания.

Магнитные моменты атомов и молекул обусловлены пространственным движением электронов (так называемые орбитальные токи и соответствующие им орбитальные магнитные моменты электронов), силовыми магнитными моментами электронов, соответствующими их собственным моментам импульса, вращательным движением молекул (вращательный магнитный момент), а также магнитными моментами атомных ядер. Магнитный момент ядра обусловлен спиновыми моментами протона и нейтрона, а также орбитальным моментом движения протона внутри ядра. Магнитным моментом обладают все ядра, у которых результирующий механический момент отличен от нуля. Магнитные моменты ядер на несколько порядков меньше орбитального и спинового магнитного моментов электрона.

Магнитное поле электрона

Вы будете перенаправлены на Автор24

На сегодняшний день науке известно почти 200 частиц и большое количество ионов, атомов и молекул. Большая часть из них возникает, и существует очень непродолжительное время, после которого происходит распад частицы. При этом говорят, что частица имеет конечное время жизни. Данное время может составлять доли секунды.

Имеется очень ограниченное число частиц с бесконечным временем жизни, это:

В состав ядер атомов входят протоны, в оболочку ядра – электроны. Эти частицы обусловили практически все явления, которые рассматривает электромагнетизм.

Электрон

Электрон относят к микроскопическим носителям заряда. Его заряд считают равным элементарному:

$|e|=1,6021892(46)bullet 10^<-19>$ Кл.

Электрон – это материальный носитель отрицательного заряда. Обычно считают, что данная частица не имеет структуры, то есть является точечным зарядом. Данное представление имеет внутренние противоречия. Поскольку энергия электрического поля точечного заряда должна быть бесконечной, это означает, что бесконечной должна быть и инертная масса электрона (как точечного заряда). Но нам известно, что экспериментально получено: масса электрона равна:

$m_e=9,1bullet 10^<-31>$ кг.

Но пока с этим противоречием мирятся, так как менее противоречивого положения о структуре электрона на настоящее время нет. Проблему с бесконечной собственной массой электрона, при вычислениях разных эффектов, преодолевают, используя прием перенормировки.

Помимо заряда электрон имеет спин и магнитный момент.

Спин не вызван вращением частицы, так как в этом случае пришлось бы допустить наличие линейной скорости при вращении, которая была бы больше скорости света в вакууме. Спин рассматривают как внутреннее свойство частицы. Со спином связывают магнитный момент заряженной частицы.

В классической физике магнитный момент электрона объясняют, рассматривая движение заряда по замкнутой траектории. Спиновый магнитный момент классическая электродинамика объяснить не может. Но магнитное поле, которое обусловлено спиновыми магнитными моментами, может быть описано феноменологически. Обычно напряженность этого поля очень мала. Классическая теория не может описать механизм появления данного поля, но само поле описывается при помощи классической теории.

Готовые работы на аналогичную тему

Магнитные моменты электрона

Рассмотрим атом. В некотором приближении можно полагать, что электроны в атоме перемещаются вокруг ядра по замкнутым круговым траекториям. Орбиту с перемещающимся по ней электроном можно уподобить контуру с током. Следовательно, она имеет магнитный момент ($p_m$), который мы вычислим.

где $r$ – радиус орбиты электрона; $v$ – скорость его движения; $T=frac<2pi r>quad$ – период обращения электрона по его орбите; $I=frac=frac$– сила тока, которую электрон создает при своем движении.

Обе части выражения (1) умножим на единичный вектор нормали $vec n$. Этот вектор ориентирован так, что если наблюдать с его конца за движением электрона, то оно будет происходить против часовой стрелки.

Рисунок 1. Магнитные моменты электрона. Автор24 — интернет-биржа студенческих работ

Принимая во внимание, что момент импульса электрона равен:

$vec L=m_evrvec n$

и зная, что электрон несет отрицательный заряд, получим:

где величину $-frac<2m_>$ называют гиромагнитным соотношением. При этом параметры $vec p_m$ и $vec L$ носят название орбитальных моментов, так как они вызваны движением электрона по орбите.

Так, любой электрон в атоме имеет орбитальный магнитный момент, который нормален плоскости его орбиты.

Кроме этого, как уже отмечалось, электроны обладают собственными моментами:

  • собственным моментом импульса (спином);
  • собственным магнитным моментом.

Наличие спина у электрона обозначает, что при взаимодействии с другими частицами электрон ведет себя как вращающаяся частица.

Собственный магнитный момент электрона говорит о том, что электрон создает около себя свое магнитное поле и взаимодействует с внешними магнитными полями подобно магнитному диполю. Собственный магнитный момент считают «врожденным» и не связывают с вращением электрона.

Магнитные моменты имеются и у ядер атомов, но они очень малы. Обычно при описании магнитных свойств вещества их не принимают во внимание. При этом магнитным моментом атома считают квантовую сумму орбитальных и собственных моментов атомарных электронов.

Квантовое суммирование производят не по правилам векторной алгебры, а по специальным правилам квантовой механики.

Магнитные свойства вещества

По современным представлениям магнетизм вещества вызван тремя причинами:

  1. Движением электронов по орбитам вокруг ядер атомов.
  2. Спинами электронов.
  3. Спином атомных ядер. Ядерный магнетизм становится существенным только при температурах близких к абсолютному нулю, при компенсации орбитальных и спиновых магнитных моментов электронов.

Атомы вещества при отсутствии внешнего магнитного поля ориентированы беспорядочно. Порождаемые ими магнитные поля компенсируют друг друга в окружающем их пространстве. При наложении внешнего магнитного поля атомы полностью или частично ориентируются вдоль поля, тогда взаимная компенсация полей нарушается. Тогда вещество считают намагниченным. Тела способные к намагничиванию назвали магнетиками.

Микроскопическое магнитное поле

Магнитное поле может быть:

Микроскопическое поле – это поле, которое порождается перемещающимися элементарными зарядами в веществе. Оно резко изменяется на расстояниях размера атома.

Макроскопическое поле получается из микроскопического путем сглаживания (усреднения по бесконечно малым пространственным объемам).

Магнитные поля, которые создают вращающиеся электроны можно уподобить токам, циркулирующим в атомах вещества (молекулярные токи).

Магнитное поле молекулярного тока запишем, ориентируясь на электрическое поле диполя (магнитный диполь изображен на рис.1 ):

где $alpha $- угол между векторами $vec p_m$ и $vec r$. (рис.1).

Величина вектора индукции магнитного поля равна при этом:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 12 04 2022

[spoiler title=”источники:”]

http://megalektsii.ru/s23189t4.html

http://spravochnick.ru/fizika/magnitnoe_pole/magnitnoe_pole_elektrona/

[/spoiler]

Источник

Добавить комментарий