Как найти орбиту группы - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 апреля 2022 года; проверки требуют 5 правок.

Циклическая группа порядка три действует на множестве вершин равностороннего треугольника поворотами вокруг его центра на углы, кратные 120°, циклически переставляя их.

Действие группы на некотором множестве — это гомоморфное сопоставление каждому элементу группы некоторого преобразования этого множества. В случае, когда множество наделено некоторой дополнительной структурой, предполагается, что преобразования сохраняют эту структуру. Действия групп позволяют изучать симметрии математических объектов с помощью аппарата теории групп.

Если группа действует на некотором объекте или структуре, она обычно действует и на связанных с ними объектах. Так, группа движений евклидова пространства действует как на этом пространстве, так и на фигурах, изображенных в нём. Например, она действует на множестве всех треугольников. Кроме того, группа симметрий некоторого многогранника действует на множествах его вершин, рёбер и граней.

В случае действий на топологических пространствах все отображения предполагаются гомеоморфизмами. Такие действия часто называются непрерывными.

Действия групп на векторных пространствах называются их линейными представлениями. В случае конечномерных векторных пространств они позволяют отождествить многие группы с подгруппами полной линейной группы ${displaystyle {rm {GL}}_{n}(K)}$ , то есть группы обратимых матриц размера над некоторым полем .

Определения[править | править код]

Действие слева[править | править код]

Говорят, что группа действует слева на множестве , если задан гомоморфизм из группы в симметрическую группу S(M) множества .
Для краткости часто записывают как g(m) , gcdot m , или .
Элементы группы называются в этом случае преобразованиями, а сама группа — группой преобразований множества . Тот факт, что сопоставление Phi является гомоморфизмом, означает то, что произведению элементов в группе соответствует композиция преобразований, а нейтральному элементу группы соответствует тождественное преобразование.

Другими словами, группа действует слева на множестве , если задано такое отображение ,
при котором образ пары обозначается g(m) , что:

для всех и ;
, где — нейтральный элемент группы .

Действие справа[править | править код]

Аналогично, правое действие группы на задаётся таким отображением , при котором образ пары обозначается , что:

;
.

Другими словами, правое действие группы на задаётся гомоморфизмом $rho :G^{op}to S(M)$ , где $G^{{op}}$ — инверсная группа группы . Или, что то же самое, левым действием группы $G^{{op}}$ на .

Разница между левыми и правыми действиями состоит в порядке, в котором произведение действует на данном элементе. В левом действии сначала действует , затем . А в правом действии сначала действует , затем .

Благодаря формуле ${displaystyle (gh)^{-1}=h^{-1}g^{-1}}$ , отображение $gmapsto g^{-1}$ осуществляет изоморфизм между инверсной группой и исходной, который позволяет, путём взятия композиции с ним, построить взаимно однозначное соответствие между левыми и правыми действиями группы.

Таким образом, для установления общих свойств действий групп достаточно рассматривать только левые действия.

Типы действий[править | править код]

Свободное, если для любых различных и любого выполняется .
Транзитивное, если для любых существует такой, что . Другими словами, действие транзитивно, если для любого элемента .
- Примитивное действие транзитивно и не сохраняет нетривиальных подможеств .
Эффективное, если для любых двух элементов в существует такой, что .
Вполне разрывное, если для любого компактного множества множество всех , для которых пересечение непусто, конечно.

На топологических пространствах и гладких многообразиях также особо рассматривают действия групп, наделённых соответствующими дополнительными структурами: топологических групп и групп Ли. Действие топологической группы на топологическом пространстве называют непрерывным, если оно непрерывно как отображение между топологическими пространствами. Аналогично определяется гладкое действие группы Ли на гладком многообразии.

Непрерывное действие группы на пространстве жёстко (или квазианалитично), если из того, что некоторый элемент группы действует как тождественное отображение на некотором открытом подмножестве пространства, следует, что это единичный элемент группы.
- Любое эффективное непрерывное действие изометриями на связном римановом многообразии обязательно жёстко, чего нельзя сказать об общих метрических пространствах. Например, действие циклической группы порядка 2 перестановкой двух рёбер на графе, образованном тремя рёбрами, выходящими из одной точки, является эффективным, но не жёстким.
Непрерывное действие группы называется кокомпактным, если факторпространство по этому действию компактен.

Орбиты[править | править код]

Подмножество

называется орбитой элемента min M (иногда обозначается как ).

Действие группы на множестве определяет на нём отношение эквивалентности

$forall n,;min M;(n,sim _{_{G}},m)Longleftrightarrow (exists gin G;:;gn=m)Longleftrightarrow (Gn=Gm).$

При этом классами эквивалентности являются орбиты элементов. Поэтому если общее число классов эквивалентности равно , то

$M=Gm_{1}sqcup Gm_{2}sqcup ldots sqcup Gm_{k},$

где $m_{1},;m_{2},;ldots ,;m_{k}in M$ попарно неэквивалентны. Для транзитивного действия k=1 .

Стабилизаторы[править | править код]

Подмножество

$G_{m}={gin Gmid gm=m}subset G$

является подгруппой группы и называется стабилизатором, или стационарной подгруппой элемента min M (иногда обозначается как ).

Стабилизаторы элементов одной орбиты сопряжены, то есть если $n,sim _{_{G}},m$ , то найдется такой элемент gin G , что

$G_{m}=gG_{n}g^{-1}.$

Количество элементов в орбите[править | править код]

$|Gm|=[G:G_{m}]$

, $G_{m}$

— стабилизатор элемента

и $[G:G_{m}]$

— индекс подгруппы $G_{m}subset G$

, в случае конечных групп равен ${frac {|G|}{|G_{m}|}}$

Размерность орбиты можно вычислить так:

${displaystyle dim |Gm|=dim |G|-dim |G_{m}|}$

, где

размерность отдельной орбиты,

${displaystyle dim |G_{m}|}$

размерность стабилизатора,

размерность группы Ли.

Если $M=Gm_{1}sqcup Gm_{2}sqcup ldots sqcup Gm_{k}$ , то

$|M|=sum _{t=1}^{k}[G:G_{m_{t}}]$

— формула разложения на орбиты.

Эта формула также влечёт следующие тождества:

$forall min M;sum _{nin Gm}|G_{n}|=|G|;$
$sum _{min M}|G_{m}|=k|G|;$
лемму Бёрнсайда.

Примеры действий[править | править код]

Действия на себе[править | править код]

Слева[править | править код]

Действие на себе слева является наиболее простым примером действия. В этом случае M=G , и гомоморфизм задан как .

Справа[править | править код]

Аналогично определяется действие на себе справа: $(Phi (g))(h)=hg^{-1}$ .

Слева и справа[править | править код]

Эти два действия являются действиями подгрупп прямого произведения на M=G с гомоморфизмом , заданным как $(Phi (g_{1},;g_{2}))(h)=g_{1}hg_{2}^{-1}$ .

Сопряжениями[править | править код]

Пусть M=G , и гомоморфизм задан как $(Phi (g))(h)=ghg^{-1}$ . При этом для каждого элемента hin G стабилизатор $G_{h}$ совпадает с централизатором C(h) :

$G_{h}={gin Gmid ghg^{-1}=h}={gin Gmid gh=hg}=C(h).$

Например, для элемента из центра группы (то есть ) имеем C(h)=G и $G_{h}=G$ .

Вариации и обобщения[править | править код]

Псевдогруппа преобразований

См. также[править | править код]

Представление группы

Литература[править | править код]

Винберг, Э. Б. Курс алгебры. — 3-е изд. — М.: Издательство «Факториал Пресс», 2002. — ISBN 5-88688-0607..
Кострикин, А. И. Введение в алгебру. Часть III. Основные структуры. — 3-е изд. — М.: ФИЗМАТЛИТ, 2004. — 272 с. — ISBN 5-9221-0489-6..

Источник

Определение:

Группа действует на множестве (англ. acts on a set) , если задано отображение (обозначается ), такое что для любого , а также для любых оно обладает свойствами:

(здесь — групповая операция)

Эквивалентность по группе

Определение:

Пусть группа действует на множестве . Введем на отношение эквивалентности для : , если . Тогда, если , то говорят, что и равны с точностью до группы.

Утверждение:

Отношение является отношением эквивалентности.

Рефлексивность. Для любого верно , значит .
Симметричность. Пусть для некоторых . Тогда существует , такое что . Пользуясь свойствами групп, получаем следующие равенства: . То есть . Значит, .
Транзитивность. Пусть и для некоторых . Тогда существуют такие , что , а . Отсюда следует, что . То есть, .

Орбита и стабилизатор

Определение:

Пусть группа действует на множество . Тогда орбитой (англ. orbit) элемента называется множество: . Множество всех орбит обозначается так: .

Иными словами, орбитой элемента множества в группе называется порожденный им класс эквивалентности по отношению . Задача подсчета количества классов эквивалентности является нетривиальной и решается в общем случае при помощи Леммы Бёрнсайда.

Определение:

Элемент называется неподвижной точкой (англ. fixed point) элемента , если

Определение:

Пусть группа действует на множество . Тогда стабилизатором (англ. stabilizer) элемента называется множество его неподвижных точек:

Далее приведены несколько несложных и полезных на практике утверждений.

Утверждение:

Заметим, что

Аналогично доказывается, что

Таким образом,

Примеры

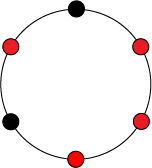
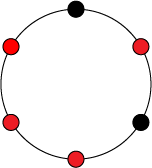
В качестве примера рассмотрим ожерелья, состоящие из бусин, которые бывают красного и черного цвета. Таким образом, множество — это множество всевозможных ожерелий из бусин, окрашенных в один из двух цветов.
Теперь введем группу , в которой будет элементов: , где будет означать поворот ожерелья на угол против часовой стрелки.

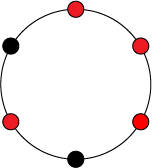
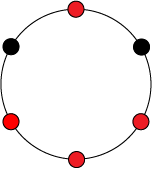
Таким образом, правое ожерелье получено из левого путем действия на него элементом . Из этого следуют, что левое и правое ожерелья равны с точностью до группы , а значит они находятся в одном классе эквивалентности.

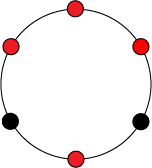
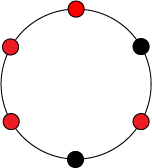
Теперь в качестве примера рассмотрим орбиту левого ожерелья — все элементы множества , полученные из элемента путем поворотов на различных углов.

Ожерелье

См. также

Теорема Кэли
Лемма Бёрнсайда и Теорема Пойа
Задача об ожерельях

Источники информации

Wikipedia | Действие группы
Wikipedia | Group action
Теория групп
MAXimal::algo::Лемма Бернсайда. Теорема Пойа

Источник

Говорят, что группа действует на множестве ,
если задан гомоморфизм из группы в группу
всех перестановок множества
. Для краткости часто записывают как .

Другими словами, группа действует на множестве , если задано отображение (обозначаемое ), такoe что

для всех , и
где есть единица .

Типы действий

Орбиты

Подмножество

называется орбитой элемента .

Действие группы на множестве определяет на нём отношение эквивалентности

${displaystyle forall n,min Mqquad left(nsim _{G}mright)quad Longleftrightarrow quad left(exists gin G gn=mright)quad Longleftrightarrow quad left(Gn=Gmright).}$

При этом классами эквивалентности являются орбиты элементов.
Поэтому, если общее число классов эквивалентности равно , то

${displaystyle M=Gm_{1}sqcup Gm_{2}sqcup dots sqcup Gm_{k}}$

где ${displaystyle m_{1},m_{2},dots ,m_{k}in M}$ попарно неэквивалентны. Для транзитивного действия .

Стабилизаторы

Подмножество

${displaystyle G_{m}={gin Gmid gm=m}subset G}$

является подгруппой группы и называется стабилизатором или стационарной подгруппой элемента .

Стабилизаторы элементов одной орбиты сопряжены, то есть если ${displaystyle nsim _{G}m}$ , то найдется такой элемент , что

${displaystyle G_{m}=g,G_{n},g^{-1}.}$

Количество элементов в орбите

${displaystyle |Gm|=[G:G_{m}]}$

, где ${displaystyle [G:G_{m}]}$

— индекс подгруппы ${displaystyle G_{m}subset G}$

, в случае конечных групп равен ${displaystyle {frac {|G|}{|G_{m}|}}}$

Если ${displaystyle M=Gm_{1}sqcup Gm_{2}sqcup dots sqcup Gm_{k}}$ , то

${displaystyle |M|=sum _{t=1}^{k}[G:G_{m_{t}}]}$

— формула разложения на орбиты.

Эта формула также влечёт следующие тождества

${displaystyle forall min Mquad sum _{nin Gm}|G_{n}|=|G|}$

${displaystyle sum _{min M}|G_{m}|=k|G|}$

и лемму Бернсайда.

Примеры действий

Действия на себе

Слева

Действие на себе слева является наиболее простым примером действия, в этом случае, и гомоморфизм задан как .

Справа

Аналогично определяется действие на себе справа, ${displaystyle (Phi (g))(h)=hg^{-1}}$ .

Сопряжениями

Пусть и гомоморфизм задан как ${displaystyle (Phi (g))(h)=ghg^{-1}}$ . При этом для каждого элемента стабилизатор ${displaystyle G_{h}}$ совпадает с централизатором :

${displaystyle G_{h}={gin Gmid ghg^{-1}=h}={gin Gmid gh=hg}=C(h)}$

Например, для элемента из центра группы (т.е. ) ), ${displaystyle G_{h}=G}$ .

Слева и справа

Все эти два действия являются действиями подгрупп действия на с гомоморфизмом заданым как ${displaystyle (Phi (g_{1},g_{2}))(h)=g_{1}hg_{2}^{-1}}$ .
eo:Grupa ago
he:פעולת חבורה
pl:Działanie grupy na zbiorze
uk:Дія групи
zh-yue:作用 (代數)

Источник

§1 Формулировка и доказательство

Лемма
Бернсайда вычисляет количество орбит
действия группы на множестве с помощью
суммы по всем элементам группы. Она
применяется в том случае, когда порядок
множества X намного больше, чем порядок
группы G.

Пусть
G
– перестановок
на множестве

Подмножество
называетсяорбитой
группы G,
если

а)
для
любогои любого;
т.е. действие перестановок изG
на элементы O
не выводит за пределы О;

б)
два
элемента из О
можно перевести друг в друга некоторой
перестановкой из G.

Всякая
группа перестановок
G
= {
имеет
орбиты.

Для
доказательства выберем произвольный
элемент
и рассмотрим множество
Оно будет орбитой группы G,
так как

а)
если
так как

б)
если
ипроизвольные
элементы изтои при этомтак
какGгруппа.

Оказывается,
что орбитами
подобного вида исчерпываются все
типы орбит.
Более точно, если Оорбита
группыG
и
,
то
=(а).
Справедливость этого утверждения
вытекает непосредственно из определения
орбиты группы.

Ясно,
что любые две орбиты О(а)
и О
(b)
либо совпадают (если bО(а)),
либо не пересекаются (если bO(а)).
Отсюда
следует, что множество
М распадается в объединение
непересекающихся подмножеств
— орбит
группы G.
В
частности, может случиться, что
единственной орбитой группы G
будет само множество М.
Группы с таким свойством называются
транзитивными.
Таким образом, группа перестановок
G
на множестве М транзитивна, если любой
элемент аМ
может быть получен из любого другого
элемента bМ
под действием подходящим способом
выбранной перестановки
:.
Все другие группы перестановок называютсяинтранзитивными.

Пусть
число
неподвижных точек перестановки
,
число
орбит группы перестановокдействующей
на множестве

Лемма
Бернсайда: Для
любой группы перестановок имеет
место равенство

Доказательство:
Рассмотрим
отношение «перестановка
сохраняет неподвижным элементm»
между перестановками группы G
и элементами множества М.
Сопоставим парам (,т),
,
m,
вершины прямоугольной сети и отметим
те из них, для которых соответствующая
пара (,т)
находится
в указанном отношении, т. е. m(a)
=
т
(рис. 4). Иными словами, построим
график
указанного отношения. Число отмеченных
точек (точек, принадлежащих графику)
можно подсчитать двумя способами:

определить
число отмеченных точек на каждой
вертикали и просуммировать полученные
величины или же определить число
таких точек по каждой горизонтали и
затем вычистить их сумму.

Рис.
4

Согласно
определению отношения на каждой вертикали
отмечаются все точки, сохраняемые
перестановкой
,
соответствующей этой вертикали. Их
число равноПоэтому число всех точек графика равно

С
другой стороны, на каждой горизонтали
отмечаются все перестановки, сохраняющие
элемент m,
отвечающий этой горизонтали. Мы
знаем, что они образуют группу G_m
—
стабилизатор элемента т
—
и их чисто равно

Поэтому
при втором способе подсчета числа
отмеченных точек графика рассматриваемого
отношения получаем выражение

Однако
если элементы i,
j
М
содержатся в одной орбите, то
и поэтомуПусть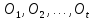— все орбиты группыG,
такие, что
,
и слагаемые в этом объединении не
пересекаются. Разобьем сумму (1) на части
так, чтобы внутри каждой из частей
суммирование шло по элементам
некоторой орбиты:

Каждое
из t
слагаемых в правой части этого равенства
можно преобразовать следующим образом:

Поэтому

Таким
образом, при втором способе подсчета
мы получили
отмеченных точек графика. Приравнивая
величины, полученные при первом и
втором способах, получим

т.е.

Лемма
доказана.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Понять, что такое орбиты, легче всего вот из какого примера. Рассмотрим группу поворотов плоскости относительно начала координат. Возьмём какую-нибудь точку $%X$%, и посмотрим, куда она может переходить при поворотах. Очевидно, что она может оказаться в любом месте окружности с центром $%O$% радиусом $%X$%. Это и есть её орбита — как если бы точка $%X$% вращалась вокруг $%O$% по окружности, подобно небесному телу. Поэтому орбитами в данном случае будут все концентрические окружности, а у начала координат $%O$% орбита из одной этой точки и состоит.

а) Рассмотрим произвольный вектор $%vin V$%. Нужно описать его орбиту, то есть множество векторов вида $%Av$%, где $%A$% — невырожденная матрица (вектор можно считать столбцом из координат с фиксированном базисе). Здесь вектор $%v$% фиксирован, а $%A$% пробегает множество всех невырожденных матриц.

Очевидно, что если $%v=0$%, то $%Av=0$%, то есть у нулевого вектора орбита одноэлементна. Если $%vne0$%, то $%Avne0$% ввиду невырожденности $%A$%. (В противном случае можно было бы написать $%v=A^{-1}Av=A^{-1}0=0$%.) Вектор $%v$%, будучи ненулевым, является частью некоторого базиса пространства $%V$%. Рассмотрим произвольный ненулевой вектор $%win V$%. Он тоже является частью некоторого базиса. Тогда для двух базисов существует и единственно линейное преобразование, переводящее векторы первого базиса в векторы второго. Обозначим его через $%A$%. Оно невырождено, так как базис переводит в базис (это эквивалентное свойство). При этом $%Av=w$%. Это означает, что $%v$% можно перевести невырожденным преобразованием в любой заданный ненулевой вектор. То есть орбитой $%v$% будет множество $%Vsetminus{0}$% всех ненулевых векторов.

Всего орбит имеется две: $%{0}$% и $%Vsetminus{0}$%.

b) Здесь рассуждение аналогично, но надо иметь в виду, что ортогональное преобразование сохраняет длину вектора. В то же время, для двух векторов одинаковой длины всегда существует ортогональное преобразование, переводящее один вектор в другой. Отсюда следует, что орбиты состоят из векторов одной и той же длины, то есть их столько же, сколько неотрицательных чисел. Для каждого $%rge0$% мы в качестве орбиты имеем сферу радиусом $%r$% в евклидовом пространстве $%V$%. Это и есть орбита любого вектора, имеющего длину $%r$%.

Источник

Определения[править | править код]

Действие слева[править | править код]

Действие справа[править | править код]

Типы действий[править | править код]

Орбиты[править | править код]

Стабилизаторы[править | править код]

Количество элементов в орбите[править | править код]

Примеры действий[править | править код]

Действия на себе[править | править код]

Слева[править | править код]

Справа[править | править код]

Слева и справа[править | править код]

Сопряжениями[править | править код]

Вариации и обобщения[править | править код]

См. также[править | править код]

Литература[править | править код]

Эквивалентность по группе

Орбита и стабилизатор

Примеры

См. также

Источники информации

Типы действий

Орбиты

Стабилизаторы

Количество элементов в орбите

Примеры действий

Действия на себе

Слева

Справа

Сопряжениями

Слева и справа

§1 Формулировка и доказательство

Вам также может понравиться

Поиск по картинке как найти фильм

Как найти массу раствора через количество вещества

Как найти своего мужчину через интернет

Добавить комментарий Отменить ответ