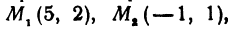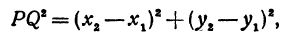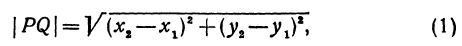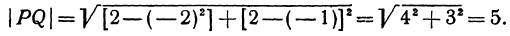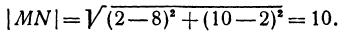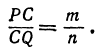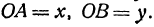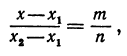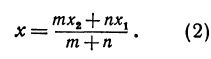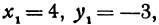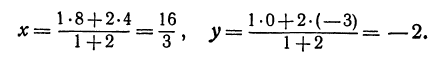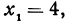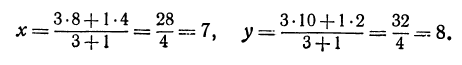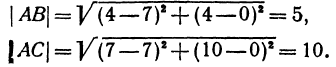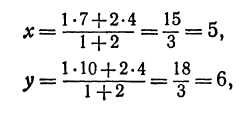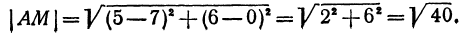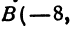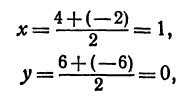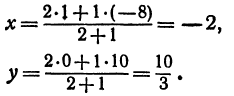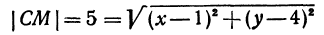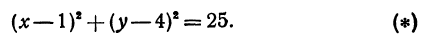Главная
Как найти ординату если известна абциса
-
- 0
-
?
Лия Зивтина
Вопрос задан 8 октября 2019 в
5 – 9 классы,
Алгебра.
-
Комментариев (0)
Добавить
Отмена
1 Ответ (-а, -ов)
- По голосам
- По дате
-
- 0
-
Если известна абсцисса (то есть имеется график функции), то надо провести линию из этой точки на оси ОХ параллельно оси ОУ до пересечения с графиком функции.
Из точки на графике проводим линию параллельно оси ОХ до пересечения с осью ОУ и там определяем ординату.
Отмена
Ева Гнедочкина
Отвечено 8 октября 2019
-
Комментариев (0)
Добавить
Отмена
Ваш ответ
Галинуха
9 декабря, 04:28
Как найти ординату если известна абциса
-
Нилыч
9 декабря, 06:20
-1
Е сли известна абсцисса (то есть имеется график функции), то надо провести линию из этой точки на оси ОХ параллельно оси ОУ до пересечения с графиком функции.
Из точки на графике проводим линию параллельно оси ОХ до пересечения с осью ОУ и там определяем ординату.
- Комментировать
- Жалоба
- Ссылка
Найди верный ответ на вопрос ✅ «Как найти ординату если известна абциса …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Как найти ординату если известна абциса.
На этой странице вы найдете ответ на вопрос Как найти ординату если известна абциса?. Вопрос
соответствует категории Алгебра и уровню подготовки учащихся 5 – 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно
ознакомиться с вариантами ответов других посетителей страницы или обсудить с
ними интересующую тему. Здесь также можно воспользоваться «умным поиском»,
который покажет аналогичные вопросы в этой категории. Если ни один из
предложенных ответов не подходит, попробуйте самостоятельно сформулировать
вопрос иначе, нажав кнопку вверху страницы.
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Как найти координаты точки
Поддержать сайт
Каждой точке координатной плоскости соответствуют две координаты.
Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.
Рассмотрим как в системе координат (на координатной плоскости):
- находить координаты точки;
- найти положение точки.
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.
Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».
Обозначают координаты точки, как указано выше (·) A (2; 3).
Пример (·) A (2; 3) и (·) B (3; 2).
Запомните!
На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.
Особые случаи расположения точек
- Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0). - Начало координат — точка O имеет координаты, равные нулю O (0,0).
- Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
- Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
- Координаты любой точки, лежащей на оси ординат имеют вид (0, y).
Как найти положение точки по её координатам
Найти точку в системе координат можно двумя способами.
Первый способ
Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:
- Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox». - Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy». - Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.
Второй способ
Чтобы найти точку D (−4 , 2) надо:
- Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−». - Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».
Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Координаты на плоскости:
Возьмем на плоскости две взаимно перпендикулярные прямые, пересекающиеся в точке
Определение: Координатными осями на плоскости называются две взаимно перпендикулярные прямые, на которых установлены: 1) направления, 2) масштаб и 3) общая точка отсчета.
Назовем одну из осей осью 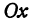
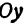
Возьмем произвольную точку 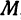
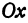
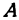
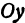
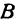
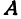
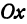
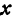
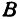
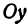
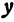
Определение. Абсциссой точки называется координата ее проекции на ось 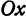
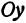
Абсциссу точки обычно обозначают буквой 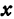
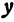
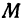
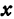
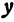
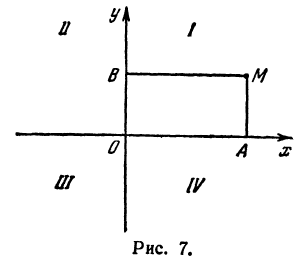
Координатные оси разделяют плоскость на четыре части, которые называют четвертями.
Первой четвертью называется та часть плоскости, в которой абсцисса и ордината положительны.
Второй четвертью — та часть, в которой абсцисса отрицательна, а ордината положительна.
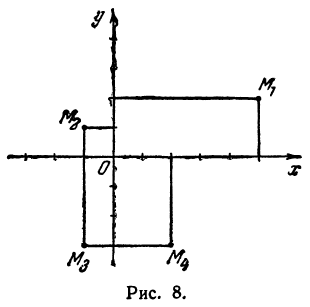
Третьей четвертью—та часть, в которой абсцисса и ордината отрицательны, и, наконец, четвертой,—та часть, в которой абсцисса положительна, а ордината отрицательна (рис. 7). На рис. 8 указаны 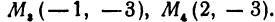
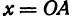
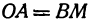
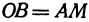
Пример:
Найти точку 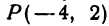
Решение:
Возьмем на оси 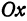
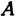
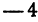
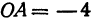
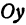
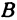
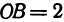
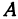
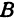
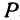
Пример:
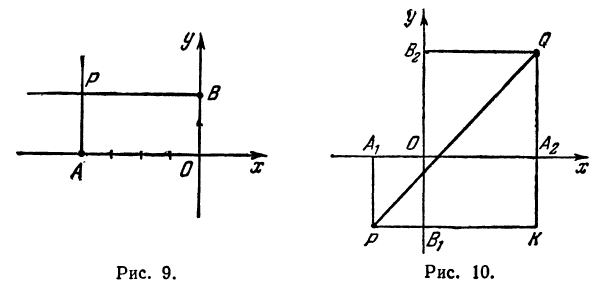
Найти расстояние между точками 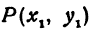
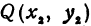
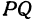
Решение:
Обозначим проекцию точки 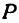
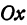
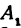
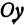
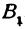
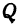
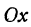
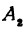
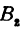
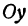
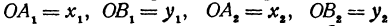
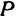
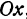
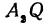
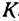
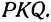
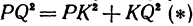
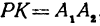
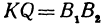
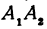
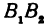
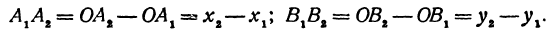
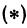
откуда
т. е. расстояние между двумя точками равно корню квадратному из суммы квадратов разностей, координат.
Примечание. Расстояние между двумя точками, так же как длина отрезка, всегда положительно, поэтому в формуле (1) перед квадратным корнем берут только знак плюс.
Пример:
Найти расстояние между точками 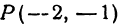
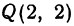
Решение:
Применяя формулу (1), получим
Пример:
Найти длину отрезка 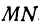
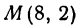
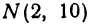
Решение:
Применяя формулу (1), получим
Пример:
Найти точку 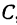
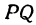
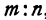
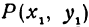
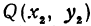
Решение:
По условию задачи надо найти такую точку 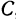
Обозначим, как и выше, проекции точки 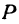
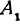
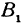
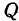
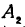
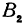
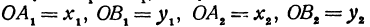
Кроме того, обозначим координаты искомой точки 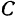
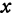
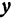
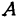
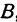
Так как прямые 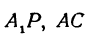
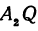
Но 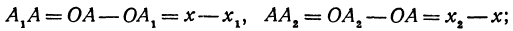
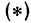
решая которое найдем абсциссу точки 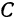
Рассуждая аналогично о проекциях на оси 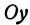
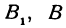
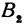
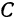
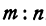
Итак, искомая точка 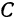
Пример:
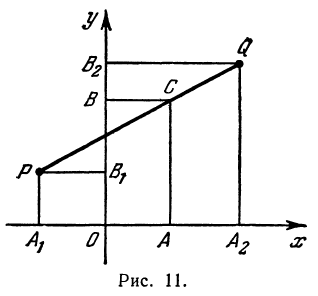
Найти точку, делящую в отношении 1:2 отрезок 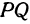
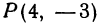
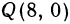
Здесь 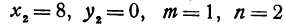
Решение:
Применяя формулы (2) и (3), получим:
- Заказать решение задач по высшей математике
Пример:
Найти точку, делящую расстояние между точками 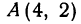
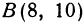
Здесь 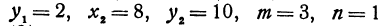
Решение:
По формулам (2) и (3) находим:
Следствие (из формул (2) и (3)). Если точка 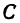
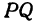
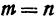
т. е. абсцисса середины отрезка равна средней арифметической абсцисс его начала и конца; ордината середины отрезка равна средней арифметической ординат его начала и конца.
Пример:
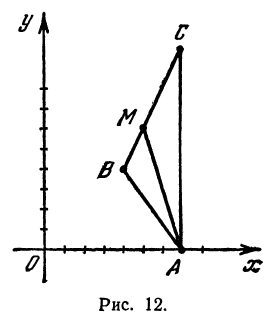
Даны три вершины треугольника: 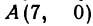
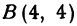
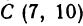
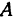
Решение:
Найдем длины сторон 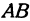
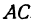
Обозначим точку пересечения биссектрисы угла 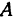
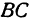
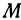
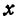
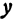
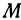
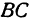
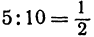
т.е. 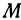
Теперь вычисляем длину биссектрисы как расстояние между точками 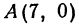
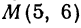
Пример:
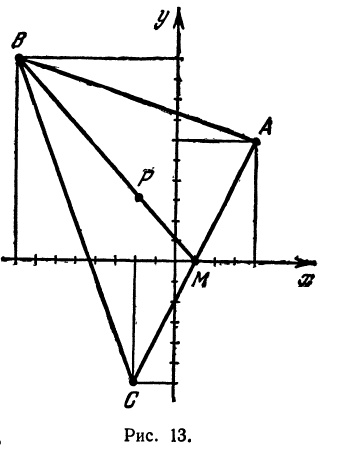
Найти точку пересечения медиан треугольника, вершинами которого являются точки 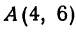

Решение:
Точка пересечения медиан делит каждую из медиан в отношении 2:1, считая от вершины треугольника. Обозначим через 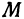
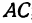
т. е. 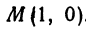
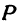
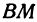
Итак, искомая точка 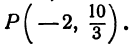
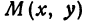
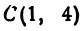
или, возводя обе части равенства в квадрат, получим
Это равенство есть уравнение с двумя неизвестными 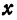
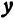
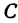
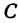
Следовательно, можно сказать, что уравнение 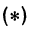
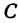
В следующих главах будут рассмотрены уравнения с двумя неизвестными 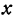
- Линейная функция
- Квадратичная функция
- Тригонометрические функции
- Производные тригонометрических функции
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
- Координаты на прямой