Как найти ординату дроби

Как найти ординату дроби

как определять координаты точек на координатном луче если они заданы смешанным числом или дробью?



Ученик

(10),
закрыт



8 лет назад

любительница музыки

Гений

(90451)


8 лет назад

Нужно знать единичный отрезок и определить, на каком расстоянии от 0 находится нужное число (дробь).
Например, чтобы отметить на координатном луче простые дроби 3/4,1/6,5/12 нужно:
выбрать единичный отрезок 12 клеток ( так будет легче отмечать дробные числа ). Тогда, чтобы отложить 3/4 надо 12:4*3 =9. То есть на девятой клетке будет стоять число 3/4. Дробь 1/6 будет через2 клетки, а 5/12 через 5 клеток..

Источник

было в ЕГЭ

в условии
в решении
в тексте к заданию
в атрибутах

Категория

Атрибут

Всего: 119    1–20 | 21–40 | 41–60 | 61–80 | 81–100 …

Добавить в вариант

Точки O(0; 0), A(10; 8), C(2; 6) и B являются вершинами параллелограмма. Найдите ординату точки B.

Точки O(0; 0), A(10; 8), B(8; 2) и C являются вершинами параллелограмма. Найдите ординату точки C.

Точки O(0; 0), B(8; 2), C(2; 6) и A являются вершинами параллелограмма. Найдите ординату точки A.

Точки O(0; 0), A(10; 8), B(8; 2), C(2; 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.

Найдите абсциссу точки пересечения прямой, заданной уравнением 3x + 2y  =  6, с осью Ox.

Найдите ординату точки пересечения прямой, заданной уравнением 3x + 2y  =  6, с осью Oy.

Найдите ординату точки пересечения прямых, заданных уравнениями 3x + 2y  =  6 и y = −x.

Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).

Найдите ординату центра окружности, описанной около треугольника, вершины которого имеют координаты (8; 0), (0; 6), (8; 6).

Найдите расстояние от точки A с координатами (4, 9) до оси абсцисс.

Найдите ординату точки, симметричной точке A(−5; 2) относительно оси Ox.

Найдите ординату точки, симметричной точке A(1, −4) относительно начала координат.

Найдите ординату середины отрезка, соединяющего точки O левая круглая скобка 0;0 правая круглая скобка и A левая круглая скобка 5;8 правая круглая скобка .

Найдите ординату точки пересечения оси Oy и отрезка, соединяющего точки A левая круглая скобка минус 4; минус 6 правая круглая скобка и B левая круглая скобка 4; 3 правая круглая скобка .

Прямая a проходит через точки с координатами (0; 2) и (2; 0). Прямая b проходит через точку с координатами (0; 4) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.

Всего: 119    1–20 | 21–40 | 41–60 | 61–80 | 81–100 …

Источник

Также, как и на координатном луче, изображение дроби на координатной прямой начинается с выбора единичного отрезка.

Самый удобный вариант — единичный отрезок взять из такого количества клеточек, каков знаменатель дроби.

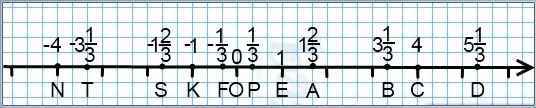
Например, требуется на координатной прямой отметить точки, координаты которых — смешанные числа и дроби со знаменателем 3. В качестве единичного  берем отрезок длиной три клеточки. В этом случае одна клеточка соответствует дроби 1/3, две клеточки — 2/3, а три клеточки — 1.

дробь на координатной прямой

    [P(frac{1}{3}),A(1frac{2}{3}),B(3frac{1}{3}),C(4),F( - frac{1}{3}),]

    [K( - 1),S( - 1frac{2}{3}),T( - 3frac{1}{3}),N( - 4),D(5frac{1}{3}).]

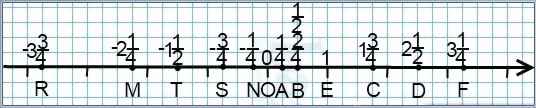
Если требуется изобразить на координатной прямой дроби со знаменателем 4, удобно в качестве единичного взять отрезок длиной 4 клеточки:

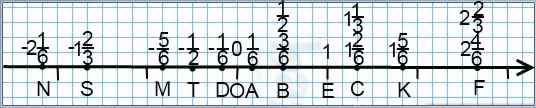
координатная прямая с дробями

    [A(frac{1}{4}),B(frac{2}{4})uB(frac{1}{2}),C(1frac{3}{4}),D(2frac{1}{2}),]

    [F(3frac{1}{4}),N( - frac{1}{4}),S( - frac{3}{4}),T( - 1frac{1}{2}),]

    [M( - 2frac{1}{4}),R( - 3frac{3}{4}).]

Если знаменатель равен 6, для изображения дроби на координатной прямой берем единичный отрезок длиной шесть клеточек:

координатная прямая с дробями

    [A(frac{1}{6}),B(frac{3}{6})uB(frac{1}{2}),C(1frac{2}{6})uC(1frac{1}{3}),]

    [D( - frac{1}{6}),K(1frac{5}{6}),F(2frac{4}{6})uF(2frac{2}{3}),]

    [T( - frac{1}{2}),M( - frac{5}{6}),S( - 1frac{2}{3}),N( - 2frac{1}{6}).]

Причем в этом случае удобно изображать не только дроби со знаменателем 6, но также дроби со знаменателем 3 и 2 (так как в этом случае 6 — их наименьший общий знаменатель).

Для изображения дроби на координатной прямой:

1) разбиваем единичный отрезок на столько частей, каков знаменатель;

2) берем из них столько частей, каков числитель.

Источник

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

На главную страницу
На главную страницу

на главную

Как найти координаты точки

Поддержать сайтспасибо

Каждой точке координатной плоскости соответствуют две координаты.

Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.

Найти координаты точки

Рассмотрим как в системе координат (на координатной плоскости):

  • находить координаты точки;
  • найти положение точки.

Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.

Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».

Координаты точки плоскости

Обозначают координаты точки, как указано выше (·) A (2; 3).

Пример (·) A (2; 3) и (·) B (3; 2).

Точки с разными координатами

Запомните!
!

На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.

Особые случаи расположения точек

  1. Если точка лежит на оси «Oy»,
    то её абсцисса равна 0. Например,
    точка С (0, 2).
  2. Если точка лежит на оси «Ox», то её ордината равна 0.
    Например,
    точка F (3, 0).
  3. Начало координат — точка O имеет координаты, равные нулю O (0,0).
    Точки на координатный осях
  4. Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
    Точки на прямой перпендикулярной оси абсцисс
  5. Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
    Точка на оси абсцисс
  6. Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
    Точка на оси абсцисс
  7. Координаты любой точки, лежащей на оси ординат имеют вид (0, y).
    Точка на оси ординат

Как найти положение точки по её координатам

Найти точку в системе координат можно двумя способами.

Первый способ

Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:

  1. Отметить на оси «Ox», точку с координатой
    «−4», и провести через неё прямую перпендикулярную оси «Ox».
  2. Отметить на оси «Oy»,
    точку с координатой 2, и провести через неё прямую перпендикулярную
    оси «Oy».
  3. Точка пересечения перпендикуляров (·) D — искомая точка.
    У неё абсцисса равна «−4», а ордината равна 2.

    Как найти точку в системе координат

Второй способ

Чтобы найти точку D (−4 , 2) надо:

  1. Сместиться по оси «x» влево на
    4 единицы, так как у нас
    перед 4
    стоит «−».
  2. Подняться из этой точки параллельно оси y вверх на 2 единицы, так
    как у нас перед 2 стоит «+».
    Как найти точку на координатной плоскости

Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.

Ваши комментарии

Важно!
Галка

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Пришелец пожимает плечами

Оставить комментарий:

Источник

Содержание

  • – Как показать дроби на числовом луче?
  • – Что необходимо отметить на прямой чтобы она стала координатной?
  • – В чем различие координатного и числового лучей?
  • – Как отметить дроби на координатной прямой?
  • – Как обозначать дроби?
  • – Как ставить дроби на координатном луче?
  • – Как сократить дробь на дробь?
  • – Как правильно складывать дроби?
  • – Как записать координаты точек 5 класс?
  • – Как правильно записывать координаты точек?
  • – Что такое координатный луч 4 класс?

Для изображения дроби на координатной прямой: 1) разбиваем единичный отрезок на столько частей, каков знаменатель; 2) берем из них столько частей, каков числитель.

Как показать дроби на числовом луче?

Дробь можно отмечать на числовом луче. Единичный отрезок разделён на 5 равных частей. Одной маленькой части единичного отрезка соответствует дробь 1 5 . Знаменатель этой дроби, число 5, говорит о том, что единичный отрезок разделили на 5 равных частей, а числитель 1 — о том, что взяли одну часть.

Что необходимо отметить на прямой чтобы она стала координатной?

Для того, чтобы лучше понять правило, следует отметить точку на координатной прямой и посмотреть, какое натуральное число соответствует отметке. Если эта точка совпадает с началом отсчета, она будет отмечена нулем.

В чем различие координатного и числового лучей?

Координатный и числовой лучи очень схожи. Различие заключается в том, что числовой луч может начинаться с любой точки и эта точка будет его началом. … Координатная прямая же, в отличие от координатного луча, может быть продлена как в право, так и в лево от начала координат.

Как отметить дроби на координатной прямой?

Для изображения дроби на координатной прямой: 1) разбиваем единичный отрезок на столько частей, каков знаменатель; 2) берем из них столько частей, каков числитель.

Как обозначать дроби?

Обозначение дроби

Обозначается дробь, как . Верхнее число дроби, называется числителем, нижнее – знаменателем.

Как ставить дроби на координатном луче?

Чтобы отметить на координатном луче нужную дробь, единичный отрезок разбиваем на столько частей, каков знаменатель, и берём таких частей столько, каков числитель. Чтобы изобразить дробь , единичный отрезок разбиваем на 12 частей и берём 7 из них.

Как сократить дробь на дробь?

Сократить дробь – значит разделить ее числитель и знаменатель на общий делитель, положительный и отличный от единицы. В результате такого действия получится дробь с новым числителем и знаменателем, равная исходной дроби.

Как правильно складывать дроби?

Чтобы сложить две обыкновенные дроби, следует:

  1. привести дроби к наименьшему общему знаменателю;
  2. сложить числители дробей, а знаменатель оставить без изменений;
  3. сократить полученную дробь;
  4. Если получилась неправильная дробь преобразовать неправильную дробь в смешанную.

Как записать координаты точек 5 класс?

Чтобы найти координаты точки на плоскости, нужно опустить из этой точки перпендикуляры на оси координат. Точка пересечения с осью «x» называется абсциссой точки «А», а с осью y называется ординатой точки «А». Обозначают координаты точки, как указано выше (·) A (2; 3). Пример (·) A (2; 3) и (·) B (3; 2).

Как правильно записывать координаты точек?

Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записываются так: A(x; y; z). Если точка находится на оси Ox, то её координаты X(x; 0; 0). Если точка находится на оси Oy, то её координаты Y(0; y; 0).

Что такое координатный луч 4 класс?

Луч OE с началом отсчёта в точке O , на котором указаны единичный отрезок и направление, называют координатным лучом. Число, соответствующее точке координатного луча, называется координатой этой точки.

Интересные материалы:

Как найти AirPods если они в чехле?
Как найти Аирподс если потерял?
Как найти соотношение сторон треугольника если известны углы?
Как оформить выплату на ребенка если нет Снилс?
Как открутить болт если он прокручивает?
Как открыть ютуб если он не открывается?
Как открыть молнию если попала ткань?
Как отменить заказ на Али если его еще не отправили?
Как перезагрузить HTC One если он завис?
Как починить молнию если слетел бегунок?

Источник

Добавить комментарий