Как найти ординату если известна абсцисса точки

Как найти ординату если известна абциса.

На этой странице вы найдете ответ на вопрос Как найти ординату если известна абциса?. Вопрос
соответствует категории Алгебра и уровню подготовки учащихся 5 – 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно
ознакомиться с вариантами ответов других посетителей страницы или обсудить с
ними интересующую тему. Здесь также можно воспользоваться «умным поиском»,
который покажет аналогичные вопросы в этой категории. Если ни один из
предложенных ответов не подходит, попробуйте самостоятельно сформулировать
вопрос иначе, нажав кнопку вверху страницы.

Источник

Главная

Как найти ординату если известна абциса

Лия Зивтина

Вопрос задан 8 октября 2019 в

5 – 9 классы,

Алгебра.

Комментариев (0)

Добавить

Отмена

1 Ответ (-а, -ов)

По голосам
По дате

Если известна абсцисса (то есть имеется график функции), то надо провести линию из этой точки на оси ОХ параллельно оси ОУ до пересечения с графиком функции.
Из точки на графике проводим линию параллельно оси ОХ до пересечения с осью ОУ и там определяем ординату.

Отмена

Ева Гнедочкина

Отвечено 8 октября 2019

Комментариев (0)

Добавить

Отмена

Ваш ответ

Источник

Решение на Упражнение 1310 из ГДЗ по Математике за 6 класс: Мерзляк А.Г.

Условие

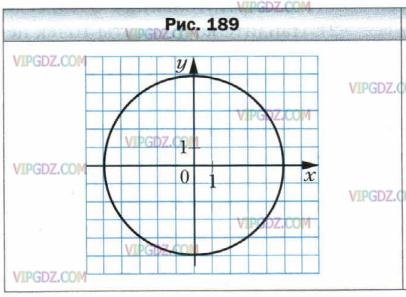
На координатной плоскости проведена окружность (рис.189).

1) Найдите ординату точки, принадлежащей этой линии, абсцисса которой равна: 5; −4.
2) Найдите абсциссу точки, принадлежащей этой линии, ордината которой равна: −5; 3; 0.

Решение 1

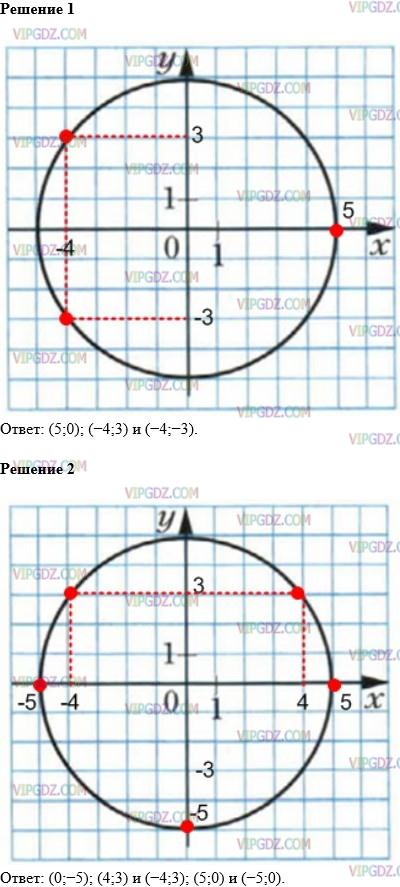
Решение 2

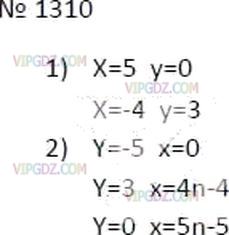
Поиск в решебнике

Дано уравнение окружности x2+y2=169.

1. Найди ординату точек на этой окружности, абсцисса которых – 13.

(запиши обе координаты точек, в точке A ординату со знаком ” – “, в точке B – со знаком ” + “; если второй точки нет, вместо координат пиши координаты первой точки).

2. Найди абсциссу точек на этой окружности, ордината которых 13.

(запиши обе координаты точек, в точке C абсциссу со знаком ” – “, в точке D – со знаком ” + “; если второй точки нет, вместо координат пиши координаты первой точки).

9 класс. Геометрия. Метод координат. Уравнение окружности.

Оглавление
Занятия
Обсуждение
О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Решение задач

Выясните, какие из данных уравнений являются уравнениями окружности.

Найдите координаты центра и радиус каждой окружности.

а)

б)

в)

г) ;

д)

Рассмотрим каждое уравнение в отдельности.

а) – окружность,

б) – окружность,

в)
Выделим полный квадрат:

уравнение не является уравнением окружности.

г) .
Выделим полный квадрат:
– окружность,

д)
Выделим полный квадрат:
– окружность,

На окружности, заданной уравнением , найдите точки

а) с абсциссой –4; б) с ординатой 3.

Решение: построим окружность с центром (0;0) радиуса 5 (рис. 1).

Рис. 1. Иллюстрация к задаче

а) Координаты точек окружности с абсциссой –4 являются решениями системы:

Получаем точку и точку

Рис. 2. Иллюстрация к задаче

б) Координаты точек окружности с ординатой 3 являются решениями системы:

Рис. 3. Иллюстрация к задаче

Получаем точку и ту же самую точку

Ответ: .

Запишите уравнение окружности радиуса r с центром в точке А, если

а)

б)

в)

г)

а) Окружность
Ответ:

б) Окружность .
Ответ:

в) Окружность
Ответ:

г) Окружность
Ответ:

Напишите уравнение окружности с центром в начале координат, проходящей через точку

Рис. 4. Иллюстрация к задаче

Найдем радиус, как расстояние ОВ:

Запишем уравнение окружности с центром О(0;0):

Для контроля проверим, удовлетворяют ли полученному уравнению координаты точки В:

значит, точка В лежит на окружности.

Ответ:

Напишите уравнение окружности, проходящей через точку А(1;3), если известно, что центр окружности лежит на оси абсцисс, а радиус равен 5.

Сколько существует таких окружностей?

Дано: А(1;3) – точка окружности,

Найти: уравнение окружности (С; r=5).

Решение: центр искомой окружности удален от точки А(1;3) на расстояние 5, значит, он лежит на окружности с центром в точке А(1;3) радиуса 5, но он еще лежит и на оси Ох. Построим окружность (А(1;3); r=5) (рис. 5).

Рис. 5. Иллюстрация к задаче

Точек, удовлетворяющих нашим условиям, на оси Ох две:

Для определения координат этих точек составим систему:

Запишем уравнения искомых окружностей:

окружность (

окружность ( и построим эти окружности (рис. 6):

Рис. 6. Иллюстрация к задаче

Ответ: две окружности.

Напишите уравнение окружности, проходящей через две заданные точки и В(0;9), если известно, что центр окружности лежит на оси ординат.

Дано: окружности ;

oкружности .

записать уравнение окружности.

Рис. 7. Иллюстрация к задаче

Запишем уравнение окружности так как окружность проходит через точки А и В, то их координаты удовлетворяют уравнению окружности:

Подставим найденные значения в уравнение.

Ответ:

Напишите уравнение окружности с центром в точке А(6;0), проходящей через точку В(-3;2).

Дано: А(6;0) – центр,

окружности.

Найти: уравнение окружности.

Рис. 8. Иллюстрация к задаче

Находим радиус как расстояние АВ:

Запишем уравнение окружности:

Ответ:

Заключение

Итак, мы рассмотрели серию задач по теме «Окружность» и в каждой задаче использовали уравнение окружности.

На следующем уроке мы выведем уравнение прямой.

[spoiler title=”источники:”]

http://urokam.net/geometrija/5356607.html

http://www.kursoteka.ru/course/2507/lesson/8218/unit/21023/5

[/spoiler]

Источник

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

на главную

Как найти координаты точки

Поддержать сайт

Каждой точке координатной плоскости соответствуют две координаты.

Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.

Рассмотрим как в системе координат (на координатной плоскости):

находить координаты точки;
найти положение точки.

Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.

Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».

Обозначают координаты точки, как указано выше (·) A (2; 3).

Пример (·) A (2; 3) и (·) B (3; 2).

Запомните!

На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.

Особые случаи расположения точек

Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2).
Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0).
Начало координат — точка O имеет координаты, равные нулю O (0,0).
Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
Координаты любой точки, лежащей на оси ординат имеют вид (0, y).

Как найти положение точки по её координатам

Найти точку в системе координат можно двумя способами.

Первый способ

Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:

Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox».
Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy».
Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.

Второй способ

Чтобы найти точку D (−4 , 2) надо:

Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−».
Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».

Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Строим графики функций y=4/x и y=4x.
1) y=4/x
Графиком является гипербола. Проходит через точки (1;4), (4;1), (2;2) и (-1;-4), (-4;-1), (-2;-2).
2) y=4x
Графиком является прямая. Для построения прямой достаточно двух точек. Пусть это будут точки (1;4) и (2;8). Можно взять ещё точки (-1;-4).
Исходя только из подготовки к построению, можно сразу увидеть ответ: общие точки (1;4) и (-1;-4).
Если всё верно построить, то графики будут пересекаться в точках (1;4) и (-1;-4).
Ответ: -1; 1

3х+2у=-27

Ответ: это а). Всё просто.

Объяснение:

$8x-6=50 \ \ 8x =56 \ \ x= 7$

По неравенству треугольника

AB + BC > AC

AC < 7 + 3

AC < 10

AB + AC > BC

AC > BC – AB

AC > 7 – 3

AC > 4

AC ∈ (4;10) отсюда из вариантов ответов подходит только AC = 8

Источник