Линией влияния в балке называется график, показывающий изменение исследуемого фактора (опорной реакции, поперечной силы, изгибающего момента и т.д.) при движении по балке единичной силы.
Любая ордината линии влияния показывает величину исследуемого фактора в тот момент, когда сила находится над этой ординатой.
Статический способ построения линий влияния в балках основан на составлении уравнений статики (уравнений равновесия). Рассмотрим простую балку на двух шарнирных опорах. По балке движется сила, равная 1. Мысленно зафиксируем силу на расстоянии z от опоры А.
1. Построение линии влияния реакции RA. Составим уравнение моментов вокруг опоры В.
Получаем аналитическое выражение для реакции RA.
Строим график по 2м точкам.
2. Аналогично строится линия влияния реакции RB. Составим уравнение моментов вокруг опоры А. 
Получаем аналитическое выражение для реакции RВ. Строим график по 2м точкам:
3. Построим линию влияния поперечной силы QK .
Возьмем произвольное сечение k, находящееся на расстоянии a от опоры A. Рассмотрим два положения силы 
— слева и справа от сечения.
a) сила находится слева от сечения K, находящееся на расстоянии a от опоры A, а рассматривать будем правую часть.Тогда 
Это значит, что линия влияния QK такая же, как линия влияния RB, но с отрицательным знаком. Строим данную линию влияния, но обводим лишь левую ее часть, так как она справедлива, когда сила слева от сечения. Значит, мы получаем левую ветвь линии влияния.
b) сила справа от сечения K, а рассматривать будем левую часть, тогда 
. Это значит, что линия влияния QK такая же, как линия влияния RА. Строим данную линию влияния, но обводим лишь правую ее часть, так как она справедлива, когда сила справа от сечения. Значит, мы получаем правую ветвь линии влияния.
При построении линии влияния поперечной силы для простой балки следует запомнить величины ординат линии влияния в сечении, а именно 
и 
.
4. Построим линию влияния изгибающего момента МK
a) сила находится слева от сечения K, а рассматривать будем правую часть, тогда 
. Это значит, что линия влияния МK такая же, как линия влияния RB, но в b раз больше. Строим данную линию влияния, но обводим лишь левую ее часть, так как она справедлива, когда сила слева от сечения. Значит, мы получаем левую ветвь линии влияния.
b) сила справа от сечения K, а рассматривать будем левую часть, тогда 
. Это значит, что линия влияния МK такая же, как линия влияния RА, но в а раз больше. Строим данную линию влияния, но обводим лишь правую ее часть, так как она справедлива, когда сила справа от сечения. Значит, мы получаем правую ветвь линии влияния.
При построении линии влияния моментов для простой балки следует запомнить величину наибольшей ординаты линии влияния, а именно 
.
Кинематический способ построения линий влияния основан на принципе возможных перемещений.
1) Для того чтобы построить линию влияния реакции какой-нибудь опоры нужно изобразить балку без этой опоры, дать данной точке возможное перемещение в положительном направлении (вверх на единицу), и зарисовать новое положение полученного механизма. 
2) Для того чтобы построить линию влияния изгибающего момента MK , нужно в данное сечение врезать шарнир 
и повернуть полученный механизм в положительном направлении на единичный угол.
3) Для того чтобы построить линию влияния поперечной силы QK, нужно в данное сечение врезать ползун 
и раздвинуть части балки в положительном направлении на единицу.
Построим линии влияния кинематическим методом в этой же балке. Линии влияния получились такие же.
Построим линии влияния поперечной силы и изгибающего момента в консольной балке кинематическим способом. Так как левая часть в этой балке неподвижна, то движется только правая часть в положительном направлении. При этом ордината линии влияния момента равна а, ордината линии влияния поперечной силы равна 1.
С помощью линий влияния можно определить любые усилия по формуле:
где сила считается положительной, если направлена вниз 
– это ордината линии влияния под силой, берется со своим знаком,
q — нагрузка считается положительной, если направлена вниз 
– это площадь в линии влияния под нагрузкой, берется со своим знаком,
М – момент считается положительным, если направлен по часовой стрелке 
— это тангенс угла наклона линии влияния над моментом, равный 
и считается положительным, если линия влияния возрастает.
Для
получения уравнения линии влияния
следует написать соответствующую
формулу, выражающую действие груза Р,
и затем принять Р =1. Такая подстановка
с алгебраической точки зрения эквивалентна
делению выражения на Р. Отсюда следует,
что ординаты линии влияния для какой-нибудь
величины Z имеют размерность.
Например,
ордината линии влияния опорных реакций
и поперечных сил, усилия в стержне имеют
размерность кг/кг, т.е. выражаются
отвлеченными числами; ординаты линии
влияния изгибающих моментов имеют
размерность
кг·м/кг = м; ординаты
линии влияния прогибов – размерность
м/кг и т.д.
Формально
можно было бы сказать, что ординаты
линий влияния, выражают собой влияние
сосредоточенного груза, равного не 1 т
или 1 кг, или какой-нибудь другой единице
сил, а равного абстрактной единице.
Ординаты
линий влияния можно рассматривать как
отношение соответствующей величины к
тому сосредоточенному грузу, которым
она вызвана. Например, если какая-либо
ордината опорной реакции равна 0,75, то
это означает, что какой угодно
сосредоточенный груз, стоящий над этой
ординатой, вызовет реакцию, величина
которой составит 0,75 от того же груза.
Можно
наконец сказать, что ордината линии
влияния представляет собой коэффициент,
стоящий при Р в соответствующей
формуле. Например, изгибающий момент в
сечении С (см. рис. 1 б) от этого груза Р,
стоящего слева, выражается формулой
.
Множитель
и служит ординатой линии влияния.
1.3Свойство прямолинейного участка линии влияния
Если
нагрузка расположена на прямолинейном
участке линии влияния, то от замены
нагрузки ее равнодействующей суммарное
влияние не изменится.
Рис.
2 Рис. 3
Для
доказательства рассмотрим рис. 2, на
котором загружен прямолинейный участок
АВ. Продолжим прямую АВ до пересечения
ее с осью абсцисс. Расположив начало
координат в точке 0, можно написать
.
Но так
как сумма моментов нескольких сил
относительно точки 0 равна моменту их
равнодействующей, то
,
следовательно:
.
Итак,
в рассмотренном случае влияния нагрузки
равно влиянию ее равнодействующей.
Этот
вывод относится не только к нагрузке,
состоящей из сосредоточенных сил, но и
к нагрузке, распределенной по длине по
любому закону.
На рис.
3 показан случай нагрузки Р1 и Р2,
равнодействующая которой расположена
за пределами прямолинейного участка
ВС линии влияния, однако в этом случае
также
.
Это
положение справедливо только для
прямолинейного участка линии влияния;
для участка другого вида тангенс угла
– переменный, и
вынесение его за знак суммы невозможно.
Следовательно, от замены нагрузки ее
равнодействующей силой влияние, вообще
говоря, изменяется.
1.4Статический способ построения линий влияния усилий
Приведенные
ниже правила используются при построении
линий влияния усилий: опорных реакций
R, поперечных сил Q
и изгибающих моментов М в поперечных
сечениях балки, продольных усилий N
в стержнях фермы.
В
соответствии со статическим методом
построения линий влияния линию влияния
какой-либо величины можно построить,
выполняя последовательно следующие
операции:
– выбрать
систему координат с осями x,
у(z). Начало координат
целесообразно выбирать на левом конце
расчетной схемы. Ось x
– ось абсцисс точки приложения единичного
груза и она же является осью абсцисс
линии влияния. Ось у (z) –
ось ординат линии влияния величины Z.
Ось x направлена
вправо, ось у – вверх;
–
единичный груз поставить в произвольное
положение (в пределах размера расчетной
схемы) и обозначить абсциссу его точки
приложения x. При этом
все действующие на конструкцию нагрузки
удаляются, т.е. конструкция рассматривается
загруженной только единичным грузом;
– считая
единичный груз неподвижным в выбранном
произвольном положении, определить
искомую величину, вызванную этим грузом,
которая выразится некоторой формулой,
содержащей x. Эта
формула будет представлять собой
уравнение линии влияния, если считать
в ней x переменным.
В
большинстве случаев единичный груз
приходится ставить в произвольное
положение поочередно на нескольких
участках. Для каждого участка получится
свое уравнение линии влияния, справедливое
только для этого участка (включая его
границы). Необходимо четко представлять
границы каждого участка, т.е. границы
справедливости соответствующего ему
уравнения линии влияния.
При
построении линий влияния усилий для
определения искомого усилия при
произвольном положении единичного
груза используются уравнения равновесия
всей конструкции (для линий влияния
опорных реакций) или части ее (для линий
влияния поперечных сил Q,
изгибающих моментов М, усилий N
в стержнях фермы).
При
определении Q, M
и N применяется метод
сечений. Он заключается в следующем.
Конструкция
мысленно рассекается на две части (рис.
4) в том месте, где требуется определить
внутренние усилия Q, M.
При
этом они становятся как бы внешними
усилиями, одинаковыми по величине для
любой из двух частей конструкции (но
противоположно направленны-
0
0
0
Рис. 4
ми) и уравновешивающими
действительные внешние нагрузки,
приложенные к рассматриваемой части
конструкции.
Из
уравнения равновесия любой из двух
частей конструкции (другая мысленно
отбрасывается) находится искомое усилие
(т.е. уравнение линии влияния).
Оставлять
для рассмотрения и составления уравнения
равновесия следует всегда ту часть
конструкции, к которой приложено меньше
внешних сил. При этом уравнение линии
влияния получается более простым.
Для
определения знаков усилий Q,
M и N,
характеризующих их направление,
пользуются специальными правилами
знаков, о чем будет сказано далее при
рассмотрении конкретных линий влияния.
При
составлении уравнений равновесия будем
пользоваться следующими соображениями:
– искомым
усилиям Q, M
и N при их изображении на
расчетной схеме задаются положительные
направления в соответствии с принятыми
правилами знаков;
– если
знак усилия при решении получится
отрицательным, то это означает, что
искомое усилие в действительности
направлено в противоположную сторону.
Момент
силы относительно некоторой моментной
точки записывается в уравнение равновесия
со знаком плюс, если он направлен против
часовой стрелки для наблюдателя,
смотрящего на чертеж сверху. При
противоположном направлении он
записывается со знаком минус.
Проекция
силы на ось записывается в уравнение
равновесия со знаком плюс, если ее
направление совпадает с положительным
направлением оси, и со знаком минус,
если направление проекции силы и оси
противоположны.
Если
при составлении уравнения равновесия
используется момент единичного груза
относительно некоторой моментной точки,
то необходимо иметь в виду следующее
обстоятельство:
– чтобы
знак этого момента оказался правильным
при любом положении единичного груза
(определяемого координатой x)
относительно моментной точки, необходимо
«плечо» этого груза, т.е. расстояние
между линией его действия и моментной
точкой, выразить положительным числом.
Для
этого необходимо это расстояние
определять как разность между наибольшей
и наименьшей в алгебраическом смысле
абсциссами двух точек – моментной точки
и точки приложения единичного груза
(или абсциссами их проекций на ось x).
При этом абсцисса моментной точки
записывается со своим знаком (она имеет
конкретное значение), а абсцисса x
точки приложения единичного груза
записывается со знаком «плюс»
(действительный ее знак учитывается,
когда x получает
конкретное значение). Поясним это на
примере (рис. 5).
0
Рис. 5
На рис.
5 начало координат в точке «0». Моментной
точкой является точка А. На основании
ранее указанного момент единичного
груза относительно точки А в уравнение
равновесия следует записать в виде +1
(-a – x).
Момент
единичного груза на рис. 5 направлен
против часовой стрелки, поэтому перед
выражением момента поставлен знак
«плюс». Величина в скобках выразится
положительным числом при любом значении
х слева от точки А, т.е. не повлияет
на правильность знака момента.
При
такой первоначальной записи момента,
соответствующей изображению на рис. 5,
его знак автоматически окажется
правильным при любом положении единичного
груза на конструкции, в том числе и
справа от точки А (следует только иметь
в виду, что при перемещении груза вправо
от точки А момент становится отрицательным).
Если
при первоначальном положении единичный
груз был бы изображен справа от моментной
точки А, то его момент следовало бы
записать в виде
–1 [x
– (–a)].
В
остальных случаях вычисления моментов
от любой другой силы для записи их в
уравнение равновесия, когда точка
приложения этой силы имеет конкретную
абсциссу, расстояние между моментной
точкой и линией действия силы принимается
равным абсолютной величине этого отрезка
(это вытекает из высказанного выше
соображения).
Избежать
возможных неточностей записей моментов
различного груза в уравнение равновесия
можно в том случае, если принимать начало
координат всегда на левом конце
конструкции и ось «x»
направлять вправо. В этом случае абсциссы
всех точек приложения единичного груза
будут положительными и «плечо» этого
груза всегда будет равно абсолютной
величине отрезка между его линией
действия и моментной точкой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Примеры решения задачи по строительной механике(линии влияния составной балки)
Примеры решения задачи по строительной механике(линии влияния составной балки)
Ниже приведены условие и решение задачи. Закачка решения в формате pdf начнется автоматически через 10 секунд.
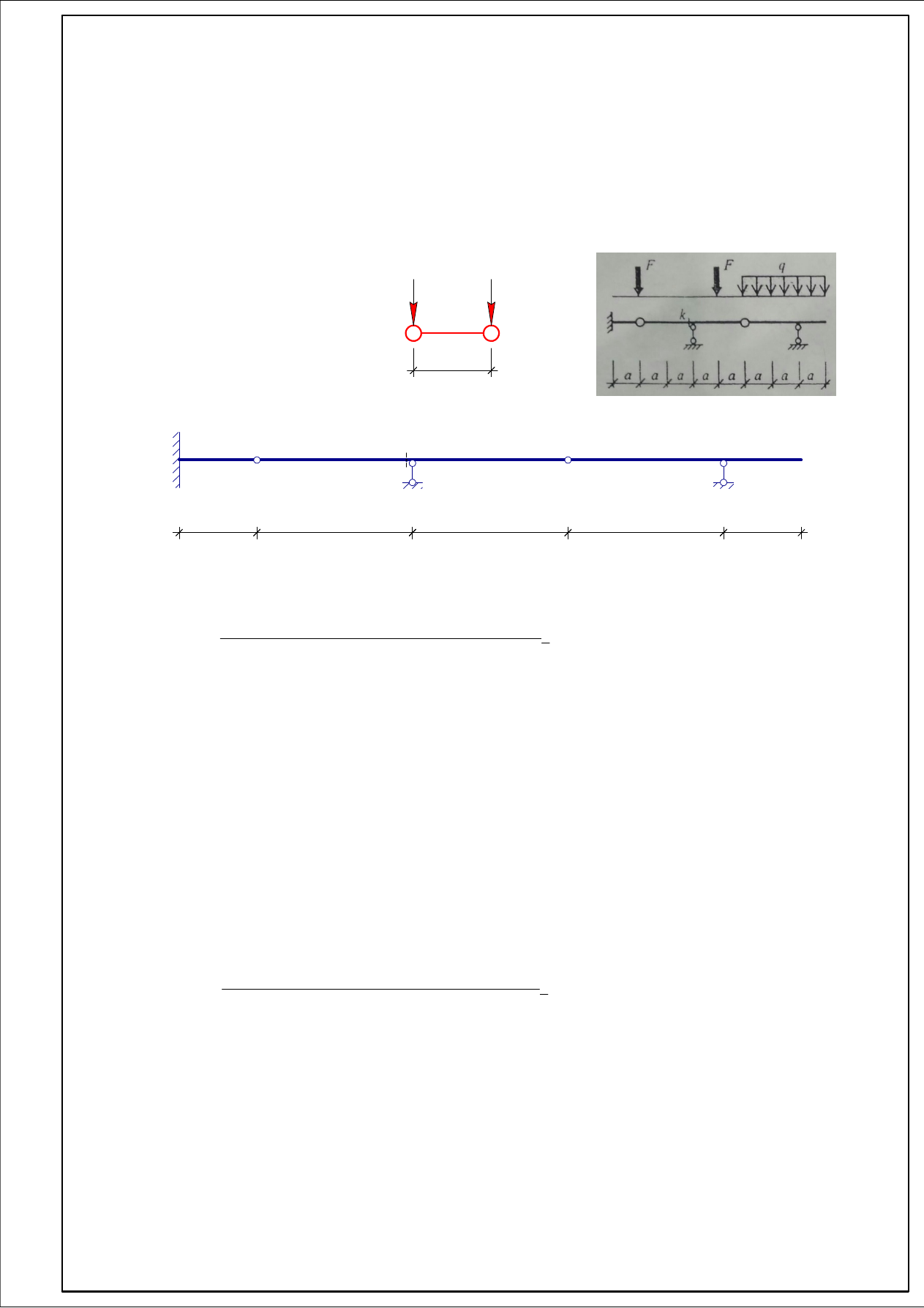
1
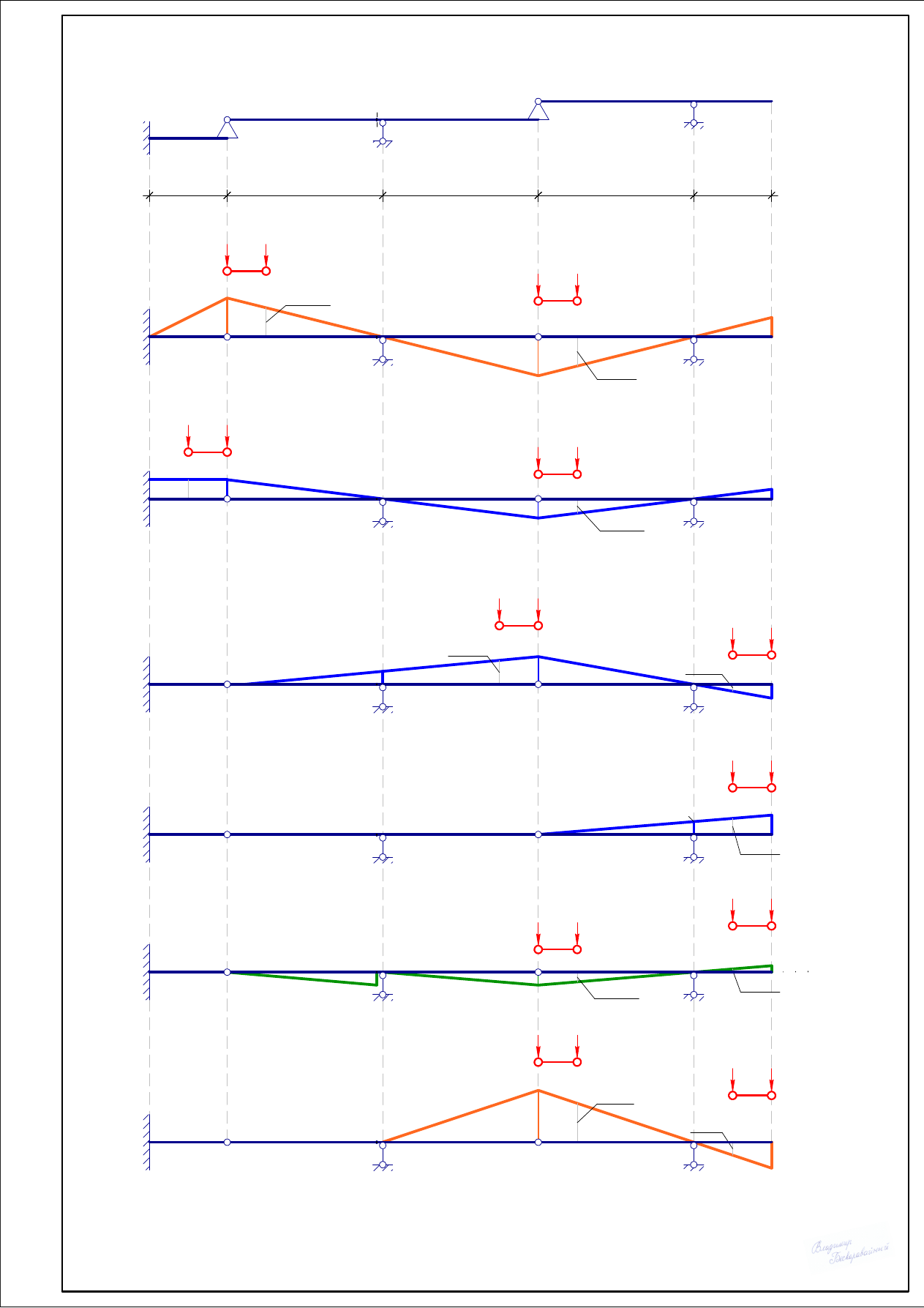
Для заданной многопролётной статически определимой балки требуется:
1. Построить линии влияния для всех опор и линии влияния Q и M для сечения K;
2. Загрузить все линии влияния заданной нагрузкой;
3. Загрузить все линии влияния наиболее опасным образом временной нагрузкой в
виде распределенной нагрузки q
вр
= 15 кН/м (рассмотреть два худших случая –
минимальное значение и максимальное значение);
4. Загрузить все линии влияния наиболее опасным образом подвижной нагрузкой в
виде двухосной тележки с давлением Q = 20 кН на каждую ось (расстояние между осями
1,5 м).
Исходные данные:
a = 3 м;
1.
Построим линии влияния для всех опор и линии влияния Q и M для сечения K.
Построим линию влияния опорного момента M
A
. Линия влияния опорного момента –
это график зависимости опорного момента от подвижной единичной силы P = 1.
Рассмотрим балку AB:
При действии единичной силы над балкой, момент составит:
M
A
= -1·x;
При действии единичной силы в защемлении момент будет нулевым, при действии
единичной силы в шарнире момент будет равен “-3”. Через найденные значения
проведём прямую.
При нахождении единичной силы над балкой BD (между сечениями B и C) нагрузка
на правый край балки будет меняться от 1 до нуля (нулевым значением будет когда
единичная сила будет находиться над опорой C), значение опорного момента M будет
меняться от “-3” до нуля. Через найденные значения проведём прямую и удлиним её до
краев балки.
При нахождении единичной силы над остальными опорами, M
A
будет равен нулю.
Изобразим полученную линию влияния.
Построим линию влияния опорной реакции V
A
. Линия влияния опорной реакции –
это график зависимости опорной реакции от подвижной единичной силы P = 1.
Рассмотрим балку AB:
При действии единичной силы в защемлении и на протяжении всей балки, опорная
реакция будет равна единице. При нахождении единичной силы над балкой BD (между
сечениями B и C) нагрузка на правый край балки будет меняться от “1” до нуля
(нулевым значением будет когда единичная сила будет находиться над опорой C). Через
найденные значения проведём прямую и удлиним её до краев балки;
При нахождении единичной силы над остальными опорами, реакция V
A
будет равна
нулю.
Изобразим полученную линию влияния.
1
A
3
6
D
6
6
3
C
B
E
K
3
6
6
6
3
1 ,5
20 кН
20 кН
1 ,5
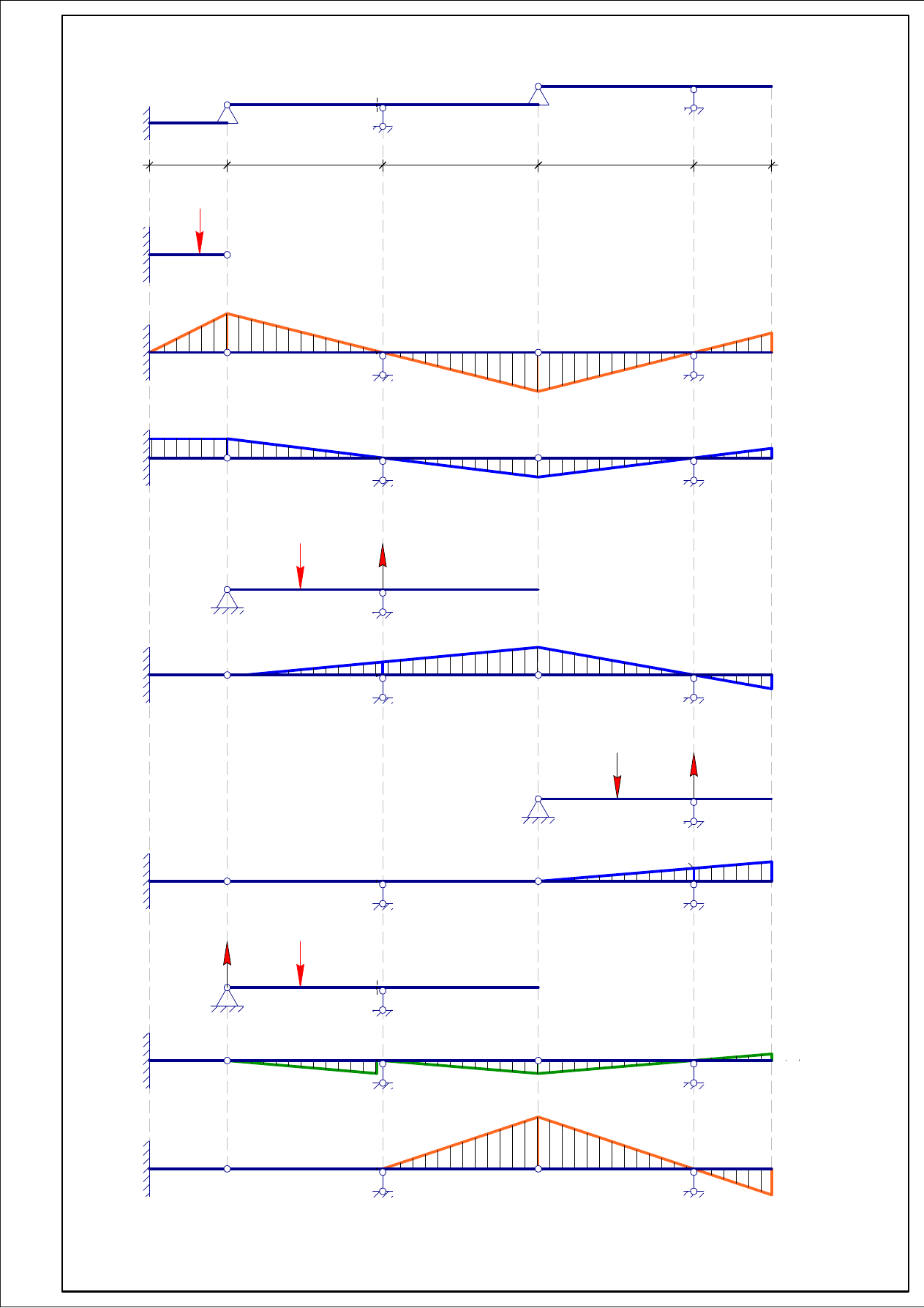
2
2
A
3
6
6
6
3
A
B
C
D
E
K
Поэтажная
схема
Л.в. Q
K
Л.в. V
C
2
1
Л.в. V
E
1
Л.в. M
K
Л.в. M
A
3
-3
-1,5
Л.в. V
A
1
0,5
-1
-1
1,5
0,5
-1
-1
3
-6
V
E
1
E
D
B
1
V
C
C
D
1
A
B
B
1
C
D
V
B
K
3
6
6
6
3
V
E
V
C
V
B
Построим линию влияния опорной реакции V
C
.
Рассмотрим балку BD:
При действии единичной силы над опорой C, опорная реакция будет равна единице.
При нахождении единичной силы над шарниром B, опорная реакция V
C
будет равна
нулю. Через найденные значения проведём прямую и удлиним её до краев балки;
Из подобия треугольников найдём значение опорной реакции при действии
единичной нагрузки на правом краю балки:
x
1
=
12
6
=> x =
12
6
= 2;
При нахождении единичной силы над остальными опорами, реакция V
C
будет равна
нулю.
При нахождении единичной силы левее шарнира B нагрузка на рассматриваемую
балку передаваться не будет.
Изобразим полученную линию влияния.
Построим линию влияния опорной реакции V
E
.
Рассмотрим балку DE:
При действии единичной силы над опорой E, опорная реакция будет равна единице.
При нахождении единичной силы над шарниром D, опорная реакция V
E
будет равна
нулю. Через найденные значения проведём прямую и удлиним её до краев балки;
При нахождении единичной силы левее шарнира D нагрузка на рассматриваемую
балку передаваться не будет.
Изобразим полученную линию влияния.
Построим линию влияния Q для сечения K.
Линия влияния поперечной силы для сечения K – график зависимости поперечной
силы в данном сечении от подвижной единичной силы P = 1.
Рассмотрим балку BD:
При нахождении единичной силы левее рассматриваемого сечения усилие в
шарнире V
B
будет:
∑
M
C
= 0:
– 1·x + V
B
·6 = 0;
V
B
=
x
6
=> Q = V
B
– 1 =
x
6
– 1;
При нахождении единичной силы в шарнире B (x = 6), Q =
6
6
– 1 = 0;
– над опорой C (x = 0), Q = 0 – 1 = -1;
При нахождении единичной силы правее опоры C усилие в шарнире V
B
будет:
∑
M
C
= 0:
1·x + V
B
·6 = 0;
V
B
= –
x
6
=> Q = – V
B
= –
x
6
;
При нахождении единичной силы в шарнире D (x = 6), Q = –
6
6
= -1;
– над опорой C (x = 0), Q = 0;
При действии единичной силы над опорами, расположенными правее, поперечная
сила будет нулевой.
При нахождении единичной силы левее шарнира B, нагрузка на рассматриваемую
балку передаваться не будет.
Изобразим полученную линию влияния.
3
3
4
Построим линию влияния изгибающего момента для сечения K.
Линия влияния изгибающего момента для сечения K – график зависимости
изгибающего момента в данном сечении от подвижной единичной силы P = 1.
Рассмотрим балку BD:
При нахождении единичной силы левее рассматриваемого сечения, усилие в
шарнире V
B
будет:
∑
M
C
= 0:
– 1·x + V
B
·6 = 0;
V
B
=
x
6
;
Изгибающий момент в сечении K будет находиться как:
M
K
= – 1·x + V
B
·6 = – 1·x +
x
6
·6 = 0;
При нахождении единичной силы правее рассматриваемого сечения, усилие в
шарнире V
B
будет:
∑
M
C
= 0:
1·x + V
B
·6 = 0;
V
B
= –
x
6
;
Изгибающий момент в сечении K:
M
K
= V
B
·6 = –
x
6
·6 = – x;
При нахождении единичной силы в шарнире D (x = 6), M
K
= -6;
– над опорой C (x = 0), M
K
= 0;
При
действии
единичной
силы
над
опорами,
расположенными
правее
рассматриваемой балки, момент M
K
будет нулевым.
При нахождении единичной силы левее шарнира B, нагрузка на рассматриваемую
балку передаваться не будет.
Изобразим полученную линию влияния.
2.
Загрузим все линии влияния заданной нагрузкой.
Для определения усилий R, Q и M по линиям влияния, используем формулу:
R =
∑
n
i= 1
P
i
·y
i
+
∑
n
i= 1
q
i
·ω
i
+
∑
n
i= 1
m
i
·tg(α
i
),
где P
i
– сосредоточенная сила, действующая на сооружение;
y
i
– ордината линии влияния под сосредоточенной силой P
i
;
q
i
– интенсивность распределенной нагрузки;
ω
i
– площадь части линии влияния R, которая находится под участком действия
равномерно распределенной нагрузки интенсивности q
i
;
m
i
– сосредоточенный момент;
tg(α
i
) – тангенс угла наклона той части линии влияния к оси балки (базовой прямой), где
приложен момент m
i
;
Нагрузка (P
i
, q
i
) направленная сверху вниз, считается положительной, а снизу вверх
– отрицательной.
Знаки для y
i
и ω
i
принимаются согласно знакам, поставленным на самой линии
влияния реакции R;
Произведение m
i
·tg(α
i
) можно считать положительным, если направляющий вектор
сосредоточенного момента М пытается «прижать» л.в. к базовой линии.
M
A
= 40·(-3) + 40·1,5 + 30·[
1
2
·3·6 +
1
2
·(-1,5)·3 ] =
142,5 кН·м
;
V
A
= 40·1 + 40·(-0,5) + 30·[
1
2
·(-1)·6 +
1
2
·0,5·3 ] =
-47,5 кН
;
V
C
= 40·1,5 + 30·[
1
2
·2·6 +
1
2
·(-1)·3 ] =
195 кН
;
V
E
= 30·(
1
2
·1,5·9) =
202,5 кН
;
Q
K
= 40·(-0,5) + 30·[
1
2
·(-1)·6 +
1
2
·0,5·3 ] =
-87,5 кН
;
M
K
= 40·(-3) + 30·[
1
2
·(-6)·6 +
1
2
·3·3 ] =
-525 кН·м
.
4
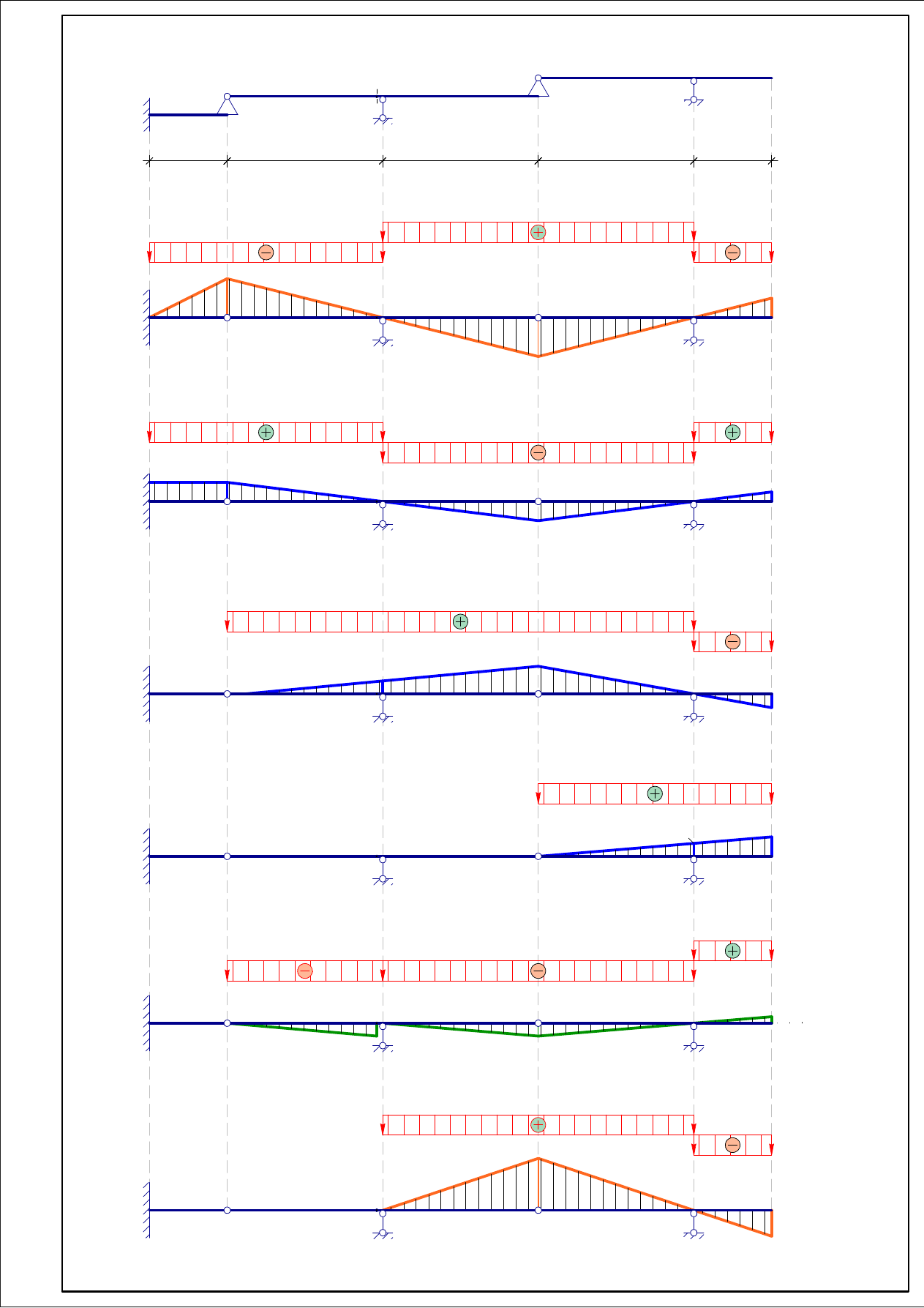
5
5
3
6
6
6
3
A
B
C
D
E
K
Л.в. Q
K
Л.в. V
C
2
1
Л.в. V
E
1
Л.в. M
K
Л.в. M
A
3
-3
-1,5
Л.в. V
A
1
0,5
-1
-1
1,5
0,5
-1
-1
3
-6
Поэтажная
схема
3
6
6
6
3
6
3.
Загрузим все линии влияния наиболее опасным образом временной нагрузкой в
виде распределенной нагрузки.
M
MAX
A
= q
вр
·(
1
2
·3·12·
1,25
2
) = 15·18 =
270 кН·м
;
M
min
A
= q
вр
·[
1
2
·(-3)·9 +
1
2
·(-1,5)·3 ] = -15·15,75 =
-236,25 кН·м
;
V
MAX
A
= q
вр
·[1·3 +
1
2
·1·6 +
1
2
·0,5·3 ] = 15·6,75 =
101,25 кН
;
V
min
A
= q
вр
·[
1
2
·(-1)·12 ] = -15·6 =
-90 кН
;
V
MAX
C
= q
вр
·[
1
2
·2·18 ] = 15·18 =
270 кН
;
V
min
C
= q
вр
·[
1
2
·(-1)·3 ] = -15·1,5 =
-22,5 кН
;
V
MAX
E
= q
вр
·[
1
2
·1,5·9 ] = 15·6,75 =
101,25 кН
;
V
min
E
=
0
;
Q
MAX
K
= q
вр
·[
1
2
·0,5·3 ] = 15·0,75 =
11,25 кН
;
Q
min
K
= q
вр
·[
1
2
·(-1)·6 +
1
2
·(-1)·12 ] = -15·9 =
-135 кН
;
M
MAX
K
= q
вр
·[
1
2
·3·3 ] = 15·4,5 =
67,5 кН·м
;
M
min
K
= q
вр
·[
1
2
·(-6)·12 ] = -15·36 =
-540 кН·м
.
4.
Загрузим все линии влияния наиболее опасным образом подвижной нагрузкой в
виде двухосной тележки.
M
MAX
A
= 20·3 + 20·2,25 =
105 кН·м
;
M
min
A
= 20·(-3) + 20·(-2,25) =
-105 кН·м
;
V
MAX
A
= 20·1 + 20·1 =
40 кН
;
V
min
A
= 20·(-1) + 20·(-0,75) =
-35 кН
;
V
MAX
C
= 20·2 + 20·1,75 =
75 кН
;
V
min
C
= 20·(-1) + 20·(-0,5) =
-30 кН
;
V
MAX
E
= 20·1,5 + 20·1,25 =
55 кН
;
V
min
E
=
0 кН
;
Q
MAX
K
= 20·0,5 + 20·0,25 =
15 кН
;
Q
min
K
= 20·(-1) + 20·(-0,75) =
-35 кН
;
M
MAX
K
= 20·3 + 20·1,5 =
90 кН·м
;
M
min
K
= 20·(-6) + 20·(-4,5) =
-210 кН·м
.
S
непод
S
M AX
вр
S
m in
вр
S
M A X
непод
S
m in
непод
S
M AX
р асч
S
m in
р асч
M
A
142,5
270
-236,25
105
-105
517,5
-198,75
V
A
-47,5
101,25
-90
40
-35
93,75
-172,5
V
C
195
270
-22,5
75
-30
540
142,5
V
E
202,5
101,25
0
55
0
358,75
202,5
Q
K
-87,5
11,25
-135
15
-35
-61,25
-257,5
M
K
-525
67,5
-540
90
-210
-367,5
-1275
6
7
7
3
6
6
6
3
Поэтажная
схема
Л.в. Q
K
Л.в. V
C
2
1
Л.в. V
E
1
Л.в. M
K
Л.в. M
A
3
-3
-1,5
Л.в. V
A
1
0,5
-1
-1
1,5
0,5
-1
-1
3
-6
-2 ,2 5
2 ,2 5
-0 ,7 5
-0 ,5
1 ,7 5
1 ,2 5
0 ,2 5
-0 ,7 5
-4 ,5
1 ,5
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
A
B
C
D
E
K
3
6
6
6
3
Имя файла: raschyot_mnogoproletnoj_balki.pdf
Размер файла: 203.75 Kb
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке
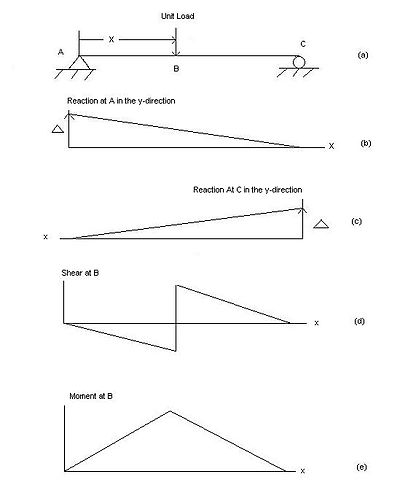
Figure 1: (a) This simple supported beam is shown with a unit load placed a distance x from the left end. Its influence lines for four different functions: (b) the reaction at the left support (denoted A), (c) the reaction at the right support (denoted C), (d) one for shear at a point B along the beam, and (e) one for moment also at point B.
Figure 2: The change in Bending Moment in a statically determinate Beam as a unit force moves from one end to the other. The bending moment diagram and the influence line for bending moment at the centre of the left-hand span, B, are shown.
In engineering, an influence line graphs the variation of a function (such as the shear, moment etc. felt in a structural member) at a specific point on a beam or truss caused by a unit load placed at any point along the structure.[1][2][3][4][5] Common functions studied with influence lines include reactions (forces that the structure’s supports must apply for the structure to remain static), shear, moment, and deflection (Deformation).[6] Influence lines are important in designing beams and trusses used in bridges, crane rails, conveyor belts, floor girders, and other structures where loads will move along their span.[5] The influence lines show where a load will create the maximum effect for any of the functions studied.
Influence lines are both scalar and additive.[5] This means that they can be used even when the load that will be applied is not a unit load or if there are multiple loads applied. To find the effect of any non-unit load on a structure, the ordinate results obtained by the influence line are multiplied by the magnitude of the actual load to be applied. The entire influence line can be scaled, or just the maximum and minimum effects experienced along the line. The scaled maximum and minimum are the critical magnitudes that must be designed for in the beam or truss.
In cases where multiple loads may be in effect, influence lines for the individual loads may be added together to obtain the total effect felt the structure bears at a given point. When adding the influence lines together, it is necessary to include the appropriate offsets due to the spacing of loads across the structure. For example, a truck load is applied to the structure. Rear axle, B, is three feet behind front axle, A, then the effect of A at x feet along the structure must be added to the effect of B at (x – 3) feet along the structure—not the effect of B at x feet along the structure.
Many loads are distributed rather than concentrated. Influence lines can be used with either concentrated or distributed loadings. For a concentrated (or point) load, a unit point load is moved along the structure. For a distributed load of a given width, a unit-distributed load of the same width is moved along the structure, noting that as the load nears the ends and moves off the structure only part of the total load is carried by the structure. The effect of the distributed unit load can also be obtained by integrating the point load’s influence line over the corresponding length of the structures.
The Influence lines of determinate structures becomes a mechanism whereas the Influence lines of indeterminate structures become just determinate.[7]
Demonstration from Betti’s theorem[edit]
Influence lines are based on Betti’s theorem. From there, consider two external force systems, 
and 
, each one associated with a displacement field whose displacements measured in the force’s point of application are represented by 
and 
.
Consider that the system represents actual forces applied to the structure, which are in equilibrium. Consider that the system is formed by a single force, 
. The displacement field associated with this forced is defined by releasing the structural restraints acting on the point where is applied and imposing a relative unit displacement that is kinematically admissible in the negative direction, represented as 
. From Betti’s theorem, we obtain the following result:
Concept[edit]
When designing a beam or truss, it is necessary to design for the scenarios causing the maximum expected reactions, shears, and moments within the structure members to ensure that no member fails during the life of the structure. When dealing with dead loads (loads that never move, such as the weight of the structure itself), this is relatively easy because the loads are easy to predict and plan for. For live loads (any load that moves during the life of the structure, such as furniture and people), it becomes much harder to predict where the loads will be or how concentrated or distributed they will be throughout the life of the structure.
Influence lines graph the response of a beam or truss as a unit load travels across it. The influence line helps designers find where to place a live load in order to calculate the maximum resulting response for each of the following functions: reaction, shear, or moment. The designer can then scale the influence line by the greatest expected load to calculate the maximum response of each function for which the beam or truss must be designed.
Influence lines can also be used to find the responses of other functions (such as deflection or axial force) to the applied unit load, but these uses of influence lines are less common.
Methods for constructing influence lines[edit]
There are three methods used for constructing the influence line. The first is to tabulate the influence values for multiple points along the structure, then use those points to create the influence line.[5] The second is to determine the influence-line equations that apply to the structure, thereby solving for all points along the influence line in terms of x, where x is the number of feet from the start of the structure to the point where the unit load is applied.[1][2][3][4][5] The third method is called the Müller-Breslau’s principle. It creates a qualitative influence line.[1][2][5] This influence line will still provide the designer with an accurate idea of where the unit load will produce the largest response of a function at the point being studied, but it cannot be used directly to calculate what the magnitude that response will be, whereas the influence lines produced by the first two methods can.
Tabulate values[edit]
To tabulate the influence values with respect to some point A on the structure, a unit load must be placed at various points along the structure. Statics is used to calculate what the value of the function (reaction, shear, or moment) is at point A. Typically an upwards reaction is seen as positive. Shear and moments are given positive or negative values according to the same conventions used for shear and moment diagrams.
R. C. Hibbeler states, in his book Structural Analysis, “All statically determinate beams will have influence lines that consist of straight line segments.”[5] Therefore, it is possible to minimize the number of computations by recognizing the points that will cause a change in the slope of the influence line and only calculating the values at those points. The slope of the inflection line can change at supports, mid-spans, and joints.
An influence line for a given function, such as a reaction, axial force, shear force, or bending moment, is a graph that shows the variation of that function at any given point on a structure due to the application of a unit load at any point on the structure.
An influence line for a function differs from a shear, axial, or bending moment diagram. Influence lines can be generated by independently applying a unit load at several points on a structure and determining the value of the function due to this load, i.e. shear, axial, and moment at the desired location. The calculated values for each function are then plotted where the load was applied and then connected together to generate the influence line for the function.
Once the influence values have been tabulated, the influence line for the function at point A can be drawn in terms of x. First, the tabulated values must be located. For the sections in between the tabulated points, interpolation is required. Therefore, straight lines may be drawn to connect the points. Once this is done, the influence line is complete.
Influence-line equations[edit]
It is possible to create equations defining the influence line across the entire span of a structure. This is done by solving for the reaction, shear, or moment at the point A caused by a unit load placed at x feet along the structure instead of a specific distance. This method is similar to the tabulated values method, but rather than obtaining a numeric solution, the outcome is an equation in terms of x.[5]
It is important to understanding where the slope of the influence line changes for this method because the influence-line equation will change for each linear section of the influence line. Therefore, the complete equation is a piecewise linear function with a separate influence-line equation for each linear section of the influence line.[5]
Müller-Breslau’s Principle[edit]
According to www.public.iastate.edu, “The Müller-Breslau Principle can be utilized to draw qualitative influence lines, which are directly proportional to the actual influence line.”[2] Instead of moving a unit load along a beam, the Müller-Breslau Principle finds the deflected shape of the beam caused by first releasing the beam at the point being studied, and then applying the function (reaction, shear, or moment) being studied to that point. The principle states that the influence line of a function will have a scaled shape that is the same as the deflected shape of the beam when the beam is acted upon by the function.
To understand how the beam deflects under the function, it is necessary to remove the beam’s capacity to resist the function. Below are explanations of how to find the influence lines of a simply supported, rigid beam (such as the one displayed in Figure 1).
-
- When determining the reaction caused at a support, the support is replaced with a roller, which cannot resist a vertical reaction.[2][5] Then an upward (positive) reaction is applied to the point where the support was. Since the support has been removed, the beam will rotate upwards, and since the beam is rigid, it will create a triangle with the point at the second support. If the beam extends beyond the second support as a cantilever, a similar triangle will be formed below the cantilevers position. This means that the reaction’s influence line will be a straight, sloping line with a value of zero at the location of the second support.
-
- When determining the shear caused at some point B along the beam, the beam must be cut and a roller-guide (which is able to resist moments but not shear) must be inserted at point B.[2][5] Then, by applying a positive shear to that point, it can be seen that the left side will rotate down, but the right side will rotate up. This creates a discontinuous influence line that reaches zero at the supports and whose slope is equal on either side of the discontinuity. If point B is at a support, then the deflection between point B and any other supports will still create a triangle, but if the beam is cantilevered, then the entire cantilevered side will move up or down creating a rectangle.
-
- When determining the moment caused by at some point B along the beam, a hinge will be placed at point B, releasing it to moments but resisting shear.[2][5] Then when a positive moment is placed at point B, both sides of the beam will rotate up. This will create a continuous influence line, but the slopes will be equal and opposite on either side of the hinge at point B. Since the beam is simply supported, its end supports (pins) cannot resist moment; therefore, it can be observed that the supports will never experience moments in a static situation regardless of where the load is placed.
The Müller-Breslau Principle can only produce qualitative influence lines.[2][5] This means that engineers can use it to determine where to place a load to incur the maximum of a function, but the magnitude of that maximum cannot be calculated from the influence line. Instead, the engineer must use statics to solve for the functions value in that loading case.
Alternate loading cases[edit]
Multiple loads[edit]
The simplest loading case is a single point load, but influence lines can also be used to determine responses due to multiple loads and distributed loads. Sometimes it is known that multiple loads will occur at some fixed distance apart. For example, on a bridge the wheels of cars or trucks create point loads that act at relatively standard distances.
To calculate the response of a function to all these point loads using an influence line, the results found with the influence line can be scaled for each load, and then the scaled magnitudes can be summed to find the total response that the structure must withstand.[5] The point loads can have different magnitudes themselves, but even if they apply the same force to the structure, it will be necessary to scale them separately because they act at different distances along the structure. For example, if a car’s wheels are 10 feet apart, then when the first set is 13 feet onto the bridge, the second set will be only 3 feet onto the bridge. If the first set of wheels is 7 feet onto the bridge, the second set has not yet reached the bridge, and therefore only the first set is placing a load on the bridge.
Also, if, between two loads, one of the loads is heavier, the loads must be examined in both loading orders (the larger load on the right and the larger load on the left) to ensure that the maximum load is found. If there are three or more loads, then the number of cases to be examined increases.
Distributed loads[edit]
Many loads do not act as point loads, but instead act over an extended length or area as distributed loads. For example, a tractor with continuous tracks will apply a load distributed over the length of each track.
To find the effect of a distributed load, the designer can integrate an influence line, found using a point load, over the affected distance of the structure.[5] For example, if a three-foot-long track acts between 5 feet and 8 feet along a beam, the influence line of that beam must be integrated between 5 and 8 feet. The integration of the influence line gives the effect that would be felt if the distributed load had a unit magnitude. Therefore, after integrating, the designer must still scale the results to get the actual effect of the distributed load.
Indeterminate structures[edit]
While the influence lines of statically determinate structures (as mentioned above) are made up of straight line segments, the same is not true for indeterminate structures. Indeterminate structures are not considered rigid; therefore, the influence lines drawn for them will not be straight lines but rather curves. The methods above can still be used to determine the influence lines for the structure, but the work becomes much more complex as the properties of the beam itself must be taken into consideration.
See also[edit]
- Beam
- Shear and Moment Diagram
- Dead and Live Loads
- Müller-Breslau’s principle
References[edit]
- ^ a b c Kharagpur. “Structural Analysis.pdf, Version 2 CE IIT” Archived 2010-08-19 at the Wayback Machine. 7 August 2008. Accessed on 26 November 2010.
- ^ a b c d e f g h Dr. Fanous, Fouad. “Introductory Problems in Structural Analysis: Influence Lines”. 20 April 2000. Accessed on 26 November 2010.
- ^ a b “Influence Line Method of Analysis”. The Constructor. 10 February 2010. Accessed on 26 November 2010.
- ^ a b “Structural Analysis: Influence Lines”. The Foundation Coalition. 2 December 2010. Accessed on 26 November 2010.
- ^ a b c d e f g h i j k l m n o Hibbeler, R.C. (2009). Structural Analysis (Seventh Edition). Pearson Prentice Hall, New Jersey. ISBN 0-13-602060-7.
- ^ Zeinali, Yasha (December 2017). “Framework for Flexural Rigidity Estimation in Euler-Bernoulli Beams Using Deformation Influence Lines”. Infrastructures. 2 (4): 23. doi:10.3390/infrastructures2040023.
- ^ “Influence Lines | Structural Analysis Review”. www.mathalino.com. Retrieved 2019-12-25.
