Как найти ординату точки егэ математика

Как найти ординату точки егэ математика

было в ЕГЭ

в условии
в решении
в тексте к заданию
в атрибутах

Категория

Атрибут

Всего: 119    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Найдите абсциссу точки, симметричной точке A(6; 8) относительно начала координат.

Найдите ординату середины отрезка, соединяющего точки O(0; 0) и A(6; 8).

Найдите ординату середины отрезка, соединяющего точки A(6; 8) и B(-2; 2).

Вектор oversetto mathopAB с началом в точке A(2; 4) имеет координаты (6; 2). Найдите ординату точки B.

Через точку А(6; 8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью Oy.

Найдите расстояние от точки A с координатами (6; 8) до оси абсцисс.

Найдите расстояние от точки A с координатами (6; 8) до оси ординат.

Найдите ординату точки, симметричной точке A(6; 8) относительно оси Ox.

Найдите абсциссу точки, симметричной точке A(6; 8) относительно начала координат.

Найдите ординату точки, симметричной точке A(6; 8) относительно начала координат.

Найдите ординату середины отрезка, соединяющего точки O (0; 0) и A (6; 8).

Найдите ординату середины отрезка, соединяющего точки A(6; 8) и B(-2; 2).

Найдите ординату точки пересечения оси Oy и отрезка, соединяющего точки A(6; 8) и B(−6; 0).

Найдите угловой коэффициент прямой, проходящей через точки с координатами (2; 0) и (0; 2).

Прямая a проходит через точки с координатами (0; 4) и (6; 0). Прямая b проходит через точку с координатами (0; 8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox

Найдите ординату точки пересечения оси Oy и прямой, проходящей через точку B(6; 4) и параллельной прямой, проходящей через начало координат и точку A(6; 8).

Точки O(0; 0), B(6; 2), C(0; 6) и A являются вершинами параллелограмма. Найдите ординату точки A.

Точки O(0; 0), A(6; 8), C(0; 6) и B являются вершинами параллелограмма. Найдите ординату точки B.

Точки O(0; 0), A(6; 8), B(6; 2) и C являются вершинами параллелограмма. Найдите ординату точки C.

Точки O(0; 0), A(6; 8), B(6; 2), C(0; 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.

Всего: 119    1–20 | 21–40 | 41–60 | 61–80 …

Источник

В ЕГЭ 2022 года добавили новую задачу на графики функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, то вот определение самой формулы часто ставит школьников в тупик. Поэтому мы разберем три разных подхода к этому вопросу.

Замечание. Про то как определяется формула у прямой и параболы я написала в этой и этой статьях. Поэтому здесь в примерах я буду использовать другие функции – дробные, иррациональные, показательные и логарифмические, но все три описанных здесь способа работают и для линейных, и для квадратичных функций в том числе.

1 способ – находим формулу по точкам

Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.

Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:

задача с гиперболой

Алгоритм:

1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому.
Пример:

находим две точки с целыми координатами

2. Подставляем эти координаты в «полуфабрикат» функции. Вместо (f(x))– координату игрек, вместо (x) – икс. Получается система.

составляем уравнения

3. Решаем эту систему и получаем готовую формулу.

решаем систему

4. Готово, функция найдена, можно переходить ко второму этапу – вычислению (f(-8)). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.

отвечаем на вопрос задачи

Давайте посмотрим метод еще раз на примере с логарифмической функцией.
Пример:

Пример с логарифмической функцией

2 способ – преобразование графиков функций

Этот способ сильно быстрее первого, но требует больше знаний. Для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют. Наиболее удобно использовать этот способ для иррациональной функции ((y=sqrt{x}) ) и функции обратной пропорциональности ((y=frac{1}{x})).

Вот как выглядит применение этого способа:

преобразование графиков функций

Для использования этого способа надо знать, как выглядят изначальные функции:

Виды функций

И понимать, как меняются функции от преобразований:

Преобразование графиков функций

примеры преобразований функций

Преобразование показательной функции Преобразование гипербол

Часто даже по «полуфабрикату» функции понятно, какие преобразования сделали с функцией:

как по формуле определить какие были преобразования с функцией

Пример:

пример с функцией обратной пропорциональности

3 способ – гибридный

Идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти. С другой стороны, независимо от оснований любая показательная функция должна проходить через точку ((0;1)), а любая логарифмическая – через точку ((1;0)).

показательная и логарифмическая функция

По смещению этих точек легко понять, как именно двигали функцию, но только если ее не растягивали, а лишь перемещали вверх-вниз, влево-вправо (как обычно и бывает в задачах на ЕГЭ).

Основание же лучше находить уже следующим действием, используя подстановку координат точки в «полуфабрикат» функции.

пример с логарифмической функцией

пример с логарифмической функцией

Как отвечать на вопросы в задаче, когда уже определили функцию

– Если просят найти (f)(любое число), то нужно это число подставить в готовую функцию вместо икса.
Пример:

что значит найти f от числа

– Если просят найти «при каком значении x значение функции равно *любому числу*», то надо решить уравнение, в одной части которого будет функция, а в другой – то самое число. Аналогично надо поступить, если просят «найти корень уравнения (f(x)=) *любое число*».
Пример:

найдите, при каком значении x значение функции равно 8

– Если просят найти абсциссу точки пересечения – надо приравнять 2 функции и решить получившееся уравнение. Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения (A)(*любое число*;*другое число*) и (B(x_0;y_0)) и просят найти (x_0).
Пример:

найдите точку пересечения функций

– Если просят найти ординату точки пересечения – надо приравнять 2 функции, найти иксы и подставить подходящий икс в любую функцию. Точно также решаем если просят найти (y_0) точки пересечения двух функций.
Пример:

найдите ординату точки пересечения

– Иногда просят найти просто какой-либо из коэффициентов функции. Тогда надо просто восстановить функцию и записать в ответ то, о чем спросили:
Пример:

найдите k

Источник

Решение:

На рисунке изображён графики двух линейных функций. Найдите ординату точки пересечения графиков.

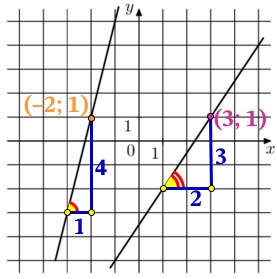
    На рисунке изображены прямые, линейных функции их вид имеет вид:

y = kx + b

    Найдём k и b функции справа. 
    k – тангенс угла наклона прямой, по отношению к оси х. Тангенс это отношение противолежащего катета, к прилежащему катету:

k=tg{color{Red}alpha}=frac{color{Blue} 3}{color{Blue} 2}=1,5

    Подставим в общий вид функции значение k и координаты точки (3; 1) найдём b:

y = kx + b
1 = 1,5·3 + b
1 = 4,5 + b
1 – 4,5 = b
–3,5 = b

    Функции справа имеет вид:

y = 1,5x – 3,5

    Найдём k и b функции слева. 

k=tg{color{Red}alpha}=frac{color{Blue} 4}{color{Blue} 1}=4

    Подставим в общий вид функции значение k и координаты точки (–2; 1) найдём b:

y = kx + b
1 = 4·(–2) + b
1 = –8 + b
1 + 8 = b
9 = b

    Функции слева имеет вид:

y = 4x + 9 

    В точке пересечения прямых значения функций (y) равны, найдём абсциссу (х) точки пересечения:

1,5x – 3,5 = 4x + 9 
1,5x – 4x = 9 + 3,5
–2,5x = 12,5
x=frac{12,5}{–2,5}=-5

    Подставим значение х = –5, в любое уравнение и найдём ординату (y) точки пересечения прямых:

y = 4·(–5) + 9 = –20 + 9 = –11

Ответ: –11.

Источник

11
Янв 2022

Категория: 10 Графики функций

Елена Репина
2022-01-11
2022-09-13

Задача 1. На рисунке изображён график функции y=kx+b.  Найдите y(-9).

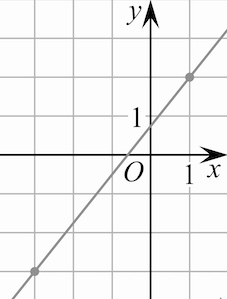
Решение: + показать

Задача 2. На рисунке изображён график функции f(x)=kx+b.   Найдите значение x, при котором f(x)=2,25. 

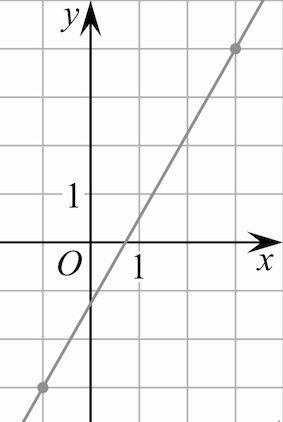
Решение: + показать

Задача 3.  На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.

Решение: + показать

Вы можете пройти тест “Линейная функция”

Автор: egeMax |

Нет комментариев

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Печать страницы

Добавить комментарий

  • Материалы для подготовки к ЕГЭ

  •    

  • Рубрики
    • 01 Геометрия (12)
    • 02 Стереометрия (9)
    • 03 Теория вероятностей ч.1 (1)
    • 04 Теория вероятностей ч.2 (1)
    • 05 Простейшие уравнения (5)
    • 06 Вычисления (5)
    • 07 Производная, ПО (4)
    • 08 «Прикладные» задачи (5)
    • 09 Текстовые задачи (7)
    • 10 Графики функций (7)
    • 11 Исследование функции (2)
    • 12 (С1) Уравнения (79)
    • 13 (С2) Стереометр. задачи (95)
    • 14 (С3) Неравенства (90)
    • 15 (С4) Практич. задачи (72)
    • 16 (С5) Планиметр. задачи (87)
    • 17 (С6) Параметры* (80)
    • 18 (С7) Числа, их свойства (38)
    • A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
    • A2 Читаем графики (нет в ЕГЭ-22) (1)
    • Видеоуроки (44)
    • ГИА (11)
      • II часть (11)
    • ЕГЭ (диагностич. работы) (70)
    • Задачи (23)
    • Иррациональные выражения, уравнения и неравенства (15)
    • Логарифмы (39)
    • МГУ (12)
    • Метод интервалов (4)
    • Метод рационализации (18)
    • Модуль (9)
    • Параметр (40)
    • Переменка (5)
    • Планиметрия (59)
    • Показательные выражения, уравнения и неравенства (8)
    • Разложение на множители (1)
    • Рациональные выражения, уравнения и неравенства (10)
    • Справочные материалы (92)
    • Стереометрия (52)
    • Т/P A. Ларина (443)
    • Текстовые задачи (12)
    • Теория чисел (2)
    • Тесты по темам (80)
    • Тригонометрические выражения, уравнения и неравенства (43)
    • Функции и графики (10)
  • Дружественные сайты

    Сайт А. Ларина
    ЕгэТренер – О. Себедаш
    Математика?Легко!
    Егэ? Ок! – И. Фельдман

  • Свежие записи
    • Задания 17 ЕГЭ 2023
  • Архивы Архивы

Источник

На рисунке изображены части графиков найдите ординату точки пересечения

На чтение 3 мин. Просмотров 1.1k.

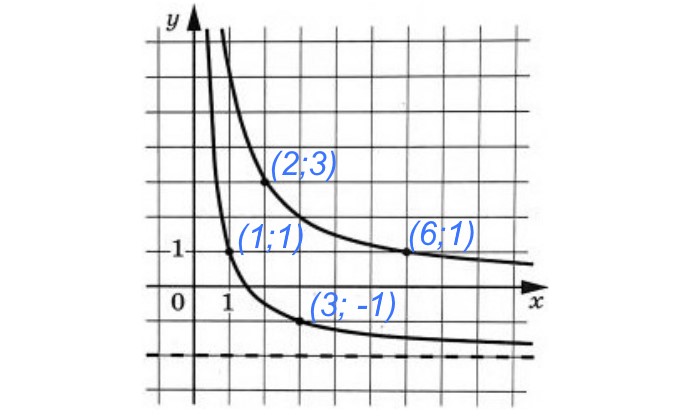
На рисунке изображены части графиков функций f(x)=displaystyle frac{k}{x} и g(x)=displaystyle frac{c}{x}+d. Найдите ординату точки пересечения графиков этих функций.

На рисунке изображены части графиков функций 1

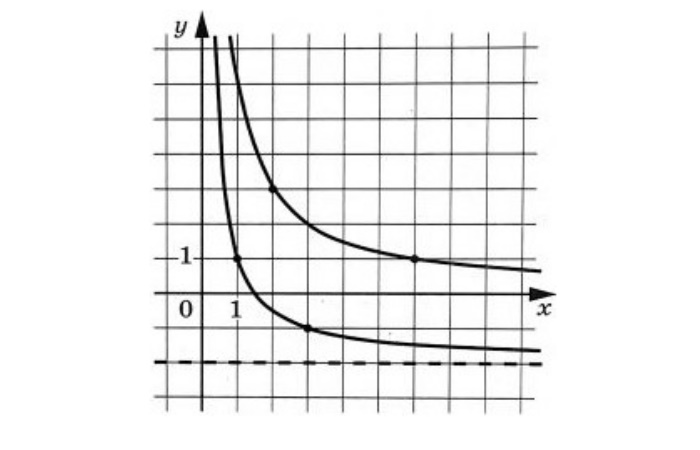
Решение:

Верхний график на рисунке не пересекает ось Ox, значит не имеет смещения вдоль оси Oy. Поэтому он принадлежит первой функции f(x)=displaystyle frac{k}{x}. Тогда второй (нижний) график на картинке принадлежит функции g(x)=displaystyle frac{c}{x}+d так как пересекает ось Ox, а значит, работает коэффициент d, смещающий график вниз.

Для первого графика даны точки (2;3) и (6;1), а для второго графика: (1;1) и (3;1). Они нам помогут определить коэффициенты k, c, d.

Графики с координатами

Подставим значения первой точки (2;3) в уравнение f(x)=displaystyle frac{k}{x} и найдем k:

3=displaystyle frac{k}{2}

k=6.

Выполним проверку, подставим теперь уже в определенной уравнение функции f(x)=displaystyle frac{6}{x} координаты второй точки (6;1):

1=displaystyle frac{6}{6}

1=1.

Итак, с первой функцией определились. Теперь определим и вторую. Поскольку во второй функции у нас два неизвестных c и d, то нам понадобится система из двух уравнений. Первое уравнение мы получим, подставив координаты первой точки (1;1), а второе уравнение получим, подставив координаты второй точки (3;1).

begin{cases} displaystyle 1=frac{c}{1}+d, \ displaystyle -1=frac{c}{3}+d, end{cases}

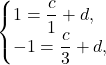
Из первого уравнения системы выразим d:

begin{cases} d=1-c, \ -1=frac{c}{3}+d, end{cases}

begin{cases} d=1-c, \ displaystyle -1=frac{c}{3}+1-c, end{cases}

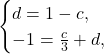
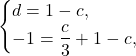
Решаем второе уравнение системы:

displaystyle -2=frac{c}{2}-c

displaystyle -2=frac{-2c}{3}

c=3

Получим:

begin{cases} d=1-c, \ c=3, end{cases}

begin{cases} d=-2, \ c=3, end{cases}

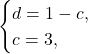
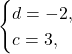
Тогда уравнение второй функции будет иметь вид: displaystyle g(x)=frac{3}{x}-2

Получили две функции displaystyle f(x)=frac{6}{x} и displaystyle g(x)=frac{3}{x}-2. В точке пересечения графиков функций значения их совпадают, значит, f(x)=g(x), получим уравнение:

displaystyle frac{6}{x}=frac{3}{x}-2

displaystyle frac{6}{x}-frac{3}{x}=-2

displaystyle frac{3}{x}=-2

displaystyle x=-frac{3}{2}.

Мы нашли абсциссу точки пересечения, но нам надо найти ординату этой точки. Подставим полученное значение в любое из уравнений f(x) или g(x).

displaystyle f(frac{-3}{2})=frac{6}{-frac{3}{2}}=frac{-12}{3}=-4.

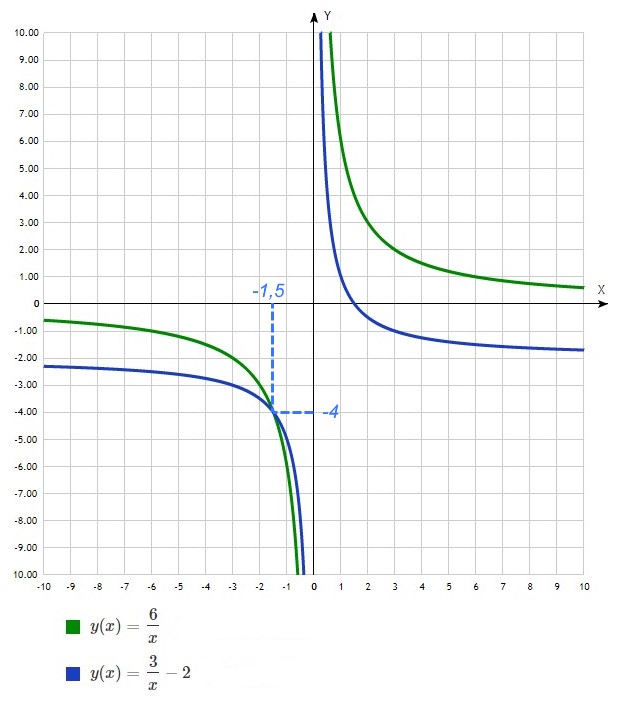
Графики функций и точка пересечения

Ответ: -4.

( 4 оценки, среднее 5 из 5 )

Источник

Добавить комментарий