Самое главное приложение производной состоит в том, что производные позволяют понять, каковы максимальные и минимальные значений исследуемой функции на каком-либо участке (конечном или бесконечном). Однако есть и другие приложения производной: производные позволяют сравнивать степень роста (или убывания) двух или нескольких функций, определять направления их выпуклости, вычислять кривизну и так далее.
Возрастание и убывание функции
Пусть нам дана функция у = f(х), графически представленная на рис. 87. Проследим за ходом изменения величины ординат точек изображенной кривой при возрастании их абсцисс.
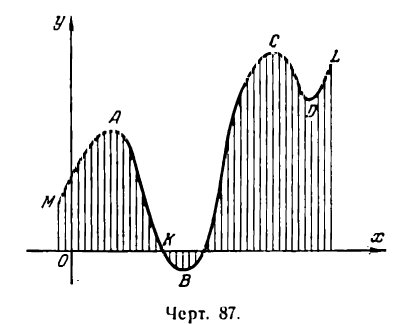
Мы видим, что при возрастании аргумента х ординаты соответствующих точек на
участке МА кривой растут,
на участке АК убывают. При
дальнейшем возрастании аргумента ординаты, принимая отрицательные значения,
продолжают убывать *) во всех точках дуги КВ,
ординаты же точек дуги ВС
возрастают и т. д.
*) Известно, что то отрицательное число меньше, у которого
абсолютная величина больше, и наоборот.
Данную функцию для участков МА, ВС и DL называют возрастающей, а для участков АВ и СD — убывающей.
Определение:
Функция у = f(х) называется возрастающей в данном промежутке значений х, если при увеличении аргумента х в этом промежутке соответствующие значения у возрастают, и убывающей, если при увеличении х значения у убывают.
В дальнейшем изложении данной главы изменения аргумента будут рассматриваться только возрастающие, а функция и ее первая и вторая производные — только непрерывные при всех рассматриваемых значениях аргумента.
Признаки возрастания и убывания функции
Теорема:
Если производная функции у = f(х) в данном промежутке значений х положительна, то функция возрастает в этом промежутке, а если производная отрицательна, то функция убывает.
Не доказывая этой теоремы, поясним ее геометрически.
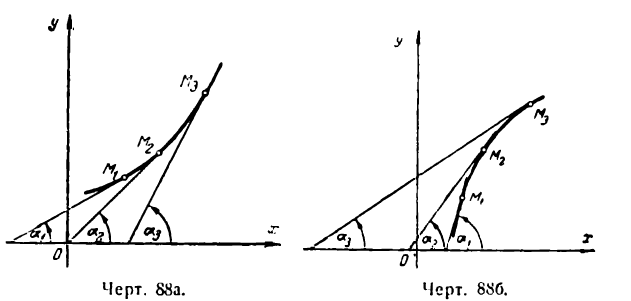
I. Пусть в данном промежутке значений х
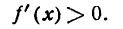
Приняв во внимание геометрический смысл производной, можно утверждать, что угловой коэффициент касательных, проведенных к графику функции у = f(х), в рассматриваемом промежутке положителен. Иначе говоря, касательные образуют с положительным направлением оси Ох острый угол (рис. 88а и 88б), а это наблюдается в том случае когда график в данном промежутке поднимается т.е. функция возрастает.
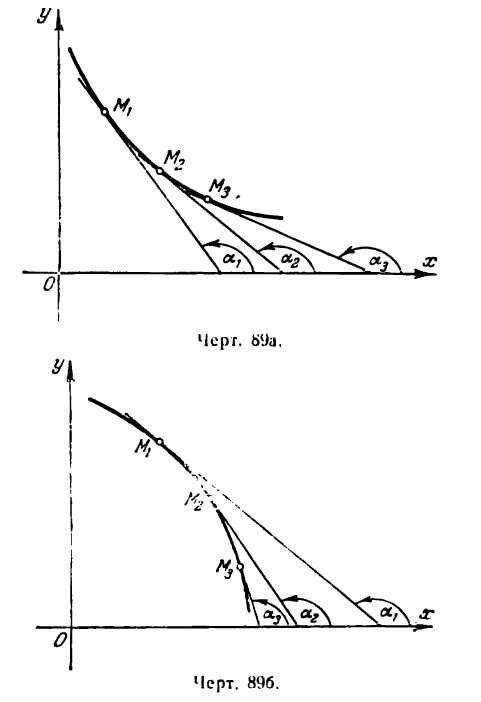
II. Положим, что в данном промежутке значений х
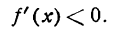
Это значит, что угловой коэффициент касательных, проведенных к графику функции у = f(х), отрицателен. Иначе говоря, касательные образуют тупой угол с положительным направлением оси Ох (рис. 89а и 89б), а это бывает в случае, когда график в рассматриваемом промежутке опускается, т. е. функция убывает.
Пример:
Определить промежутки возрастания и убывания функции
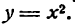
Решение:
Найдем производную данной функции
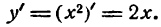
Величина 2х имеет положительное значение при всяком положительном х и отрицательное — при любом отрицательном его значении.
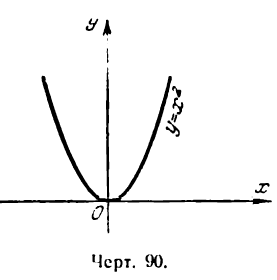
Отсюда следует, что данная функция убывающая при х < 0 и возрастающая при х > 0 (рис. 90).
Максимум и минимум функции
Рассматривая ход изменения функции на рис. 87, мы можем отметить, что ординаты точек на участках МА и ВС возрастают, достигая в точках А и С кривой наибольшей величины сравнительно со значениями ординат ближайших к ним точек, и убывают на участках АВ и СD до наименьшей величины в точках В и D сравнительно со значениями ординат соседних к ним точек.
Те значения аргумента, при которых функция имеет наибольшую или наименьшую величину, называются соответственно точками максимума или минимума функции, а значение функции при этих значениях аргумента — максимумом или минимумом ее.
Как видно, точка максимума служит границей перехода от возрастания функции к ее убыванию, а точка минимума— границей перехода от убывания функции к ее возрастанию.
Определение:
Функция у = f(х) имеет максимум при х — а, если при всех х, достаточно близких к а, выполняется неравенство
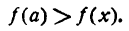
Определение:
Функция у = f(х) имеет минимум при если при всех х, достаточно близких к а выполняется неравенство
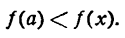
Признаки максимума и минимума функции
I. Пусть точке А графика функции у = f(х) соответствует максимум при х = а (рис. 91). Как видно из рисежа, во всех точках, расположенных левее А, касательные образуют с положительным направлением оси Ох острые углы. Поэтому
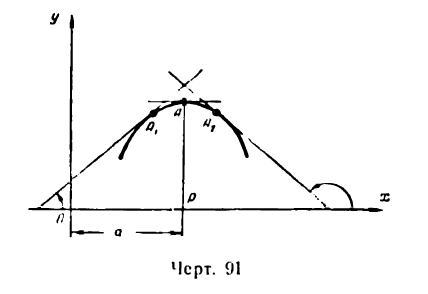
тангенс этих углов, а согласно геометрическому смыслу производной и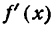 
в указанных точках имеет положительное значение.
В точках же, лежащих правее А, касательные образуют с положительным направлением оси Ох тупые углы, а потому тангенс этих углов, а также первая производная имеет отрицательное значение.
Так как производная функции непрерывна, то ее значение должно меняться без скачков, и, следовательно, при переходе от положительных значений к отрицательным пройдет при х = а через нуль, т. е. в точке А
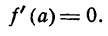
Если функция у = f(x) при х = а имеет максимум, то
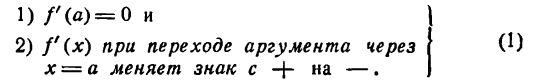
II. Положим, что точке В графика функции у = f(х) соответствует минимум при х = а (рис. 92). Рассуждая так же, придем к выводу, что в этом случае первая производная
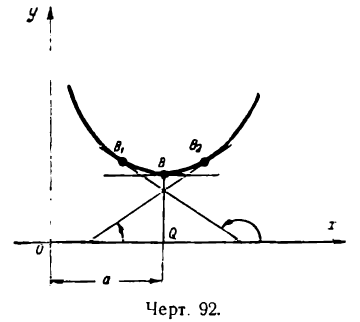
при возрастании х меняет отрицательные значения на положительные и, будучи непрерывной, обращается при х = а в нуль, т. е. в точке В
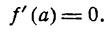
Таким образом, если функция у = f(x) при х = а имеет минимум, то
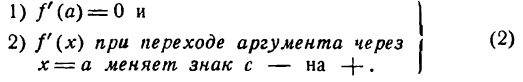
Справедливы обратные утверждения. Функция y = f(x) при х = а имеет максимум, если
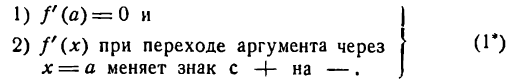
Функция у = f(х) при х = а имеет минимум, если
Признаки (1 * ) и (2*) являются достаточными признаками максимума и минимума функции, т. е. такими признаками, наличие которых влечет за собой или максимум или минимум функции.
*) Бывают случаи, когда в точках кривой, соответствующих максимуму или минимуму функции, касательная параллельна не оси Ох, а оси Оу. Такие функции исключаются нами из рассмотрения.
Как видно из равенства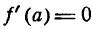 
, касательная, проведенная в точках А и В графиков, параллельна оси Ох*).
III. Может, однако, случиться, что первая производная функции, обращаясь в нуль при х = а, не меняет знака при переходе аргумента через х = а. В этом случае функция не имеет ни максимума ни минимума. На рис. 93 показано, что касательная в точке А кривой у = f(х) параллельна оси Ох, т. е. 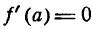, но 
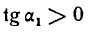и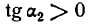 
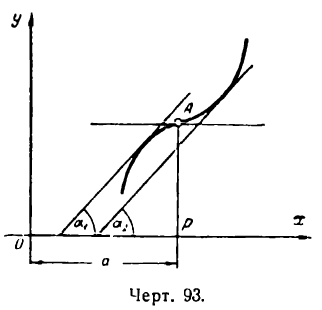
Следовательно, первая производная функции у = f(х) при переходе аргумента через х = а не меняет знака. Функция, как показывает рисеж, не имеет при х = а ни максимума ни минимума.
Значения аргумента, обращающие первую производную в нуль, будем называть критическими значениями аргумента.
Правило нахождения максимума и минимума функции
Пусть дана функция у = f(х). Для исследования ее на максимум и минимум прежде всего нужно решить уравнение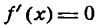 
для нахождения критических значений аргумента. Пусть действительными корнями этого уравнения будут х1, х2, х3 и т. д. **).
**) Этих корней будет ограниченное число, если мы исключим из рассмотрения бесконечно колеблющиеся функции.
Затем нужно исследовать знак f'(x) для найденных критических значений х, начиная с х1 (наименьшего); с этой целью определяют знак производной сначала для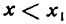 
подставляя какое-либо число, меньшее 
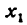(производная при всех значениях 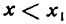не обращается в нуль, а потому ее знак в силу непрерывности сохраняется неизменным при 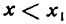как это следует из выводов).
После этого определяют знак производной при каком-либо значении х в промежутке между х1 и х2 (в промежутке между x1 и х2 производная сохраняет один и тот же знак по тому же свойству непрерывной функции).
Найдя таким образом знаки производной для значений х, сначала меньшего, а потом большего чем x1, устанавливают, существует ли при этом значении х= х1 максимум или минимум функции или нет ни того ни другого.
Точно так же исследуют знак f'(x) для остальных критических значений х.
Первое правило. Таким образом, для исследования функции y = f(x) на максимум и минимум нужно:
I. Найти производную функции у’ = f'(x).
П. Приравняв ее нулю, найти действительные корни полученного уравнения) пусть они будут х1, x2, х3 и т. д.
III. Расположив значения x1, х2, х3, … в порядке их возрастания, подставить в производную сначала какое-либо число, меньшее х1, затем подставить число, заключенное в промежутке между х1 и х2;
если при этом знак производной меняется с + на —, то при х = x1| имеет место максимум;
если с — на + , то при х—х1 имеет место минимум;
если же знак производной не меняется, функция при х = х1 не имеет ни максимума ни минимума;
таким же образом определить знак производной до х2 и после х2 и т. д.
IV. Найти максимальные и минимальные значения функции, т. е. вычислить f(x1), f(x2), f(x3) и т. д.
Четвертый пункт этого правила нужен только в том случае, если есть необходимость знать положение точек на кривой, соответствующих максимуму и минимуму функции.
Рассмотрим несколько примеров.
Пример:
Исследовать на максимум и минимум функцию
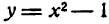
Решение:
Находим производную функции:
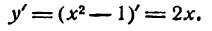
II. Приравниваем ее нулю:
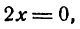
откуда
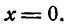
III. Определяем знак производной для значения x < 0, например для х = —1:
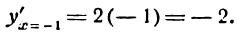
Теперь находим знак производной для х > 0, например для х — 1:
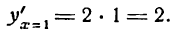
Изменение знака производной с минуса на плюс показывает, что данная функция при x = 0 имеет минимум.
IV. Находим минимальное значение функции, т. е. f(0):
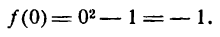
Теперь мы можем представить на рисеже положение найденной точки A(0; — 1) и вид кривой вблизи нее (рис. 94).
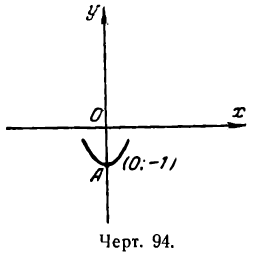
Пример:
Исследовать на максимум и минимум функцию
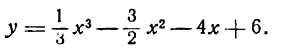
Решение:
Согласно правилу имеем:
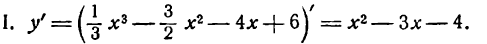
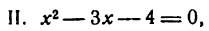
откуда
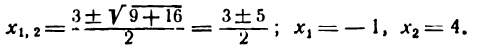
III. 1) Исследуем критическое значение х1 = —1. Берем значение х < — 1, например х = — 2; тогда
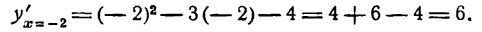
Возьмем значение х > — 1, например х = 0; тогда
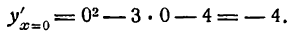
Перемена знака производной с плюса на минус показывает, что функция при х = —1 имеет максимум.
2) Исследуем критическое значение x2 = 4. Беря для x < 4 значение x = 0, а для х > 4 значение х = 5, имеем:
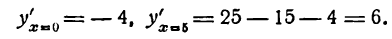
Следовательно, при х = 4 функция имеет минимум.
IV. Максимальное и минимальное значения функции будут:
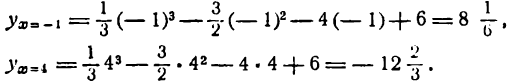
Результат вычисления запишем в таблицу:
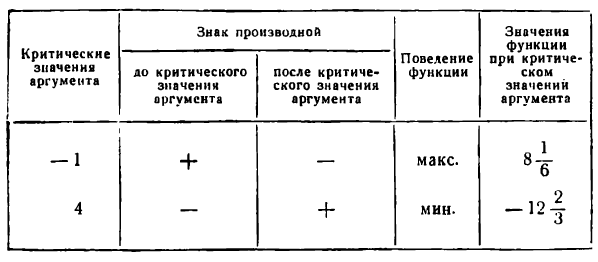
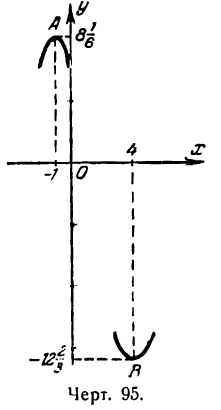
Обозначив точки графика функции, соответствующие максимуму и минимуму ее через А и В, напишем:
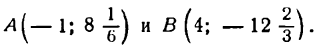
Положение точек A и В и вид кривой вблизи них представлены на рис. 95.
Пример:
Исследовать на максимум и минимум функцию
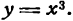
Решение:
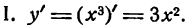
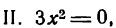
откуда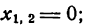 
III. Для х < 0, например для х = -1
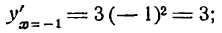
для х > 0, например для x = 1,
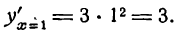
Знаки производной оказались одинаковыми при переходе через критическое значение х = 0; следовательно, данная функция при х = 0 не имеет ни максимума ни минимума (рис. 71).
Выпуклость и вогнутость кривой
Рассмотрим кривую, изображенную на рис. 96. Проведя касательную, например АВ, мы видим, что точки кривой, смежные с точкой касания А и лежащие по обе стороны от нее, располагаются ниже касательной. В таком случае говорят, что кривая выпукла вверх в точке А; если часть кривой между точками М и N удовлетворяет этому условию, то эту часть кривой называют выпуклой вверх или просто выпуклой.
Возьмем кривую, изображенную на рис. 97.
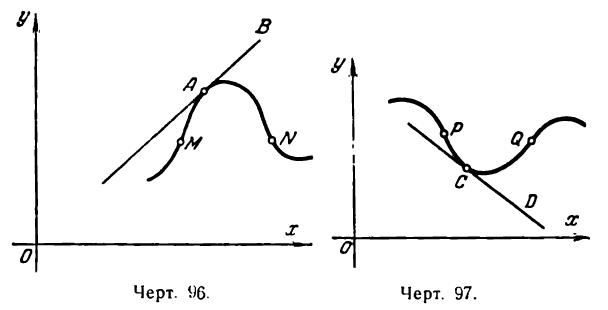
Здесь мы наблюдаем другое явление, а именно: точки кривой, близкие к точке касания С и расположенные по разным сторонам от нее, лежат выше касательной СD. В этом случае говорят, что кривая в точке С вогнута вверх и часть кривой между точками Р и Q, удовлетворяющей этому условию, называют вогнутой вверх или просто вогнутой.
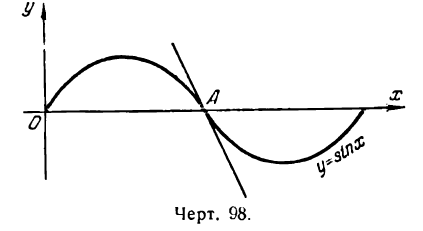
Бывают случаи, когда кривая в одной своей части выпукла, а в другой вогнута; так, например, синусоида (рис. 98) имеет и выпуклость (выше оси Ох) и вогнутость (ниже оси Ох), причем точка А служит границей между ними. Касательная, проведенная к кривой в этой точке, является общей для выпуклой и вогнутой части ее; эта касательная в то же время пересекает кривую в точке касания; поэтому синусоида в точке А ни выпукла ни вогнута. Эта точка носит название тонки перегиба.
Признаки выпуклости и вогнутости кривой
Теорема:
Если вторая производная функции у = f(x) в данном промежутке значений х положительна, то кривая вогнута в этом промежутке, а если отрицательна, — то выпукла.
Поясним эту теорему геометрически.
I. Пусть в данном промежутке значений х
Так как f»(x) является производной функции f'(x), то, применяя признак возрастания и убывания к функции f'(x) , скажем, что при условии (1) f'(x) возрастает с возрастанием х в данном промежутке. Но тогда согласно геометрическому смыслу первой производной возрастает и угловой коэффициент касательных, проведенных к графику функции y = f(x) в точках данного промежутка, т. е. растет тангенс угла наклона этих касательных, а следовательно, и угол их наклона к положительному направлению оси Ох.
Итак, при условии (1) с возрастанием х угол, образованный касательными к кривой y — f(х) с положительным направлением оси Ох, растет, а это наблюдается только в случае, когда касательные проведены в точках, лежащих на вогнутом участке кривой (рис. 99).
II. Пусть в данном промежутке значений х
При этом условии с возрастанием х функция f'(x) убывает, а потому убывает и угловой коэффициент касательных, проведенных к графику функции у = f(x) в точках данного промежутка, т. е. убывает тангенс угла наклона этих касательных, а следовательно, и угол их наклона к положительному направлению оси Ох.
Таким образом, при условии (2) с возрастанием х угол между касательными к кривой у=f(х) и положительным направлением оси Ох убывает, а это имеет место только в случае, когда касательные проведены на выпуклом участке кривой (рис. 100).
Пример:
Узнать, выпукла или вогнута кривая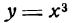 
в точке, абсцисса которой равна —2.
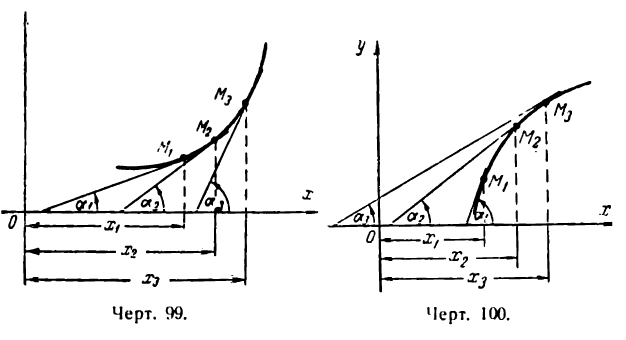
Решение:
Находим вторую производную данной функции и определяем ее знак при х = — 2:
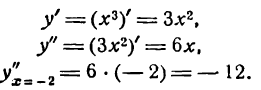
Вторая производная отрицательна; следовательно, кривая 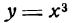в данной точке выпукла (рис. 71).
Нахождение точки перегиба
Определение:
Точкой перегиба кривой называется точка, которая отделяет выпуклую часть кривой от вогнутой.
Если график функции у=f(х) меняет выпуклость на вогнутость или наоборот, то при этом вторая производная данной функции должна менять свой знак, обращаясь в нуль в точке перегиба.
Легко показать, что справедливо и обратное утверждение: если при данном х вторая производная функции у = f(х) равна нулю и при переходе аргумента через данное значение х меняет знак, то при этом график функции имеет точку перегиба.
Это является достаточным признаком точки перегиба. Отсюда имеем следующее правило.
Чтобы найти точку перегиба кривой у =f(х), нужно:
I.Отыскать вторую производную функции у = f(х).
II. Приравняв ее нулю, решить полученное уравнение; пусть действительными корнями его будут х1, х2, х3 и т. д. *).
*) Предполагается, что уравнение имеет ограниченное число корней.
III. Расположив значения х1, х2, х3, … в порядке их возрастания, подставить во вторую производную сначала любое число, меньшее х1, затем — любое число, заключенное между х1 и х2 если в обоих случаях получатся разные знаки, то при х = х1 имеется точка перегиба, если же одинаковые, то точки перегиба нет; таким же образом определить знак второй производной до и после х2 и т. д.
IV. Найти ординаты точек перегиба, т. е. вычислить функцию для тех значений аргумента, для которых имеет место перегиб.
Пример:
Найти точку перегиба кривой .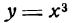
Решение:
Согласно правилу находим;
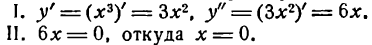
III. Определяем знак:
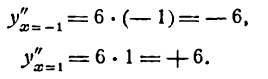
Как видно, при х = 0 имеет место точка перегиба.
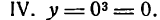
Кривая 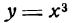имеет точку перегиба в начале координат и здесь меняет выпуклость на вогнутость, как это видно из чередования знаков второй производной (рис. 71).
Второе правило нахождения максимума и минимума функции
Теорема:
Если для некоторой функции у=f(х)
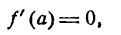
то данная функция при х = а имеет
максимум, если f» (а) < 0 и минимум, если f» (а) > 0
Покажем справедливость теоремы следующими соображениями.
При условии f’ (а) = 0 функция у = f(x) имеет максимум или минимум или точку перегиба. Но согласно теореме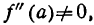 
поэтому точка перегиба исключается.
При f»(а) < 0 точка с абсциссой х = а лежит на выпуклой части графика функции, а при f»(а) >0 — на вогнутой его части. Следовательно, в первом случае имеет место максимум, во втором — минимум, что и требовалось показать.
Может однако случиться, что при f'(а) = 0 также и f»(а ) = 0, тогда при помощи второй производной нельзя установить, что имеет функция: максимум или минимум. В этом случае для решения вопроса нужно прибегнуть к первому правилу.
Таким образом, имеем второе правило для нахождения максимума и минимума функции:
Найти вторую производную функции и подставить в нее каждое из критических значений аргумента; если в результате подстановки одного из них вторая производная будет отрицательной, то при этом значении аргумента функция имеет максимум, если положительной,— то минимум, а если же вторая производная обращается в нуль, то для решения вопроса нужно обратиться к первому правилу.
Рассмотрим несколько примеров.
Пример:
Исследовать на максимум и минимум функцию
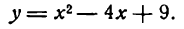
Решение:
Согласно правилу имеем:
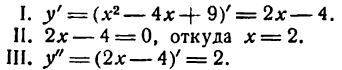
Вторая производная оказалась положительной; следовательно, при х = 2 имеет место минимум.
Пример:
Исследовать на максимум и минимум функцию
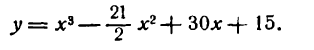
Решение:
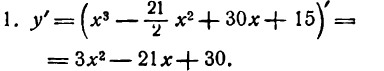
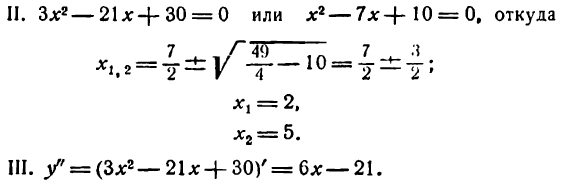
Подставим во вторую производную вместо х поочередно значения 2 и 5:
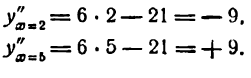
Как видно, при х =2 функция имеет максимум, при х = 5 — минимум.
Пример:
Исследовать на максимум и минимум функцию
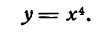
Решение:
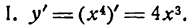
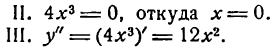
Подставив значение x = 0, получим:
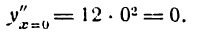
Вторая производная оказалась равной нулю, поэтому указанным способом установить максимум и минимум нельзя. Обратившись к первому правилу, будем иметь:
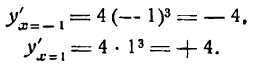
Перемена знака первой производной показывает, что при x = 0 функция имеет минимум.
Задачи на максимум и минимум функции
Теория максимума и минимума функции имеет большое применение как в самой математике, так и в технических дисциплинах. Решим несколько задач.
Задача:
Разбить число 20 на два слагаемых, произведение которых имело бы наибольшее значение.
Решение:
Будем искать эти слагаемые. Обозначим одно из них буквой х; тогда другое слагаемое выразится в виде 20 — х. Произведение этих слагаемых есть переменная величина, меняющаяся с изменением слагаемого х. Обозначая произведение буквой у, запишем:
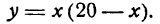
Мы получили функцию, выражающую зависимость произведения у от величины слагаемого х. В задаче требуется найти такое х, при котором у принимает наибольшее значение, т. е. задача свелась к нахождению максимума функции.
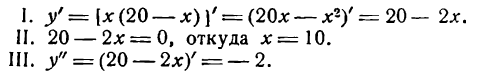
Следовательно, при x = 10 функция имеет максимум.
Число 20 нужно разбить на два равных слагаемых, тогда их произведение будет наибольшим.
Задача:
Найти высоту конуса наибольшего объема, который можно вписать в шар радиуса, равного R.
Решение:
Обозначив радиус основания, высоту и объем конуса соответственно буквами r, h и v, запишем:
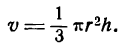
Это равенство выражает зависимость v от двух переменных r и h исключим одну из этих величин, а именно r. Для этого из прямоугольного треугольника АВО (рис. 101)
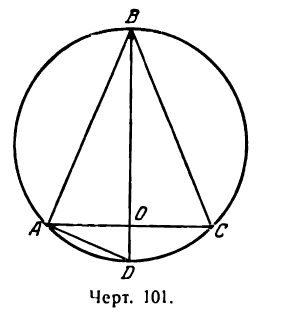
выводим (по теореме о квадрате перпендикуляра, опущенного из вершины прямого угла на гипотенузу):
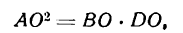
или
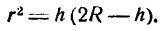
Подставив значение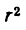 
в формулу объема конуса, получим:
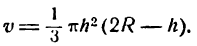
Мы видим, что объем v конуса, вписанного в шар радиуса R, есть функция от высоты этого конуса h. Найти высоту, при которой вписанный конус имеет наибольший объем, это значит найти такое h , при котором функция v имеет максимум.
Ищем максимум функции v:
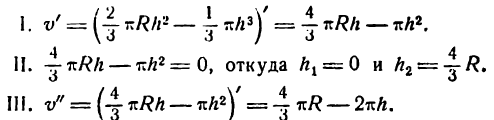
Подставив вместо h сначала h1 = 0, а потом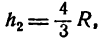 
получим:
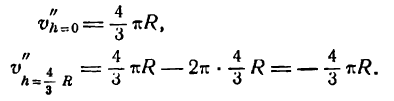
В первом случае имеем минимум, во втором — искомый
максимум.
Следовательно, при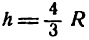 
конус, вписанный в шар радиуса /?, имеет наибольший объем.
Задача:
Окно имеет форму прямоугольника, завершенного полукругом; периметр фигуры окна равен 6 м. Каковы должны быть его размеры, чтобы оно пропускало максимум света (рис. 102).
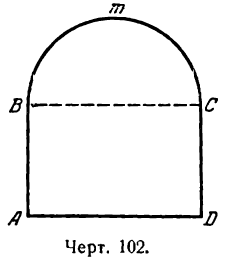
Решение:
Как известно, количество света, проходящего через окно, тем больше, чем больше площадь окна. Обозначим:
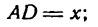
тогда длина полуокружности В m С будет равна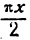 
, а высота окна
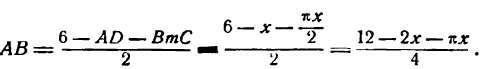
Площадь всего окна состоит из площадей прямоугольника АВСD и полукруга ВmС, По соответствующим формулам найдем:
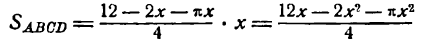
Обозначив площадь окна буквой у, получим:
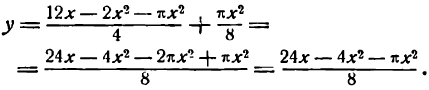
Мы видим, что площадь окна у в условиях нашей задачи является функцией его основания х, и задача свелась к нахождению максимума функции у.
Исследуем полученную функцию на максимум:
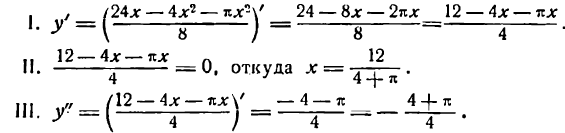
Вторая производная оказалась отрицательной, значит, при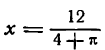
площадь окна наибольшая.
Для прохождения наибольшего количества света через окно с контуром в 6 м нужно, чтобы ширина его была равна
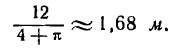
Графики функций
В настоящей главе мы познакомились с тем, как изучаются свойства функции с помощью ее производных. Знание этих свойств позволяет нам получить представление о функции, а также построить ее график.
Пример:
Построить график функции
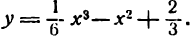
Решение:
Исследуем данную функцию на максимум и минимум.
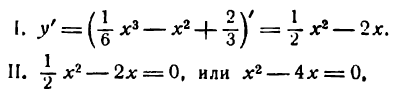
откуда x1 = 0 и х2 = 4.
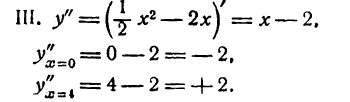
При x = 0 функция имеет максимум, при x = 4 — минимум.
IV. Найдем ординаты точек, соответствующих максимуму и минимуму функции:
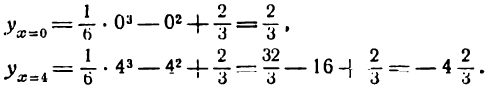
Координаты искомых точек суть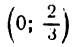 
и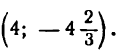 
Исследуем теперь данную функцию на точку перегиба; для этого найденную вторую производную приравняем нулю:
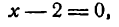
откуда
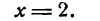
Чтобы убедиться, что при х = 2 имеет место перегиб, определим знаки второй производной для х < 2 и для х > 2; в результате получим:
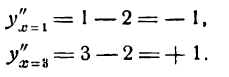
Смена знаков второй производной показывает, что аргументу х = 2 соответствует точка перегиба. Найдя ее ординату, будем иметь:
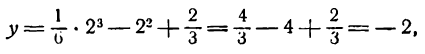
и координаты точки перегиба (2; — 2).
Чтобы яснее представить график данной функции, вычислим координаты еще нескольких точек *).
*) Часто бывает полезно найти точки пересечения кривой с осями координат, однако это нередко связано с большими трудностями при решении уравнений высших степеней.
Положив, например, х = — 2 и х = 6, получим:
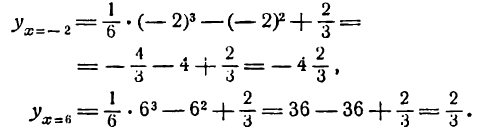
Координаты дополнительных точек суть 
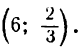
Составим таблицу найденных значений координат точек:
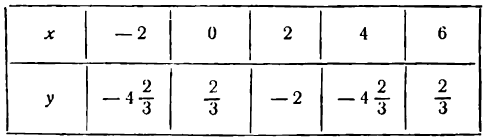
Построим все эти точки и проведем через них плавную линию (рис.103).
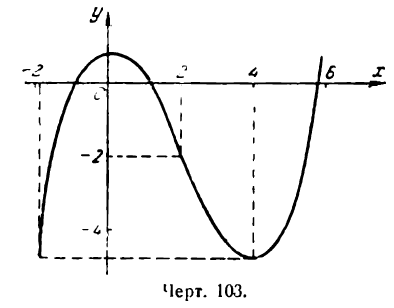
Для построения графика функции следует придерживаться такой схемы.
- Найти значения х, при которых данная функция имеет максимум или минимум.
- Найти значения х, при которых график функции имеет точки перегиба.
- Вычислить значения ординат точек, соответствующие найденным значениям абсцисс; присоединив к этим точкам еще несколько дополнительных, записать найденные значения х и у в таблицу.
- Построить найденные точки и провести через них плавную линию.
Приложение производных к исследованию функций
Использование производных позволяет прояснить многие особенности в поведении функций. Наиболее важными особенностями функций являются интервалы монотонности и точки экстремумов функций. Кроме того, для приложений нужно уметь находить полиномы, значения которых вместе с производными совпадают со значениями функции в известной точке. Такие полиномы называют приближающими. Если функция относится к классу монотонных функций, то ее производная сохраняет знак на интервале монотонности, причем возрастающая функция имеет положительную производную, а убывающая — отрицательную. Действительно, если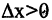 
и так как
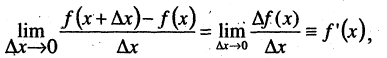
то знак производной совпадает со знаком приращения функции. Для возрастающих функций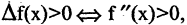 
для убывающих функций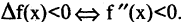 
Функция имеет локальный максимум (минимум) в точке 
, если она определена как в точке , так и в окрестности этой точки и значение функции в точке больше (меньше), чем ее
значения во всех соседних точках: т. е.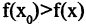 
в точках максимума и 
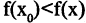в точках минимума для всех х из окрестности точки .
Функция имеет локальный максимум (минимум) в точке , если она определена как в точке , так и в окрестности этой точки и значение функции в точке больше (меньше), чем ее значения во всех соседних точках: т. е. 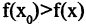в точках максимума и 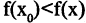в точках минимума для всех х из окрестности точки .
Минимумы и максимумы функции объединены единым понятием — экстремумы. До точки максимума функция возрастает, следовательно, ее производная положительна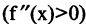 
, после точки максимума — убывает, производная отрицательна 
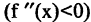. Для точки минимума первоначально функция убывает 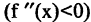, а потом возрастает 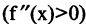. В самих точках экстремумов производная или равна нулю (обычный экстремум) или не существует (острый экстремум). На рис. 3.6 функция имеет экстремумы в точках 
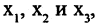причем в точке 
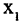— острый максимум, а в точках 
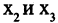— обычный минимум и максимум. Тем самым в точках экстремумов функции производная равна нулю или не существует (необходимое условие экстремума) и меняет знак с «+» на «-» в точках максимумов и с «-» на «+» в точках минимумов (достаточные условия экстремума).
Замечание:
Не надо путать наибольшее и наименьшее значение и экстремум. Экстремум достигается всегда внутри промежутка, а наибольшее и наименьшее значения могут достигаться и в точках экстремумов, и на границах промежутка, и в точках разрыва. На рис. 3.6 точка х3 является точкой максимума и в ней достигается наибольшее значение, наименьшее значение достигается в точке а, т.е. на границе промежутка.
Формула Тейлора
Пусть функция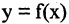 
в интервале (а,b) имеет производные до 
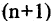-го порядка включительно. Приближающий полином п-ой степени, значение которого и его производных до порядка п включительно совпадают со значением функции и ее производных в точке , имеет вид
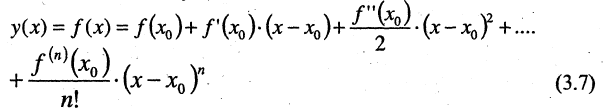
В окрестности точки замена функции полиномом дает некоторую ошибку. Формула Тейлора обеспечивает возможность точной замены данной функции полиномом
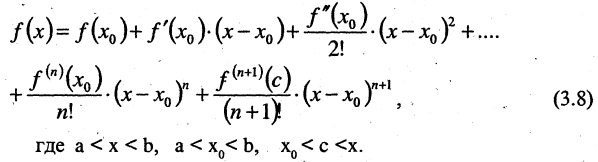
Выражение
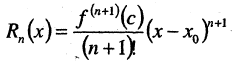
называется остаточным членом формулы Тейлора в форме Лагранжа. Величина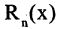 
определяет погрешность, возникающую при замене функции полиномом степени п. Форма Лагранжа позволяет при вычислениях найти оценку сверху для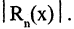 
Если учесть, что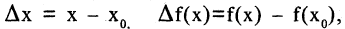 
а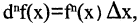 
то получим дифференциальную форму формулы Тейлора
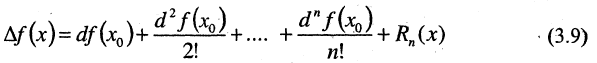
Формула Маклорена — частный случай формулы Тейлора, когда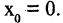 
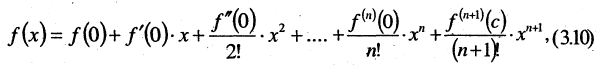
Пример:
Вычислить значение числа е.
Решение. Построим формулу Тейлора для функции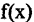 
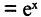в окрестности точки 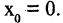Прежде всего вычислим производные:
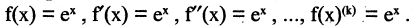
Отсюда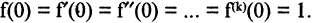 
Из (4.16) для 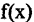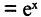имеем
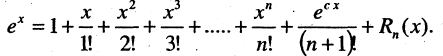
Эта формула получена для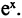 
Если в правой части положить 
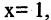то
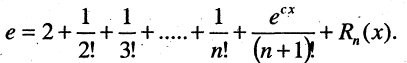
В зависимости от требований задачи эта формула позволяет получить сколь угодно точные значения величины е. Так
для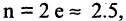 
ошибка не превышает величины 0.23,
для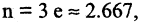 
ошибка не превышает величины 0.052,
для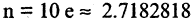 
и ошибка не более, чем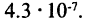 
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.
Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:
У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).
Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.
Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.
Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:
– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
– если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
– если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
– если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.
Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.
Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью
Экстремумы функции
Необходимое условие экстремума функции одной переменной
Достаточное условие экстремума функции одной переменной
Если в точке x * выполняется условие:
Пример №1 . Найти наибольшее и наименьшее значения функции: 
на отрезке [1; 3].
Решение.
Критическая точка одна x1 = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)= 5 /2, f(3)=3 8 /81
Ответ: fmin= 5 /2 при x=2; fmax=9 при x=1
Пример №2 . С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π /3+2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x= π /3+2πk, k∈Z – точки минимума функции; , значит x=- π /3+2πk, k∈Z – точки максимума функции.
Пример №3 . Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x0 или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.
Пример №4 . Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x – первое слагаемое. Тогда (49-x) – второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
или
49x – x 2
Максимумы, минимумы и экстремумы функций
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.
Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:
У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).
Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.
Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.
Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
Все вышесказанное можно обобщить следующими выводами:
– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
– если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
– если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
– если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.
Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.
Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Исследование графика функции
На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:
- область определения функции
- область значений функции
- нули функции
- промежутки возрастания и убывания
- точки максимума и минимума
- наибольшее и наименьшее значение функции на отрезке.
Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось .
Ось ординат — вертикальная ось, или ось .
Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается .
Другими словами, мы сами выбираем , подставляем в формулу функции и получаем .
Область определения функции — множество тех (и только тех) значений аргумента , при которых функция существует.
Обозначается: или .
На нашем рисунке область определения функции — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.
Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок — от самого нижнего до самого верхнего значения .
Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .
Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .
Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.
Функция возрастает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.
Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Для убывающей функции большему значению соответствует меньшее значение . График идет вправо и вниз.
На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .
Определим, что такое точки максимума и минимума функции.
Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.
На нашем рисунке — точка максимума.
Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».
На нашем рисунке — точка минимума.
Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и на нашем графике не может быть точкой минимума.
Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это и .
А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.
Аналогично, максимум нашей функции равен . Он достигается в точке .
Можно сказать, что экстремумы функции равны и .
Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.
В нашем случае наименьшее значение функции на отрезке равно и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно . Оно достигается в левом конце отрезка.
В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.
[spoiler title=”источники:”]
http://cos-cos.ru/math/327/
http://ege-study.ru/ru/ege/materialy/matematika/issledovanie-grafika-funkcii/
[/spoiler]
Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.
Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.
Возрастание и убывание функции на интервале
Функция y=f(x) будет возрастать на интервале x, когда при любых x1∈X и x2∈X , x2>x1неравенство f(x2)>f(x1) будет выполнимо. Иначе говоря, большему значению аргумента соответствует большее значение функции.
Функция y=f(x) считается убывающей на интервале x, когда при любых x1∈X, x2∈X, x2>x1 равенство f(x2)>f(x1) считается выполнимым. Иначе говоря, большему значению функции соответствует меньшее значение аргумента. Рассмотрим рисунок, приведенный ниже.
Замечание: Когда функция определенная и непрерывная в концах интервала возрастания и убывания, то есть (a;b), где х=а, х=b, точки включены в промежуток возрастания и убывания. Определению это не противоречит, значит, имеет место быть на промежутке x.
Основные свойства элементарных функций типа y=sinx – определенность и непрерывность при действительных значениях аргументах. Отсюда получаем, что возрастание синуса происходит на интервале -π2; π2, тогда возрастание на отрезке имеет вид -π2; π2.
Точки экстремума, экстремумы функции
Точка х0 называется точкой максимума для функции y=f(x), когда для всех значений x неравенство f(x0)≥f(x) является справедливым. Максимум функции – это значение функции в точке, причем обозначается ymax.
Точка х0 называется точкой минимума для функции y=f(x), когда для всех значений x неравенство f(x0)≤f(x) является справедливым. Минимум функции – это значение функции в точке, причем имеет обозначение вида ymin.
Окрестностями точки х0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.
Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.
Первый рисунок говорит о том, что необходимо найти наибольшее значение функции из отрезка [a;b]. Оно находится при помощи точек максимума и равняется максимальному значению функции, а второй рисунок больше походит на поиск точки максимума при х=b.
Достаточные условия возрастания и убывания функции
Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.
Первое достаточное условие экстремума
Пусть задана функция y=f(x), которая дифференцируема в ε окрестности точки x0, причем имеет непрерывность в заданной точке x0. Отсюда получаем, что
- когда f'(x)>0 с x∈(x0-ε; x0) и f'(x)<0 при x∈(x0; x0+ε), тогда x0 является точкой максимума;
- когда f'(x)<0 с x∈(x0-ε; x0) и f'(x)>0 при x∈(x0; x0+ε), тогда x0 является точкой минимума.
Иначе говоря, получим их условия постановки знака:
- когда функция непрерывна в точке x0, тогда имеет производную с меняющимся знаком, то есть с + на -, значит, точка называется максимумом;
- когда функция непрерывна в точке x0, тогда имеет производную с меняющимся знаком с – на +, значит, точка называется минимумом.
Алгоритм для нахождения точек экстремума
Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:
- найти область определения;
- найти производную функции на этой области;
- определить нули и точки, где функция не существует;
- определение знака производной на интервалах;
- выбрать точки, где функция меняет знак.
Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.
Найти точки максимума и минимума заданной функции y=2(x+1)2x-2.
Решение
Область определения данной функции – это все действительные числа кроме х=2. Для начала найдем производную функции и получим:
y’=2x+12x-2’=2·x+12’·(x-2)-(x+1)2·(x-2)'(x-2)2==2·2·(x+1)·(x+1)’·(x-2)-(x+1)2·1(x-2)2=2·2·(x+1)·(x-2)-(x+2)2(x-2)2==2·(x+1)·(x-5)(x-2)2
Отсюда видим, что нули функции – это х=-1, х=5, х=2, то есть каждую скобку необходимо приравнять к нулю. Отметим на числовой оси и получим:
Теперь определим знаки производной из каждого интервала. Необходимо выбрать точку, входящую в интервал, подставить в выражение. Например, точки х=-2, х=0, х=3, х=6.
Получаем, что
y'(-2)=2·(x+1)·(x-5)(x-2)2x=-2=2·(-2+1)·(-2-5)(-2-2)2=2·716=78>0, значит, интервал -∞; -1 имеет положительную производную. Аналогичным образом получаем, что
y'(0)=2·(0+1)·0-50-22=2·-54=-52<0y'(3)=2·(3+1)·(3-5)(3-2)2=2·-81=-16<0y'(6)=2·(6+1)·(6-5)(6-2)2=2·716=78>0
Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.
Получим, что в точке х=-1 функция будет непрерывна, значит, производная изменит знак с + на -. По первому признаку имеем, что х=-1 является точкой максимума, значит получаем
ymax=y(-1)=2·(x+1)2x-2x=-1=2·(-1+1)2-1-2=0
Точка х=5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид
ymin=y(5)=2·(x+1)2x-2x=5=2·(5+1)25-2=24
Графическое изображение
Ответ: ymax=y(-1)=0, ymin=y(5)=24.
Стоит обратить внимание на то, что использование первого достаточного признака экстремума не требует дифференцируемости функции с точке x0, этим и упрощает вычисление.
Найти точки максимума и минимума функции y=16×3=2×2+223x-8.
Решение.
Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:
-16×3-2×2-223x-8, x<016×3-2×2+223x-8, x≥0
После чего необходимо найти производную:
y’=16×3-2×2-223x-8′, x<016×3-2×2+223x-8′, x>0y’=-12×2-4x-223, x<012×2-4x+223, x>0
Точка х=0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:
lim y’x→0-0=lim yx→0-0-12×2-4x-223=-12·(0-0)2-4·(0-0)-223=-223lim y’x→0+0=lim yx→0-012×2-4x+223=12·(0+0)2-4·(0+0)+223=+223
Отсюда следует, что функция непрерывна в точке х=0, тогда вычисляем
lim yx→0-0=limx→0-0-16×3-2×2-223x-8==-16·(0-0)3-2·(0-0)2-223·(0-0)-8=-8lim yx→0+0=limx→0-016×3-2×2+223x-8==16·(0+0)3-2·(0+0)2+223·(0+0)-8=-8y(0)=16×3-2×2+223x-8x=0=16·03-2·02+223·0-8=-8
Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:
-12×2-4x-223, x<0D=(-4)2-4·-12·-223=43×1=4+432·-12=-4-233<0x2=4-432·-12=-4+233<0
12×2-4x+223, x>0D=(-4)2-4·12·223=43×3=4+432·12=4+233>0x4=4-432·12=4-233>0
Все полученные точки нужно отметить на прямой для определения знака каждого интервала. Поэтому необходимо вычислить производную в произвольных точках у каждого интервала. Например, у нас можно взять точки со значениями x=-6, x=-4, x=-1, x=1, x=4, x=6. Получим, что
y'(-6)=-12×2-4x-223x=-6=-12·-62-4·(-6)-223=-43<0y'(-4)=-12×2-4x-223x=-4=-12·(-4)2-4·(-4)-223=23>0y'(-1)=-12×2-4x-223x=-1=-12·(-1)2-4·(-1)-223=236<0y'(1)=12×2-4x+223x=1=12·12-4·1+223=236>0y'(4)=12×2-4x+223x=4=12·42-4·4+223=-23<0y'(6)=12×2-4x+223x=6=12·62-4·6+223=43>0
Изображение на прямой имеет вид
Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что
x=-4-233, x=0, x=4+233, тогда отсюда точки максимума имеют значениx=-4+233, x=4-233
Перейдем к вычислению минимумов:
ymin=y-4-233=16×3-22+223x-8x=-4-233=-8273ymin=y(0)=16×3-22+223x-8x=0=-8ymin=y4+233=16×3-22+223x-8x=4+233=-8273
Произведем вычисления максимумов функции. Получим, что
ymax=y-4+233=16×3-22+223x-8x=-4+233=8273ymax=y4-233=16×3-22+223x-8x=4-233=8273
Графическое изображение
Ответ:
ymin=y-4-233=-8273ymin=y(0)=-8ymin=y4+233=-8273ymax=y-4+233=8273ymax=y4-233=8273
Второй признак экстремума функции
Если задана функция f'(x0)=0, тогда при ее f”(x0)>0 получаем, что x0 является точкой минимума, если f”(x0)<0, то точкой максимума. Признак связан с нахождением производной в точке x0.
Найти максимумы и минимумы функции y=8xx+1.
Решение
Для начала находим область определения. Получаем, что
D(y): x≥0x≠-1⇔x≥0
Необходимо продифференцировать функцию, после чего получим
y’=8xx+1’=8·x’·(x+1)-x·(x+1)'(x+1)2==8·12x·(x+1)-x·1(x+1)2=4·x+1-2x(x+1)2·x=4·-x+1(x+1)2·x
При х=1 производная становится равной нулю, значит, точка является возможным экстремумом. Для уточнения необходимо найти вторую производную и вычислить значение при х=1. Получаем:
y”=4·-x+1(x+1)2·x’==4·(-x+1)’·(x+1)2·x-(-x+1)·x+12·x'(x+1)4·x==4·(-1)·(x+1)2·x-(-x+1)·x+12’·x+(x+1)2·x'(x+1)4·x==4·-(x+1)2x-(-x+1)·2x+1(x+1)’x+(x+1)22x(x+1)4·x==-(x+1)2x-(-x+1)·x+1·2x+x+12x(x+1)4·x==2·3×2-6x-1x+13·x3⇒y”(1)=2·3·12-6·1-1(1+1)3·(1)3=2·-48=-1<0
Значит, использовав 2 достаточное условие экстремума, получаем, что х=1 является точкой максимума. Иначе запись имеет вид ymax=y(1)=811+1=4.
Графическое изображение
Ответ: ymax=y(1)=4..
Третье достаточное условие экстремума
Функция y=f(x) имеет ее производную до n-го порядка в ε окрестности заданной точки x0 и производную до n+1-го порядка в точке x0. Тогда f'(x0)=f”(x0)=f”'(x0)=…=fn(x0)=0.
Отсюда следует, что когда n является четным числом, то x0 считается точкой перегиба, когда n является нечетным числом, то x0 точка экстремума, причем f(n+1)(x0)>0, тогда x0 является точкой минимума, f(n+1)(x0)<0, тогда x0 является точкой максимума.
Найти точки максимума и минимума функции yy=116(x+1)3(x-3)4.
Решение
Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что
y’=116x+13′(x-3)4+(x+1)3x-34’==116(3(x+1)2(x-3)4+(x+1)34(x-3)3)==116(x+1)2(x-3)3(3x-9+4x+4)=116(x+1)2(x-3)3(7x-5)
Данная производная обратится в ноль при x1=-1, x2=57, x3=3. То есть точки могут быть точками возможного экстремума. Необходимо применить третье достаточное условие экстремума. Нахождение второй производной позволяет в точности определить наличие максимума и минимума функции. Вычисление второй производной производится в точках ее возможного экстремума. Получаем, что
y”=116x+12(x-3)3(7x-5)’=18(x+1)(x-3)2(21×2-30x-3)y”(-1)=0y”57=-368642401<0y”(3)=0
Значит, что x2=57 является точкой максимума. Применив 3 достаточный признак, получаем, что при n=1 и f(n+1)57<0.
Необходимо определить характер точек x1=-1, x3=3. Для этого необходимо найти третью производную, вычислить значения в этих точках. Получаем, что
y”’=18(x+1)(x-3)2(21×2-30x-3)’==18(x-3)(105×3-225×2-45x+93)y”'(-1)=96≠0y”'(3)=0
Значит, x1=-1 является точкой перегиба функции, так как при n=2 и f(n+1)(-1)≠0. Необходимо исследовать точку x3=3. Для этого находим 4 производную и производим вычисления в этой точке:
y(4)=18(x-3)(105×3-225×2-45x+93)’==12(105×3-405×2+315x+57)y(4)(3)=96>0
Из выше решенного делаем вывод, что x3=3 является точкой минимума функции.
Графическое изображение
Ответ: x2=57 является точкой максимума, x3=3 – точкой минимума заданной функции.
Как найти точки минимума и максимума функции
Содержание:
-
Минимум и максимум функции
- Точка минимума, минимум функции
- Точка максимума, максимум функции
- Исследование функций на экстремумы
- Примеры задач
Минимум и максимум функции
Минимумом и максимумом функции, другими словами экстремумами, называют точки, в которых функция меняет характер монотонности (с возрастания на убывание и наоборот). Важно понимать, что экстремумы это не максимальные и минимальные значения функции. Обозначаются следующим образом:
- (y_{min}, y_{max}) — минимум, максимум функции или экстремумы;
- (x_{min}, x_{max}) — точки минимума, максимума функции;
- (y_{наиб}, y_{наим}) — наибольшее (максимальное), наименьшее (минимальное) значение функции.
Точка минимума, минимум функции
Точка минимума — такая точка (x_0), если у неё существует окрестность, для всех точек которой выполняется неравенство (f(x)geq f(x_0))
Минимум функции — значение функции в точке минимума (x_0)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Простыми словами, точка минимума — это та, где убывание функции меняется на возрастание.
Точка максимума, максимум функции
Точка максимума — такая точка (x_0), если у неё существует окрестность, для всех точек которой выполняется неравенство (f(x)leq f(x_0))
Максимум функции — значение функции в точке максимума (x_0)
Простыми словами, точка максимума — это та, где возрастание функции меняется на убывание.
Точки максимума и минимума на графике:
Исследование функций на экстремумы
Теорема. Если функция f(x) имеет экстремум в точке (x=x_0,) то в ней производная либо равна 0, либо не существует.
Алгоритм нахождения экстремумов с помощью производной:
-
Найти область определения функции — D(y).
-
Определить производную — f ‘(x).
-
Определить стационарные точки y = f(x), т.е. те, которые принадлежат D(y), f ‘(x) в них обращается в ноль, отыскать критические точки, в которых производной не существует (пример: (f^,(x)=frac1{2sqrt x}), производной не существует при x = 0).
-
Исследовать характер изменения функции f (x) и знак f ‘(x) в промежутках, на которые найденные критические точки делят область определения (при отрицательном знаке производной функция убывает, при положительном — возрастает).
-
Относительно каждой критической точки определить, является ли она точкой максимума, минимума (возрастание меняется на убывание — точка максимума, убывание на возрастание — минимума) или не является точкой экстремума (то есть, меняется ли знак производной при переходе через исследуемую точку).
-
Вычислить значения функции в точках экстремума.
Примеры задач
Задача 1
Исследовать на экстремумы функцию (f(x)=x^3-3x^2.)
Решение задачи по алгоритму:
1) (D(y): xin(-infty;+infty)), т.е. x — любое число.
2) Производная: (f'(x)=3x^2-6x) .
3) Из пункта 1 следует, что критических точек нет. Найдем стационарные:
Приравниваем f ‘(x) к 0, решаем квадратное уравнение (3x^2-6x=0), получаем (x_1=0),(;x_2=2.)
4) Отметим на горизонтальной оси координат точки 0 и 2. Подставим любое x из интервала ((-infty;0)) в f'(x), например, пусть x = -1, тогда (f'(x)=3{(-1)}^2-6(-1)=3+6=9). Получаем f ‘(x)>0, значит на исследуемом интервале f(x) возрастает. Аналогично рассмотрим оставшиеся интервалы. Итого, на отрезке (0;2) производная отрицательна, функция убывает, а на интервале ((2;+infty)) производная положительна, возрастает. Из этого следует, что x=0 – точка максимума, а x=2 – минимума.
5) Найдем значение экстремумов функции.
(f(0)=0-3times0=0)
(f(2)=2^3-3times2^2=8-12=-4)
Ответ: (x_{min}=2,;y_{min}=-4;;x_{max}=0,;y_{max}=0) или (0;0) – минимум функции, (2;-4) – максимум.
Задача 2
Найти промежутки монотонности функции (f(x)=frac x{x^2-4}).
1) (D(y): xinmathbb{R},;)кроме(;pm2)
2) (f'(x)=frac{1(x^2-4)-xtimes2x}{{(x^2-4)}^2}=-frac{x^2+4}{{(x^2-4)}^2})
3) Итак, как выяснилось в пункте 1, критические точки 2 и -2. Если мы приравняем f ‘(x) к 0, чтобы найти стационарные точки, то увидим, что уравнение не будет иметь корней. Значит, стационарных точек нет. Из этого следует, что функция монотонна на всей области определения. Проверим, возрастает она или убывает. Для этого решаем неравенство (-frac{x^2+4}{{(x^2-4)}^2}leq0) и получим, что неравенство верно при любом x, значит функция убывает.
Не забываем, что в ответе, указывая промежуток, обязательно нужно исключить критические точки -2 и 2 т.к. в них функция не определена.
Ответ: f(x) убывает на промежутке ((-infty;-2)cup(-2;2)cup(2;+infty)).
Задача 3
Докажите, что функция (f(x)=x^5+2x^3-4) возрастает на всех числовой прямой.
1) (D(y): xinmathbb{R}), значит критических точек нет.
2) (f'(x)=5x^4+6x)
3) Приравняем f'(x) к 0 и найдем корень: x = 0. Отметим 0 на числовой прямой и определим знак производной на промежутках ((-infty;0)) и ((0;+infty)). Получим, что производная положительна на обоих промежутках, следовательно функция возрастает на всей числовой прямой.
Утверждение доказано
