и абциссе/ординате этой окружности абциссу или ординату? Например. Цитирую “Дано уравнение окружностиx2+y2=400.
1. Найди ординату точек на этой окружности, абсцисса которых 16.
(запиши обе координаты точек; если второй точки нет, вместо координат пиши координаты первой точки) .
2. Найди абсциссу точек на этой окружности, ордината которых 12.
(запиши обе координаты точек; если второй точки нет, вместо координат пиши координаты первой точки) .
“
Важно узнать как вы это сделали. Просто ответ не прокатит) ) Решение нужно. Что бы понять и простить.. .
Спасибо за ответ) )
Прямоугольная система координат. Ось абсцисс и ординат
О чем эта статья:
Прямоугольная декартова система координат
Французский математик Рене Декарт предложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.
Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Координаты точки в декартовой системе координат
Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.
Каждая точка М, которая расположена на Ох, равна действительному числу xM. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.
Число xM — это координата точки М на заданной координатной прямой.
Пусть точка будет проекцией точки Mx на Ох, а My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения Mx и My.Тогда у точки Mx на оси Оx есть соответствующее число xM, а My на Оу — yM. Как это выглядит на координатных осях:
Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (xM, yM), которые называются ее координатами. Абсцисса М — это xM, ордината М — это yM.
Обратное утверждение тоже верно: каждая пара (xM, yM) имеет соответствующую точку на плоскости.
Формулы для вычисления координат точки
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы выведем формулы для определения координат точки с помощью понятий синуса и косинуса.
Вначале решим типовую задачу на данную тему и на ее примере рассмотрим, как выражаются координаты точки через длину отрезка и угол. Далее выразим координаты вектора и точки через произведение тригонометрических функций и длины отрезка и проанализируем знаки полученных координат.
На примере типовой задачи решим несколько конкретных задач на нахождение координат точки через синус и косинус угла.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»
Как найти абсциссу и ординату точки?
Как найти абсциссу точки?
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки перпендикуляры на оси координат. Точка пересечения с осью «x» называется абсциссой точки «А», а с осью y называется ординатой точки «А».
Что значит найти абсциссу точки?
Абсциссой (лат. abscissa — отрезок) точки A называется координата этой точки на оси X в прямоугольной системе координат (рис. 1).
Где находится абсцисса и ордината?
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо. Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек).
Что такое абсцисс?
Абсциссой (лат. abscissa — отрезок) точки A называется координата этой точки на оси X’X в прямоугольной системе координат. Величина абсциссы точки A равна длине отрезка OB (см.
Как считать Абсциссы?
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки перпендикуляры на оси координат. Точка пересечения с осью «x» называется абсциссой точки «А», а с осью y называется ординатой точки «А».
Как называется ось Х?
называется осью абсцисс. При построении графиков функций ось абсцисс обычно используется как содержащая область определения функции.
Как располагается ось абсцисс?
Положительные абсциссы обычно располагаются на оси XX’ справа от начала координат; положительные ординаты – вверх по оси YY’ от начала координат. На рис.
Что такое ордината точки?
Смотреть что такое “ордината точки” в других словарях: ОРДИНАТА — (от лат. ordinatus расположенный в порядке) одна из декартовых координат точки, обычно вторая, обозначаемая буквой y … . В системе координат аналитической геометрии перпендикуляр на плоскости, опущенный из точки на ось абсцисс.
Как называется ось о игрек?
Горизонтальная ось OX называется осью абсцисс (осью x), вертикальная ось OY — осью ординат (осью y). Точка O, стоящая на пересечении осей, называется началом координат. . Положительные числа изображаются на оси абсцисс точками вправо, а на оси ординат — точками вверх от нулевой точки.
Как называется ось Z?
Эти векторы задают три координатных оси: Ox − ось абсцисс, Oy − ось ординат и Oz − ось аппликат.
Что значит на оси абсцисс?
Абсциссой (лат. abscissa — отрезок) точки A называется координата этой точки на оси X’X в прямоугольной системе координат. . В прямоугольной системе координат ось X’X называется «осью абсцисс». При построении графиков функций, ось абсцисс обычно используется как область определения функции.
Где ось Х А где у?
Система координат основана на пересечении двух осей под углом в 90°, горизонтальная ось называется осью Х и вертикальная – осью Y. Единственная точка пересечения осей имеет координаты (0,0).
Что такое ось Y?
3.20 ось Y (Y axis): Направление, перпендикулярное к движению сканирующего луча и номинально параллельное штрихам линейного символа.
Что значит по оси?
Ось — стержень, не передающий крутящего момента, на котором держатся вращающиеся детали. . Ось координат — прямая с указанными на ней направлением, началом отсчёта и выбранной масштабной единицей: ось абсцисс, ось ординат, ось аппликат.
[spoiler title=”источники:”]
http://interneturok.ru/lesson/geometry/9-klass/sinus-kosinus-i-tangens-ugla/formuly-dlya-vychisleniya-koordinat-tochki
http://topobzor10.ru/kak-naiti-abstsissu-i-ordinatu-tochki
[/spoiler]
Предмет: Математика,
автор: greyonecat
Ответы
Автор ответа: PinkesRose
23
Ответ:
Пошаговое объяснение:
Приложения:
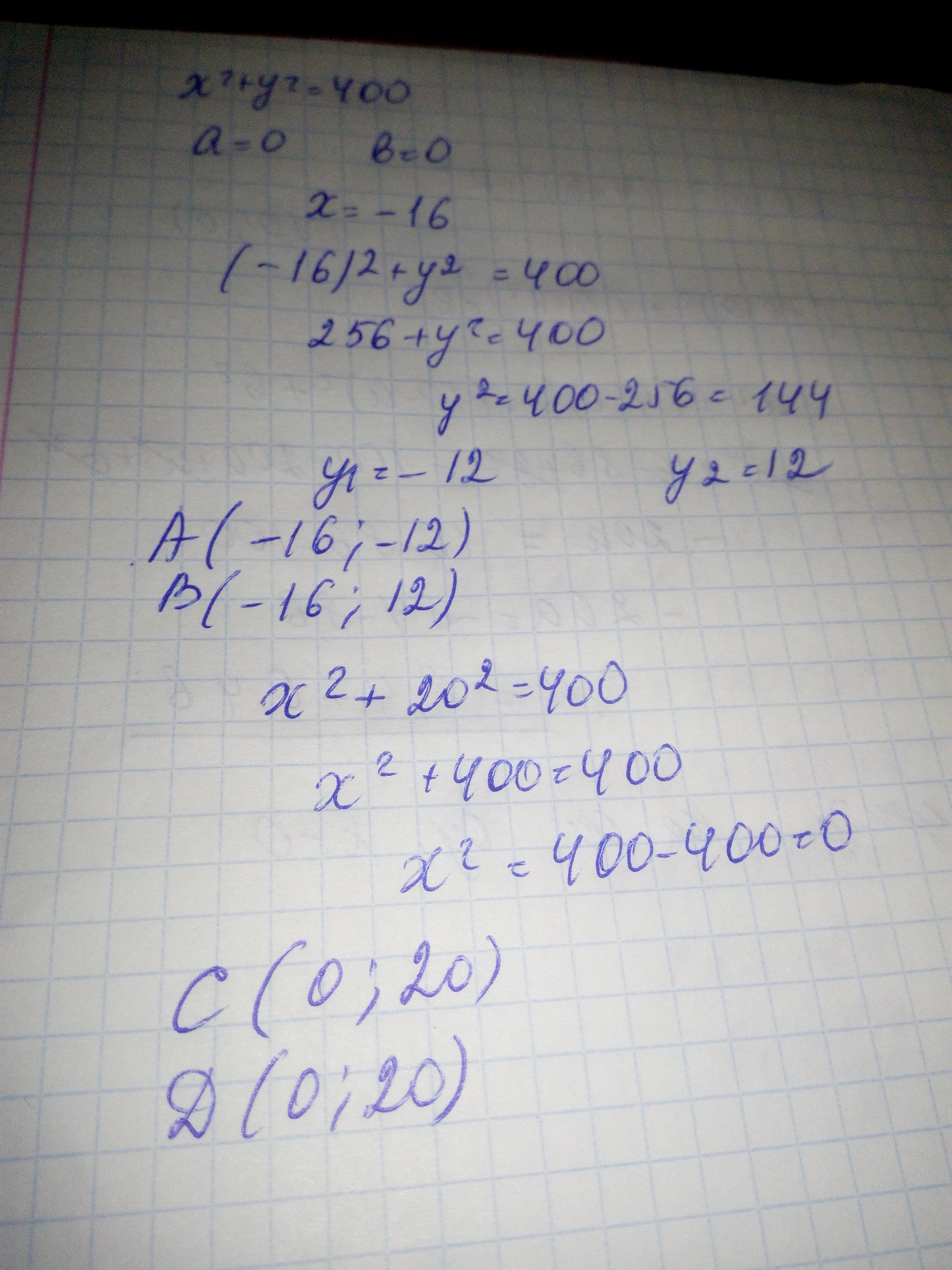
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Английский язык,
автор: lordlordik666
СРОЧНО ДАЮ 10 БАЛЛОВ
3 года назад
Предмет: Қазақ тiлi,
автор: azizazgaliev
көмектесіңіздерші?!?!
3 года назад
Предмет: Английский язык,
автор: prostchelovek222
Помогите очень много баллов!!! Writing a good film review Put the sentences into the correct order.
while to a film. she watching the was came Tom kitchen cinema.
go week the we will Next to film.
watching drama like do not I Back Check
3 года назад
Предмет: Математика,
автор: таня1965
вычислить-5,7-(-1,3)
6 лет назад
Предмет: Математика,
автор: igorc1323
начерти прямоугольник площадь которого равна 18см2 а длина одной из сторон 9см
6 лет назад
Александров-Ответ
Ответ:
1) Уравнение окружности имеет вид: (x-x0)^2+(y-y0)^2=R^2, где x0 и y0 – координаты центра окружности, а R – её радиус.
Координаты центра заданной окружности (2; 3).
1. То, что окружность касается оси Ох, значит, что её радиус равен расстоянию от центра окружности до оси абсцисс. На оси Ох ордината равна нулю, а значит, радиус окружности равен 3. Таким образом, уравнение окружности в этом случае: (x-2)^2+(y-3)^2=9
2. То, что окружность касается оси Оy, значит, что её радиус равен расстоянию от центра окружности до оси ординат. На оси Oy абсцисса равна нулю, а значит, радиус окружности равен 2. Таким образом, уравнение окружности в этом случае: (x-2)^2+(y-3)^2=4.
2)
1.
A(13; 0) и B(13; 0)
Пошаговое объяснение:
Если абсцисса равна 13, то нужно подставить 13 в уравнение вместо x и найти у:
y²+13²=169
y²+169=169
y²=0
y=0
2.
С(5; -12) и D (5; 12)
Пошаговое объяснение:
Если ордината равна -12, то нужно подставить в уравнение -12 вместо y и найти x:
(-12)²+x²=169
144+x²=169
x²=25
x=±5
Расположим числовую окружность в координатной плоскости так, чтобы центр окружности совместился с началом координат, а её радиус принимаем за единичный отрезок.
Начальная точка числовой окружности (A) совмещена с точкой ((1;0)).
Каждая точка числовой окружности имеет в координатной плоскости свои координаты.
Найдём сначала координаты тех точек координатной плоскости, которые получены на макетах числовой окружности.
 |
Точка Mπ4 — середина (I) четверти. Опустим перпендикуляр (MP) на прямую (OA) и рассмотрим треугольник (OMP). Так как дуга (AM) составляет половину дуги (AB), то ∡MOP=45° . Значит, треугольник ( OMP ) — равнобедренный прямоугольный треугольник и (OP = MP), т. е. у точки (M) абсцисса и ордината равны: (x = y). Координаты точки (M(x;y)) удовлетворяют уравнению числовой окружности x2+y2=1 , Поэтому их найдём из системы уравнений: x2+y2=1x=y |
Заменим в первом уравнении (y) на (x):
x2+x2=1;2×2=1;x2=12;x=12=22;y=x=22.
Мы выбрали положительный корень уравнения, так как абсцисса точки (M) больше нуля.
Получили, что координаты точки (M), соответствующей числу
π4
, будут
Mπ4=M22;22
.
Аналогично можно получить координаты и других точек первого макета числовой окружности, учитывая только знаки координат в каждой четверти.
Полученные результаты запишем в таблицу.
|
(0) |
π4 |
π2 |
3π4 |
π |
5π4 |
3π2 |
7π4 |
2π |
|
|
Абсцисса (x) |
(1) |
22 |
(0) |
−22 |
(-1) |
−22 |
(0) |
22 |
(1) |
|
Ордината (y) |
(0) |
22 |
(1) |
22 |
(0) |
−22 |
(-1) |
−22 |
(0) |
Рассуждаем аналогично для точки (M), если теперь она соответствует числу
π6
.
 |
Треугольник (MOP) прямоугольный. Так как дуга (AM) составляет третью часть дуги (AB), то ∡MOP=30° . Катет (MP) лежит против угла (30) градусов в прямоугольном треугольнике, значит, равен половине гипотенузы, т. е. ордината точки (M) равна MP=12;y=12 |
Абсциссу (x) точки (M) найдём, решив уравнение:
x2=1−122=1−14=34;x=32.
При решении учитываем, что абсцисса точки (M) положительна.
Получили, что координаты точки (M), соответствующей числу
π6
, будут
Mπ6=M32;12
.
Аналогично можно получить координаты и других точек второго макета числовой окружности, учитывая только знаки координат в каждой четверти.
Полученные результаты запишем в таблицу.
|
π6 |
π3 |
2π3 |
5π6 |
7π6 |
4π3 |
5π3 |
11π6 |
|
|
Абсцисса (x) |
32 |
12 |
−12 |
−32 |
−32 |
−12 |
12 |
32 |
|
Ордината (y) |
12 |
32 |
32 |
12 |
−12 |
−32 |
−32 |
−12 |




