было в ЕГЭ
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 119 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Найдите абсциссу точки, симметричной точке A(6; 8) относительно начала координат.
Найдите ординату середины отрезка, соединяющего точки O(0; 0) и A(6; 8).
Найдите ординату середины отрезка, соединяющего точки A(6; 8) и B(-2; 2).
Вектор с началом в точке A(2; 4) имеет координаты (6; 2). Найдите ординату точки B.
Через точку А(6; 8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью Oy.
Найдите расстояние от точки A с координатами (6; 8) до оси абсцисс.
Найдите расстояние от точки A с координатами (6; 8) до оси ординат.
Найдите ординату точки, симметричной точке A(6; 8) относительно оси Ox.
Найдите абсциссу точки, симметричной точке A(6; 8) относительно начала координат.
Найдите ординату точки, симметричной точке A(6; 8) относительно начала координат.
Найдите ординату середины отрезка, соединяющего точки O (0; 0) и A (6; 8).
Найдите ординату середины отрезка, соединяющего точки A(6; 8) и B(-2; 2).
Найдите ординату точки пересечения оси Oy и отрезка, соединяющего точки A(6; 8) и B(−6; 0).
Найдите угловой коэффициент прямой, проходящей через точки с координатами (2; 0) и (0; 2).
Прямая a проходит через точки с координатами (0; 4) и (6; 0). Прямая b проходит через точку с координатами (0; 8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox
Найдите ординату точки пересечения оси Oy и прямой, проходящей через точку B(6; 4) и параллельной прямой, проходящей через начало координат и точку A(6; 8).
Точки O(0; 0), B(6; 2), C(0; 6) и A являются вершинами параллелограмма. Найдите ординату точки A.
Точки O(0; 0), A(6; 8), C(0; 6) и B являются вершинами параллелограмма. Найдите ординату точки B.
Точки O(0; 0), A(6; 8), B(6; 2) и C являются вершинами параллелограмма. Найдите ординату точки C.
Точки O(0; 0), A(6; 8), B(6; 2), C(0; 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.
Всего: 119 1–20 | 21–40 | 41–60 | 61–80 …
Решение:
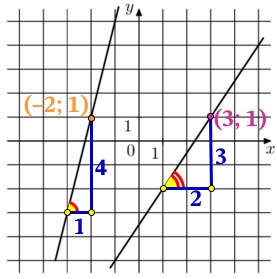
На рисунке изображены прямые, линейных функции их вид имеет вид:
y = kx + b
Найдём k и b функции справа.
k – тангенс угла наклона прямой, по отношению к оси х. Тангенс это отношение противолежащего катета, к прилежащему катету:
k=tg{color{Red}alpha}=frac{color{Blue} 3}{color{Blue} 2}=1,5
Подставим в общий вид функции значение k и координаты точки (3; 1) найдём b:
y = kx + b
1 = 1,5·3 + b
1 = 4,5 + b
1 – 4,5 = b
–3,5 = b
Функции справа имеет вид:
y = 1,5x – 3,5
Найдём k и b функции слева.
k=tg{color{Red}alpha}=frac{color{Blue} 4}{color{Blue} 1}=4
Подставим в общий вид функции значение k и координаты точки (–2; 1) найдём b:
y = kx + b
1 = 4·(–2) + b
1 = –8 + b
1 + 8 = b
9 = b
Функции слева имеет вид:
y = 4x + 9
В точке пересечения прямых значения функций (y) равны, найдём абсциссу (х) точки пересечения:
1,5x – 3,5 = 4x + 9
1,5x – 4x = 9 + 3,5
–2,5x = 12,5
x=frac{12,5}{–2,5}=-5
Подставим значение х = –5, в любое уравнение и найдём ординату (y) точки пересечения прямых:
y = 4·(–5) + 9 = –20 + 9 = –11
Ответ: –11.
В ЕГЭ 2022 года добавили новую задачу на графики функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, то вот определение самой формулы часто ставит школьников в тупик. Поэтому мы разберем три разных подхода к этому вопросу.
Замечание. Про то как определяется формула у прямой и параболы я написала в этой и этой статьях. Поэтому здесь в примерах я буду использовать другие функции – дробные, иррациональные, показательные и логарифмические, но все три описанных здесь способа работают и для линейных, и для квадратичных функций в том числе.
1 способ – находим формулу по точкам
Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.
Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:

Алгоритм:
1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому.
Пример:

2. Подставляем эти координаты в «полуфабрикат» функции. Вместо (f(x))– координату игрек, вместо (x) – икс. Получается система.

3. Решаем эту систему и получаем готовую формулу.

4. Готово, функция найдена, можно переходить ко второму этапу – вычислению (f(-8)). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.

Давайте посмотрим метод еще раз на примере с логарифмической функцией.
Пример:

2 способ – преобразование графиков функций
Этот способ сильно быстрее первого, но требует больше знаний. Для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют. Наиболее удобно использовать этот способ для иррациональной функции ((y=sqrt{x}) ) и функции обратной пропорциональности ((y=frac{1}{x})).
Вот как выглядит применение этого способа:

Для использования этого способа надо знать, как выглядят изначальные функции:

И понимать, как меняются функции от преобразований:




Часто даже по «полуфабрикату» функции понятно, какие преобразования сделали с функцией:

Пример:

3 способ – гибридный
Идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти. С другой стороны, независимо от оснований любая показательная функция должна проходить через точку ((0;1)), а любая логарифмическая – через точку ((1;0)).

По смещению этих точек легко понять, как именно двигали функцию, но только если ее не растягивали, а лишь перемещали вверх-вниз, влево-вправо (как обычно и бывает в задачах на ЕГЭ).
Основание же лучше находить уже следующим действием, используя подстановку координат точки в «полуфабрикат» функции.


Как отвечать на вопросы в задаче, когда уже определили функцию
– Если просят найти (f)(любое число), то нужно это число подставить в готовую функцию вместо икса.
Пример:

– Если просят найти «при каком значении x значение функции равно *любому числу*», то надо решить уравнение, в одной части которого будет функция, а в другой – то самое число. Аналогично надо поступить, если просят «найти корень уравнения (f(x)=) *любое число*».
Пример:

– Если просят найти абсциссу точки пересечения – надо приравнять 2 функции и решить получившееся уравнение. Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения (A)(*любое число*;*другое число*) и (B(x_0;y_0)) и просят найти (x_0).
Пример:

– Если просят найти ординату точки пересечения – надо приравнять 2 функции, найти иксы и подставить подходящий икс в любую функцию. Точно также решаем если просят найти (y_0) точки пересечения двух функций.
Пример:

– Иногда просят найти просто какой-либо из коэффициентов функции. Тогда надо просто восстановить функцию и записать в ответ то, о чем спросили:
Пример:

23
Сен 2022
Категория: 10 Графики функций
2022-09-23
2022-10-20
Задача 1. На рисунке изображены графики функций и
которые пересекаются в точках A и B. Найдите абсциссу точки B.
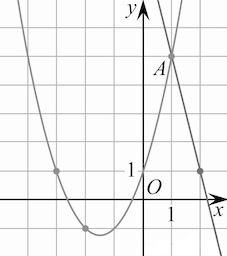
Решение: + показать
Задача 2. На рисунке изображены графики функций и
которые пересекаются в точках A и B. Найдите абсциссу точки B.

Решение: + показать
Задача 3. На рисунке изображены графики функций и
которые пересекаются в точке A. Найдите ординату точки A.

Решение: + показать

Пройти тест
Автор: egeMax |
Нет комментариев
Задачи ЕГЭ профиль
-
1. Планиметрия
-
1.1. Треугольники
-
1.2. Многоугольники
-
1.3. Окружности
-
-
2. Стереометрия
-
2.1. Многогранники
-
2.2. Тела вращения
-
2.3. Составные тела
-
-
3. Классическое определение вероятности
-
4. Теория вероятностей
-
4.1. Несовместные и независимые события
-
4.2. Условная и полная вероятность
-
-
5. Уравнения
-
5.1. Алгебраические уравнения
-
5.2. Рациональные уравнения
-
5.3. Иррациональные уравнения
-
5.4. Показательные уравнения
-
5.5. Логарифмические уравнения
-
5.6. Тригонометрические уравнения
-
-
6. Нахождение значений выражений
-
6.1. Рациональные выражения
-
6.2. Выражения со степенями
-
6.3. Иррациональные выражения
-
6.4. Логарифмические выражения
-
6.5. Тригонометрические выражения
-
-
7. Производная
-
7.1. Геометрический смысл производной
-
7.2. Физический смысл производной
-
7.3. Первообразная
-
-
8. Задачи прикладного содержания
-
8.1. Задачи с рациональными и иррациональными выражениями
-
8.2. Задачи с показательными и логарифмическими выражениями
-
8.3. Задачи с тригонометрическими выражениями
-
-
9. Текстовые задачи
-
9.1. Движение по прямой
-
9.2. Движение по окружности
-
9.3. Движение по воде
-
9.4. Работа
-
9.5. Смеси, сплавы
-
9.6. Проценты, прогрессии
-
-
10. Функции и графики
-
10.1. Прямые
-
10.2. Параболы
-
10.3. Гиперболы
-
10.4. Корни
-
10.5. Логарифмические функции
-
10.6. Показательные функции
-
10.7. Тригонометрические функции
-
10.8. Пересечения графиков
-
10.9. Модули
-
-
11. Исследование функций
-
11.1. Степенные функции
-
11.2. Дробно-рациональные функции
-
11.3. Логарифмические функции
-
11.4. Показательные функции
-
11.5. Тригонометрические функции
-
11.6. Исследование без производной
-
-
12. Сложные уравнения
-
12.1. Тригонометрические уравнения
-
12.2. Тригонометрические уравнения с учетом ОДЗ
-
12.3. Показательные уравнения
-
12.4. Смешанные уравнения
-
-
13. Стереометрия
-
14. Неравенства
-
15. Экономические задачи
-
16. Планиметрия
-
17. Параметры
-
18. Теория чисел
На рисунке изображены графики функций (f(x)=dfrac{k}{x}) и (g(x)=ax+b), которые пересекаются в точках A и B. Найдите ординату точки B.
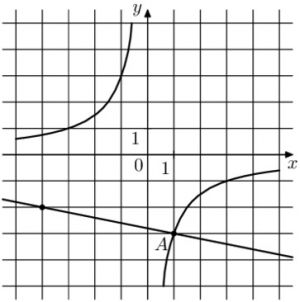
На рисунке изображены графики функций (f(x)=dfrac{k}{x}) и (g(x)=ax+b), которые пересекаются в точках A и B. Найдите ординату точки B.
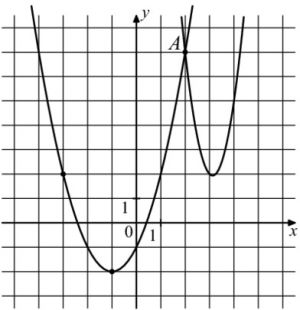
На рисунке изображены графики функций (f(x)=4x^2-25x+41) и (g(x)=ax^2+bx+c), которые пересекаются в точках A и B. Найдите абсциссу точки B.
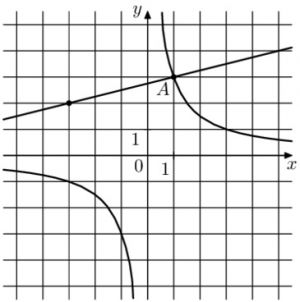
На рисунке изображены графики функций (f(x)=dfrac{k}{x}) и (g(x)=ax+b), которые пересекаются в точках A и B. Найдите абсциссу точки B.
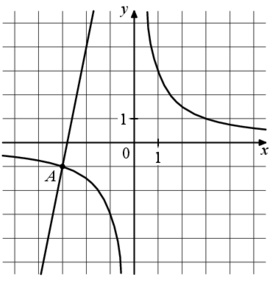
На рисунке изображены графики функций (f(x)=asqrt{x}) и (g(x)=kx+b), которые пересекаются в точке A. Найдите ординату точки A.
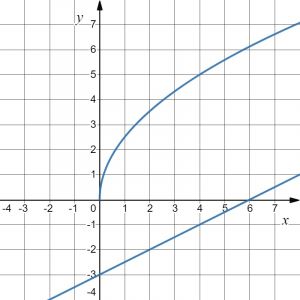
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
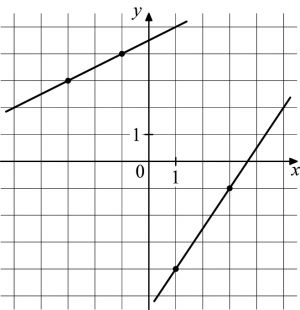
На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
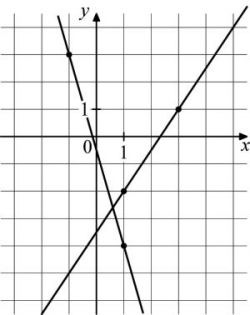
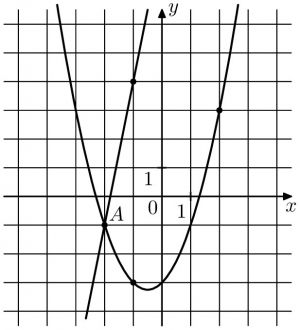
На рисунке изображены графики функций (f(x)=3x+3) и (g(x)=ax^2+bx+c), которые пересекаются в точках (A(-1;0)) и (B(x_0;y_0)). Найдите (y_0).
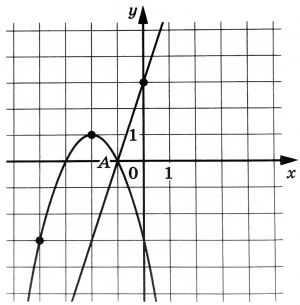
На рисунке изображены графики функций (f(x)=dfrac{k}{x}) и (g(x)=ax+b), которые пересекаются в точках (A(-2;-3)) и (B(x_0;y_0)). Найдите (x_0).
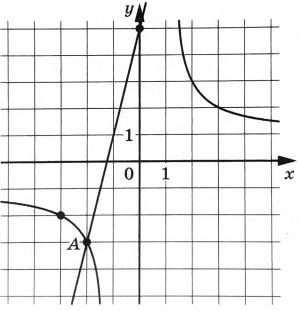
На рисунке изображены графики функций (fleft(xright)=5x+9) и (gleft(xright)=ax^2+bx+c), которые пересекаются в точках А и В. Найдите абсциссу точки В.