Как найти ординату точки вершины параллелограмма

Как найти ординату точки вершины параллелограмма


СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

1 мая

Новый сервис: можно исправить ошибки!

1 мая

Бесплатные курсы подготовки к ЕГЭ и ОГЭ

29 апреля

Разместили актуальные шкалы ЕГЭ  — 2023

24 апреля

Учителю: обновленный классный журнал

7 апреля

Новый сервис: ссылка, чтобы записаться к учителю

30 марта

Решения досрочных ЕГЭ по математике

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Задания

Версия для печати и копирования в MS Word

Задания Д5 № 27674

Точки O(0; 0), A(6; 8), B(6; 2) и C являются вершинами параллелограмма. Найдите ординату точки C.

Спрятать решение

Решение.

Так как у параллелограмма противоположные стороны попарно равны, то BA= корень из левая круглая скобка 6 минус 6 правая круглая скобка в квадрате плюс левая круглая скобка 8 минус 2 правая круглая скобка в квадрате =6, BA=OC=6. Известно, что C имеет координаты левая круглая скобка 0;y правая круглая скобка , следовательно,

OC= корень из левая круглая скобка 0 минус 0 правая круглая скобка в квадрате плюс левая круглая скобка y минус 0 правая круглая скобка в квадрате = корень из y в квадрате =6.

Поэтому y=6.

Ответ: 6.

Аналоги к заданию № 27674: 26405 Все

Спрятать решение

·

Помощь

О проекте · Редакция · Правовая информация · О рекламе

© Гущин Д. Д., 2011—2023

Источник
Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

  • Все категории
  • экономические
    43,651
  • гуманитарные
    33,653
  • юридические
    17,917
  • школьный раздел
    611,896
  • разное
    16,900

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Источник

Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?

В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.

Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.

Примеры.

1)

najti-koordinaty-vershiny-parallelogramma Дано: ABCD — параллелограмм,

A(-3;11), B(12;-4), C(1;-7)

Найти: D.

Решение:

najti-4-vershinu-parallelogramma1) Найдём координаты точки O — середины диагонали AC.

По формуле координат середины отрезка

    [x_O = frac{{x_A + x_C }}{2} = frac{{ - 3 + 1}}{2} = - 1;]

    [y_O = frac{{y_A + y_C }}{2} = frac{{11 + ( - 7)}}{2} = 2.]

То есть O(-1;2).

2) По свойству диагоналей параллелограмма, точка O также является серединой BD:

    [x_O = frac{{x_B + x_D }}{2}; - 1 = frac{{12 + x_D }}{2};x_D = - 14;]

    [y_O = frac{{y_B + y_D }}{2};2 = frac{{ - 4 + y_D }}{2};y_D = 8.]

Ответ: D (-14; 8).

2)

Дано: ABCD — параллелограмм,

B(7;4), C(-5;10), D(-1;-2)

Найти: A.

Решение:

1) Ищем координаты точки O — середины отрезка BD:

    [x_O = frac{{x_B + x_D }}{2};x_O = frac{{7 + ( - 1)}}{2} = 3;]

    [y_O = frac{{y_B + y_D }}{2};x_O = frac{{4 + ( - 2)}}{2} = 1.]

Итак, O (3;1).

2) Точка O также является серединой AC:

    [x_O = frac{{x_A + x_C }}{2};3 = frac{{x_A + ( - 5)}}{2};x_A = 11;]

    [y_O = frac{{y_A + y_C }}{2};1 = frac{{y_A + 10}}{2};y_A = - 8.]

Ответ: A (11;-8).

Источник

Условие

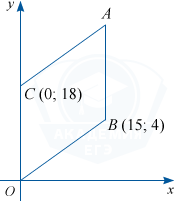
Точки O(0; 0), B(15; 4), C(0; 18) и A являются вершинами параллелограмма. Найдите ординату точки A.

Параллелограмм на координатной плоскости

Показать решение

Решение

Стороны параллелограмма CO и AB равны и параллельны оси ординат Oy. Значит, ординату точки A можно найти следующим образом: y_a=y_b+AB, при этом AB=OC=18, y_B=4.

Тогда y_A=4+18=22.

Ответ

22

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Лучшие онлайн-курсы для подготовки к ЕГЭ

Лучшие репетиторы для сдачи ЕГЭ

Лучшие репетиторы для сдачи ЕГЭ

Источник

A(2 ; 7 ; – 1)B( – 5 ; 3 ; – 5)C(1 ; – 3 ; 1) A)найдите координаты вершины D параллелограмма ABCD b)на оси ординат Найдите точку равноудаленную от точек B и C.

На этой странице находится вопрос A(2 ; 7 ; – 1)B( – 5 ; 3 ; – 5)C(1 ; – 3 ; 1) A)найдите координаты вершины D параллелограмма ABCD b)на оси ординат Найдите точку равноудаленную от точек B и C?. Здесь же – ответы на него,
и похожие вопросы в категории Геометрия, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 10 – 11 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.

Источник

Добавить комментарий