Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Как найти координаты точки
Поддержать сайт
Каждой точке координатной плоскости соответствуют две координаты.
Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.
Рассмотрим как в системе координат (на координатной плоскости):
- находить координаты точки;
- найти положение точки.
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.
Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».
Обозначают координаты точки, как указано выше (·) A (2; 3).
Пример (·) A (2; 3) и (·) B (3; 2).
Запомните!
На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.
Особые случаи расположения точек
- Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0). - Начало координат — точка O имеет координаты, равные нулю O (0,0).
- Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
- Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
- Координаты любой точки, лежащей на оси ординат имеют вид (0, y).
Как найти положение точки по её координатам
Найти точку в системе координат можно двумя способами.
Первый способ
Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:
- Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox». - Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy». - Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.
Второй способ
Чтобы найти точку D (−4 , 2) надо:
- Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−». - Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».
Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
было в ЕГЭ
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 119 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Найдите абсциссу точки, симметричной точке A(6; 8) относительно начала координат.
Найдите ординату середины отрезка, соединяющего точки O(0; 0) и A(6; 8).
Найдите ординату середины отрезка, соединяющего точки A(6; 8) и B(-2; 2).
Вектор с началом в точке A(2; 4) имеет координаты (6; 2). Найдите ординату точки B.
Через точку А(6; 8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью Oy.
Найдите расстояние от точки A с координатами (6; 8) до оси абсцисс.
Найдите расстояние от точки A с координатами (6; 8) до оси ординат.
Найдите ординату точки, симметричной точке A(6; 8) относительно оси Ox.
Найдите абсциссу точки, симметричной точке A(6; 8) относительно начала координат.
Найдите ординату точки, симметричной точке A(6; 8) относительно начала координат.
Найдите ординату середины отрезка, соединяющего точки O (0; 0) и A (6; 8).
Найдите ординату середины отрезка, соединяющего точки A(6; 8) и B(-2; 2).
Найдите ординату точки пересечения оси Oy и отрезка, соединяющего точки A(6; 8) и B(−6; 0).
Найдите угловой коэффициент прямой, проходящей через точки с координатами (2; 0) и (0; 2).
Прямая a проходит через точки с координатами (0; 4) и (6; 0). Прямая b проходит через точку с координатами (0; 8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox
Найдите ординату точки пересечения оси Oy и прямой, проходящей через точку B(6; 4) и параллельной прямой, проходящей через начало координат и точку A(6; 8).
Точки O(0; 0), B(6; 2), C(0; 6) и A являются вершинами параллелограмма. Найдите ординату точки A.
Точки O(0; 0), A(6; 8), C(0; 6) и B являются вершинами параллелограмма. Найдите ординату точки B.
Точки O(0; 0), A(6; 8), B(6; 2) и C являются вершинами параллелограмма. Найдите ординату точки C.
Точки O(0; 0), A(6; 8), B(6; 2), C(0; 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.
Всего: 119 1–20 | 21–40 | 41–60 | 61–80 …
Математика 5-6 класс
10 баллов
как найти абсциссу и ординату точки на координатной плоскости?
Влад Тихонов
15.07.2019 15:46:22
Чтобы найти абсциссу, нужно по оси x выбрать то число, которое указано в координатах на первом месте. Чтобы найти ординату, нужно по оси y выбрать то число, которое указано в координатах на втором месте.
Все предметы
Рейтинг пользователей

- Калькуляторы
- Справочник
- Словарь
Решение:
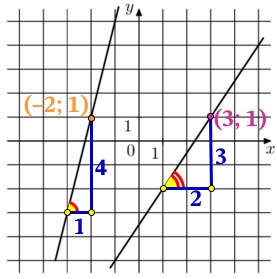
На рисунке изображены прямые, линейных функции их вид имеет вид:
y = kx + b
Найдём k и b функции справа.
k – тангенс угла наклона прямой, по отношению к оси х. Тангенс это отношение противолежащего катета, к прилежащему катету:
k=tg{color{Red}alpha}=frac{color{Blue} 3}{color{Blue} 2}=1,5
Подставим в общий вид функции значение k и координаты точки (3; 1) найдём b:
y = kx + b
1 = 1,5·3 + b
1 = 4,5 + b
1 – 4,5 = b
–3,5 = b
Функции справа имеет вид:
y = 1,5x – 3,5
Найдём k и b функции слева.
k=tg{color{Red}alpha}=frac{color{Blue} 4}{color{Blue} 1}=4
Подставим в общий вид функции значение k и координаты точки (–2; 1) найдём b:
y = kx + b
1 = 4·(–2) + b
1 = –8 + b
1 + 8 = b
9 = b
Функции слева имеет вид:
y = 4x + 9
В точке пересечения прямых значения функций (y) равны, найдём абсциссу (х) точки пересечения:
1,5x – 3,5 = 4x + 9
1,5x – 4x = 9 + 3,5
–2,5x = 12,5
x=frac{12,5}{–2,5}=-5
Подставим значение х = –5, в любое уравнение и найдём ординату (y) точки пересечения прямых:
y = 4·(–5) + 9 = –20 + 9 = –11
Ответ: –11.
Сегодня, просматривая различные задания в сборнике под ред. Ф.Ф. Лысенко, наткнулась на интересное и простое задание №9. Здесь мы уже привыкли видеть различные уравнения (линейные или квадратные). В этот раз задание звучало немного нестандартно 🧐 Само задание простое, но не будет лишним повторить некоторые моменты.
ЗАДАНИЕ №9 (сборник “40 вариантов ОГЭ 2022 математика” под ред. Ф.Ф. Лысенко)
Две прямые пересекаются в точке А. Найдите ординату точки А.
ВСПОМИНАЕМ:
1) Ордината точки – это значение координаты “y”
2) Пересечение графиков алгебраически записывается системой уравнений. Решение системы это значение координат точки пересечения.
Записываем систему из двух уравнений и решаем методом сложения:
Нашли значение абсциссы (“x”) точки А. Теперь найдем “y”
ОТВЕТ: -3
Единственное, что может сбить с решения этого задания, сама формулировка. Т.к. зачастую ученики готовятся к решению явно заданных уравнений или систем уравнений. А волнение накладывает свой отпечаток 😬
Продолжение следует…