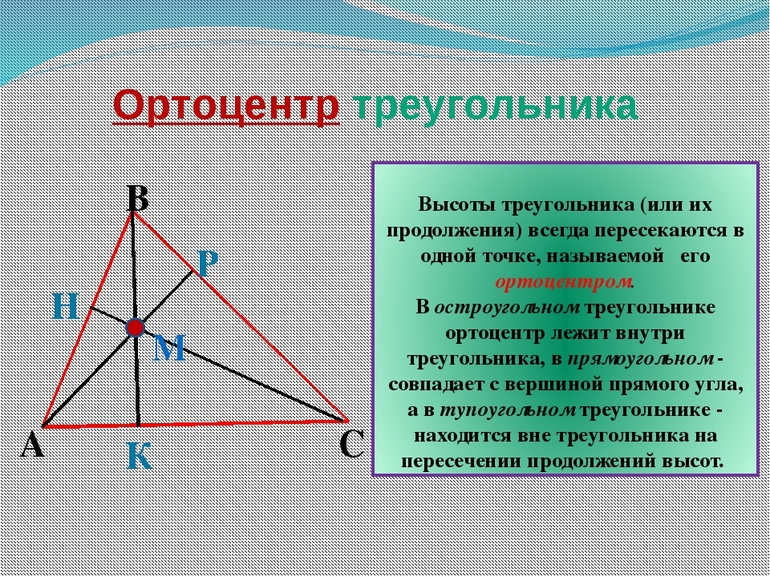
Как найти ортоцентр в треугольнике - Сайт, где вы сможете решить свои вопросы

A simple polygon having three sides and three vertices are called a triangle. The intersection point of the three altitudes of a triangle is called the “orthocenter of a triangle,” and it is generally represented by the letter “H.” An altitude of a triangle is a line segment drawn from each vertex to the opposite side that is perpendicular to its opposite side. As a triangle has three vertices and three sides, it has three altitudes, and the point of intersection of these three sides is called the orthocenter.

For every triangle, the position of the orthocenter varies; i.e; for an equilateral triangle, the orthocenter, circumcenter, incenter, and centroid are the same, but in the case of the other triangles,, the position will be different.

In the case of an acute-angled triangle, the orthocenter lies inside the triangle.
In the case of an obtuse-angled triangle, the orthocenter lies outside the triangle.
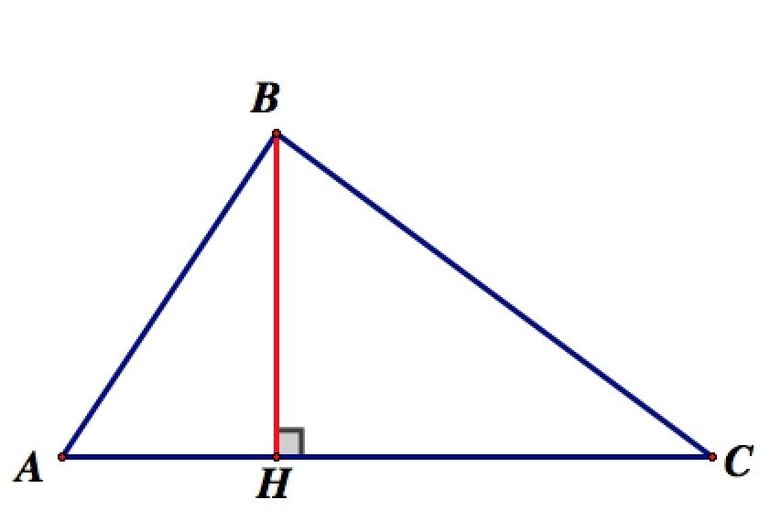
In the case of a right-angled triangle, the orthocenter lies on the vertex of the right angle.

Determining the orthocenter of a triangle

Let’s consider a triangle ABC to determine the orthocenter of a triangle. AD, BE, and CF are the perpendiculars drawn from the vertices A (x₁, y₁), B (x₂, y₂), and C (x₃, y₃) to their respective opposite sides BC, AC, and AB and “H” is the point of their intersection.

Step 1: Calculate the slopes of the sides of the triangle ABC using the slope formula;

m = (y₂ – y₁)/(x₂ – x₁)

Let the slope of the AB be m_AB.

m_AB = (y₂ – y₁)/(x₂ – x₁)

Let the slope of the BC be m_BC

So, m_BC = (y₃ – y₂)/(x₃ – x₂)

Step 2: Using the slopes of the sides of a triangle, find the slopes of altitudes.

We know that the altitude is perpendicular to the side.

Product of slopes of two perpendicular slopes lines = m₁× m₂ = -1

So, the slope of the altitude = -1/slope of the side = -1/m

Now, the slopes of the respective altitudes CF and AD are,

m_CF = -1/m_AB

m_AD = -1/m_BC

Step 4: With the help of the point-slope form equation, find the equations of the altitudes using the slopes and the coordinates of the opposite vertices.

The equation of CF is (y – y₃) = m_CF(x – x₃)

The equation of AD is (y – y₁) = m_AD(x – x₁)

Step 4: Solve the equations of any two altitudes and the values of x and y obtained by solving both equations are the coordinates of the orthocenter of the triangle.

Sample Problems

Problem 1: Determine the coordinates of the orthocenter of a triangle whose vertices are A (3, 1), B (-5, 2), and C (0, 4).

Solution:

Given,

The vertices of a triangle are A (x₁, y₁) = (3,1), B (x₂, y₂) = (-5,2) and C (x₃, y₃) = (0,4)

Now, the slope of the side AB = (y₂ – y₁)/(x₂ – x₁)

⇒ m_AB = (2 – 1)/(-5 -3) = -(1/8)

The slope of the line perpendicular to AB i.e., slope of CF = -(1/slope of AB) = 8

So, the equation of the line CF with point C (0,4) and slope = 8 is y – y₃ = m(x – x₃) [point-slope form]

⇒ y – 4 = 8 (x – 0)

⇒ y – 4 = 8x

⇒ 8x – y = -4 ⇢ (1)

Slope of the side BC = (y₃ – y₂)/(x₃ – x₂)

⇒ m_BC = (4 – 2)/(0 – (-5)) = 2/5

Now, the slope of the line perpendicular to BC i.e., the slope of AD = -(1/slope of BC) = -(5/2)

So, the equation of the line AD with point A (3,1) and slope = -(5/2) is y – y₁ = m(x – x₁) [point slope form]

⇒ y – 1 = -(5/2) (x – 3)

⇒ 2(y – 1) = -5(x – 3)

⇒ 2y – 2 = -5x + 15

⇒ 5x + 2y = 17 ⇢ (2)

Now, multiply the equation (1) with “2” on both sides and add both equations (1) and (2).

16x – 2y = -8

5x + 2y = 17

21x = 9 ⇒ x = 3/7

Now, substitute the value of x = 3/7 in equation (1)

⇒ 8(3/7) – y = -4

⇒ y = 24/7 + 4 = 52/7

Hence, the coordinates of the orthocenter (H) are (3/7, 52/7).

Problem 2: Determine the coordinates of the orthocenter of a triangle whose vertices are A (5, -3), B (7, 0), and C (4, 9).

Solution:

Given,

The vertices of a triangle are A (x₁, y₁) = (5, -3), B (x₂, y₂) = (7, 0) and C (x_3, y₃) = (4, 9).

Now, the slope of the side AB = (y₂ – y₁)/(x₂ – x₁)

⇒ m_AB = (0 – (-3))/(7 – 5) = 3/2

The slope of the line perpendicular to AB i.e., slope of CF = -(1/slope of AB) = -(2/3)

So, the equation of the line CF with point C (4, 9) and slope = -(2/3) is y – y₃= m(x – x₃) [point-slope form]

⇒ y – 9 = -(2/3) (x – 4)

⇒ 3(y – 9) = -2(x – 4)

⇒ 3y – 27 = -2x + 8

⇒ 2x + 3y = 35 ⇢ (1)

Slope of the side BC = (y₃ – y₂)/(x₃ – x₂)

⇒ m_BC = (9 – 0)/(4 – 7) = -(9/3) = -3

Now, the slope of the line perpendicular to BC i.e., the slope of AD = -(1/slope of BC) = 1/3

So, the equation of the line AD with point A (5, -3) and slope = 1/3 is y – y₁ = m(x – x₁) [point slope form]

⇒ y – (-3) = (1/3) (x – 5)

⇒ 3(y + 3) = x – 5

⇒ 3y + 9 = x – 5

⇒ x – 3y = 14 ⇢ (2)

Now, add equations (1) and (2)

2x + 3y = 35

x – 3y = 14

3x = 49 ⇒ x =49/3

Now, substitute the value of x = 49/3 in equation (2)

⇒ 49/3 – 3y = 14 ⇒ 3y = -1

⇒ y =7/9

Hence, the coordinates of the orthocenter (H) are (49/3, 7/9).

Problem 3: Find the orthocenter of a triangle whose vertices are A (2, -7), B (6, 3), and C (-8, 0).

Solution:

Given,

The vertices of a triangle are A (x₁, y₁) = (5, -3), B (x₂, y₂) = (7, 0) and C (x₃, y₃) = (4, 9)

Now, the slope of the side AB = (y₂ – y₁)/(x₂ – x₁)

⇒ m_AB = (3 – (-7))/(6 – 2) = 10/4 = 5/2

The slope of the line perpendicular to AB i.e., slope of CF = -(1/slope of AB) = -(2/5)

So, the equation of the line CF with point C (-8, 0) and slope = -(2/5) is y – y₃= m(x – x₃) [point-slope form]

⇒ y – 0 = -(2/5) (x – (-8))

⇒ 5y = -2(x + 8)

⇒ 5y = -2x -16

⇒ 2x + 5y = -16 ⇢ (1)

Slope of the side AC = (y₃ – y₁)/(x₃ – x₁)

⇒ m_AC = (0 – (-7))/(-8 – 2) = -(7/10)

Now, the slope of the line perpendicular to AC i.e., the slope of BE = -(1/slope of AC) = 10/7

So, the equation of the line BE with point B (6, 3) and slope = 10/7 is y – y₂ = m(x – x₂) [point slope form]

⇒ y – 3 = (10/7) (x – 6)

⇒ 7(y – 3) = 10(x – 6)

⇒ 7y – 21 = 10x – 60

⇒ 10x – 7y = 39 ⇢ (2)

Multiply equation (1) with “5” on both sides and subtract both equations.

10x + 25y = -80

10x – 7y = 39

(-) (+) (-)

——————

32y = -119 ⇒ y = – 119/32

Now, substitute the value of y = -119/32 in equation (1)

2x + 5(-119/32) = -16

⇒ 2x – 595/32 = -16 ⇒ 2x = 595/32 – 16

⇒ 2x = 83/32 ⇒ x = 83/64

Hence, the coordinates of the orthocenter (H) are (83/64, -119/32).

Problem 4: Find the orthocenter of a triangle whose vertices are A (6, 2), B (1, 1), and C (-4, 7).

Given,

The vertices of a triangle are A (x₁, y₁) = (6, 2), B (x₂, y₂) = (1, 1) and C (x₃, y₃) = (-4, 7).

Now, the slope of the side AC = (y₃ – y₁)/(x₃– x₁)

⇒ m_AC = (7 – 2)/(-4 – 6) = -(5/10) = -1/2

The slope of the line perpendicular to AC i.e., slope of BE = -(1/slope of AC) = 2

So, the equation of the line BE with point B (1,1) and slope = 2 is y – y₂ = m(x – x₂) [point-slope form]

⇒ y – 1 = 2(x – 1)

⇒ y – 1 = 2x – 2

⇒ 2x – y = 1 ⇢ (1)

Slope of the side BC = (y₃ – y₂)/(x₃ – x₂)

⇒ m_BC =(7 – 1)/(-4 – 1) = -(6/5)

Now, the slope of the line perpendicular to BC i.e., the slope of AD = -(1/slope of BC) = 5/6

So, the equation of the line BE with point A (6, 2) and slope = 10/7 is y – y₁ = m(x – x₁) [point slope form]

⇒ y – 2 = (5/6) (x – 6)

⇒ 6(y – 2) = 5(x – 6)

⇒ 6y – 12 = 5x – 30

⇒ 5x – 6y = 18 ⇢ (2)

Now, multiply equation (1) with “6” on both sides and subtract both equations.

12x – 6y = 6

5x – 6y = 18

(-) (+) (-)

——————

7x = -12 ⇒ x = -12/7

Now, substitute the value of x = -12/7 in equation (1)

2(-12/7) – y = 1

⇒ y = -24/7 – 1 ⇒ y = -31/7

Hence, the coordinates of the orthocenter (H) are (-12/7, -31/7).

Problem 5: Determine the coordinates of the orthocenter of a triangle whose vertices are A (0,-5), B (3,-2), and C (-6, 0).

Given,

The vertices of a triangle are A (x₁, y₁) = (3,1), B (x₂, y₂) = (-5,2) and C (x₃, y₃) = (0,4)

Slope of the side BC = (y₃– y₂)/(x₃ – x₂)

⇒ m_BC =(0 – (-2))/(-6 – 3) = -(2/9)

Now, the slope of the line perpendicular to BC i.e., the slope of AD = -(1/slope of BC) = (9/2)

So, the equation of the line AD with point A (3,1) and slope = (9/2) is y – y₁ = m(x – x₁) [point slope form]

⇒ y – (-5) = (9/2) (x – 0)

⇒ 2(y + 5) = 9x

⇒ 2y + 10 = 9x

⇒ 9x – 2y = 10 ⇢ (1)

Now, the slope of the side AB = (y₂ – y₁)/(x₂ – x₁)

⇒ m_AB = (-2 – (-5))/(3 – 0) = 3/3 = 1

The slope of the line perpendicular to AB i.e., slope of CF = -(1/slope of AB) = -1

So, the equation of the line CF with point C (-6, 0) and slope = -1 is y – y₃ = m(x – x₃) [point-slope form]

⇒ y – 0 = (-1)(x – (-6))

⇒ y = -(x + 6)

⇒ y = -x – 6

⇒ x + y = -6 ⇢ (2)

Now, multiply equation (2) with “2” on both sides and add both equations.

9x – 2y = 10

2x + 2y = -12

11x = -2 ⇒ x = -2/11

Now, substitute the value of x = -2/11 in equation (2)

⇒ -2/11 + y = -6

⇒ y = -6 + 2/11 ⇒ y = -64/11

Now, by solving the equations of the lines AD and CF we get the coordinates of the orthocenter (H) are (-2/11, -64/11).

Источник

Точка пересечения высот треугольника – свойства, координаты и расположение ортоцентра

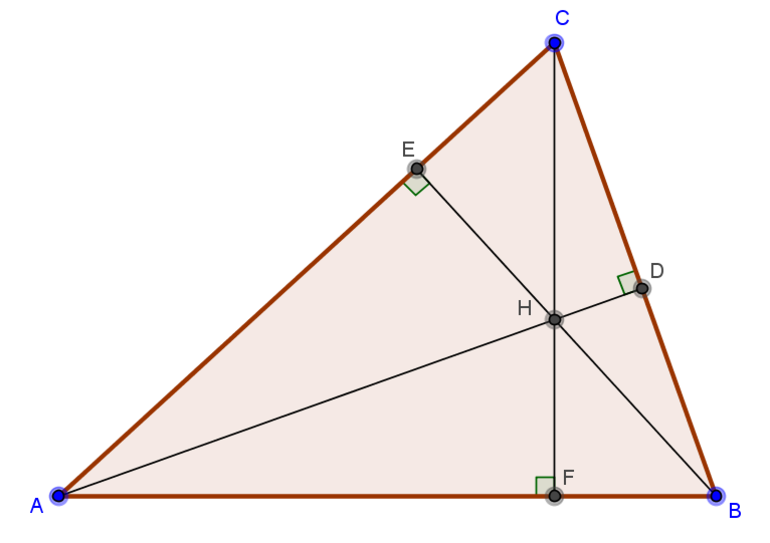
Что такое высота

Если из вершины опустить перпендикуляр на противоположную сторону, получится отрезок, который именуется высотой. В равнобедренном треугольнике 2 отрезка равны, а в равностороннем равны все 3.

У фигур с углами 90 и более градусов высота попадает на противоположную сторону. В случае острого угла дело обстоит иначе. Прямая попадет только на продолжение противоположной стороны и будет находиться вне самой фигуры. Таким образом, если все углы острые, отрезки будут находиться внутри, как и ортоцентр. В тупоугольной фигуре два из трех отрезков будут проходить за его пределами — ортоцентр окажется вне фигуры.

Свойства ортоцентра

Свойства высот треугольника, пересекающихся в одной точке, давно изучены и описаны. Согласно основному из них, все 3 высоты всегда пересекаются в одном месте. Иногда, чтобы найти это место, отрезки нужно продлить, превратив в ортогональные прямые.

Ортоцентр по отношению к фигуре может быть расположен:

внутри;
снаружи;
в вершине (у прямоугольных треугольников)

Ортоцентр — важная в геометрии характеристика, влияющая на нахождение золотого сечения.

Так называется маленький треугольник, расположенный внутри основного, находящийся на пересечении его трех параметров:

Золотое сечение может представлять собой не только треугольную фигуру, но и отрезок. В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку.

Полезные факты

Местонахождение ортоцентра имеет некоторые закономерности. Их знание принесет пользу при решении задач.

Пусть:

H — ортоцентр в ABC;
О — центр описанной окружности.

Тогда:

окружности, описанные вокруг АБС, АНВ, CHB, HCA, равны:
отрезок BH вдвое длиннее отрезка АС;
середины отрезков AC и BH разделены расстоянием, равным радиусу описанной окружности.

Задача Фаньяно

Это классическая теорема. Она возникла в процессе поиска фигур с наименьшим периметром. Теорему доказал Фаньяно — итальянский математик и инженер. Это произошло еще в начале XVIII века.

Формулировка: ортотреугольник, то есть фигура, полученная соединением трех оснований треугольника, проведенный внутри остроугольного треугольника, имеет самый маленький периметр изо всех возможных, вписанных в данную фигуру.

Площадь ортотреугольника рассчитывается по формуле:

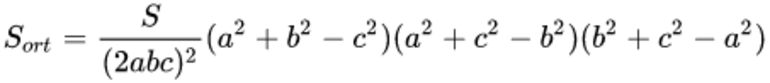
Здесь S — площадь, а, b, c — стороны.

Существует понятие ортоцентрической системы. Оно включает в себя 3 вершины и место пересечения их высот. Любая из данных четырех точек будет являться ортоцентром треугольника, образованного тремя остальными.

История изучения

Важное значение имеет место пересечения медиан или центр тяжести. Вместе с ортоцентром это еще одна «замечательная точка», которая была известна еще древним грекам. Так их стали называть начиная с 18 века, другое название «особенные».

Исследование этих точек стало началом для создания геометрии треугольника, основателем которой считается Леонард Эйлер. Ученый показал, что в любом треугольнике точки соединения высот, медиан и центр описанного круга находятся на одной линии, которую позже назвали прямой Эйлера.

В позапрошлом веке была обнаружена окружность 9 точек или Фейербаха. Она состоит из оснований медиан, высот и центров высот. Оказалось, что все эти точки лежат на общей окружности, центр которой находится на линии Эйлера.

Каждый отрезок, прочерченный из ортоцентра до соединения с описанной окружностью, всегда будет делиться линией Эйлера на 2 равные части.

Треугольник — удивительная фигура, изучением которой занимается целый раздел геометрии. Ортоцентр и его свойства имеют широкое применение в практической жизни, например, в строительстве. Этот показатель настолько важен и распространен, что существуют калькуляторы, позволяющие определить местонахождение точки по координатам вершин.

Ортоцентр.

Ортоцентр — точка пересечения прямых, содержащих высоты треугольника.

Ортоцентр остроугольного треугольника лежит внутри треугольника.

Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.

Ортоцентр тупоугольного треугольника лежит вне треугольника.

Свойства:

Точка, симметричная ортоцентру относительно стороны треугольника, лежит на описанной около него окружности.
Точка, симметричная ортоцентру относительно середины стороны треугольника, лежит на описанной окружности и диаметрально противоположна вершине треугольника, противолежащей стороне.
Расстояние от вершины треугольника до ортоцентра в два раза больше расстояния от центра описанной окружности до противолежащей стороны.
Сумма квадратов расстояния от вершины треугольника до ортоцентра и длины стороны, противолежащей этой вершине, равна квадрату диаметра описанной окружности.
Радиус описанной окружности, проведенный к вершине треугольника, перпендикулярен соответствующей стороне ортотреугольника.
При изогональном сопряжении ортоцентр переходит в центр описанной окружности.
Ортоцентр в остроугольном треугольнике является инцентром ортотреугольника.
Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих равные радиусы описанных окружностей. При этом одинаковый радиус этих трех окружностей равен радиусу окружности, описанной около исходного остроугольного треугольника.

Свойства высот треугольника. Ортоцентр

Схема 1. В треугольнике АВС проведены высоты АМ и СК.
Н – точка пересечения высот треугольника (ортоцентр), Н=АМ∩СК

Запомните этот рисунок. Перед вами – схема, из которой можно получить сразу несколько полезных фактов.

1. Треугольники МВК и △АВС, подобны, причем коэффициент подобия
, если , и , если

Четырехугольник АКМС можно вписать в окружность. Эта вспомогательная окружность поможет решить множество задач.
Четырехугольник ВКМН также можно вписать в окружность.
Радиусы окружностей, описанных вокруг треугольников АВС, АНС, ВНС и АВН, равны.
,где R – радиус описанной окружности .

Докажем эти факты по порядку.

1) Заметим, что на рисунке есть подобные треугольники. Это АВМ и СВК, прямоугольные треугольники с общим углом В, и они подобны по двум углам

Мы получили, что в треугольниках МВК и АВС стороны, прилежащие к углу В, пропорциональны. Получаем, что по углу и двум сторонам.

2) Докажем, что вокруг четырехугольника АКМС можно описать окружность. Для этого необходимо и достаточно, чтобы суммы противоположных углов четырехугольника АКМС были равны .

Пусть ∠ACB=∠BKM=γ (поскольку треугольники МВК и АВС подобны), тогда
– как смежный с углом ВКМ. Получили, что , и это значит, что четырехугольник AKMC можно вписать в окружность.

3) Рассмотрим четырехугольник KBMH. Его противоположные углы ВКН и ВМН – прямые, их сумма равна , и значит, четырехугольник КВМН можно вписать в окружность.

4) По теореме синусов, радиус окружности, описанной вокруг треугольника АВС,

Радиус окружности, описанной вокруг треугольника АНС,
Мы помним, что . Значит, синусы углов АВС и АНС равны, и радиусы окружностей, описанных вокруг треугольников АВС и АНС равны.

5) Докажем, что ,где R – радиус описанной окружности . Поскольку четырехугольник КВМН можно вписать в окружность и углы ВКН и ВМН – прямые, отрезок ВН является диаметром этой окружности. Треугольник МВК также вписан в эту окружность, и по теореме синусов, .

Диаметр окружности, описанной вокруг треугольника АВС, равен Поскольку треугольники МВК и АВС подобны, отношение диаметров описанных вокруг них окружностей равно . Получили, что

Задача ЕГЭ по теме «Высоты треугольника» (Профильный уровень, №16)

2. В остроугольном треугольнике KMN проведены высоты KB и NA.

а) Докажите, что угол ABK равен углу ANK.

б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и

а) Докажем, что
(по двум углам). Запишем отношение сходственных сторон:
Но это значит, что (по углу и двум сторонам), причем .

– смежный с углом ,
,
,четырехугольник ABNK можно вписать в окружность.
(опираются на одну дугу).

[spoiler title=”источники:”]

http://anasta8ia.ru/ortocentr/

http://ege-study.ru/materialy-ege/svojstva-vysot-treugolnika-ortocentr/

[/spoiler]

Источник

Ортоцентр
Высоты и ортоцентр
Барицентрические координаты
Трилинейные координаты	${displaystyle {frac {1}{cos A}}:{frac {1}{cos B}}:{frac {1}{cos C}}}$
Код ЭЦТ	X(4)
Связанные точки
Изогонально сопряженная	центр описанной окружности
Дополнительная^[es]	центр описанной окружности
Антидополнительная^[es]	точка де Лоншама^[en]

Ортоцентр (от др.-греч. ὀρθός «прямой») — точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой . В зависимости от вида треугольника ортоцентр может находиться внутри треугольника (в остроугольном), вне его (в тупоугольном) или совпадать с вершиной (в прямоугольном — совпадает с вершиной при прямом угле). Ортоцентр относится к замечательным точкам треугольника и перечислен в энциклопедии центров треугольника Кларка Кимберлинга как точка X(4).

Свойства[править | править код]

Если в четвёрке точек , , , точка является точкой пересечения высот треугольника , то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четвёрку иногда называют ортоцентрической системой точек (см. рис.).
- Более того, при любом разбиении множества ортоцентрической системы точек на две пары, например, и или при любом другом подобном разбиении, всегда перпендикулярны образующиеся два отрезка прямых с концами в данных точках множеств (в нашем случае перпендикулярно ) независимо от выбора этих двух пар
- Радиусы окружностей, проходящих через любые три точки ортоцентрической системы, равны (следствие теоремы Гамильтона для окружности Эйлера). Их часто называют окружностями Джонсона.
- Последнее утверждение можно сформулировать так: Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих равные радиусы описанных окружностей (следствие теоремы Гамильтона для окружности Эйлера). При этом одинаковый радиус этих трех окружностей равен радиусу окружности, описанной около исходного остроугольного треугольника.

Точки, симметричные ортоцентру относительно сторон, лежат на описанной окружности.

Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника.
Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности (см. рисунок)^[1].
Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
Если — центр описанной окружности , то .
При изогональном сопряжении ортоцентр переходит в центр описанной окружности.
Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью, всегда делится окружностью Эйлера пополам. Это следует из того, что ортоцентр есть центр гомотетии этих двух окружностей с коэффициентом .
Четыре попарно пересекающиеся прямые, никакие три из которых не проходят через одну точку (четырёхсторонник), при пересечении образуют четыре треугольника. Их ортоцентры лежат на одной прямой (на прямой Обера).
Если считать, что ортоцентр треугольника делит первую высоту на части длиной и , вторую высоту на части длиной и , третью высоту на части длиной и , тогда ^[4]^[5].
Цепочка уравнений в последнем пункте: по сути означает, что три пары отрезков, на которые ортоцентр разделяет три высоты остроугольного треугольника, подчиняются правилу хорд, пересекающихся внутри окружности, например: . Отсюда автоматически следует то, что через четыре конца любых двух высот остроугольного треугольника всегда можно провести окружность (высоты в ней будут пересекающимися хордами). Оказывается, это утверждение сохраняет силу и для тупоугольного, и прямоугольного треугольников.
Расстояние от стороны до центра описанной окружности равно половине расстояния от противоположной ей вершины до ортоцентра^[6]^[7].
Сумма квадратов расстояний от вершин до ортоцентра плюс сумма квадратов сторон равна двенадцати квадратам радиуса описанной окружности^[8].
Три основания высот остроугольного треугольника или три проекции ортоцентра на стороны треугольника образуют ортотреугольник.

Ортоцентрическая ось (Orthic axis) — трилинейная поляра ортоцентра

Трилинейной полярой ортоцентра является ортоцентрическая ось (Orthic axis) (см. рис.)

Четыре ортоцентра четырёх треугольников, образованных четырьмя попарно пересекающимися прямыми, никакие три из которых не проходят через одну точку, лежат на одной прямой (Прямая Обера четырёхугольника). Здесь используются те же четыре треугольника, что и при построении точки Микеля.

Существует формула Карно^[9]:

${displaystyle R+r=k_{a}+k_{b}+k_{c}={frac {1}{2}}(d_{A}+d_{B}+d_{C})}$ ,

где ${displaystyle k_{a}}$

, ${displaystyle k_{b}}$

, ${displaystyle k_{c}}$

— расстояния от центра описанной окружности соответственно до сторон

треугольника, $d_{A}$

, $d_{B}$

, ${displaystyle d_{C}}$

— расстояния от ортоцентра соответственно до вершин

треугольника.

В ортоцентрической системе 4 точек любая точка является ортоцентром треугольника, образованного 3 остальными точками.

Ортоцентрическая система. Здесь O₁, O₂, O₃ и O₄ — центры окружностей четырех возможных треугольников, образованных из ортоцентрических точек A₁, A₂, A₃ и A₄ (см. рис.). Три из них вершины исходного треугольника, а четвертая — его ортоцентр. Радиусы всех четырех окружностей равны. Центры трех из четырех окружностей (кроме описанной исходного треугольника) образуют вершины треугольника, равного исходному, со сторонами, попарно параллельными сторонам исходного треугольника.

Ортоцентрическая система. Здесь O₁, O₂, O₃ и O₄ — центры окружностей четырех возможных треугольников, образованных из ортоцентрических точек A₁, A₂, A₃ и A₄.

*Если прямая ℓ ортополюса P проходит через ортоцентр Q треугольника, то точка, расположенная на продолжении отрезка PQ, соединяющего ортополюс с ортоцентром, по другую сторону на расстоянии, равном PQ, лежит на окружности Эйлера этого треугольника.^[10]

История[править | править код]

Утверждение: «Все 3 высоты треугольника пересекаются в одной точке», называемой теперь ортоцентром, в «Началах» Евклида отсутствует. Ортоцентр впервые в греческой математике использован в «Книге лемм» Архимеда, хотя явного доказательства существования ортоцентра Архимед не привёл.

Часть историков приписывает это утверждение Архимеду и называют его теоремой Архимеда^[11]. До середины девятнадцатого века, ортоцентр нередко называли архимедовой точкой^[12].

В явном виде это утверждение («Все 3 высоты треугольника пересекаются в одной точке») встречается у Прокла (410—485) — комментатора Евклида^[13].

Другие историки математики считают автором первого доказательства Уильяма Чеппла (англ.) (рус. (Miscellanea Curiosa Mathematica, 1749 год)^[14].

Термин ортоцентр впервые был использован У. Х. Безантом (англ.) (рус. в работе «Конические сечения, исследованные геометрически (1869)» (^[15])^[16].

См. также[править | править код]

Высота треугольника
Высота (геометрия)
Замечательные точки треугольника
Центр вписанной окружности
Ортотреугольник
Ортоцентроидная окружность
Центроид

Примечания[править | править код]

↑ Honsberger, 1995, p. 18.
↑ Marie-Nicole Gras, «Distances between the circumcenter of the extouch triangle and the classical centers»,
Forum Geometricorum 14 (2014), 51-61. http://forumgeom.fau.edu/FG2014volume14/FG201405index.html Архивная копия от 28 апреля 2021 на Wayback Machine
↑ Smith, Geoff, and Leversha, Gerry, «Euler and triangle geometry», Mathematical Gazette 91, November 2007, 436—452.
↑ Altshiller-Court, 2007, p. 94.
↑ Honsberger, 1995, p. 20.
↑ Altshiller-Court, 2007, p. 99.
↑ Honsberger, 1995, p. 17, 23.
↑ Altshiller-Court, 2007, p. 102.
↑ Зетель С. И. Новая геометрия треугольника. Пособие для учителей. — 2-е изд. — М.: Учпедгиз, 1962. — С. 120—125 (задача), параграф 57, с. 73.
↑ College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle. Nathan Altshiller-Court. (Параграф: G. The Orthopole. Пункт. 699. Теорема. Fig. 156. С.290-291). Mineola, New York: Dover Publication, Inc., 2012. 292 p.
↑ Ефремов Д. Новая геометрия треугольника. Одесса, 1902. С. 9, п. 16. Высоты треугольника. Теорема Архимеда.
↑ Maureen T. Carroll, Elyn Rykken. Geometry: The Line and the Circle. Дата обращения: 10 апреля 2020.
↑ Nathan Altshiller-Court. «College Geometry. An Introduction to the Modern Geometry of the Triangle and the Circle». Second Edition. Mineola, New York: Dover Publications, Inc. 2007. P. 298, § 175.
↑ Bogomolny, Alexander, A Possibly First Proof of the Concurrence of Altitudes, <https://www.cut-the-knot.org/triangle/Chapple.shtml>. Проверено 17 ноября 2019. Архивная копия от 7 мая 2021 на Wayback Machine
↑ Conic Sections Treated Geometrically, 1869. Ссылка: 1895: Conic sections treated geometrically Архивная копия от 18 апреля 2018 на Wayback Machine from Cornell University Historical Math Monographs.
↑ Nathan Altshiller-Court. «College Geometry. An Introduction to the Modern Geometry of the Triangle and the Circle». Second Edition. Mineola, New York: Dover Publications, Inc. 2007. § 176, p. 94; § 176, p. 298

Литература[править | править код]

Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 37—39. — ISBN 5-94057-170-0.
Nathan Altshiller-Court. College geometry : an introduction to the modern geometry of the triangle and the circle. — Dover Publications, Inc., 2007. — ISBN 0-486-45805-9.
Ross Honsberger. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. — Mathematical Association of America, 1995. — Vol. 37. — P. 17—26. — (New Mathematical Library). — ISBN 0-88385-639-5 (Vol. 37). — ISBN 0-88385-600-X (complete set).

Ссылки[править | править код]

Живой чертёж
Weisstein, Eric W. Orthocenter (англ.) на сайте Wolfram MathWorld.
Bernard Gibert Circumcubic K006 (недоступная ссылка)
Clark Kimberling, «Encyclopedia of triangle centers».
Weisstein, Eric W. «Orthocentric System.» From MathWorld–A Wolfram Web Resource. [1]

Источник

Чтобы найти ортоцентр треугольника, можно воспользоваться калькулятором, где следует внести координаты. В автоматическом режиме с помощью формул произведется расчет. Можно также все расчеты произвести самостоятельно.

Например, имеются следующие данные точек:
А – 4,3;
В – 0,5;
С – 3,-6.

Первое , что необходимо найти наклон сторон, который обозначается – m , используется формула :

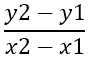
Из этого следует:

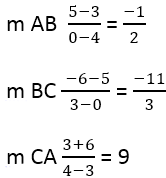
Далее необходимо найти наклон перпендикулярных сторон, для этого используется формула:

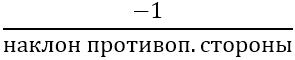
Имеем:

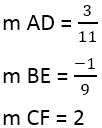
Когда найден наклон перпендикуляров, можно использовать уравнение линий, например, для линии AD, где точка 4,3, а наклон равен 3/11:

y-y1 = m(x-x1) y-3 = 3/11(x-4)

С помощью упрощения, имеем: 3х – 11у=-21
Для линии ВЕ, где точка 0,5, а наклон -1/9, имеем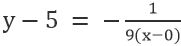

Упрощение дает: х+9у=45.
И последние линии CF, где точка 3, -6, а наклон 2, имеем уравнение y+6 = 2(x-3).
И упрощение, 2x — y = 12.
Если решить два из трех уравнений будут найдены значения х и у. Для данного примера:
Значение х = 8,05263;
Значение у = 4,10526.
Которые в данном случае являются координатами искомого Ортоцентра.

Источник

Ортоцентр – это точка пересечения высот треугольника.

Рассмотрим остроугольный треугольник ABC:
O – ортоцентр,
∠ BAC = a,
∠ ABC = b,
∠ ACB = c.

Утверждения.
1. Треугольник ABC подобен треугольнику, образованному вершиной B и основанием двух высот:
Δ ABC ∼ Δ H₃BH₂,
коэффициент подобия:
H₃B / AB = H₂B / CB = H₃H₂ / AC = cos b.

2. Соотношение отрезков, на которые ортоцентр делит высоту, можно вычислить по формуле:
BO / OH₁ = cos b / (cos a * cos c).

3. Высоты треугольника можно вычислить по формуле:
BH₁ = AC * sin a * sin c / sin b.

4. Расстояние от ортоцентра до вершины треугольника:
OB = AC / tg b.

5. 1 / BH₁ + 1 / CH₂ + 1 / AH₃ = 1 / r,
r – радиус вписанной окружности.

Докажем эти утверждения.
1.

В треугольнике ABC проведены высоты BD и CE.
Докажем, что треугольник ABC подобен треугольнику ADE.

Решение.
Рассмотрим Δ ABD:
cos A = AD / AB.
Рассмотрим Δ ACE:
cos A = AE / AC.
Таким образом,
cos A = AD / AB = AE / AC.
Значит, Δ ABC ∼ Δ ADE по двум сторонам и углу между ними.

2.

Диагонали трапеции ABCD пересекаются под прямым углом.
CH – высота, проведенная к большему основанию AD.
∠ CAD = a,
∠ ACD = c,
∠ ADC = d.
Найдем отношение, в котором диагональ трапеции делит высоту CH.

Решение.
Пусть K – точка пересечения диагоналей трапеции,
O – точка пересечения диагонали BD и высоты CH.
Найдем соотношение CO / OH.

Δ BOC подобен Δ DOH по двум углам,
так как ∠ BCO = ∠ DHO = 90,
∠ BOC = ∠ DOH как вертикальные.
Значит,
CO / OH = BC / DH. (*)

Рассмотрим Δ CKD:
KC = CD * cos c.
Рассмотрим Δ BCK:
BC = KC / cos a = (CD * cos c) / cos a.
Рассмотрим Δ CHD:
HD = CD * cos d.

Из (*) и последних трех равенств получаем:
CO / OH = BC / DH =
( (CD * cos c) / cos a ) : (CD * cos d) =

Таким образом, мы нашли соотношение отрезков, на которые ортоцентр O треугольника ABD делит высоту CH:

3.

Найдем расстояние от ортоцентра треугольника до его вершины, и высоту, проведенную из этой вершины, если известны углы треугольника и противолежащая сторона.