Как найти ортогональное дополнение онлайн

Оглавление — Линейная алгебра

---

Ортогональные дополнения евклидова пространства

Ортогональным дополнением непустого подмножества [math]M[/math] евклидова пространства [math]mathbb{E}[/math] называется множество векторов, ортогональных каждому вектору из [math]M[/math]. Ортогональное дополнение обозначается

[math]M^{perp}= Bigl{ mathbf{v}colon, langle mathbf{v},mathbf{w}rangle=0,~ forall mathbf{w}in M Bigr}.[/math]

Рассмотрим примеры ортогональных дополнений евклидова пространства.

1. Ортогональным дополнением нулевого подпространства [math]{mathbf{o} } triangleleft mathbb{E}[/math] служит все пространство [math]mathbb{E} colon, {mathbf{o} }^{perp}= mathbb{E}[/math]. Ортогональным дополнением всего пространства является его нулевое подпространство [math]mathbb{E}^{perp}= {mathbf{o} }[/math].

2. Пусть в пространстве [math]{V_3 }[/math] радиус-векторов (с началом в точке [math]O[/math]) за даны три взаимно перпендикулярных радиус-вектора [math]overrightarrow{OA}[/math], [math]overrightarrow{OB}[/math] и [math]overrightarrow{ OC }[/math]. Тогда ортогональным дополнением вектора [math]overrightarrow{OA}[/math] является множество радиус- векторов на плоскости, содержащей векторы [math]overrightarrow{ OB }[/math] и [math]overrightarrow{ OC }[/math], точнее, [math]{overrightarrow{OA}}^{perp}= operatorname{Lin}(overrightarrow{OB},overrightarrow{OC})[/math]. Ортогональным дополнением векторов [math]overrightarrow{OA}[/math] и [math]overrightarrow{OB}[/math] служит множество радиус-векторов на прямой, содержащей вектор [math]overrightarrow{OC}colon {overrightarrow{OA},overrightarrow{OB}}^{perp}= operatorname{Lin} (overrightarrow{OC})[/math]. Ортогональным дополнение трех заданных векторов служит нулевой радиус-вектор: [math]{overrightarrow{OA}, overrightarrow{OB}, overrightarrow{OC}}^{perp}= {overrightarrow{OO}}[/math].

3. В пространстве [math]P_2(mathbb{R})[/math] многочленов степени не выше второй со скалярным произведением (8.29) задано подмножество [math]P_0(mathbb{R})[/math] – многочленов нулевой степени. Найдем ортогональное дополнение этого подмножества. Для этого приравняем нулю скалярное произведение многочлена [math]p_2(x)=ax^2+bx+c[/math] на постоянный многочлен [math]p_0(x)=dcolon[/math] [math]langle p_2(x),p_0(x)rangle= acdot0+bcdot0+ccdot d=0[/math]. Поскольку величина [math]d[/math] произвольная, то [math]c=0[/math]. Следовательно, ортогональным дополнением подмножества [math]P_0(mathbb{R})[/math] является множество многочленов из [math]P_0(mathbb{R})[/math] с нулевым свободным членом.

---

Свойства ортогонального дополнения

Рассмотрим свойства ортогональных дополнений подмножеств n-мерного евклидова пространства [math]mathbb{E}[/math].

1. Ортогональное дополнение [math]M^{perp}[/math] непустого подмножества [math]Msubset mathbb{E}[/math] является линейным подпространством, т.е. [math]M^{perp} triangleleft mathbb{E}[/math], и справедливо включение [math]Msubset (M^{perp})^{perp}[/math].

В самом деле, множество [math]M^{perp}[/math] замкнуто по отношению к операциям сложения векторов и умножения вектора на число, так как сумма двух век торов, ортогональных [math]M[/math], ортогональна [math]M[/math], и произведение вектора, ортогонального [math]M[/math], на любое число является вектором, ортогональным [math]M[/math]. До кажем включение [math]Msubset (M^{perp})^{perp}[/math]. Пусть [math]mathbf{w}in M[/math], тогда [math]langle mathbf{w},mathbf{v}rangle=0[/math] для любого вектора [math]mathbf{v}in M^{perp}[/math]. Но это означает, что [math]mathbf{w}subset (M^{perp})^{perp}[/math].

2. Пересечение любого непустого подмножества [math]Msubset mathbb{E}[/math] со своим ортогональным дополнением есть нулевой вектор: [math]Mcap M^{perp}= {mathbf{o}}[/math].

Действительно, только нулевой вектор ортогонален самому себе.

3. Если [math]L[/math] – подпространство [math]mathbb{E}~ (Ltriangleleft mathbb{E})[/math], то [math]mathbb{E}=Loplus L^{perp}[/math].

Действительно, возьмем в [math]L[/math] ортогональный базис [math](mathbf{e})= (mathbf{e}_1, ldots,mathbf{e}_k)[/math]. До полним его векторами [math](mathbf{f})= (mathbf{f}_{k+1},ldots, mathbf{f}_n)[/math] до ортогонального базиса [math](mathbf{e}),,(mathbf{f})[/math] всего пространства [math]mathbb{E}[/math]. Тогда произвольный вектор [math]mathbf{w}in mathbb{E}[/math] можно представить в виде суммы

[math]mathbf{w}= underbrace{sum_{i=1}^{k}mathbf{w}_i mathbf{e}_i}_{mathbf{u}}+ underbrace{sum_{j=k+1}^{n}mathbf{w}_j mathbf{f}_j}_{mathbf{v}} =mathbf{u}+ mathbf{v},[/math]

где [math]mathbf{u}in L[/math], а [math]mathbf{v}in L^{perp}[/math], так как [math]langle mathbf{v},mathbf{e}_irangle= sum_{j=k+1}^{n}mathbf{w}langle mathbf{f}_j, mathbf{e}_i rangle_{{}_{=0}}=0[/math] для [math]i=1,ldots,k[/math]. Следовательно, любой вектор пространства [math]mathbb{E}[/math] раскладывается по подпространствам [math]L[/math] и [math]L^{perp}[/math], т.е. [math]mathbb{E}= L+L^{perp}[/math]. Эта алгебраическая сумма является прямой суммой по свойству 2, поскольку [math]Lcap L^{perp}={mathbf{o}}[/math]. Следовательно, [math]mathbb{E}=Loplus L^{perp}[/math].

4. Если [math]Ltriangleleft mathbb{E}[/math], то [math]dim{L^{perp}}= dimmathbb{E}-dim{L}[/math].

5. Если [math]L[/math] – подпространство [math]mathbb{E}[/math], то [math]L=(L^{perp})^{perp}[/math].

Из первого свойства следует включение [math]Lsubset(L^{perp})^{perp}[/math]. Докажем, что [math](L^{perp})^{perp}subset L[/math]. Действительно, пусть [math]mathbf{w}in (L^{perp})^{perp}[/math]. По свойству 3: [math]mathbf{w}=mathbf{u}+mathbf{v}[/math], где [math]mathbf{u}in L,~ mathbf{v}in L^{perp}[/math]. Найдем скалярное произведение

[math]underbrace{langle mathbf{w},mathbf{v}rangle}_{0}= langle mathbf{w}+ mathbf{v}, mathbf{v}rangle= underbrace{langle mathbf{u},mathbf{v}rangle }_{0}+langle mathbf{v}, mathbf{v}rangle= langle mathbf{v},mathbf{v}rangle.[/math]

Следовательно, [math]langle mathbf{v},mathbf{v}rangle=0[/math], и согласно аксиоме 4 скалярного произведения [math]mathbf{v}=mathbf{o}[/math], поэтому [math]mathbf{w}=mathbf{u}+ mathbf{v}= mathbf{u}+mathbf{0}=mathbf{u}in L[/math]. Значит, [math](L^{perp})^{perp}subset L[/math]. Из двух включений [math]Lsubset (L^{perp})^{perp}[/math] и [math](L^{perp})^{perp} subset L[/math] следует равенство [math]L=(L^{perp})^{perp}[/math].

6. Если [math]L_1triangleleft mathbb{E}[/math] и [math]L_2triangleleft mathbb{E}[/math], то [math](L_1+L_2)^{perp}=L_1^{perp}cap L_2^{perp}[/math] и [math](L_1cap L_2)^{perp}= L_1^{perp}+ L_2^{perp}[/math].

Последние свойства аналогичны свойствам алгебраических дополнений.

---

Нахождение ортогонального дополнения подпространства

Ранее для описания подпространств линейных пространств использовались два способа описания (внешний и внутренний). Рассмотрим применение этих способов описания для нахождения ортогональных дополнений подпространств. Учитывая изоморфизм евклидовых пространств, будем рассматривать арифметическое пространство [math]mathbb{R}^n[/math] со скалярным произведением (8.27).

Для заданного подпространства [math]Ltriangleleft mathbb{R}^n[/math] требуется найти его ортогональное дополнение [math]L^{perp}[/math]. В зависимости от способа описания подпространства [math]L[/math] используем одно из следующих двух утверждений.

1. Если подпространство [math]Ltriangleleft mathbb{R}^n[/math] задано как линейная оболочка [math]L=operatorname{Lin}(a_1,ldots,a_k)[/math] столбцов матрицы [math]A= begin{pmatrix}a_1&cdots&a_kend{pmatrix}[/math], то множество решений однородной системы [math]Ax=o[/math] является его ортогональным дополнением [math]L^{perp}triangleleft mathbb{R}^n[/math], т.е.

2. Если подпространство [math]Ltriangleleft mathbb{R}^n[/math] задано как множество решений однородной системы [math]Ax=o[/math] [math]m[/math] уравнений с [math]n[/math] неизвестными, то линейная оболочка столбцов [math]a_1^T,ldots,a_m^T[/math] транспонированной матрицы [math]A^T=begin{pmatrix}a_1^T&cdots&a_m^Tend{pmatrix}[/math] является его ортогональным дополнением [math]L^{perp}triangleleft mathbb{R}^n[/math], т.е.

где [math]a_i^T[/math] – i-й столбец матрицы [math]A^T[/math].

Докажем, например, первое утверждение. Линейное однородное уравнение

[math]a_{i,1}cdot x_1+a_{i,2}cdot x_2+ldots+a_{i,n}cdot x_n=0[/math]

можно записать при помощи скалярной произведения [math]langle mathbf{a}_{i},mathbf{x} rangle=0[/math], так как [math]langle mathbf{a}_{i},mathbf{x} rangle=(a_{i})^Tx[/math] по формуле (8.27). Тогда множество [math]{langle mathbf{a}_{i},mathbf{x} rangle=o}[/math] решений одного уравнения совпадает с множеством векторов, ортогональных [math]mathbf{i}_i[/math]. Поэтому множество [math]{A^Tx=o}[/math] совпадает с множеством векторов, ортогональных каждому из векторов [math]mathbf{a}_1,ldots,mathbf{a}_k[/math], значит, и их линейной оболочке [math]L= operatorname{Lin}(mathbf{a}_1,ldots,mathbf{a}_k)[/math]. Таким образом, [math]L^{perp}={A^Tx=o}[/math].

Замечания 8.13

1. В отличие от алгебраического дополнения [math]L^{+}[/math] подпространстве [math]Ltriangleleft mathbb{E}[/math] ортогональное дополнение [math]L^{perp}[/math] находится однозначно.

2. Ортогональное дополнение [math]L^{perp}[/math] подпространства [math]Ltriangleleft mathbb{E}[/math] в силу свойства 3 является также и алгебраическим дополнением. Это обстоятельстве учитывалось при нахождении алгебраических дополнений при помощи утверждений (8.16) и (8.17), которые по существу совпадают с утверждениями (8.34) и (8.35).

---

Пример 8.19. В примере 8.10 для линейного подпространства [math]L= operatorname{Lin}[(t-1)^2,(t+1)^3][/math] пространства [math]P_3(mathbb{R})[/math] многочленов не более, чем 3-й степени, было найдено алгебраическое дополнение

[math]L^{+}= operatorname{Lin}!left[left(-dfrac{9}{5}-dfrac{2}{5},t+t^2right)!, left(-dfrac{2}{5}-dfrac{1}{5},t+t^3right)right].[/math]

Доказать, что это алгебраическое дополнение является ортогональным дополнением подпространства [math]L[/math] евклидова пространства [math]P_3(mathbb{R})[/math] со скалярным произведением (8.29).

Решение. Для решения задачи достаточно показать, что образующие подпространства [math]L:[/math]

[math]p_1(t)=(t-1)^2= 0cdot t^3+1cdot t^2+(-2)cdot t+1;quad p_2(t)=(t+1)^3= 1cdot t^3+3cdot t^2+3cdot t+1[/math]

ортогональны образующим алгебраического дополнения [math]L^{+}:[/math]

[math]q_1(t)=0cdot t^3+1cdot t^2+frac{-2}{5}cdot t+frac{-9}{5},quad q_2(t)= 1cdot t^3+0cdot t^2+frac{-1}{5}cdot t+frac{-2}{5},.[/math]

По формуле (8.29) находим

[math]begin{aligned}langle p_1(t),q_1(t)rangle&= 0cdot0+1cdot1+(-2)cdot!left(-dfrac{2}{5}right)+1cdot!left(-frac{9}{5}right)=0;\[2pt] langle p_1(t),q_2(t)rangle&= 0cdot1+1cdot0+(-2)cdot!left(-dfrac{1}{5}right)+1cdot!left(-frac{2}{5}right)=0;\[2pt] langle p_2(t),q_1(t)rangle&= 1cdot0+3cdot1+3cdot!left(-dfrac{2}{5}right)+1cdot!left(-frac{9}{5}right)=0;\[2pt] langle p_2(t),q_2(t)rangle&= 1cdot1+3cdot0+3cdot!left(-dfrac{1}{5}right)+1cdot!left(-frac{2}{5}right)=0. end{aligned}[/math]

Следовательно, [math]L=L^{+}[/math].

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Два
подпространства
называются ортогональными,
если каждый вектор одного подпространства
ортогонален каждому вектору другого
подпространства . Ортогональность
подпространств
и
обозначается

Для
того чтобы вектор
был ортогонален к подпространству
необходимо и достаточно, чтобы он был
ортогонален ко всем векторам какого-либо
базиса подпространства

Для
того чтобы два подпространства были
ортогональными, необходимо и достаточно
, чтобы каждый вектор какого-либо базиса
одного подпространства был ортогонален
ко всем векторам какого-либо базиса
другого подпространства.

Сумма

подпространств
называется ортогональной
и обозначается
если подпространства попарно ортогональны.

Ортогональная
сумма ненулевых подпространств всегда
является прямой суммой.

Совокупность
всех векторов, ортогональных к линейному
подпространству
евклидова пространства
называется ортогональным
дополнением подпространства

и обозначается

Евклидово
пространство
есть ортогональная сумма любого своего
линейного подпространства
и его ортогонального дополнения
т.е.

Любой
вектор
из евклидова пространства
всегда можно представить, причём
единственным образом, в виде

где

принадлежит некоторому подпространству
,

ортогонален к
Вектор
называется ортогональной
проекцией
вектора

на
подпространство

а –
перпендикуляром,
опущенным из
на

Пример
1.
Докажите, что

Доказательство.
Пусть
Тогда
В силу того, что
где ,
а .
Следовательно,
Если в последнем равенстве выбрать
то из условия
заключаем, что
Полагая
получаем, что
или
Другими словами, из условия
вытекает, что Пусть
теперь .
Тогда ,
т.к.
и .
Значит, .
Таким образом, мы получили, что если ,
то .
И, наоборот, если ,
то .
Сказанное равносильно равенству .

Пример
2.
Линейное подпространство
задано системой уравнений:

Найдите
базис ортогонального дополнения .

Решение.
Найдем базис .
Для этого решим данную однородную
систему уравнений:

–
свободные переменные;

Таким
образом, общее решение имеет вид:
.
Выбирая значения свободных переменных
в соответствии с таблицей

получаем
базисные векторы подпространства :

.

Поскольку
,
а ортогональная сумма есть прямая сумма,

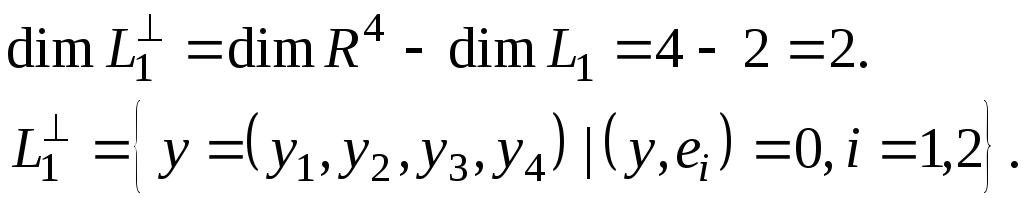
Таким
образом,
определяется системой уравнений

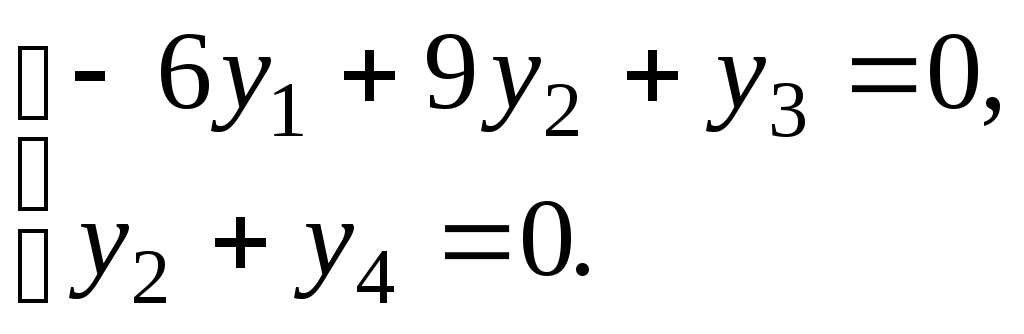
Найдя
фундаментальную систему решений этой
однородной системы уравнений, получим
базис .

.

–
свободные переменные;

.

Общее
решение имеет вид:
.

Выбирая
значения свободных переменных в
соответствии с таблицей

получаем
базис ортогонального дополнения :

.

Пример
3.
Найдите ортогональную проекцию
и перпендикуляр ,
опущенный из вектора
на подпространство ,
порожденное векторами
и .

Решение.
Система векторов
образует базис подпространства .
Т.к.
такие, что .
Кроме того, справедливо (причем
единственное) представление ,
в котором .
Последнее означает, что .
Отсюда

т.е.
получили неоднородную систему уравнений
относительно
и ,
которая в матричном виде выглядит так:

.

Поскольку

система

эквивалентна следующей:

.

Отсюда

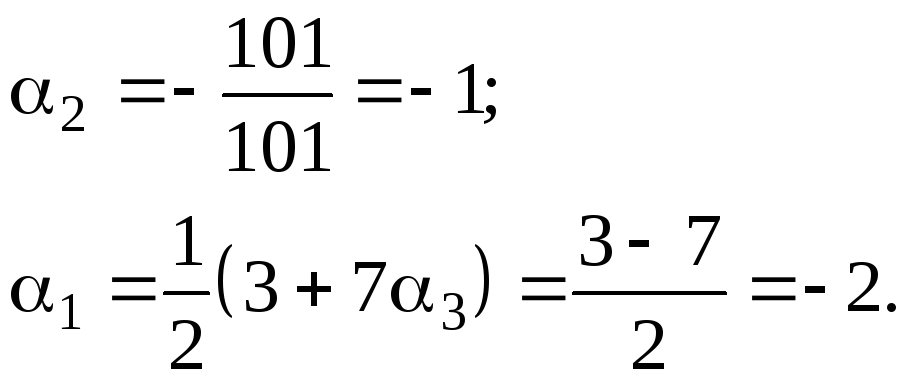
Следовательно,

5.3.1.
Докажите, что ортогональное дополнение
к линейному подпространству евклидова
пространства
обладает свойствами:

если
,
то

Здесь
–
нулевое подпространство, содержащее
лишь нулевой вектор.

5.3.2.
Найдите базис ортогонального дополнения

линейной оболочки
следующей системы векторов пространства
:

5.3.3.
Найдите ортогональный базис ортогонального
дополнения ,
если

и

5.3.4.
В пространстве
многочленов степени
с действительными коэффициентами
скалярное произведение многочленов
и
определяется формулой

.

Найдите
ортогональное дополнение подпространства
всех многочленов, удовлетворяющих
условию

5.3.5.
Найдите ортогональную проекцию и
перпендикуляр, опущенный из вектора
на подпространство :

натянуто
на векторы

натянуто
на векторы

задано
системой уравнений:

натянуто
на векторы

Соседние файлы в папке Задачник-1

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Ортогональное дополнение. Ортогональная проекция вектора на подпространство

Пусть Е — евклидово пространство, а L — его подпространство. Множество L 1 – векторов в Е, ортогональных к каждому вектору подпространства L, называют ортогональным дополнением к подпространству L.

Теорема 8.6. Ортогональное дополнение IA к подпространству L евклидова пространства Е является подпространством в Е.

> Пусть уi,y2 € ZA. Тогда для любого вектора х ? L имеем: (ж, г/1) = 0 и (х,у2) = 0. Следовательно,

т.е. вектор у + у2 ортогонален любому вектору х € L. Это означает, что У1+У2 € ZA. Мы доказали, что сумма любых двух векторов множества ZA принадлежит ZA. Аналогично для любого действительного числа Л и любого х € L имеем:

т.е. вектор Л у ортогонален любому вектору х е L, а значит, принадлежит ZA. Таким образом, множество ZA замкнуто относительно сложения векторов и умножения векторов на числа и, следовательно, является подпространством. ?

Теорема 8.7. Конечномерное евклидово пространство Е является прямой суммой любого своего подпространства L и его ортогонального дополнения ZA, т.е. ортогональное дополнение к подпространству является его прямым дополнением.

> Пусть в пространстве L выбран ортогональный базис, состоящий из векторов ai, 02, . а&. Дополним его до ортогонального базиса пространства Е векторами fk+i, fk+2, •••, fn и по построенному базису

разложим произвольный вектор х из Е. Тогда получим где положено

Вектор у принадлежит подпространству Z, поскольку он является линейной комбинацией векторов базиса в L. Покажем, что вектор z принадлежит ортогональному дополнению LА Для этого замечаем, что по построению векторы fk+i, fk+2, fn ортогональны базисным

векторам ai, Это очевидное следствие теоремы о размерности суммы подпространств (см. теорему 4.23). ?

Следствие 8.3. Ортогональным дополнением к подпространству ZA является подпространство L.

> Так как каждый вектор из L ортогонален каждому вектору из ZA, то подпространство L содержится в (ZA)A Кроме того, выполняются соотношения Е = L 0 ZA, Е = (L– L )- L ф ZA, и по предыдущему следствию подпространства L и (ZA) 1 – имеют одинаковую размерность. Поэтому эти подпространства совпадают. ?

Следствие 8.4. Если L — подпространство в евклидовом пространстве Е, то любой вектор х € Е имеет разложение

где хо G L, х 1 – G /А. Такое разложение единственно.

> Это утверждение — фактически расшифровка утверждения, что Е = L Ф ZA. ?

Пример 8.9. В четырехмерном пространстве Е± скалярное произведение в заданном базисе определено формулой (8.5). Построить ортогональное дополнение ZA для подпространства L = (а^аг), где a, = (1,1,1, l) r , а₂ = (1, -1,1,1) т .

Решение. Векторы а и а2 составляют базис в L. Дополним эту систему до базиса в Е± векторами Ъ и 62, удовлетворяющими условиям

и положим L = (61,62)- Векторы 61, 62 являются решениями системы из двух уравнений (ai,x) = 0, (а,2,х) = 0, и в качестве их можно взять любую фундаментальную систему решений, например, 61 = (—1,0,1,0) т , 62 = (—1,0,0,1) т . Из выбора векторов 61 и 62 следует, что они составляют базис в L L , т.е. L = L L . ?

Пусть L — подпространство евклидова пространства Е. Каждый вектор у ? Е может быть единственным способом представлен в виде

где уо ? L, а вектор у 1 – ортогонален к каждому вектору из L, т.е. у 1 – ? L х . Вектор уо называют ортогональной проекцией вектора у на пространство L и обозначают прьУ, а вектор y L называют ортогональной составляющей вектора у. Очевидно, что если у ? L, то прьу = у, и, наоборот, если прьу = : Действительно, пусть у — произвольный вектор, опущенный из конца вектора х на подпространство L и х 1 – — ортогональная составляющая вектора х, т.е. перпендикуляр, опущенный из конца вектора х на подпространство L. Тогда

поскольку концы векторов у их 1 лежат в L. Поэтому

так как векторы у — х 1 – их 1 ортогональны. ?

Доказанные утверждения является естественным обобщением известного из элементарной геометрии утверждения о том, что перпендикуляр короче любой наклонной, опущенной из той же точки на плоскость.

Длину ортогональной составляющей х 1 – вектора х принимают за кратчайшее расстояние от вектора х до подпространства L.

Ортогональная проекция вектора у на подпространство L является частным случаем проекции вектора на подпространство параллельно подпространству L₂, являющемуся прямым дополнением к L (см. разд. 4.11). В случае ортогональной проекции Ь₂ = Ь 1 .

На практике при отыскании ортогональной проекции вектора х на подпространство L = (ai, а₂, •••?> &fc) поступают следующим образом. В разложении

вектора х на ортогональную проекцию жо = np_LT и ортогональную составляющую х 1 – вектор Xq можно представить в виде линейной комбинации

Тогда равенство х = Хо + х 1 принимает вид:

Для отыскания коэффициентов oi, 02, . о& умножим равенство (8.16) скалярно на векторы а, а₂, . ак- Учитывая, что (а^аг 1- ) = = (а₂,х ± ) = . = (ак,х?*?) = 0, получаем систему линейных уравнений

относительно неизвестных оц, а₂, . а к. Из этой системы находят коэффициенты oi, а₂, . о^. В матричной форме равенство (8.15) и система (8.17) записываются в виде

где А = (oi, а₂. а*,) — матрица, для которой столбцами являются столбцы координат векторов а, а₂, . а&; о — (01,02, . о*;) т — столбец высоты к. Использование системы (8.17), или, что тоже самое системы (8.19), указывает на то (см. п.8.21), что отыскание коэффициентов ai, а₂, . ак для равенства (8.15) равносильно решению методом наименьших квадратов системы А о = х с неизвестным столбцом

Если система векторов oi, 2, • ••, ftfc линейно независимая, то в равенстве (8.19) матрица А т А невырожденная, так как она представляет собой матрицу Грама этой системы векторов (см. теорему 8.1). В этом случае из уравнения (8.19) однозначно определяется столбец а:

Учитывая равенство (8.18), заключаем, что

Пример 8.10. Для вектора х = (3,6,0) т найти ортогональную проекцию Xq на подпространство L = (а^аг) и ортогональную составляющую т х , если ay = (1, —1,0) т , т .

Решение. Запишем xq = np_L.x в виде хд = ау ау + Коэффициенты ау и «2 можно найти, решив систему (8.17), которая в данном случае имеет вид:

Вычислим все скалярные произведения. В результате получим

Решая систему относительно неизвестных од иаг, находим, что од = = су2 = 3. Таким образом, пр/,т = Зау + Заг = (0,3,3) т и х^ = = х — np_LT = (3,3, —3) т .

Поскольку векторы а у, а2 линейно независимые, то можно также воспользоваться формулой (8.20). Вычислив

Заметим, что если е = (ei, е₂,е_п) — ортоиормированный базис в евклидовом пространстве Е, а подпространство L является линейной оболочкой части базисных векторов, например, L = (ei, е₂. е*,), то для любого вектора

ортогональная проекция прь-т совпадает с суммой слагаемых в разложении х по базису, соответствующих векторам, порождающим L. а ортогональная проекция — с суммой всех остальных слагаемых, т.е.

Например, для вектора х = (1,2, 3,4,5) т проекция на подпространство L = (б1,е2,ез) равна Xq = (1,2,3,0,0) т , и его ортогональная составляющая х 1 – = (0,0,0,4, 5) т . ?

Ортогональные дополнения евклидова пространства

Ортогональным дополнением непустого подмножества [math]M[/math] евклидова пространства [math]mathbb[/math] называется множество векторов, ортогональных каждому вектору из [math]M[/math] . Ортогональное дополнение обозначается

forall mathbfin M Bigr>.[/math]

Рассмотрим примеры ортогональных дополнений евклидова пространства.

1. Ортогональным дополнением нулевого подпространства [math] <mathbf> triangleleft mathbb[/math] служит все пространство [math]mathbb colon, <mathbf>^<perp>= mathbb[/math] . Ортогональным дополнением всего пространства является его нулевое подпространство [math]mathbb^<perp>= <mathbf>[/math] .

2. Пусть в пространстве [math][/math] радиус-векторов (с началом в точке [math]O[/math] ) за даны три взаимно перпендикулярных радиус-вектора [math]overrightarrow[/math] , [math]overrightarrow[/math] и [math]overrightarrow< OC >[/math] . Тогда ортогональным дополнением вектора [math]overrightarrow[/math] является множество радиус- векторов на плоскости, содержащей векторы [math]overrightarrow< OB >[/math] и [math]overrightarrow< OC >[/math] , точнее, [math]<overrightarrow>^<perp>= operatorname(overrightarrow,overrightarrow)[/math] . Ортогональным дополнением векторов [math]overrightarrow[/math] и [math]overrightarrow[/math] служит множество радиус-векторов на прямой, содержащей вектор [math]overrightarrowcolon <overrightarrow,overrightarrow>^<perp>= operatorname (overrightarrow)[/math] . Ортогональным дополнение трех заданных векторов служит нулевой радиус-вектор: [math]<overrightarrow, overrightarrow, overrightarrow>^<perp>= <overrightarrow>[/math] .

3. В пространстве [math]P_2(mathbb)[/math] многочленов степени не выше второй со скалярным произведением (8.29) задано подмножество [math]P_0(mathbb)[/math] – многочленов нулевой степени. Найдем ортогональное дополнение этого подмножества. Для этого приравняем нулю скалярное произведение многочлена [math]p_2(x)=ax^2+bx+c[/math] на постоянный многочлен [math]p_0(x)=dcolon[/math] [math]langle p_2(x),p_0(x)rangle= acdot0+bcdot0+ccdot d=0[/math] . Поскольку величина [math]d[/math] произвольная, то [math]c=0[/math] . Следовательно, ортогональным дополнением подмножества [math]P_0(mathbb)[/math] является множество многочленов из [math]P_0(mathbb)[/math] с нулевым свободным членом.

Свойства ортогонального дополнения

Рассмотрим свойства ортогональных дополнений подмножеств n-мерного евклидова пространства [math]mathbb[/math] .

1. Ортогональное дополнение [math]M^<perp>[/math] непустого подмножества [math]Msubset mathbb[/math] является линейным подпространством, т.е. [math]M^ <perp>triangleleft mathbb[/math] , и справедливо включение [math]Msubset (M^<perp>)^<perp>[/math] .

В самом деле, множество [math]M^<perp>[/math] замкнуто по отношению к операциям сложения векторов и умножения вектора на число, так как сумма двух век торов, ортогональных [math]M[/math] , ортогональна [math]M[/math] , и произведение вектора, ортогонального [math]M[/math] , на любое число является вектором, ортогональным [math]M[/math] . До кажем включение [math]Msubset (M^<perp>)^<perp>[/math] . Пусть [math]mathbfin M[/math] , тогда [math]langle mathbf,mathbfrangle=0[/math] для любого вектора [math]mathbfin M^<perp>[/math] . Но это означает, что [math]mathbfsubset (M^<perp>)^<perp>[/math] .

2. Пересечение любого непустого подмножества [math]Msubset mathbb[/math] со своим ортогональным дополнением есть нулевой вектор: [math]Mcap M^<perp>= <mathbf>[/math] .

Действительно, только нулевой вектор ортогонален самому себе.

3. Если [math]L[/math] – подпространство [math]mathbb

(Ltriangleleft mathbb)[/math] , то [math]mathbb=Loplus L^<perp>[/math] .

Действительно, возьмем в [math]L[/math] ортогональный базис [math](mathbf)= (mathbf_1, ldots,mathbf_k)[/math] . До полним его векторами [math](mathbf)= (mathbf_,ldots, mathbf_n)[/math] до ортогонального базиса [math](mathbf),,(mathbf)[/math] всего пространства [math]mathbb[/math] . Тогда произвольный вектор [math]mathbfin mathbb[/math] можно представить в виде суммы

где [math]mathbfin L[/math] , а [math]mathbfin L^<perp>[/math] , так как [math]langle mathbf,mathbf_irangle= sum_^mathbflangle mathbf_j, mathbf_i rangle_<<>_<=0>>=0[/math] для [math]i=1,ldots,k[/math] . Следовательно, любой вектор пространства [math]mathbb[/math] раскладывается по подпространствам [math]L[/math] и [math]L^<perp>[/math] , т.е. [math]mathbb= L+L^<perp>[/math] . Эта алгебраическая сумма является прямой суммой по свойству 2, поскольку [math]Lcap L^<perp>=<mathbf>[/math] . Следовательно, [math]mathbb=Loplus L^<perp>[/math] .

4. Если [math]Ltriangleleft mathbb[/math] , то [math]dim>= dimmathbb-dim[/math] .

5. Если [math]L[/math] – подпространство [math]mathbb[/math] , то [math]L=(L^<perp>)^<perp>[/math] .

Из первого свойства следует включение [math]Lsubset(L^<perp>)^<perp>[/math] . Докажем, что [math](L^<perp>)^<perp>subset L[/math] . Действительно, пусть [math]mathbfin (L^<perp>)^<perp>[/math] . По свойству 3: [math]mathbf=mathbf+mathbf[/math] , где [math]mathbfin L,

mathbfin L^<perp>[/math] . Найдем скалярное произведение

Следовательно, [math]langle mathbf,mathbfrangle=0[/math] , и согласно аксиоме 4 скалярного произведения [math]mathbf=mathbf[/math] , поэтому [math]mathbf=mathbf+ mathbf= mathbf+mathbf<0>=mathbfin L[/math] . Значит, [math](L^<perp>)^<perp>subset L[/math] . Из двух включений [math]Lsubset (L^<perp>)^<perp>[/math] и [math](L^<perp>)^ <perp>subset L[/math] следует равенство [math]L=(L^<perp>)^<perp>[/math] .

6. Если [math]L_1triangleleft mathbb[/math] и [math]L_2triangleleft mathbb[/math] , то [math](L_1+L_2)^<perp>=L_1^<perp>cap L_2^<perp>[/math] и [math](L_1cap L_2)^<perp>= L_1^<perp>+ L_2^<perp>[/math] .

Последние свойства аналогичны свойствам алгебраических дополнений.

Нахождение ортогонального дополнения подпространства

Ранее для описания подпространств линейных пространств использовались два способа описания (внешний и внутренний). Рассмотрим применение этих способов описания для нахождения ортогональных дополнений подпространств. Учитывая изоморфизм евклидовых пространств, будем рассматривать арифметическое пространство [math]mathbb^n[/math] со скалярным произведением (8.27).

Для заданного подпространства [math]Ltriangleleft mathbb^n[/math] требуется найти его ортогональное дополнение [math]L^<perp>[/math] . В зависимости от способа описания подпространства [math]L[/math] используем одно из следующих двух утверждений.

1. Если подпространство [math]Ltriangleleft mathbb^n[/math] задано как линейная оболочка [math]L=operatorname(a_1,ldots,a_k)[/math] столбцов матрицы [math]A= begina_1&cdots&a_kend[/math] , то множество решений однородной системы [math]Ax=o[/math] является его ортогональным дополнением [math]L^<perp>triangleleft mathbb^n[/math] , т.е.

2. Если подпространство [math]Ltriangleleft mathbb^n[/math] задано как множество решений однородной системы [math]Ax=o[/math] [math]m[/math] уравнений с [math]n[/math] неизвестными, то линейная оболочка столбцов [math]a_1^T,ldots,a_m^T[/math] транспонированной матрицы [math]A^T=begina_1^T&cdots&a_m^Tend[/math] является его ортогональным дополнением [math]L^<perp>triangleleft mathbb^n[/math] , т.е.

где [math]a_i^T[/math] – i-й столбец матрицы [math]A^T[/math] .

Докажем, например, первое утверждение. Линейное однородное уравнение

1. В отличие от алгебраического дополнения [math]L^<+>[/math] подпространстве [math]Ltriangleleft mathbb[/math] ортогональное дополнение [math]L^<perp>[/math] находится однозначно.

2. Ортогональное дополнение [math]L^<perp>[/math] подпространства [math]Ltriangleleft mathbb[/math] в силу свойства 3 является также и алгебраическим дополнением. Это обстоятельстве учитывалось при нахождении алгебраических дополнений при помощи утверждений (8.16) и (8.17), которые по существу совпадают с утверждениями (8.34) и (8.35).

Пример 8.19. В примере 8.10 для линейного подпространства [math]L= operatorname[(t-1)^2,(t+1)^3][/math] пространства [math]P_3(mathbb)[/math] многочленов не более, чем 3-й степени, было найдено алгебраическое дополнение

Доказать, что это алгебраическое дополнение является ортогональным дополнением подпространства [math]L[/math] евклидова пространства [math]P_3(mathbb)[/math] со скалярным произведением (8.29).

Решение. Для решения задачи достаточно показать, что образующие подпространства [math]L:[/math]

ортогональны образующим алгебраического дополнения [math]L^<+>:[/math]

[spoiler title=”источники:”]

http://mathhelpplanet.com/static.php?p=ortogonalnye-dopolneniya-evklidov-prostranstv

[/spoiler]

Как следует из теоремы 2.7, в произвольном линейном пространстве L любое линейное подпространство H имеет прямое дополнение, т.е. такое линейное подпространство H’, что H ⊕ H’ = L. Такое линейное подпространство H’ не является единственным. Однако в случае евклидова пространства
среди всех возможных прямых дополнений к данному линейному подпространству одно выделяется.

Определение 3.8. Ортогональным дополнением линейного подпространства H в евклидовом пространстве Ε называют множество H^⊥ всех векторов х ∈ Ε, ортогональных каждому вектору линейного подпространства H.

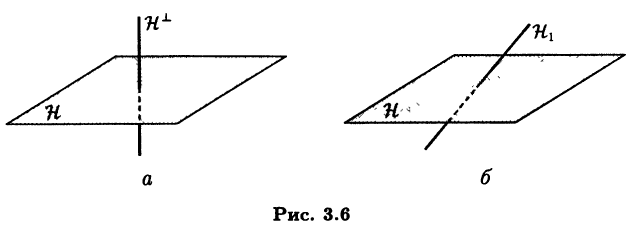
Пример 3.15. В евклидовом пространстве V₃ свободных векторов рассмотрим линейное подпространство H векторов, параллельных данной плоскости (см. пример 2.1). Тогда ортогональным дополнением H^⊥ будет множество векторов, перпендикулярных к этой плоскости (рис. 3.6, а), в то время как в качестве прямого дополнения H₁ можно взять подпространство векторов, коллинеарных произвольной прямой, пересекающей плоскость в единственной точке, т.е. не параллельной плоскости и не лежащей в этой плоскости (рис. 3.6,6). Отметим, что в данном случае H^⊥ является линейным подпространством в V₃.

Теорема 3.6. Ортогональное дополнение H^⊥ линейного подпространства Н в евклидовом подпространстве Ε является линейным подпространством в Ε, причем Ε = Н ⊕ H^⊥ и dimH + dimH^⊥ = dimΕ.

◄ Чтобы доказать, что H^⊥ является линейным подпространством в Ε, нужно проверить условия 1) и 2) определения 2.1. Взяв два произвольных вектора x и у, принадлежащих H^⊥, умножим скалярно их сумму на произвольный вектор h ∈ Н. Получим:

(x + у, h) – (x, h) + (у, h) = 0 + 0 = 0,

т.е. для любых векторов x и у из множества H^⊥ их сумма x + у принадлежит тому же множеству.

Теперь рассмотрим произведение вектора x ∈ H^⊥ на про-извольное действительное число λ. Для произвольного вектора h ∈ H

(λx, h) = λ (x, h) = λ • 0 = 0,

и поэтому λx ∈ H^⊥ если x ∈ H^⊥. Следовательно, H^⊥ является линейным подпространством в Ε.

Отметим, что любой вектор x, принадлежащий пересечению Н ∩ H^⊥, ортогонален самому себе: (x, x) = 0, так как любой вектор из H^⊥ ортогонален любому вектору подпространства H. Но вектор ортогонален самому себе лишь в том случае, когда он нулевой (аксиома г) скалярного умножения). Поэтому Н ∩ H^⊥ = {0}, а сумма Н + H^⊥ рассматриваемых линейных
подпространств является прямой (см. теорему 2.3). Докажем, что эта прямая сумма совпадает со всем евклидовым пространством Ε.

Выберем некоторый ортонормированный базис f₁, … , f_m в линейном подпространстве H и дополним его до базиса f₁, …, f_m, f_m+1, … , f_n во всем евклидовом пространстве Ε, dimΕ = n. Исходя из этого базиса построим при помощи процесса Грама – Шмидта ортонормированный базис е = (e₁ … е_m e_m+1 … е_n) в Ε. Так как первые m векторов f₁, … , f_m исходного базиса попарно ортогональны и имеют единичную длину, процесс ортогонализации оставит их без изменения, т.е. е₁ = f₁, i = 1,m. Векторы e_m+1, …, е_n ортогональны каждому из векторов e₁, …, е_m базиса линейного подпространства Н и, следовательно, ортогональны Н, так как H = span{e₁,… ,е_m}. Поэтому все они попадают в ортогональное дополнение H^⊥.

Рассмотрим произвольный вектор х ∈ Ε и запишем его разложение по базису е:

x = x₁e₁+ … + x_ne_n.

Легко увидеть, что х₁ = x₁e₁ + … + х_mе_m есть вектор из Н, x₂ = x_m+1e_m+1 + … + х_nе_n есть вектор из H^⊥, при этом x = x₁ + x₂. Следовательно, x ∈ H ⊕ H^⊥, и так как вектор х выбирался произвольно, то H ⊕ H^⊥ = Ε.

Согласно следствию из теоремы 2.5, из соотношения H ⊕ H^⊥ = Ε вытекает следующее равенство для размерностей: dimΕ = dimH + dimH^⊥ . ►

Следствие 3.1. Каково бы ни было линейное подпространство Н в евклидовом пространстве Ε, любой вектор x ∈ Ε можно однозначно представить в виде

x = h + h^⊥ (3.11)

где h ∈ H, h^⊥ ∈ H^⊥.

◄ Действительно, это утверждение означает, что Ε = H ⊕ H^⊥. ►

Вектор h в разложении (3.11) называют ортогональной проекцией вектора х на линейное подпространство H, а вектор h^⊥ – ортогональной составляющей вектора х относительно линейного подпространства H.

Как построить ортогональное дополнение к данному линейному подпространству? Пусть линейное подпространство H определено наиболее распространенным способом – как линейная оболочка некоторой системы векторов a₁,… , а_m. Согласно определению 3.8 ортогонального дополнения, любой вектор х ∈ H^⊥ должен быть ортогонален каждому из векторов а_i:

(a_i,x)=0, i = l,m. (3.12)

Наоборот, если вектор х удовлетворяет системе равенств (3.12), т.е. он ортогонален каждому из векторов а_i, то этот вектор ортогонален и любой линейной комбинации системы векторов a₁, …, a_m (см. 3.5). Значит, х ортогонален каждому вектору линейного подпространства H = span{a₁,… ,a_m} и принадлежит линейному подпространству H^⊥.

Итак, система уравнений (3.12) описывает ортогональное дополнение линейного подпространства Н. Запишем эту систему в координатах в некотором ортонормированием базисе е = (e₁ … е_n). Пусть векторы а_i в этом базисе имеют разложения

a₁ = a₁₁e₁ + … + a_1ne_n,

………………………….

a_i = a_i1e₁ + … + a_ine_n,

………………………….

a_m = a_m1e₁ + … + a_mne_n.

Координаты произвольного вектора х в том же базисе обозначим х₁, …, х_n т.е. полагаем, что

х = х₁e₁ + … + х_nе_n.

Тогда в ортонормированном базисе е

(a₁,x) = (a_i1e₁ + … + a_ine_n, x₁e₁ + … + x_ne_n) = a_i1x₁ + … + a_inx_n, i = 1,m.

Таким образом, система (3.12), записанная в координатах относительно ортонормированного базиса е, имеет вид

a₁₁x₁ + … + a_1nx_n = 0,

……………….. (3.13)

a_m1x₁ + … + a_mnx_n = 0,

т.е. представляет собой однородную систему из m линейных алгебраических уравнений с п неизвестными. Строки матрицы А этой системы совпадают с наборами координат векторов a₁, …, а_m. Поэтому матрица А имеет ранг, равный рангу системы векторов a₁, …, a_m, т.е. этот ранг совпадает с размерностью линейного подпространства Н.

Каждое решение системы (3.13) представляет собой набор координат некоторого вектора из H^⊥ и наоборот, любой вектор из H^⊥ описывает решение системы (3.13). Поэтому можно сказать, что множество всех решений этой системы есть линейное подпространство H^⊥. Согласно теореме 3.6, это подпространство имеет размерность n – dimH = n – RgА. Множество решений однородной системы линейных алгебраических уравнений (СЛАУ) описывается при помощи фундаментальной системы решений. Напомним, что столбцы фундаментальной системы решений линейно независимы, а любое решение однородной СЛАУ представляется в виде линейной комбинации столбцов фундаментальной системы решений. Другими словами, фундаментальная система решений – это базис в подпространстве всех решений данной однородной СЛАУ. Каждый столбец фундаментальной системы решений представляет собой координатную запись вектора линейного подпространства Н^⊥ в выбранном базисе е евклидова пространства Ε, при этом такие векторы в совокупности образуют базис подпространства H^⊥. Мы здесь можем не различать фундаментальную систему решений системы (3.13) и соответствующий ей базис ортогонального дополнения H^⊥.

Пример 3.16. Пусть линейное подпространство Н представляет собой линейную оболочку системы векторов, заданных координатами в некотором фиксированном ортонормированием базисе е четырехмерного евклидова пространства Ε:

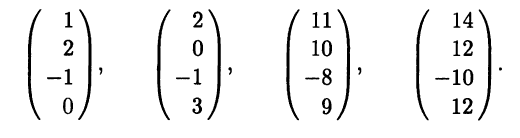
Найдем какой-либо базис ортогонального дополнения H^⊥.

Записываем систему вида (3.13), используя координаты векторов a_i.

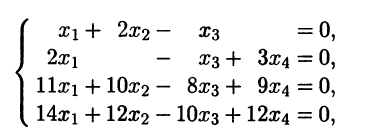
и находим ее фундаментальную систему решений. Это можно сделать, например, с помощью приведения матрицы системы к ступенчатому виду методом элементарных преобразований [III]. В качестве базисных переменных выберем x₁ и x₂. Тогда фундаментальная система решений будет содержать два решения, например:

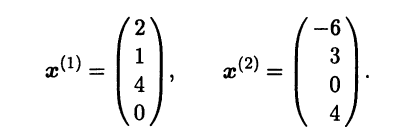
Cтолбцы найденной фундаментальной системы решений представляют собой координаты двух векторов f₁, f₂ из Ε, образующих базис линейного подпространства H^⊥, но этот базис не является ортонормированным. Чтобы получить ор-онормированный базис H^⊥, достаточно применить процесс ортогонализации Грама – Шмидта. Сделав это, находим векторы g₁ = f₁,

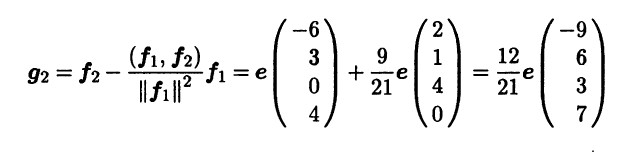
и ортонормированный базис в линейном пространстве H^⊥:

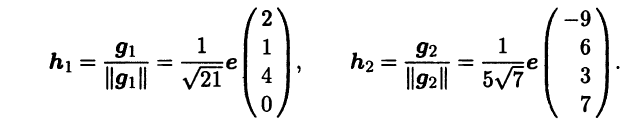
Дополнение 3.1. Нормы матриц

В линейном пространстве М_n(R) квадратных матриц порядка n норму можно задавать различными способами. Например, это линейное пространство можно трактовать как n²–мерное линейное арифметическое пространство со стандартным скалярным умножением, которому соответствует евклидова норма. Для матрицы А = (a_ij) ∈ М_n(R) эта норма имеет вид

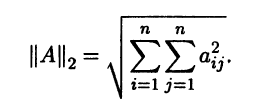
Ее называют евклидовой нормой или l₂-нормой.

Евклидова норма матрицы никак не связана с расположением элементов матрицы по строкам и столбцам. Это обычно нежелательно, и поэтому она используется редко. Больший интерес представляют нормы матриц, использующие специфику записи матриц. Такая норма может быть связана с некоторой нормой, заданной для столбцов матрицы. Важно также и то, как норма связала с операцией умножения матриц. В этом разделе векторы линейных арифметических пространств удобно записывать как матрицы-столбцы, отождествляя векторы со столбцами их координат в стандартном базисе (см. замечание 1.4).

Определение 3.9. Пусть в линейном арифметическом пространстве Rⁿ задана норма ||•||_*. Норму ||•||_m в линейном пространстве М_n(R) называют согласованной с нормой ||•||_*, если для любой матрицы А ∈ М_n(R) и любого столбца x ∈ Rⁿ выполняется соотношение

||Ax||_* ≤ ||Ax||_m||x||_* (3.14)

Каждая ли норма в Rⁿ имеет согласованную с ней норму в М_n(R)? Ответ на этот вопрос утвердительный. Приведем пример такой нормы. Пусть в Rⁿ задана норма ||•||_*. На линейном пространстве матриц М_n(R) рассмотрим функцию

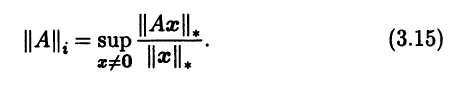
Из формулы не ясно, всегда ли определена указанная функция, т.е. всегда ли точная верхняя грань имеет конечное значение. Отметим, что, согласно аксиомам нормы и свойствам матричного умножения,

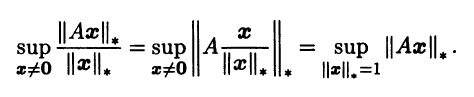
Следовательно, значение ||А||_i равно точной верхней грани функции ||Ax||_*, на множестве {x ∈ Rⁿ: ||x||_* = 1}. Можно покаказать, что это множество замкнутое и ограниченное (в частных случаях это показывает пример 3.8), а функция ||Ax||_*
непрерывна на нем. На замкнутом ограниченном множестве непрерывная функция ограничена и достигает точной верхней грани [V]. Значит, величина ||Ax||_i конечна, причем существует такой вектор у ∈ Rⁿ единичной нормы, что ||А||_i = ||Ау||_*.

Итак, соотношение (3.15) корректно задает функцию на линейном пространстве М_n(R). Покажем, что эта функция является нормой, т.е. верны три аксиомы нормы. Выполнение аксиомы а) очевидно. Проверим аксиому б):

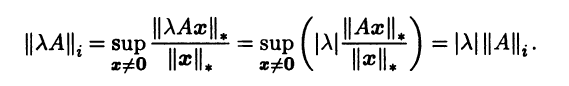
Аксиома в) нормы также верна:

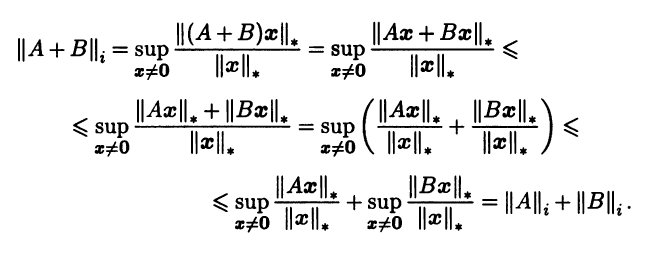
Норму, определенную соотношением (3.15), называют индуцированной (или подчиненной, операторной) и используют для нее то же обозначение, что и для порождающей ее исходной нормы в Rⁿ:

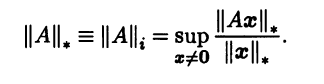
Индуцированная норма всегда согласована с исходной нормой в Rⁿ, так как для любой матрицы А и любого x ≠ 0

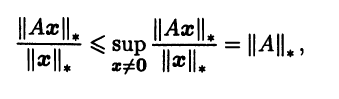
что эквивалентно (3.14) при ||А||_m = ||A||_*. Индуцированная норма является наименьшей из всех норм, согласованных с данной нормой в Rⁿ. Действительно, пусть задана норма ||•|| в линейном пространстве матриц М_n(R), согласованная с нормой ||•||_* в Rⁿ. Выберем произвольную матрицу А, а в качестве вектора х выберем тот, на котором функция ||Аx||_* достигает наибольшего значения на множестве {||x|| = 1} всех векторов единичной нормы. Тогда

||A||_* = ||Ax||_* ≤ ||A||||x||_* = ||A||,

так как норма ||•||согласована с нормой ||•||_*.

Говорят, что норма ||•|| в линейном пространстве матриц M_n(R) является матричной, или кольцевой, если

||AB||≤||A||||B||.

Первый термин не совсем удачен, так как более естественно назвать матричной любую норму, заданную в линейном пространстве матриц. Отметим, что любая индуцированная норма является кольцевой, так как

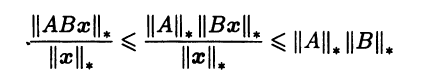
для любого ненулевого столбца x в силу согласованности индуцированной нормы. Поэтому

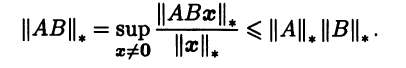
Задавая различные нормы в Rⁿ, мы получаем индуцированные нормы в линейном пространстве матриц М_n(R). Выберем в Rⁿ евклидову норму ||•||₂:

||x||₂ = √(x²₁ + … + x²_n)

где х = (x₁, … , х_n). Индуцированную ею норму в линейном пространстве матриц М_n(R) называют спектральной нормой. Это название вызвано тем, что спектральная норма ||A||₂ матрицы А равна √λ, где λ – максимальное собственное значение матрицы А^TА.

Задав в Rⁿ l₁ – норму

||x||₁ = |x₁| + … + |x_n|,

в качестве индуцированной получим следующую норму:

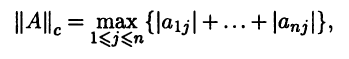
т.е. нормой матрицы А = (а_ij) ∈ М_n(R) является максимальная из l₁ – норм столбцов этой матрицы. Поэтому ее называют максимальной столбцевой или октаэдрической.

В качестве нормы в Rⁿ выберем l∞-норму

||x||_∞ = max{|x₁|,…,|x_n|}.

Тогда индуцированной нормой будет функция

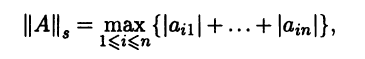
т.е. нормой матрицы А = (a_ij) ∈ М_n(R) будет максимальная из l₁-норм строк этой матрицы. Поэтому ее называют максимальной строчной или кубической.

Особо стоит евклидова норма матриц ||A||₂, которая не является индуцированной. Действительно, непосредственно из определения (3.15) индуцированной нормы следует, что, какова бы ни была норма в Rⁿ, индуцированная норма единичной матрицы всегда равна единице. Однако нетрудно убедиться, что евклидова норма единичной матрицы Е ∈ М_n(R) равна √n > 1 (при n > 1).

Евклидова норма матриц является кольцевой. Действительно, пусть даны квадратные матрицы А = (a_ij) и В = (b_jk) порядка n. Их произведением будет матрица С = (с_ikx) с элементами
c_ik = а_i1b_1k + а_i2b_2k + … +а_inb_nk. Так как, согласно неравенству Коши,

c²_ik ≤ (а²_i1+ … + а²_in)(b²_1k+ … + b²_nk),

заключаем, что

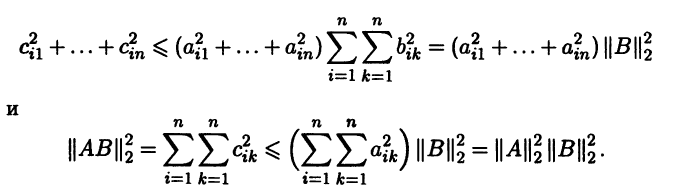
В линейном пространстве матриц М_n(R), интерпретируя его как линейное арифметическое пространство Rⁿ , можно задать l₁-норму

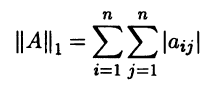
и l_∞ -норму

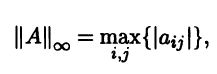
где А = (a_ij) ∈ M_n(R). В приложениях теории матриц первая норма заметного интереса не представляет. Вторая норма оце-нивает величину матрицы по максимальному из абсолютных значений ее элементов и необходима при изучении свойств различных методов вычислений. Можно показать, что l_∞-норма в М_n(R) не является кольцевой, а потому она не согласована ни с какой нормой в Rⁿ. Этот недостаток можно нейтрализовать, модифицировав эту норму. Новая норма

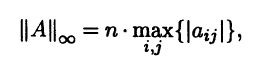
отличающаяся от старой корректирующим множителем n, равным порядку матрицы, уже является кольцевой и согласована с тремя основными нормами в Rⁿ: евклидовой, l₁-нормой и l_∞-нормой.

Дополнение 3.2. Метод наименьших квадратов

Постановка задачи. Рассмотрим систему из n линейных алгебраических уравнений (СЛАУ) относительно к неизвестных

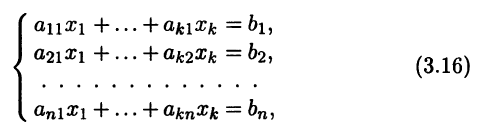
или в матричной записи

Ax = b. (3.17)

Каждому набору значений неизвестных сопоставим числа

d_i = b_i – (a_1ix₁ + … + a_kix_k), i = 1,n,

которые называют невязками уравнений системы для задан-ного набора значений неизвестных. Очевидно, что набор зна-чений неизвестных является решением системы тогда и только тогда, когда соответствующие ему невязки всех уравнений си-стемы равны нулю.

Отметим, что функция

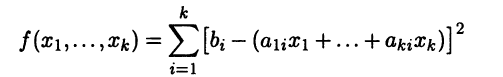
на решениях системы равна нулю и положительна в остальных случаях. Поэтому ее можно рассматривать как оценку отклоне-ния набора значений неизвестных от точного решения системы. Если система несовместна, то часто возникает задача найти вместо отсутствующих решений такой набор значений неизвестных, который приводит к наименьшему значению функции f. Такой подход в решении некорректной (т.е. не имеющей решений) задачи называют методом наименьших квадратов, поскольку ищется минимум функции, являющейся суммой квадратов.

Сформулированная задача по своему типу относится к классу задач минимизации функций многих переменных [V] и мо-жет быть решена общими методами поиска минимума. Однако ей можно придать алгебро-геометрическую интерпретацию и полностью решить методами линейной алгебры. Для придания задаче такой интерпретации будем трактовать столбцы коэф-фициентов при неизвестных, столбец правых частей уравнений (3.16) как столбцы координат векторов a₁, …, а_k;, b евклидова арифметического пространства Rⁿ в стандартном базисе, отождествляя при этом векторы с их столбцами координат (см. замечание 1.4). Тогда и набор невязок уравнений системы мож-но рассматривать как вектор d = (d₁, …, d_n) ∈ Rⁿ, который, согласно определению невязок, определяется соотношением

d = b – (x₁a₁ + … + x_ka_k).

Число ||d|| назовем невязкой СЛАУ (3.17). Вычислив скалярный квадрат вектора d, находим

||d||² = f (x₁, … , x_k)

Следовательно, задача сводится к определению таких действи-тельных коэффициентов х₁, …, x_k при которых величина ||d|| имеет наименьшее значение.

Решение задачи. Введем линейное подпространство H = span{a₁,…,a_k} и его ортогональное дополнение H^⊥. Разложим вектор b на его ортогональную проекцию на линейное подпространство Н и соответствующую ортогональную составляющую:

b = h + h^⊥, h ∈ H, h^⊥ ∈ H^⊥.

Тогда

d = h + h^⊥ – (x₁a₁ + … + x_ka_k) = h^⊥ + (h – x₁a₁ – … – x_ka_k) = h^⊥ + d₀,

где

d₀ = h – x₁a₁ – … – x_ka_k ∈ H.

Так как d₀ ⊥ h^⊥,то по теореме Пифагора заключаем, что

||d||² = ||d₀||² + ||h^⊥||²

Ортогональная составляющая h^⊥ вектора невязок постоянна и от выбора коэффициентов х_i не зависит. Поэтому минимизация величины ||d||² сводится к поиску минимума величины ||d₀||². Эта величина является неотрицательной и достигает минимума, если обращается в нуль, т.е. при условии, что d₀ = 0. А это равносильно тому, что d = h^⊥, т.е. вектор невязок принадлежит ортогональному дополнению H^⊥ и поэтому является решением системы

(a_j, d) = 0, j = 1,k, (3.18)

или

(а_j, b – x₁a₁ – … – х_kа_k) = 0, j = 1,k,

(см. 3.9). После преобразований получаем СЛАУ

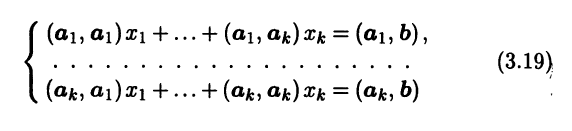
относительно неизвестных х₁, …, х_k. Матрица этой системы Г = ((а_i,а_j)) – это квадратная матрица порядка k, представляющая собой матрицу Грама для системы векторов a₁, …, a_k.

Теорема 3.7. Если система векторов а₁, …, а_k линейно независима, то ее матрица Грама является невырожденной.

◄ Докажем равносильное утверждение, что если матрица Грама системы векторов а₁, …, а_k вырождена, то эта система векторов линейно зависима. Вырожденность матрицы Грама означает, что ее столбцы линейно зависимы и один из них, например первый, является линейной комбинацией остальных [III]:

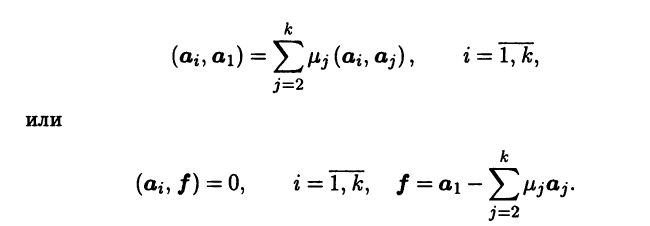
Следовательно, вектор f принадлежит ортогональному дополнению линейного подпространства span{a₁,…,a_k}, а поскольку f ∈ span{a₁,…,a_k}, то f = 0, т.е.

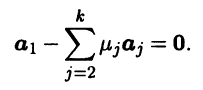
Это равенство означает, что векторы a₁, … , a_k линейно зависимы, так как коэффициент при a₁ не равен нулю. ►

Отметим, что система линейных алгебраических уравнений (3.19) всегда совместна: ее решениями являются коэффициенты разложения вектора h ∈ H = span{a₁,… ,a_k} по системе векторов a₁, …, а_k, так как в этом случае вектор d = b – h = h^⊥ – решение системы (3.18). Если система векторов a₁, …, а_k линейно независима, то, согласно доказанной теореме, матрица СЛАУ (3.19) невырождена и эта система имеет единственное решение, которое дает решение исходной задачи. Если же указанная система векторов линейно зависима, то матрица СЛАУ
(3.19) вырождена. В этом случае квадратная СЛАУ (3.19), будучи совместной, имеет бесконечно много решений и каждое из них дает решение исходной задачи. Среди этих решений можно выбирать те, которые удовлетворяют каким-то дополнительным условиям.

Дополнение 3.3. Псевдорешения и псевдообратная матрица

Рассмотрим систему линейных алгебраических уравнений (СЛАУ) Ах = b, вообще говоря, несовместную, с матрицей А типа n × k. Мы остановимся на тех столбцах x, которые для рассматриваемой системы дают минимальную невязку. Если СЛАУ Ах = b совместна, то такие столбцы представляют собой ее решения. Если же СЛАУ несовместна, то столбцы, дающие минимальную невязку, можно находить при помощи метода наименьших квадратов. В этом разделе изложим другой метод их нахождения, используя отождествление векторов евклидова арифметического пространства Rⁿ с матрицами-столбцами их координат в стандартном базисе.

СЛАУ Ах = b соответствует СЛАУ А^TАх = А^Tb, которую называют нормальной.

Пусть a₁, …, a_k ∈ Rⁿ – столбцы матрицы А. СЛАУ Ах = b может быть записана в векторной форме:

x₁a₁ + … + x_kа_k = b.

Совместность СЛАУ Ах = b означает, что вектор b ∈ Rⁿ попадает в линейную оболочку H системы векторов a₁, …, а_k. Пусть b ∉ Н. Разложим вектор b в сумму b = h + h^⊥, где h – ортогональная проекция вектора b на линейное подпространство
H, a h^⊥ – ортогональная составляющая этого вектора. Введенные обозначения используем в формулировках и доказательстве следующих трех теорем.

Теорема 3.8. Для любой СЛАУ Ах = b следующие множества совпадают:

– множество столбцов, дающих минимальную невязку для этой СЛАУ;

– множество решений СЛАУ Ах = h;

– множество решений нормальной СЛАУ А^TАх = А^Tb.

◄ Норма вектора h^⊥ представляет собой минимальную невязку СЛАУ Ах = b (см. Д.3.2), а множество векторов, дающих такую невязку, представляют собой решения СЛАУ Ах = h.

Условие h^⊥ ∈ Н^⊥ равносильно тому, что вектор h^⊥ ортогонален каждому из векторов a₁, …, a_k, т.е.

(a_i,h^⊥) = 0, i = 1,k.

Мы имеем СЛАУ относительно компонент столбца h^⊥, которая в матричной форме имеет вид A^Th^⊥ = 0.

Умножим СЛАУ Ах = h, решения которой дают для си-стемы Ах = b минимальную невязку, на матрицу А^T слева. Учитывая, что А^TА = 0, получим

А^TАх = A^Th = A^Th + A^Th^⊥ = А^⊥b.

Значит, все векторы х, дающие для СЛАУ Ах = b минимальную невязку, являются решениями СЛАУ А^TАх = А^Tb. Верно и обратное: если вектор х является решением системы A^TАх = А^Tb, то для СЛАУ Ах = b он дает минимальную невязку. Действительно, если А^TАх = А^Tb, то А^T(b – Ах) = 0, а это означает, что вектор b’ = b – Ах ортогонален векторам a₁, …, а_k и, следовательно, принадлежит линейному пространству, Н^T. Поскольку b” = Ах ∈ Н, то b = b” + b’. Согласно следствию 3.1, последнее равенство совпадает с разложением b = h + h^⊥. Поэтому b’ = h^⊥, а норма вектора b’, представляющая собой невязку, будет минимальной. ►

Теорема 3.9. Нормальная система линейных алгебраических уравнений всегда совместна.

◄ СЛАУ Ах = b соответствует нормальная СЛАУ А^TАх = А^Tb. Решениями нормальной СЛАУ являются векторы х, дающие минимальную невязку для исходной СЛАУ Ах = b и являющиеся решениями СЛАУ Ах = h. Последняя же система всегда имеет решения, так как в векторной форме она имеет вид x₁a₁ + … + x_ka_k = h, где h ∈ H = span{a₁,… ,a_k}. ►

Теорема 3.10. Для того чтобы нормальная СЛАУ А^TАх = А^Tb имела единственное решение, необходимо и достаточно, чтобы:

– однородная СЛАУ Ах = 0 была определенной;

– ранг матрицы А совпадал с количеством ее столбцов;

– векторы a₁, …, а_k были линейно независимы.

◄ Так как множества решений систем Ах = h и А^TАх = А^Tb совпадают, то из теоремы о структуре общего решения СЛАУ [III] следует, что тогда совпадают и множества решений соответствующих однородных систем Ах = 0 и А^T Ах = 0. Если эти однородные системы определенны, т.е. имеют единственное решение, то СЛАУ Ах = b имеет единственный вектор с минимальной невязкой и наоборот. Для того чтобы однородная система Ах = 0 имела единственное решение, необходимо и достаточно, чтобы ранг матрицы А был равен количеству столбцов в ней, или, другими словами, чтобы столбцы матрицы были линейно независимы [III]. ►

Псевдорешения и их свойства. Если для системы Ах = b бесконечное количество векторов х дает минимальную невязку, то обычно выбор останавливают на том из них, который имеет минимальную норму. Такой вектор называют нормальным псевдорешением (или просто псевдорешением) СЛАУ Ах = b. Таким образом, псевдорешение системы линейных ал-гебраических уравнений – это такой вектор, который дает минимальную невязку в этой системе и среди таких векторов имеет минимальную норму.

Теорема 3.11. Любая СЛАУ имеет псевдорешение, и притом единственное.

◄ Множество всех векторов х, дающих минимальную невязку для СЛАУ Ах = b, описывается формулой

x = x_x + x_о, (3.20)

где х_ч – некоторое частное решение соответствующей нормальной СЛАУ; х_о – общее решение однородной СЛАУ А^TАх = 0, которое является общим решением и однородной СЛАУ Ах = 0 (см. доказательство теоремы 3.10).

Обозначим через K линейное подпространство всех решений однородной СЛАУ Ах = 0. Тогда имеет место представление х_ч = х^⊥_ч + х°_ч, где х°_ч ∈ K, х^⊥_ч ∈ K^⊥, и поскольку х°_ч + х_о ∈ K, то для любого x вида (3.20), согласно теореме Пифагора, имеем

||x||² = ||x_ч + x_о||² = ||x^⊥_ч + (x^о_ч + x_о)||² + ||x^⊥_ч||² + ||x^о_ч + x^о||² ≥ ||x^⊥_ч||²

Равенство ||x|| = ||x^⊥_ч||² возможно и притом лишь в единственном
случае, когда x°_ч + х_o = 0, или х = х 1/ч. Следовательно, среди векторов, дающих минимальную невязку СЛАУ Ах = b, минимальную норму будет иметь вектор и только он. Этот вектор является ортогональной составляющей (любого) частного решения нормальной СЛАУ относительно линейного подпространства K всех решений соответствующей однородной СЛАУ Ах = 0. ►

Оказывается, что для любой СЛАУ можно построить такую другую СЛАУ, единственным решением которой является псевдорешение исходной СЛАУ. Для нахождения такой СЛАУ воспользуемся тем, что, согласно доказательству теоремы 3.11, условие минимальности нормы псевдорешения СЛАУ Ах = b означает его ортогональность всем векторам линейного подпространства K решений соответствующей однородной системы Ах = 0. Ортогональность линейному подпространству K равносильна тому, что псевдорешение ортогонально каждому из векторов произвольно выбранной фундаментальной системы решений СЛАУ Ах = 0. Условия ортогональности представляют собой линейные уравнения, добавив которые к нормальной СЛАУ, мы и получим такую СЛАУ, единственным решением которой будет псевдорешение системы Ах = b.

Пример 3.17. Если матрица А нулевая, то псевдорешением СЛАУ Ах = b является нулевой вектор. Действительно,в этом случае невязка не зависит от выбора вектора х и равна ||b||. Минимальную же норму среди всех векторов линейного арифметического пространства имеет нулевой вектор.

Пример 3.18. Если матрица А является квадратной и невырожденной, то псевдорешение СЛАУ Ах = b совпадает с ее обычным решением, так как минимальная невязка, равная нулю, будет достигаться на единственном векторе, являющемся решением этой системы. Псевдорешение совпадет с решением и в случае, когда матрица А не является квадратной, но имеет ранг, совпадающий с количеством столбцов. Это возможно в том случае, когда число строк превышает число столбцов. Такую систему можно заменить эквивалентной ей квадратной, отбрасывая лишние уравнения.

Пример 3.19. Рассмотрим простейшую систему

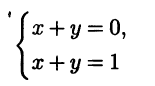
двух уравнений с двумя неизвестными. Видно, что эта система несовместна. Последовательно вычисляем

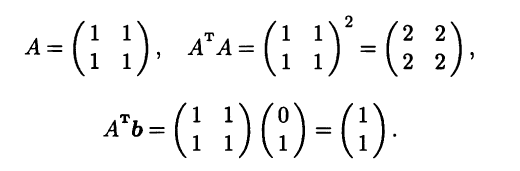
Таким образом, нормальная СЛАУ в этом случае состоит из двух одинаковых уравнений:

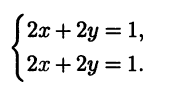
Множество решений нормальной системы, т.е. множество пар х, у, дающих минимальную невязку в исходной системе, на плоскости изображается прямой х + у = 0,5 (рис. 3.7), а псевдорешением будет точка этой прямой, ближайшая к началу координат, т.е. точка с координатами х = 0,25, у = 0,25. Этой точке соответствует радиус-вектор с наименьшей нормой среди всех радиус-векторов точек прямой х + у = 0,5.

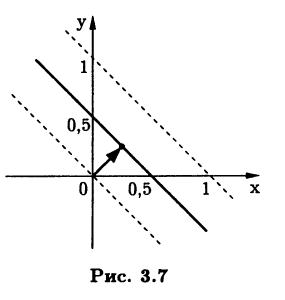
Если одно из уравнений исходной системы умножить на ко-эффициент, то и множество решений нормальной системы, и псевдорешение данной системы изменятся. Это достаточно очевидно, так как умножение уравнения на коэффициент изме-няет, вообще говоря, его невязку. Например, умножив второе уравнение рассматриваемой системы на 2:

и вычислив

находим, что нормальная СЛАУ и в этом случае будет состоять из двух идентичных уравнений 5х + 5у = 4, но они уже другие. Псевдорешением рассматриваемой системы будет х = 0,4, y = 0,4.

Пример 3.20. Рассмотрим на плоскости треугольник с вершинами (1; 1), (2;2), (3;1) (рис. 3.8). Прямые, на которых лежат стороны этого треугольника, опишем при помощи нормальных уравнений и составим из них систему

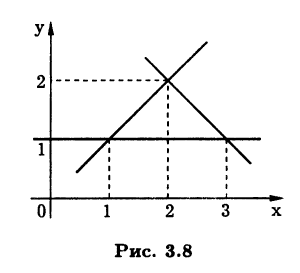
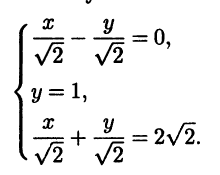
Полученная система несовместна, так как три прямых не имеют общей точки.

Определим для полученной системы нормальную СЛАУ. Для этого последовательно находим:

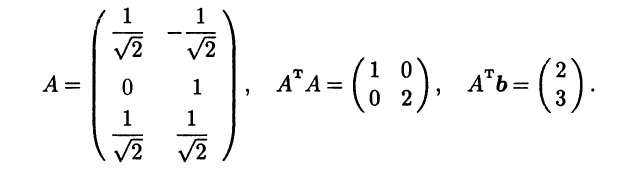
Нормальная СЛАУ A^T Ax = A^Tb имеет единственное решение х = 2, у = 1,5, являющееся (в силу единственности) псевдорешением исходной системы.

Так как прямые плоскости заданы нормальными уравнени-ями, квадрат невязки системы для вектора (х₀, у₀) будет равен сумме квадратов расстояний от точки (x₀;y₀) до трех прямых. Найденному псевдорешению на плоскости соответствует точка (2;1,5), сумма квадратов расстояний от которой до трех сторон треугольника является минимальной. #

Псевдорешения сохраняют линейные свойства решений ли-нейных систем.

Теорема 3.12. Если х₁ – псевдорешение системы Ах = b₁, x₂ – псевдорешение системы Ах = b₁, то λ₁x₁ + λ₂x₂ – псевдорешение системы Ах = λ₁b₁ + λ₂b₂.

◄ Из условий теоремы вытекает, что x_i является решением нормальной СЛАУ А^TАх = A^Tb_i, i = 1,2. Значит, λ₁x₁ + λ₂x₂ является решением нормальной СЛАУ А^TАх = А^Tλ₁b₁ + А^Tλ₂b₂, и нам остается показать, что при этом λ₁x₁ + λ₂x₂ имеет минимальную норму или, что то же самое, λ₁x₁ + λ₂x₂ и любое решение у однородной СЛАУ Ау = 0 ортогональны.

Отметим, что псевдорешения x_i ортогональны всем решениям СЛАУ Ау = 0 как псевдорешения систем, различающихся лишь правыми частями. Это значит, что (у, x_i) = 0, если Ау = 0. Поэтому

(у, λ₁x₁ + λ₂x₂) = λ₁(у, x₁) + λ₂ (у, x₂) = 0,

если Ау = 0. ►

Псевдообратная матрица. Решение СЛАУ Ах = b с квадратной невырожденной матрицей А может быть записано с помощью обратной матрицы в виде x = А^-1b [III]. Обратная матрица А^-1 является решением матричного уравнения АХ = Е, где Е – единичная матрица, а столбцы с_i обратной матрицы являются решениями систем Ag_i = е_i, i = 1,n, где е₁, …, е_n – стандартный базис в линейном пространстве Rⁿ (столбец е_i является также i-м столбцом единичной матрицы). Для b = (b₁ … b_n)^T справедливо разложение b = b₁e₁ + … + b_ne_n, и поэтому формула x = А^-1b в векторной форме записывается в виде x = b₁g₁ + … + b_ng_n т.е. в виде линейной комбинации решений g_i, коэффициентами в которой служат правые части b_i уравнений системы.

Этот подход позволяет обобщить понятие обратной матрицы и использовать это обобщение для нахождения псевдорешений примерно так же, как обратную матрицу для построения обычных решений.

Рассмотрим СЛАУ Ах = b с произвольной матрицей А типа n × k. Пусть g_i – псевдорешение системы Ах = е_i, где е₁, …, е_n – стандартный базис в Rⁿ. Матрицу А⁺ = (g₁ … g_n), составленную из столбцов g_i, называют псевдообратной к матрице А. Отметим, что матрица А⁺ имеет тип k×n, т.е. тот же, что и транспонированная матрица А^T.

Теорема 3.13. Псевдорешением СЛАУ Ах = b является вектор х = А⁺b.

◄ Действительно, если g_i – псевдорешение системы Ах = е_i, i = 1,n, то, согласно теореме 3.12, х = b₁g₁ +… + b_ng_n является псевдорешением системы с той же матрицей и правой частью b₁e₁ +… + b_nе_n = b , т.е. рассматриваемой системы Аx = b. ►

Как вытекает из изложенного, любая матрица имеет псевдообратную. Если матрица А квадратная невырожденная, то ее псевдообратная матрица А⁺ совпадает с обратной А^-1, так как в этом случае псевдорешения g_i систем Аx = е_i будут совпадать с обычными решениями и, следовательно, будут столбцами обратной матрицы.

Пример 3.21. Если А – нулевая матрица типа n × k, то А⁺ – также нулевая, но типа k × n. В этом случае псевдорешением системы Аx = е_i, i = 1,n, будет нулевой столбец высоты k (см. пример 3.17).

Пример 3.22. Рассмотрим матрицу

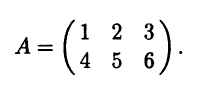
Эта матрица имеет ранг 2, а соответствующая СЛАУ при любой правой части, согласно теореме Кронекера – Капелли, будет совместна, так как ранг расширенной матрицы не может превышать двух и потому совпадает с рангом матрицы системы. Поэтому псевдорешение СЛАУ Аx = b является одним и

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ

Помогаю со студенческими работами здесь

Найти ортогональный базис подпространства
Посредством процесса ортогонализации найти ортогональный базис подпространства, натянутого на…

Дополнить базис подпространства до базиса всего пространства
Доказать, что векторы вида (3a+2b, -a-b, 2a+4b) образуют линейное подпространство в пространстве…

Найдите какой-нибудь базис и определите размерность подпространства
Найдите какой-нибудь базис и определите размерность подпространства 6-мерного пространства векторов…

Найти любые два вектора, образующие базис подпространства
Рассмотрим плоскость в трехмерном пространстве R3, задаваемую уравнением вида x−2y+3z=0.
Все…

Искать еще темы с ответами

Или воспользуйтесь поиском по форуму: