Как найти ортогональный вектор к прямой

Ортогональность векторов. Перпендикулярность векторов.

Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).

рис. 1

Примеры задач на ортогональность векторов

Примеры плоских задач на ортогональность векторов

Так в случае плоской задачи для векторов a = < a_x ; a_y > и b = < b_x ; b_y > , условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) = 2 – 2 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 3 · 7 + (-1) · 5 = 21 – 5 = 16

Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 = 2 n + 4
2 n + 4 = 0
2 n = -4
n = -2

Ответ: вектора a и b будут ортогональны при n = -2.

Примеры пространственных задач на ортогональность векторов

Так в случае пространственной задачи для векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z >, условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 – 2 + 0 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 + 1 · (-8)= 2 n + 4 – 8 = 2 n – 4
2 n – 4 = 0
2 n = 4
n = 2

Ответ: вектора a и b будут ортогональны при n = 2.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Ортогональные векторы

В данной публикации мы рассмотрим, какие векторы называются ортогональными, какое условие при этом должно выполняться. Также разберем примеры решения задач по этой теме.

Условие ортогональности векторов

Векторы a и b являются ортогональными, если угол между ними прямой (т.е. равен 90°).

Примечание: Скалярное произведение ортогональных векторов равняется нулю. Это и есть существенное условие их ортогональности.

a · b = 0

То есть, если в плоскости и , то

Примеры задач

Задание 1
Докажем, что векторы и ортогональны.

Решение:
a · b = 2 · (-2) + 4 · 1 = 0

Следовательно, заданные векторы являются ортогональными, так как их скалярное произведение равняется нулю.

Задание 2
При каком значении n векторы и ортогональны.

Решение:
a · b = 3 · 6 + (-9) · n = 0
18 – 9n = 0
n = 2

Таким образом, a и b ортогональны при n, равном двум.

Ортогональные векторы и условие ортогональности

В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.

Ортогональные векторы: определение и условие

Ортогональные векторы — это векторы a ¯ и b ¯ , угол между которыми равен 90 0 .

Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.

Примеры решения задач на ортогональность векторов

Плоские задачи на ортогональность векторов

Если дана плоская задача, то ортогональность для векторов a ¯ = < a x × a y >и b ¯ = < b x × b y >записывают следующим образом:

a ¯ × b ¯ = a x × b x + a y × b y = 0

Задача 1. Докажем, что векторы a ¯ = < 1 ; 2 >и b ¯ = < 2 ; – 1 >ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( – 1 ) = 2 – 2 = 0

Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.

Задача 2. Докажем, что векторы a ¯ = < 3 ; – 1 >и b ¯ = < 7 ; 5 >ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 3 × 7 + ( – 1 ) × 5 = 21 – 5 = 16

Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.

Задача 3. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 >и b ¯ = < n ; 1 >будут ортогональными.

Как решить?

Найдем скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 = 2 n + 4 2 n + 4 = 0 2 n = – 4 n = – 2

Ответ: векторы являются ортогональными при значении n = 2 .

Примеры пространственных задач на ортогональность векторов

При решении пространственной задачи на ортогональность векторов a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; – 1 ; 10 >условие записывается следующим образом: a ¯ × b ¯ = a x × b x + a y × b y + a z × b z = 0 .

Задача 4. Докажем, что векторы a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; – 1 ; 10 >являются ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( – 1 ) + 0 × 10 = 2 – 2 = 0

Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.

Задача 5. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 ; 1 >и b ¯ = < n ; 1 ; – 8 >будут являться ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 + 1 × ( – 8 ) = 2 n + 4 – 8 = 2 n – 4 2 n – 4 = 0 2 n = 4 n = 2

Ответ: векторы a ¯ и b ¯ будут ортогональными при значении n = 2 .

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/vektory/ortogonalnye-vektory-i-uslovie-ortogonalnosti/

[/spoiler]



2.5.8. Как найти проекцию вектора на прямую?

Об ортогональной проекции вектора на вектор мы говорили ранее, и фактически было установлено

следующее:

Чтобы найти ортогональную проекцию вектора на прямую, нужно найти его проекцию на любой направляющий вектор этой прямой.

…возможно, не всем понятен термин «ортогональная» – это такая проекция, при которой на вектор «падают лучи света» строго

перпендикулярно по отношению к прямой (см. рис. ниже). Существует куча иных («косых») проекций, когда проецирование осуществляется под

другими углами, но для данной книги этот материал не столь актуален.

Решим символическую задачку:

Задача 85

Найти проекцию вектора  на прямую

Решение: найдём какой-нибудь направляющий вектор прямой, проще и быстрее

взять стандартный вариант: .
Проекция вектора на прямую – есть его проекция на любой направляющий вектор этой прямой, по

соответствующей формуле:

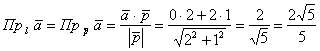
Ответ:

Напоминаю, что проекция – это длина «тени» вектора  (красный цвет):

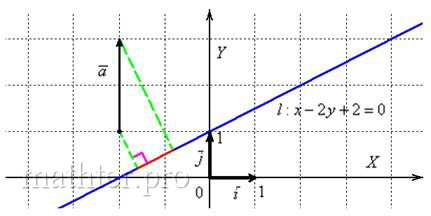
Желающие могут взять любые точки  прямой, найти направляющий вектор  и убедиться в том, что проекция  будет такой же, как вариант, со знАком «минус».

Ну вот и подошло к концу наше путешествие по основным задачам с «плоской» прямой, и никакого Кащея Бессмертного тут нет…. – Здесь есть я, с

новыми знаниями и задачами J  Потому что Бабу-Ягу никто не отменял =)

2.6. Линейные неравенства

2.5.7. Как найти угол между прямыми?

| Оглавление |



Автор: Aлeксaндр Eмeлин

В данной публикации мы рассмотрим, какие векторы называются ортогональными, какое условие при этом должно выполняться. Также разберем примеры решения задач по этой теме.

• Условие ортогональности векторов
• Примеры задач

Условие ортогональности векторов

Векторы a и b являются ортогональными, если угол между ними прямой (т.е. равен 90°).

Примечание: Скалярное произведение ортогональных векторов равняется нулю. Это и есть существенное условие их ортогональности.

a · b = 0

То есть, если в плоскости a = {a_x; a_y} и b = {b_x; b_y}, то a · b = a_x · b_x + a_y · b_y = 0

Примеры задач

Задание 1
Докажем, что векторы a = {2; 4} и b = {-2; 1} ортогональны.

Решение:
a · b = 2 · (-2) + 4 · 1 = 0

Следовательно, заданные векторы являются ортогональными, так как их скалярное произведение равняется нулю.

Задание 2
При каком значении n векторы a = {3; -9} и b = {6; n} ортогональны.

Решение:
a · b = 3 · 6 + (-9) · n = 0
18 – 9n = 0
n = 2

Таким образом, a и b ортогональны при n, равном двум.

Пусть

Тогда

Доказательство.

а) Необходимость().
Пусть

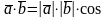
=0.

а) Достаточность().
Пусть

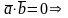
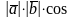
=0.
Так как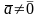
и

, то

и

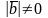
cos
=0

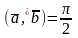
(поскольку

Î
[0, π])

.

Раздел
№4.

1.1)Параметрические
уравнения прямой по точке и направляющему
вектору.

1. Пусть М(x,y)
– произвольная точка, лежащая на прямой

.
Покажем, что ee координаты
удовлетворяют уравнению (2).

Так как
М(x,y)∈
l и М₀(x₀,y₀)∈
l , то

.
Тогда

.
Следовательно,

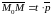
для некоторого

.
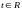
В координатной форме:

(2) параметрические уравнения
прямой по точке


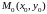
и направляющему вектору

.
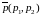
t – параметр.

1.2)Каноническое
уравнение прямой по точке и направляющему
вектору.

Выразим
из обоих уравнений (2) параметр t.

каноническое
уравнение прямой по точке


и направляющему вектору

.

1.3) Уравнение прямой, проходящей через 2 точки

Пусть
на прямой l заданы
точки

и

.
Тогда вектор

является направляющим вектором для

.

Согласно
(3), уравнение

по точке

и направляющему вектору

имеет вид

– уравнение прямой, проходящей через
точки M₁(x₁,y₁)
и M₂(x₂,y₂)

1.4) Уравнение прямой в отрезках на осях

Пусть
прямая

проходит через точки А(а, 0) и В(0,
b).

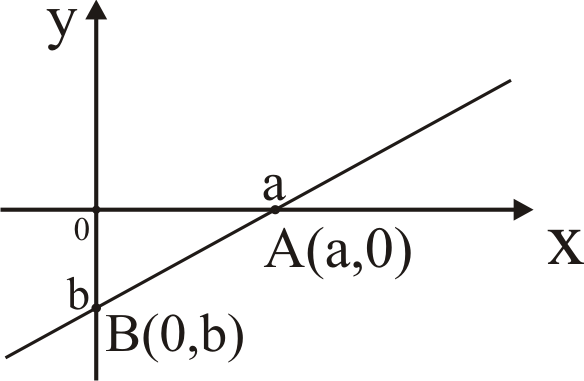
Согласно
(4), её уравнение имеет вид:

;

;

;
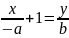
отсюда

(5) – уравнение прямой, отсекающей на
координатных осях отрезки a
и b
соответственно.

1.5) Общее уравнение прямой

Теорема
1. В аффинной системе координат всякое
уравнение первой степени

Ах+Ву+С=0, где А²+В²
0 (7)

задает
прямую с направляющим вектором

.

Обратно, любая прямая на плоскости имеет
уравнение вида (7) – общее уравнение
прямой.

Доказательство:
1) Пусть в аффинной системе координат
дано уравнение Ах+Ву+С=0,

.
Покажем, что все точки, координаты
которых удовлетворяют (7), лежат на одной
прямой с направляющим вектором

Пусть

–
фиксированная точка, координаты которой
удовлетворяют (7), а

– любая другая точка, удовлетворяющая
(7), тогда

Если A0
и B0, то

(*). Получаем, что координаты точки

удовлетворяют уравнению (*), которое
является уравнением прямой вида (3) по
точке

и направляющему вектору

.
Таким образом, все точки, удовлетворяющие
уравнению (7), лежат на прямой (*).

Если
А=0, то By+C=0;

(**) – уравнение прямой, параллельной оси
Оx.

Если
В=0, то Ax+C=0;

(***) – уравнение прямой параллельной оси
Оy.

Таким
образом, в любом случае все точки

,
удовлетворяющие уравнению (7) лежат на
одной прямой на плоскости.

2)
Пусть прямая

на плоскости проходит через точку

с направляющим вектором

.
Покажем, что её уравнение можно привести
к виду (7).

Если
A0
и B0, согласно
(3), уравнение

:

.
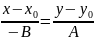
Умножим обе части уравнения на АВ:

.

Обозначив
–Ax₀–By₀=C,
получим, что прямая l имеет уравнение
вида

–
уравнение вида (7)

Если
A=0 получаем согласно
(2), уравнение l:

,
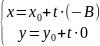
откуда при t∈ℝ
получаем x∈ℝ
a у=у₀. Таким
образом, уравнение данной прямой
приводится к виду у-у₀=0
– уравнение вида (7) где А=0, В=1, С=-y₀

Теорема
доказана.

2)Параметрические
уравнения плоскости

Пусть

– направляющие векторы плоскости

,

∦
.
Отложим

и

от точки

.

1. Покажем,
что

,
ее координаты удовлетворяют уравнениям
(1). Поскольку M₀∈,
M∈,
тогда

лежит в плоскости .
Отложим векторы

и

от точки M₀, тогда

,

,

∦
.
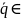
Следовательно

и

образуют на плоскости 
аффинную систему координат. Тогда вектор

разлагается по векторам

и

:

для некоторых u, v∈ℝ.
Запишем это равенство в координатной
форме:

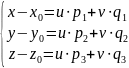
откуда

(1) – параметрические уравнения
плоскости

по точке


и направляющим векторам

,
u, v∈ℝ
параметры.

3.1)
Уравнение прямой в пространстве
по точке и направляющему вектору

Пусть
в аффинной системе координат

,

и

.

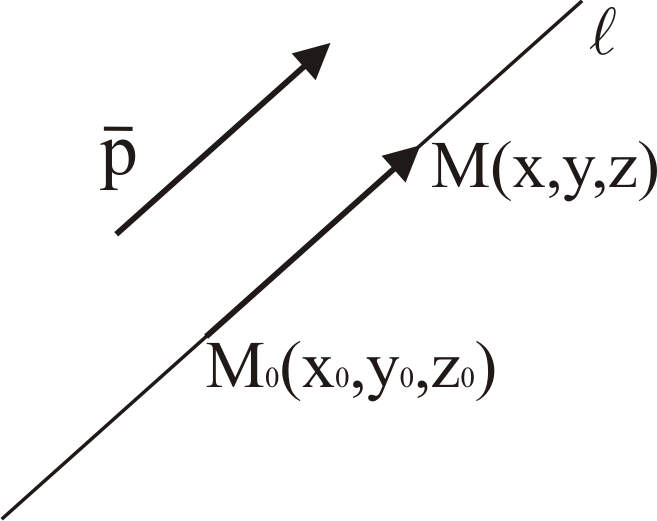
Заметим, что

для некоторого t∈ℝ


t ∈ℝ
(1) – параметрические уравнения прямой
в пространстве по точке


и направляющему вектору

.

3.2)Выразим
параметр t из каждого
уравнения (1)

–
канонические уравнения прямой в
пространстве по точке

и
направляющему вектору

.

3.3)Уравнение прямой
в пространстве по двум точкам.

Пусть в
аффинной системе координат

заданы
координаты двух точек на прямой

.
Запишем, согласно (2) канонические
уравнения прямой

по точке

и направляющему вектору

.

–
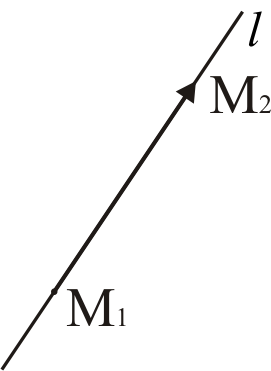
уравнения прямой в пространстве,
проходящей через две точки

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #

  30.05.201548.1 Mб31Delphi_Kuzan.pdf

• #
• #
• #
• #
• #
• #
• #
• #
• #