1) Составить характеристическое уравнение линейного оператора |A – l.E| = 0.
2) Найдем все корни характеристического уравнения.
3) Вычислим собственные векторы линейного оператора A, решая матричное уравнение (A – l.E)X=0.
4) Ортонормируем, полученный базис.
Пример. Линейный оператор A, действующий в евклидовом пространстве Е3, имеет в ортонормированном базисе E1, E2, E3 матрицу
 .
.
Найти в Е3 ортонормированный базис из собственных векторов оператора A и составить матрицу оператора A в этом базисе.
Решение. 1) Составить характеристическое уравнение линейного оператора |A – l.E| = 0.

2) Найдем все корни характеристического уравнения: l1=-1, l2 = l3 = 1. Тогда матрица линейного оператора в ортонормированном базисе, составленном из собственных векторов имеет вид
![]() .
.
3) Вычислим собственные векторы линейного оператора A, решая матричное уравнение (A – l.E)X=0.
Пусть l1=-1. Матричное уравнение (A – l1E)X=0 принимает вид:

Решая систему, находим решение X = C(1,-2,1), C€R.
Пусть l2 = l3 = 1. Матричное уравнение (A – l1E)X=0 принимает вид:

Решая систему, находим решение X = C1(2,1,0) + C2(-1,0,1), C€R.
4) Ортонормируем, полученный базис.
A1 = (1,-2,1), A2 = (2,1,0), A3 =(-1,0,1).
B1 = (1,-2,1), B2 = (2,1,0), B3 = A3 + k b2, ![]() , b3 =(-1/5, 2/5, 1/5).
, b3 =(-1/5, 2/5, 1/5).
 .
.
| < Предыдущая | Следующая > |
|---|
104. Построение ортонормированного базиса из собственных векторов самосопряженного оператора
1) Составить характеристическое уравнение линейного оператора |A – l.E| = 0.
2) Найдем все корни характеристического уравнения.
3) Вычислим собственные векторы линейного оператора A, решая матричное уравнение (A – l.E)X=0.
4) Ортонормируем, полученный базис.
Пример. Линейный оператор A, действующий в евклидовом пространстве Е3, имеет в ортонормированном базисе E1, E2, E3 матрицу
 .
.
Найти в Е3 ортонормированный базис из собственных векторов оператора A и составить матрицу оператора A в этом базисе.
Решение. 1) Составить характеристическое уравнение линейного оператора |A – l.E| = 0.

2) Найдем все корни характеристического уравнения: l1=-1, l2 = l3 = 1. Тогда матрица линейного оператора в ортонормированном базисе, составленном из собственных векторов имеет вид
 .
.
3) Вычислим собственные векторы линейного оператора A, решая матричное уравнение (A – l.E)X=0.
Пусть l1=-1. Матричное уравнение (A – l1E)X=0 принимает вид:

Пусть l2 = l3 = 1. Матричное уравнение (A – l1E)X=0 принимает вид:

4) Ортонормируем, полученный базис.
B1 = (1,-2,1), B2 = (2,1,0), B3 = A3 + k b2,  , b3 =(-1/5, 2/5, 1/5).
, b3 =(-1/5, 2/5, 1/5).
 .
.
Собственные числа и собственные векторы линейного оператора
Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x 1, x 2, . x m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x 1, x 2, . x m оператора A с попарно различными собственными числами λ1, λ2, …, λm линейно независимы.
3. Если собственные числа λ1=λ2= λm= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.
Итак, если имеется n линейно независимых собственных векторов x 1, x 2, . x n, соответствующих различным собственным числам λ1, λ2, …, λn, то они линейно независимы, следовательно, их можно принять за базис пространства Rn. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 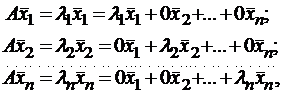 тогда
тогда  .
.
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.
Теорема. Матрица линейного оператора A в базисе < ε i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса – собственные векторы оператора A.
Правило отыскания собственных чисел и собственных векторов
Система (1) имеет ненулевое решение, если ее определитель D равен нулю
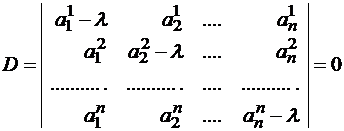
Пример №1 . Линейный оператор A действует в R3 по закону A· x =(x1-3x2+4x3, 4x1-7x2+8x3, 6x1-7x2+7x3), где x1, x2, . xn – координаты вектора x в базисе e 1=(1,0,0), e 2=(0,1,0), e 3=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e 1=(1,4,6)
A· e 2=(-3,-7,-7)
A· e 3=(4,8,7) 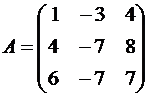 .
.
Составляем систему для определения координат собственных векторов:
(1-λ)x1-3x2+4x3=0
x1-(7+λ)x2+8x3=0
x1-7x2+(7-λ)x3=0
Составляем характеристическое уравнение и решаем его:
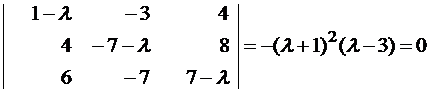
Пример №2 . Дана матрица  .
.
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.
Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x – собственный вектор



Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой ai k =ak i .
Замечания .
- Все собственные числа симметрической матрицы вещественны.
- Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.
В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.
[spoiler title=”источники:”]
http://math.semestr.ru/math/vector.php
[/spoiler]

Построение ортонормированного базиса из собственных
векторов для симметричного линейного оператора
На прошлой лекции мы изучили ортогональные и симметричные операторы в евклидовом пространстве.
Мы выяснили, что
Ортогональная матрица может не иметь действительных собственных значений.
Симметрическая матрица ВСЕГДА имеет действительное собственное значение.
Все собственные значения симметрической матрицы – действительные числа.
Собственные векторы симметрической матрицы, принадлежащие различным собственным значениям, ортогональны.
Для любой симметрической вещественной матрицы A существует ортогональная матрица U, такая, что матрица U-1AU – диагональная матрица.
Алгоритм нахождения ортонормированного базиса из собственных векторов симметрической матрицы:
I. Найти характеристические числа i заданной симметрической матрицы.
II. Если i – простой корень характеристического уравнения, то ему отвечает с точностью до множителя один собственный вектор. Нормируем его и получаем единичный вектор.
Если i – корень кратности k , то ему отвечают k линейно независимых собственных векторов. В этом случае их необходимо отогонализировать и подвергнуть нормировке – получаем k линейно независимых ортонормированных вектора,
отвечающих собственному значению i . Так как собственные векторы, отвечающие различным характеристическим числам, ортогональны, то, собирая их вместе,
получаем ортонормированный базис из собственных векторов.

Пример 1. Привести к диагональному виду с помощью ортогональной матрицы
|
1 |
2 |
2 |
|||
|
симметрическую матрицу A |
2 |
1 |
2 |
. Указать ортонормированный базис. |
|
|
2 |
2 |
1 |
|||
Решение.
На первом шаге необходимо найти собственные значения данного линейного оператора.
Составим характеристическое уравнение данного преобразования: Ae E 0 .
|
2 |
2 |
II III |
5 |
5 |
5 |
|||||||||||
|
1 |
||||||||||||||||
|
Ae E |
2 |
1 |
2 |
2 |
1 |
2 |
||||||||||
|
2 |
2 |
1 |
2 |
2 |
1 |
|||||||||||
|
1 |
1 |
1 |
1 |
1 |
||||||||||||
|
1 |
||||||||||||||||
|
(5 ) |
2 |
1 |
2 |
2I |
(5 ) |
0 |
1 |
0 |
(5 )(1 )2 |
0 |
||||||
|
2 |
2 |
1 |
2II |
0 |
0 |
1 |
||||||||||
|
1, алг кратность 2 |
|||
|
Корни уравнения |
1 |
– собственные значения линейного |
|
|
2 |
5, алг кратность 1 |
|
ˆ |
|||||||||||||||||||
|
оператора A . |
|||||||||||||||||||
|
На втором шаге найдем собственные векторы, относящиеся к каждому |
|||||||||||||||||||
|
собственному значению. |
|||||||||||||||||||
|
1. 1 1 |
. Решим матричное уравнение (Ae 1 E)X 0 . |
||||||||||||||||||
|
2 2 |
2 x |
0 |
|||||||||||||||||
|
1 |
|||||||||||||||||||
|
( Ae E) |
X |
2 2 |
2 |
x2 |
0 |
||||||||||||||
|
2 2 |
2 |
0 |
|||||||||||||||||
|
x3 |
|||||||||||||||||||
|
1 |
1 |
||||||||||||||||||
|
Решением |
является |
вектор |
U |
С1 |
1 |
С2 |
0 |
, C1,C2 |
0 , базис |
||||||||||
|
1 |
|||||||||||||||||||
|
0 |
1 |
||||||||||||||||||
|
пространства решений образуют векторы u ( 1;1;0)T , u |
2 |
( 1;0;1)T |
|||||||||||||||||
|
1 |
|||||||||||||||||||
|
2. 2 5 . Решим матричное уравнение (Ae 5 E)X 0 . |
|||||||||||||||||||
|
4 |
2 |
2 x |
0 |
||||||||||||||||
|
1 |
|||||||||||||||||||
|
( Ae 5E) X |
2 |
4 2 |
x2 |
0 |
|||||||||||||||
|
2 |
2 4 x |
0 |
|||||||||||||||||
|
3 |

|
1 |
||||||||
|
векторы U 2 |
С3 |
C3 0 , |
||||||
|
Решением являются |
1 , |
базисом |
пространства |
|||||
|
1 |
||||||||
|
решений является вектор u |
(1;1;1)T . |
|||||||
|
3 |
||||||||
|
Вектор |
u3 (1;1;1) |
ортогонален векторам |
u1 ( 1;1;0) и |
u2 ( 1;0;1) , |
||||
|
поскольку они относятся к различным собственным значениям. |
||||||||
|
Ортогонализируем векторы u1 ( 1;1;0) |
и u2 |
( 1;0;1) . |
||||||
|
Пусть |
f1 u1 |
|||||||
|
f2 u2 f1 . Выберем |
таким |
образом, |
чтобы |
векторы |
f1, f2 были |
ортогональны, то есть ( f1, f2 ) 0 ( f1, f2 ) ( f1, u2 f1) ( f1, u2 ) ( f1, f1) 0
( f1,u2 ) (u1,u2 ) 1 ( f1, f1) (u1,u1) 2
|
f |
u |
1 |
f |
1 |
( 1;1;0) ( 1;0;1) ( |
1 |
; |
1 |
;1) |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
1 |
2 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Теперь векторы |
f1, f2 , u3 |
ортогональны. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
f |
2 , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Нормируем их. |
f |
2 |
, |
u |
3 . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
2 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
1 |
1 |
1 |
1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
h ( |
; |
;0) |
h |
( |
1 |
; |
1 |
; |
2 |
) |
h ( |
; |
; |
) |
|||||||||||||||||||||||||||||||||||||||||||||
|
Векторы |
, |
, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
2 |
2 |
2 |
6 |
6 |
3 |
3 |
3 |
3 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||
составляют искомый ортономированный базис.
|
1 |
1 |
1 |
||||||||||
|
2 |
6 |
3 |
||||||||||
|
1 |
1 |
1 |
||||||||||
|
Ортогональная матрица U |
||||||||||||
|
2 |
6 |
3 |
||||||||||
|
0 |
2 |
1 |
||||||||||
|
3 |
3 |
|||||||||||
Матрица обратная к U совпадает с UТ, то есть
|
1 |
1 |
||||||||||||
|
0 |
|||||||||||||
|
2 |
2 |
||||||||||||
|
U 1 |
1 |
1 |
2 |
||||||||||
|
6 |
6 |
3 |
|||||||||||
|
1 |
1 |
1 |
|||||||||||
|
3 |
3 |
3 |
|||||||||||
f (x1, x2,…, xn ) с
f (x1, x2,…, xn ) .
f (x1, x2,…, xn ) ,
преобразование
|
ˆ |
||||
|
Матрица оператора A в базисе из собственных векторов имеет вид |
||||
|
1 |
0 |
0 |
||
|
Ah U 1AeU |
0 |
1 |
0 |
|
|
0 |
0 |
5 |
||
ОРТОГОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ, ПРИВОДЯЩЕЕ КВАДРАТИЧНУЮ ФОРМУ К КАНОНИЧЕСКОМУ ВИДУ
Ранее мы говорили о методе Лагранжа приведения квадратичной формы к каноническому виду – методе выделения полных квадратов. В результате получалось некоторое линейное преобразование, в общем случае не однозначно определенное, но
среди всех таких матриц всегда можно выбрать ортогональную.
С другой стороны, рассмотренная нами выше формула приведения матрицы к диагональному виду с помощью ортогонального преобразования D = U-1AU= UTAU ( в
силу U-1= UT) аналогична преобразованию симметрической матрицы A квадратичной формы с линейным преобразованием неизвестных U. Поскольку диагональную матрицу имеет квадратичная форма, приведенная к каноническому виду, получаем
следующую теорему.
Теорема 1. Для каждой действительной квадратичной формы
заданной в евклидовом пространстве, можно указать ортогональное неизвестных, приводящее ее к каноническому виду.
Геометрически такой выбор матрицы означает переход к новой декартовой системе координат, определяемой ортонормированным базисом собственных векторов матрицы A. Новые оси координат называют в этом случае главными осями матрицы A
и соответствующей квадратичной формы Теорема 1 называется
теоремой о приведении действительной квадратичной формы к главным осям.
Теорема 2. Каково бы ни было ортогональное преобразование, приводящее к
каноническому виду квадратичную форму матрицей A,
коэффициентами этого канонического вида будут характеристические корни матрицы
A, взятые с их кратностями.
В матричной формулировке теорема 2 может быть переписана в виде
Теорема 3. Какова бы ни была ортогональная матрица, приводящая к диагональному виду симметрическую матрицу A, на главной диагонали полученной
f (x1, x2,…, xn )
диагональной матрицы будут стоять характеристические корни матрицы A, взятые с их кратностями.
Приведению квадратичной формы к главным осям можно
придать следующую геометрическую формулировку: в евклидовом пространстве уравнение f (x1, x2,…, xn ) С определяет некоторую поверхность второго порядка.
Ортогональное преобразование X Ce f Y , приводящее форму к каноническому
виду означает поворот декартовых осей, осуществляющий преобразование уравнения
|
поверхности второго порядка |
к каноническому виду, по которому легко узнать тип |
|||||
|
данной поверхности. |
||||||
|
Пример 2. Найти ортогональное преобразование, приводящее к каноническому |
||||||
|
виду квадратичную форму f (x , x ) 17x2 |
12x x |
8x2 |
||||
|
1 |
2 |
1 |
1 |
2 |
2 |
|
|
Решение. |
||||||
|
17 |
6 |
|||||
|
Матрица квадратичной формы: |
A |
|||||
|
6 |
||||||
|
8 |
|
Найдем корни характеристического уравнения |
Ae E |
0 . |
|||||||||||
|
Ae E |
17 |
6 |
20 |
||||||||||
|
8 |
2 |
25 100 |
( 20)( 5) |
0 1 |
– |
||||||||
|
6 |
2 |
5 |
собственные значения.
Найдем собственные векторы, относящиеся к каждому собственному значению:
|
1 20 . Решим матричное уравнение (Ae 20Е)X 0 . |
||||||||||||||||||||||||
|
3 |
6 |
x1 |
0 |
3 |
6 |
1 2 |
||||||||||||||||||
|
, |
12 |
|||||||||||||||||||||||
|
6 |
12 |
x |
0 |
6 |
0 0 |
|||||||||||||||||||
|
2 |
||||||||||||||||||||||||
|
Решением |
являются |
векторы |
U |
2 |
C 0 |
, |
базисом пространства |
|||||||||||||||||
|
1 |
С |
, |
||||||||||||||||||||||
|
1 |
1 |
|||||||||||||||||||||||
|
1 |
||||||||||||||||||||||||
|
решений является вектор u1 (2;1)T . |
Нормируем его: |
h1 ( |
2 |
; |
1 |
) |
||||||||||||||||||
|
5 |
5 |
|||||||||||||||||||||||
|
2 5 . Решим матричное уравнение (Ae 5Е)X 0 . |
||||||||||||||||||||||||
|
12 |
6 |
x1 |
0 |
, |
12 |
6 |
2 |
1 |
||||||||||||||||
|
0 |
||||||||||||||||||||||||
|
6 |
3 |
x2 |
0 |
6 |
3 |
0 |

|
Решением являются векторы |
U |
С |
1 |
, |
C |
0 |
, базисом пространства |
||||
|
2 |
2 |
2 |
|||||||||
|
2 |
|||||||||||
|
решений является вектор u2 ( 1;2)T . Нормируем его: |
h2 |
( |
1 |
; |
2 |
) |
|||||||||||||||||||||||||||||||||||||||
|
5 |
5 |
||||||||||||||||||||||||||||||||||||||||||||
|
2 |
1 |
||||||||||||||||||||||||||||||||||||||||||||
|
5 |
5 |
||||||||||||||||||||||||||||||||||||||||||||
|
U |
|||||||||||||||||||||||||||||||||||||||||||||
|
1 |
2 |
||||||||||||||||||||||||||||||||||||||||||||
|
5 |
|||||||||||||||||||||||||||||||||||||||||||||
|
5 |
|||||||||||||||||||||||||||||||||||||||||||||
|
2 |
1 |
||||||||||||||||||||||||||||||||||||||||||||
|
y |
|||||||||||||||||||||||||||||||||||||||||||||
|
X UY |
5 |
5 |
|||||||||||||||||||||||||||||||||||||||||||
|
Искомое преобразование |
1 |
||||||||||||||||||||||||||||||||||||||||||||
|
1 |
2 |
||||||||||||||||||||||||||||||||||||||||||||
|
y2 |
|||||||||||||||||||||||||||||||||||||||||||||
|
5 |
|||||||||||||||||||||||||||||||||||||||||||||
|
5 |
|||||||||||||||||||||||||||||||||||||||||||||
|
x |
2 |
y |
1 |
y |
|||||||||||||||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||
|
1 |
5 |
1 |
5 |
||||||||||||||||||||||||||||||||||||||||||
|
1 |
2 |
||||||||||||||||||||||||||||||||||||||||||||
|
x |
y |
y |
|||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||||||||||||||||
|
5 |
1 |
5 |
|||||||||||||||||||||||||||||||||||||||||||
|
Канонический вид квадратичной формы: |
f 20 y2 |
5y2 |
||||||||
|
1 |
2 |
|||||||||
|
Пример 3. Найти ортогональное преобразование, приводящее к каноническому |
||||||||||
|
виду квадратичную форму f (x , x , x ) 2x2 |
x2 |
x2 |
4x x |
4x x |
2x x |
|||||
|
1 |
2 |
3 |
1 |
2 |
3 |
1 2 |
1 3 |
2 |
3 |
|
|
Решение. |
||||||||||
|
2 |
2 |
2 |
||||||||
|
Матрица квадратичной формы |
A |
2 |
1 |
1 |
||||||
|
2 |
1 |
1 |
||||||||
Составим характеристическое уравнение данного преобразования: Ae E 0 .
|
2 |
2 |
2 |
|||||||
|
A E |
2 |
1 |
1 |
(2 )2 (4 ) 0 |
|||||
|
e |
|||||||||
|
2 |
1 |
1 |
|||||||
|
Корни уравнения |
2 |
– собственные значения. |
|||||||
|
1 |
|||||||||
|
2 |
4 |
На втором шаге найдем собственные векторы, относящиеся к каждому собственному значению.
1. 1 2 , решая матричное уравнение (Ae 2 E)X 0 ,
|
4 |
2 |
2 x1 |
0 |
||||||||||||
|
( Ae |
2E) X |
2 |
1 |
1 |
x2 |
0 |
|||||||||
|
2 |
0 |
||||||||||||||
|
1 1 x3 |
|||||||||||||||
|
4 |
2 |
2 |
2 |
1 1 |
|||||||||||
|
2 |
1 |
1 |
0 |
0 0 |
|||||||||||
|
2 |
1 1 |
0 |
0 0 |
||||||||||||
|
1 |
1 |
||||||||||
|
Решением является вектор U 1 |
С2 |
||||||||||
|
С1 |
2 |
0 |
, C1,C2 |
0 , базис пространства |
|||||||
|
0 |
2 |
||||||||||
|
решений образуют векторы u ( 1;2;0)T , |
u |
2 |
(1;0;2)T . Ортогонализируем их. |
||||||||
|
1 |
|||||||||||
|
Пусть f1 u1 |
|||||||||||
|
f2 u2 f1 . Выберем |
таким |
образом, |
чтобы |
векторы f1, f2 были |
ортогональны, то есть ( f1, f2 ) 0 ( f1, f2 ) ( f1, u2 f1) ( f1, u2 ) ( f1, f1) 0
( f1,u2 ) (u1,u2 ) 1 ( f1, f1) (u1,u1) 5
f2 u2 12 f1 15 ( 1;2;0) (1;0;2) ( 54 ; 52 ;2)
Теперь векторы f1, f2 ортогональны.
|
2 |
30 |
|||||||||||||||||||||||||||||||||||||||||
|
Нормируем их. |
f |
5 , |
f |
2 |
||||||||||||||||||||||||||||||||||||||
|
1 |
5 |
|||||||||||||||||||||||||||||||||||||||||
|
1 |
2 |
|||||||||||||||||||||||||||||||||||||||||
|
h ( |
; |
;0) |
h |
( |
2 |
; |
1 |
; |
5 |
) |
||||||||||||||||||||||||||||||||
|
, |
||||||||||||||||||||||||||||||||||||||||||
|
1 |
5 |
5 |
2 |
30 |
30 |
30 |
||||||||||||||||||||||||||||||||||||
|
2. 2 |
4 . Решим матричное уравнение (Ae 4 E)X 0 . |
|||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
2 x |
0 |
|||||||||||||||||||||||||||||||||||||||
|
1 |
||||||||||||||||||||||||||||||||||||||||||
|
( Ae 4E) X 2 |
5 1 |
x2 |
0 |
|||||||||||||||||||||||||||||||||||||||
|
2 |
1 5 |
0 |
||||||||||||||||||||||||||||||||||||||||
|
x3 |
||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 1 |
|||||||||||||||||||||||||||||||||||
|
2 |
5 1 |
0 |
3 3 |
0 1 |
1 |
|||||||||||||||||||||||||||||||||||||
|
2 |
1 5 |
0 |
3 3 |
0 0 |
0 |
|||||||||||||||||||||||||||||||||||||

|
2 |
||||||||
|
Решением является |
векторы U 2 |
С3 |
1 |
, |
C3 0 , базисом |
пространства |
||
|
1 |
||||||||
|
решений является вектор u |
( 2; 1;1)T . |
|||||||
|
3 |
||||||||
|
Вектор u3 ( 2; 1;1) ортогонален векторам |
u1 ( 1;1;0) и |
u2 ( 1;0;1) , |
поскольку они относятся к различным собственным значениям и, как следствие,
|
( |
2 |
1 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
векторам h1 |
и h2 |
. Нормируем его. |
u3 |
6 , h3 |
; |
; |
) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
6 |
6 |
6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
h ( |
1 |
; |
2 |
;0) |
h |
( |
2 |
; |
1 |
; |
5 |
) |
h |
( |
2 |
; |
1 |
; |
1 |
) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Векторы |
, |
, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
5 |
5 |
2 |
30 |
30 |
30 |
3 |
6 |
6 |
6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
составляют искомый ортономированный базис. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
30 |
6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ортогональная матрица U |
2 |
1 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
30 |
6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
30 |
6 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
30 |
6 |
y |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
1 |
1 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Искомое преобразование X UY |
y2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
30 |
6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
5 |
1 |
y3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
30 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
1 |
y |
2 |
y |
2 |
y |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
5 |
1 |
30 |
6 |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
y1 |
1 |
y2 |
1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x2 |
y3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
30 |
6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
y2 |
1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x3 |
y3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
30 |
6 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Канонический вид квадратичной формы: f 2y12 2y22 4y32 .
Применим рассмотренный алгоритм приведения квадратичной формы к каноническому виду с помощью ортогонального преобразования для классификации кривых и поверхностей второго порядка.

Пример 4. Найти тип и каноническое уравнение кривой второго порядка
9x2 6y2 4xy 16x 8y 2 0
Решение. Рассмотрим уравнение кривой: 9x2 6 y2 4xy 16x 8y 2 0
|
квадратичная часть |
|||
|
Выпишем матрицу квадратичной части: |
|||
|
Матрица квадратичной формы: |
9 |
2 |
|
|
A |
|||
|
6 |
|||
|
2 |
|
Найдем корни характеристического уравнения |
Ae E |
0 . |
5 |
||||||||||||
|
9 |
2 |
||||||||||||||
|
Ae |
E |
2 |
6 |
2 |
15 50 ( 5)( 10) 0 |
1 |
– |
||||||||
|
10 |
|||||||||||||||
|
2 |
собственные значения.
Найдем собственные векторы, относящиеся к каждому собственному значению:
|
1 5 . Решим матричное уравнение |
(Ae 5Е)X 0 . |
|||||||||||||||
|
4 |
2 |
x |
0 |
4 |
2 |
2 |
1 |
|||||||||
|
, |
||||||||||||||||
|
1 |
0 |
|||||||||||||||
|
2 1 |
y |
0 |
2 |
0 |
||||||||||||
|
Решением |
являются |
векторы |
U |
С |
1 |
C 0 |
, базисом пространства |
|||||||||
|
1 |
, |
|||||||||||||||
|
1 |
2 |
1 |
||||||||||||||
|
решений является вектор u (1;2)T . |
Нормируем его: h1 ( |
1 |
; |
2 |
) |
||||||||||||||||||||||||||||
|
1 |
5 |
5 |
|||||||||||||||||||||||||||||||
|
2 10 . Решим матричное уравнение (Ae 10Е)X 0 . |
|||||||||||||||||||||||||||||||||
|
1 |
2 |
x |
0 |
1 |
2 |
1 |
2 |
||||||||||||||||||||||||||
|
, |
|||||||||||||||||||||||||||||||||
|
4 |
4 |
||||||||||||||||||||||||||||||||
|
2 |
y |
0 |
2 |
0 |
0 |
||||||||||||||||||||||||||||
|
Решением |
являются |
векторы |
U |
С |
2 |
, C |
0 , |
базисом |
|||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||||||
|
1 |
|||||||||||||||||||||||||||||||||
|
решений является вектор u ( 2;1)T |
. Нормируем его: h2 ( |
2 |
; |
1 |
) |
||||||||||||||||||||||||||||
|
2 |
5 |
5 |
|||||||||||||||||||||||||||||||
|
H {h1, h2} – собственный ортонормированный базис. |
|||||||||||||||||||||||||||||||||
|
Перейдем |
к новым координатам |
(x’, y’) |
с |
помощью |
матрицы |
исходного ортонормированного базиса {i, j} к собственному ортонормированному
базису {h1, h2}
|
1 |
2 |
||||||||
|
5 |
5 |
||||||||
|
U |
– матрица перехода |
||||||||
|
2 |
1 |
||||||||
|
5 |
5 |
||||||||
|
1 |
||||||
|
x |
x‘ |
|||||
|
5 |
||||||
|
U |
||||||
|
Искомое преобразование |
2 |
|||||
|
y |
y‘ |
|||||
|
5 |
||||||
Выпишем преобразование координат:
|
1 |
2 |
|||||||||
|
x |
x‘ |
y‘ x‘cos y‘sin |
||||||||
|
5 |
5 |
|||||||||
|
2 |
1 |
|||||||||
|
y |
x‘ |
y‘ x‘sin y‘cos |
||||||||
|
5 |
5 |
|||||||||
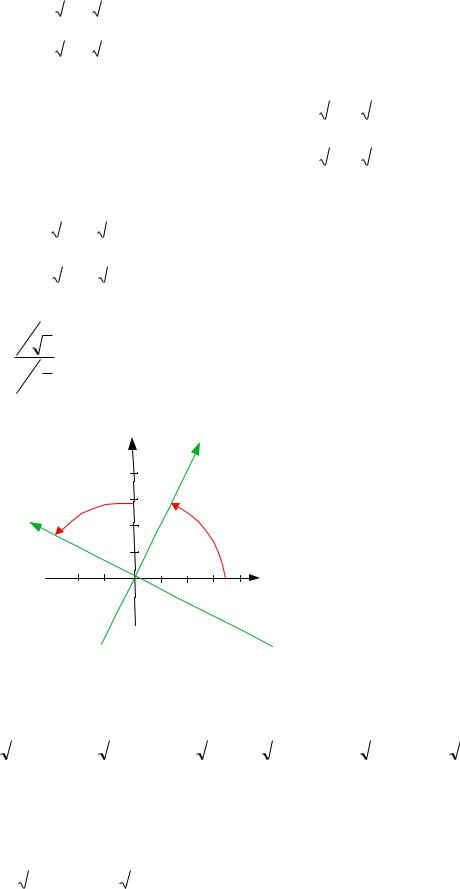
Данное преобразование соответствуют повороту системы координат на угол :
2
tg 1 5 2 против часовой стрелки (т.к. угол положительный): по y 2 единицы,

 5
5
по x – 1 единица
|
y |
x’ |
|
|
4 |
||
|
y’ |
3 |
|
|
2 |
||
|
1 |
||
|
x |
||
|
-3 -2 -1 0 1 2 3 4 |
Перейдем к новым координатам, подставив x’ и y’ в уравнение кривой:
|
x‘ 2 y‘ 2 |
2x‘ y‘ 2 |
x‘ 2 y‘ |
2x‘ y‘ |
x‘ 2 y‘ |
2x‘ y‘ |
|||||||||||||||||||||||||
|
9 |
6 |
4 |
16 |
8 |
2 |
0 |
||||||||||||||||||||||||
|
5 |
5 |
5 |
5 |
5 |
5 |
Раскроем скобки и приведем подобные слагаемые:
|
9 |
x‘2 |
4x‘ y‘ 4 y‘2 |
6 |
4x‘2 |
4x‘ y‘ y‘2 2 |
4 |
2x‘2 3x‘ y‘ 2 y‘2 |
||||||||||||
|
5 |
5 |
5 |
|||||||||||||||||
|
16x‘ 32 y‘ |
16x‘ 8y‘ |
||||||||||||||||||
|
2 |
0 |
||||||||||||||||||
|
5 |
5 |
Соседние файлы в папке Лекции Пронина Е.В.
- #
- #
- #
- #
- #
- #
- #
Решение.
Найдем собственные вектора заданного линейного оператора.
Число  есть собственное число оператора
есть собственное число оператора  в том и только том случае, когда
в том и только том случае, когда 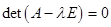 . Запишем характеристическое уравнение:
. Запишем характеристическое уравнение:
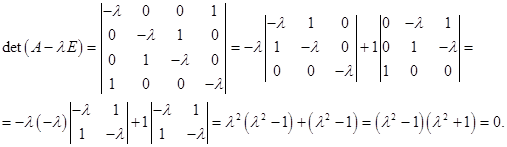
Решая его, имеем
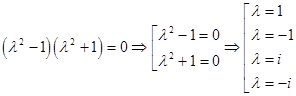
Таким образом, получаем собственные числа оператора:
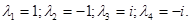
Для каждого из полученных собственных значений найдем собственные векторы.
Их можно найти их системы 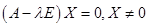 .
.
А) 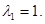
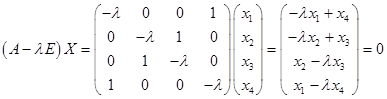
Решим однородную систему уравнений.
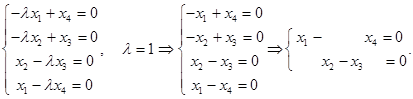
Матрица коэффициентов 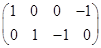 имеет ранг 2. Выберем в качестве базисного минора
имеет ранг 2. Выберем в качестве базисного минора 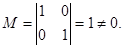 Тогда, полагая
Тогда, полагая 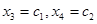 , имеем
, имеем
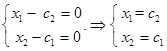
Таким образом, общее решение системы
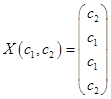 .
.
Из общего решения находим фундаментальную систему решений:
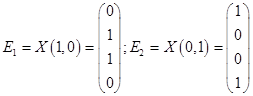 .
.
С использованием фундаментальной системы решений, общее решение может быть записано в виде .
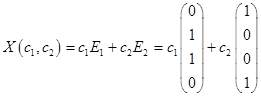
Б) 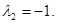
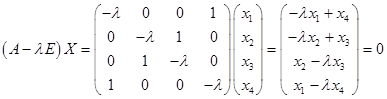
Решим однородную систему уравнений
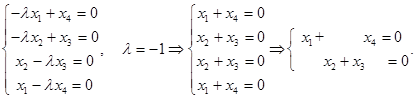 .
.
Матрица коэффициентов 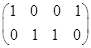 имеет ранг 2. Выберем в качестве базисного минора
имеет ранг 2. Выберем в качестве базисного минора 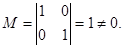 Тогда, полагая
Тогда, полагая 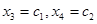 , имеем
, имеем 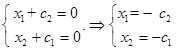
Таким образом, общее решение системы 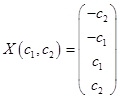 .
.
Из общего решения находим фундаментальную систему решений:
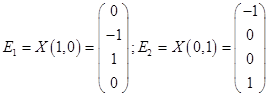 .
.
С использованием фундаментальной системы решений, общее решение может быть записано в виде
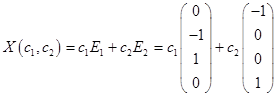 .
.
В) 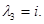
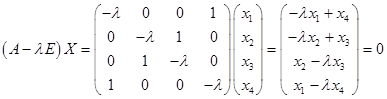
Решим однородную систему уравнений.
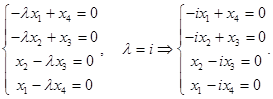
Матрица коэффициентов 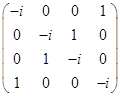 имеет ранг 4, поскольку
имеет ранг 4, поскольку
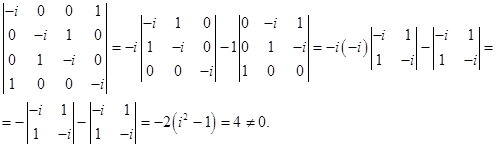
Так как ранг равен количеству неизвестных, то система имеет только тривиальное решение.
Г) 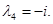
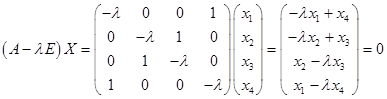
Решим однородную систему уравнений.
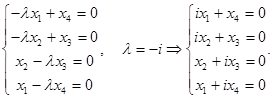
Матрица коэффициентов 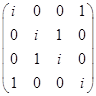 имеет ранг 4, поскольку
имеет ранг 4, поскольку
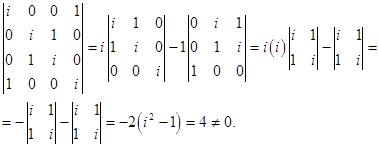
Так как ранг равен количеству неизвестных, то система имеет только тривиальное решение.
Таким образом, имеем собственные вектора 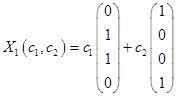 и
и 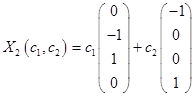 .
.
Выберем в качестве ортогонального базиса вектора 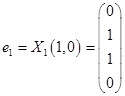 ,
, 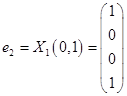 ,
, 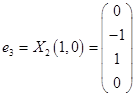 ,
, 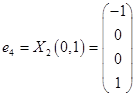 .
.
Нормируем найденный ортогональный базис:
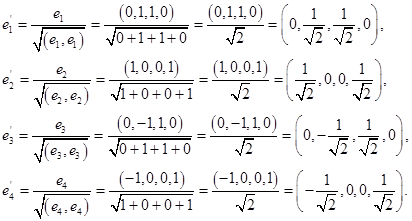
Ответ: 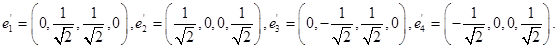
Теорема 6.4. Собственные векторы самосопряженного оператора, отвечающие различным собственным значениям, ортогональны.
◄ Рассмотрим самосопряженный оператор А и два его собственных вектора x1 и х2, отвечающие различным собственным значениям λ1 и λ2. Тогда Ах1 = λ1x1 и Ах2 = λ2x2. Поэтому
(Ах1,x2) = (λ1x1,x2) = λ1(x1,x2) (6.6)
Но так как А является самосопряженным оператором, то (Ax1,x2) = (x1,Ax2) . Значит,
(Ax1,x2) = (x1,Ax2) = (x1, λ2x2) = λ2(x1,x2) (6.7)
Приравнивая правые части соотношений (6.6) и (6.7), получаем
λ1(x1,x2) = λ2(x1,x2)
или
(λ1 – λ2)(x1,x2) = 0. (6.8)
Так как λ1 ≠ λ2, из равенства (6.8) следует, что (x1,x2) = 0, что и означает ортогональность векторов x1 и x2. ►
Теорема 6.5. Если собственные значения λ1, …, λn самосопряженного оператора А, действующего в n-мерном евклидовом пространстве Ε, попарно различны, то в Ε существует ортонормированный базис, в котором матрица этого линейного оператора А имеет диагональный вид, причем диагональными элементами такой матрицы являются собственные значения λ1, …, λn.
◄ Поскольку собственные значения λ1, …, λn попарно различны, то, выбрав для каждого λi соответствующий ему собственный вектор еi, получим систему е ненулевых векторов, которые по теореме 6.4 попарно ортогональны. Поэтому е – ортогональная система векторов. Согласно теореме 5.5, она линейно независима и, имея n векторов, является базисом (см. теорему 1.4). Этот базис является ортогональным, а чтобы его превратить в ортонормированный, необходимо каждый вектор еi нормировать делением на его длину.
Таким образом, в условиях теоремы существует базис из собственных векторов самосопряженного оператора А. По теореме 5.6 матрица линейного оператора в базисе из собственных векторов является диагональной, а диагональные элементы ма-трицы представляют собой собственные значения. ►
Хотя все корни характеристического уравнения самосопряженного оператора действительны (см. теорему 6.3), среди них могут быть кратные, и тогда теорема 6.5 неприменима. Однако и в этом случае матрица самосопряженного оператора в некотором базисе имеет диагональный вид.
Теорема 6.6. Для любого самосопряженного оператора А существует ортонормированный базис, состоящий из соб-ственных векторов этого линейного оператора. Матрица А самосопряженного оператора А в этом базисе имеет диагональный вид, на ее диагонали расположены собственные значения оператора А, повторяющиеся столько раз какова их кратность. #
Доказательство этой теоремы приведено в Д.6.1.
Следствие 6.4. Любая симметрическая матрица М порядка n подобна некоторой диагональной, т.е. существует такая невырожденная матрица Р порядка n, что
P-1MP = diag(λ1, …, λn).
Последовательность λ1, …, λn из n чисел представляет собой перечень всех корней характеристического уравнения матрицы М с учетом их кратностей.
◄ Рассмотрим в n-мерном евклидовом пространстве Rn стандартный ортонормированный базис, и пусть матрица М является матрицей в этом базисе некоторого линейного оператора М. Тогда этот оператор будет самосопряженным. По теореме 6.6 для него существует ортонормированный базис, в котором его матрица М’ имеет диагональный вид М’ = diag (λ1, …, λ1n). Матрица М’ получается из исходной матрицы М при помощи матрицы перехода Р из стандартного базиса в указанный ортонормированный базис: М’ = Р-1МР. ►
Дополнение 6.1. Инвариантные подпространства самосопряженного оператора
Теорема 6.7. Если H – инвариантное подпространство самосопряженного оператора А, действующего в евклидовом пространстве Ε, то его ортогональное дополнение H⊥ – также является инвариантным подпространством этого оператора А.
◄ Нам достаточно проверить, что для любого вектора у линейного подпространства H⊥ его образ Ау тоже принадлежит H⊥, т.е. что для любого вектора х ∈ H выполнено условие (Ау, х) = 0.
Пусть у ∈ H⊥, х ∈ H. Так как оператор А самосопряженный, выполнено равенство (Ау, х) = (у, Ах). Но H – инвариантное подпространство оператора А, т.е. Ах ∈H для вектора х ∈ H. Поэтому (у, Ах) = 0, так как вектор у ∈ H⊥ ортогонален любому вектору из H, в частности вектору Ах. Следовательно, (Ау, х) = 0, что и требовалось доказать. ►
Мы видели, что кратность собственного значения и размерность соответствующего собственного подпространства линейного оператора могут не совпадать (см. пример 5.7). Эти две характеристики совпадают, если линейный оператор, действующий в евклидовом пространстве, является самосопряженным.
Теорема 6.8. Пусть λ – собственное значение самосопряженного оператора А, действующего в евклидовом пространстве Ε. Тогда кратность собственного значения λ равна размерности отвечающего этому значению собственного под-пространства £(А,λ) линейного оператора А.
◄ Собственное подпространство £(А, λ) самосопряженного оператора А является инвариантным подпространством этого оператора. Поэтому, согласно теореме 6.7, ортогональное дополнение £(А, λ)⊥ также является инвариантным подпространством самосопряженного оператора А. Пусть dim£(A, λ) = k, a dim£(A,λ)⊥ = l. Выберем в линейных подпространствах £(А,λ) и £(А,λ)⊥ базисы е = (e1 … еk) и g = (g1 … gl) соответственно.
Так как £(А, λ) ⊕ £(А, λ)⊥ = Ε, система векторов (е g) является базисом евклидова пространства Ε. Рассмотрим в этом базисе матрицу А оператора А. Для любого вектора еi системы е имеем Aei = λеi, так как еi принадлежит собственному подпространству £(А, λ) линейного оператора, отвечающему собственному значению λ. Для каждого вектора gj системы g имеем Agj = aj1g1 + … + aglgl, так как £(А,λ)⊥ – инвариантное подпространство оператора А, а g – базис этого подпространства. Эти разложения означают, что матрица А оператора А в базисе (е g) имеет блочный вид:
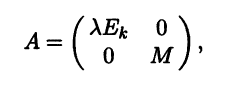
где Еk обозначает единичную матрицу порядка k, а блок М представляет собой квадратную матрицу порядка l, состоящую из коэффициентов разложения векторов Agj в базисе (е g):

Исходя из блочного представления матрицы А получаем вид ее характеристического уравнения:
ΧA( τ) = det(A – τЕn) = (λ – τ)k det(M – τЕl) =
(λ – τ)kΧM(τ), (6.9)
где Еn и El – единичные матрицы порядков n и l.
Отметим, что матрица М представляет собой матрицу в базисе g линейного оператора, являющегося ограничением линейного оператора А на его инвариантное подпространство £(А,λ)⊥. Оператор А не имеет в подпространстве £(А,λ)⊥ собственных векторов с собственным значением λ. Поэтому λ не является собственным значением матрицы М, и из представления (6.9) заключаем, что собственное значение λ матрицы А имеет кратность k. ►
Доказательство теоремы 6.6 опирается на свойства инвари-антных подпространств.
◄ Пусть λ1, …, λk – собственные значения самосопряженного оператора A, a r1, …, rk – их кратности. Так как характеристическое уравнение самосопряженного оператора имеет только действительные корни, сумма кратностей r1 + … + rk собственных значений равна размерности n евклидова пространства Ε. Рассмотрим собственное подпространство Hi оператора А, соответствующее собственному значению λi. Размерность этого линейного подпространства, согласно теореме 6.8, совпадает с кратностью ri собственного значения λi. Выберем ортонормированный базис в линейном подпространстве Hi, который будет состоять из ri, собственных векторов самосопряженного оператора А, попарно ортогональных и имеющих единичную длину. Объединив выбранные базисы в одну систему, получим систему из n собственных векторов единичной длины, любые два из которых ортогональны. Действительно, либо оба вектора одновременно входят в базис некоторого подпространства Hi и будут ортогональны согласно выбору, либо они попадают в разные инвариантные подпространства Hi и Hj и будут ортогональны как собственные векторы, отвечающие различным собственным значениям (см. теорему 6.4).
Итак, мы выбрали систему из п попарно ортогональных векторов единичной длины. Согласно теореме 3.4, эта система линейно независима, а так как количество векторов в ней совпадает с размерностью пространства, она является ортонормиро- ванным базисом. Согласно теореме 5.6, матрица оператора А в этом базисе является диагональной и на ее диагонали расположены собственные значения, повторяющиеся столько раз, какова их кратность, поскольку построенный базис состоит из соответствующих наборов собственных векторов. ►
Вопросы и задачи
- Известно, что матрица линейного оператора в некото-ром ортонормированном базисе диагональна. Является ли этот линейный оператор самосопряженным?
- Известно, что в некотором базисе, не являющемся ортогональным, матрица оператора А симметрическая. Можно ли утверждать, что: а) А – самосопряженный оператор; б) А не является самосопряженным оператором. Что можно утверждать, если базис ортогональный, но не ортонормированный?
- Линейный оператор, действующий в n-мерном линейном пространстве, имеет в некотором базисе симметрическую матрицу. Докажите, что этот оператор имеет базис го собственных векторов, даже если линейное пространство не является евклидовым.
- Докажите, что: а) (А + В)* = А* + В*; б) (АВ)* = В*А*; в) если линейный оператор А имеет обратный, то и оператор А* имеет обратный, причем (А-1)* = (А*)-1.
- Рассмотрим в пространстве V2 линейный оператор Rφ поворота вектора на угол φ, 0 < φ < π. Найдите оператор, сопряженный к оператору Rφ.
- Пусть Ε – евклидово пространство, е – произвольный, вообще говоря, неортогональный базис в Ε, Г – матрица Грама для системы векторов е. Докажите, что если линейный оператор А в базисе е имеет матрицу А, то сопряженный к нему оператор А* имеет в том же базисе матрицу А* = Г-1ATГ.
- В базисе
- Докажите, что для любого евклидова пространства Ε отображение L(Ε,Ε) → L(Ε,Ε), сопоставляющее линейному оператору из L(Ε,Ε) ему сопряженный, является изоморфизмом линейного пространства L(Ε,Ε). Зависит ли этот изоморфизм от выбора базиса в евклидовом пространстве Ε? Когда этот изоморфизм является тождественным отображением?
- Для симметрической матрицы
b1 = (1, 1, 1, 1), b2 = (1, 1, 1,0),
b3 = (1, 1, 0, 0), b4 = (1, 0, 0, 0)
линейного арифметического пространства Rn матрица линейного оператора А имеет вид
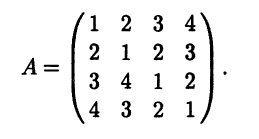
Найдите матрицу сопряженного оператора А* в том же базисе (b1 b2 b3 b4). В пространстве Rn предполагается стандартное скалярное произведение.
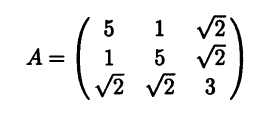
найдите подобную ей диагональную матрицу А’ = Р-1АР и соответствующую матрицу Р.
-
Линейные операции над векторами
-
Базис. Cкалярное произведение
-
Векторное и смешанное произведения векторов
-
Декартова система координат. прямая на плоскости
-
Плоскость в пространстве
-
Прямая в пространстве
-
Кривые второго порядка — I
-
Кривые второго порядка — II
-
Поверхности второго порядка
-
Матрицы и операции с ними
-
Обратная матрица
-
Ранг матрицы
-
Системы линейных алгебраических уравнений
-
Свойства решений однородных и неоднородных СЛАУ
