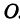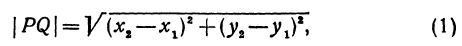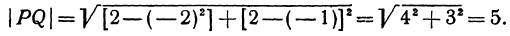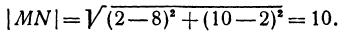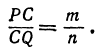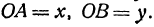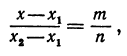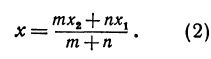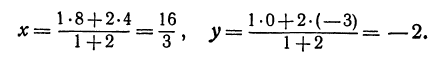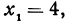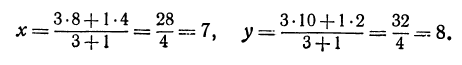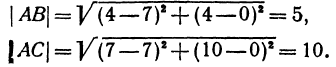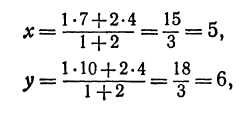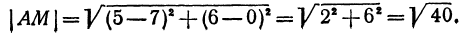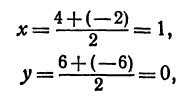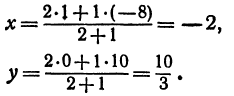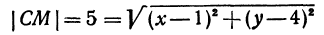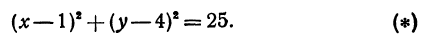Декартовы координаты точек плоскости. Уравнение окружности
Числовая ось
Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление
указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.
Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .
Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .
Прямоугольная декартова система координат на плоскости
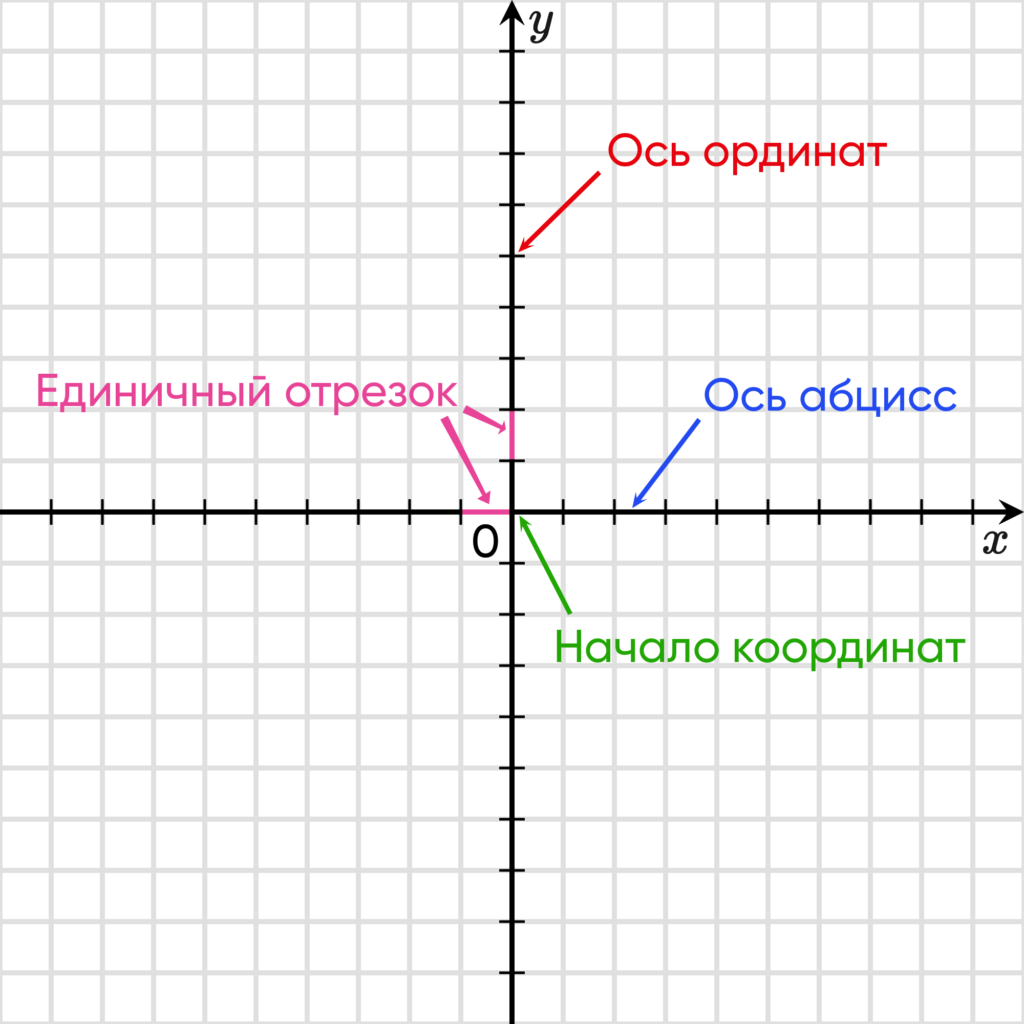
Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).
Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.
Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA1 и AA2 на прямые Ox и Oy соответственно (рис.3).
Определение 4 . Абсциссой точки A называют координату точки A1 на числовой оси Ox , ординатой точки A называют координату точки A2 на числовой оси Oy .
Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).
Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .
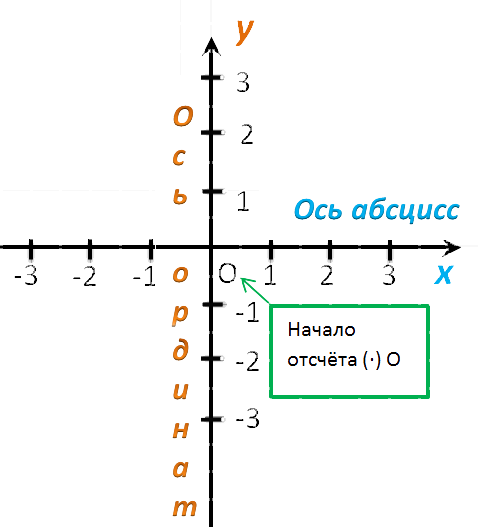
Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).
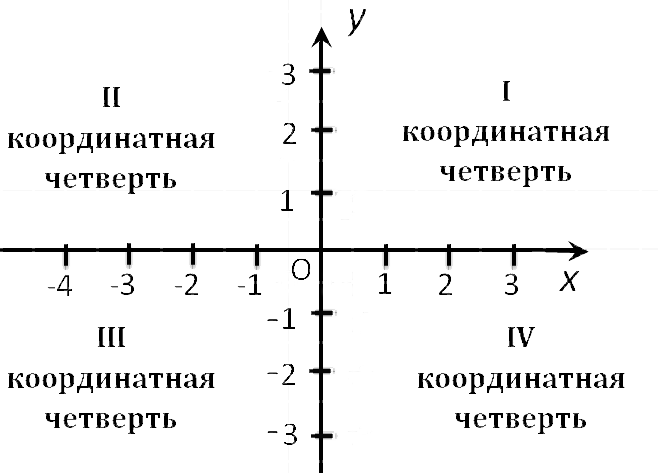
Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.
Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .
Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.
Формула для расстояния между двумя точками координатной плоскости
Утверждение 1 . Расстояние между двумя точками координатной плоскости
вычисляется по формуле
Доказательство . Рассмотрим рисунок 6.
| | A1A2| 2 = = ( x2 – x1) 2 + ( y2 – y1) 2 . |
(1) |
что и требовалось доказать.
Уравнение окружности на координатной плоскости
Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:
Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A0 (x0 ; y0) .
Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид
Как найти синус и косинус без тригонометрической таблицы?
В статье мы рассмотрим, как найти значения:
и других тригонометрических выражений без тригонометрической таблицы .
Для начала внимательно прочтите статью о числовой окружности . Вы должны научиться находить точки на окружности в числах с Пи .
Уже умеете? Тогда два ключевых утверждения:
– косинус числа равен абсциссе точки на числовой окружности
– синус числа равен ординате точки на числовой окружности
Например, пусть нам нужно найти синус и косинус числа (frac<π><6>). Обозначим на числовой окружности точку со значением (frac<π><6>).
Если построить все точно и крупно, то можно убедиться, что абсцисса этой точки будет равна (0,866…) , что соответствует числу (frac<sqrt<3>><2>) , а ордината равна (0,5), то есть (frac<1><2>).
Аналогично и для любой другой точки: значение абсциссы совпадает со значением косинуса, а ординаты – синуса. Поэтому:
В тригонометрии ось абсцисс часто называют «ось косинусов», а ординат – «ось синусов».
И обычно на них не наносят значения в десятичных ((0,1); (0,2); (0,3) и т.д.), а сразу отмечают стандартные значения для синуса и косинуса: (frac<1> <2>=0,5); (frac<sqrt<2>> <2>≈0,707); (frac<sqrt<3>><2>≈0,866), причем, как со знаком плюс, так и минус. Почему стандартные значения синуса и косинуса именно (frac<1><2>),(frac<sqrt<2>><2>) и (frac<sqrt<3>><2>) вы можете узнать из этого видео .
Как находить значения синуса и косинуса без таблицы, а только с помощью круга?
- Начертите круг и оси косинусов и синусов.
- Отметьте на круге число, синус и косинус которого надо найти. Если с этим возникают проблемы, прочитайте здесь о том, как расставлять числа на числовой окружности.
- Найдите координаты точки, используя картинку ниже.
Пример. Найдите синус и косинус для числа (-frac<7π><6>).
Решение:(-frac<7π><6>=-frac<6π><6>-frac<π><6>=-π-frac<π><6>) , то есть, чтобы отметить на окружности точку (-frac<7π><6>) сначала находим число (-π) и от него в отрицательную сторону откладываем дугу длиной (frac<π><6>).
Отмечаем число, синус и косинус которого надо найти:
Точка (frac<5π><2>) совпадает с (1) на оси синусов, значит (sinfrac<5π><2>=1). А если провести перпендикуляр из точки (frac<5π><2>) до оси косинусов, то можно убедиться, что он попадет в (0). Поэтому (cosfrac<5π><2>=0).
И тут некоторые из вас подумали: «с кругом, на котором подписаны числа, каждый дурак сможет посчитать, а что делать, когда его под рукой нет? Что делать на ЕГЭ?» Ответ прост – нарисуйте круг сами! Для этого вам будет нужно понять логику расположения чисел на осях (подробнее об этом читайте в статье « Как запомнить тригонометрический кру г »).
Пример. Найдите а) (sinfrac<3π><2>), б) (cosfrac<3π><4>), в) (sin(-frac<π><3>)) .
Решение: а) Чертим круг, оси и отмечаем число (frac<3π><2>). Обращаем внимание на ось синусов и понимаем, что точка совпала с (-1), получается (sinfrac<3π><2>=-1).
б) (frac<3π><4>=frac<4π><4>-frac<π><4>=π-frac<π><4>) – отмечаем число на круге. Проводим перпендикуляр до оси косинусов и вспоминаем, что точки со знаменателем (4) находятся посередине. Мы еще попали и в отрицательную часть оси косинусов, получается (cosfrac<3π><4>=-frac<sqrt<2>><2>).
в) (-frac<π><3>) – отмечаем число на круге. Видим, что перпендикуляр к оси синусов попал в точку близкую к (-1), значит (sin(-frac<π><3>)=-frac<sqrt<3>><2>).
Как видите не обязательно рисовать, очень красивую или очень большую окружность – вы можете определить нужное вам значение, быстро набросав круг. И ничего не надо учить!
Если вы хотите еще примеров с вычислением синусов и косинусов без тригонометрической таблицы, то прочтите эту статью.
Урок на тему Числовая окружность на координатной плоскости
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Занимательная математика Алгебра и начала математического анализа, 10 класс. Урок на тему: Числовая окружность на координатной плоскости.
Числовая окружность на координатной плоскости. Что будем изучать: Определение. Важные координаты числовой окружности. Как искать координату числовой окружности? Таблица основных координат числовой окружности. Примеры задач.
Определение. Числовая окружность на координатной плоскости. Расположим числовую окружность в координатной плоскости так, чтобы центр окружности совместился с началом координат, а её радиус принимаем за единичный отрезок. Начальная точка числовой окружности A совмещена с точкой (1;0). Каждая точка числовой окружности имеет в координатной плоскости свои координаты х и у, причем: x > 0, у > 0 в первой четверти; х 0 во второй четверти; х 0, у
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 987 человек из 79 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 310 человек из 69 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 677 человек из 75 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 533 935 материалов в базе
Материал подходит для УМК
«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.
§ 5. Числовая окружность на координатной плоскости
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 20.10.2017
- 2615
- 42
- 20.10.2017
- 1255
- 0
- 19.10.2017
- 1961
- 8
- 19.10.2017
- 387
- 0
- 19.10.2017
- 374
- 0
- 19.10.2017
- 444
- 2
- 19.10.2017
- 1516
- 25
- 18.10.2017
- 3535
- 188
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 20.10.2017 4150
- PPTX 425.6 кбайт
- 22 скачивания
- Рейтинг: 4 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Поцелуева Елена Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 1 месяц
- Подписчики: 6
- Всего просмотров: 128018
- Всего материалов: 42
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Тульской области ввели школьные каникулы со 2 по 11 февраля
Время чтения: 1 минута
В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид
Время чтения: 1 минута
В Курской области с 7 по 20 февраля ввели дистанционное обучение для школьников
Время чтения: 1 минута
Путин поручил обучать педагогов работе с девиантным поведением
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Рязанских школьников с 5 по 8 классы переведут на дистанционное обучение
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
[spoiler title=”источники:”]
http://cos-cos.ru/ege/zadacha209/356/
http://infourok.ru/urok-na-temu-chislovaya-okruzhnost-na-koordinatnoy-ploskosti-2197437.html
[/spoiler]
Координаты на плоскости:
Возьмем на плоскости две взаимно перпендикулярные прямые, пересекающиеся в точке
Определение: Координатными осями на плоскости называются две взаимно перпендикулярные прямые, на которых установлены: 1) направления, 2) масштаб и 3) общая точка отсчета.
Назовем одну из осей осью 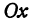
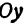
Возьмем произвольную точку 
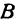
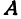
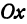
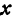
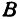
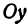
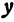
Определение. Абсциссой точки называется координата ее проекции на ось 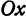
Абсциссу точки обычно обозначают буквой 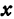
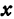
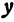
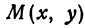
Координатные оси разделяют плоскость на четыре части, которые называют четвертями.
Первой четвертью называется та часть плоскости, в которой абсцисса и ордината положительны.
Второй четвертью — та часть, в которой абсцисса отрицательна, а ордината положительна.
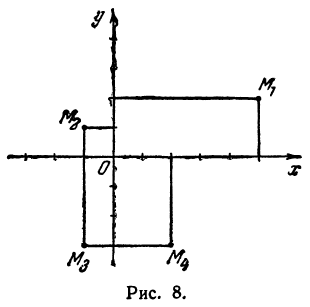
Третьей четвертью—та часть, в которой абсцисса и ордината отрицательны, и, наконец, четвертой,—та часть, в которой абсцисса положительна, а ордината отрицательна (рис. 7). На рис. 8 указаны 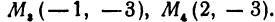
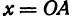
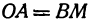
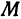
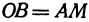
Пример:
Найти точку 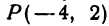
Решение:
Возьмем на оси 
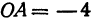
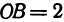
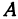
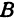
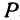
Пример:
Найти расстояние между точками 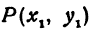
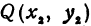
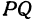
Решение:
Обозначим проекцию точки 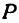
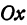
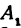
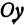
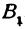
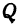
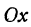
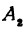
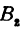
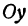
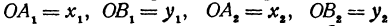
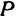
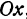
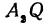
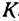
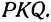
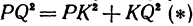
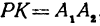
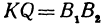
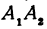
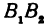
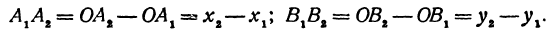
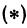
откуда
т. е. расстояние между двумя точками равно корню квадратному из суммы квадратов разностей, координат.
Примечание. Расстояние между двумя точками, так же как длина отрезка, всегда положительно, поэтому в формуле (1) перед квадратным корнем берут только знак плюс.
Пример:
Найти расстояние между точками 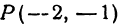
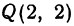
Решение:
Применяя формулу (1), получим
Пример:
Найти длину отрезка 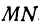
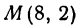
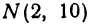
Решение:
Применяя формулу (1), получим
Пример:
Найти точку 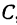
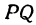
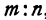
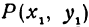
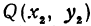
Решение:
По условию задачи надо найти такую точку 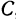
Обозначим, как и выше, проекции точки 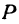
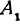
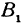
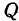
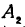
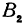
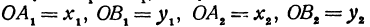
Кроме того, обозначим координаты искомой точки 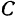
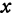
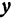
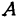
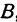
Так как прямые 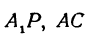
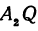
Но 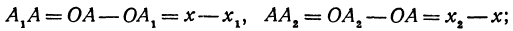
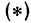
решая которое найдем абсциссу точки 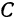
Рассуждая аналогично о проекциях на оси 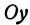
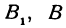
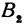
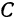
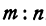
Итак, искомая точка 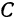
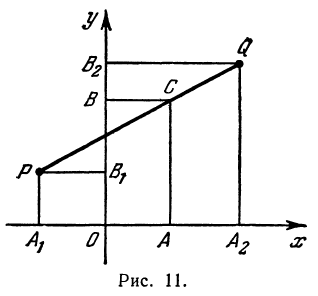
Пример:
Найти точку, делящую в отношении 1:2 отрезок 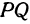
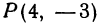
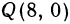
Здесь 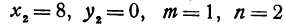
Решение:
Применяя формулы (2) и (3), получим:
- Заказать решение задач по высшей математике
Пример:
Найти точку, делящую расстояние между точками 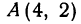
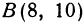
Здесь 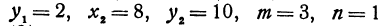
Решение:
По формулам (2) и (3) находим:
Следствие (из формул (2) и (3)). Если точка 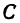
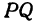
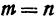
т. е. абсцисса середины отрезка равна средней арифметической абсцисс его начала и конца; ордината середины отрезка равна средней арифметической ординат его начала и конца.
Пример:
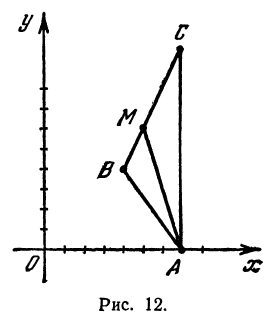
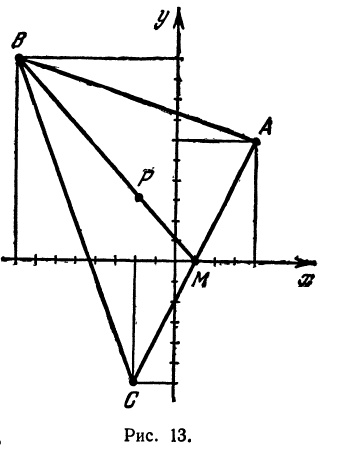
Даны три вершины треугольника: 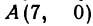
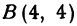
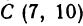
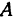
Решение:
Найдем длины сторон 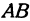
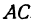
Обозначим точку пересечения биссектрисы угла 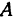
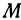
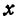
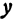
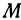
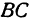
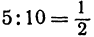
т.е. 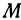
Теперь вычисляем длину биссектрисы как расстояние между точками 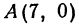
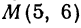
Пример:
Найти точку пересечения медиан треугольника, вершинами которого являются точки 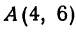

Решение:
Точка пересечения медиан делит каждую из медиан в отношении 2:1, считая от вершины треугольника. Обозначим через 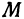
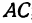
т. е. 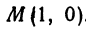
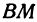
Итак, искомая точка 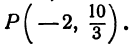
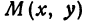
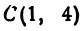
или, возводя обе части равенства в квадрат, получим
Это равенство есть уравнение с двумя неизвестными 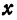
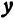
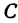
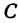
Следовательно, можно сказать, что уравнение 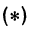
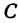
В следующих главах будут рассмотрены уравнения с двумя неизвестными 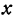
- Линейная функция
- Квадратичная функция
- Тригонометрические функции
- Производные тригонометрических функции
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
- Координаты на прямой
В повседневной жизни часто можно услышать фразу: «Оставь мне свои координаты».
В ответ человек обычно оставляет свой адрес или номер телефона, то есть данные, по которым его можно найти.
Координаты могут обозначаться самыми разными наборами цифр или букв.
Например, номер автомобиля — это координаты, потому что по номеру машины можно определить из какого
она города и кто ёё владелец.
Важно!
Координаты — это набор данных, по которому определяется положение того или иного объекта.
Примерами координат являются: номер вагона и места в поезде, широта и долгота на географической карте,
запись положения фигуры на шахматной доске, положение точки на числовой оси и т.д.
Всегда, когда мы по определенным правилам однозначно обозначаем какой-то объект набором букв, чисел или
других символов, мы задаём координаты объекта.
Декартова система координат
Французкий математик Рене Декарт (1596–1650) предложил задавать положение точки на плоскости с помощью двух координат.
Для нахождения координат нужны ориентиры, от которых ведётся отсчёт.
- На плоскости такими ориентирами будут служить две числовые оси. На чертеже обычно первую ось рисуют горизонтально, её
называют осью АБСЦИСС и обозначают буквой «X», записывают ось
«Ox». Положительное направление на оси абсцисс выбирают
слева направо и
показывают стрелкой. - Вторую ось проводят вертикально, её называют
осью ОРДИНАТ и обозначают буквой «Y», записывают ось
«Oy».
Положительное направление на оси ординат выбирают
снизу вверх и
показывают стрелкой.
Оси взаимно перпендикулярны (т.е. угол между ними равен 90°) и
пересекаются в точке, которую обозначают «O».
Точка «O» является началом отсчёта для каждой из осей.
Запомните!
Система координат — это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является
началом отсчёта для каждой из них.
Координатные оси — это прямые, образующие систему координат.
Ось абсцисс «Ox» — горизонтальная ось.
Ось ординат «Oy» — вертикальная ось.
Координатная плоскость — плоскость, в которой построена система координат.
Обозначается плоскость как «x0y».
Обращаем ваше внимание на выбор длины единичных отрезков по осям.
Цифры, обозначающие числовые значения на осях можно располагать как справа, так и слева
от оси «Oy». Цифры
на оси «Ox», как правило, пишут внизу под осью.
Обычно единичный отрезок на оси «0y» равен единичному
отрезку на оси «0x». Но бывают случаи,
когда они не равны друг другу.
Оси координат делят плоскость на 4 угла, которые называют координатными четвертями. Четверть, образованная положительными
полуосями (правый верхний угол), считают первой I.
Отсчитываем четверти (или координатные углы) против часовой стрелки.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
28 сентября 2016 в 11:11
Вероника Диянова
Профиль
Благодарили: 0
Сообщений: 1
Вероника Диянова
Профиль
Благодарили: 0
Сообщений: 1
На оси абсцисс найти точку, расстояние которой от прямой 8х+15у+10=0 равно 1. Сделать чертеж
0
Спасибо
Ответить
28 сентября 2016 в 15:07
Ответ для Вероника Диянова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Графиком функции является прямая. Задайте два значения x, получите y и проведите линию через 2 точки, думаю это не самая сложная задача. Далее либо по графику, либо аналитически решаем задачу. Аналитически: если надо найти точку удалённую от оси абсцис на 1, значит нужно подставить вместо y = 1.
8x + 15 · 1 + 10 = 0.
8x = ?25
x = ? = ? 3 = ? 3,125
Если построите график, то увидите, что это так.
Ответ: (1; ? 3,125)
0
Спасибо
Ответить
1 октября 2016 в 22:35
Ответ для Вероника Диянова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
(7/8; 0); (?27/8; 0).
? = = 1. => |8a + 10| = 17.
0
Спасибо
Ответить
6 сентября 2016 в 15:15
Николай Шамов
Профиль
Благодарили: 0
Сообщений: 1
Николай Шамов
Профиль
Благодарили: 0
Сообщений: 1
Вообщем, прошу помочь, проблема касется изображения на координатной оси объединение и пересечения.Т.е. допустим, задание «Изобразите на координатной оси числовые промежутики A и B, найдите их объединение и пересечение, если: A=[-3;4],B=[0;7). Я понимаю, что Объединение [-3;7)
Пересечение [0;4]
но не понимаю, как это изобразить это на координатной оси, прошу помощи
0
Спасибо
Ответить
19 сентября 2016 в 14:31
Ответ для Николай Шамов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Проще всего изобразить это цветными карандашами или ручками. Нарисовать на одной оси оба промежутка и выделив разными цветами объединение и пересечение.
0
Спасибо
Ответить
Математика 5-6 класс
10 баллов
как найти абсциссу и ординату точки на координатной плоскости?
Влад Тихонов
15.07.2019 15:46:22
Чтобы найти абсциссу, нужно по оси x выбрать то число, которое указано в координатах на первом месте. Чтобы найти ординату, нужно по оси y выбрать то число, которое указано в координатах на втором месте.
Все предметы
Рейтинг пользователей

- Калькуляторы
- Справочник
- Словарь
Чтобы найти на плоскости какой-то объект, его описывают двумя значениями. Так каждое место в зале кинотеатра имеет два параметра: ряд и место. Каждая клетка на шахматной доске или при игре в «морской бой» описывается номером строки и буквой, обозначающей столбец.
В математике определение местоположения объекта на плоскости придумали быстро находить с помощью системы координат, образованной двумя прямыми, называемых координатными осями (или осями координат).
Абсцисса, ордината, начало координат и единичный отрезок
Эти оси имеют общепринятые наименования. А именно, горизонтальную ось именуют осью абсцисс и на письме обозначают $Оx$
Вертикальную ось называют осью ординат и на письме обозначают $Оy$
Оси пересекаются под прямым углом перпендикулярно друг к другу, поэтому такая система координат и называется прямоугольной.
Место пересечения осей координат является началом отсчета. Обычно эту точку обозначают буквой $О$ и называют началом координат. Ее называют еще иногда нулевой точкой.
На каждой оси выбирается единичный отрезок, с помощью которого вычисляются координаты объекта. Длиной единичного отрезка может выступать любая единица измерения, но она должна быть одинаковой на каждой из осей. То есть, если единичный отрезок на оси абсцисс задан, например, равным 1 см, то и на оси ординат единичный отрезок тоже должен быть равен одному сантиметру.
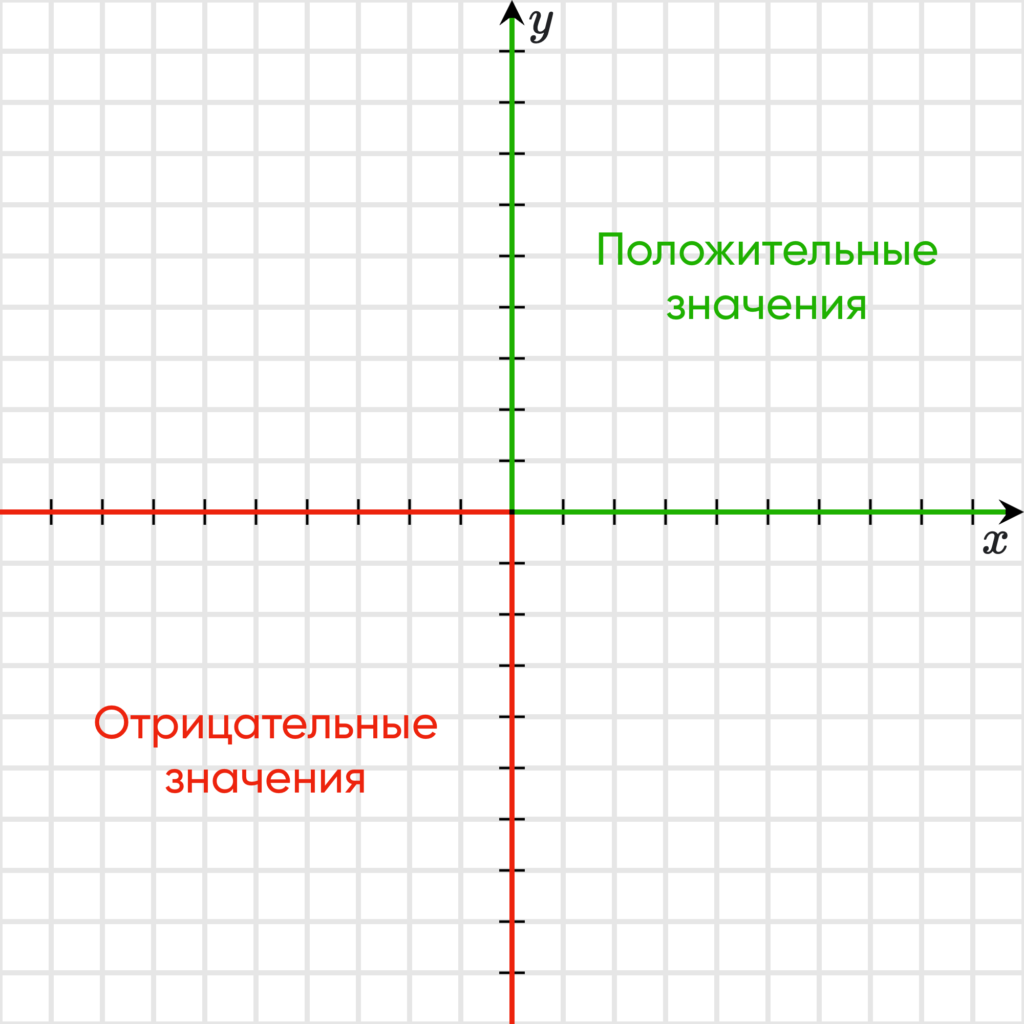
Положительное и отрицательное направление
У осей стрелкой задается положительное направление:
- так обычно у оси $Оx$ положительным считается направление вправо;
- у оси $Оy$ положительным считается направление снизу вверх.
В таком случае часть прямой $Оx$ левее точки $О$ будет принимать отрицательные значения. Аналогично часть прямой $Оy$ ниже точки отсчета $О$ будет также принимать отрицательные значения.
Таким образом, все вместе:
- начало координат $О$
- пересекающиеся под прямым углом оси $Оx$ и $Оy$ с заданными направлениями
- заданный единичный отрезок
образуют в математике прямоугольную систему координат, плоскость называют координатной.
Или другими словами:
Прямоугольная система координат – это две взаимно перпендикулярные координатные оси с заданными направлениями, единицей длины и точкой отсчета в месте их пересечения.
На письме система координат обозначается $Оxy$
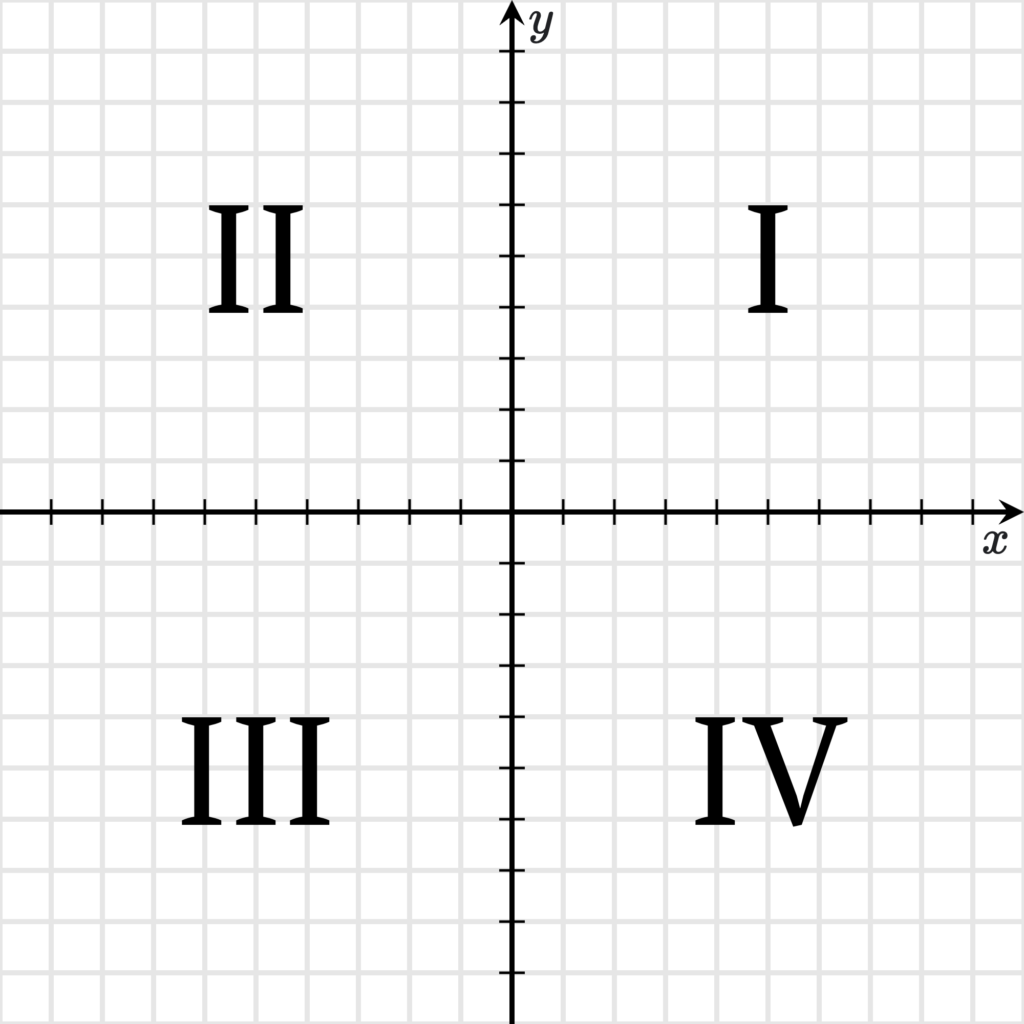
Четверти
Осями координат плоскость делится на 4 части, их обозначают римскими цифрами. Каждая часть называется «квадрант». Другие названия: «координатный угол» или «четверть». Нумерация четвертей принята против часовой стрелки в том порядке, в котором указано на рисунке ниже.
В квадранте I значения $x$ и $y$ будут положительными. Отсюда следует, что если координаты объекта $x$ и $y$ – числа положительные, то он находится в I квадранте.
В квадранте II значение $y$ будет положительными, а $x$ отрицательным.
В квадранте III обе координаты $x$ и $y$ будут иметь отрицательные значения.
В последнем IV квадранте значение $x$ будет положительным, а $y$ отрицательным.
Немного из истории
В латинском языке слово «координаты» получилось из двух других: co – «совместно» и ordinatus – «определенный», «упорядоченный».
Впервые необходимость нахождения координат объектов возникла в географии и астрономии. Для этого использовали широту и долготу, определяющие расположение точки на небесной сфере или на поверхности земного шара.
Таким образом начали вычислять координаты точек еще в 14 веке. Но упорядочил и систематизировал все знания в 17 веке французский математик по имени Рене Декарт. Поэтому прямоугольную систему координат также называют еще и «декартовой».