Содержание
- Введение системы координат
- Координаты куба
- Координаты трехгранной призмы
- Координаты шестигранной призмы
- Координаты четырехугольной пирамиды
- Координаты правильной треугольной призмы
Введение системы координат
Метод координат — это, конечно, очень хорошо, но в настоящих задачах C2 никаких координат и векторов нет. Поэтому их придется вводить. Да-да, вот так взять и ввести: указать начало отсчета, единичный отрезок и направление осей x, y и z.
Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения, как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.
Тем не менее, приведу некоторые рекомендации, как лучше ввести систему координат для самых часто встречающихся в задаче C2 многогранников. С указанием конкретных точек. Во всех случаях упор делается на минимизацию объема вычислений.
Координаты куба
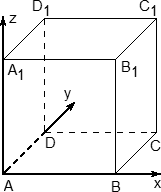
Если в задаче C2 будет куб — считайте, что вам повезло. Это самый простой многогранник, все двугранные углы которого равны 90°.
Система координат также вводится очень просто:
- Начало координат — в точке A;
- Чаще всего ребро куба не указано, поэтому принимаем его за единичный отрезок;
- Ось x направляем по ребру AB, y — по ребру AD, а ось z — по ребру AA1.
Обратите внимание: ось z направляется вверх! После двумерной системы координат это несколько непривычно, но на самом деле очень логично.
Итак, теперь у каждой вершины куба есть координаты. Соберем их в таблицу — отдельно для нижней плоскости куба:
| Точка | A | B | C | D |
| Координаты | (0; 0; 0) | (1; 0; 0) | (1; 1; 0) | (0; 1; 0) |
| Точка | A1 | B1 | C1 | D1 |
| Координаты | (0; 0; 1) | (1; 0; 1) | (1; 1; 1) | (0; 1; 1) |
Несложно заметить, что точки верхней плоскости отличаются соответствующих точек нижней только координатой z. Например, B = (1; 0; 0), B1 = (1; 0; 1). Главное — не запутаться!
Координаты трехгранной призмы
Призма — это уже намного веселее. При правильном подходе достаточно знать координаты только нижнего основания — верхнее будет считаться автоматически.
В задачах C2 встречаются исключительно правильные трехгранные призмы (прямые призмы, в основании которых лежит правильный треугольник). Для них система координат вводится почти так же, как и для куба. Кстати, если кто не в курсе, куб — это тоже призма, только четырехгранная.
Итак, поехали! Вводим систему координат:
- Начало координат — в точке A;
- Сторону призмы принимаем за единичный отрезок, если иное не указано в условии задачи;
- Ось x направляем по ребру AB, z — по ребру AA1, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC.
Здесь требуются некоторые пояснения. Дело в том, что ось y НЕ совпадает с ребром AC, как многие считают. А почему не совпадает? Подумайте сами: треугольник ABC — равносторонний, в нем все углы по 60°. А углы между осями координат должны быть по 90°, поэтому сверху картинка будет выглядеть так:

Надеюсь, теперь понятно, почему ось y не пойдет вдоль AC. Проведем в этом треугольнике высоту CH. Треугольник ACH — прямоугольный, причем AC = 1, поэтому AH = 1 · cos A = cos 60°; CH = 1 · sin A = sin 60°. Эти факты нужны для вычисления координат точки C.
Теперь взглянем на всю призму вместе с построенной системой координат:
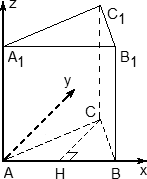
Получаем следующие координаты точек:
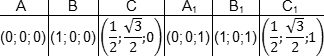
Как видим, точки верхнего основания призмы снова отличаются от соответствующих точек нижнего лишь координатой z. Основная проблема — это точки C и C1. У них есть иррациональные координаты, которые надо просто запомнить. Ну, или понять, откуда они возникают.
Координаты шестигранной призмы
Шестигранная призма — это «клонированная» трехгранная. Можно понять, как это происходит, если взглянуть на нижнее основание — обозначим его ABCDEF. Проведем дополнительные построения: отрезки AD, BE и CF. Получилось шесть треугольников, каждый из которых (например, треугольник ABO) является основанием для трехгранной призмы.
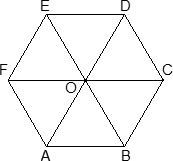
Теперь введем собственно систему координат. Начало координат — точку O — поместим в центр симметрии шестиугольника ABCDEF. Ось x пойдет вдоль FC, а ось y — через середины отрезков AB и DE. Получим такую картинку:
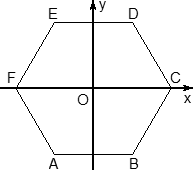
Обратите внимание: начало координат НЕ совпадает с вершиной многогранника! На самом деле, при решении настоящих задач вы обнаружите, что это очень удобно, поскольку позволяет значительно уменьшить объем вычислений.
Осталось добавить ось z. По традиции, проводим ее перпендикулярно плоскости OXY и направляем вертикально вверх. Получим итоговую картинку:
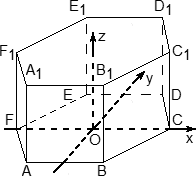
Запишем теперь координаты точек. Предположим, что все ребра нашей правильной шестигранной призмы равны 1. Итак, координаты нижнего основания:
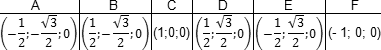
Координаты верхнего основания сдвинуты на единицу по оси z:
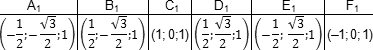
Координаты четырехугольной пирамиды
Пирамида — это вообще очень сурово. Мы разберем только самый простой случай — правильную четырехугольную пирамиду, все ребра которой равны единице. Однако в настоящих задачах C2 длины ребер могут отличаться, поэтому ниже приведена и общая схема вычисления координат.
Итак, правильная четырехугольная пирамида. Это такая же, как у Хеопса, только чуть поменьше. Обозначим ее SABCD, где S — вершина. Введем систему координат: начало в точке A, единичный отрезок AB = 1, ось x направим вдоль AB, ось y — вдоль AD, а ось z — вверх, перпендикулярно плоскости OXY. Для дальнейших вычислений нам потребуется высота SH — вот и построим ее. Получим следующую картинку:
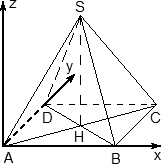
Теперь найдем координаты точек. Для начала рассмотрим плоскость OXY. Здесь все просто: в основании лежит квадрат, его координаты известны. Проблемы возникают с точкой S. Поскольку SH — высота к плоскости OXY, точки S и H отличаются лишь координатой z. Собственно, длина отрезка SH — это и есть координата z для точки S, поскольку H = (0,5; 0,5; 0).
Заметим, что треугольники ABC и ASC равны по трем сторонам (AS = CS = AB = CB = 1, а сторона AC — общая). Следовательно, SH = BH. Но BH — половина диагонали квадрата ABCD, т.е. BH = AB · sin 45°. Получаем координаты всех точек:
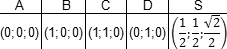
Вот и все с координатами пирамиды. Но не с координатами вообще. Мы рассмотрели лишь самые распространенные многогранники, однако этих примеров достаточно, чтобы самостоятельно вычислить координаты любых других фигур. Поэтому можно приступать, собственно, к методам решения конкретных задач C2.
Источник
Координаты правильной треугольной призмы
Решение заданий №14 ЕГЭ по математике координатно-векторным методом
С помощью данных методических рекомендаций можно научиться решать задачи на вычисление углов и расстояний в стереометрии с помощью координатно-векторного метода. Для учеников 10-11 классов самой главной проблемой является подготовка к ЕГЭ. Причем не все ученики уверенно решают задания II части , а некоторые и не берутся за их решение.
Координатно-векторный метод основан на введении прямоугольной системы координат и создании геометрически-алгебраической модели решения задач, тем самым упрощая громоздкие и достаточно сложные преобразования и выкладки.
Достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных конфигураций.
Выражаю огромную благодарность своим ученикам 11 класса 2016 – 2017 учебного года: Комаровой Ангелине, Тарбаеву Наилю, Бекмурзаеву Тимуру, Утегеновой Аимгуль, Абылхатаевой Карине, Кункашевой Арине, Юсуповой Аделине, Успанову Гелиму, которые сыграли большую роль в создании данного методического сборника
Если у вас имеются серьезные проблемы с пониманием определений, с чтением или построением сложного стереометрического рисунка, если вам никак не удается подобрать необходимые дополнительные построения, мне кажется, что стоит заняться изучением координатно-векторного метода. Особенно это актуально в условиях экстренной помощи, когда до ЕГЭ остается всего лишь 2-3 месяца.
Данный курс не претендует на научность, а является небольшим методическим пособием при подготовке к ЕГЭ для выпускника, нацеленного на высокий балл при сдаче экзамена. Курс является кратким, в нем рассмотрены лишь наиболее часто встречающиеся типы заданий, как в сборниках, так и в контрольно-измерительных материалах.
Метод координат — это довольно несложный способ, но в настоящих задачах №14 никаких координат и векторов нет. Поэтому их придется вводить: указать начало отсчета, единичный отрезок и направление осей x, y и z.
Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения, как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.
Основные понятия.
Метод координат —эффективный и универсальный способ нахождения любых углов или расстояний между стереометрическими объектами в пространстве. Данный метод заключается во введении декартовой системы координат, а затем – нахождение образующихся векторов (их длин и углов между ними). Достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных конфигураций. Алгоритм применения метода координат к решению геометрических задач сводится к следующему:
— Выбираем в пространстве систему координат
— Находим координаты необходимых, по условию задачи, точек.
— Решаем задачу, используя основные задачи метода координат.
— Переходим от аналитических соотношений к геометрическим.
Для начала разбора метода координат для стереометрических задач рассмотрим, что же представляет собой прямоугольная (декартова) система координат в пространстве. Прямоугольная (декартова) система координат в пространстве – совокупность точки О (называемой началом координат), единицы измерения и трёх попарно перпендикулярных прямых Ox, Oy иOz (называемых осями координат: Ox – ось абсцисс, Oy – ось ординат, Oz – ось аппликат), на каждой из которых указано направление положительного отсчёта. Плоскости хОу, уОz и zOx называют координатными плоскостями. Каждой точке пространства ставится в соответствие тройка чисел, называемых её координатами.
 z
z

 0 у
0 у
Для того чтобы использовать метод координат, надо хорошо знать формулы:
1. Нахождение расстояния между двумя точками, заданными своими координатами.
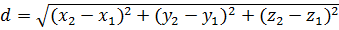 , где
, где
2. Нахождение координат середины отрезка
A(x 1 ; y 1 ; z 1), B(x 2 ; y 2 ; z 2) 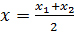
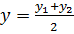
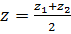
3. Нахождение косинуса угла между векторами
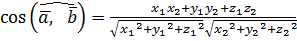 , где
, где 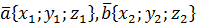
4. Координаты x, y, z точки М, которая делит отрезок , ограниченный точками А(х1, у1,z1 ) и B(x2,y2,z2 ), в отношении , определяется по формулам 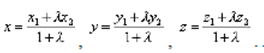
5. Расстояние от точки до плоскости
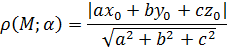
Для решения задач необходимо научиться находить координаты вершин основных многогранников при помещении их в прямоугольную систему координат.
Ниже представлены координаты вершин некоторых многогранников, помещенных в систему координат.
Координаты куба
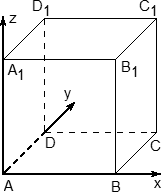
Это самый простой многогранник, все двугранные углы которого равны 90°.
Система координат также вводится очень просто:
1. Начало координат — в точке A;
2. Чаще всего ребро куба не указано, поэтому принимаем его за единичный отрезок;
3. Ось x направляем по ребру AB, y — по ребру AD, а ось z — по ребру AA1.
Обратите внимание: ось z направляется вверх! После двумерной системы координат это несколько непривычно, но на самом деле очень удобно и логично.
Итак, теперь у каждой вершины куба есть координаты. Соберем их в таблицу — отдельно для нижней плоскости куба:
| Точка | A | B | C | D |
| Координаты | (0; 0; 0) | (1; 0; 0) | (1; 1; 0) | (0; 1; 0) |
| Точка | A1 | B1 | C1 | D1 |
| Координаты | (0; 0; 1) | (1; 0; 1) | (1; 1; 1) | (0; 1; 1) |
Несложно заметить, что точки верхней плоскости отличаются от соответствующих точек нижней только координатой z. Например, B = (1; 0; 0), B1 = (1; 0; 1).
Координаты правильной треугольной призмы
При правильном подходе достаточно знать координаты только нижнего основания — верхнее будет считаться автоматически.
В задачах №14 встречаются исключительно правильные трехгранные призмы (прямые призмы, в основании которых лежит правильный треугольник). Для них система координат вводится почти так же, как и для куба.
1. Начало координат — в точке A;
2. Сторону призмы принимаем за единичный отрезок, если иное не указано в условии задачи;
3. Ось x направляем по ребру AB, z — по ребру AA1, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC.

Получаем следующие координаты точек:
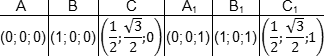
Как видим, точки верхнего основания призмы снова отличаются от соответствующих точек нижнего лишь координатой z. Основная проблема — это точки C и C1. У них есть иррациональные координаты, и для того чтобы довольно просто решить задание №14 эти иррациональные координаты надо просто запомнить. Или можно вывести.
Дата добавления: 2021-03-18 ; просмотров: 582 ; Мы поможем в написании вашей работы!
Источник
Что такое ось призмы? (прямой правильной треугольной)
Угон Харлеев
Знаток
(325),
закрыт
14 лет назад
Лучший ответ
Leonid
Высший разум
(388685)
14 лет назад
Линия, соединящая центры симметрии оснований (они же центры тяжести и прочие цуентры правильных треугольников, лежащих в основаниях призмы).
Остальные ответы
Ayrat
Гуру
(3591)
14 лет назад
это линия проходящая через 2 точки, в плоскости основания призмы, полученные в результате пересечения биссектрис.
Похожие вопросы
Содержание:
Ранее вы уже знакомились с призмой, т. е. многогранником, две грани которого — равные 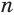
Что такое призма
Равные грани-многоугольники призмы лежат в параллельных плоскостях и называются основаниями призмы, а остальные грани-параллелограммы — боковыми гранями. Ребра боковых граней, не принадлежащие основаниям, называют боковыми ребрами. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называют диагональю призмы (рис. 1). Плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани, называется диагональной плоскостью, а сечение призмы диагональной плоскостью — диагональным сечением. На рисунке 2 показаны два диагональных сечения призмы.
Призмы разделяют на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон их оснований. Призма, изображенная на рисунке 1, — шестиугольная, а на рисунке 2, — девятиугольная.
Отличают прямые и наклонные призмы в зависимости от того, перпендикулярны или не перпендикулярны боковые ребра призмы ее основаниям. Обычно при изображении прямой призмы ее боковые ребра проводят вертикально.
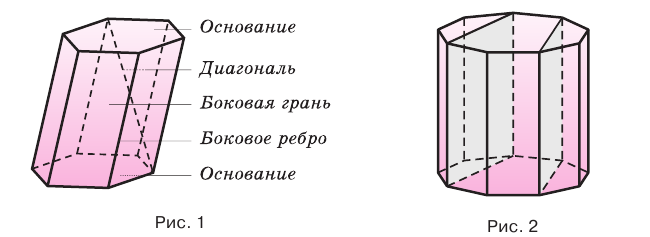
Прямая призма, основаниями которой являются правильные многоугольники, называется правильной призмой. В прямой призме все боковые грани — прямоугольники, а в правильной — равные прямоугольники.
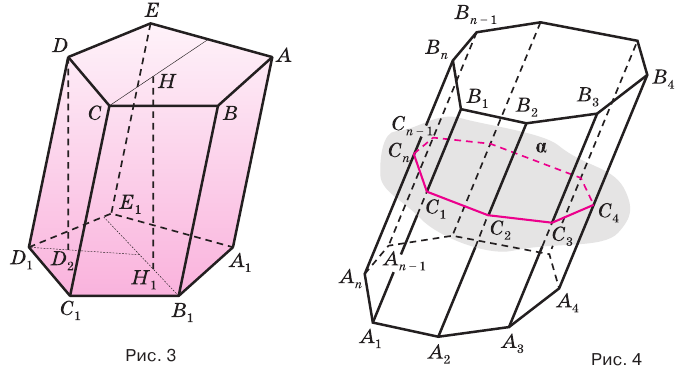
Перпендикуляр, проведенный из какой-либо точки одного основания призмы к плоскости другого основания, называется высотой призмы. На рисунке 3 показаны две высоты 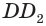 и
и 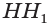 призмы
призмы 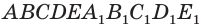 . У прямой призмы ее высота равна боковому ребру.
. У прямой призмы ее высота равна боковому ребру.
Боковые грани составляют боковую поверхность призмы, а боковые грани вместе с основаниями — полную поверхность призмы.
Теорема 1.
Площадь боковой поверхности призмы равна произведению периметра ее перпендикулярного сечения и длины бокового ребра:
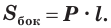
Доказательство:
Пусть имеется 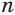 -угольная призма
-угольная призма 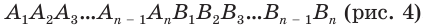 . Пересечем ее плоскостью
. Пересечем ее плоскостью 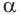 , перпендикулярной боковому ребру. Получим перпендикулярное сечение
, перпендикулярной боковому ребру. Получим перпендикулярное сечение 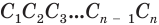 , стороны которого перпендикулярны сторонам параллелограммов, составляющим боковую поверхность призмы. Поэтому для боковой поверхности
, стороны которого перпендикулярны сторонам параллелограммов, составляющим боковую поверхность призмы. Поэтому для боковой поверхности 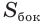 получим:
получим:
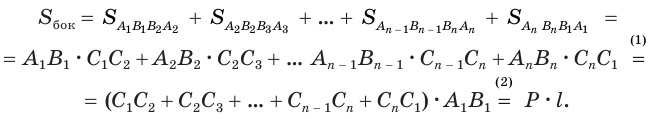
При переходе (1) мы учли, что все боковые ребра призмы равны друг другу, при переходе (2) — то, что сумма  выражает периметр
выражает периметр 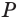 перпендикулярного сечения призмы, а множитель
перпендикулярного сечения призмы, а множитель 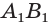 — длину
— длину 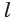 бокового ребра.
бокового ребра.
Следствие 1.
Площадь боковой поверхности прямой призмы равна произведению периметра ее основания и высоты.
Действительно, перпендикулярное сечение прямой призмы равно ее основанию, а боковое ребро является высотой.
Частным видом призмы является параллелепипед, т. е. призма, основанием которой является параллелограмм. Параллелепипед, как и призма, может быть прямым или наклонным. Прямой параллелепипед, основаниями которого являются прямоугольники, называется прямоугольным параллелепипедом. Прямоугольный параллелепипед, у которого три ребра, выходящие из одной вершины, равны друг другу, называется кубом.
У параллелепипеда все грани — параллелограммы, из которых у прямого параллелепипеда прямоугольниками являются боковые грани, а у прямоугольного параллелепипеда — все грани.
12 ребер параллелепипеда разделяются на три четверки равных ребер (рис. 5), его 6 граней — на три пары равных граней (рис. 6), а 4 диагонали пересекаются в одной точке, являющейся центром симметрии параллелепипеда (рис. 7).
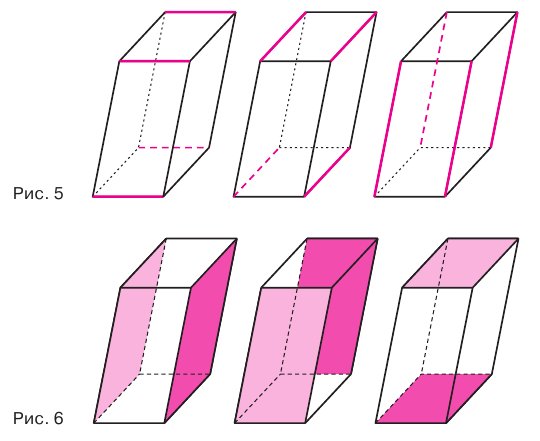
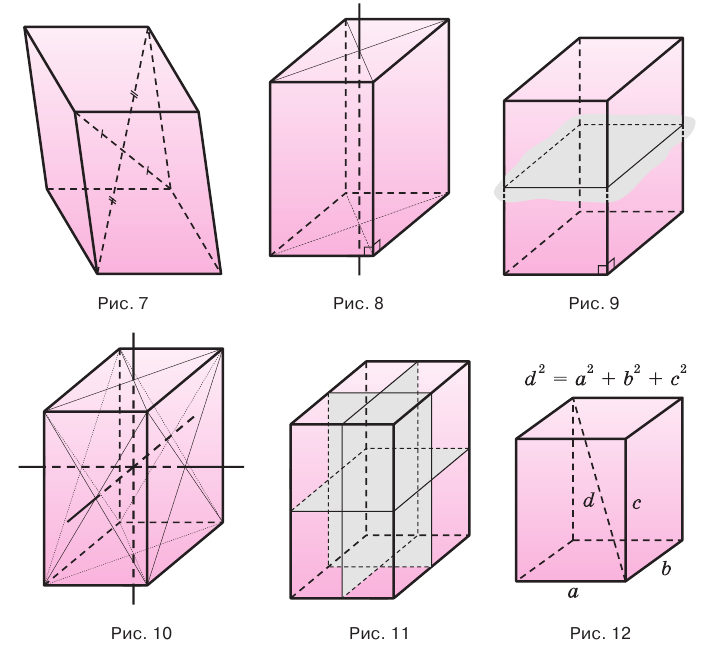
Прямой параллелепипед еще имеет ось симметрии (рис. 8) и плоскость симметрии (рис. 9). Прямоугольный параллелепипед имеет три оси симметрии (рис. 10) и три плоскости симметрии (рис. 11).
Ребра прямоугольного параллелепипеда, выходящие из одной вершины, называют измерениями прямоугольного параллелепипеда. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (рис. 12), и все его диагонали равны друг другу.
Важной характеристикой плоской фигуры является ее площадь. Подобной характеристикой тела является его объем. Будем считать, что изучаемые нами тела имеют объем.
За единицу объема принимают объем куба с ребром 1. На практике пользуются разными единицами объема: как метрическими — кубический миллиметр, кубический сантиметр, кубический дециметр, кубический метр, кубический километр, так и неметрическими — галлон, барель, бушель, кварта.
Для объема тела выполняются его основные свойства:
- равные тела имеют равные объемы;
- если тело разделено на части, то его объем равен сумме объемов этих частей.
При этом равными фигурами называют фигуры, которые преобразуются друг в друга определенным движением. Например, равными являются две шестиугольные правильные призмы, у которых соответственно равны стороны оснований и высоты (рис. 13), или два цилиндра с соответственно равными радиусами оснований и образующими (рис. 14). Тело, изображенное на рисунке 15, можно разделить на цилиндр и конус, и его объем равен сумме объемов этих цилиндра и конуса.
Два тела с равными объемами называют равновеликими телами. Равные тела являются равновеликими, но не наоборот.
Вы знаете, что объем 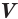 прямоугольного параллелепипеда равен произведению трех его измерений
прямоугольного параллелепипеда равен произведению трех его измерений 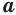 ,
, 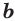 ,
, 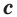 (рис. 16):
(рис. 16): 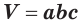 .
.
Учитывая, что в формуле 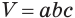 произведение
произведение 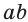 выражает площадь
выражает площадь 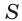 основания прямоугольного параллелепипеда, а число
основания прямоугольного параллелепипеда, а число 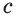 — его высоту
— его высоту 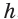 , получим, что объем
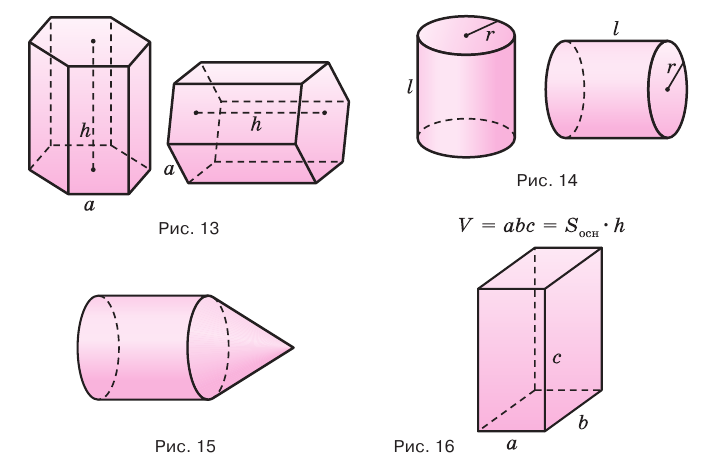
, получим, что объем 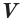 прямоугольного параллелепипеда равен произведению площади его основания и высоты:
прямоугольного параллелепипеда равен произведению площади его основания и высоты:  .
.
Теорема 2.
Объем произвольного параллелепипеда равен произведению площади его основания и высоты:
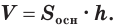
Доказательство:
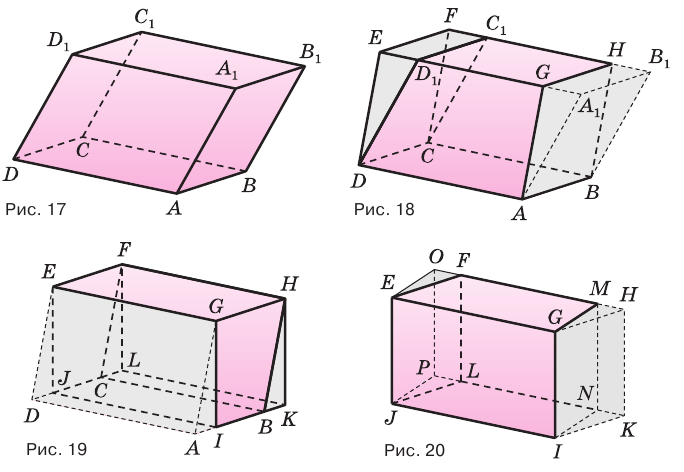
Пусть имеется произвольный параллелепипед 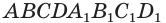 (рис. 17). Через ребро
(рис. 17). Через ребро 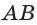 проведем плоскость, перпендикулярную ребру
проведем плоскость, перпендикулярную ребру 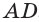 , она отсечет от параллелепипеда треугольную призму
, она отсечет от параллелепипеда треугольную призму 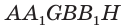 (рис. 18). После параллельного сдвига этой призмы в направлении отрезка
(рис. 18). После параллельного сдвига этой призмы в направлении отрезка 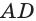 получим призму
получим призму 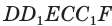 . Параллелепипед
. Параллелепипед 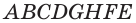 равновелик с данным параллелепипедом
равновелик с данным параллелепипедом 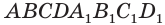 . Выполненное преобразование параллелепипеда также сохраняет объем параллелепипеда, площадь его основания и высоту.
. Выполненное преобразование параллелепипеда также сохраняет объем параллелепипеда, площадь его основания и высоту.
У параллелепипеда 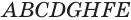 его боковые грани
его боковые грани 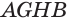 и
и  перпендикулярны плоскости основания. К граням
перпендикулярны плоскости основания. К граням 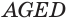 и
и 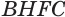 , которые не перпендикулярны плоскости основания, применим такое же преобразование, в результате которого получим прямой параллелепипед
, которые не перпендикулярны плоскости основания, применим такое же преобразование, в результате которого получим прямой параллелепипед 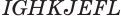 (рис. 19), в котором сохраняются объем, площадь основания и высота.
(рис. 19), в котором сохраняются объем, площадь основания и высота.
Наконец, применив еще раз такое преобразование к граням 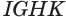 и
и  прямого параллелепипеда
прямого параллелепипеда 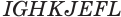 , получим прямоугольный параллелепипед
, получим прямоугольный параллелепипед 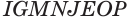 (рис. 20), сохранив объем параллелепипеда, площадь его основания и высоту.
(рис. 20), сохранив объем параллелепипеда, площадь его основания и высоту.
Значит,
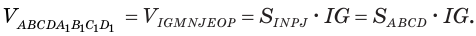
Множитель 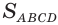 есть площадь основания параллелепипеда
есть площадь основания параллелепипеда 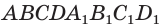 , а множитель
, а множитель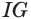 выражает его высоту, так как
выражает его высоту, так как 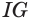 есть перпендикуляр, возведенный из точки
есть перпендикуляр, возведенный из точки 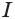 основания
основания 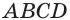 к другому основанию
к другому основанию 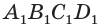 . Значит, объем произвольного параллелепипеда равен произведению площади его основания и высоты.
. Значит, объем произвольного параллелепипеда равен произведению площади его основания и высоты.
Теорема 3.
Объем призмы равен произведению площади ее основания и высоты:
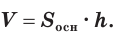
Доказательство:
Рассмотрим сначала треугольную призму 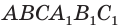 (рис. 21). Дополним ее до параллелепипеда
(рис. 21). Дополним ее до параллелепипеда 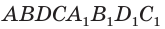 (рис. 22). Точка
(рис. 22). Точка 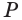 пересечения диагоналей диагонального сечения
пересечения диагоналей диагонального сечения 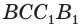 этого параллелепипеда является его центром симметрии. Это означает, что достроенная призма
этого параллелепипеда является его центром симметрии. Это означает, что достроенная призма 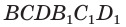 симметрична данной призме
симметрична данной призме 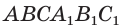 относительно центра
относительно центра 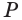 , а потому эти призмы равны друг другу. Значит, объем параллелепипеда
, а потому эти призмы равны друг другу. Значит, объем параллелепипеда 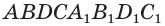 равен удвоенному объему данной призмы.
равен удвоенному объему данной призмы.
Объем параллелепипеда 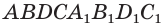 равен произведению площади его основания
равен произведению площади его основания 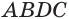 и высоты. Но площадь его основания
и высоты. Но площадь его основания 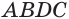 равна удвоенной площади основания
равна удвоенной площади основания  данной призмы, а высота параллелепипеда равна высоте призмы.
данной призмы, а высота параллелепипеда равна высоте призмы.
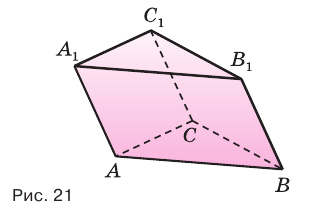
Отсюда следует, что объем призмы  равен площади ее основания
равен площади ее основания  и высоты. Теперь рассмотрим произвольную призму
и высоты. Теперь рассмотрим произвольную призму 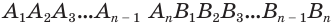 (рис. 23).
(рис. 23).
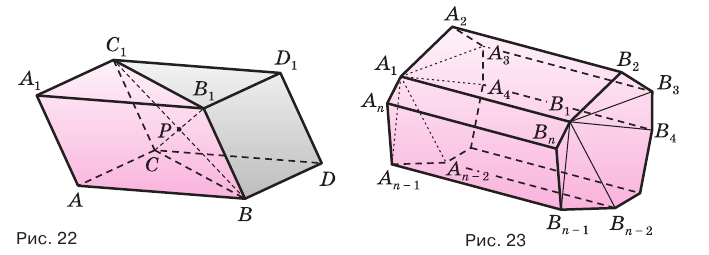
Диагональными сечениями, проходящими через вершину 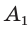 , разобьем ее на треугольные призмы-части
, разобьем ее на треугольные призмы-части 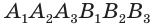 ,
, 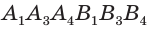 , …,
, …, 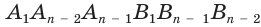 ,
, 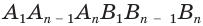 , которые все имеют одну и ту же высоту, равную высоте
, которые все имеют одну и ту же высоту, равную высоте 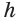 данной призмы. Объем данной призмы равен сумме объемов призм-частей. По уже доказанному для объема
данной призмы. Объем данной призмы равен сумме объемов призм-частей. По уже доказанному для объема 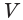 данной призмы получим:
данной призмы получим:
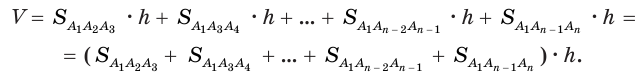
Учитывая, что сумма в скобках выражает площадь S основания данной призмы, получим:
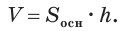
Следствие 2.
Объем прямой призмы равен произведению площади ее основания и бокового ребра.
Призма и её сечения
С призмой вы уже знакомы. Несмотря на это, мы напомним определение призмы и её свойства.
Призма -это многогранник, две грани которого равные n-угольники (основания), лежащие в параллельных плоскостях, а остальные n граней – параллелограммы (рис. 22).
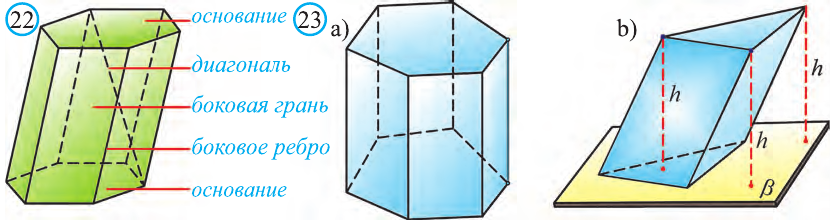
В зависимости от того перпендикулярны ли боковые грани призмы его основаниям или нет, призмы делят на прямые или наклонные. На рисунке 23.а изображена прямая призма, а на рисунке 23.b – наклонная. Очевидно, что боковые грани прямой призмы – прямоугольники.
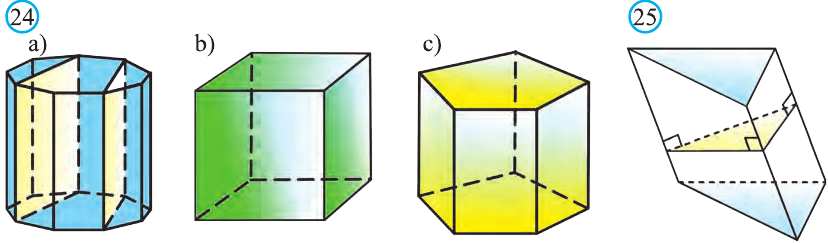
Если основания прямой призмы являются правильными многоугольниками, то её называют правильной (рис. 24). Боковые грани правильной призмы это равные между собой прямоугольники.
Перпендикуляр, опущенный из некоторой точки одного основания к другому, называют его перпендикуляром (рис. 23.b).
Сечение призмы, проходящее через соответствующие диагонали его оснований, называют диагональным сечением (рис. 24.а) и их число равно числу диагоналей одного из оснований.
Перпендикулярным сечением призмы называют сечение перпендикулярное всем его боковым рёбрам (рис. 25). так как 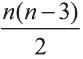 число диагоналси выпуклого n-угольника, то число диагональных сeчeний n-угольной призмы также равно
число диагоналси выпуклого n-угольника, то число диагональных сeчeний n-угольной призмы также равно 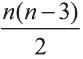 .
.
В каждом диагональном сечении призмы можно провести две диагонали. Следовательно, n-угольная призма имеет 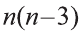 диагоналей.
диагоналей.
Пример:
В наклонной треугольной призме расстояния между боковыми ребрами соответственно равны 7 см, 15 см и 20 см. Найдите расстояние между большей боковой гранью и противолежащим боковым ребром.
Решение:
Известно, что расстояние между параллельными прямыми равно длине перпендикуляра, опущенного из произвольной точки одной прямой на другую. Тогда длины сторон перпендикулярного сечения ABC (рис. 26). Наибольшая грань призмы проходит через наибольшую сторону АС= 20 см этого сечения. Расстояние от рёбра призмы В2В1 до плоскости грани 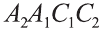 равно высоте BD треугольника ABC.
равно высоте BD треугольника ABC.
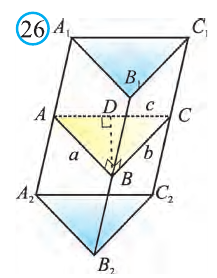
Тогда по формуле Герона получаем:
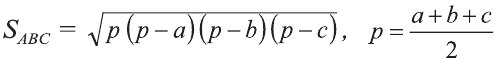
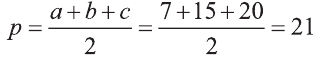 ,
,
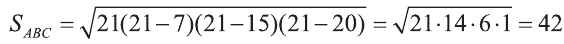 .
.
С другой стороны, 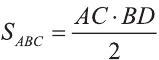 .
.
Отсюда 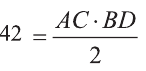 или
или 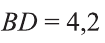 см.
см.
Ответ: 4,2 см.
Параллелепипед и куб
Призма, основаниями которой являются параллелограммы, называют параллелепипедом (рис. 27). Параллелепипеды также как и призмы могут быть прямыми (рис. 27.а) и наклонными (рис. 27.b). 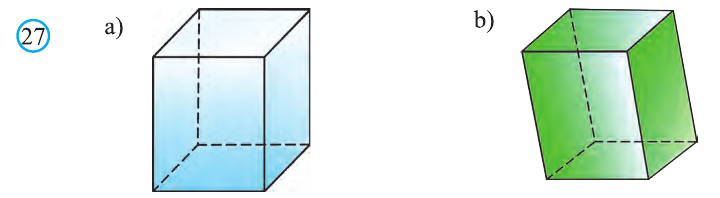
Грани параллелепипеда, не имеющие общую вершину, называют противоположными гранями.
У параллелепипеда:
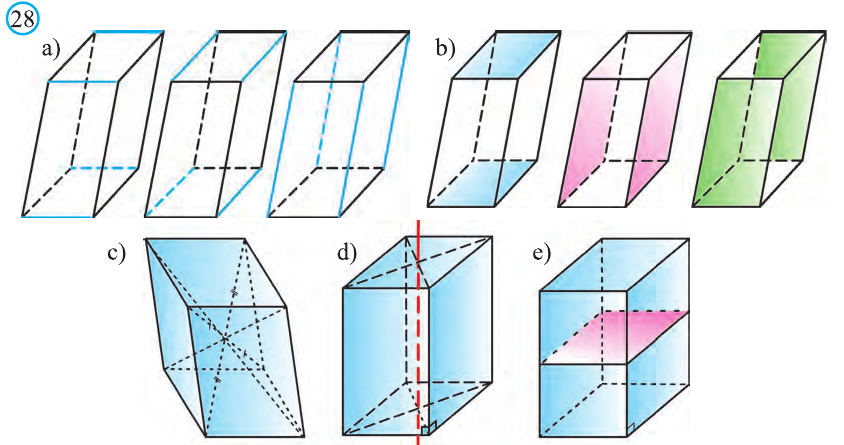
- —12 рёбер, каждые четыре из которых равны (рис. 28.а),
- —6 граней, которые попарно параллельны и равны (рис. 28.b),
- —4 диагонали, которые пересекаются и точкой пересечения делятся пополам (рис. 28.с),
- —точка пересечения диагоналей – центр его симметрии (рис. 28.с). Прямой параллелепипед имеет ось симметрии (рис. 28.d) и плоскость симметрии (рис. 28.e).
Прямой параллелепипед, основания которого являются прямоугольники, называют прямоугольным параллелепипедом (рис. 29). Очевидно, что все грани прямоугольного параллелепипеда являются прямоугольниками.
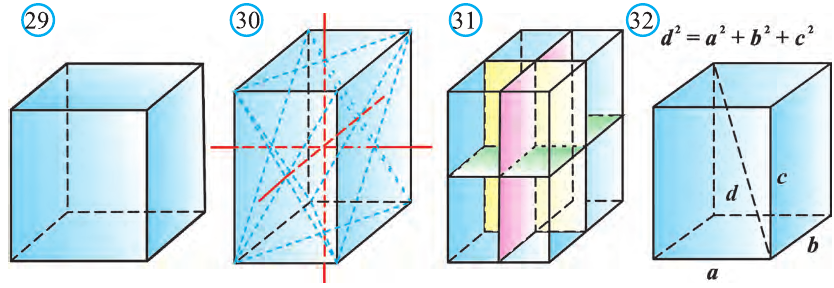
Прямоугольный параллелепипед имеет три оси симметрии (рис. 30) и три плоскости симметрии (рис. 31).
Длины трех рёбер, исходящих из одной вершины прямоугольного параллелепипеда называют его измерениями.
Свойство: В прямоугольном параллелепипеде квадрат любой диагонали d равен сумме квадратов его измерений: а, b и с (рис.32):
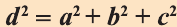 .
.
Прямоугольный параллелепипед, все измерения которого равны, называют кубом. Очевидно, что все грани куба являются равными квадратами. Куб имеет один центр симметрии, 9 осей симметрии и 9 плоскостей симметрии.
Выше были перечислены свойства призмы. Некоторые из них были показаны в 10 классе. Доказательства остальных свойств проще, поэтому их доказательства вы можете провести самостоятельно.
Площади боковой и полной поверхности призмы
На рисунке 33 проведены высоты НН1 DD1 призмы
АВСDЕ–А1В1С1D1Е1. Очевидно, что высоты правильной призмы будут равны её боковому рёбру. 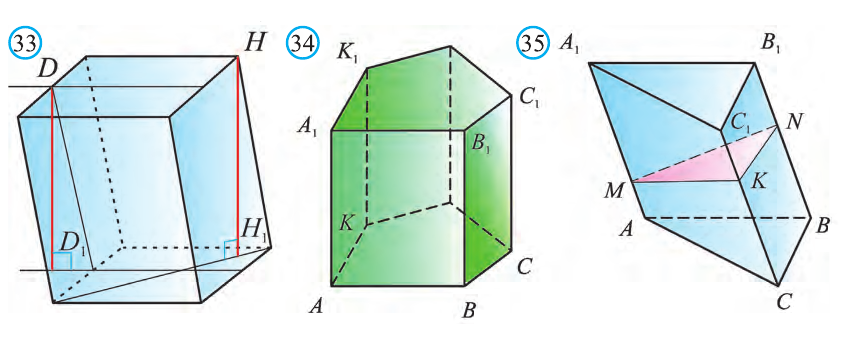
Боковая поверхность призмы (точнее, площадь боковой поверхности)равна сумме боковых поверхностей ее граней, а полная поверхнасть равна сумме боковой поверхности и площадей двух ее оснований. 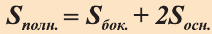
Теорема. Боковая поверхность прямой призмы равна произведению периметра ее основания на высоту: 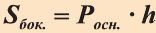
Доказательство. Пусть высота данной прямой призмы равна 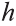 , а периметр основания
, а периметр основания 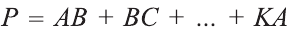 (рис. 34). Известно, что каждая грань прямой призмы является прямоугольником. Основания прямоугольников равны соответствующим сторонам основания призмы, а высоты равны высоте призмы.
(рис. 34). Известно, что каждая грань прямой призмы является прямоугольником. Основания прямоугольников равны соответствующим сторонам основания призмы, а высоты равны высоте призмы.
Тогда 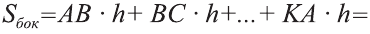
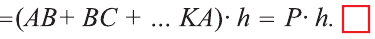
Теорема. Боковая поверхность произвольной призмы равна произведению периметра перпендикулярного сечения призмы на ее боковое ребро: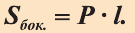
Доказательство. Пусть периметр перпендикулярного сечения призмы равен Р (рис. 35). Сечение делит призму на две части (рис. 36.а). Совершим параллельный перенос одной из этих частей так, чтобы основания нашей призмы совпали. В результате мы получим новую прямую призму (рис. 36.b). Очевидно, что, боковая поверхность этой призмы равна боковой поверхности данной. Её основанием является перпендикулярное сечение, а боковое ребро равно 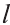 .
.
Тогда по доказанной выше теореме: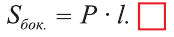
Объем призмы
Одним из свойств, характеризующих геометрические тела в пространстве, является понятие объема. Каждый предмет (тело) занимает некоторую часть пространства. Например, кирпич по сравнению со спичечным коробком занимает большую часть пространства. Для сравнения этих частей между собой вводится понятие объёма.
Объём – это величина, численное значение которой обладает следующими свойствами:
- Любое тело имеет определённый объём, выраженный положительным числом.
- Равные тела имеют равные объёмы.
- Если тело разбито на несколько частей, то его объём равен сумме объёмов этих частей.
- Объём куба, ребро которого равно единице, равен единице.
Объём – также как длина и площадь, является величиной. В зависимости от выбора единицы длины, объём единого куба измеряют в кубических единицах:
1 см3, 1 дм3, 1 м3 и т. д.
Объёмы тел измеряют различными способами или вычисляют. Например, объёмы маленьких предметов можно измерить с помощью сосудов (мензурки) с мелкими делениями (шкалами) (рис. 46). А объём ведра можно измерить с помощью сосуда, имеющего единичный объём, наполнив его водой (рис. 47). Но таким способом мы не можем измерить объёмы всех тел. В таких случаях объём вычисляют различными способами. Ниже рассмотрим их без доказательств. 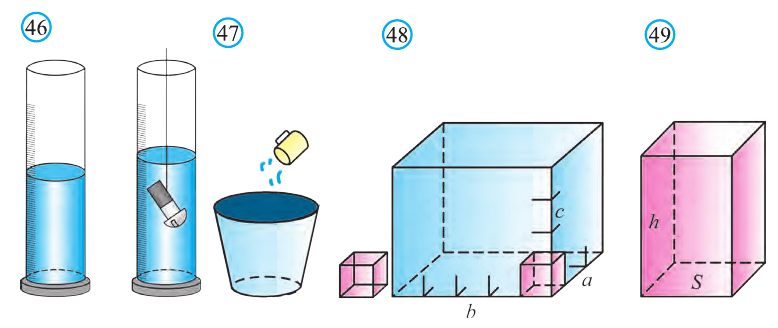
Объём параллелепипеда
Теорема. Объём прямоугольного параллелепипеда равен произведению трех его измерeний (рис.48): 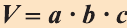 .
.
Следствие. Объём прямоугольного параллелепипеда равен произведению площади его основания на высоту (рис. 49): 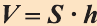 .
.
Теорема. Объём произвольного параллелепипеда равен произведению площади его основания на высоту (рис. 50): 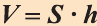 .
.
Это свойство вытекает из вышеупомянутого следствия. На рисунке 50 показано как данный параллелепипед преобразовать в прямоугольный параллелепипед. Воспользовавшись этим самостоятельно обоснуйте свойство. 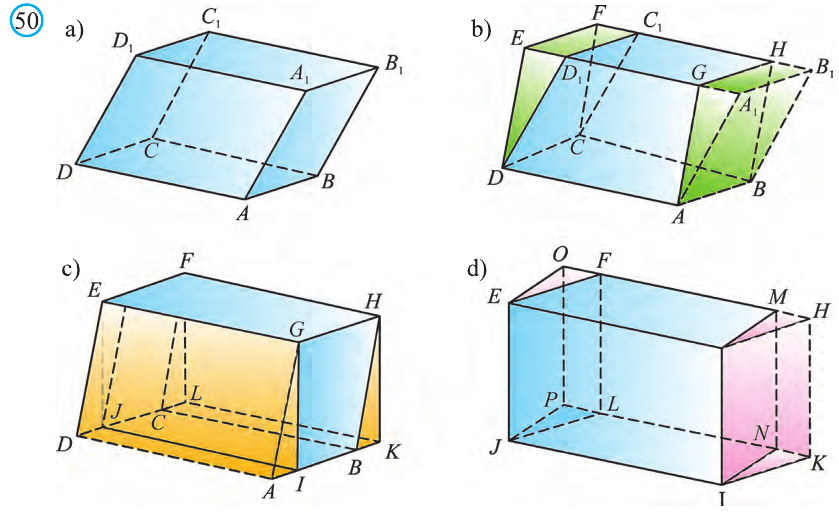
Нахождение объёма призмы
Теорема. Объём прямой призмы равен произведению площади его основания на высоту (рис. 51): 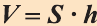 .
.
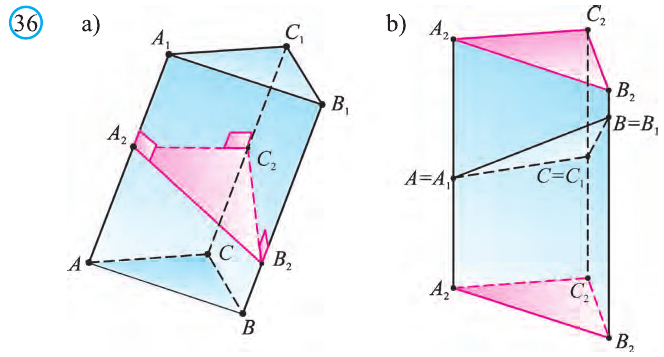
Доказательство. 1 случай. Пусть основанием призмы будет прямоугольный треугольник (рис 51.а). Эту призму можно дополнить равной ей призмой до прямоугольного параллелепипеда (рис. 51 .b).
Если объём данной призмы, площадь её основания и высота V, S и h, то объём полученного прямоугольного параллелепипеда, площадь его основания и высота будут соответственно равны 2V, 2S и h.
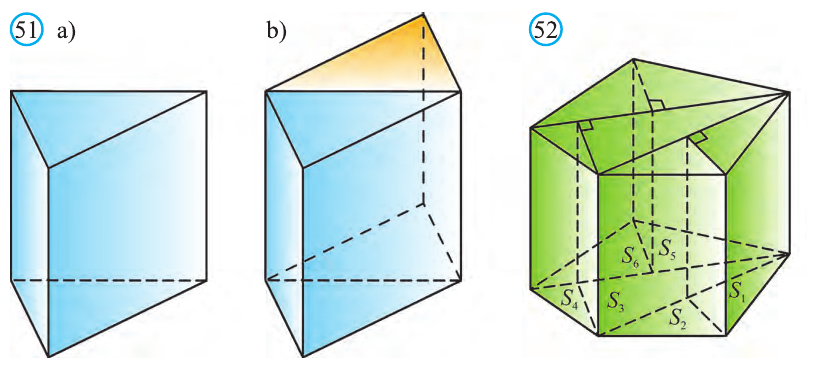
Следовательно 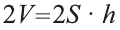 или
или 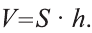
2 случай. Пусть S – площадь произвольной n – угольной прямой призмы и h – её высота. Основание призмы – n-угольник делится диагоналями на треугольники, каждый из которых можно разделить на прямоугольные треугольники (рис. 52). В результате данная призма разделится на конечное число прямых призм, основания которых являются прямоугольными треугольниками. Высоты этих призм равны h , а сумма площадей оснований этих призм равна площади основания данной призмы: 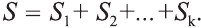
Объём данной призмы равен сумме объёмов составляющих её треугольных призм:
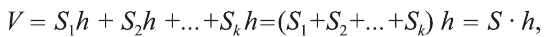
или 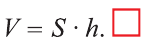
Теорема. Объём произвольной призмы равен произведению площади его основания на высоту: 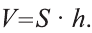
По рисунку 5.3 докажите эту теорему самостоятельно, сначала для треугольной призмы (рис. 5.3.а), затем для любой призмы (рис. 5.3.b).
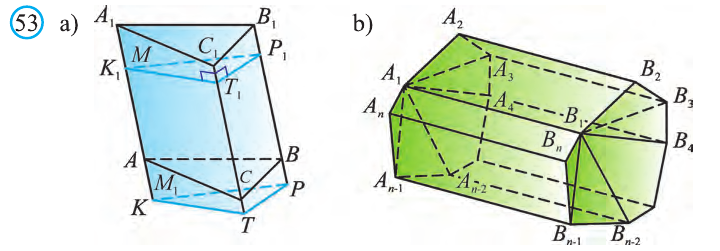
Пример:
Стороны основания прямого параллелепипеда равны а и b, а угол между ними 30°. Найдите его объём, если площадь его боковой поверхности равна S.
Решение:
Обозначим высоту параллелепипеда h(рис. 54).
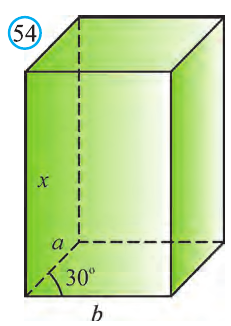
Тогда по условию задачи:
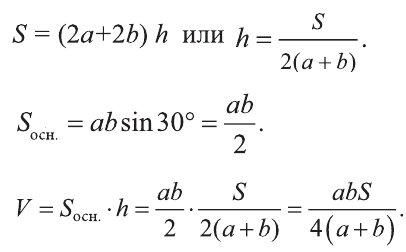
- Цилиндр в геометрии
- Пирамида в геометрии
- Конус в геометрии
- Сфера в геометрии
- Возникновение геометрии
- Геометрические преобразования в геометрии
- Планиметрия – формулы, определение и вычисление
- Стереометрия – формулы, определение и вычисление
Макеты страниц
Напомним, что правильной называется прямая призма, в основании которой лежит правильный многоугольник. Симметричность правильных призм определяется симметричностью их оснований (рис. 7.13), а так же перпендикулярностью основаниям боковых ребер и граней.
У правильной П-угольной призмы имеется П плоскостей симметрии, проходящих через соответствующие оси симметрии оснований призмы (рис. 7.14). Кроме того, у нее имеется еще одна плоскость симметрии, которая проходит через середины боковых ребер (рис. 7.15).

Рис. 7.14
Осями симметрии правильной  -угольной призмы всегда являются
-угольной призмы всегда являются  осей симметрии сечения этой призмы, проходящего через середины боковых ребер (рис. 7.16). Если к тому же
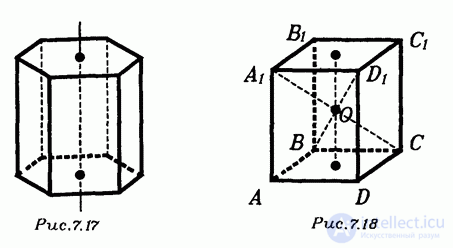
осей симметрии сечения этой призмы, проходящего через середины боковых ребер (рис. 7.16). Если к тому же  четно, то осью симметрии является еще прямая, которая соединяет центры оснований (рис. 7.17). Если же
четно, то осью симметрии является еще прямая, которая соединяет центры оснований (рис. 7.17). Если же  нечетно, то это не так и других осей симметрии нет.
нечетно, то это не так и других осей симметрии нет.
Отрезок, соединяющий центры оснований правильной призмы, называется ее осью (рис. 7.17).
Если П четно, то середина оси правильной  -угольной призмы является центром симметрии этой призмы (рис. 7.18). Если же
-угольной призмы является центром симметрии этой призмы (рис. 7.18). Если же  нечетно, то центра симметрии у правильной призмы нет (как и у ее основания).
нечетно, то центра симметрии у правильной призмы нет (как и у ее основания).
Итак, симметричность правильной  -угольной призмы определяется симметричностью ее основания — правильного П-угольника. Но, как известно из планиметрии, правильные П-угольники имеют еще один вид симметрии — вращательную, т. е. они самосовмещаются при повороте вокруг своего центра на угол
-угольной призмы определяется симметричностью ее основания — правильного П-угольника. Но, как известно из планиметрии, правильные П-угольники имеют еще один вид симметрии — вращательную, т. е. они самосовмещаются при повороте вокруг своего центра на угол  (рис. 7.19), а также на любой угол, кратный
(рис. 7.19), а также на любой угол, кратный  . Аналогично, правильные
. Аналогично, правильные  -угольные призмы самосовмещаются при повороте вокруг своей оси на такой же угол
-угольные призмы самосовмещаются при повороте вокруг своей оси на такой же угол  (рис. 7.20).
(рис. 7.20).
Подробнее это означает следующее. Плоскости, перпендикулярные оси правильной  -угольной призмы Р, параллельны ее основанию. Поэтому все сечения призмы Р такими плоскостями равны ее основанию и проектируются на него. Центры этих правильных
-угольной призмы Р, параллельны ее основанию. Поэтому все сечения призмы Р такими плоскостями равны ее основанию и проектируются на него. Центры этих правильных  -угольников лежат на оси призмы. Поэтому, если эти многоугольники одновременно повернуть в их плоскостях в одном направлении на угол
-угольников лежат на оси призмы. Поэтому, если эти многоугольники одновременно повернуть в их плоскостях в одном направлении на угол  вокруг их центров, то все они самосовместятся. А потому при таком преобразовании и призма Р самосовместится. Такое преобразование призмы называется поворотом вокруг прямой — оси призмы — на угол
вокруг их центров, то все они самосовместятся. А потому при таком преобразовании и призма Р самосовместится. Такое преобразование призмы называется поворотом вокруг прямой — оси призмы — на угол  Тем самым призма среди симметрий имеет и поворотную симметрию.
Тем самым призма среди симметрий имеет и поворотную симметрию.
Заметим еще, что осевая симметрия в пространстве является поворотом на 180° вокруг оси симметрии. Действительно, в результате поворота на 180° вокруг

Рис. 7.15

Рис. 7.16

Рис. 7.17

Рис. 7.18

Рис. 7.19

Рис. 7.20
прямой а точка X, не лежащая на прямой а, перейдет в такую точку X, что прямая а перпендикулярна отрезку  и пересекает его в середине.
и пересекает его в середине.
Привет, Вы узнаете про симметрии в призме, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
симметрии в призме, симметрии в пирамиде , настоятельно рекомендую прочитать все из категории Стереометрия.
Симметрия прямой призмы
Плоскость симметрии, проходящая через середины боковых ребер .
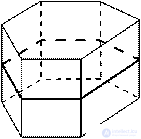
Симметрия правильной призмы
1. Центр симметрии при четном числе сторон основания — точка пересечения диагоналей правильной призмы
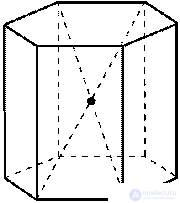
2. Плоскости симметрии: плоскость, проходящая через середины боковых ребер; при четном числе сторон основания — плоскости, проходящие через противолежащие ребра
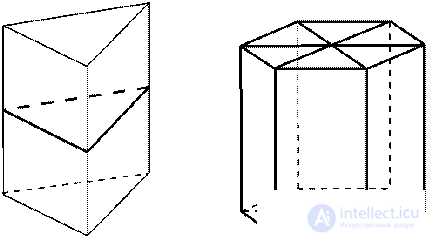
3. Оси симметрии: при четном числе сторон основания — ось симметрии, проходящая через центры оснований, и оси симметрии, проходящие через точки пересечения диагоналей противолежащих боковых граней .

Симметрия правильной призмы
Напомним, что правильной называется прямая призма, в основании которой лежит правильный многоугольник. Симметричность правильных призм определяется симметричностью их оснований (рис. 1), а так же перпендикулярностью основаниям боковых ребер и граней.
У правильной n-угольной призмы имеется n плоскостей симметрии, проходящих через соответствующие оси симметрии оснований призмы (рис. 2).
Кроме того, у нее имеется еще одна плоскость симметрии, которая проходит через середины боковых ребер (рис. 7/15).
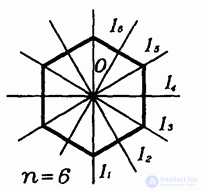
рис . Об этом говорит сайт https://intellect.icu . 1
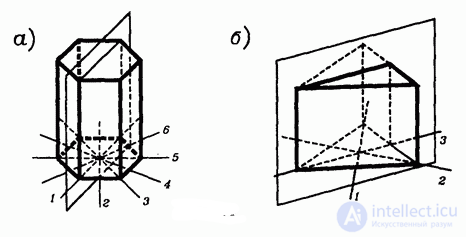
рис. 2
Осями симметрии правильной n -угольной призмы всегда являются n осей симметрии сечения этой призмы, проходящего через середины боковых ребер (рис. 7.16). Если к тому же четно, то n осью симметрии является еще прямая, которая соединяет центры оснований (рис. 7.17). Если же нечетно, то это не так и других n осей симметрии нет.
Отрезок, соединяющий центры оснований правильной призмы, называется ее осью (рис. 7.17).
Если n – четно, то середина оси правильной -угольной призмы является центром симметрии этой призмы (рис. 7.18).
Если же n – нечетно, то центра симметрии у правильной призмы нет (как и у ее основания).
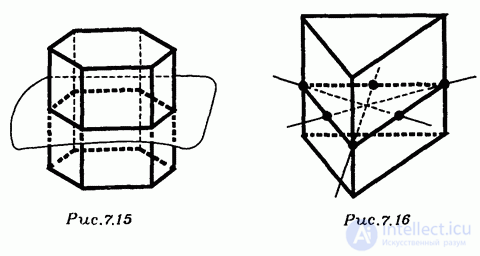
Итак, симметричность правильной n-угольной призмы определяется симметричностью ее основания — правильного n-угольника. Но, как известно из планиметрии, правильные n-угольники имеют еще один вид симметрии — вращательную, т. е. они самосовмещаются при повороте вокруг своего центра на угол 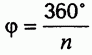 (рис. 7.19), а также на любой угол, кратный . Аналогично, правильные n -угольные призмы самосовмещаются при повороте вокруг своей оси на такой же угол
(рис. 7.19), а также на любой угол, кратный . Аналогично, правильные n -угольные призмы самосовмещаются при повороте вокруг своей оси на такой же угол  (рис. 7.20).
(рис. 7.20).
Подробнее это означает следующее. Плоскости, перпендикулярные оси правильной n -угольной призмы Р, параллельны ее основанию. Поэтому все сечения призмы Р такими плоскостями равны ее основанию и проектируются на него. Центры этих правильных n -угольников лежат на оси призмы. Поэтому, если эти многоугольники одновременно повернуть в их плоскостях в одном направлении на угол 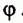 вокруг их центров, то все они самосовместятся. А потому при таком преобразовании и призма Р самосовместится. Такое преобразование призмы называется поворотом вокруг прямой — оси призмы — на угол
вокруг их центров, то все они самосовместятся. А потому при таком преобразовании и призма Р самосовместится. Такое преобразование призмы называется поворотом вокруг прямой — оси призмы — на угол 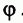 Тем самым призма среди симметрий имеет и поворотную симметрию.
Тем самым призма среди симметрий имеет и поворотную симметрию.
Заметим еще, что осевая симметрия в пространстве является поворотом на 180° вокруг оси симметрии. Действительно, в результате поворота на 180° вокруг
прямой а точка X, не лежащая на прямой а, перейдет в такую точку X`, что прямая а перпендикулярна отрезку XX` и пересекает его в середине.
Симметрия правильной пирамиды
1. Плоскости симметрии: при четном числе сторон основания — плоскости, проходящие через противолежащие боковые ребра; и плоскости, проходящие через медианы, проведенные к основанию противолежащих боковых граней (рис. 15).
2. Ось симметрии: при четном числе сторон основания — ось симметрии, проходящая через вершину правильной пирамиды и центр основания .
См. также
- понятие симметрии , виды симметрии ,
- симметрия шара , симметрия сферы ,
- центральная симметрия параллелепипеда , симметрия параллелепипеда ,
- свойство симметрии относительно точки ,
- симметрия относительно прямой , ось симметрии ,
- симметрия относительно точки , центр симметрии ,
- Симметрии в физике
- Суперсимметрия
- Трансляционная симметрия
- Симметрии в биологии
- Асимметрия
- диссимметрии
- сферическая симметрия
- аксиальная симметрия
- радиальная симметрия
- трансляционная симметрия
- двусторонняя (билатеральная) симметрия
- Симметрия в химии
- Анизотропия
- Симметрия в религии и культуре
В общем, мой друг ты одолел чтение этой статьи об симметрии в призме. Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках.
Надеюсь, что теперь ты понял что такое симметрии в призме, симметрии в пирамиде
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Стереометрия
Из статьи мы узнали кратко, но емко про симметрии в призме
