Сколько осей симметрии у круга?
оси симметрии круга Они бесконечны. Эти оси делят любую геометрическую форму на две точно равные половины.
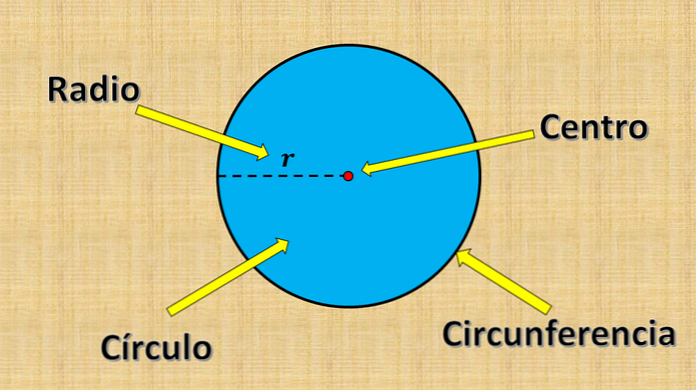
И круг состоит из всех точек, чье расстояние до фиксированной точки меньше или равно некоторому значению «r».
Упомянутая выше фиксированная точка называется центром, а значение «r» называется радиусом. Радиус – это наибольшее расстояние, которое может быть между точкой на окружности и центром..
С другой стороны, любой отрезок, концы которого находятся на краю окружности (окружности) и проходит через центр, называется диаметром. Его измерение всегда равно удвоенному радиусу.
Круг и окружность
Не путайте круг с кругом. Окружность относится только к точкам, которые находятся на расстоянии «r» от центра; то есть только край круга.
Однако при поиске осей симметрии безразлично, работаете ли вы с кругом или с кругом.
Что такое ось симметрии?
Ось симметрии – это линия, которая делит на две равные части определенную геометрическую фигуру. Другими словами, ось симметрии действует как зеркало.
Валы симметрии круга
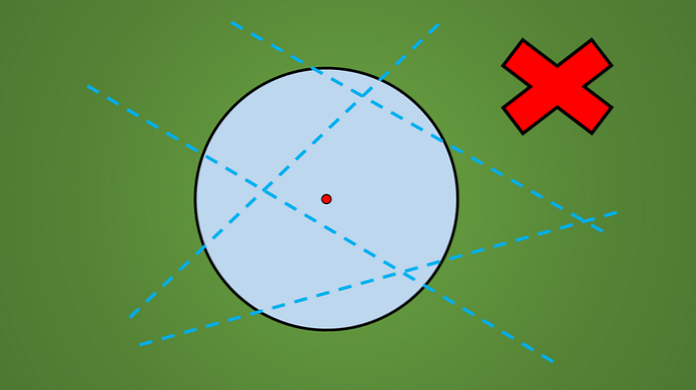
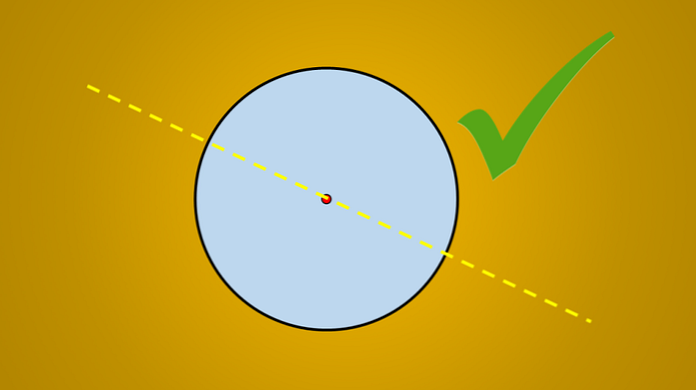
Если вы наблюдаете любой круг, независимо от его радиуса, вы можете видеть, что не каждая линия, которая пересекает его, является осью симметрии..
Например, ни одна из линий, нарисованных на следующем рисунке, не является осью симметрии..
Простой способ проверить, является ли линия осью симметрии или нет, состоит в том, чтобы перпендикулярно отразить геометрическую фигуру к противоположной стороне линии..
Если отражение не соответствует исходному рисунку, то эта линия не является осью симметрии. Следующее изображение иллюстрирует эту технику.
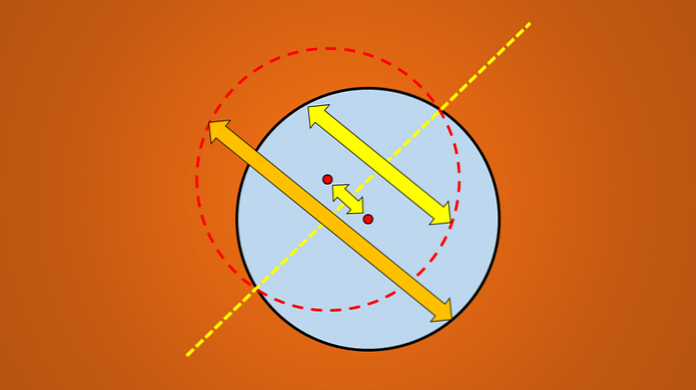
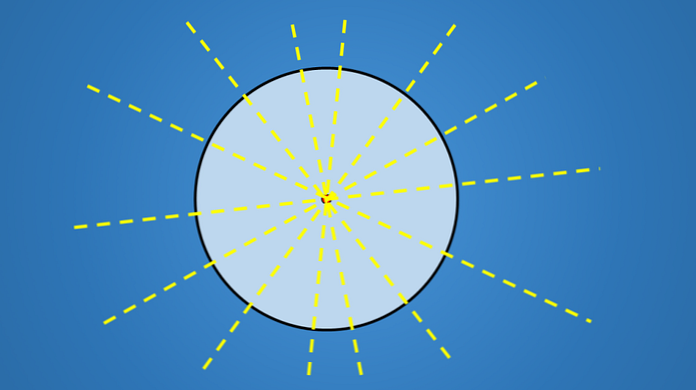
Но если рассматривается следующее изображение, хорошо известно, что нарисованная линия является осью симметрии круга.
Вопрос: есть ли еще оси симметрии? Ответ – да. Если повернуть эту линию на 45 ° против часовой стрелки, полученная линия также является осью симметрии круга.
То же самое происходит, если вы поворачиваете на 90 °, 30 °, 8 ° и вообще на любое количество градусов.
Важной особенностью этих линий является не склонность, которую они имеют, но все они проходят через центр круга. Следовательно, любая линия, содержащая диаметр окружности, является осью симметрии..
Таким образом, поскольку круг имеет бесконечное число диаметров, то он имеет бесконечное количество осей симметрии.
Другие геометрические фигуры, такие как треугольник, четырехугольник, пятиугольник, шестиугольник или любой другой многоугольник, имеют конечное число осей симметрии.
Причина, по которой круг имеет бесконечное число осей симметрии, заключается в том, что у него нет сторон.
Осевая и центральная симметрия
О чем эта статья:
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1. Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
- Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
- С другой стороны прямой отложим такие же расстояния.
- Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
- Получаем два треугольника, симметричных относительно оси симметрии.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
- Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
- Измеряем расстояние от вершин до точек на прямой.
- Откладываем такие же расстояния на другой стороне оси симметрии.
- Соединяем точки и строим треугольник A1B1C1.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
- Проводим через точку А прямую, перпендикулярную прямой l.
- Проводим через точку В прямую, перпендикулярную прямой l.
- Измеряем расстояния от точек А и В до прямой l.
- Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A1 и B1.
- Соединяем точки A1 и B1.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).
- Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
- Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
- Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.
- Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
- Измеряем расстояние от точки B до точки О и от точки А до точки О.
- Проводим прямую из точки А через точку О и выводим ее на другую сторону.
- Проводим прямую из точки B через точку О и выводим ее на другую сторону.
- Чертим на противоположной стороне отрезки А1О и B1О, равные отрезкам АО и АB.
- Соединяем точки A1 и B1 и получаем отрезок A1B1, симметричный данному.
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Симметрия окружности
Есть ли симметрия в окружности? Сколько осей симметрии имеет окружность? Что является центром симметрии окружности?
Окружность имеет бесконечно много осей симметрии.
Осью симметрии окружности является любая прямая, содержащая диаметр окружности.
Проведём произвольный диаметр AB окружности.
Отметим на окружности произвольную точку X.
Из точки X проведём хорду, перпендикулярную диаметру.
Обозначим точки пересечения этой прямой с диаметром AB как P и X1.
Так как хорда перпендикулярна диаметру, то диаметр проходит через середину.
Следовательно, XP=X1P, а значит, точка X1 симметрична точке X относительно прямой, содержащей диаметр AB.
Имеем: точка, симметричная произвольной точке окружности относительно произвольного диаметра, также принадлежит окружности. Следовательно, любой диаметр окружности является её осью симметрии.
Что и требовалось доказать .
Окружность — центрально-симметричная фигура.
Осью симметрии окружности является её центр.
Отметим на окружности произвольную точку X.
Проведем через точку X диаметр XX1.
XO=X1O (как радиусы).
Таким образом, точка, симметричная произвольной точке окружности относительно её центра, также принадлежит окружности. Значит, окружность — центрально-симметричная фигура, а центр симметрии окружности — это центр окружности.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/osevaya-i-centralnaya-simmetriya
[/spoiler]
Есть ли симметрия в окружности? Сколько осей симметрии имеет окружность? Что является центром симметрии окружности?
Утверждение

Осью симметрии окружности является любая прямая, содержащая диаметр окружности.
Доказательство:

Отметим на окружности произвольную точку X.
Из точки X проведём хорду, перпендикулярную диаметру.
Обозначим точки пересечения этой прямой с диаметром AB как P и X1.
Так как хорда перпендикулярна диаметру, то диаметр проходит через середину.
Следовательно, XP=X1P, а значит, точка X1 симметрична точке X относительно прямой, содержащей диаметр AB.
Имеем: точка, симметричная произвольной точке окружности относительно произвольного диаметра, также принадлежит окружности. Следовательно, любой диаметр окружности является её осью симметрии.
Что и требовалось доказать.
Утверждение
Окружность — центрально-симметричная фигура.
Осью симметрии окружности является её центр.
Доказательство:

Проведем через точку X диаметр XX1.
XO=X1O (как радиусы).
Следовательно, точки X и X1 симметричны относительно точки O.
Таким образом, точка, симметричная произвольной точке окружности относительно её центра, также принадлежит окружности. Значит, окружность — центрально-симметричная фигура, а центр симметрии окружности — это центр окружности.
Что и требовалось доказать.
113. Мы уже знакомы с происхождением круга и некоторыми его свойствами. Теперь надлежит пополнить наши сведения о круге более детальным его изучением. Мы знаем, что положение прямой линии определяется двумя точками. Возникает такой же вопрос о круге:
Сколькими точками определяется положение круга?
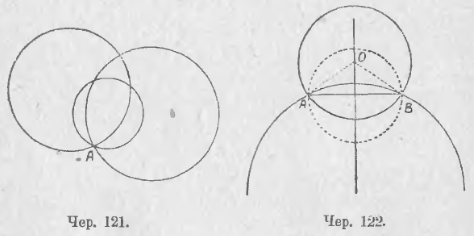
Пусть имеем точку A (чер. 121); требуется построить круг, проходящий чрез эту точку. Ясно, что таких кругов можно построить бесчисленное множество (на чертеже построено 3 круга), причем центр круга можно брать где угодно, а радиус круга должен равняться расстоянию от взятого произвольно центра до точки A.
Пусть теперь имеем 2 точки A и B (чер. 122); требуется построить круг, проходящий чрез эти 2 точки. Если нам удалось найти центр O искомого круга, то отрезки AO и OB должны служить его радиусами, и, следов., AO = OB, т. е. искомый центр должен быть равноудален от точек A и B; но мы знаем, что геометрическим местом точек, равноудаленных от двух данных точек A и B, является перпендикуляр к отрезку AB чрез его середину. Поэтому заключаем, что чрез 2 данных точки также можно построить бесчисленное множество кругов, но центры их нельзя выбирать совсем произвольно: здесь произвол ограничен, – центры можно брать где-либо на перпендикуляре к отрезку AB чрез его середину.
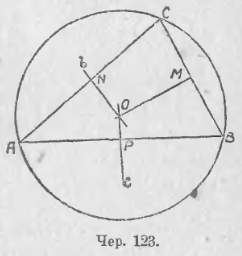
Пусть теперь даны 3 точки A, B и C, не лежащие на одной прямой (чер. 123); требуется построить круг, проходящий чрез A, B и C. Центр искомого круга должен быть равноудален от трех данных точек. В п. 98 была предложена задача (2), в которой требуется найти точку, равноудаленную от трех данных. Дадим здесь ее решение. Мы знаем, что если соединить точки A и B и чрез середину P отрезка AB построить к нему перпендикуляр c, то на этом перпендикуляре c расположены все точки, равноудаленные от A и B. Построив также перпендикуляр b к отрезку AC чрез его середину N, найдем все точки, равноудаленные от A и C. Отсюда заключаем, что точкою, равноудаленной и от A, и от B, и от C, явится точка, принадлежащая обоим перпендикулярам. Если b и c пересекаются в точке O, то эта точка O и должна служить искомым центром. (Проверка: так как O лежит на перпендикуляре c к отрезку AB через его середину, то эта точка O одинаково удалена от A и B; так как O лежит на перпендикуляре b к отрезку AC чрез его середину, то точка O одинаково удалена от точек A и C; следовательно, точка O одинаково удалена и от A, и от B, и от C). Легко видеть, что центром может служить только одна точка (перпендикуляры b и c пересекаются только в одной точке). За радиус искомого круга мы должны принять одно из равных расстояний OA = OB = OC. Итак, чрез три точки, не лежащие на одной прямой, можно построить только один круг.
114. Если мы соединим еще точки B и C и заметим, что точка O, будучи равноудалена от B и C, должна (п. 97) лежать на перпендикуляре OM к отрезку BC чрез его середину, то придем к заключению, что
Перпендикуляры, построенные к сторонам треугольника чрез их середины, пересекаются в одной точке, которая является центром круга, описанного около треугольника.
Самый круг, проходящий чрез точки A, B и C, называется кругом, описанным около треугольника ABC.
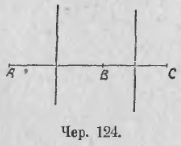
115. Если данные три точки A, B и C располагаются на одной прямой (чер. 124), то, построив перпендикуляры к отрезкам AB и BC чрез их середины, мы увидим, что эти перпендикуляры не пересекаются (они параллельны, так как перпендикулярны к одной прямой, – см. п. 75). Отсюда заключаем, что чрез точки A, B и C в этом случае построить круга нельзя. Итак, теперь возможно дать ответ на вопрос п. 113:
Положение круга определяется тремя точками: если эти три точки не расположены на одной прямой, то чрез них можно построить круг и только один, а если три точки расположены на одной прямой, то чрез них нельзя построить ни одного круга.
116. Упражнения.
- Найти геометрическое место центров кругов, имеющих данный радиус и проходящих через данную точку.
- Построить круг данным радиусом, проходящий чрез 2 данных точки.
- Дан тупоугольный треугольник: описать около него круг. (Центр искомого круга лежит вне треугольника.)
- Дан круг (или его дуга); найти центр этого круга (или дуги).
117. Вторым вопросом, подлежащим исследованию, является:
Каковы могут быть различные случаи взаимного расположения прямой и круга?
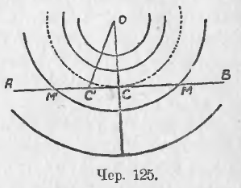
Пусть имеем прямую AB (чер. 125) и пусть точка O, лежащая вне этой прямой, служит центром круга. Случай, когда центр круга лежит на прямой, был разобран в п. 21.
Станем строить, принимая O за центр, круги различными радиусами. Построим OC ⊥ AB.
Если мы построим круги радиусами, меньшими перпендикуляра OC, то легко видеть, что все точки прямой удалены от центра O на расстояние, большее радиуса круга, и, следовательно, круг и прямая, если радиус круга меньше перпендикуляра, опущенного из его центра на прямую, не имеют общих точек (не пересекаются).
Если станем строить круги радиусами, большими перпендикуляра OC, то точка C должна лежать внутри одного из таких кругов, а так как прямая AB тянется без конца, то всегда на ней можно найти точки, лежащие вне такого круга. Нам очевидно, что перейти по прямой AB от точки C, лежащей внутри круга, к точкам, лежащим вне его, можно лишь, пересекая самый круг (соображение, сходное с тем, какое дано в начале п. 25), т. е. в этом случае прямая AB пересекается с нашим кругом. Пусть точка M есть точка пересечения; тогда OM есть радиус этого круга. Отложив отрезок CM’ = CM по другую сторону точки C по прямой AB и соединив O с M’, найдем, что OM’ = OM, как наклонные с равными проекциями (п. 99). Следовательно, окружность пересекает прямую AB еще в точке M’. Других общих точек у окружности и прямой быть не может, ибо нельзя из O построить еще наклонных к AB, равных OM и OM’. Итак, если радиус окружности больше перпендикуляра, опущенного из ее центра на данную прямую, то эта окружность имеет с прямою две общих точки (пересекаются в двух точках).
Построим, наконец, окружность радиусом, равным перпендикуляру OC, тогда точка C принадлежит и кругу и прямой; но всякая другая точка C’, расположенная на прямой AB, не может лежать на круге: соединив C’ с O, получим наклонную OC’, которая больше радиуса круга OC, – следовательно, точка C’ лежит вне круга. Итак, в этом случае окружность и прямая имеют только одну общую точку. Такое особенное расположение выражают словами: «круг касается прямой», или «прямая касается круга»; прямая называется в этом случае касательной к кругу, и общая точка C называется точкою касания.
Итак, могут быть 3 случая расположения круга и прямой:
1) Круг и прямая не имеют общих точек (признак: радиус круга меньше расстояния прямой от центра), 2) круг и прямая имеют 2 общих точки (признак: радиус круга больше расстояния прямой от центра) и 3) прямая и круг касаются (признак: радиус круга равен расстоянию прямой от центра).
118. Итак,
Прямая касается круга, если ее расстояние от цента этого круга равно его радиусу.
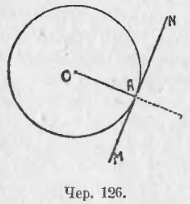
На основании этого мы можем построить касательную к данному кругу чрез одну из его точке. Пусть., напр., дан круг O (чер. 126) и точка A этого круга. Требуется построить касательную к кругу чрез точку A (очевидно, что точкою касания должна служить сама точка A). Построим радиус OA и затем прямую MN, расстояние которой от центра O равно радиусу OA, или, другими словами, прямую MN чрез точку A перпендикулярно к OA (для этого придется, согласно п. 69, продолжить OA).
119. В п. 23 была установлена зависимость между дугами одного круга (или равных кругов) и соответствующими им центральными углами: равным дугам соответствуют равные центральные углы, большей дуге соответствует больший центральный угол, и обратно. Теперь, пользуясь этим, установим зависимость между дугами одного (или равных) круга и стягивающими их хордами.
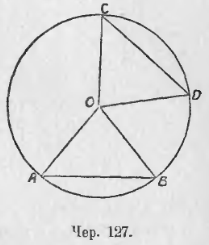
Пусть имеем круг O и две дуги ◡AB и ◡CD (чер. 127), причем примем, что каждая дуга меньше полукруга. Соединив концы этих дуг с центром O, получим ∆OAB и ∆OCD. Если ◡CD = ◡AB, то (п. 23) и ∠COD = ∠AOB, а так как, кроме того, OA = OB = OC = OD, как радиусы, то и ∆OAB и ∆OCD и, следовательно, хорда AB = хорде CD. Если ◡CD > ◡AB, то ∠COD > ∠AOB; тогда наши треугольники имеют по 2 равных стороны, но углы между ними не равны. Поэтому к этим треугольникам применима мысль: «против большего угла лежит большая сторона» (п. 87); следовательно, будем иметь: хорда CD > хорды AB. Наоборот, если нам известно, что хорда AB = хорде CD, то ∆AOB = ∆COD (три стороны одного равны соответственно трем сторонам другого) и, следовательно, ∠AOB = ∠COD, откуда, на основании п. 23, заключаем, что ◡AB = ◡CD. Если имеем, что хорда CD > хорды AB, то наши треугольники имеют по две равных стороны, а третьи стороны у них не равны; тогда (п. 88) против большей стороны лежит больший угол и, следовательно, ∠COD > ∠AOB, откуда, на основании п. 23, имеем ◡CD > ◡AB.
Собирая вместе результаты этих исследований, имеем:
В круге (или в равных кругах) равные дуги стягиваются равными хордами, большая дуга стягивается большею хордою. Обратно: равные хорды стягивают равные дуги, большая хорда стягивает большую дугу.
120. В п. 24 мы нашли, что окружность симметрична относительно диаметра, т. е., если перегнуть плоскость по диаметру, то одна ее часть совпадет с другою.
Чтобы найти при помощи симметрии новые свойства круга, разберем сначала вспомогательный вопрос:
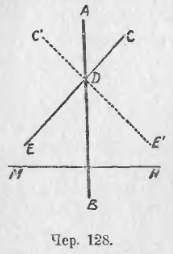
Пусть AB (чер. 128) есть ось симметрии. Построить как-либо другую прямую, чтобы она была симметрична относительно оси AB, т. е., чтобы при перегибании плоскости по AB одна часть этой прямой совпала с другою.
Если мы построим какую попало прямую, напр., CDE, то при перегибании она займет положение C’DE’ так, что ∠E’DB = ∠BDE. Теперь легко увидать, что для того, чтобы прямая совпала сама с собою при перегибании по AB, надо построить ее так, чтобы она была перпендикулярна к AB. Если MN ⊥ AB, то AB служит осью симметрии для прямой MN.
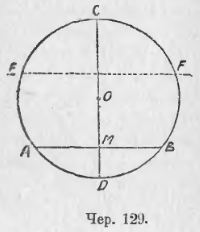
121. Пусть имеем круг O и какую-нибудь хорду AB (чер. 129). Мы можем найти ось симметрии для всей фигуры, – этою осью будет служить диаметр CD, перпендикулярный к хорде AB: в самом деле, раз CD есть диаметр, то круг симметричен относительно CD, раз AB ⊥ CD, то AB (п. 120) симметрична относительно CD. Поэтому при перегибании по CD фигура CBMD должна совместиться с фигурою CAMD, и, следовательно, имеем: 1) AM = MB, 2) ◡AD = ◡DB. Поэтому:
Диаметр, перпендикулярный к хорде, делит пополам и хорду и стягиваемую ею дугу.
122. Если построим еще какую-либо хорду EF ⊥ CD (чер. 129), то EF также симметрична относительно диаметра CD и, перегибая всю фигуру по CD, найдем: ◡EA = ◡FB. Так как, кроме того, мы знаем, что EF || AB, то придем к заключению:
Дуги, заключенные между параллельными хордами, равны.
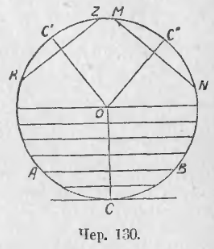
123. Пусть имеем круг O (чер. 130); построим какую-либо хорду AB и вообразим, что эта хорда перемещается параллельно самой себе (другими словами, будем строить ряд других хорд, параллельных AB). Пусть OC есть радиус, перпендикулярный к AB. Станем хорду AB удалять от центра; тогда дуга, стягиваемая хордою, станет уменьшаться, а, следовательно, и сама хорда (п. 119) уменьшается, то есть:
Хорда уменьшается с удалением ее от центра.
Есть две границы для расстояния хорды от центра: 1) если это расстояние равно нулю, т. е. хорда проходит чрез центр, тогда хорда делается наибольшею и обращается в диаметр; 2) если расстояние хорды от центра равно радиусу, тогда мы знаем, что прямая обращается в касательную, и сама хорда исчезает (делается равной нулю).
(Что диаметр есть наибольшая из хорд, можно увидать, напр., из ∆AOB (чер. 127). На основании п. 90 имеем AB < AO + OB, т. е. хорда меньше суммы двух радиусов, а диаметр равен сумме двух радиусов: следовательно, хорда меньше диаметра.)
Пусть теперь имеем две каких-либо хорды KZ и MN (чер. 130). Пусть OC’ ⊥ KZ и OC’ ⊥ MN. Повернув всю систему рассмотренных выше хорд, перпендикулярных к радиусу OC, около центра O так, чтобы радиус OC пошел по OC’ — тогда точка C совместится с C’ и среди системы хорд, перпендикулярных к OC, найдется одна, которая совместится с KZ. (Построить эту хорду легко: ◡KZ делится в точке C’ пополам (п. 121); отложим от C дугу, равную дуге C’K◡ и построим чрез полученную точку перпендикуляр к OC). Точно так же среди нашей системы хорд можем найти одну, с которою совмещается MN, если OC совместится с OC’. Тогда 1) если хорды KZ и MN равны, то они совмещаются с одною и тою же хордою нашей системы, – следовательно, их расстояния от центра одинаковы, 2) Если хорда MN больше хорды KZ, то MN совмещается с большею хордою, чем хорда KZ, из нашей системы, и поэтому хорда MN ближе к центру. Итак:
Равные хорды равно удалены от центра, большая хорда ближе к центру.
124. 1. Построить касательную к данному кругу, параллельную данной прямой.
Надо построить диаметр, перпендикулярный к данной прямой, и через его концы построить к нему перпендикуляры.
Упражнения на свойства хорд и дуг и на свойства, вытекающие из симметрии круга.
2. Разделить пополам данную дугу круга.
3. Построен круг и две его хорды. Существует ли для полученной фигуры (состоящей из круга и двух хорд) ось симметрии? (Вообще говоря, не существует.)
Как надо построить эти 2 хорды, чтобы у полученной фигуры оказалась ось симметрии? Разобрать различные возможные случаи расположения двух хорд при условии, что ось симметрии существует. Построить для каждого случая ось симметрии (особенно обратить внимание на случай, когда хорды не параллельны). Какие следствия возможно здесь получить для дуг, определяемых концами наших хорд?
4. Если построить хорду и параллельную ей касательную, то дуга, стягиваемая хордою, делится в точке касания пополам.
5. Через точку, данную внутри круга, построить хорду так, чтобы она делилась в этой точке пополам.
6. Найти геометрическое место середин равных хорд круга.
7. Построить в круге хорду, чтобы она была равна данному отрезку и параллельна данной прямой.
8. Прямые, соединяющие концы двух параллельных хорд, пересекаются на диаметре, перпендикулярном к хордам.
9. Построен круг и хорда AB. Продолжаем эту хорду на отрезок BC, равный радиусу круга, и чрез C строим диаметр CED. Тогда ◡AD = 3◡BE. (Соединить центр с точкою B, Построить чрез B хорду BM || CD и чрез M построить новый диаметр MN; тогда MN || AC и т. д.).
125. Задача 1. Построить круг, касательный к данной прямой.
Легко видеть, что таких кругов можно построить бесчисленное множество, причем центры их можно брать где угодно; радиусом должно служить расстояние выбранного центра от данной прямой.
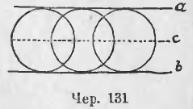
Задача 2. Построить круг, касательный к двум данным параллельным прямым.
Чтобы круг касался данных прямых a и b (чер. 131), центр его должен быть равноудален и от a и от b. Но геометрическим местом точек, равноудаленных от двух данных параллельных прямых, служит (п. 102) прямая, параллельная данным и находящаяся на середин расстояния между ними. Построив это геометрическое место — прямую c (c || a || b), увидим, что центр искомого круга можно брать где угодно на прямой c, а радиус равен половине расстояния между параллельными a и b. Таких кругов можно построить бесчисленное множество, и все они имеют одинаковые радиусы.
Задача 3. Построить круг, касающийся двух пересекающихся прямых.
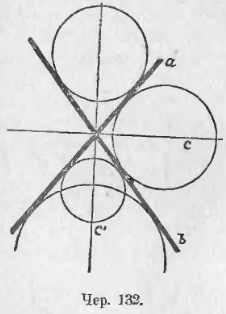
Пусть даны две пересекающихся прямых a и b (чер. 132). Центр искомого круга должен быть одинаково удален от a и b. Пользуясь п. 103, найдем, что центр должен лежать на одном из биссекторов углов, составляемых прямыми a и b. Построив эти биссекторы, увидим, что любую точку их можно принять за центр искомого круга, радиус должен равняться расстоянию выбранного центра от любой из прямых a или b. Таких кругов можно построить бесчисленное множество.
Задача 4. Построить круг, касающийся трех пересекающихся в трех точках прямых.
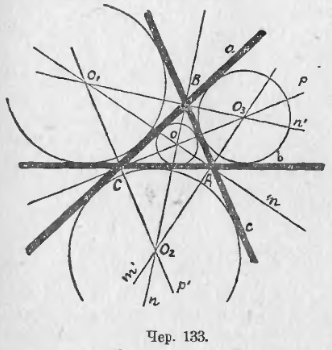
Пусть даны прямые a, b и c (чер. 133), пересекающиеся в точках A, B и C. Так как искомый круг должен касаться всех трех прямых, то его центр должен быть одинаково удален и от a, и от b, и от c. Построим сначала биссекторы углов, образованные прямыми a и b при точке C; пусть эти биссекторы суть p и p’; тогда на них располагаются все точки, равноудаленные от a и b, – следовательно, и искомый центр должен лежать на одном из этих биссекторов p и p’.
Найдем также геометрическое место точек, равноудаленных от a и c, для чего построим биссекторы n и n’ углов при точке B. На одном из этих биссекторов также должен лежать искомый центр. Отсюда заключаем, что центром искомого круга должна служить любая из точек пересечения первой пары (p и p’) биссекторов со второю парою (n и n’). Таких точек 4: O, O1, O2 и O3; одна из них O располагается внутри ∆ABC, а остальные вне его. Следовательно, искомых кругов 4, радиусом каждого из них служит расстояние его центра от любой из данных прямых. Круг, центром которого служит точка O, называется кругом, вписанным в треугольник ABC; остальные три круга с центрами O1, O2 и O3 называются вневписанными кругами в ∆ABC.
126. Мы нашли в предыдущем п., что точки O и O1 одинаково удалены от всех трех данных прямых a, b и c, а, следовательно, и от двух последних b и c; поэтому точки O и O1 должны лежать на биссекторе m внутреннего угла A треугольника ABC. Отсюда имеем:
Три биссектора внутренних углов треугольника пересекаются в одной точке, а именно — в центре вписанного круга.
Точки O2 и O3 так же одинаково удалены от прямых b и c; поэтому они должны лежать на биссекторе m’ внешнего угла A треугольника ABC. Поэтому имеем:
Биссекторы внутренних и внешних углов треугольника пересекаются по три в четырех точках, служащих центрами кругов, касающихся сторон треугольника («сторону треугольника» здесь надо понимать в смысле бесконечной прямой).
127. Упражнения.
- Построить круг касательный к двум данным пересекающимся прямым и одной из них в данной точке (2 решения).
- Построить круг, касательный к двум параллельным прямым и проходящий чрез точку, данную между параллельными (2 решения).
- Даны две параллельных и секущая. Построить круг, касающийся всех трех прямых (2 решения).
- Найти геометрическое место центров кругов, имеющих данный радиус и касающихся данной прямой.
- Построить круг, имеющий данный радиус и касающийся двух данных пересекающихся прямых (4 решения).
- Построить круг, проходящий чрез данную точку и касающийся данной прямой в другой данной точке.
- Построить данным радиусом круг, касающийся данной прямой и проходящий чрез данную точку (2 решения).
128. Теперь нам предстоит рассмотреть различные случаи расположения двух кругов. В пп. 25 и 26 мы уже изучали вопрос о пересечении двух кругов, и нашли, что две общие точки двух кругов располагаются симметрично относительно лини центров. Теперь мы можем окончательно установить, что более двух общих точек у двух кругов быть не может: в самом деле, мы знаем (п. 115), что через три точки можно построить или один круг, или ни одного, а допущение, что два круга имеют три общих точки, повело бы к тому, что чрез 3 точки проходило бы 2 круга.
Итак, 2 круга могут иметь или две общих точки — тогда говорят, что круги пересекаются, или одну — тогда говорят, что круги касаются, или ни одной — тогда говорят, что круги не пересекаются.
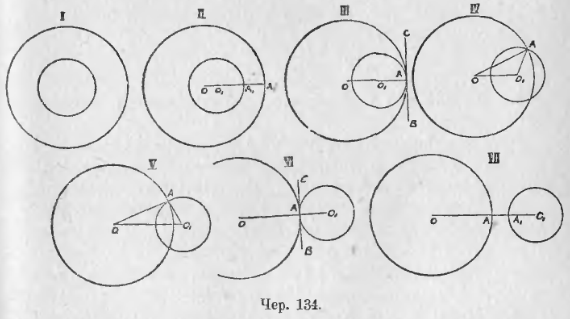
Возьмем два круга, радиусы которых обозначим одною буквою каждый: R и r (причем будем считать R > r). Пусть наши 2 круга помещены так, что их центры совпадают (чер. 134, положение I); мы знаем, что в этом случае круги не имеют общих точек и называются концентрическими. Станем затем круг с меньшим радиусом отодвигать вправо, – перейдем к положению II; здесь один круг лежит внутри другого (общих точек у них нет), но их центры O и O1 не совпадают. Назовем расстояние OO1 между центрами чрез d. Мы имеем (см. положение II): OA – O1A1 = OO1 + A1A или OA – O1A1 > OO1, или R – r > d, или d < R – r; с другой стороны, очевидно, d < R + r.
Эти два неравенства
d < R – r и d < R + r
служат характерною особенностью рассматриваемого положения II.
Передвигая меньший круг дальше в том же направлении, придем к положению III, в котором круги имеют одну общую точку. Прежде всего надо заметить, что эта общая точка непременно лежит на линии центров; в самом деле, предположение, что эта точка лежит вне линии центров, влечет за собой следствие, что у кругов имеется и другая общая точка, симметричная с первой относительно линии центров. Пусть эта общая точка есть A, так что OO1A есть прямая линия. Тогда имеем: OO1 = OA – O1A или d = R – r; с другой стороны, очевидно, что d < R + r. Поэтому для положения III имеем:
d = R – r и d < R + r
Говорят, что в этом случае круги имеют внутреннее касание.
Передвигая круг O1 дальше, придем к положению IV или V, в которых круги имеют 2 общих точки. Рассматривая здесь ∆OO1A и пользуясь пп. 90 и 91, имеем:
OO1 > OA – O1A и OO1 < OA + O1A
или d > R – r и d < R + r.
Передвигая дальше круг O1, перейдем к положению VI, в котором один круг лежит вне другого, и оба круга имеют общую точку A, лежащую на линии центров OO1. Здесь имеем: OO1 = OA = O1A или d = R + r; с другой стороны, очевидно, что d > R – r. Итак, для VI положения имеем:
d > R – r и d = R + r.
Говорят, что в этом случае круги имеют внешнее касание.
Передвигая круг O1 еще дальше, придем в положение VII, где круги расположены один вне другого и общих точек не имеют. Здесь имеем: OO1 = OA + AA1 + A1O1 или OO1 > OA + A1O1, или d > R + r; с другой стороны, очевидно, что d > R – r. Поэтому для положения VII имеем:
d > R – r и d > R + r.
Присоединим еще сюда, что для положения I (круги концентричны) имеем d = 0 (это есть частный случай положения II).
Для каждого из 5 возможных случаев положения двух кругов (II, III, IV и V, VI, VII) имеется своя зависимость между расстоянием центров, суммою и разностью радиусов. Поэтому обратно: каждая из этих зависимостей может служить признаком, по которому можно судить о расположении двух кругов (см. упражнения п. 130).
129. Рассмотрим положения III и VI (чер. 134); здесь круги касаются. Если через точку касания A построить BC ⊥ OA, то будем иметь BC ⊥ O1A и, следовательно, BC окажется касательной и к кругу O и кругу O1, то есть
Два касающихся круга имеют в точке касания общую касательную.
130. Упражнения.
- Построена трапеция, имеющая площадь; затем построены два круга, диаметрами которых служат параллельные стороны трапеции, а расстояние между их центрами равно средней линии этой трапеции. Каково расположение этих кругов?
- Одна из параллельных сторон трапеции, имеющей площадь, в два раза более другой. Построены 2 круга, радиусами которых служат параллельные стороны этой трапеции, а расстояние между их центрами равно средней линии этой трапеции. Каково расположение этих кругов?
- Построена трапеция, не имеющая площади; затем построены два круга, диаметрами которых служат параллельные стороны этой трапеции, а их центры расположены на расстоянии, равном средней линии этой трапеции. Каково расположение этих кругов?
- Построен круг; его радиус разделен на 5 равных частей и затем строят новый круг, принимая за его центр точку, отстоящую от центра на расстояние, равное 1/5 радиуса первого круга, и за его радиус отрезок, равный 2/5 радиуса первого круга. Каково расположение этих кругов?
- Радиусы двух кругов равны соответственно двум сторонам данного треугольника, а расстояние между их центрами равно периметру этого треугольника. Каково расположение этих кругов?
- Дан треугольник, стороны которого равны a, b и c. Затем построены два круга: диаметр одного из них равен a, диаметр другого = b + c и расстояние между центрами равно медиане этого треугольника, делящей пополам сторону a. Каково расположение этих кругов (см. п. 95)?
- Если через точку пересечения двух кругов провести их диаметры, то концы этих диаметров лежат на одной прямой с другою точкою пересечения кругов.
- Если 2 круга касаются, то прямая, проходящая чрез точку касания, пересекает эти 2 круга в двух таких точках, что радиусы кругов, проходящие чрез эти точки, параллельны.
131. Задачи на построение.
- Найти геометрическое место центров кругов, касающихся двух данных концентрических кругов.
Это геометрическое место распадается на два: на одном расположены центры тех кругов, которые имеют с одним из данных внутреннее касание, а с другим — внешнее; на другом расположены центры кругов, имеющих с обоими данными внутреннее касание. - Даны 2 концентрические круга и точка между ними. Построить круг, касающийся обоих данных и проходящий чрез данную точку.
- Построить круг, касающийся данной прямой и данного круга, последнего в данной точке.
Так как искомый круг касается данного, то в точке касания, которая дана, эти круги имеют общую касательную, которую можем построить. Тогда задача сведется к построению круга касательного к двум данным прямым и одной из них в данной точке. - Построить данным радиусом круг, касающийся данного круга и проходящий чрез данную точку.
Сначала откинем последнее требование, чтобы круг проходил чрез данную точку, и найдем, где расположены центры кругов данного радиуса, касающихся данного круга. Потом отбросим требование, чтобы круг касался данного круга и найдем, где расположены центы кругов данного радиуса, проходящих чрез данную точку. После этого легко найти центры кругов, удовлетворяющих обоим требованиям. - Построить данным радиусом круг, касающийся двух данных кругов.
Тот же прием, как для предыдущей задачи. - Построить данным радиусом круг, касательный к данной прямой и к данному кругу. (Тот же прием.)
- Построить круг, проходящий чрез данную точку и касательный к данному кругу в данной точке.
Сначала найдем геометрическое место центров кругов, касающихся данного в данной точке, затем геометрическое место центров кругов, проходящих чрез две данные точки. - Построить круг, касающийся данного круга и данной прямой, последней в данной точке.
- Чрез точку пересечения двух кругов построить прямую так, чтобы получить две равных хорды.
Предположим, что задача решена; построим чрез центры кругов перпендикуляры к нашей прямой. Тогда получим трапецию, средняя линия которой вполне определена и может быть построена предварительно, – она соединяет точку пересечения кругов с серединою расстояния их центров.
-
Nauka.Club | Образовательный портал
-
Вопросы
-
Сколько осей симметрии имеет круг?
Сколько осей симметрии имеет круг?
У круга может быть бесконечное множество осей симметрии, т.к. любая линия, проходящая через центр круга, делит его на 2 симметричные части и будет являться осью симметрии этого круга.
Автор:
John Stephens
Дата создания:
27 Январь 2021
Дата обновления:
15 Май 2023
Содержание
- Круг и окружность
- Что такое ось симметрии?
- Линии симметрии круга
- Ссылки
В линии симметрии круга они бесконечны. Эти оси делят любую геометрическую фигуру на две точно равные половины. А круг состоит из всех точек, расстояние до фиксированной точки которых меньше или равно некоторому значению «r».
Упомянутая выше неподвижная точка называется центром, а значение «r» – радиусом.Радиус – это наибольшее расстояние, которое может быть между точкой на окружности и центром.
С другой стороны, любой отрезок прямой, концы которого находятся на краю окружности (окружности) и проходят через центр, называется диаметром. Его мера всегда равна удвоенному радиусу.
Круг и окружность
Не путайте круг с окружностью. Окружность относится только к точкам, которые находятся на расстоянии «r» от центра; то есть только край круга.
Однако при поиске линий симметрии не имеет значения, работаете ли вы с кругом или с кругом.
Что такое ось симметрии?
Ось симметрии – это линия, разделяющая определенную геометрическую фигуру на две равные части. Другими словами, ось симметрии действует как зеркало.
Линии симметрии круга
Если наблюдается любой круг, независимо от его радиуса, можно увидеть, что не каждая пересекающая его линия является осью симметрии.
Например, ни одна из линий, нарисованных на следующем изображении, не является осью симметрии.
Самый простой способ проверить, является ли линия осью симметрии или нет, – это отразить геометрическую фигуру перпендикулярно противоположной стороне линии.
Если отражение не соответствует исходной фигуре, то эта линия не является осью симметрии. Следующее изображение иллюстрирует эту технику.
Но если рассмотреть следующее изображение, то заметно, что проведенная линия является осью симметрии круга.
Возникает вопрос: есть ли еще линии симметрии? Ответ положительный. Если эту линию повернуть на 45 ° против часовой стрелки, полученная линия также будет осью симметрии окружности.
То же самое верно, если вы поворачиваете на 90 °, 30 °, 8 ° и, как правило, на любое количество градусов.
В этих линиях важно не их наклон, а то, что все они проходят через центр круга. Следовательно, любая линия, содержащая диаметр круга, является осью симметрии.
Итак, поскольку круг имеет бесконечное количество диаметров, значит, он имеет бесконечное количество линий симметрии.
Другие геометрические фигуры, такие как треугольник, четырехугольник, пятиугольник, шестиугольник или любой другой многоугольник, имеют конечное число линий симметрии.
Причина, по которой круг имеет бесконечное количество линий симметрии, заключается в том, что у него нет сторон.
Ссылки
- Басто, Дж. Р. (2014). Математика 3: Основы аналитической геометрии. Grupo Editor Patria.
- Билльштейн, Р., Либескинд, С., и Лотт, Дж. У. (2013). Математика: подход к решению проблем для учителей начального образования. Редакторы Лопеса Матеоса.
- Булт, Б., и Хоббс, Д. (2001). Математическая лексика (Иллюстрированный ред.). (Ф. П. Кадена, Trad.) AKAL Editions.
- Кальехо, И., Агилера, М., Мартинес, Л., и Альдеа, К. С. (1986). Математика. Геометрия. Реформа верхнего цикла E.G.B. Министерство образования.
- Шнайдер В. и Сапперт Д. (1990). Практическое пособие по техническому черчению: введение в основы промышленного черчения. Reverte.
- Томас, Г. Б., и Вейр, М. Д. (2006). Расчет: несколько переменных. Pearson Education.