Если середину отрезка провести перпендикулярную прямую, то она будет осью симметрии данного отрезка.

Есть утверждения, что если через этот отрезок провести прямую, то она будет второй осью симметрии для данного отрезка.

Давайте рассмотрим более подробнее этот случай и для начала ознакомимся с определением некоторых вещей
Определение точки

Определение линии

Определение прямой

Определение отрезка
Отрезок – это часть прямой линии, он имеет длину, но не имеет ширины и толщины, следовательно – разделить его вдоль никак нельзя и поэтому, он имеет только одну ось симметрии.
Теперь рассмотрим случай с прямой.
Проведем две перпендикулярных прямых к прямой а – одну посередине отрезка АА1, который лежит на этой прямой, другую немного правее

Первая прямая будет осью симметрии и для отрезка АА1 и для прямой а, вторая – только для прямой а (для любых точек А и А1 всегда найдем симметричные).
Прямая линия имеет бесконечное количество осей симметрии, но все они должны быть к ней перпендикулярны.
Осевая и центральная симметрии
Если прямая  проходит через середину отрезка А1А2 и перпендикулярна к нему, то точки А1 и А2 называются симметричными относительно прямой
проходит через середину отрезка А1А2 и перпендикулярна к нему, то точки А1 и А2 называются симметричными относительно прямой  . Каждая точка прямой
. Каждая точка прямой  симметрична самой себе.
симметрична самой себе.
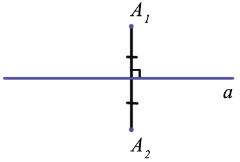
Фигура называется симметричной относительно прямой  , если для каждой точки фигуры симметричная ей точка относительно прямой
, если для каждой точки фигуры симметричная ей точка относительно прямой  также принадлежит этой фигуре. Прямая
также принадлежит этой фигуре. Прямая  – ось симметрии фигуры.
– ось симметрии фигуры.
Пример (синим цветом обозначены оси симметрии):
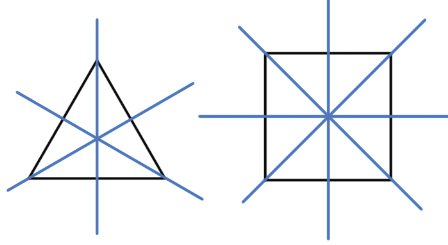
Точки А1 и А2 называются симметричными относительно точки О, если О – середина отрезка А1А2. Точка О считается симметричной самой себе.
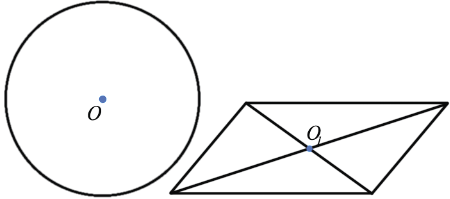
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры.
Пример (синим цветом обозначены центры симметрии):
Поделись с друзьями в социальных сетях:
Осевая и центральная симметрия

О чем эта статья:
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1. Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
- Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
- С другой стороны прямой отложим такие же расстояния.
- Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
- Получаем два треугольника, симметричных относительно оси симметрии.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
- Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
- Измеряем расстояние от вершин до точек на прямой.
- Откладываем такие же расстояния на другой стороне оси симметрии.
- Соединяем точки и строим треугольник A1B1C1.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.

- Проводим через точку А прямую, перпендикулярную прямой l.
- Проводим через точку В прямую, перпендикулярную прямой l.
- Измеряем расстояния от точек А и В до прямой l.
- Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A1 и B1.
- Соединяем точки A1 и B1.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).
- Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
- Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
- Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.
- Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
- Измеряем расстояние от точки B до точки О и от точки А до точки О.
- Проводим прямую из точки А через точку О и выводим ее на другую сторону.
- Проводим прямую из точки B через точку О и выводим ее на другую сторону.
- Чертим на противоположной стороне отрезки А1О и B1О, равные отрезкам АО и АB.
- Соединяем точки A1 и B1 и получаем отрезок A1B1, симметричный данному.
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Ось симметрии – что это такое? Фигуры, имеющие ось симметрии
Что же такое ось симметрии? Это множество точек, которые образуют прямую, являющуюся основой симметрии, то есть, если от прямой отложили определенное расстояние с одной стороны, то оно отразится и в другую сторону в таком же размере. Осью может выступать все, что угодно, – точка, прямая, плоскость и так далее. Но об этом лучше говорить на наглядных примерах.
Симметрия
Для того чтобы понять, что такое ось симметрии, нужно вникнуть в само определение симметрии. Это соответствие определенного фрагмента тела относительно какой-либо оси, когда его структура неизменна, а свойства и форма такого объекта остаются прежними относительно его преобразований. Можно сказать, что симметрия – свойство тел к отображению. Когда фрагмент не может иметь подобного соответствия, это называется асимметрией или же аритмией.
 Вам будет интересно: Как сдать физику и что нужно для этого сделать?
Вам будет интересно: Как сдать физику и что нужно для этого сделать?
Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.
 Вам будет интересно: Гибкость: определение, средства и методы развития гибкости
Вам будет интересно: Гибкость: определение, средства и методы развития гибкости

Виды симметрии
Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:
История симметрии
Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.
В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то “центрального огня”, вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.
А философ Платон считал многогранники олицетворением четырех природных стихий:
- тетраэдр – огонь, так как его вершина направлена вверх;
- куб – земля, так как это самое устойчивое тело;
- октаэдр – воздух, нет каких-либо объяснений;
- икосаэдр – вода, так как тело не имеет грубых геометрических форм, углов и так далее;
- образом всей Вселенной являлся додекаэдр.
Из-за всех этих теорий правильные многогранники называют телами Платона.
Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.

Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины “День и ночь”.
Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. “Богатыри”.
Что уж там говорить, симметрия – ключевое понятие для всех деятелей искусства на протяжении многих веков, но в XX веке ее смысл оценили также все деятели точных наук. Точным свидетельством являются физические и космологические теории, например, теория относительности, теория струн, абсолютно вся квантовая механика. Со времен Древнего Вавилона и, заканчивая передовыми открытиями современной науки, прослеживаются пути изучения симметрии и открытия ее основных законов.
Симметрия геометрических фигур и тел
Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.
А с геометрическими фигурами дело обстоит иначе. Ось симметрии прямоугольника – также прямая, но их несколько. Можно провести ось параллельно отрезкам ширины, а можно – длины. Но не все так просто. Вот прямая не имеет осей симметрии, так как ее конец не определен. Могла существовать только центральная симметрия, но, соответственно, и таковой не будет.
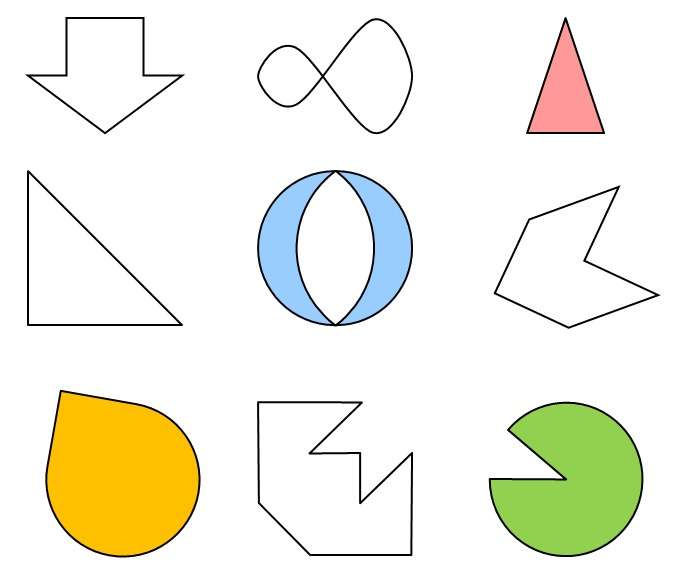
Следует также знать то, что некоторые тела имеют множество осей симметрии. Об этом догадаться несложно. Даже не нужно говорить о том, сколько осей симметрии имеет окружность. Любая прямая, проходящая через центр окружности, является таковой и этих прямых – бесконечное множество.
У некоторые четырехугольников может быть две оси симметрии. Но вторые должны быть перпендикулярны. Это происходит в случае с ромбом и прямоугольником. В первом оси симметрии – диагонали, а во втором – средние линии. Множество таковых осей только у квадрата.
Симметрия в природе
Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.

А сколько примеров окружает нас постоянно! Это цветы, листья, лепестки, овощи и фрукты, животные и даже соты пчел имеют ярко выраженную геометрическую форму и симметрию. Вся природа устроена упорядоченно, всему есть свое место, что еще раз подтверждает совершенство законов природы, в которых симметрия – основное условие.
Вывод
Нас постоянно окружают какие-либо явления и предметы, например, радуга, капля, цветы, лепестки и так далее. Их симметрия – очевидна, в какой-то степени она обусловлена гравитацией. Часто в природе под понятием “симметрия” понимают регулярную смену дня и ночи, времен года и так далее.

Подобные свойства наблюдаются везде, где есть порядок и равенство. Также и сами законы природы – астрономические, химические, биологические и даже генетические подчинены определенным принципам симметрии, так как имеют совершенную системность, а значит, сбалансированность имеет всеохватывающий масштаб. Следовательно, осевая симметрия – один из основополагающих законов мироздания в целом.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/osevaya-i-centralnaya-simmetriya
http://1ku.ru/obrazovanie/10576-os-simmetrii-chto-eto-takoe-figury-imeyushhie-os-simmetrii/
[/spoiler]
Что называется осевой симметрией
Содержание:
- Что такое осевая симметрия в геометрии
- Свойства осевой симметрии
- Теорема и доказательство
- Фигуры, обладающие симметрией
- Симметрия в повседневной жизни
Что такое осевая симметрия в геометрии
Симметрия – это свойство геометрических фигур отражаться. Симметрия относительно точки называется центральной. Осевая симметрия – это симметрия относительно прямой.
Если точка A и точка B симметричны относительно прямой n, то прямая называется осью симметрии n и проходит через середину отрезка AB. Обозначение осевой симметрии – Sn, таким образом симметрия точек A и B обозначается так:
Sn (А) = В.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Другое название осевой симметрии – вращательная – применяется в естественных науках. Данное понятие означает отражение предметов касательно поворотов вокруг прямой.
Свойства осевой симметрии
- Осевая симметрия переводит прямую в прямую, луч – в луч, отрезок – в отрезок, плоскость в плоскость.
- Неподвижными являются: ось симметрии и все точки на ней, все прямые и плоскости, перпендикулярные оси симметрии.
- Обратное преобразование осевой симметрии есть та же осевая симметрия.
- Осевая симметрия – это поворот относительно оси симметрии на 180°.
Теорема и доказательство
Теорема
Осевая симметрия – это движение, то есть при преобразовании осевой симметрии расстояние между точками сохраняется.
Если отрезок MN симметричен отрезку M1N1 относительно прямой a, то MN = M1N1.
Чтобы доказать, что MN = M1N1, сделаем дополнительные построения:
- P – это точка пересечения MM1 и прямой a;
- Q – это точка пересечения NN1 и прямой a;
- построим отрезок MK, перпендикулярный NN1;
- тогда точка K отразится в точку K1.
Докажем, что прямоугольные треугольники MNK и M1N1K1 равны. Стороны MN и M1N1 являются гипотенузами данных треугольников, поэтому, нужно доказать равенство катетов.
МК = М1К1 , так как перпендикулярны к параллельным прямым.
По построению:
NK = NQ – KQ,
N1K1 = N1Q – K1Q.
Точка N отобразилась в точку N1, значит:
NK = N1K1.
Итак, треугольники равны по двум катетам, следовательно, их гипотенузы равны, то есть MN = M1N1, что и требовалось доказать.
Фигуры, обладающие симметрией
Осевой симметрией обладает угол, а биссектриса является осью симметрии.
Пример №1
Из произвольной точки одной стороны угла опустим перпендикуляр к биссектрисе и продлим его до другой стороны угла:
Рассмотрим Δ KAO и Δ MAO:
- AO – общая сторона
- Из свойства биссектрисы: ∠ MAO = ∠KAO
- Треугольники KAO и MAO прямоугольные,
Отсюда следует, что KO = OM, поэтому точки K и M симметричны касательно биссектрисы угла.
Следовательно, равнобедренный треугольник тоже симметричен относительно биссектрисы, проведенной к основанию.
Пример №2
Равносторонний треугольник имеет три оси симметрии – биссектрисы, медианы, высоты каждого угла:
Пример №3
У прямоугольника две оси симметрии. Каждая из них проходит через середины противоположных сторон.
Пример №4
Ромб обладает двумя осями симметрии – это прямые, содержащие его диагонали.
Пример №5
Квадрат имеет 4 оси симметрии, так как он одновременно и ромб, и прямоугольник.
Пример №6
У окружности бесконечное множество осей симметрии – это все прямые, проведенные через центр круга.
Симметрия в повседневной жизни
Симметрия стала частью жизни человека уже в древние времена. Орнаменты с признаками зеркального отражения встречаются на античных зданиях, древнегреческих вазах. Свойство пропорционального расположения заимствовано в науку из природы.
Зеркальное отражение часто встречается в живой и неживой природе. Этой характеристикой обладают снежинки. В растительном мире одинаково расположены противоположные элементы растений: большинство листьев зеркально отражаются сравнительно среднего стебля. В животном мире законы симметрии проявляются в наличии у животных правой и левой сторон. Большинство представителей фауны обладает парными частями тела: уши, лапы, глаза, крылья, рога. Ярким образцом зеркальной симметрии считается бабочка. Прямая, условно проведенная вдоль туловища насекомого по центру, является осью симметрии.
Поскольку человек – это часть природы, в своем творчестве он использует принцип симметрии. В искусстве свойство отражения применяется для создания красоты и гармонии. В архитектуре пропорциональность выполняет практическую функцию – придает зданиям устойчивость и надежность. В предметах быта можно встретить одинаковость в расположении частей узоров на коврах, принтов на ткани, рисунков обоев.
Стремление к созданию симметричного, предположительно, связано с притяжением Земли – гравитацией. Человек интуитивно считает симметрию формулой устойчивости. Принцип зеркального отражения играет важную роль в человеческой жизни. Тяга к гармонии и красоте побуждает человечество придерживаться правил пропорциональности.
Что же такое ось симметрии? Это множество точек, которые образуют прямую, являющуюся основой симметрии, то есть, если от прямой отложили определенное расстояние с одной стороны, то оно отразится и в другую сторону в таком же размере. Осью может выступать все, что угодно, – точка, прямая, плоскость и так далее. Но об этом лучше говорить на наглядных примерах.
Симметрия
Для того чтобы понять, что такое ось симметрии, нужно вникнуть в само определение симметрии. Это соответствие определенного фрагмента тела относительно какой-либо оси, когда его структура неизменна, а свойства и форма такого объекта остаются прежними относительно его преобразований. Можно сказать, что симметрия – свойство тел к отображению. Когда фрагмент не может иметь подобного соответствия, это называется асимметрией или же аритмией.
 Вам будет интересно:Как сдать физику и что нужно для этого сделать?
Вам будет интересно:Как сдать физику и что нужно для этого сделать?
Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.
 Вам будет интересно:Гибкость: определение, средства и методы развития гибкости
Вам будет интересно:Гибкость: определение, средства и методы развития гибкости

Виды симметрии
Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:
История симметрии
Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.
В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то “центрального огня”, вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.
А философ Платон считал многогранники олицетворением четырех природных стихий:
- тетраэдр – огонь, так как его вершина направлена вверх;
- куб – земля, так как это самое устойчивое тело;
- октаэдр – воздух, нет каких-либо объяснений;
- икосаэдр – вода, так как тело не имеет грубых геометрических форм, углов и так далее;
- образом всей Вселенной являлся додекаэдр.
Из-за всех этих теорий правильные многогранники называют телами Платона.
Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.

Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины “День и ночь”.
Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. “Богатыри”.
Что уж там говорить, симметрия – ключевое понятие для всех деятелей искусства на протяжении многих веков, но в XX веке ее смысл оценили также все деятели точных наук. Точным свидетельством являются физические и космологические теории, например, теория относительности, теория струн, абсолютно вся квантовая механика. Со времен Древнего Вавилона и, заканчивая передовыми открытиями современной науки, прослеживаются пути изучения симметрии и открытия ее основных законов.
Симметрия геометрических фигур и тел
Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.
А с геометрическими фигурами дело обстоит иначе. Ось симметрии прямоугольника – также прямая, но их несколько. Можно провести ось параллельно отрезкам ширины, а можно – длины. Но не все так просто. Вот прямая не имеет осей симметрии, так как ее конец не определен. Могла существовать только центральная симметрия, но, соответственно, и таковой не будет.

Следует также знать то, что некоторые тела имеют множество осей симметрии. Об этом догадаться несложно. Даже не нужно говорить о том, сколько осей симметрии имеет окружность. Любая прямая, проходящая через центр окружности, является таковой и этих прямых – бесконечное множество.
У некоторые четырехугольников может быть две оси симметрии. Но вторые должны быть перпендикулярны. Это происходит в случае с ромбом и прямоугольником. В первом оси симметрии – диагонали, а во втором – средние линии. Множество таковых осей только у квадрата.
Симметрия в природе
Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.

А сколько примеров окружает нас постоянно! Это цветы, листья, лепестки, овощи и фрукты, животные и даже соты пчел имеют ярко выраженную геометрическую форму и симметрию. Вся природа устроена упорядоченно, всему есть свое место, что еще раз подтверждает совершенство законов природы, в которых симметрия – основное условие.
Вывод
Нас постоянно окружают какие-либо явления и предметы, например, радуга, капля, цветы, лепестки и так далее. Их симметрия – очевидна, в какой-то степени она обусловлена гравитацией. Часто в природе под понятием “симметрия” понимают регулярную смену дня и ночи, времен года и так далее.

Подобные свойства наблюдаются везде, где есть порядок и равенство. Также и сами законы природы – астрономические, химические, биологические и даже генетические подчинены определенным принципам симметрии, так как имеют совершенную системность, а значит, сбалансированность имеет всеохватывающий масштаб. Следовательно, осевая симметрия – один из основополагающих законов мироздания в целом.
Сегодня на уроке мы вспомним такое понятие как
осевая симметрия на плоскости, введём понятие осевой симметрии в пространстве,
проверим, будет ли осевая симметрия движением пространства.
Давайте вспомним, что фигура называется симметричной
относительно прямой , если для
каждой точки фигуры симметричная ей точка относительно прямой также
принадлежит этой фигуре. Прямая называется осью
симметрии фигуры. Про такую фигуру говорят, что она обладает осевой
симметрией.
Давайте приведём примеры таких фигур
из жизни и геометрии.
Ещё мы давали такое определение:
Точки и
называются симметричными
относительно прямой , если прямая
проходит через
середину отрезка и
перпендикулярна к этому отрезку.
Прямая называется осью
симметрии.
Каждая точка прямой считается
симметричной самой себе.
В курсе планиметрии мы доказывали, что осевая
симметрия является движением.
Напомним это доказательство.
Пусть точки М и N
– какие-нибудь точки плоскости, а точки М1, и N1
– симметричные им точки относительно прямой А. Здесь может быть несколько
вариантов расположения точек на плоскости.
Рассмотрим один из таких вариантов.
По построению симметричных точек относительно прямой
А, прямая А перпендикулярна прямым ММ1 и NN1
и делит эти отрезки пополам, значит, в треугольниках МОМ1 и NОN1
отрезки ОК и ОЕ будут являться медианами и высотами, проведёнными к
основанию, то есть это равнобедренные треугольники.
.
.
Заменив отрезок равным ему
отрезком , а отрезок
– равным ему
отрезком , получим, что
.
Вывод: таким образом, мы
доказали, что расстояние между точками М и N
равно расстоянию между симметричными им точками М один и N1.
Получаем, что осевая симметрия – пример движения
плоскости.
В пространстве осевой симметрией с осью мы назовем
такое отображение пространства на себя, при котором любая точка переходит в
симметричную ей точку относительно
оси .
Теперь давайте проверим, будет ли осевая симметрия в
пространстве движением пространства.
Для этого введём прямоугольную систему координат Оxyz
так, чтобы ось Оz совпала с осью
симметрии. Теперь давайте попробуем найти связь между координатами точки М с
координатами x, y,
z и точки М1 с
координатами x1,
y1,z1,
симметричных относительно оси Оz.
Если точка М не лежит на оси Оz,
то по определению оси симметрии, ось Оz
проходит через середину отрезка ММ1 и перпендикулярна к этому
отрезку. Поскольку Оz – середина
отрезка ММ1, и абсциссы и ординаты точек оси Оz
равны нулю, то можно записать, что и
.
То есть ,
.
Условие того, что ось Оz
перпендикулярно прямой ММ1 даёт нам, то что аппликаты точек М и М1
равны .
Если же точка М лежит на оси Оz,
то она отображается сама на себя, по определению оси симметрии, значит, и в
этом случае будут выполнятся полученные равенства.
Вывод: для симметричный точек
относительно оси Оz абсциссы и
ординаты противоположны, а аппликаты равны.
Возникает вопрос, а если ось симметрии совпадает не
с осью Оz, а, например, Оx
или Оy. Тогда связь между
координатами симметричных точек М и М1 будет такая: если ось
симметрии проходит через ось Оx,
то точки М и М1 имеют такие координаты ,
.
Если осью симметрии будет ось Оy,
то точки М и М1 имеют такие координаты ,
.
Теперь давайте рассмотрим любые две точки и
. По только что
доказанным формулам для координат симметричных точек получим, что точка . Точка
.
Теперь давайте найдём расстояние .
Получим, что .
Теперь давайте найдём расстояние между точками и
.
Очевидно, что оба эти выражения равны, то есть
получим, что . То есть
расстояние между точками при осевой симметрии в пространстве сохраняется,
значит, осевая симметрия в пространстве также является движением,
но уже не плоскости, а пространства.
Задача:
найти координаты точек, в которые переходят точки ,
,
при осевой
симметрии относительно координатных осей.
Решение:
сначала найдём координаты точек в которые переходит точки ,
,
при осевой
симметрии относительно оси Ох.
Если точка симметрична
точке относительно
оси то справедливы
формулы: .
Точка отобразится в
точку .
Точка отобразится в
точку .
Точка отобразится в
точку .
Если точка симметрична
точке относительно
оси то справедливы
формулы: .
Точка отобразится в
точку .
Точка отобразится в
точку .
Точка отобразится в
точку .
Если точка симметрична
точке относительно
оси то справедливы
формулы: .
Точка отобразится в
точку .
Точка отобразится в
точку .
Точка отобразится в
точку .
Итоги:
Сегодня на уроке мы ввели понятия осевой симметрии в
пространстве. Показали, что и в пространстве осевая симметрия будет примером
движения. Решили несколько задач.
