Как найти ось симметрии отрезка 4 класс

Как найти ось симметрии отрезка 4 класс

содержание

Проверочная работа 2. Вариант 1.

1. Для актового зала в первый день купили 6 кресел, а во второй — 4 кресла по той же цене. За все кресла заплатили 34 000 р. Сколько рублей заплатили в первый день?
1) 6 + 4 = 10 (к.) — купили за два дня.
2) 34 000 : 10 = 3 400 (p.) — стоит одно кресло.
3) 3 400 * 6 = 20 400 (p.) — заплатили в первый день.
Ответ: 20 400 рублей.

2. Два всадника выехали одновременно навстречу друг другу из двух посёлков и встретились через 2 ч. Скорость одного всадника 15 км/ч, а другого — 13 км/ч. Найди расстояние между посёлками.
1) 15 + 13 = 28 (км/ч) — скорость сближения.
2) 28 * 2 = 56 (км) — расстояние между посёлками.
Ответ: 56 км.

3*. Начерти:
1) ось симметрии отрезка CD;
2) ось симметрии четырёхугольника ABCD.

Источник

Если середину отрезка провести перпендикулярную прямую, то она будет осью симметрии данного отрезка.

Есть утверждения, что если через этот отрезок провести прямую, то она будет второй осью симметрии для данного отрезка.

Давайте рассмотрим более подробнее этот случай и для начала ознакомимся с определением некоторых вещей

Определение точки

Определение линии

Определение прямой

Определение отрезка

Отрезок – это часть прямой линии, он имеет длину, но не имеет ширины и толщины, следовательно – разделить его вдоль никак нельзя и поэтому, он имеет только одну ось симметрии.

Теперь рассмотрим случай с прямой.

Проведем две перпендикулярных прямых к прямой а – одну посередине отрезка АА1, который лежит на этой прямой, другую немного правее

Первая прямая будет осью симметрии и для отрезка АА1 и для прямой а, вторая – только для прямой а (для любых точек А и А1 всегда найдем симметричные).

Прямая линия имеет бесконечное количество осей симметрии, но все они должны быть к ней перпендикулярны.

Источник

Задание 1.

Для библиотеки в первый день купили 5 стеллажей для книг, а во второй – 4 стеллажа по той же цене. За все стеллажи заплатили 27 000. Сколько денег заплатили за стеллажи в первый день?

Подсказка:

Чтобы решить задачу, нужно узнать, сколько стеллажей купили всего.

1) 5 + 4 = 9 (шт).

Далее, узнаем цену 1 стеллажа.

2) 27 000 : 9 = 3 000 (р).

Затем, отвечая на вопрос задачи, узнаем, сколько денег заплатили за стеллажи в первый день.

3) 3 000 * 5 = 15 000 (р.).

Ответ:

15 000 р.

Задание 2.

Два лыжника вышли одновременно навстречу друг другу из двух посёлков, расстояние между которым 48 км. Скорость одного лыжника 11 км/ч, а другого – 13 км/ч. Через сколько часов лыжники встретятся?

Подсказка:

Чтобы решить задачу, нужно узнать общую скорость сближения.

1) 11 + 13 = 24 (км/ч).

Далее, найдем время, через которое лыжники встретятся.

2) t = S : V = 48 : 24 = 2 (ч).

Ответ:

2 ч

Задание 3.

Начерти:

1) ось симметрии отрезка BC;

2) ось симметрии четырёхугольника KCMN.

Ответ:

1) Отрезок имеет 1 ось симметрии – ту, которая ему перпендикулярна и проходит через центр.

2) Четырёхугольник KCMN – это ромб. Он имеет 2 оси симметрии – они соответствуют его диагоналям (KM, CN).

Источник
  1. Главная
  2. Справочники
  3. Справочник по математике 5-9 класс
  4. Координаты на плоскости
  5. Осевая и центральная симметрии

Осевая симметрия

Рассмотрим построение точки, симметричной данной точке А относительно данной прямой .

Пусть дана точка А и прямая .

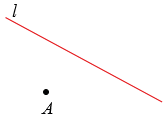
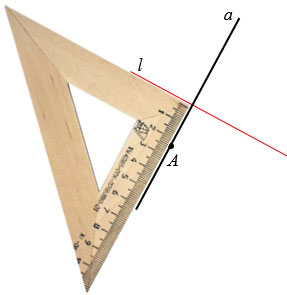
Точку симметричную точке А относительно прямой , можно построить так. Проведем через точку А прямую , перпендикулярную прямой . Для этого используем чертежный угольник. Прикладываем чертежный угольник так, как показано на рисунке ниже и проводим прямую через точку А.

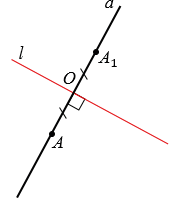
Пусть прямые и пересекаются в точке О. Отложим при помощи линейки на прямой отрезок ОА1, равный отрезку ОА.

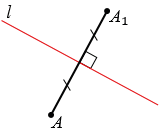
Получаем точки А и А1, которые симметричны относительно прямой .

Также можно построить фигуры, симметричные относительно прямой.

Построим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой .

Пусть дан треугольник АВС и прямая .

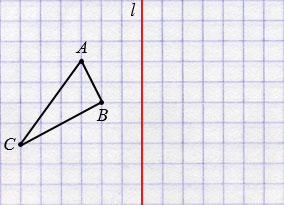
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно прямой (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой .

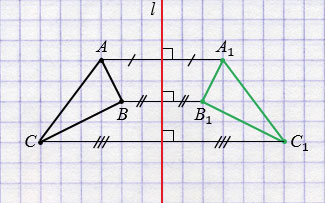
Обратите внимание, любые две фигуры, симметричные относительно прямой, равны.

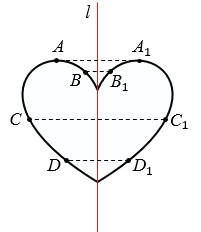
Если фигура имеет ось симметрии (прямая  ) то, все точки этой фигуры, не принадлежащие этой оси, можно разделить на пары симметричных точек.

Центральная симметрия

Точки М и М1 называют симметричными относительно точки О, если точка О является серединой отрезка ММ1 (смотри рисунок ниже).

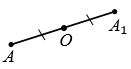
Рассмотрим построение точки, симметричной данной точке М относительно данной точки О.

Пусть даны точки М и О. Точку, симметричную точке М относительно точки О, можно построит так. Проведем луч МО.

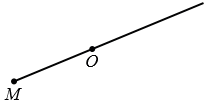
На луче МО отложим отрезок ОN , равный отрезку ОМ.

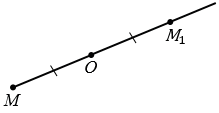
Точки М и М1, которые симметричны относительно точки О.

Также можно построить фигуры, симметричные относительно точки.

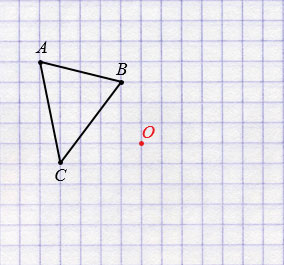
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.

Пусть дан треугольник АВС и точки О.

Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно точки О (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.

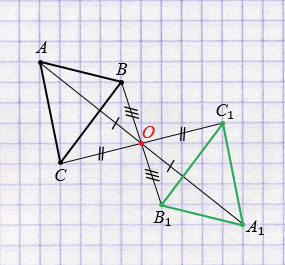
Обратите внимание, любые две фигуры, симметричные относительно точки, равны.

Рассмотрим окружность с центром в точке О. Все точки окружности можно разбить на пары точек, симметричных относительно точки О.

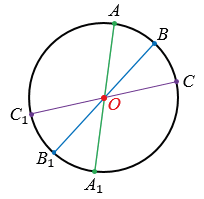
В таком случае говорят, что окружность имеет центр симметрии – точку О.

Также центр симметрии имеют такие фигуры, как отрезок, прямоугольник, эллипс.

Советуем посмотреть:

Перпендикулярные прямые

Параллельные прямые

Координатная плоскость

Координаты на плоскости


Правило встречается в следующих упражнениях:

6 класс

Номер 1245,
Мерзляк, Полонский, Якир, Учебник

Номер 1257,
Мерзляк, Полонский, Якир, Учебник

Номер 1260,
Мерзляк, Полонский, Якир, Учебник

Номер 1261,
Мерзляк, Полонский, Якир, Учебник

Номер 1262,
Мерзляк, Полонский, Якир, Учебник

Номер 1270,
Мерзляк, Полонский, Якир, Учебник

Номер 1272,
Мерзляк, Полонский, Якир, Учебник

Номер 1273,
Мерзляк, Полонский, Якир, Учебник

Номер 1334,
Мерзляк, Полонский, Якир, Учебник

Номер 3,
Мерзляк, Полонский, Якир, Учебник

Источник

Что же такое ось симметрии? Это множество точек, которые образуют прямую, являющуюся основой симметрии, то есть, если от прямой отложили определенное расстояние с одной стороны, то оно отразится и в другую сторону в таком же размере. Осью может выступать все, что угодно, – точка, прямая, плоскость и так далее. Но об этом лучше говорить на наглядных примерах.

Симметрия

Для того чтобы понять, что такое ось симметрии, нужно вникнуть в само определение симметрии. Это соответствие определенного фрагмента тела относительно какой-либо оси, когда его структура неизменна, а свойства и форма такого объекта остаются прежними относительно его преобразований. Можно сказать, что симметрия – свойство тел к отображению. Когда фрагмент не может иметь подобного соответствия, это называется асимметрией или же аритмией.

Как сдать физику и что нужно для этого сделать?Вам будет интересно:Как сдать физику и что нужно для этого сделать?

Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.

Гибкость: определение, средства и методы развития гибкостиВам будет интересно:Гибкость: определение, средства и методы развития гибкости

Виды симметрии

Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:

  • Осевая. Осью симметрии является прямая, проходящая через центр тела. Как это? Если наложить части вокруг оси симметрии, то они будут равными. Это можно увидеть на примере сферы.
  • Зеркальная. Осью симметрии здесь является прямая, относительно которой тело можно отразить и получить обратное отображение. Например, крылья бабочки зеркально симметричны.
  • Центральная. Осью симметрии является точка в центре тела, относительно которой при всех преобразованиях части тела равны при наложении.

    • История симметрии

    Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.

    В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то “центрального огня”, вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.

    А философ Платон считал многогранники олицетворением четырех природных стихий:

    • тетраэдр – огонь, так как его вершина направлена вверх;
    • куб – земля, так как это самое устойчивое тело;
    • октаэдр – воздух, нет каких-либо объяснений;
    • икосаэдр – вода, так как тело не имеет грубых геометрических форм, углов и так далее;
    • образом всей Вселенной являлся додекаэдр.

    Из-за всех этих теорий правильные многогранники называют телами Платона.

    Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.

    Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины “День и ночь”.

    Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. “Богатыри”.

    Что уж там говорить, симметрия – ключевое понятие для всех деятелей искусства на протяжении многих веков, но в XX веке ее смысл оценили также все деятели точных наук. Точным свидетельством являются физические и космологические теории, например, теория относительности, теория струн, абсолютно вся квантовая механика. Со времен Древнего Вавилона и, заканчивая передовыми открытиями современной науки, прослеживаются пути изучения симметрии и открытия ее основных законов.

    Симметрия геометрических фигур и тел

    Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.

    А с геометрическими фигурами дело обстоит иначе. Ось симметрии прямоугольника – также прямая, но их несколько. Можно провести ось параллельно отрезкам ширины, а можно – длины. Но не все так просто. Вот прямая не имеет осей симметрии, так как ее конец не определен. Могла существовать только центральная симметрия, но, соответственно, и таковой не будет.

    Следует также знать то, что некоторые тела имеют множество осей симметрии. Об этом догадаться несложно. Даже не нужно говорить о том, сколько осей симметрии имеет окружность. Любая прямая, проходящая через центр окружности, является таковой и этих прямых – бесконечное множество.

    У некоторые четырехугольников может быть две оси симметрии. Но вторые должны быть перпендикулярны. Это происходит в случае с ромбом и прямоугольником. В первом оси симметрии – диагонали, а во втором – средние линии. Множество таковых осей только у квадрата.

    Симметрия в природе

    Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.

    А сколько примеров окружает нас постоянно! Это цветы, листья, лепестки, овощи и фрукты, животные и даже соты пчел имеют ярко выраженную геометрическую форму и симметрию. Вся природа устроена упорядоченно, всему есть свое место, что еще раз подтверждает совершенство законов природы, в которых симметрия – основное условие.

    Вывод

    Нас постоянно окружают какие-либо явления и предметы, например, радуга, капля, цветы, лепестки и так далее. Их симметрия – очевидна, в какой-то степени она обусловлена гравитацией. Часто в природе под понятием “симметрия” понимают регулярную смену дня и ночи, времен года и так далее.

    Подобные свойства наблюдаются везде, где есть порядок и равенство. Также и сами законы природы – астрономические, химические, биологические и даже генетические подчинены определенным принципам симметрии, так как имеют совершенную системность, а значит, сбалансированность имеет всеохватывающий масштаб. Следовательно, осевая симметрия – один из основополагающих законов мироздания в целом.

    Источник

    Добавить комментарий