Как найти ось симметрии равнобедренного треугольника

Есть ли симметрия в равнобедренном треугольнике? Сколько осей симметрии имеет равнобедренный треугольник? Есть ли в у равнобедренного треугольника центр симметрии?

Утверждение

Равнобедренный треугольник имеет одну ось симметрии.

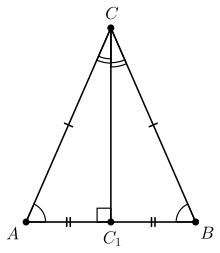
Осью симметрии равнобедренного треугольника является прямая, перпендикулярная основанию и проходящая через его середину.

Доказательство:

Пусть дан равнобедренный треугольник ABC с основанием AC.

Через середину основания — точку F- проведём прямую BF,

   

В треугольнике ABC BF — высота и биссектриса, проведённые к основанию. По свойству равнобедренного треугольника BF является также его биссектрисой.

Отметим на стороне AB произвольную точку X.

Проведём из точки X прямую XX1, перпендикулярную BF,

   

Рассмотрим прямоугольные треугольники XBK и X1BK.

1) BK — общий катет.

2) ∠XBK=∠X1BK (так как BF — биссектриса ∠ABC).

Следовательно, треугольники XBK и X1BK равны (по катету и острому углу).

Отсюда, XK=X1K.

Значит, точки X и X1 симметричны относительно прямой BF.

Таким образом, точка, симметричная произвольной точке равнобедренного треугольника относительно прямой BF, также принадлежит этому треугольнику.

Точки B и F симметричны относительно прямой BF сами себе.

Следовательно, прямая прямая BF является осью симметрии треугольника ABC.

Что и требовалось доказать.

Центра симметрии равнобедренный треугольник не имеет.

Симметрия в равнобедренном треугольнике

Есть ли симметрия в равнобедренном треугольнике? Сколько осей симметрии имеет равнобедренный треугольник? Есть ли в у равнобедренного треугольника центр симметрии?

Равнобедренный треугольник имеет одну ось симметрии.

Осью симметрии равнобедренного треугольника является прямая, перпендикулярная основанию и проходящая через его середину.

Пусть дан равнобедренный треугольник ABC с основанием AC.

Через середину основания — точку F- проведём прямую BF,

В треугольнике ABC BF — высота и биссектриса, проведённые к основанию. По свойству равнобедренного треугольника BF является также его биссектрисой.

Отметим на стороне AB произвольную точку X.

Проведём из точки X прямую XX1, перпендикулярную BF,

Рассмотрим прямоугольные треугольники XBK и X1BK.

1) BK — общий катет.

2) ∠XBK=∠X1BK (так как BF — биссектриса ∠ABC).

Следовательно, треугольники XBK и X1BK равны (по катету и острому углу).

Таким образом, точка, симметричная произвольной точке равнобедренного треугольника относительно прямой BF, также принадлежит этому треугольнику.

Точки B и F симметричны относительно прямой BF сами себе.

Следовательно, прямая прямая BF является осью симметрии треугольника ABC.

Что и требовалось доказать .

Центра симметрии равнобедренный треугольник не имеет.

Осевая и центральная симметрия

О чем эта статья:

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С другой стороны прямой отложим такие же расстояния.
4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
5. Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

1. Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
2. Измеряем расстояние от вершин до точек на прямой.
3. Откладываем такие же расстояния на другой стороне оси симметрии.
4. Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Проводим через точку А прямую, перпендикулярную прямой l.
2. Проводим через точку В прямую, перпендикулярную прямой l.
3. Измеряем расстояния от точек А и В до прямой l.
4. Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
5. Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
4. Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

1. Измеряем расстояние от точки B до точки О и от точки А до точки О.
2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.
4. Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
5. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Please wait.

We are checking your browser. mathvox.ru

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d3823b77cf84971 • Your IP : 85.95.179.65 • Performance & security by Cloudflare

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/osevaya-i-centralnaya-simmetriya

http://mathvox.ru/geometria/treugolniki/treugolniki-glava-6/simmetriya-v-ravnobedrennom-treugolnike-utverjdenie-1/

[/spoiler]

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 апреля 2023 года; проверки требуют 7 правок.

Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием. Каждый правильный треугольник также является равнобедренным, но обратное утверждение неверно^[1].

Терминология[править | править код]

Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании^[1].

Евклид определил равнобедренный треугольник как треугольник, который имеет две равные стороны, но современная трактовка^[2] предпочитает определение, где треугольник имеет хотя бы две равные стороны, определяя таким образом равносторонний треугольник как частный случай равнобедренного.

Симметрия[править | править код]

Треугольник с двумя равными сторонами имеет одну ось симметрии, которая проходит через вершинный угол и середину основания. Эта ось симметрии совпадает с биссектрисой вершинного угла, медианой, проведённой к основанию, высотой, проведённой из вершинного угла и с серединным перпендикуляром^{[3][уточнить]}.

Свойства[править | править код]

Основной источник: ^[1]

В равнобедренном треугольнике углы при основании равны. Также равны биссектрисы, медианы и высоты, проведённые из этих углов.

Биссектриса, медиана, высота и серединный перпендикуляр, проведённые к основанию, совпадают между собой. Центры вписанной и описанной окружностей лежат на этой линии.

Пусть a — длина равных боковых сторон, b — длина основания, h — высота к основанию, R — радиус описанной окружности

Радиус вписанной окружности может быть выражен пятью способами в зависимости от того, какие два параметра равнобедренного треугольника известны:

• 
• 
• 
• 
• 

Углы могут быть выражены следующими способами:

Периметр равнобедренного треугольника находится следующими способами:

Площадь треугольника находится следующими способами:

Теорема Лемуса-Штейнера[править | править код]

Основной источник: ^[4]

Если две биссектрисы треугольника равны, то этот треугольник — равнобедренный.

Лемус, Штейнер, XIX в.

Доказан этот признак равнобедренного треугольника был только в XIX веке двумя математиками, Лемусом и Штейнером, которые обменивались письмами в течение нескольких лет.

См. также[править | править код]

• Теорема о равнобедренном треугольнике
• Равнобедренный прямоугольный треугольник

Примечания[править | править код]

Литература[править | править код]

• Выгодский М. Я. Справочник по элементарной математике. — 25-е изд. — М.: Наука, 1978. — 336 с.
  • Переиздание: М.: АСТ, 2006, ISBN 5-17-009554-6, 509 с.

Осевая симметрия

Мы выделили несколько особых видов треугольников: равнобедренные (и их частные случаи – равносторонние) и прямоугольные (см. рис. 1).

Рис. 1. Сверху-вниз: равнобедренный, равносторонний и прямоугольный треугольники

Остановимся подробнее на их свойствах, т. к. они являются удобными инструментами как для изучения других треугольников, так и для изучения многоугольников вообще. Мы уже видели это на конкретном примере, когда выводили формулу площади произвольного треугольника через формулу площади прямоугольного треугольника.

Если у треугольника две стороны равны, то мы его называем равнобедренным. Обычно его ставят на третью сторону, называемую основанием. Равные стороны оказываются по бокам, их называют боковыми.

Если у треугольника равны все три стороны, то его называют равносторонним. Естественно, равносторонний треугольник является равнобедренным, т. е. он обладает и свойствами равнобедренного треугольника, и своими собственными.

Рассмотрим равнобедренный треугольник  с основанием ,  – боковые стороны (см. рис. 2).

Рис. 2. Равнобедренный треугольник  с основанием  и боковыми сторонами   и

Если вырезать такой треугольник из бумаги и согнуть вдоль вертикальной линии, проходящей через точку , то образовавшиеся половины совпадут (см. рис. 3).

Рис. 3. Бумажный равнобедренный треугольник согнули вдоль вертикальной линии, проходящей через точку

Если разрезать треугольник по линии сгиба и приставить одну из половинок к зеркалу, то мы снова увидим исходный треугольник (см. рис. 4).

Рис. 4. Половину разрезанного по линии сгиба треугольника приставили к зеркалу

Такое свойство фигуры называется осевой симметрией, т. е. фигура симметрична относительно оси.

---

Осевая симметрия

Равнобедренный треугольник не единственная фигура, обладающая осью симметрии. Несложно доказать, что у равностороннего треугольника сразу три таких оси (можно рассматривать его как равнобедренный относительно каждой из трех сторон – оснований) (см. рис. 5).

Рис. 5. Равносторонний треугольник имеет три оси симметрии

Из других известных нам фигур: у прямоугольника и ромба есть по две оси симметрии (см. рис. 6), у квадрата – четыре (см. рис. 7), у окружности таких осей бесконечно много (любая прямая, проходящая через центр) (см. рис. 8).

Рис. 6. У прямоугольника и ромба есть две оси симметрии

Рис. 7. У квадрата есть четыре оси симметрии

Рис. 8. У окружности бесконечно много осей симметрии

Мы дали интуитивное определение оси симметрии. Сформулируем строгое определение.

Точка называется симметричной точке  относительно прямой (оси) , если  перпендикулярен прямой ; если  пересекает прямую  в точке , то  (см. рис. 9).

Рис. 9. Точка  симметрична точке  относительно прямой

---

Свойства равнобедренного треугольника

Чтобы доказать симметричность равнобедренного треугольника, докажем сначала несколько важных свойств.

Теорема 1

У равнобедренного треугольника углы при основании равны.

Доказательство

Проведем биссектрису  (см. рис. 10).

Рис. 10. Равнобедренный треугольник  с проведенной биссектрисой

Треугольники  и  равны по первому признаку:

1.  – боковые стороны;
2.  – общая;
3. , т. к.  – биссектриса.

Следовательно, .

Теорема доказана.

Из равенства треугольников  и  мы получаем еще два факта:

1. , т. е.  – середина ;
2. , а т. к. они еще и смежные (, следовательно, ), значит, они прямые. Т. е. отрезок  перпендикулярен .

Объединим эти два факта в одну теорему.

Теорема 2

Биссектриса в равнобедренном треугольнике, проведенная к основанию, является одновременно медианой и высотой.

Т. е., если мы проводим отрезок  как биссектрису (делим  пополам), то он одновременно будет являться и медианой, и высотой (см. рис. 11).

Рис. 11. В равнобедренном треугольнике биссектриса, проведенная к основанию, является и медианой, и высотой

Как вы думаете, если мы начнем строить отрезок  как медиану или высоту, будет ли он сразу являться и всем остальным? Конечно, да. Доказательство тоже очень простое. Попробуйте это сделать самостоятельно, а ознакомиться с доказательствами можно ниже.

---

Доказательство

Теорема 1

Медиана, проведенная к основанию в равнобедренном треугольнике, является биссектрисой и высотой.

Доказательство

Проведем в равнобедренном треугольнике  медиану  (см. рис. 12).

Рис. 12. Равнобедренный треугольник  с проведенной медианой

Треугольники  и  равны по третьему признаку:

1.  – боковые стороны равнобедренного треугольника.
2. , т. к.  – медиана.
3.  – общая.

Тогда , следовательно,  – биссектриса.

Аналогично . Учитывая, что они смежные, то , откуда: , т. е.  – высота.

Теорема доказана.

Теорема 2

Высота, проведенная к основанию в равнобедренном треугольнике, является биссектрисой и медианой.

Доказательство

Если предположить, что высота  не является биссектрисой, т. е. другая биссектриса, которая обязана быть высотой (по доказанной ранее теореме). Значит, у нас будет две высоты из точки . Но это невозможно, т. к. из точки на прямую можно опустить только один перпендикуляр. Значит,  также является биссектрисой, а значит, и медианой.

Теорема доказана.

С помощью доказанных теорем можно строго доказать, что равнобедренный треугольник обладает осевой симметрией. Причем осью симметрии будет являться высота (она же биссектриса, высота), проведенная из точки .

Рассмотрим произвольную точку  равнобедренного треугольника на боковой стороне (см. рис. 13) (для точек основания проведите доказательство самостоятельно).

Рис. 13. На боковой стороне равнобедренного треугольника отметили произвольную точку

Опустим из точки  перпендикуляр на высоту  и продлим его до пересечения со второй боковой стороной (точкой ) (см. рис. 14).

Рис. 14. Из произвольной точки  опустили перпендикуляр и продлили его до пересечения со второй боковой стороной

Наша задача: доказать, что . Рассмотрим треугольники  и , в них:

1.  – общая сторона;
2. ;
3.  (т. к.  – биссектриса).

Тогда треугольники  и  равны по второму признаку равенства. Значит,  и равнобедренный треугольник является симметричным относительно оси .

Теорема доказана.

---

Признак равнобедренного треугольника

Итак, если треугольник равнобедренный, то он симметричен. У него равны углы при основании и совпадают три элемента – биссектриса, медиана и высота, проведенные к основанию. Для неравнобедренного треугольника это не так. Это не так уже даже для нашего равнобедренного треугольника, если биссектрису, медиану и высоту проводить из вершины при основании (см. рис. 15).

Рис. 15. В равнобедренном треугольнике биссектриса, медиана, высота, проведенные к боковой стороне, не совпадают

А работает ли эта связь в обратную сторону? Т. е. если известно только, что два угла у треугольника равны, можно ли сделать вывод, что и две соответствующие стороны равны, что он равнобедренный? Интуитивно мы понимаем, что это так. Докажем это строго.

Теорема 3.

Если в треугольнике два угла равны, то он равнобедренный.

Доказательство

Пусть в треугольнике  углы . Опустим высоту  (см. рис. 16).

Рис. 16. Треугольник   с проведенной высотой

В треугольниках  и :

1.  – общая;
2. ;
3. .

Тогда треугольники  и  равны по второму признаку равенства (сторона и два угла). Откуда следует, что , т. е. треугольник  равнобедренный.

Теорема доказана.

Полученное утверждение не путаем с определением равнобедренного треугольника: если в треугольнике две стороны равны, то треугольник называется равнобедренным.

А наше утверждение – это признак равнобедренного треугольника: достаточно заметить, что в треугольнике два угла равны, тогда можно утверждать, что он является равнобедренным.

Итак, у равнобедренного треугольника есть такой набор свойств и признаков:

1. Если треугольник равнобедренный, то углы при основании равны.
2. Если углы при основании равны, то треугольник равнобедренный.
3. В равнобедренном треугольнике медиана, биссектриса и высота, проведенные к основанию, совпадают.

Используя такой инструмент, как равнобедренный треугольник и его свойства, мы теперь можем доказать ряд утверждений, которые до этого считали верными без строгого доказательства.

Теорема о внешнем угле треугольника

Прежде чем перейти к ранее не доказанным утверждениям, рассмотрим еще один полезный инструмент для доказательства различных фактов, связанных с треугольниками.

Если в треугольнике продолжить одну из сторон, то мы получим угол, смежный с одним из углов треугольника. Такой угол будем называть внешним углом треугольника (см. рис. 17), а углы внутри треугольника – внутренними.

Рис. 17. Внешний угол треугольника

Теорема 4 (о внешнем угле треугольника).

Внешний угол треугольника больше любого внутреннего, не смежного с ним.

На самом деле, мы уже знаем более сильное утверждение о внешнем угле. Сумма углов треугольника равна , поэтому внешний угол равен сумме двух внутренних, не смежных с ним:

Из этого очевидно следует, что он больше каждого из этих двух внутренних в отдельности.

Но мы не можем использовать для доказательства этой теоремы тот факт, что сумма углов треугольника равна , т. к. мы его пока формально не доказали. Более того, для того чтобы доказать теорему о сумме углов треугольника, мы будем использовать теорему о внешнем угле. Поэтому доказывать эту теорему мы будем только с использованием уже доказанных нами фактов. Как именно – можно почитать ниже.

---

Доказательство

Теорема (о внешнем угле треугольника)

Внешний угол треугольника больше любого внутреннего, не смежного с ним.

Доказательство

Самый разумный способом показать, что один угол больше другого, – это сравнить меньший угол с частью большего. Давайте попробуем. Продолжим сторону  треугольника  (см. рис. 18).

Рис. 18. Продлили сторону  и отметили точку

Докажем, что внешний угол , т. е.  больше внутренних углов  и , например .

Разделим сторону  точкой  пополам, т. е. . Проведем луч  и отметим на нем точку  так, чтобы . Соединим  и  (см. рис. 19).

Рис. 19. Разделили сторону  точкой  пополам и отметили на луче  точку  так, что , соединили  и

Зачем мы это сделали? Мы получили два треугольника  и . В одном есть , а в другом – часть внешнего . Осталось их сравнить.

Треугольники равны по первому признаку (двум сторонам и углу между ними):

1.  (потому что мы так выбирали точку );
2.  (потому что мы так выбирали точку );
3.  (как вертикальные углы).

Следовательно . Но  – это часть внешнего . Значит,  меньше внешнего . Аналогично можно доказать и то, что  меньше внешнего .

Теорема доказана.

---

Признаки параллельности двух прямых

Теперь у нас есть все инструменты для того, чтобы приступить к доказательству ранее не доказанных утверждений.

На первом уроке мы оставили без доказательства тот факт, что диагонали прямоугольника равны (см. рис. 20).

Рис. 20. Прямоугольник  с равными диагоналями

Попробуйте самостоятельно доказать это утверждение, используя первый признак равенства треугольников  и , а также то, что по определению у прямоугольника равны противоположные стороны, а все углы прямые.

На третьем уроке мы рассматривали один из возможных случаев расположения трех прямых на плоскости: две прямые параллельны и пересекаются третьей прямой (секущей) (см. рис. 21).

Рис. 21. Две прямые параллельны и пересекаются третьей прямой

И оставили без доказательства утверждение, что соответственные углы в таком случае будут равны. Докажем сначала признак параллельности двух прямых (т. е. условие, выполнение которого гарантирует нам параллельность прямых).

Теорема 5

Если при пересечении двух прямых третьей внутренние накрест лежащие углы равны, то прямые параллельны.

Доказательство

Пусть имеются прямые  и . Нам пока не известно, параллельны они или нет. Они пересекаются третьей прямой:  (см. рис. 22).

Рис. 22. Прямые  и  пересекаются третьей прямой:

Докажем, что прямые  и  обязаны быть параллельными. Предположим противное: прямые  и  непараллельны. Значит, они пересекаются в некой точке  (пусть и очень далекой). Тогда мы получаем треугольник  (см. рис. 23).

Рис. 23. Полученный треугольник

Для этого треугольника  является внешним. Но тогда, по недавно доказанной теореме о внешнем угле, он больше  (ведь это внутренний угол треугольника, не смежный с ним). Но это противоречит условию. Получили противоречие, значит, прямые не могут пересекаться, т. е. они параллельны.

Теорема доказана.

Используя данный признак, несложно доказать еще два признака параллельности прямых:

1. Если соответственные углы равны, то прямые параллельны.
2. Если внутренние односторонние углы в сумме равны , то прямые параллельны.

Попробуйте провести эти доказательства самостоятельно, используя принцип «вылить воду из чайника», т. е. свести задачу к уже решенной. Докажите, что из условия 1 или условия 2 следует, что внутренние накрест лежащие углы также равны. Тогда параллельность прямых будет следовать из доказанной только что теоремы.

Более того, теперь мы доказали ранее сформулированный нами признак параллельности прямых, который звучал так: если две прямые перпендикулярны третьей прямой, то они параллельны.

Действительно, если две прямые перпендикулярны секущей, то все углы, образованные при пересечении, прямые – равны по . Но это значит, что внутренние накрест лежащие углы равны, как и соответственные углы, поэтому прямые параллельны по только что доказанной теореме (см. рис. 24).

Рис. 24. Внутренние накрест лежащие углы равны, поэтому прямые параллельны

Теорема о внутренних накрест лежащих углах

Теперь можно доказать обратное утверждение.

Теорема 6

Если две прямые параллельны, то при пересечении их третьей прямой внутренние накрест лежащие углы будут равны.

Попробуйте доказать его самостоятельно, если не получится – смотрите доказательство ниже.

---

Доказательство

Воспользуемся методом от противного: пусть  (см. рис. 25).

Рис. 25. Внутренние накрест лежащие углы  и , образованные при пересечении двух параллельных прямых третьей

Проведем прямую , которая проходит через точку  так, что  (см. рис. 26).

Рис. 26. Прямая  проходит через точку  так, что

Но тогда прямые  и  параллельны (у них равны внутренние накрест лежащие углы при секущей ). Получается, что через точку  проходит две прямых, которые параллельны прямой .

Это противоречит одной из сформулированных нами аксиом – пятому постулату Евклида (в плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной). Значит, исходное предположение неверно и .

Теорема доказана.

---

Из этой теоремы следуют и другие:

1. Соответственные углы при параллельных прямых равны.
2. Внутренние односторонние углы при параллельных прямых дают в сумме .

Попробуйте доказать эти утверждения самостоятельно, используя равенство внутренних накрест лежащих углов при параллельных прямых.

Теорема о сумме углов треугольника

Закроем вопрос о сумме углов треугольника.

Теорема 7

Сумма углов треугольника равна .

Доказательство

Рассмотрим произвольный треугольник  (см. рис. 27).

Рис. 27. Произвольный треугольник

Нужно доказать, что сумма его внутренних углов равна . Проведем через точку  прямую , параллельную  (см. рис. 28).

Рис. 28. Прямые  и  параллельны

Прямые  и  – секущие для параллельных прямых  и .

Следовательно,  (внутренние накрест лежащие), аналогично  (см. рис. 29).

Рис. 29. Внутренние накрест лежащие углы: ,

Тогда:

Но углы  составляют развернутый угол . Значит, и сумма углов треугольника равна .

Теорема доказана.

Теорема, связывающая углы и стороны треугольника

Мы также обсуждали, что углы и стороны треугольника связаны между собой. Действительно, если у треугольника два угла равны, то равны и стороны, которые им противолежат (свойство равнобедренного треугольника).

Если же начать раздвигать две стороны треугольника, то третья сторона начнет увеличиваться. Чем больше противоположная сторона, тем больше и угол. Если взять треугольник с сильно отличающимися сторонами, то легко увидеть, что напротив большей стороны лежит больший угол. Эти наблюдения приводят в гипотезе, которую мы сформулируем в виде теоремы.

Теорема 8

В произвольном треугольнике против большей стороны лежит больший угол.

Доказательство попробуйте провести самостоятельно. Подсказка: отложите на большей стороне меньшую сторону от общей вершины и рассмотрите полученные равнобедренные треугольники (см. рис. 30). Само доказательство приведено ниже.

Рис. 30. В треугольнике на большей стороне отложена меньшая сторона от общей вершины

---

Доказательство

Пусть в произвольном треугольнике :  (см. рис. 31). Докажем, что .

Рис. 31. Произвольный треугольник , где

Отложим на длинной стороне короткую сторону: пусть . Получили равнобедренный треугольник  (см. рис. 32).

Рис. 32. Равнобедренный треугольник

Следовательно,  (по свойству равнобедренного треугольника). Но  является внешним углом треугольника . По теореме о внешнем угле он больше внутренних углов, не смежных с ним, значит, в частности, он больше .

Получаем:

Теорема доказана.

---

 Самостоятельно сформулируйте и докажите обратное утверждение. Ознакомиться с доказательством можете ниже.

---

Обратная теорема и ее доказательство

Теорема

Против большего угла треугольника лежит большая сторона.

Доказательство

Пусть  (см. рис. 33). Докажем, что .

Рис. 33. Треугольник , где

Предположим, что это не так. Тогда возможны два варианта:

1. . Но тогда треугольник равнобедренный и  (по свойству равнобедренного треугольника), а это противоречит условию. Значит, такой случай невозможен.
2. . Но против большей стороны лежит больший угол. Тогда , что тоже противоречит условию.

Теорема доказана.

---

 Эта теорема очень важна, ведь она позволяет сделать вывод о связи углов и сторон треугольника (до этого мы говорили либо только о сторонах, либо только об углах).

Более того, с ее помощью мы можем доказать несколько важных утверждений, которые ранее оставили без доказательства, а именно: утверждение о том, что перпендикуляр всегда короче наклонной, и неравенство треугольника. Для этого рассмотрим еще один обещанный инструмент – прямоугольный треугольник.

Доказательство неравенства треугольника

Прямоугольным называется треугольник, если у него есть прямой угол (см. рис. 34).

Рис. 34. Прямоугольный треугольник , где

Что можно сказать о двух оставшихся углах? Теорема о сумме углов треугольника утверждает, что, поскольку один угол уже равен , сумма двух остальных углов также равна . Значит, каждый из них меньше , т. е. острый.

Итак, в прямоугольном треугольнике один угол прямой и два острых. Сторона напротив прямого угла называется гипотенузой, а остальные стороны – катетами. Что можно сказать о соотношении гипотенузы и катетов? Гипотенуза длиннее любого из катетов.

Почему? Гипотенуза лежит напротив самого большого угла – прямого. А напротив большего угла лежит большая сторона. Значит, гипотенуза – самая большая сторона в прямоугольном треугольнике.

Из этого утверждения несложно понять, почему наклонная всегда длиннее перпендикуляра. Ведь наклонная – это гипотенуза в прямоугольном треугольнике, в котором перпендикуляр – это катет. А из этого утверждения уже можно доказать неравенство треугольника: любая сторона меньше суммы двух других.

Рассмотрим остроугольный треугольник . Проведем в нем высоту  (см. рис. 35).

Рис. 35. Остроугольный треугольник  с проведенной высотой 

В прямоугольных треугольниках  и :  и  (гипотенузы длиннее катетов). Но тогда: . Это рассуждение можно повторить для всех трех сторон. Неравенство треугольника доказано.

Мы рассмотрели остроугольный треугольник. В чем отличие прямоугольного и тупоугольного треугольников? Дело в том, что в остроугольном треугольнике высота всегда лежит внутри треугольника и будет разбивать сторону на два отрезка. В прямоугольном и тупоугольном треугольнике это не всегда так (см. рис. 36).

Рис. 36. Высоты в остроугольном, прямоугольном и тупоугольном треугольниках

Попробуйте доказать неравенство треугольника для прямоугольного и тупоугольного треугольников самостоятельно – используйте тот же подход, что и для остроугольного.

Признаки равенства прямоугольных треугольников

Вернемся к изучению нашего нового инструмента – прямоугольных треугольников. Мы знаем три признака равенства треугольников (по двум сторонам и углу между ними; по двум углам и стороне между ними; по трем сторонам). Но у всех прямоугольных треугольников есть один равный элемент – у них один из углов равен .

Поэтому признаки равенства прямоугольных треугольников можно переформулировать:

• по двум катетам;
• по катету и острому углу.

Признак «по трем сторонам» для прямоугольных треугольников не формулируют, т. к. в нем требуется избыточное равенство сразу четырех элементов: трех сторон и прямого угла.

Но для прямоугольных треугольников иногда формулируют «уникальный» признак:

• по гипотенузе и катету.

Это самостоятельный признак, не являющийся новой формулировкой одного из прежних признаков. Доказательство его совсем не сложно. Выполните его самостоятельно и проверьте себя, ознакомившись с ним ниже.

---

Доказательство

Теорема

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны.

Доказательство

Пусть в прямоугольных треугольниках  и : , катеты  и гипотенузы  (см. рис. 37).

Рис. 37. Прямоугольные треугольники  с равными катетами  и гипотенузами

Докажем, что треугольники равны. Приставим один к другому равными катетами (см. рис. 38).

Рис. 38. Прямоугольные треугольники  и  приставили равными катетами друг к другу

Тогда  и  образуют развернутый угол, т. е.  – это отрезок прямой. Тогда  – равнобедренный треугольник . Откуда следует, что  ( – высота и биссектриса в равнобедренном треугольнике) и треугольники  и  равны по первому признаку равенства (катет, гипотенуза и угол между ними).

Теорема доказана.

На самом деле, иногда формулируют и доказывают более общий признак: два треугольника равны, если у них равны две стороны и больший из углов (важное отличие от первого признака: не требуется, чтобы этот угол лежал между равными сторонами). Несложно убедиться, что только что доказанный признак равенства для прямоугольных треугольников – это частный случай данного признака.

---

Заключение

Итак, мы рассмотрели два важных инструмента – равнобедренные и прямоугольные треугольники – и посмотрели, как их можно использовать для доказательства различных утверждений. В дальнейшем мы изучим использование этих и других известных нам инструментов для решения задач.

Список литературы

1. Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия, 7 класс. Учебник. – М.: «Просвещение», 2017.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия, 7 класс. Учебник. – М.: «Просвещение», 2017.
3. Мерзляк А.Г., Полонский В.Б., Якир М.С., Геометрия, 7 класс. Учебник. – М.: издательский центр «ВЕНТАНА-ГРАФ», 2018.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал yaklass.ru (Источник)
2. Интернет-портал school-assistant.ru (Источник)
3. Интернет-портал treugolniki.ru (Источник)

Домашнее задание

1. Прямые  и  параллельны. Чему равны углы при основании  равнобедренного треугольника , если ?

2. Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна . Найти градусные меры этих углов.

3. Площадь равнобедренного треугольника , в котором проведена биссектриса  см, равна . Найти площадь треугольника , если .