Как найти ось симметрии в треугольнике

Осевая симметрия — это симметрия относительно прямой.

Пусть дана некоторая прямая g.

Чтобы построить точку, симметричную некоторой точке A относительно прямой g, надо:

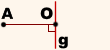1) Провести из точки A к прямой g перпендикуляр AO.

2) На продолжении перпендикуляра с другой стороны от прямой g отложить отрезок OA1, равный отрезку AO: OA1=AO.

Полученная точка A1 симметрична точке A относительно прямой g.

Прямая g называется осью симметрии.

Таким образом, точки A и A1 симметричны относительно прямой g, если эта прямая проходит через середину отрезка AA1 и перпендикулярна к нему.

Если точка A лежит на прямой g, то симметричная ей точка есть сама точка A.

Преобразование фигуры F  в фигуру F1, при котором каждая её точка A переходит в точку A1, симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g.

Фигуры F и F1 называются фигурами, симметричными относительно прямой g.

Чтобы построить треугольник, симметричный данному относительно прямой g, достаточно построить точки, симметричные вершинам треугольника, и соединить их отрезками.

Например, треугольники ABC и A1B1C1 симметричны относительно прямой g.

Если преобразование симметрии относительно прямой g переводит фигуру в себя, то такая фигура называется симметричной относительно прямой g, а прямая g называется её осью симметрии.

Симметричная фигура своей осью симметрии делится на две равные половины. Если симметричную фигуру нарисовать на бумаге, вырезать и согнуть по оси симметрии, то эти половинки совпадут.

Примеры фигур, симметричных относительно прямой.

1) Прямоугольник.

Прямоугольник имеет 2 оси симметрии: прямые, проходящие через точку пересечения диагоналей параллельно сторонам.

2) Ромб.

Ромб имеет две оси симметрии:

прямые, на которых лежат его диагонали.

3) Квадрат, как ромб и прямоугольник, имеет четыре оси симметрии: прямые, содержащие его диагонали, и прямые, проходящие через точку пересечения диагоналей параллельно сторонам.

4) Окружность.

Окружность имеет бесконечное множество осей симметрии:

любая прямая, содержащая диаметр, является осью симметрии окружности.

5) Прямая.

Прямая также имеет бесконечное множество осей симметрии: любая перпендикулярная ей прямая является для данной прямой осью симметрии.

6) Равнобедренная трапеция.

Равнобедренная трапеция — фигура, симметричная относительно прямой,перпендикулярной основаниям и проходящей через их середины.

7) Равнобедренный треугольник.

Равнобедренный треугольник имеет одну ось симметрии:

прямую, проходящую через высоту (медиану, биссектрису), проведённую к основанию.

8) Равносторонний треугольник.

Равносторонний треугольник имеет три оси симметрии:

прямые, содержащие его высоты (медианы, биссектрисы).

9) Угол.

Угол — фигура, симметричная относительно прямой, содержащей его биссектрису.

Теорема.

Осевая симметрия является движением.

ВИДЕОУРОК

Симметрия – слово греческого происхождения. Оно означает соразмерность, наличие
определённого порядка, закономерности в расположении частей.

Люди с давних времён
использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре,
художестве, строительстве.

Симметрия широко распространена и в природе, где
не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и
цветов растений, в расположении различных органов животных, в форме кристаллических
тел, в порхающей бабочке, загадочной снежинке, морской звезде.

Симметрия
в геометрии – свойство геометрических фигур.

Рассмотрим две симметрии на плоскости относительно точки и прямой.

ОСЕВАЯ СИММЕТРИЯ

Ось симметрии.

Две
точки, лежащие на одном перпендикуляре к данной плоскости (или прямой) по
разные стороны и на одинаковом расстоянии от неё, называются симметричными
относительно этой плоскости (или прямой). Фигура (плоская или пространственная)
симметрична относительно прямой (оси симметрии) или плоскости (плоскости
симметрии), если её точки попарно обладают указанным свойством.

Фигура симметрична
относительно прямой, если для каждой точки фигуры симметричная ей точка
относительно прямой также принадлежит этой фигуре. Прямая – ось симметрии фигуры, а фигура обладает
осевой симметрией.

Фигура, обладающая
осевой симметрией – это неразвёрнутый угол, который имеет одну ось симметрии –
прямую на которой расположена биссектриса угла.

Осевая симметрия – это симметрия относительно проведённой
прямой (оси).

Две точки  А 
и  В 
симметричны относительно прямой  а (оси симметрии), если эта прямая проходит через середину отрезка
АВ  и перпендикулярна
к нему.

Проведем прямую 
ЕF  через
середины  Е  и  F  сторон  АВ  и  СD  прямоугольника  АВСD.

Эта прямая делит прямоугольник пополам. Если прямоугольник перегнуть по этой
прямой, то обе две половины совпадут. Говорят, что прямоугольник симметричный относительно
прямой  ЕF, а прямую  ЕF  называют осью симметрии прямоугольника. У
прямоугольника  АВСD  есть другая ось симметрии – прямая  NК.

Вообще, фигуру называют симметричной относительно прямой  l, если эта прямая делит фигуру на две части, которые совпадают при перегибании
по этой прямой. Прямую  l  называют осью симметрии этой фигуры.

Две
точки  А  и  В, которые совпадают при перегибании плоскости по
прямой  l, называют симметричными относительно этой
прямой. Если точки  А  и  В  симметричные относительно прямой  l, то:

1) отрезок  АВ 
перпендикулярен прямой  l.

2) прямая  l  делит этот отрезок пополам.

Окружность имеет бесконечное количество осей симметрии. Любая прямая, которая
проходит через центр окружности, будет его осью симметрии.

Ось симметрии имеют изображения многих фигур (предметов), которые часто
встречаются в природе и технике.

Каждая точка прямой  а  симметрична самой себе.

ПРИМЕР:

АО
= ОВ, АВ ⊥
а.

Точка  А 
симметрична сама себе.

Фигура симметрична относительно прямой – если для каждой точки фигуры симметричная ей точка
относительно прямой также принадлежит этой фигуре.

Прямая – ось симметрии фигуры, а
фигура обладает осевой симметрией.

Фигуры, симметричные относительно прямой, равны.

Иногда у фигур несколько осей симметрии.

Фигуры, обладающие осевой симметрией.

ПРИМЕР:

Неразвёрнутый угол имеет одну ось симметрии –
прямую, на которой расположена биссектриса угла.

Равнобедренный
треугольник имеет одну ось симметрии.

Равносторонний
треугольник имеет три оси симметрии.

Квадрат имеет четыре оси
симметрии.

Прямоугольник имеет две
оси симметрии

Ромб имеет две оси
симметрии

Окружность имеет
бесконечно много осей симметрии – любая прямая, проходящая через центр,
является осью симметрии.

Примером фигур, у которых нет ни одной оси симметрии, являются
параллелограмм и треугольник, все стороны которого различны.

Алгоритм построения фигуры, симметричной относительно некоторой прямой.

ПРИМЕР:

Построим треугольник  А₁В₁С₁, симметричный треугольнику  АВС 
относительно красной прямой линии (ось симметрии).

Для этого проведём из вершины
треугольника  АВС  прямые,
перпендикулярные оси симметрии, и продолжим их дальше на другой стороне оси.

Измерим расстояние от вершин треугольника
до получившихся точек на прямой и отложим с другой стороны прямой такие же
расстояния.

Соединим получившиеся точки отрезками и
получим треугольник  А₁В₁С₁, симметричный данному треугольнику  АВС.

ЗАДАЧА:

Дан отрезок  АВ.
Построить его симметрию относительно прямой 
l,
не пересекающий данный отрезок.

РЕШЕНИЕ:

Изобразим схематически условие задачи.

Так как осевая симметрия
является движением, то отрезок  АВ 
отобразится на равный ему отрезок 
А’В’.

Для его построения сделаем
следующее: проведём через точки  А  и  В  прямые  m  и  n  перпендикулярно
прямой  l.
Пусть 

m ∩ l = Х, n ∩ l = Y.

Далее проведём отрезки 

А’Х
= АХ  и 
В’Y = ВY.

ЗАДАЧА:

Построить симметричный
треугольник для данного треугольника относительно какой-либо его стороны.

РЕШЕНИЕ:

Пусть нам дан треугольник  АВС. Будем строить его
симметрию относительно стороны  ВС.

Сторона  ВС  при осевой симметрии перейдёт в саму себя (следует из
определения). Точка  А  перейдёт в точку  А₁  следующим образом:

АА₁ ⊥ ВС, АН = НА₁.

Треугольник  АВС  перейдёт в треугольник  А₁ВС.

ЦЕНТРАЛЬНАЯ СИММЕТРИЯ

Симметрию относительно точки называют центральной
симметрией.

Две точки  А  и  В 
симметричны относительно точки  О, если  О – середина отрезка  АВ. Точка  О  называется центром симметрии.

Точка  О  симметрична самой
себе.

Фигура
симметрична относительно точки (центр симметрии), если её точки попарно лежат
на прямых, проходящих через центр симметрии, по разные стороны и на равных
расстояниях от него.

Фигура симметрична относительно точки, если для каждой точки фигуры симметричная ей точка
относительно данной точки также принадлежит этой фигуре. Данная точка – центр симметрии фигуры, а фигура обладает центральной симметрией.

Фигуры, симметричные относительно некоторой точки, равны.

Фигуры, обладающие центром симметрии.

ПРИМЕР:

Окружность, центр окружности
является её центром симметрии.

Параллелограмм, его центром
симметрии является точка пересечения диагоналей.

Прямая имеет бесконечно много
центров симметрии, так как любая точка прямой является её центром симметрии.

Примером фигуры, не имеющей центра симметрии, является треугольник.

Алгоритм построения центрально-симметричных фигур.

ПРИМЕР:

Построим треугольник  А₁В₁С₁, симметричный треугольнику  АВС 
относительно центра (точки)  О.

Для этого соединим точки  А,В,С  с центром  О  и продолжим эти отрезки.

Измерим отрезки  АО,
ВО, СО  и отложим с
другой стороны от точки  О  равные им отрезки 

АО
= ОА₁, ВО = ОВ₁, СО = ОС₁.

Соединим получившиеся точки
отрезками и получим треугольник  

А₁В₁С₁, симметричный данному треугольнику  АВС.

ЗАДАЧА:

Дан отрезок  АВ.
Построить его симметрию относительно точки 
С, лежащей на прямой  l.

РЕШЕНИЕ:

Изобразим схематически условие задачи.

Так как центральная симметрия
является движением, то отрезок  АВ 
отобразится на равный ему отрезок 
А”В”.

Для его построения сделаем
следующее: проведём прямые  АС  и  ВС. Далее проведём отрезки  

х‘ =
х,

у‘ =
–у.

3) При повороте на  90°  вокруг начала координат ось  Ох 
переходит в ось  Оу  так, что положительное направление переходит
в положительное, а ось  Оу  отображается на ось  Ох  так, что
положительное направление переходит в отрицательное. Поэтому  Р(х, у)  отображается на
точку  Р’

с координатами:

х‘ =
–у,

у‘ =
х.

4) При центральной симметрии

каждая из осей координат
отображается на себя, но так, что положительное направление оси переходит в
отрицательное и наоборот: отрицательное в положительное. Поэтому

Объединим результаты в таблицу

Прежде, чем ответить на вопрос о том, сколько осей симметрии имеет треугольник, сначала нужно вообще вспомнить, что такое ось симметрии.

Так вот, говоря просто, в геометрии ось симметрии – это линия, если по которой согнуть фигуру, то получим одинаковые половинки.

но стоит помнить, что треугольники тоже бывают разными.

Так вот, равнобедренный треугольник (треугольник с двумя равными сторонами) имеет одну ось симметрии.

Равносторонний треугольник соответственно имеет 3 оси симметрии, так как все стороны у этого треугольника равны.

А вот разносторонний треугольник вообще осей симметрии не имеет. Хоть как его складывай и хоть где прямые линии проводи, но раз стороны разные, то и двух одинаковых половиной не получится.

Осевая симметрия

Цели
урока:  создать
содержательные и организационные условия для развития умений строить
симметричные фигуры и находить оси симметрии в треугольниках.

Задачи
урока:

·        
Образовательные: продолжить изучение понятия осевой
симметрии, показать явления симметрии в природе, архитектуре и технике, уметь
находить симметричные объекты в окружающем мире, приобретение навыков
самостоятельной работы.

·        
Развивающие: развитие логического мышления, творческой
активности, познавательного интереса. Развивать умение кратко излагать свои
мысли.

Теоретическая
часть:

Что
такое симметрия? Основные понятия.

Симметрия — это соразмерность, пропорциональность
частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если
обе части от центра одинаковы, то это симметрия.

Ось
симметрии фигуры — это
прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять,
что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой
пересекаются все оси симметрии.Осевая

Осевой
симметрией называется
симметрия, проведенная относительно прямой. При осевой симметрии любой точке,
расположенной по одну сторону прямой, всегда соответствует другая точка на
второй стороне этой прямой.

При
этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

          

На рисунке осевая симметрия: отрезки AB
и А1В1 симметричны относительно прямой

Осевая симметрия часто встречается в повседневной жизни:

Давайте
разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1.
Постройте треугольник A₁B₁C₁ ,симметричный
треугольнику ABC относительно прямой.

1. Проведем
   из вершин треугольника ABC три прямые, перпендикулярные оси симметрии,
   выведем эти прямые на другую сторону оси симметрии.
2. Найдем
   расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С
   другой стороны прямой отложим такие же расстояния.
4. Соединяем
   точки отрезками и строим треугольник A₁B₁C₁,
   симметричный треугольнику ABC.
5. Получаем
   два треугольника, симметричных относительно оси симметрии.

Пример
2. Постройте треугольник, симметричный треугольнику ABC относительно прямой.

1. Строим
   по уже известному алгоритму. Проводим прямые из вершин треугольника ABC и
   выводим их на другую сторону оси симметрии.
2. Измеряем
   расстояние от вершин до точек на прямой.
3. Откладываем
   такие же расстояния на другой стороне оси симметрии.
4. Соединяем
   точки и строим треугольник A₁B₁C₁.

Пример
3. Построить отрезок A₁B₁, симметричный отрезку AB
относительно прямой.

1. Измеряем
   расстояние от точки B до прямой и от точки A до прямой.
2. Проводим
   прямую от точки А через прямую под прямым углом к прямой, выводя за ось
   симметрии.
3. Проводим
   прямую от точки B через прямую под прямым углом к прямой, выводя за ось
   симметрии.
4. Соединяем
   точки A₁ и B₁ и получаем отрезок A₁B₁,
   симметричный данному.

Задачи:

1.     
Постройте фигуру, симметричную данной
относительно прямой.

2.     
Постройте фигуру, симметричную данной
относительно прямой.