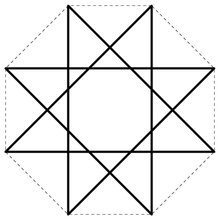
Как найти ось симметрии звезды - Сайт, где вы сможете решить свои вопросы

Сколько всего есть оси симметрии?

Светлана Мерзлякова

29 ноября 2018 · 933

Для удобства рассмотрим случай в двухмерном пространстве. Нарисуем две взаимоперпендикулярные прямые. Пусть это будут оси симметрии для фигуры звезда с четырьмя лучами. Мы разделим прямой угол между лучами этой звезды, например, на 2 и проведем еще оси симметрии, затем достроим фигуру уже до звезды с 8 лучами. И так по аналогии можно разделить угол на сколь угодно большое количество дополнительных лучей, поэтому осей симметрии может быть бесконечно много в пространстве, начиная с двухмерного. В одномерном самая прямая – это уже единственная ось симметрии.

689

Комментировать ответ…Комментировать…

Источник

В геометрии правильная звезда – это обычно невыпуклый правильный многоугольник , все ребра которого имеют одинаковую длину.

Правильные звезды зеркально-симметричны и вращательно-симметричны . Центр симметрии – это центр окружности и вписанной окружности . Следовательно, углы , длина и площади, которые имеют одинаковое положение относительно центра симметрии, одинаковы. Помимо прочего, все стороны и внутренние углы одинаковы.

Термин звезда для такого плоского многоугольника дополнительно ограничивается в комбинаторной геометрии условием, что прямые линии, на которых лежат края звезды, всегда проходят через два выпуклых внешних угла звезды и затем называются звездным многоугольником . В качестве альтернативы звездообразный многоугольник определяется в комбинаторной геометрии как правильный ( равносторонний и равноугольный ) перевернутый, невыпуклый, плоский многоугольник. Переворот означает, что стороны могут пересекаться внутри многоугольника. Термин звездный многоугольник появился только в 20 веке, когда геометры начали изучать тротуары комбинаторным способом. Эти звездообразные многоугольники построены намного старше, например, пентаграмма и гексаграмма , также известные как Звезда Давида .

Рассматриваемые в топологии и анализе звездные области , к которым также принадлежат выпуклые множества и которые не обязательно должны быть многоугольными, должны отличаться от этого.

строительство

Обычная звезда образуется в результате реакции, в плоском регулярном соединении -Eck каждую вершину с несмежной вершиной прямой линией, и этот процесс продолжается, снова достигается до исходной угловой точки. Пронумерованы ли углы индексами и только те, которые соединены прямой линией, чьи последовательные индексы имеют разницу . Периметр разделен эквидистантна в дуги .

Обычные звезды можно построить из правильного угла. Они называются звезды, с на символ Шлефли с . Если и взаимно просты , звезда соединена, может быть нарисована за один раз и также называется звездным многоугольником . В противном случае он разбивается на столько правильных многоугольников, сколько указывает наибольший общий делитель . Следовательно, количество углов этих многоугольников одинаково . Когда это простое число , подключены все -звезды. Если учесть количество соединенных звездообразных многоугольников для заданного количества углов, вы получите последовательность A055684 в OEIS . Этот номер такой же . Здесь называется фи – функция Эйлера .
$2 leq q leq left lfloor tfrac {p-1} {2} right rfloor$ ${ displaystyle { tfrac {p} { operatorname {ggT} (p, q)}}}$ ${ displaystyle { tfrac { varphi (p)} {2}} - 1}$

Параметры

угол

Внутренние углы в звезде {8/2} ( восьмерка ) равны 90 °.

Внутренние углы звезды {8/3} ( восьмерка ) равны 45 °.

Углы правильной звезды лежат и совмещены на общем круге. Обычная звезда имеет периметр с радиусом периметра . Кроме того, углы на окружности равноудалены , то есть углы, расположенные рядом друг с другом, появляются под одним и тем же центральным углом. RU}

${ displaystyle mu = { frac {1} {p}} cdot 360 ^ { circ} = { frac {2 pi} {p}}}$

Следовательно, такая звезда также имеет вписанный круг с вписанным радиусом . Вписанный круг касается сторон в центрах сторон. Центр круга совпадает с центром окружности.
$г_ {я}$

Если соединить соседние углы штатной звезды, получится правильный угол. В диагоналях , которые начинаются с одного угла этого многоугольника формы равных углов, которые в два раз меньше из центральных углов и каждый из них .
${ displaystyle { frac { pi} {p}}}$

Это можно увидеть, посмотрев на равнобедренные треугольники , образованные одной из диагоналей и двумя окружными радиусами. Другая возможность – повернуть диагонали вокруг угла с центральной точкой в качестве центра вращения или использовать угол окружности, установленный для окружности .
${ displaystyle { frac {2 pi} {p}}}$

Между двумя соседними сторонами звезды расположены диагонали, которые делят внутренний угол на равные по величине углы . Отсюда следует, что все внутренние углы правильной -звезды равны
${ displaystyle { frac { pi} {p}}}$

${ displaystyle alpha = (p-2q) cdot { frac { pi} {p}} = pi - { frac {2q pi} {p}}}$

находятся.

Стороны звезды образуют пересечения . Каждая сторона звезды вырезана с разных сторон, потому что углы находятся на более короткой дуге над стороной, а две другие стороны встречаются в каждом из углов, каждая из которых соединяет этот угол с углом на более длинной дуге над рассматриваемой стороной. Каждая сторона образует с другими сторонами углы пересечения и , где есть. Каждая точка пересечения принадлежит 2 сторонам, поэтому пересечений есть всего . Каждый из этих углов пересечения встречается несколько раз, потому что каждый угол пересечения состоит из 2 противоположных углов для каждой стороны .
q-1 q-1 ${ displaystyle { frac {2m pi} {p}}}$ ${ displaystyle pi - { frac {2m pi} {p}}}$ ${ Displaystyle { tfrac {1} {2}} cdot p (2q-2) = p (q-1)}$

Например, для углов в правильных звездах получаются следующие значения:

звезда	Центральный угол	Внутренний угол	Угол среза
Степень	Радианы	Степень	Радианы	Степень
{p / q} звезда	${ displaystyle { frac {1} {p}} cdot 360 ^ { circ}}$	${ displaystyle { frac {2 pi} {p}}}$	${ displaystyle { frac {p-2q} {p}} cdot 180 ^ { circ}}$	${ displaystyle pi - { frac {2q pi} {p}}}$	${ displaystyle { frac {2m} {p}} cdot 180 ^ { circ}, { frac {p-2m} {p}} cdot 180 ^ { circ}}$
{5/2} звезда	$72 ^ { circ}$	${ tfrac {2} {5}} pi$	$36 ^ { circ}$	${ tfrac {1} {5}} pi$	${ displaystyle 72 ^ { circ}, 144 ^ { circ}}$
{6/2} звезда	$60 ^ { circ}$	${ tfrac {1} {3}} pi$	$60 ^ { circ}$	${ tfrac {1} {3}} pi$	${ displaystyle 60 ^ { circ}, 120 ^ { circ}}$
{8/2} звезда	$45 ^ { circ}$	${ tfrac {1} {4}} pi$	$90 ^ { circ}$	${ tfrac {1} {2}} pi$	${ displaystyle 45 ^ { circ}, 135 ^ { circ}}$
{8/3} звезда	$45 ^ { circ}$	${ tfrac {1} {4}} pi$	$45 ^ { circ}$	${ tfrac {1} {4}} pi$	${ displaystyle 90 ^ { circ}, 45 ^ { circ}, 135 ^ { circ}, 90 ^ { circ}}$
{10/2} звезда	$36 ^ { circ}$	${ tfrac {1} {5}} pi$	$108 ^ { circ}$	${ tfrac {3} {5}} pi$	${ displaystyle 36 ^ { circ}, 144 ^ { circ}}$
{10/3} звезда	$36 ^ { circ}$	${ tfrac {1} {5}} pi$	$72 ^ { circ}$	${ tfrac {2} {5}} pi$	${ displaystyle 72 ^ { circ}, 36 ^ { circ}, 144 ^ { circ}, 108 ^ { circ}}$
{10/4} звезда	$36 ^ { circ}$	${ tfrac {1} {5}} pi$	$36 ^ { circ}$	${ tfrac {1} {5}} pi$	${ displaystyle 108 ^ { circ}, 72 ^ { circ}, 36 ^ { circ}, 144 ^ { circ}, 108 ^ { circ}, 72 ^ { circ}}$
{12/2} звезда	$30 ^ { circ}$	${ tfrac {1} {6}} pi$	$120 ^ { circ}$	${ tfrac {2} {3}} pi$	${ displaystyle 30 ^ { circ}, 150 ^ { circ}}$
{12/3} звезда	$30 ^ { circ}$	${ tfrac {1} {6}} pi$	$90 ^ { circ}$	${ tfrac {1} {2}} pi$	${ displaystyle 60 ^ { circ}, 30 ^ { circ}, 150 ^ { circ}, 120 ^ { circ}}$
{12/4} звезда	$30 ^ { circ}$	${ tfrac {1} {6}} pi$	$60 ^ { circ}$	${ tfrac {1} {3}} pi$	${ displaystyle 90 ^ { circ}, 60 ^ { circ}, 30 ^ { circ}, 150 ^ { circ}, 120 ^ { circ}, 90 ^ { circ}}$
{12/5} звезда	$30 ^ { circ}$	${ tfrac {1} {6}} pi$	$30 ^ { circ}$	${ tfrac {1} {6}} pi$	${ displaystyle 120 ^ { circ}, 90 ^ { circ}, 60 ^ { circ}, 30 ^ { circ}, 150 ^ { circ}, 120 ^ { circ}, 90 ^ { circ} }, 60 ^ { circ}}$

Длина

Наиболее важные параметры правильных звезд можно определить с помощью треугольника определения, который образован центром и двумя смежными углами многоугольника. Треугольник определения является равнобедренным с углом при вершине , углами основания , ногами , основанием и высотой . Если треугольник определения по высоте ( апофема ) разделен на два прямоугольных треугольника, в результате получится вышеупомянутый центральный угол и тригонометрические функции ( синус и косинус , тангенс и котангенс, а также секанс и косеканс ), следующие соотношения между страницей длина ,
${ tfrac { alpha} {2}}$ RU} $г_ {я}$

Круговой радиус и радиус вписанной окружности :
RU} $г_ {я}$

${ displaystyle a = 2 , r_ {u} cdot sin left ({ frac {q pi} {p}} right) = 2 , r_ {i} cdot tan left ({ frac {q pi} {p}} right)}$

${ displaystyle r_ {u} = { frac {a} {2}} cdot csc left ({ frac {q pi} {p}} right) = r_ {i} cdot sec влево ({ frac {q pi} {p}} right)}$

${ displaystyle r_ {i} = { frac {a} {2}} cdot cot left ({ frac {q pi} {p}} right) = r_ {u} cdot cos влево ({ frac {q pi} {p}} right)}$

Если и имеют общий множитель , то для обычной -звезды такие же отношения длин между , и для обычной -звезды.
RU} $г_ {я}$ ${ displaystyle {{ tfrac {p} {m}} / { tfrac {q} {m}} }}$

Для некоторых значений могут быть указаны явные формулы для значений функций тригонометрических функций (см. Сборник формул тригонометрии ) и, следовательно, для длин в обычных звездах, например:

звезда	Длина стороны с учетом	Циркумрадиус задан	Указанный радиус задан $г_ {я}$
Радиус периметра	Вписанный радиус	Длина стороны	Вписанный радиус	Длина стороны	Радиус периметра
{p / q} звезда	${ displaystyle { frac {a} {2}} cdot csc left ({ frac {q pi} {p}} right)}$	${ displaystyle { frac {a} {2}} cdot cot left ({ frac {q pi} {p}} right)}$	${ displaystyle 2 , r_ {u} cdot sin left ({ frac {q pi} {p}} right)}$	${ displaystyle r_ {u} cdot cos left ({ frac {q pi} {p}} right)}$	${ displaystyle 2 , r_ {i} cdot tan left ({ frac {q pi} {p}} right)}$	${ displaystyle r_ {i} cdot sec left ({ frac {q pi} {p}} right)}$
{5/2} звезда	${ displaystyle a cdot { sqrt {{ tfrac {1} {10}} left (5 - { sqrt {5}} right)}}}$	${ displaystyle a cdot { tfrac {1} {2}} { sqrt {{ tfrac {1} {5}} left (5-2 { sqrt {5}} right)}}}$	${ displaystyle r_ {u} cdot { sqrt {{ tfrac {1} {2}} left (5 + { sqrt {5}} right)}}}$	${ displaystyle r_ {u} cdot { tfrac {1} {4}} left ({ sqrt {5}} - 1 right)}$	${ displaystyle r_ {i} cdot 2 { sqrt {5 + 2 { sqrt {5}}}}}$	${ displaystyle r_ {i} cdot left (1 + { sqrt {5}} right)}$
{6/2} звезда	$а cdot { tfrac {1} {3}} { sqrt {3}}$	$а cdot { tfrac {1} {6}} { sqrt {3}}$	$г_ {и} cdot { sqrt {3}}$	$г_ {и} cdot { tfrac {1} {2}}$	$r_ {i} cdot 2 { sqrt {3}}$	$г_ {i} cdot 2$
{8/2} звезда	$а cdot { tfrac {1} {2}} { sqrt {2}}$	$а cdot { tfrac {1} {2}}$	$г_ {и} cdot { sqrt {2}}$	$r_ {u} cdot { tfrac {1} {2}} { sqrt {2}}$	$г_ {i} cdot 2$	$r_ {i} cdot { sqrt {2}}$
{8/3} звезда	${ displaystyle a cdot { sqrt {{ tfrac {1} {2}} left (2 - { sqrt {2}} right)}}}$	${ displaystyle a cdot { tfrac {1} {2}} left ({ sqrt {2}} - 1 right)}$	${ displaystyle r_ {u} cdot { sqrt {2 + { sqrt {2}}}}}$	${ displaystyle r_ {u} cdot { tfrac {1} {2}} { sqrt {2 - { sqrt {2}}}}}$	${ displaystyle r_ {i} cdot left (2 + 2 { sqrt {2}} right)}$	${ displaystyle r_ {i} cdot { sqrt {4 + 2 { sqrt {2}}}}}$
{10/2} звезда	${ displaystyle a cdot { sqrt {{ tfrac {1} {10}} left (5 + { sqrt {5}} right)}}}$	${ displaystyle a cdot { tfrac {1} {2}} { sqrt {{ tfrac {1} {5}} left (5 + 2 { sqrt {5}} right)}}}$	${ displaystyle r_ {u} cdot { sqrt {{ tfrac {1} {2}} left (5 - { sqrt {5}} right)}}}$	${ displaystyle r_ {u} cdot { tfrac {1} {4}} left (1 + { sqrt {5}} right)}$	$r_ {i} cdot 2 { sqrt {5-2 { sqrt {5}}}}$	${ displaystyle r_ {i} cdot left ({ sqrt {5}} - 1 right)}$
{10/3} звезда	${ displaystyle a cdot { tfrac {1} {2}} left ({ sqrt {5}} - 1 right)}$	${ displaystyle a cdot { tfrac {1} {2}} { sqrt {5-2 { sqrt {5}}}}}$	${ displaystyle r_ {u} cdot { tfrac {1} {2}} left (1 + { sqrt {5}} right)}$	${ displaystyle r_ {u} cdot { tfrac {1} {2}} { sqrt {{ tfrac {1} {2}} left (5 - { sqrt {5}} right)}} }$	${ displaystyle r_ {i} cdot 2 { sqrt {{ tfrac {1} {5}} left (5 + 2 { sqrt {5}} right)}}}$	${ displaystyle r_ {i} cdot 2 { sqrt {{ tfrac {1} {10}} left (5 + { sqrt {5}} right)}}}$
{10/4} звезда	${ displaystyle a cdot { sqrt {{ tfrac {1} {10}} left (5 - { sqrt {5}} right)}}}$	${ displaystyle a cdot { tfrac {1} {2}} { sqrt {{ tfrac {1} {5}} left (5-2 { sqrt {5}} right)}}}$	${ displaystyle r_ {u} cdot { sqrt {{ tfrac {1} {2}} left (5 + { sqrt {5}} right)}}}$	${ displaystyle r_ {u} cdot { tfrac {1} {4}} left ({ sqrt {5}} - 1 right)}$	${ displaystyle r_ {i} cdot 2 { sqrt {5 + 2 { sqrt {5}}}}}$	${ displaystyle r_ {i} cdot left (1 + { sqrt {5}} right)}$
{12/2} звезда		$а cdot { tfrac {1} {2}} { sqrt {3}}$	$г_ {и} cdot 1$	$r_ {u} cdot { tfrac {1} {2}} { sqrt {3}}$	$r_ {i} cdot { tfrac {2} {3}} { sqrt {3}}$	$r_ {i} cdot { tfrac {2} {3}} { sqrt {3}}$
{12/3} звезда	$а cdot { tfrac {1} {2}} { sqrt {2}}$	$а cdot { tfrac {1} {2}}$	$г_ {и} cdot { sqrt {2}}$	$r_ {u} cdot { tfrac {1} {2}} { sqrt {2}}$	$г_ {i} cdot 2$	$r_ {i} cdot { sqrt {2}}$
{12/4} звезда	$а cdot { tfrac {1} {3}} { sqrt {3}}$	$а cdot { tfrac {1} {6}} { sqrt {3}}$	$г_ {и} cdot { sqrt {3}}$	$г_ {и} cdot { tfrac {1} {2}}$	$r_ {i} cdot 2 { sqrt {3}}$	$г_ {i} cdot 2$
{12/5} звезда	${ displaystyle a cdot { tfrac {1} {2}} left ({ sqrt {6}} - { sqrt {2}} right)}$	${ displaystyle a cdot { tfrac {1} {2}} left (2 - { sqrt {3}} right)}$	${ displaystyle r_ {u} cdot { tfrac {1} {2}} left ({ sqrt {6}} + { sqrt {2}} right)}$	${ displaystyle r_ {u} cdot { tfrac {1} {4}} left ({ sqrt {6}} - { sqrt {2}} right)}$	${ displaystyle r_ {i} cdot left (4 + 2 { sqrt {3}} right)}$	${ displaystyle r_ {i} cdot left ({ sqrt {6}} + { sqrt {2}} right)}$

Боковые секции

Каждая из страниц вырезана из других страниц и разделена на разделы. Длину этих участков можно определить следующим образом:

Расстояние от середины стороны до пересечения или конечной точки стороны образует прямоугольный треугольник вместе с радиусом вписанной окружности и соединительным расстоянием между центром вписанной окружности и точкой пересечения или конечной точки . Эти точки обозначаются началом от центральной точки . Расстояние от середины одной стороны до пересечения или конечной точки находится в прямоугольном треугольнике напротив угла , где -. Это следует из рассмотрения половинного центрального угла . В результате получается длина этого маршрута:
${ Displaystyle S_ {1}, S_ {2}, S_ {3}, ldots, S_ {q}}$ $S_ {m}$ ${ displaystyle { frac {m pi} {p}}}$

${ displaystyle a_ {m} = r_ {i} cdot tan left ({ frac {m pi} {p}} right) = r_ {u} cdot cos left ({ frac { q pi} {p}} right) cdot tan left ({ frac {m pi} {p}} right)}$

Длина отрезка между точками и тогда такая же
${ displaystyle s_ {m}}$ ${ displaystyle S_ {m-1}}$ $S_ {m}$

${ Displaystyle s_ {m} = a_ {m} -a_ {m-1} = r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot tan left ({ frac {m pi} {p}} right) -r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot tan left ({ frac {(m-1) pi} {p}} right) = r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot left ( tan left ({ frac {m pi} {p}} right) - tan left ({ frac {(m-1) pi} {p}} right) right) right )}$

Согласно теореме Пифагора , расстояние между точкой и центром звезды одинаково.
$S_ {m}$

${ displaystyle r_ {m} = { sqrt {r_ {i} ^ {2} + a_ {m} ^ {2}}} = { sqrt {r_ {i} ^ {2} + left (r_ { i} cdot tan left ({ frac {m pi} {p}} right) right) ^ {2}}} = r_ {i} cdot { sqrt {1+ tan ^ { 2} left ({ frac {m pi} {p}} right)}} = { frac {r_ {i}} { cos left ({ frac {m pi} {p}}) right)}} = r_ {i} cdot sec left ({ frac {m pi} {p}} right) = r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot sec left ({ frac {m pi} {p}} right)}$

Использовалась связь между касательной и секущей (см. Тригонометрическая функция – отношения между функциями ). Поскольку обычная звезда зеркально-симметрична и вращательно-симметрична , это расстояние одинаково для всех сторон. Следовательно, точки для данного с лежат на окружности с радиусом .
$S_ {m}$ r_m

При заданном радиусе для длин маршрутов, длин участков и радиусов получаются следующие значения :
$r_ {u} = 1$ ${ displaystyle s_ {m}}$ r_m

звезда	Длина маршрутов	Длина секций ${ displaystyle s_ {m}}$	Радиусы
{p / q} звезда	${ displaystyle r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot tan left ({ frac {m pi} {p}} right )}$	${ displaystyle r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot left ( tan left ({ frac {m pi} {p}) } right) - tan left ({ frac {(m-1) pi} {p}} right) right)}$	${ displaystyle r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot sec left ({ frac {m pi} {p}} right )}$
	$а_ {1}$		$а_ {3}$	$s_ {1}$	$s_ {2}$		$г_ {1}$	$г_ {2}$
{5/2} звезда	0,224513988	0,951056516		0,224513988	0,726542528		0,381966011	1.000000000
{6/2} звезда	0,288675135	0,866025404	0,288675135	0,577350269	0,577350269	1.000000000
{7/2} звезда	0,300256864	0,781831482	0,300256864	0,481574619	0,692021472	1.000000000
{7/3} звезда	0,107160434	0,279032425	0,974927912	0,107160434	0,171871992	0,695895487	0,246979604	0,356895868	1.000000000
{8/2} звезда	0,292893219	0,707106781		0,292893219	0,414213562		0,765366865	1.000000000
{8/3} звезда	0,158512668	0,382683432	0,923879533	0,158512668	0,224170765	0,541196100	0,414213562	0,541196100	1.000000000

Периметр и площадь

Окружность регулярной звезды состоит из двух наружных секций с каждой стороны. Это единственные секции, которых нет в интерьере звезды. Есть такие участки с длиной . Это дает возможность:
${ displaystyle s_ {q}}$

${ Displaystyle U = 2 , p , s_ {q} = 2 , p , r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot left ( tan left ({ frac {q pi} {p}} right) - tan left ({ frac {(q-1) pi} {p}} right) right) right )}$

Область покрыта регулярные результаты звезды от разницы между площадью правильного многоугольника , который создается путем соединения соседних углов, а площадь равнобедренных треугольников , каждый из которых состоят из одной стороны наружного регулярного угла и образуются две внешние части Сторон звезды. Внешний правильный угол имеет длину стороны и площадь .
${ displaystyle 2 , r_ {u} cdot sin left ({ frac { pi} {p}} right)}$ ${ displaystyle { frac {p , r_ {u} ^ {2}} {2}} cdot sin left ({ frac {2 pi} {p}} right) = p , r_ {u} ^ {2} cdot sin left ({ frac { pi} {p}} right) cdot cos left ({ frac { pi} {p}} right)}$

Эти равнобедренные треугольники иметь базовую длину , угол базы , на высоту и площадь . Это дает площадь обычной звезды:
${ displaystyle 2 , r_ {u} cdot sin left ({ frac { pi} {p}} right)}$ ${ displaystyle { frac {(q-1) pi} {p}}}$ ${ displaystyle r_ {u} cdot sin left ({ frac { pi} {p}} right) cdot tan left ({ frac {(q-1) pi} {p} } верно)}$ ${ displaystyle r_ {u} ^ {2} cdot sin ^ {2} left ({ frac { pi} {p}} right) cdot tan left ({ frac {(q- 1) pi} {p}} right)}$

${ displaystyle A = p , r_ {u} ^ {2} cdot sin left ({ frac { pi} {p}} right) cdot cos left ({ frac { pi } {p}} right) -p , r_ {u} ^ {2} cdot sin ^ {2} left ({ frac { pi} {p}} right) cdot tan left ({ frac {(q-1) pi} {p}} right) = p , r_ {u} ^ {2} cdot sin left ({ frac { pi} {p} } right) cdot left ( cos left ({ frac { pi} {p}} right) - sin left ({ frac { pi} {p}} right) cdot tan left ({ frac {(q-1) pi} {p}} right) right)}$

Внутренние части всех сторон звезды вместе образуют край правильного многоугольника, который находится внутри звезды. Внутренний правильный угол имеет длину стороны и площадь .
${ displaystyle a_ {1} = 2 , r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot tan left ({ frac { pi } {p}} right)}$ ${ displaystyle { frac {p , a_ {1} ^ {2}} {4}} cdot cot left ({ frac { pi} {p}} right) = { frac {p } {4}} cdot left (4 , r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot tan left ({ frac { pi} {p}} right) right) ^ {2} cdot cot left ({ frac { pi} {p}} right) = p , r_ {u} ^ {2} cdot cos ^ {2} left ({ frac {q pi} {p}} right) cdot tan left ({ frac { pi} {p}} right)}$

При заданном окружном радиусе для окружности и площади получаются следующие значения :
$r_ {u} = 1$

звезда	объем	Площадь	Площадь наружного правильного угла	Площадь внутреннего правильного угла
{p / q} звезда	${ displaystyle 2 , p , r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot left ( tan left ({ frac {q pi} {p}} right) - tan left ({ frac {(q-1) pi} {p}} right) right)}$	${ displaystyle p , r_ {u} ^ {2} cdot sin left ({ frac { pi} {p}} right) cdot left ( cos left ({ frac { pi} {p}} right) - sin left ({ frac { pi} {p}} right) cdot tan left ({ frac {(q-1) pi} {p }} верно-верно)}$	${ displaystyle p , r_ {u} ^ {2} cdot sin left ({ frac { pi} {p}} right) cdot cos left ({ frac { pi} { p}} right)}$	${ displaystyle p , r_ {u} ^ {2} cdot cos ^ {2} left ({ frac {q pi} {p}} right) cdot tan left ({ frac { pi} {p}} right)}$
{5/2} звезда	7,265425280	1,122569941	2,377641291	0,346893189
{6/2} звезда	6,928203230	1,732050808	2,598076211	0,866025404
{7/2} звезда	6,742044663	2.101798046	2,736410189	1,310449647
{7/3} звезда	9,742536814	1.083959195	2,736410189	0,166918079
{8/2} звезда	6,627416998	2,343145751	2,828427125	1,656854249
{8/3} звезда	8,659137602	1,656854249	2,828427125	0,485281374

Частичные области

Страницы обычного -Sterns делят его область на подобласти, а именно: внутренний правильный -Eck, равнобедренные треугольники и квадраты воздушных змеев , которые квадраты с диагональной осью симметрии . В этом можно убедиться, добавляя части всех сторон звезды поэтапно, начиная с центра сторон. Каждая из двух внутренних частей длины образует стороны внутреннего правильного многоугольника. Вместе с соседними секциями длиной , они образуют боковые стороны конгруэнтных равнобедренных треугольников. Таким образом , эти равнобедренный треугольник имеет длины сторон , и . Две последовательные части длины и стороны равных квадратов дракона. Эти квадраты воздушного змея имеют две смежные стороны длиной и .
$s_ {1}$ $s_ {2}$ ${ displaystyle 2s_ {1}}$ $s_ {2}$ $s_ {2}$ ${ displaystyle s_ {m-1}}$ ${ displaystyle s_ {m}}$ ${ displaystyle s_ {m-1}}$ ${ displaystyle s_ {m}}$

Если вы посмотрите на боковые части обычной -звезды, вы увидите, что внутренние части всех сторон образуют обычную -звезду. Ибо есть внутренний правильный угол. У этой правильной звезды есть длина стороны и радиус периметра . В результате получится область (см. Разделы страницы ) :
m = 1 ${ displaystyle 2s_ {1} + 2s_ {2} + 2s_ {3} + ldots + 2s_ {m} = 2a_ {m}}$ r_m ${ displaystyle r_ {m} = r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot sec left ({ frac {m pi} { p}} right)}$

${ displaystyle { begin {align} & , p , r_ {m} ^ {2} cdot sin left ({ frac { pi} {p}} right) cdot left ( cos left ({ frac { pi} {p}} right) - sin left ({ frac { pi} {p}} right) cdot tan left ({ frac {( m-1) pi} {p}} right) right) \ = & , p , left (r_ {u} cdot cos left ({ frac {q pi} {p }} right) cdot sec left ({ frac {m pi} {p}} right) right) ^ {2} cdot sin left ({ frac { pi} {p }} right) cdot left ( cos left ({ frac { pi} {p}} right) - sin left ({ frac { pi} {p}} right) cdot tan left ({ frac {(m-1) pi} {p}} right) right) \ = & , p , r_ {u} ^ {2} cdot cos ^ {2} left ({ frac {q pi} {p}} right) cdot sin left ({ frac { pi} {p}} right) cdot { frac {1} { cos ^ {2} left ({ frac {m pi} {p}} right)}} cdot left ( cos left ({ frac { pi} {p}} right ) - sin left ({ frac { pi} {p}} right) cdot tan left ({ frac {(m-1) pi} {p}} right) right) \ = & , p , r_ {u} ^ {2} cdot cos ^ {2} left ({ frac {q pi} {p}} right) cdot sin left ( { frac { pi} {p}} right) cdot { frac { cos left ({ frac { pi} {p}} right) - sin left ({ frac { пи} {p}} r ight) cdot tan left ({ frac {(m-1) pi} {p}} right)} { cos left ({ frac { pi} {p}} + { frac {(m-1) pi} {p}} right) cdot cos left ({ frac {m pi} {p}} right)}} \ = & , p , r_ {u} ^ {2} cdot cos ^ {2} left ({ frac {q pi} {p}} right) cdot sin left ({ frac { pi} {p} } right) cdot { frac { cos left ({ frac { pi} {p}} right) - sin left ({ frac { pi} {p}} right) cdot tan left ({ frac {(m-1) pi} {p}} right)} { left ( cos left ({ frac { pi} {p}} right) cdot cos left ({ frac {(m-1) pi} {p}} right) - sin left ({ frac { pi} {p}} right) cdot sin left ({ frac {(m-1) pi} {p}} right) right) cdot cos left ({ frac {m pi} {p}} right)}} \ = & , p , r_ {u} ^ {2} cdot cos ^ {2} left ({ frac {q pi} {p}} right) cdot sin left ({ frac { pi} {p}} right) cdot { frac { cos left ({ frac { pi} {p}} right) - sin left ({ frac { pi} {p}} right) cdot tan left ({ frac {(m-1) pi} {p}} right)} { left ( cos left ({ frac { pi} {p}} right) - sin left ({ frac { pi} {p}} right) cdot tan left ({ frac {(m-1) pi} {p}} right) right) cdot cos left ({ frac {(m-1) pi} {p}} right) cdot cos left ({ frac {m pi} {p}} right)}} \ = & , p , r_ {u} ^ {2} cdot cos ^ {2} left ({ frac {q pi} {p}} right) cdot sin left ({ frac { pi} {p }} right) cdot { frac {1} { cos left ({ frac {(m-1) pi} {p}} right) cdot cos left ({ frac {m pi} {p}} right)}} \ = & , p , r_ {u} ^ {2} cdot cos ^ {2} left ({ frac {q pi} {p }} right) cdot sin left ({ frac { pi} {p}} right) cdot sec left ({ frac {(m-1) pi} {p}} right) cdot sec left ({ frac {m pi} {p}} right) end {align}}}$

Теорема сложения использовалась для косинуса и определения секущей .

Если вы удалите внешние равные квадраты дракона с длинами сторон и с поверхности обычной -звезды, то останется обычная -звезда. Таким образом, общая площадь этих четырехугольников воздушного змея является разницей между площадью обычной -звезды и обычной -звезды. Площадь кайта квадрата это различие:
${ displaystyle s_ {m-1}}$ ${ displaystyle s_ {m}}$ ${ displaystyle { tfrac {1} {p}}}$

${ displaystyle { begin {align} & , { frac {1} {p}} , left (p , r_ {u} ^ {2} cdot cos ^ {2} left ({ frac {q pi} {p}} right) cdot sin left ({ frac { pi} {p}} right) cdot sec left ({ frac {(m-1 ) pi} {p}} right) cdot sec left ({ frac {m pi} {p}} right) -p , r_ {u} ^ {2} cdot cos ^ {2} left ({ frac {q pi} {p}} right) cdot sin left ({ frac { pi} {p}} right) cdot sec left ({ frac {(m-2) pi} {p}} right) cdot sec left ({ frac {(m-1) pi} {p}} right) right) \ = & , r_ {u} ^ {2} cdot cos ^ {2} left ({ frac {q pi} {p}} right) cdot sin left ({ frac { pi } {p}} right) cdot sec left ({ frac {(m-1) pi} {p}} right) cdot left ( sec left ({ frac {m pi} {p}} right) - sec left ({ frac {(m-2) pi} {p}} right) right) end {align}}}$

Эта область также может быть рассчитана с использованием длин диагоналей на площади кайта . Длина диагонали, лежащей на оси симметрии , равна разности радиусов и . Остальные диагональные пробеги ортогонально и формы равнобедренный треугольник с двумя радиусами . Эта диагональ лежит в равнобедренном треугольнике напротив центрального угла, поэтому она имеет длину . Это дает площадь квадрата дракона:
r_m ${ displaystyle r_ {m-2}}$ ${ displaystyle r_ {m-1}}$ ${ displaystyle { frac {2 pi} {p}}}$ ${ displaystyle 2 , r_ {m-1} cdot sin left ({ frac { pi} {p}} right)}$

${ displaystyle { begin {align} & , { frac {1} {2}} , left (2 , r_ {m-1} cdot sin left ({ frac { pi}) {p}} right) right) cdot left (r_ {m} -r_ {m-2} right) \ = & , r_ {m-1} cdot sin left ({ frac { pi} {p}} right) cdot left (r_ {m} -r_ {m-2} right) \ = & , r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot sec left ({ frac {(m-1) pi} {p}} right) cdot sin left ({ frac { pi} {p}} right) cdot left (r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot sec left ({ frac {m pi} {p}} right) -r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot sec left ({ frac {(m-2) pi} {p}} right) right) \ = & , r_ {u} cdot cos left ({ frac {q pi} {p}} right ) cdot sec left ({ frac {(m-1) pi} {p}} right) cdot sin left ({ frac { pi} {p}} right) cdot r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot left ( sec left ({ frac {m pi} {p}} right ) - sec left ({ frac {(m-2) pi} {p}} right) right) \ = & , r_ {u} ^ {2} cdot cos ^ {2 } left ({ frac {q pi} {p}} right) cdot sin left ({ frac { pi} {p}} right) cdot sec left ({ frac {(m-1) pi} {p}} right) cdot left ( sec left ({ frac {m pi} {p}} right) - sec left ({ frac {(m-2) pi} {p}} right) right) end {выравнивается}}}$

Для случая , пограничного, это дает область равнобедренных треугольников , которые имеют одну стороны вместе с регулярным внутренним углом. Он
м = 2

${ displaystyle r_ {u} ^ {2} cdot cos ^ {2} left ({ frac {q pi} {p}} right) cdot sin left ({ frac { pi } {p}} right) cdot sec left ({ frac { pi} {p}} right) cdot left ( sec left ({ frac {2 pi} {p} } right) -1 right)}$

Представление с координатами и векторами

Декартовы координаты

Углы правильной звезды соответствуют углам правильного угла. Их можно представить в декартовых координатах . Единичный круг можно принять за периметр с радиусом . Тогда центральная точка совпадает с началом координат, а угол имеет координаты
${ Displaystyle P_ {1}, P_ {2}, P_ {3}, ldots, P_ {p}}$ $r_ {u} = 1$ P_k

${ displaystyle P_ {k} = { begin {pmatrix} r_ {u} cdot cos left ({ frac {2k pi} {p}} right) \ r_ {u} cdot sin left ({ frac {2k pi} {p}} right) end {pmatrix}}, quad k = 1,2,3, ldots, p}$

Тогда стороны этой правильной звезды являются двумерными векторами направления :
${ Displaystyle { overline {P_ {k} P_ {k + q}}}}$

${ displaystyle { overrightarrow {P_ {k} P_ {k + q}}} = { begin {pmatrix} -a cdot sin left ({ frac {(2k + 2q + 1) pi} { 2p}} right) \ a cdot cos left ({ frac {(2k + 2q + 1) pi} {2p}} right) end {pmatrix}} = { begin {pmatrix} -2 , r_ {u} cdot sin left ({ frac {q pi} {p}} right) cdot sin left ({ frac {(2k + 2q + 1) pi } {2p}} right) \ 2 , r_ {u} cdot sin left ({ frac {q pi} {p}} right) cdot cos left ({ frac { (2k + 2q + 1) pi} {2p}} right) end {pmatrix}}, quad k = 1,2,3, ldots, p}$

Каждая из страниц вырезана из других страниц (см. Разделы страницы ). В точках пересечения имеют следующие декартовы координаты :

${ Displaystyle S_ {к, m} = { begin {pmatrix} r_ {m} cdot cos left ({ frac {2k pi} {p}} right) \ r_ {m} cdot sin left ({ frac {2k pi} {p}} right) end {pmatrix}} = { begin {pmatrix} r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot sec left ({ frac {m pi} {p}} right) cdot cos left ({ frac {2k pi} {p}} right) \ r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot sec left ({ frac {m pi} {p}} right) cdot sin left ({ frac {2k pi} {p}} right) end {pmatrix}}, quad k = 1,2,3, ldots, p, quad 0 <m leq q, quad qm , mathrm {даже}}$

${ Displaystyle S_ {к, m} = { begin {pmatrix} r_ {m} cdot cos left ({ frac {(2k-1) pi} {p}} right) \ r_ { m} cdot sin left ({ frac {(2k-1) pi} {p}} right) end {pmatrix}} = { begin {pmatrix} r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot sec left ({ frac {m pi} {p}} right) cdot cos left ({ frac { (2k-1) pi} {p}} right) \ r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot sec left ( { frac {m pi} {p}} right) cdot sin left ({ frac {(2k-1) pi} {p}} right) end {pmatrix}}, quad k = 1,2,3, ldots, p, quad 0 <m leq q, quad qm , mathrm {odd}}$

Радиус этого расстояние точек пересечения от центра звезды.
r_m

Полярные координаты

Комплексные решения уравнения деления окружности можно использовать для вычисления угловых точек правильной звезды . В полярных координатах угловых точек регулярной звезды, происхождение от координат в качестве центра и радиус окружности имеют простой вид
$г ^ {п} = 1$ $(r_ {k}, varphi _ {k})$ RU}

${ displaystyle (r_ {k}, varphi _ {k}) = left (r_ {u}, { frac {2k pi} {p}} right), quad k = 1,2,3 , ldots, p}$

Следующие полярные координаты получаются для точек пересечения сторон :

${ displaystyle (r_ {k}, varphi _ {k}) = left (r_ {m}, { frac {2k pi} {p}} right) = left (r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot sec left ({ frac {m pi} {p}} right), { frac {2k pi } {p}} right), quad k = 1,2,3, ldots, p, quad 0 <m leq q, quad qm , mathrm {even}}$

${ displaystyle (r_ {k}, varphi _ {k}) = left (r_ {m}, { frac {2 (k-1) pi} {p}} right) = left (r_ {u} cdot cos left ({ frac {q pi} {p}} right) cdot sec left ({ frac {m pi} {p}} right), { гидроразрыв {2 (k-1) pi} {p}} right), quad k = 1,2,3, ldots, p, quad 0 <m leq q, quad qm , mathrm {странный}}$

Радиус этого расстояние точек пересечения от центра звезды.
r_m

Симметрии

Группа симметрии правильной -звезды – это группа диэдра . Группа диэдра показывает порядок и состоит из
${ displaystyle D_ {p}}$

Если он прямой, то одна половина осей симметрии проходит через два противоположных угла, а другая половина – через два центра на противоположных сторонах. Если он нечетный, то все оси симметрии проходят через угол и центр противоположной стороны.

Каждая правильная звезда с четным числом углов также точечно-симметрична относительно своего центра.

Интерпретации звездного многоугольника

Три возможных интерпретации звездного многоугольника {5/2}.

Поскольку определение звездного многоугольника происходит из комбинаторной геометрии, а не из евклидовой геометрии, строго говоря, звездный многоугольник – это еще не геометрическая звезда в смысле евклидовой геометрии , а объект из теории графов, канонически встроенный в евклидову плоскость. Это становится ясным, если спросить себя, что именно представляют собой углы , края и поверхность объекта и что нужно понимать под геометрической звездой.

Эту «свободу интерпретации» звездного многоугольника как геометрической звезды можно увидеть на левом рисунке: желтая звезда – это геометрическая звезда, рядом с ней – плоский соответствующий звездный многоугольник, а затем еще две значимые интерпретации звездного многоугольника как математические. звезда. Красная звезда – типичная интерпретация в теории мозаик . Две средние звезды имеют по 5 углов и 5 краев, а желтая и зеленая звезды имеют по 10 углов и 10 или 15 краев. Желтая звезда определила края с помощью правила вращения четности , зеленая звезда – свои поверхности с правилом вращения четности, которое является результатом спецификации конструкции звездообразного многоугольника.

Геометрические параметры

Половина внутреннего угла (желтый), половина центрального угла ( пурпурный), окружной радиус (синий и голубой) и радиус (красный) звезды. Наконечник нарисован черным цветом. ${ tfrac { alpha} {2}}$ ${ displaystyle { tfrac { pi} {p}}}$ RU} $г_ {1}$

Если половина центр угла , то по окружности радиуса , а радиус звезды заданы, то из – за двух треугольных отношений и в соответствии с законом синуса , то применяется следующее . Согласно теореме Пифагора , длина ребра звезды, построенной таким образом, равна, а ее площадь равна .
${ displaystyle { tfrac { pi} {p}}}$ RU} $г_ {1}$ ${ displaystyle tan left ({ frac { alpha} {2}} right) = { frac {r_ {1} cdot sin left ({ frac { pi} {p}} right)} {r_ {u} -r_ {1} cdot cos left ({ frac { pi} {p}} right)}}}$ ${ displaystyle { frac {r_ {1}} { sin left ({ frac { alpha} {2}} right)}} = { frac {r_ {u}} { sin left ( pi - left ({ frac { alpha} {2}} + { frac { pi} {p}} right) right)}}}$ ${ displaystyle { frac {r_ {1}} {r_ {u}}} = { frac { sin left ({ frac { alpha} {2}} right)} { sin left ( { frac { alpha} {2}} + { frac { pi} {p}} right)}}}$ ${ displaystyle { sqrt { left (r_ {u} -r_ {1} cdot cos left ({ frac { pi} {p}} right) right) ^ {2} + left (r_ {1} cdot sin left ({ frac { pi} {p}} right) right) ^ {2}}} = { sqrt {r_ {u} ^ {2} -2r_ {u} r_ {1} cdot cos left ({ frac { pi} {p}} right) + r_ {1} ^ {2}}}}$ ${ displaystyle pr_ {u} r_ {1} cdot sin left ({ tfrac { pi} {p}} right)}$

Примеры

Классический случай, который приводит к правильным многоугольникам, не связанным со звездой, – это то, что эти прямые линии расположены точно посередине между кончиками звезды – см., Например, геометрию звезды Вергинаса (художественное украшение 16- конечной звезды как солнечный символ древности) или восьмиконечная звезда Штернбергера (геральдическая фигура из средневековья). Другими примерами являются трехконечная звезда Mercedes (в логотипе этой автомобильной марки как плоская звезда) с углом при вершине 360 ° / 18 – и, таким образом, «содержащаяся» в многоугольнике звезды, четырехконечная звезда НАТО (производная от четырехконечной розы компаса ) или шестиконечной звезды на гербе Таминя (муниципалитет в Швейцарии) с острым углом точно 45 °. Вот восемь-луч звезды старого компаса – может здесь очень хорошо внутри и реализовать вписанный круг и (как часть точности изображения) , чтобы определить.
${ Displaystyle { tfrac {r_ {1}} {r_ {u}}}}$ ${ tfrac {1} {4}}$

4-конечная звезда НАТО
6-конечная звезда муниципалитета Таминс в Граубюндене (Швейцария)

В некоторых национальных флагах в качестве символов флага используются правильные звезды, которые не являются звездообразным многоугольником ( пентаграммой ). Если вы измените формулу выше, вы получите общие

${ displaystyle tan left ({ frac { alpha} {2}} right) = { frac { sin left ({ frac { pi} {p}} right)} {{ frac {r_ {u}} {r_ {1}}} - cos left ({ frac { pi} {p}} right)}}}$

и в этом случае неравенство
${ displaystyle r_ {u} = 2r_ {1}}$

${ displaystyle { frac { pi} {p}}> sin left ({ frac { pi} {p}} right)> { frac { sin left ({ frac { pi } {p}} right)} {2- cos left ({ frac { pi} {p}} right)}} = tan left ({ frac { alpha} {2}} right)> { frac { alpha} {2}}}$

Для большого количества углов хорошим приближением является угол при вершине. Для прямой , углы и отношения длины такой звезды приближаются к многоугольнику звезды.
${ displaystyle alpha приблизительно { tfrac {2 pi} {p}}}$ ${ displaystyle left {p / { tfrac {p-2} {2}} right }}$

Асимптотика

Круг как форма границы

При увеличивающемся числе сторон и постоянстве форма правильного угла с постоянным окружным радиусом все больше приближается к окружности . Соотношение длины окружности и радиуса периметра стремится к предельному значению.

${ displaystyle lim _ {p to infty} 2 , p cdot cos left ({ frac {q pi} {p}} right) cdot left ( tan left ({ frac {q pi} {p}} right) - tan left ({ frac {(q-1) pi} {p}} right) right) = 2 pi}$

Соотношение суммы длин сторон и радиуса периметра приближается к

${ displaystyle lim _ {p to infty} 2 , p cdot sin left ({ frac {q pi} {p}} right) = 2q pi}$

Соотношение площади и квадрата окружного радиуса стремится к предельному значению для возрастающих и постоянных значений.

${ displaystyle lim _ {p to infty} p cdot sin left ({ frac { pi} {p}} right) cdot left ( cos left ({ frac { pi} {p}} right) - sin left ({ frac { pi} {p}} right) cdot tan left ({ frac {(q-1) pi} {p }} right) right) = pi}$

Формальное доказательство может быть выполнено с помощью теоремы де Л’Оспаля (см. Правильный многоугольник – сходимость ).

Это также относится к радиусу вписанной окружности , потому что при увеличении и постоянстве радиус вписанной окружности приближается к радиусу окружности : Из следует .
${ displaystyle r_ {i} = r_ {u} cdot cos left ({ frac {q pi} {p}} right)}$ ${ displaystyle lim _ {p to infty} r_ {i} = lim _ {p to infty} r_ {u} cdot cos left ({ frac {q pi} {p} } right) = r_ {u}}$

конвергенция

Для определения сходимости вместо нее используется действительная переменная и выводятся предельные значения функций для площади и периметра . Здесь важно, чтобы эти функции и их факторы (или частные) были дифференцируемыми . Предполагается , что это примерно пропорционально к , а именно с действительными числами и .
Икс ${ Displaystyle 0 <с leq { tfrac {1} {2}}}$

объем

В предельном значении результатов для сферы

${ displaystyle { begin {align} & , lim _ {x to infty} 2 , x , r_ {u} cdot cos left ({ frac {q pi} {x}) } right) cdot left ( tan left ({ frac {q pi} {x}} right) - tan left ({ frac {(q-1) pi} {x} } right) right) \ = & , lim _ {x to infty} 2 , x , r_ {u} cdot cos left ({ frac {q pi} {x }} right) cdot left ({ frac { left (1+ tan left ({ frac {q pi} {x}} right) cdot tan left ({ frac { pi} {x}} right) right) cdot tan left ({ frac {q pi} {x}} right)} {1+ tan left ({ frac {q pi} {x}} right) cdot tan left ({ frac { pi} {x}} right)}} - { frac { tan left ({ frac {q pi} {x}} right) - tan left ({ frac { pi} {x}} right)} {1+ tan left ({ frac {q pi} {x}} right ) cdot tan left ({ frac { pi} {x}} right)}} right) \ = & , lim _ {x to infty} 2 , x , r_ {u} cdot cos left ({ frac {q pi} {x}} right) cdot { frac { left (1+ tan ^ {2} left ({ frac {q pi} {x}} right) right) cdot tan left ({ frac { pi} {x}} right)} {1+ tan left ({ frac {q pi } {x}} right) cdot tan left ({ frac { pi} {x}} right)}} \ = & , lim _ {x to infty} 2 , х , г_ {и} cdot cos left ({ frac {q pi} {x}} right) cdot { frac { cos ^ {- 2} left ({ frac {q pi} {x}} right) cdot tan left ({ frac { pi} {x}} right)} {1+ tan left ({ frac {q pi} {x}} right) cdot tan left ({ frac { pi} {x}} right)}} \ = & , lim _ {x to infty} 2 , x , r_ {u} cdot tan left ({ frac { pi} {x}} right) cdot sec left ({ frac {q pi} {x}} right) cdot { frac {1} {1+ tan left ({ frac {q pi} {x}} right) cdot tan left ({ frac { pi} {x}} right)}} \ = & , lim _ {x to infty} 2 , x , r_ {u} cdot tan left ({ frac { pi} {x}} right) cdot lim _ {x to infty} sec left ({ frac {q pi} {x}} right) cdot lim _ {x to infty} { frac {1} {1+ tan left ({ frac {q pi} {x}} right) cdot tan left ({ frac { pi} {x}} right)}} \ = & , 2 , pi , r_ {u} cdot lim _ {x to infty} sec left (c pi + { frac {d pi} {x}} right) cdot lim _ {x to infty } { frac {1} {1+ tan left (c pi + { frac {d pi} {x}} right) cdot tan left ({ frac { pi} {x }} right)}} \ = & , 2 , pi , r_ {u} cdot sec left (c pi right) cdot { frac {1} {1+ tan влево (с пи вправо) cdot tan left (0 right)}} \ = & , 2 , pi , r_ {u} cdot sec left (c pi right) end {align}}}$

Теорема сложения использовалась для касательной и отношения между касательной и секущей (см. Тригонометрическая функция – отношения между функциями ).

Для и , например, звезд , , , , подходы степени значения . Это временная окружность периметра .
${ displaystyle c = { tfrac {1} {4}}}$ ${ displaystyle 2 , pi , r_ {u} cdot sec left ({ tfrac { pi} {4}} right) = 2 { sqrt {2}} , pi , RU}}$

Площадь

Для области , полученной для на пределе ${ displaystyle c <{ tfrac {1} {2}}}$

${ displaystyle { begin {align} & , lim _ {x to infty} x , r_ {u} ^ {2} cdot sin left ({ frac { pi} {x} } right) cdot left ( cos left ({ frac { pi} {x}} right) - sin left ({ frac { pi} {x}} right) cdot tan left ({ frac {(q-1) pi} {x}} right) right) \ = & , lim _ {x to infty} x , r_ {u} ^ {2} cdot sin left ({ frac { pi} {x}} right) cdot cos left ({ frac { pi} {x}} right) -x , r_ {u} ^ {2} cdot sin ^ {2} left ({ frac { pi} {x}} right) cdot tan left (c pi + { frac {(d -1) pi} {x}} right) \ = & , lim _ {x to infty} { frac {x , r_ {u} ^ {2}} {2}} cdot sin left ({ frac {2 pi} {x}} right) - lim _ {x to infty} 2 , x , r_ {u} cdot sin left ({ frac { pi} {x}} right) cdot lim _ {x to infty} { frac {r_ {u}} {2}} cdot sin left ({ frac { pi} {x}} right) cdot tan left (c pi + { frac {(d-1) pi} {x}} right) \ = & , pi , r_ {u} ^ {2} -2 , pi , r_ {u} cdot { frac {r_ {u}} {2}} cdot sin left (0 right) cdot tan left (c pi right) \ = & , pi , r_ {u} ^ {2} end {align}}}$

Затем площадь приближается к площади периметра .

Для , что есть предел получается ${ displaystyle c = { tfrac {1} {2}}}$ ${ displaystyle q = { tfrac {p} {2}} + d}$

${ displaystyle { begin {align} & , lim _ {x to infty} x , r_ {u} ^ {2} cdot sin left ({ frac { pi} {x} } right) cdot left ( cos left ({ frac { pi} {x}} right) - sin left ({ frac { pi} {x}} right) cdot tan left ({ frac {(q-1) pi} {x}} right) right) \ = & , lim _ {x to infty} x , r_ {u} ^ {2} cdot sin left ({ frac { pi} {x}} right) cdot cos left ({ frac { pi} {x}} right) -x , r_ {u} ^ {2} cdot sin ^ {2} left ({ frac { pi} {x}} right) cdot tan left ({ frac { pi} {2} } + { frac {(d-1) pi} {x}} right) \ = & , lim _ {x to infty} { frac {x , r_ {u} ^ { 2}} {2}} cdot sin left ({ frac {2 pi} {x}} right) - lim _ {x to infty} 2 , x , r_ {u} cdot sin left ({ frac { pi} {x}} right) cdot lim _ {x to infty} { frac {r_ {u}} {2}} cdot sin left ({ frac { pi} {x}} right) cdot tan left ({ frac { pi} {2}} + { frac {(d-1) pi} {x }} right) \ = & , pi , r_ {u} ^ {2} -2 , pi , r_ {u} cdot lim _ {x to infty} { frac {r_ {u}} {2}} cdot sin left ({ frac { pi} {x}} right) cdot cot left ({ frac {(1-d) pi} {x}} right) \ = & , pi , r_ {u} ^ {2} -2 , pi , r_ {u} cdot lim _ {x to infty} { frac {r_ {u} cdot sin left ({ frac { pi} {x}} right)} {2 cdot загар left ({ frac {(1-d) pi} {x}} right)}} end {align}}}$

Были использованы предельные значения и (см. Сходимость правильного многоугольника с заданным радиусом ). Согласно теореме де Л’Оспаля , пересечение границы на бесконечности выглядит следующим образом:
${ displaystyle lim _ {x to infty} { frac {x , r_ {u} ^ {2}} {2}} cdot sin left ({ frac {2 pi} {x }} right) = pi , r_ {u} ^ {2}}$ ${ displaystyle lim _ {x to infty} 2 , x , r_ {u} cdot sin left ({ frac { pi} {x}} right) = 2 , pi , RU}}$

${ displaystyle { begin {align} & , pi , r_ {u} ^ {2} -2 , pi , r_ {u} cdot lim _ {x to infty} { frac {r_ {u} cdot sin left ({ frac { pi} {x}} right)} {2 cdot tan left ({ frac {(1-d) pi} { x}} right)}} \ = & , pi , r_ {u} ^ {2} -2 , pi , r_ {u} cdot lim _ {x to infty} { frac {{ frac { mathrm {d} ^ {1}} { mathrm {d} x ^ {1}}} , r_ {u} cdot sin left ({ frac { pi } {x}} right)} {{ frac { mathrm {d} ^ {1}} { mathrm {d} x ^ {1}}} , 2 cdot tan left ({ frac {(1-d) pi} {x}} right)}} \ = & , pi , r_ {u} ^ {2} -2 , pi , r_ {u} cdot lim _ {x to infty} { frac {r_ {u} cdot cos left ({ frac { pi} {x}} right) cdot left (- { frac { pi} { mathrm {x} ^ {2}}} right)} {2 cdot cos ^ {- 2} left ({ frac {(1-d) pi} {x}} right ) cdot left (- { frac {(1-d) pi} { mathrm {x} ^ {2}}} right)}} \ = & , pi , r_ {u} ^ {2} -2 , pi , r_ {u} cdot lim _ {x to infty} { frac {r_ {u} cdot cos left ({ frac { pi} {x}} right) cdot cos ^ {2} left ({ frac {(1-d) pi} {x}} right)} {2 (1-d)}} \ = & , pi , r_ {u} ^ {2} -2 , pi , r_ {u} cdot { frac {r_ {u}} {2 (1-d)}} \ = & , pi , r_ {u} ^ {2} , left (1 - { frac {1} {1-d}} right) end {align}}}$

Для и так звезд , , , , подходы МЕРЕ значение . То есть область в периметре .
${ displaystyle c = { tfrac {1} {2}}}$ ${ displaystyle d = - { tfrac {1} {2}}}$ ${ displaystyle pi , r_ {u} ^ {2} , left (1 - { frac {1} {1- left (- { tfrac {1} {2}} right)}} right) = { frac { pi , r_ {u} ^ {2}} {3}}}$ ${ displaystyle { tfrac {1} {3}}}$

Для и так звезд , , , , подходы МЕРЕ значение . То есть половина площади по периметру .
${ displaystyle c = { tfrac {1} {2}}}$ ${ displaystyle pi , r_ {u} ^ {2} , left (1 - { frac {1} {1- left (-1 right)}} right) = { frac { пи , г_ {и} ^ {2}} {2}}}$

Теоретические свойства графа

График , может быть получен от обычной звезды , так что каждая угловая точка , и каждая точка пересечения соответствует в узел , каждая сторона раздела соответствует на край и каждая частичная зона соответствует на поверхность графика. У звезды есть угловые точки и точки пересечения, потому что каждая из сторон пересекается с другими сторонами, и каждая точка пересечения принадлежит 2 сторонам. Итак, у графа есть узлы. Каждая сторона звезды разделена на части (см. Разделы на странице ). Количество боковых секций и, следовательно, количество ребер графа равно . После Эйлера Polyedersatz число поверхностей дает результат: . Также учитывается внешняя область графика.

Это также можно увидеть геометрически , добавляя сечения всех сторон звезды, начиная с центра сторон, шаг за шагом. После первого шага создается внутренний правильный многоугольник . На каждом из следующих шагов создаются равнобедренные треугольники или квадраты дракона . Вместе с внешней поверхностью это поверхности.
q-1

В узлах на графике , которые соответствуют в вершины звезды имеют узел степени 2. Другие узлы , которые соответствуют на пересечения имеют степень узла 4. Поскольку степени всех узлов даже, граф имеет Эйлер круги .

Иллюстрации

Звезды и звездные многоугольники с малым индексом Шлефли

В следующем обзоре показаны правильные звезды и звездные многоугольники с индексом Шлефли для , т.е. максимум 9 углов. В отличие от звезды, многоугольник звезды можно нарисовать в одну линию.

{7/3} звездообразный многоугольник ,
гептаграмма
{9/3} -звезда , (3 треугольника)
эннеаграмма
{9/4} звездный многоугольник ,
эннеаграмма

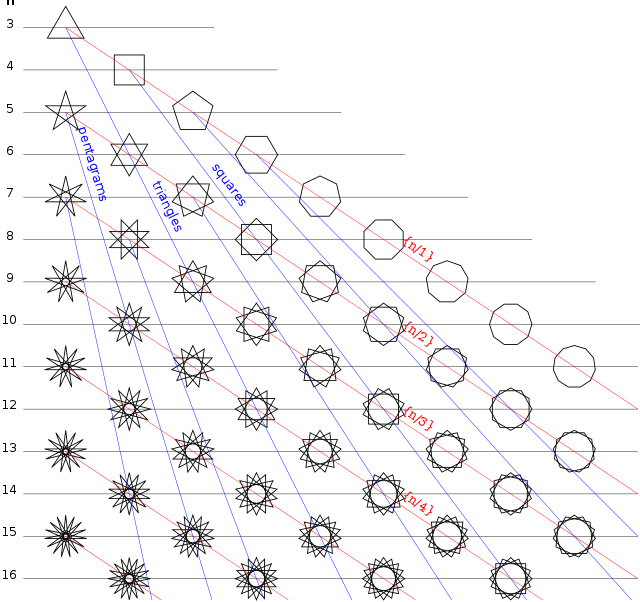
На следующей схеме показаны звезды или многоугольники с максимум 16 углами. Красные линии проходят через правильные многоугольники или звезды и т. Д. С такими же . Синие линии проходят через правильные многоугольники или звезды , которые состоят из одинаковых звездных многоугольников и, следовательно, имеют одинаковые внутренние углы .
${ displaystyle alpha = (kp-2kq) cdot { frac { pi} {p}} = pi - { frac {2q pi} {p}}}$

программирование

Следующий пример в C # языке программирования показывает осуществление метода , который рисует очередную звездочку. В параметрах метода являются р и д, радиус периметра, углом поворота и два булевыми переменными , которые определяют ли периметр и радиус вписанного или периметр и вписанный имеет радиус обращаются.

private void PaintRegularStar(int p, int q, float circumRadius, float angle, bool drawRadiuses, bool drawCircles)
{
	// Definiert Farben mit RGB-Werten.
	Color blue = Color.FromArgb(0, 0, 255), white = Color.FromArgb(255, 255, 255), black = Color.FromArgb(0, 0, 0);
	int gcd = GreatestCommonDivisor(p, q); // Berechnet den größten gemeinsamen Teiler von p und q, die Anzahl der Sternpolygone, in die der regelmäszige Stern zerfällt
	int starPolygonCount = p / gcd; // Anzahl der Ecken der Sternpolygone
	PointF[] regularPolygon = new PointF[starPolygonCount];
	for (int j = 0; j < gcd; j++) // for-Schleife mit Index j, die Sternpolygone durchläuft
	{
		for (int i = 0; i < starPolygonCount; i++) // for-Schleife mit Index i, die die Ecken erzeugt
		{
			// Berechnet die Koordinaten der Ecken des regelmäszigen Vielecks
			double centralAngle = 2 * (q * i + j) * Math.PI / p + angle; // Berechnet den Mittelpunktswinkel
			regularPolygon[i] = new PointF((float) (circumRadius * Math.Cos(centralAngle)), (float) (circumRadius * Math.Sin(centralAngle))); // Erzeugt eine Ecke mit den Koordinaten
		}
		graphics.FillPolygon(new SolidBrush(blue), regularPolygon); // Füllt das regelmäszige Sternpolygon mit einer Farbe
	}
	if (drawRadiuses) // Wenn CheckBox gesetzt, dann Radien zeichnen
	{
		for (int j = 0; j < gcd; j++) // for-Schleife mit Index j, die Sternpolygone durchläuft
		{
			for (int i = 0; i < starPolygonCount; i++) // for-Schleife mit Index i, bei jedem Durchlauf wird jeweils 1 Umkreisradius und 1 Inkreisradius gezeichnet
			{
				double centralAngle = 2 * (q * i + j) * Math.PI / p + angle; // Berechnet den Mittelpunktswinkel
				graphics.DrawLine(new Pen(white), 0, 0, (float) (circumRadius * Math.Cos(centralAngle)), (float) (circumRadius * Math.Sin(centralAngle))); // Zeichnet den Umkreisradius
				float inradius = (float) (circumRadius * Math.Cos(q * Math.PI / p)); // Berechnet den Inkreisradius
				centralAngle = (2 * (q * i + j) + 1) * Math.PI / p + angle; // Berechnet den Mittelpunktswinkel
				graphics.DrawLine(new Pen(white), 0, 0, (float) (inradius * Math.Cos(centralAngle)), (float) (inradius * Math.Sin(centralAngle))); // Zeichnet den Inkreisradius
			}
		}
	}
	if (drawCircles) // Wenn CheckBox gesetzt, dann Umkreis und Inkreis zeichnen
	{
		graphics.DrawEllipse(new Pen(black), -circumRadius, -circumRadius, 2 * circumRadius, 2 * circumRadius); // Zeichnet den Umkreis
		float inradius = (float) (circumRadius * Math.Cos(q * Math.PI / p)); // Berechnet den Inkreisradius
		graphics.DrawEllipse(new Pen(black), -inradius, -inradius, 2 * inradius, 2 * inradius); // Zeichnet den Inkreis
	}
}

веб ссылки

Commons : Star – коллекция изображений, видео и аудио файлов.

Эрик В. Вайсштейн: MathWorld – Звездный многоугольник. (Английский)
Онлайн-руководство по созданию звезды с помощью PHP. Геометрические основы звезды, математические формулы и реализация в виде исходного кода.
Клипарт галерея звездных многоугольников. (Английский)
Генератор звездообразных многоугольников
Desmos, Inc.: https://www.desmos.com/calculator/jf7n00td1q?lang=en (веб-приложение для рисования)
Desmos, Inc.: https://www.desmos.com/calculator/hpglbai0jg?lang=en (веб-приложение для рисования)
GeoGebra: Regular star polygons (веб-приложение для рисования)
GeoGebra: исследование звездного полигона (веб-приложение для рисования)

Индивидуальные доказательства

^ Гарольд Скотт Макдональд Кокстер : Введение в геометрию. 2-е издание. Wiley, New York 1969, §2.8 (Звездные многоугольники), стр. 36–38. (Немецкий: Immortal Geometry. 2-е издание. Birkhäuser, Базель, 1981.)
↑ C # Helper: нарисуйте звезду с заданным количеством точек на C #

Источник

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

Все категории
экономические
43,655
гуманитарные
33,653
юридические
17,917
школьный раздел
611,944
разное
16,904

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Источник

Как построить пятиконечную звезду

Форма пятиконечной звезды повсеместно используется человеком с древних времен. Мы считаем ее форму прекрасной, так как бессознательно различаем в ней соотношения золотого сечения, т.е. красота пятиконечной звезды обоснована математически. Первым описал построение пятиконечной звезды Евклид в своих “Началах”. Давайте же приобщимся к его опыту.

Вам понадобится

линейка;
карандаш;
циркуль;
транспортир.

Инструкция

Построение пятиконечной звезды сводится к построению правильного пятиугольника с последующим соединением его вершин друг с другом последовательно через одну. Для того чтобы построить правильный пятиугольник необходимо разбить окружность на пять равных частей.
Постройте произвольную окружность при помощи циркуля. Обозначьте ее центр точкой O.

Отметьте на окружности точку A и при помощи линейки начертите отрезок ОА. Теперь необходимо разделить отрезок OA пополам, для этого из точки А проведите дугу радиусом ОА до пересечения ее с окружностью в двух точках M и N. Постройте отрезок MN. Точка Е, в которой MN пересекает OA, будет делить отрезок OA пополам.

Восстановите перпендикуляр OD к радиусу ОА и соедините точку D и E. Сделайте засечку B на диаметре OA из точки E радиусом ED.

Теперь при помощи отрезка DB разметьте окружность на пять равных частей. Обозначьте вершины правильного пятиугольника последовательно цифрами от 1 до 5. Соедините точки в следующей последовательности: 1 с 3, 2 с 4, 3 с 5, 4 с 1, 5 с 2. Вот и готова правильная пятиконечная звезда, вписанная в правильный пятиугольник. Именно таким способом строил пятиконечную звезду Евклид около 2300 лет тому назад.

Во времена Евклида не было транспортиров, поэтому приходилось прибегать к этому, достаточно сложному способу построения. Если у вас есть транспортир, вы можете справиться с построением пятиконечной звезды быстрее. Начертите окружность и проведите оси симметрии через ее центр. Поставьте транспортир параллельно одной из осей симметрии и отмерьте 72 градуса от точки A пересечения другой оси симметрии с окружностью. Обозначьте получившуюся точку буквой B. Поставьте острие циркуля в точку А, а грифель в точку B. Полученной длинной разделите окружность на пять равных частей. Соедините получившие точки так же, как в первом способе.

Видео по теме

Источники:

Б. И. Аргунов, М. Б. Балк Геометрические построения на плоскости. Пособие для студентов педагогических институтов. — Издание второе. — М.: Учпедгиз, 1957.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Сколько всего есть оси симметрии?

строительство

Параметры

угол

Длина

Боковые секции

Периметр и площадь

Частичные области

Представление с координатами и векторами

Декартовы координаты

Полярные координаты

Симметрии

Интерпретации звездного многоугольника

Геометрические параметры

Примеры

Асимптотика

Круг как форма границы

конвергенция

объем

Площадь

Теоретические свойства графа

Иллюстрации

Звезды и звездные многоугольники с малым индексом Шлефли

программирование

веб ссылки

Индивидуальные доказательства

Как построить пятиконечную звезду

Вам также может понравиться

Стихотворение как найти любимого

Как найти мгновенное ускорение точки

Как найти серебряную руду в майнкрафте

Добавить комментарий Отменить ответ