В физике для описания инерционных качеств поступательного или линейного движения пользуются понятием массы тела. Если же движение рассматривается вокруг некоторой оси вращения, то используют несколько иную физическую характеристику – момент инерции. В данной статье рассмотрим, что это за величина и как можно рассчитать момент инерции тонкого стержня.
Вращение и момент инерции
Инерции момент проще всего ввести для материальной точки. Когда она, обладая массой M, вращается вокруг оси, описывая окружность радиусом R, то момент инерции для нее определяется по формуле:
I = M*R2.
Любое реальное тело, какой бы сложной геометрической формой оно не обладало, можно представить как совокупность материальных точек. Это означает, что для всего тела или системы твердых тел величину I можно вычислить, если проинтегрировать по элементарным массам dm выражение выше. Общая формула для определения момента инерции имеет вид:
I = ∫m(r2*dm).
Через объем и плотность это равенство записывается в таком виде:
I = ∫V(ρ*r2*dV).
Его часто применяют для вычисления значений I конкретных геометрических объектов.
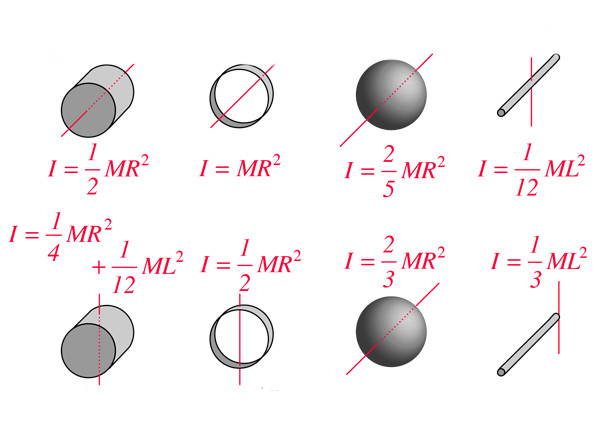
Физический смысл инерции момента I заключается в том, что он определяет, насколько “сложно” данной силе, создающей некоторый крутящий момент, раскрутить или остановить вращающуюся систему. Иными словами, I характеризует инерционные свойства изучаемой системы.
Самым известным примером использования момента инерции является маховик двигателя внутреннего сгорания в автомобилях. Благодаря большому значению величины I, маховик обеспечивает плавность движения автомобиля, сглаживая любые резкие воздействия на коленчатый вал. Пример иного характера, где также важно знать момент инерции, – это закон сохранения момента импульса. Применяется он для поворота вокруг оси искусственных спутников в космическом пространстве Земли.
Тонкий стержень и оси вращения
Далее будет рассмотрен момент инерции стержня относительно осей (разных). Вычисления будут проводиться для тонкого стержня, который обладает однородным распределением массы, то есть его плотность во всех точках является постоянной величиной. Под тонким понимают такой стержень, у которого ширина (толщина) намного меньше, чем его длина L. Для обозначения его массы будем использовать букву M.
Из приведенных выше формул следует, что величина I зависит от относительного положения тела и оси вращения. Для стержня можно выделить три основных оси. Одна из них проходит через длину всего стержня. Поскольку его толщина стремится к нулю, то момент инерции для такого положения тела также будет стремиться к этому значению.
Две другие оси перпендикулярны длине рассматриваемого тела. Одна из них проходит через центр масс, назовем ее O1, вторая – через конец стержня, обозначим ее O2. Относительно них и вычислим величину I.
Момент инерции относительно O1
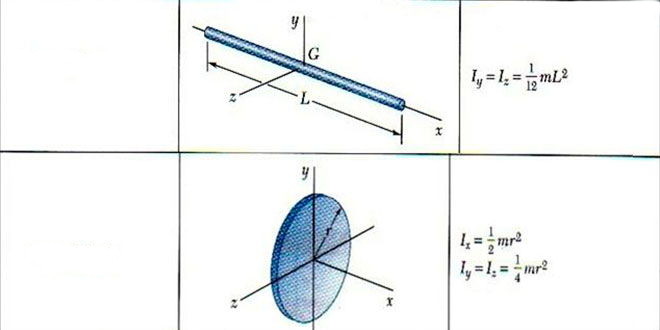
В первую очередь выпишем общую формулу. Имеем:
I = ∫V(ρ*r2*dV).
Обозначим площадь сечения стержня буквой S. Очевидно, что она стремится к нулю, поскольку стержень тонкий. Но это обозначение удобно ввести для выполнения дальнейших расчетов.
Теперь мысленно разобьем стержень на бесконечное количество мелких кусочков, каждый из которых будет иметь сечение S и толщину dl. Заменяя r на l в формуле выше, получаем:
I = ∫L(ρ*S*l2*dl).
Остается только подставить правильные пределы интегрирования и записать конечную формулу. Поскольку ось O1 проходит через середину стержня, то пределы интегрирования будут следующими:
I = ∫-L/2L/2(ρ*S*l2*dl).
Результатом вычисления этого интеграла является следующая формула:
I = M*L2/12.
Таким образом, момент инерции тонкого стержня определяется его массой и длиной.
Инерции момент относительно O2
Теперь рассмотрим ситуацию, когда ось вращения будет проходить через любой из концов стержня и будет ему перпендикулярна. Соответствующую формулу можно получить из записанного выше интеграла, если правильно подставить пределы интегрирования. Однако мы пойдем несколько иным путем и определим инерции момент с помощью теоремы Штейнера.
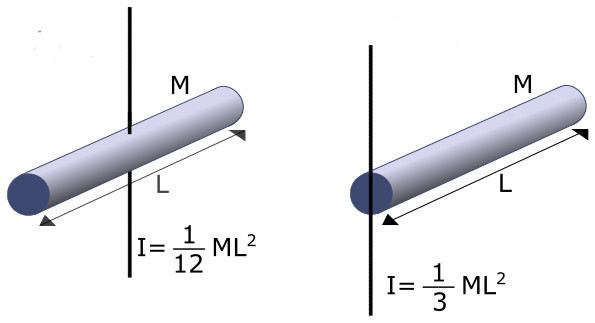
Она говорит о том, что если две оси являются параллельными друг другу и одна из них (ось O) проходит через центр масс тела, то момент инерции относительно второй оси может быть вычислен с помощью такого равенства:
I = I0 + M*h2.
Здесь I0 – момент инерции стержня относительно оси O, h – дистанция между осями.
Эту формулу можно с успехом применить для нашего случая. Поскольку I0 мы рассчитали в предыдущем пункте статьи относительно оси O1, и расстояние между O1 и O2 составляет L/2, то с использованием теоремы Штейнера получаем следующий результат:
I = I0 + M*h2 = M*L2/12 + M*L2/4 = M*L2/3.
Таким образом, для стержня величина I относительно оси O2 в 4 раза больше, чем относительно оси O1. Это означает, что для придания одинакового углового ускорения стержню в случае вращения вокруг оси O2 следует приложить в 4 раза больший крутящий момент, чем в случае оси O1.
Пример задачи
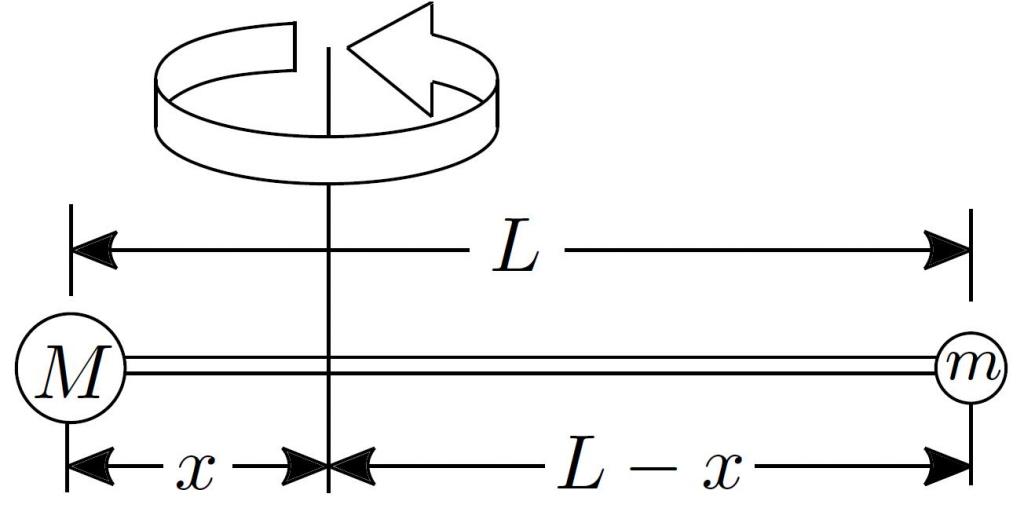
Дан тонкий стержень длиною 0,5 м и массой 5 кг. На расстоянии 2/5 от его конца расположена ось вращения, перпендикулярная стержню. Чему равен момент инерции системы?
Для решения задачи воспользуемся теоремой Штейнера. Расстояние между осями O1 и заданной в задаче равно:
h = 0,25 – 0,2 = 0,05 м.
Тогда получаем момент инерции стержня (однородного):
I = I0 + M*h2 = 5*0,52/12 + 5*0,052 = 0,117 кг*м2.
В СИ момент инерции стержня измеряется в указанных единицах.
11
Механика твердого тела
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Лекция 6
-
Момент инерции
материальной точки
Момент инерции м.
т. и тел является скалярной величиной
и широко применяется не только в физике,
но и ряде других дисциплин: теоретическая,
прикладная механика и т. д.
Моментом инерции
м. т. относительно полюса называют
скалярную величину, равную произведению
массы этой точки на квадрат расстояния
до полюса.
Момент инерции м.
т. можно найти по формуле
I0
= m
R2,
(6.1)
где m – масса м.
т.; R – расстояние до полюса 0.
Единицей
измерения момента инерции в СИ является
килограмм, умноженный на метр в квадрате
(кгм2).
-
Момент инерции
системы материальных точек
Тело можно
представить состоящим из большого числа
м.т., поэтому момент инерции системы м.
т.
 ,
,
(6.2)
где
mi
– масса i-й м. т.; Ri
– ее расстояние до полюса 0.
Моментом
инерции системы м. т. или тела относительно
полюса (точки) называют алгебраическую
сумму произведений масс м. т., из которых
состоит тело, на квадрат расстояния их
до полюса 0.
При
непрерывном распределении массы по
объему тела момент инерции относительно
полюса находится по формуле
 (6.3)
(6.3)
В случае момента
инерции относительно полюса массу dm
умножают на квадрат расстояния до
неподвижной точки (полюса), а в случае
момента инерции относительно оси – до
неподвижной оси.
В
декартовой системе координат сумма
моментов инерции тела относительно
трех взаимно перпендикулярных осей,
пересекающих в одной точке 0, равна
удвоенному моменту инерции этого тела
относительно этого же начала:
Ix
+ Iy+
Iz
= 2I0
.
(6.4)
6.3. Теорема Штейнера

Рис. 6.1
Для установления
связи (рис. 5.1) между моментом инерции
тел относительно двух параллельных
осей применяется теорема Штейнера
(Штейнера –
Гюйгенса):
I
= Ic
+ md2.
(6.5)
Момент
инерции тела относительно произвольной
оси равен моменту инерции относительно
оси, параллельной данной, проходящей
через центр масс, плюс произведение
массы тела на квадрат расстояния между
осями.
6.4. Момент инерции однородного стержня
Моменты
инерции различных тел можно найти по
формуле I = mR2,
где m
– коэффициент пропорциональности,
который зависит от формы тела и его
расположения относительно оси вращения.
Найдем
момент инерции однородного стержня
относительно оси, проходящей через один
из его концов, перпендикулярно продольной
геометрической оси симметрии (рис. 6.2).
Пусть ось вращения ВВ проходит через
правый конец стержня (т. Г), тогда
I
= mmL2,
где
L –
длина стержня.
Согласно
теореме Штейнера, имеем
![]() .
.

Рис. 6.2
Величину момента
инерции Ic
относительно
оси, проходящей через центр масс (точка
С), представим как сумму моментов инерции
двух стержней с длинами ДС = СГ = L/2
и массой
каждого, равной m/2 стержня, т. е.
![]() .
.
Подставим
значения момента инерции I и Ic
в формулу теоремы Штейнера – Гюйгенса
и найдем :
![]() .
.
После
преобразования получим, что m
= 1 / 3.
Следовательно,
момент инерции стержня относительно
оси, проходящей через центр масс,
![]()
(6.6)
относительно
оси ВВ,
![]()
(6.7)
Содержание:
Вращение твердого тела вокруг неподвижной точки:
Вращением твердого тела вокруг неподвижной точки называют такое движение, при котором одна точка тела остается все время неподвижной. Это вращение часто называют сферическим движением твердого тела в связи с тем, что траектории всех точек тела при таком движении располагаются на поверхностях сфер, описанных из неподвижной точки. Тело, совершающее вращение вокруг неподвижной точки, имеет три степени свободы, так как закрепление одной точки тела уменьшает число степеней свободы на три единицы, а свободное тело имеет шесть степеней свободы. Одной из главных задач при изучении вращения тела вокруг неподвижной точки является установление величин, характеризующих это движение, т. е. углов Эйлера, угловой скорости, углового ускорения, и вывод формул для вычисления скоростей и ускорений точек тела.
Уравнения вращения твердого тела вокруг неподвижной точки (Углы Эйлера)
Три степени свободы, которые имеет тело при вращении вокруг неподвижной точки, требуют для задания положения тела относительно какой-либо системы координат трех независимых величин. Эти три величины, или параметра, можно задать различными способами. В теоретической механике наибольшее применение получили так называемые углы Эйлера, рассмотренные ниже.
Через неподвижную точку 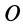
Первый из этих углов—угол прецессии 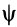 — определяет положение линии узлов
— определяет положение линии узлов  , которая является линией пересечения координатных плоскостей
, которая является линией пересечения координатных плоскостей 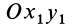 и
и 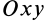 относительно неподвижной координатной оси
относительно неподвижной координатной оси 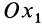 . Для изменения этого угла тело должно вращаться вокруг координатной оси
. Для изменения этого угла тело должно вращаться вокруг координатной оси 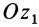 , которую называют осью прецессии. Положение линии узлов при движении тела изменяется как относительно неподвижной системы координат
, которую называют осью прецессии. Положение линии узлов при движении тела изменяется как относительно неподвижной системы координат 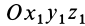 , так и относительно движущегося тела, т. е. подвижной системы координат
, так и относительно движущегося тела, т. е. подвижной системы координат 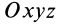 . Угол
. Угол 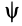 от положительной части оси
от положительной части оси 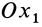 до положительного направления линии узлов
до положительного направления линии узлов  считается положительным, когда он отсчитывается против часовой стрелки, если смотреть с положительного направления оси
считается положительным, когда он отсчитывается против часовой стрелки, если смотреть с положительного направления оси 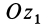 . За положительное направление на линии узлов
. За положительное направление на линии узлов  выбираем то ее направление, с которого поворот оси
выбираем то ее направление, с которого поворот оси 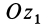 к оси
к оси 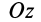 на наименьший угол виден происходящим против часовой стрелки.
на наименьший угол виден происходящим против часовой стрелки.
Вторым углом Эйлера является угол между координатными плоскостями 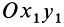 и
и 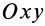 . Его измеряют углом
. Его измеряют углом 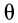 между перпендикулярами к этим координатным плоскостям, которыми являются оси
между перпендикулярами к этим координатным плоскостям, которыми являются оси 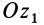 и
и 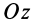 . Угол
. Угол 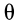 отсчитывают от оси
отсчитывают от оси 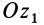 до оси
до оси 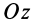 в положительном направлении, если направление поворота оси
в положительном направлении, если направление поворота оси 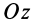 с положительного направления линии узлов
с положительного направления линии узлов  происходит против часовой стрелки.
происходит против часовой стрелки.
Угол 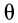 называют углом нутации, а ось
называют углом нутации, а ось  , вокруг которой вращается тело при изменении угла
, вокруг которой вращается тело при изменении угла 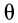 , соответственно называют осью нутации или линией узлов.
, соответственно называют осью нутации или линией узлов.
Для полного определения положения рассматриваемого тела относительно системы координат 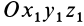 нужно задать угол между подвижной осью координат
нужно задать угол между подвижной осью координат 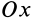 и положительным направлением линии узлов
и положительным направлением линии узлов  —угол собственного вращения
—угол собственного вращения 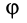 . Угол
. Угол 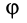 от линии узлов
от линии узлов  до оси
до оси 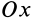 считается положительным, если вокруг оси
считается положительным, если вокруг оси 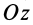 поворот оси
поворот оси 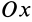 от линии
от линии  виден происходящим против часовой стрелки.
виден происходящим против часовой стрелки.
При изменении угла 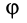 тело вращается вокруг так называемой оси собственного вращения
тело вращается вокруг так называемой оси собственного вращения 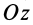 , перпендикулярной плоскости, в которой лежат прямые
, перпендикулярной плоскости, в которой лежат прямые  и
и 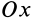 , образующие этот угол. Таким образом, угол
, образующие этот угол. Таким образом, угол 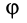 определяет положение подвижной координатной оси
определяет положение подвижной координатной оси 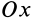 относительно линии узлов
относительно линии узлов  .
.
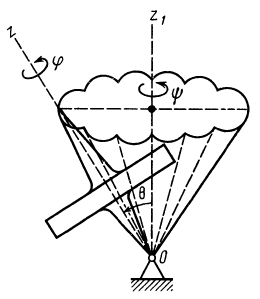
Рис. 74
Углы Эйлера широко применяются в теории гироскопов. Движение гироскопа, т. е. симметричного тела, имеющего неподвижную точку на оси симметрии и быстро вращающегося вокруг этой оси, в общем случае можно представить состоящим из трех движений (рис. 74): вращения с большой угловой скоростью вокруг оси симметрии, или оси собственного вращения, при котором изменяется угол собственного вращения (р; вращения гироскопа вместе со своей осью симметрии вокруг неподвижной оси 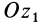 , при котором изменяется угол прецессии
, при котором изменяется угол прецессии 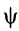 . Третье движение совершает ось симметрии, которая, участвуя в прецессионном движении, описывает коническую поверхность с вершиной в неподвижной точке, а вследствие изменения угла нутации
. Третье движение совершает ось симметрии, которая, участвуя в прецессионном движении, описывает коническую поверхность с вершиной в неподвижной точке, а вследствие изменения угла нутации 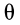 описывает в общем случае волнистую поверхность.
описывает в общем случае волнистую поверхность.
Если угол 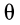 не изменяется, то коническая поверхность является круговым конусом. Если коническую поверхность пересечь плоскостью, перпендикулярной оси прецессии, то получится кривая линия, на которой возможны узловые точки, или точки возврата. Известно, например, что земной шар кроме собственного вращения вокруг своей оси еще прецессирует и совершает нутационное движение.
не изменяется, то коническая поверхность является круговым конусом. Если коническую поверхность пересечь плоскостью, перпендикулярной оси прецессии, то получится кривая линия, на которой возможны узловые точки, или точки возврата. Известно, например, что земной шар кроме собственного вращения вокруг своей оси еще прецессирует и совершает нутационное движение.
В технике особенно важное значение имеет так называемая регулярная прецессия, когда угловые скорости вращения вокруг оси собственного вращения и вокруг неподвижной оси прецессии постоянны и угол между этими осями (угол нутации) остается тоже постоянным.
При вращении тела вокруг неподвижной точки в общем случае изменяются все три угла Эйлера: 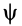 ,
, 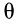 и
и 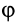 . Углы Эйлера являются независимыми параметрами, или обобщенными координатами, характеризующими положение тела с одной неподвижной точкой относительно неподвижной системы координат. Задание трех углов Эйлера для тела, вращающегося вокруг неподвижной точки, как функций времени является необходимым и достаточным для полного описания такого движения тела.
. Углы Эйлера являются независимыми параметрами, или обобщенными координатами, характеризующими положение тела с одной неподвижной точкой относительно неподвижной системы координат. Задание трех углов Эйлера для тела, вращающегося вокруг неподвижной точки, как функций времени является необходимым и достаточным для полного описания такого движения тела.
Итак, для определения положения тела с одной неподвижной точкой в любой момент времени надо задать углы Эйлера как однозначные функции времени, т. е.
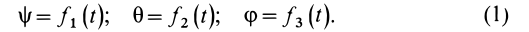
Уравнения (1) являются уравнениями вращения твердого тела вокруг неподвижной точки. Если эти уравнения заданы, то в любой момент времени известно положение твердого тела относительно системы координат 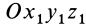 .
.
Отметим, что углы Эйлера не являются единственной комбинацией трех независимых углов для тела, имеющего одну неподвижную точку. Существуют и другие комбинации углов, определяющих положение одной системы координат относительно другой.
Теорема о конечном перемещении твердого тела, имеющего одну неподвижную точку
Тело, имеющее одну неподвижную точку, из одного положения в любое другое можно перевести одним поворотом вокруг оси, проходящей через неподвижную точку. Эту ось называют осью конечного вращения.
Положение тела с неподвижной точкой относительно некоторой системы отсчета можно полностью определить, если задать на какой-либо неподвижной сфере, описанной из неподвижной точки тела, положение сферической фигуры, скрепленной с этим телом. За сферическую фигуру можно принять любую часть поверхности сферы таким же радиусом, что и радиус неподвижной сферы, который обычно принимают равным единице. За сферическую фигуру можно принять также всю сферу единичного радиуса.
При движении тела вокруг неподвижной точки скрепленная с движущимся телом сфера единичного радиуса движется по неподвижной сфере того же радиуса. Положение сферы полностью определяется заданием на этой сфере дуги большого круга, крепленной со сферой.
Пусть положение 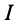 тела характеризуется дугой большого круга
тела характеризуется дугой большого круга 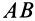 , описанной из неподвижной точки тела, а в положении
, описанной из неподвижной точки тела, а в положении 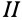 —той же дугой, но в другом положении на сфере
—той же дугой, но в другом положении на сфере 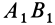 (рис. 75). Аналогично тому, как находится центр конечного вращения для плоской фигуры при плоском перемещении, найдем точку
(рис. 75). Аналогично тому, как находится центр конечного вращения для плоской фигуры при плоском перемещении, найдем точку 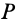 на сфере в случае тела, имеющего одну неподвижную точку. Для этого соединяем точки
на сфере в случае тела, имеющего одну неподвижную точку. Для этого соединяем точки 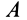 с
с 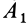 и
и 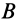 с
с 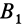 дугами большого круга, проведенными из неподвижной точки тела и целиком лежащими на неподвижной сфере. В серединах дуг
дугами большого круга, проведенными из неподвижной точки тела и целиком лежащими на неподвижной сфере. В серединах дуг 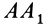
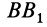 из точек
из точек 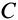 и
и 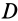 проводим сферические перпендикуляры, т. е. дуги большого круга
проводим сферические перпендикуляры, т. е. дуги большого круга 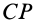 и
и 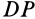 касательные к которым перпендикулярны в точках
касательные к которым перпендикулярны в точках 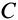 и
и 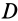 соответственно касательным дуг
соответственно касательным дуг 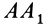 и
и 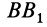 .
.
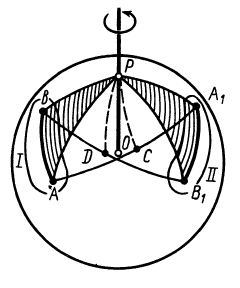
Рис. 75
Эти перпендикуляры, лежащие на сфере, пересекутся в точке 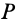 . Из равенства прямоугольных сферических треугольников
. Из равенства прямоугольных сферических треугольников 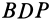 и
и 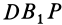 , имеющих общий катет
, имеющих общий катет 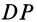 и равные катеты
и равные катеты 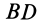 и
и 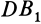 , следует, что гипотенузы этих сферических треугольников тоже равны, т. е. точки 5 и й, равноудалены от точки Р.
, следует, что гипотенузы этих сферических треугольников тоже равны, т. е. точки 5 и й, равноудалены от точки Р.
Аналогично доказывается, что точки 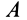 и
и 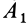 тоже одинаково удалены от точки
тоже одинаково удалены от точки 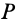 . Если повернуть заштрихованный сферический треугольник
. Если повернуть заштрихованный сферический треугольник 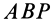 вокруг оси, проходящей через точку
вокруг оси, проходящей через точку 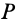 и неподвижную точку
и неподвижную точку 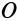 , то этот треугольник, перемещаясь по сфере, совпадет всеми своими точками с равным ему по трем сторонам сферическим треугольником
, то этот треугольник, перемещаясь по сфере, совпадет всеми своими точками с равным ему по трем сторонам сферическим треугольником 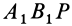 , так как сферический угол на сфере, на который надо повернуть вокруг
, так как сферический угол на сфере, на который надо повернуть вокруг 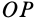 дугу
дугу 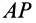 до совпадения с дугой
до совпадения с дугой 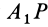 , равен сферическому углу на той же сфере, на который надо повернуть дугу
, равен сферическому углу на той же сфере, на который надо повернуть дугу 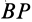 до совпадения с дугой
до совпадения с дугой 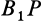 .
.
Итак, путем поворота вокруг оси, перпендикулярной поверхности сферы и проходящей через точку 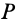 и, следовательно, проходящей также и через центр сферы, где расположена неподвижная точка, тело можно переместить из одного положения в любое другое. Для каждых двух положений тела получаются соответствующая точка
и, следовательно, проходящей также и через центр сферы, где расположена неподвижная точка, тело можно переместить из одного положения в любое другое. Для каждых двух положений тела получаются соответствующая точка 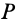 и, следовательно, соответствующая ось конечного вращения, проходящая через эту точку и неподвижную точку тела.
и, следовательно, соответствующая ось конечного вращения, проходящая через эту точку и неподвижную точку тела.
Мгновенная ось вращения (Аксоиды)
Ось, вокруг которой следует вращать тело, имеющее одну неподвижную точку, для перевода его из одного положения в другое, бесконечно близкое первому, называют мгновенной осью вращения (или мгновенной осью) для данного момента времени.
Любое движение тела вокруг неподвижной точки можно заменить последовательностью вращений вокруг совокупности мгновенных осей. Геометрическое место мгновенных осей относительно неподвижных осей координат, по отношению к которым рассматривается движение тела, называется неподвижным аксоидом. Неподвижный аксоид является конической поверхностью с вершиной в неподвижной точке тела, так как все мгновенные оси проходят через неподвижную точку.
Геометрическое место мгновенных осей в движущемся теле представляет подвижный аксоид, являющийся также конической поверхностью. Для каждого движения твердого тела вокруг неподвижной точки имеется пара аксоидов. При этом, когда тело совершает вращение вокруг неподвижной точки, подвижный аксоид катится по неподвижному без скольжения, так как общая образующая этих аксоидов в каждый момент времени служит мгновенной осью, вокруг которой вращается тело, и, следовательно, все точки оси в рассматриваемый момент времени неподвижны. Если подвижный аксоид катится без скольжения по неподвижному аксоиду, то осуществляется движение тела вокруг неподвижной точки.
Очевидно, что при плоском движении твердого тела конические аксоиды являются цилиндрическими поверхностями, которые в пересечении с плоскостью движения плоской фигуры образуют центроиды для этой фигуры.
Практически понятие аксоидов используется для классификации видов прецессионных движений гироскопов.
Угловая скорость и угловое ускорение при вращении тела вокруг неподвижной точки
Так как движение тела, имеющего одну неподвижную точку, в каждый момент времени можно считать вращением вокруг мгновенной оси, то в качестве величин, характеризующих это движение, можно ввести мгновенную угловую скорость и мгновенное угловое ускорение вращения твердого тела вокруг неподвижной точки. Очевидно, вводимая угловая скорость является векторной величиной, направленной в каждый момент времени по соответствующей мгновенной оси, и при использовании правой системы координат вектор угловой скорости 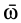 направлен по мгновенной оси так, что с направления этого вектора видно вращение тела вокруг мгновенной оси против часовой стрелки. Модуль вектора угловой скорости можно выразить через элементарный угол поворота
направлен по мгновенной оси так, что с направления этого вектора видно вращение тела вокруг мгновенной оси против часовой стрелки. Модуль вектора угловой скорости можно выразить через элементарный угол поворота 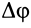 вокруг мгновенной оси за время
вокруг мгновенной оси за время 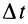 :
:
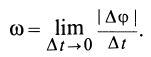
Элементарный угол поворота 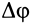 , аналогично случаю вращения тела вокруг неподвижной оси, следует рассматривать как угол между двумя положениями в моменты
, аналогично случаю вращения тела вокруг неподвижной оси, следует рассматривать как угол между двумя положениями в моменты 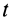 и
и 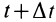 подвижной плоскости, скрепленной с телом и проходящей через мгновенную ось в момент времени
подвижной плоскости, скрепленной с телом и проходящей через мгновенную ось в момент времени 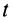 .
.
Введенный таким образом вектор угловой скорости 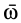 характеризует угловую скорость вращения вокруг мгновенной оси, направление мгновенной оси и направление вращения тела вокруг этой оси. Вектор угловой скорости
характеризует угловую скорость вращения вокруг мгновенной оси, направление мгновенной оси и направление вращения тела вокруг этой оси. Вектор угловой скорости 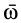 можно прикладывать в любой точке мгновенной оси (рис. 76).
можно прикладывать в любой точке мгновенной оси (рис. 76).
За вектор углового ускорения 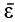 при вращении тела вокруг неподвижной точки принимают вектор, который характеризует изменение угловой скорости со в данный момент как по числовой величине, так и по направлению. Известно, что такой характеристикой является производная по времени от вектора угловой скорости
при вращении тела вокруг неподвижной точки принимают вектор, который характеризует изменение угловой скорости со в данный момент как по числовой величине, так и по направлению. Известно, что такой характеристикой является производная по времени от вектора угловой скорости 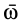 . Таким образом, угловое ускорение
. Таким образом, угловое ускорение
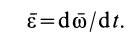
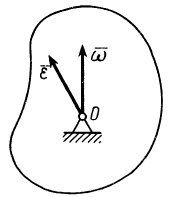
Рис. 76
Так как угловая скорость может изменяться по модулю и направлению, то в общем случае угловое ускорение не направлено по мгновенной оси, а имеет направление как производная по времени от вектора 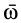 , параллельное касательной к годографу этого вектора. Условимся угловое ускорение
, параллельное касательной к годографу этого вектора. Условимся угловое ускорение 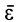 изображать в любой точке прямой, параллельной этой касательной годографа
изображать в любой точке прямой, параллельной этой касательной годографа 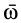 , но проходящей через неподвижную точку тела.
, но проходящей через неподвижную точку тела.
Скорости точек тела при вращательном движении вокруг неподвижной точки
При рассмотрении вращательного движения тела вокруг неподвижной оси получена векторная формула Эйлера, по которой скорости точек тела полностью характеризуются общей для всех точек тела угловой скоростью вращения и расположением точек тела относительно оси вращения.
Формула Эйлера справедлива и для случая вращения твердого тела вокруг неподвижной точки.
В этом случае в каждый момент времени тело вращается вокруг мгновенной оси, проходящей через неподвижную точку, с угловой скоростью со, направленной по мгновенной оси. Точки тела, лежащие на мгновенной оси, имеют скорости, равные нулю, как и в случае неподвижной оси вращения.
Следовательно, линейные скорости точек тела при вращении вокруг неподвижной точки можно вычислять также по векторной формуле Эйлера, как и в случае вращения вокруг неподвижной оси, только радиус-вектор каждой точки удобно проводить из неподвижной точки тела.
Итак, скорость 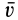 какой-либо точки
какой-либо точки 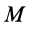 тела (рис. 77), по векторной формуле Эйлера,
тела (рис. 77), по векторной формуле Эйлера,

Модуль скорости
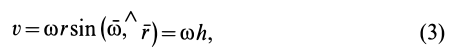
где 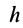 — кратчайшее расстояние от рассматриваемой точки до мгновенной оси.
— кратчайшее расстояние от рассматриваемой точки до мгновенной оси.
Таким образом, скорости точек тела пропорциональны расстояниям от этих точек до мгновенной оси. Направление скорости какой-либо точки тела перпендикулярно плоскости, в которой находятся векторы 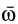 и
и 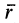 , а следовательно, перпендикулярно отрезку
, а следовательно, перпендикулярно отрезку 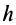 .
.
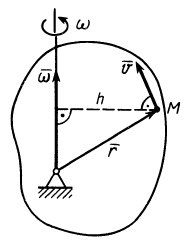
Рис. 77
Если требуется найти модуль угловой скорости тела в определенный момент времени, то для этого, согласно (3), достаточно разделить скорость какой-либо точки в этот же момент времени на кратчайшее расстояние от этой точки до мгновенной оси.
Мгновенную ось в конкретных задачах часто находят из механических условий задачи, т. е. в рассматриваемый момент времени она всегда проходит через две неподвижные точки тела. Так, если движущееся тело касается в какой-либо точке неподвижной поверхности другого тела и при этом нет скольжения, то мгновенная ось проходит через эту неподвижную в данный момент времени точку.
В случае качения без скольжения одного конуса по другому, неподвижному, конусу (рис. 78) мгновенной осью является та общая образующая этих конусов 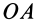 , вдоль которой в данный момент времени они касаются друг друга. Если, например, скорость
, вдоль которой в данный момент времени они касаются друг друга. Если, например, скорость 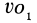 точки
точки 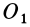 известна, то угловая скорость подвижного конуса
известна, то угловая скорость подвижного конуса
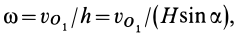
где 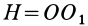 и
и 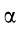 — угол полураствора подвижного конуса.
— угол полураствора подвижного конуса.
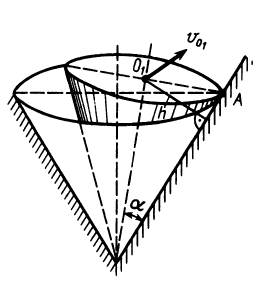
Рис. 78
Проекции угловой скорости тела 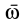 как на подвижные, так и неподвижные оси координат можно определить также через углы Эйлера как функции времени, характеризующие положение тела относительно неподвижной системы координат.
как на подвижные, так и неподвижные оси координат можно определить также через углы Эйлера как функции времени, характеризующие положение тела относительно неподвижной системы координат.
Если спроецировать правую и левую части (2) на координатные оси, то получим формулы Эйлера для проекций скоростей 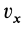 ,
, 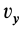 и
и 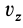 :
:
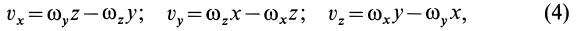
где 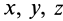 — координаты точек тела, скорости которых определяются.
— координаты точек тела, скорости которых определяются.
Если взять точки тела, лежащие на мгновенной оси в рассматриваемый момент времени, то для них скорости равны нулю, а следовательно, приняв равными нулю 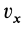 ,
, 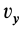 ,
,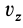 , из (4) получим следующие уравнения для координат этих точек:
, из (4) получим следующие уравнения для координат этих точек:
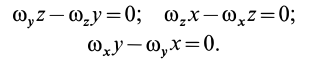
Эти уравнения можно представить в виде
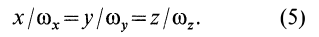
Для определенного момента времени формула (5) является уравнением мгновенной оси. Если же величины, входящие в (5), рассматривать как функции времени, то она будет представлять собой уравнения подвижного или неподвижного аксоида (в параметрической форме) в зависимости от того, в какой системе координат она составлена.
Если 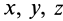 являются текущими координатами точки мгновенной оси относительно подвижных осей, скрепленных с движущимся телом, а
являются текущими координатами точки мгновенной оси относительно подвижных осей, скрепленных с движущимся телом, а 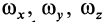 — проекции угловой скорости тела на эти оси, то формула (5) является уравнением подвижного аксоида.
— проекции угловой скорости тела на эти оси, то формула (5) является уравнением подвижного аксоида.
Если вместо подвижных осей координат взять неподвижные оси, относительно которых рассматривается движение тела, и проекции угловой скорости тоже взять на эти оси, то тогда формула (5) будет уравнением неподвижного аксоида.
Скорость какой-либо точки можно вычислить как первую производную по времени от радиуса-вектора 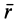 этой точки, проведенного из неподвижной точки. С другой стороны, скорость точки тела, вращающегося вокруг неподвижной точки, можно вычислить по векторной формуле Эйлера (2). Следовательно, производная по времени от радиуса-вектора любой точки твердого тела, вращающегося вокруг неподвижной точки, определится по формуле
этой точки, проведенного из неподвижной точки. С другой стороны, скорость точки тела, вращающегося вокруг неподвижной точки, можно вычислить по векторной формуле Эйлера (2). Следовательно, производная по времени от радиуса-вектора любой точки твердого тела, вращающегося вокруг неподвижной точки, определится по формуле

Длина радиуса-вектора 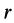 как расстояние между двумя точками твердого тела является постоянной величиной при движении этого тела. Следовательно, равенство (6) можно рассматривать как формулу для вычисления производной по времени от вектора, модуль которого постоянен, и изменение этого вектора происходит только вследствие вращения его с угловой скоростью со вместе с телом вокруг неподвижной точки.
как расстояние между двумя точками твердого тела является постоянной величиной при движении этого тела. Следовательно, равенство (6) можно рассматривать как формулу для вычисления производной по времени от вектора, модуль которого постоянен, и изменение этого вектора происходит только вследствие вращения его с угловой скоростью со вместе с телом вокруг неподвижной точки.
Если взять подвижную систему координат 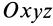 , скрепленную с телом, которое вращается вокруг неподвижной точки с угловой скоростью
, скрепленную с телом, которое вращается вокруг неподвижной точки с угловой скоростью 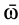 , то для единичных векторов
, то для единичных векторов 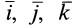 , направленных по этим осям координат, как для векторов, модули которых постоянны, на основании (6) имеем:
, направленных по этим осям координат, как для векторов, модули которых постоянны, на основании (6) имеем:
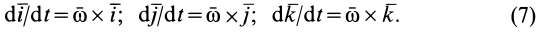
Формулы (7) называют формулами Пуассона.
Ускорения точек тела при вращении вокруг неподвижной точки
Формулу для ускорения какой-либо точки 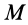 тела, вращающегося вокруг неподвижной точки, нельзя получить непосредственно используя формулу для ускорения при вращательном движении вокруг неподвижной оси, так как в рассматриваемом случае угловое ускорение в общем случае не направлено по оси вращения, а следовательно, и по а>. Во всем остальном формулы для ускорения в этих случаях полностью аналогичны.
тела, вращающегося вокруг неподвижной точки, нельзя получить непосредственно используя формулу для ускорения при вращательном движении вокруг неподвижной оси, так как в рассматриваемом случае угловое ускорение в общем случае не направлено по оси вращения, а следовательно, и по а>. Во всем остальном формулы для ускорения в этих случаях полностью аналогичны.
Формулу для ускорения какой-либо точки тела 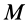 можно получить путем дифференцирования по времени вектора скорости, учитывая, что скорость вычисляют по формуле (2). Выполняя это дифференцирование, получаем
можно получить путем дифференцирования по времени вектора скорости, учитывая, что скорость вычисляют по формуле (2). Выполняя это дифференцирование, получаем
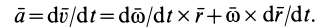
Так как
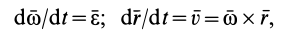
то

Формулу (8) часто называют формулой Ривальса. Часть общего ускорения точки

называют вращательным ускорением, а другую часть

— осестремительным ускорением. Следовательно, формула (8) примет вид

т. е. ускорение точки тела, вращающегося вокруг неподвижной точки, равно векторной сумме вращательного и осестремительного ускорений.
В общем случае вращательное и осестремительное ускорения не перпендикулярны; следовательно, модуль ускорения 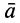 вычисляют как диагональ параллелограмма по формуле
вычисляют как диагональ параллелограмма по формуле
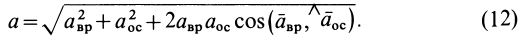
Рассмотрим вращательное и осестремительное ускорения по отдельности. Вращательное ускорение вычисляют по формуле (9), аналогичной формуле (2) для скорости точки. Только здесь вместо угловой скорости 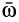 входит угловое ускорение
входит угловое ускорение 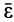 . Поэтому вращательное ускорение
. Поэтому вращательное ускорение 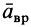 направлено аналогично скорости
направлено аналогично скорости 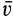 если тело вращается в рассматриваемый момент времени с угловой скоростью, равной угловому ускорению
если тело вращается в рассматриваемый момент времени с угловой скоростью, равной угловому ускорению 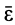 .
.
Модуль вращательного ускорения 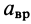 определяют аналогично модулю скорости
определяют аналогично модулю скорости 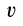 [см. формулу (3)]:
[см. формулу (3)]:

где 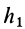 — кратчайшее расстояние от точки тела до линии, по которой направлено угловое ускорение
— кратчайшее расстояние от точки тела до линии, по которой направлено угловое ускорение 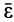 (рис. 79). Формула (13) для
(рис. 79). Формула (13) для 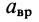 получается из (9):
получается из (9):
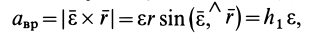
где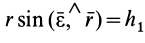 .
.
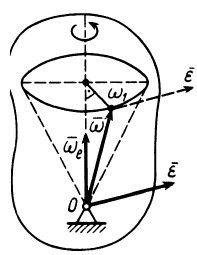
Рис. 79
Из (13) следует, что вектор углового ускорения 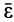 расположен на прямой линии, проходящей через неподвижную точку. В противном случае эта точка имела бы не равное нулю вращательное ускорение.
расположен на прямой линии, проходящей через неподвижную точку. В противном случае эта точка имела бы не равное нулю вращательное ускорение.
Модуль осестремительного ускорения 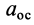 можно получить из формулы (10):
можно получить из формулы (10):
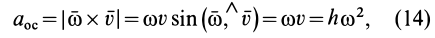
так как угловая скорость 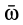 перпендикулярна скорости
перпендикулярна скорости 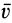 .
.
Осестремительное ускорение направлено по перпендикуляру к мгновенной оси, опущенному из точки, для которой оно вычисляется, т. е. по отрезку 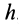 , так как, являясь векторным произведением
, так как, являясь векторным произведением 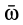 и
и 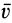 , оно перпендикулярно плоскости, где находятся эти векторы, и имеет направление вектора этого векторного произведения. Если ввести вектор
, оно перпендикулярно плоскости, где находятся эти векторы, и имеет направление вектора этого векторного произведения. Если ввести вектор 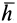 , направленный по перпендикуляру от мгновенной оси к рассматриваемой точке, то
, направленный по перпендикуляру от мгновенной оси к рассматриваемой точке, то

В случае вращения твердого тела вокруг неподвижной оси угловое ускорение и угловая скорость направлены по этой оси; тогда расстояния 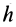 и
и 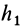 , равны. Следовательно, вращательное ускорение превращается в касательное ускорение, а осестремительное— в нормальное или центростремительное ускорение.
, равны. Следовательно, вращательное ускорение превращается в касательное ускорение, а осестремительное— в нормальное или центростремительное ускорение.
Таким образом, вращение тела вокруг неподвижной точки можно рассматривать как более общее движение, чем вращение тела вокруг неподвижной оси.
Вычисление углового ускорения
Для вычисления ускорения точек тела необходимо знать угловое ускорение 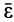 . Рассмотрим два основных способа его вычисления.
. Рассмотрим два основных способа его вычисления.
1. Если известны проекции угловой скорости на подвижные или неподвижные оси координат 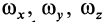 , то проекции углового ускорения на те же оси определяют по формулам
, то проекции углового ускорения на те же оси определяют по формулам
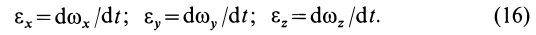
По проекциям легко найти модуль углового ускорения и косинусы его углов с осями координат.
2. Другой способ определения углового ускорения 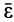 основан на его разложении на две взаимно перпендикулярные составляющие. Если ввести единичный вектор
основан на его разложении на две взаимно перпендикулярные составляющие. Если ввести единичный вектор 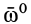 , направленный по
, направленный по 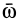 , то
, то
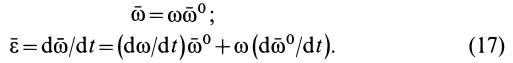
Составляющая 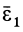 полного углового ускорения
полного углового ускорения 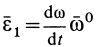 направлена по вектору
направлена по вектору 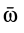 , когда
, когда 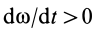 , и противоположно ему при
, и противоположно ему при 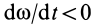 .
.
Составляющая 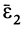 полного углового ускорения
полного углового ускорения 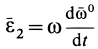 всегда перпендикулярна
всегда перпендикулярна 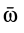 , так как производная по времени от единичного вектора
, так как производная по времени от единичного вектора 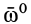 есть вектор, перпендикулярный дифференцируемому единичному вектору и, следовательно, перпендикулярный вектору
есть вектор, перпендикулярный дифференцируемому единичному вектору и, следовательно, перпендикулярный вектору 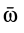 .
.
Составляющая углового ускорения 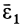 является полным угловым ускорением при вращении тела вокруг неподвижной оси, так как составляющая
является полным угловым ускорением при вращении тела вокруг неподвижной оси, так как составляющая 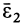 в этом случае равна нулю. Вычислим составляющую углового ускорения
в этом случае равна нулю. Вычислим составляющую углового ускорения 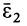 . Часто угловая скорость постоянна по модулю и изменяется только по направлению. В этом случае составляющая
. Часто угловая скорость постоянна по модулю и изменяется только по направлению. В этом случае составляющая 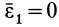 и полное угловое ускорение совпадает с
и полное угловое ускорение совпадает с 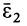 .
.
Если же угловое ускорение 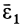 не равно нулю, то его можно вычислить отдельно и затем, сложив с составляющей
не равно нулю, то его можно вычислить отдельно и затем, сложив с составляющей 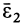 , определить полное угловое ускорение
, определить полное угловое ускорение 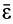 . Итак, если угловая скорость постоянна, то
. Итак, если угловая скорость постоянна, то
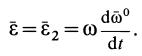
В этом случае воспользуемся определением углового ускорения через угловую скорость непосредственно:
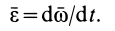
Учитывая, что 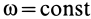 , и применяя формулу, аналогичную производной по времени от радиуса-вектора [см. формулу (6)], когда радиус-вектор постоянен по длине, будем иметь
, и применяя формулу, аналогичную производной по времени от радиуса-вектора [см. формулу (6)], когда радиус-вектор постоянен по длине, будем иметь

где 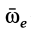 — угловая скорость вращения дифференцируемого по времени вектора
— угловая скорость вращения дифференцируемого по времени вектора 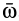 , т. е. угловая скорость вращения мгновенной оси, по которой направлен вектор
, т. е. угловая скорость вращения мгновенной оси, по которой направлен вектор 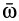 . Модуль углового ускорения можно найти аналогично скорости точки, т. е.
. Модуль углового ускорения можно найти аналогично скорости точки, т. е.

где расстоянием 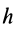 является
является 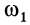 — кратчайшее расстояние от конца вектора
— кратчайшее расстояние от конца вектора 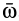 до оси, по которой направлена угловая скорость
до оси, по которой направлена угловая скорость 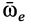 (рис. 80).
(рис. 80).
Вектор углового ускорения 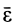 пройдет через неподвижную точку и будет параллелен касательной к годографу вектора
пройдет через неподвижную точку и будет параллелен касательной к годографу вектора 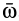 . Окончательно направление
. Окончательно направление 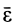 берут в соответствии с формулой (18), т. е. по направлению вращения мгновенной оси в зависимости от угловой скорости
берут в соответствии с формулой (18), т. е. по направлению вращения мгновенной оси в зависимости от угловой скорости 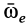 .
.
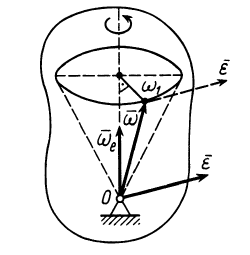
Рис. 80
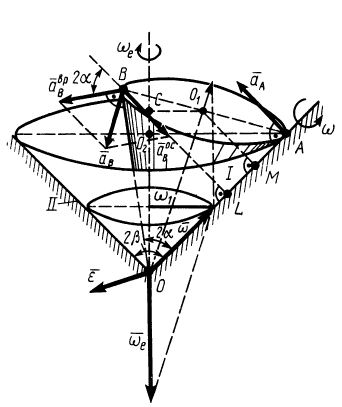
Рис. 81
Рассмотрим теперь пример на вычисление угловой скорости, углового ускорения и линейных скоростей и ускорений точек тела, вращающегося вокруг неподвижной точки.
- Заказать решение задач по теоретической механике
Пример с решением
Круговой конус I с углом раствора 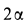 катится без скольжения по внутренней стороне неподвижного конуса II с углом раствора
катится без скольжения по внутренней стороне неподвижного конуса II с углом раствора 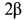 (рис. 81). Скорость точки
(рис. 81). Скорость точки 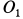 подвижного конуса постоянна и равна
подвижного конуса постоянна и равна 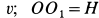 .
.
Определить угловую скорость и угловое ускорение подвижного конуса, а также скорости и ускорения точек 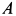 и
и 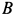 этого конуса.
этого конуса.
Решение. Мгновенной осью конуса I является образующая 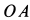 . Если скорость точки
. Если скорость точки 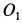 направлена от плоскости
направлена от плоскости 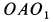 во внешнюю сторону, то угловая скорость конуса
во внешнюю сторону, то угловая скорость конуса 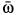 направлена по мгновенной оси от точки
направлена по мгновенной оси от точки 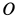 к точке
к точке 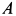 . Числовое значение угловой скорости
. Числовое значение угловой скорости
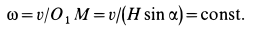
Скорость точки 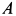 равна нулю, так как эта точка находится на мгновенной оси. Скорость точки
равна нулю, так как эта точка находится на мгновенной оси. Скорость точки 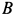 вычисляем по формуле
вычисляем по формуле
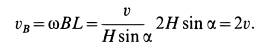
Скорость 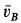 перпендикулярна плоскости
перпендикулярна плоскости 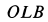 и направлена от нее во внешнюю сторону.
и направлена от нее во внешнюю сторону.
Угловое ускорение 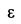 вычисляем по формуле (19):
вычисляем по формуле (19):
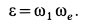
Годографом вектора 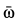 является окружность радиуса
является окружность радиуса 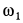 :
:
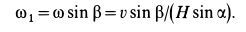
Если рассмотреть плоскость, в которой находятся мгновенная ось 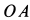 , ось подвижного конуса
, ось подвижного конуса 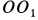 и ось неподвижного конуса
и ось неподвижного конуса 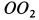 (плоскость рисунка), то при движении конуса I эта плоскость вращается вокруг оси неподвижного конуса
(плоскость рисунка), то при движении конуса I эта плоскость вращается вокруг оси неподвижного конуса 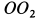 , расположенной в указанной плоскости, а следовательно, вокруг этой оси вращается и мгновенная ось
, расположенной в указанной плоскости, а следовательно, вокруг этой оси вращается и мгновенная ось 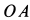 , находящаяся в этой плоскости. Угловую скорость этого вращения
, находящаяся в этой плоскости. Угловую скорость этого вращения 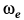 можно определить, если скорость какой-либо точки этой плоскости, участвующей только во вращении вокруг
можно определить, если скорость какой-либо точки этой плоскости, участвующей только во вращении вокруг 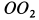 и не имеющей другого движения, разделить на кратчайшее расстояние от этой точки до оси
и не имеющей другого движения, разделить на кратчайшее расстояние от этой точки до оси 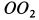 . Отмеченными выше свойствами обладают все точки, расположенные на оси подвижного конуса
. Отмеченными выше свойствами обладают все точки, расположенные на оси подвижного конуса 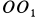 . Выбрав на этой оси точку
. Выбрав на этой оси точку 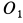 , имеем
, имеем
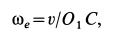
где 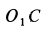 —кратчайшее расстояние от точки
—кратчайшее расстояние от точки 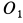 до
до 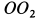 . Так как
. Так как
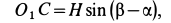
то
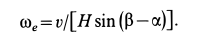
Таким образом,
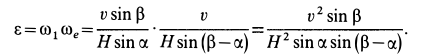
Так как скорость точки 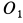 направлена во внешнюю сторону от рисунка, то мгновенная ось
направлена во внешнюю сторону от рисунка, то мгновенная ось 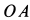 вращается вокруг
вращается вокруг 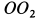 по часовой стрелке и, следовательно, угловое ускорение
по часовой стрелке и, следовательно, угловое ускорение 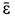 направлено перпендикулярно плоскости
направлено перпендикулярно плоскости 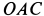 во внешнюю сторону.
во внешнюю сторону.
Ускорение какой-либо точки подвижного конуса можно определить по формуле
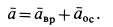
Для точки 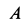 расстояние
расстояние 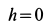 и поэтому
и поэтому 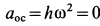 . Для вращательного ускорения имеем
. Для вращательного ускорения имеем
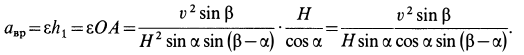
Ускорение 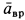 , а следовательно, и полное ускорение
, а следовательно, и полное ускорение 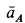 этой точки направлены перпендикулярно
этой точки направлены перпендикулярно 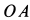 и находятся в плоскости
и находятся в плоскости 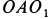 . С положительного направления вектора
. С положительного направления вектора 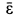 направление
направление 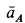 должно быть направлено как скорость при вращении против часовой стрелки вокруг
должно быть направлено как скорость при вращении против часовой стрелки вокруг 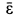 . Для точки
. Для точки 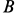
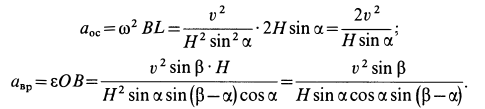
Ускорение 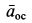 направлено по
направлено по 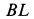 от точки
от точки 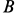 к точке
к точке 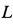 , а ускорение
, а ускорение 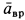 —перпендикулярно
—перпендикулярно 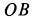 и расположено в плоскости
и расположено в плоскости 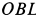 .
.
Полное ускорение точки 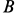 вычисляется как диагональ параллелограмма, построенного на ускорениях
вычисляется как диагональ параллелограмма, построенного на ускорениях 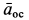 и
и 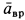 , т. е.
, т. е.
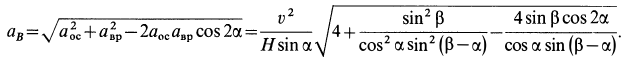
Отметим, что 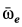 можно получить, если угловую скорость
можно получить, если угловую скорость 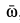 , направленную по мгновенной оси, разложить по правилу параллелограмма по осям подвижного и неподвижного конусов. Тогда составляющая по оси неподвижного конуса и будет угловой скоростью
, направленную по мгновенной оси, разложить по правилу параллелограмма по осям подвижного и неподвижного конусов. Тогда составляющая по оси неподвижного конуса и будет угловой скоростью 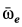 .
.
Общий случай движения свободного твердого тела
Разложение движения свободного твердого тела на поступательное и вращательное
Рассмотрим общий случай движения свободного твердого тела, т. е. тела, имеющего шесть степеней свободы. Покажем, что самое общее движение свободного твердого тела можно представить состоящим из поступательного движения вместе с какой-либо точкой тела и вращательного движения вокруг этой точки.
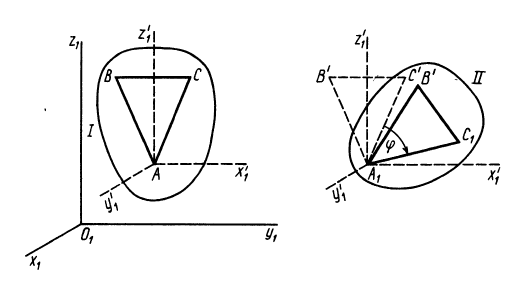
Рис. 82
Положение тела относительно какой-либо системы координат 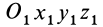 полностью определяется заданием трех точек тела, не лежащих на одной прямой, или заданием треугольника, скрепленного с телом (рис. 82). Треугольник
полностью определяется заданием трех точек тела, не лежащих на одной прямой, или заданием треугольника, скрепленного с телом (рис. 82). Треугольник 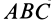 , а следовательно, и тело, скрепленное с ним, из одного положения I в любое другое положение II можно переместить одним поступательным перемещением вместе с какой-либо точкой тела (например, точкой
, а следовательно, и тело, скрепленное с ним, из одного положения I в любое другое положение II можно переместить одним поступательным перемещением вместе с какой-либо точкой тела (например, точкой 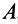 , когда подвижная система координат
, когда подвижная система координат 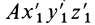 перемещается поступательно) и поворотом относительно подвижной системы координат
перемещается поступательно) и поворотом относительно подвижной системы координат 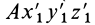 , т. е. вокруг оси, проходящей через эту точку.
, т. е. вокруг оси, проходящей через эту точку.
Поступательная часть перемещения тела зависит от выбора точки, вместе с которой перемещается тело, а вращательная часть перемещения вокруг оси или вокруг точки не зависит от выбора точки. Поступательную часть перемещения можно поменять местами с вращательной частью, и, наконец, их можно выполнять одновременно, т. е. пока тело совершает поступательное перемещение из одного положения в другое, за это же время можно осуществить и поворот тела вокруг точки на требующийся угол.
Если два положения тела бесконечно близки, то истинное элементарное перемещение свободного твердого тела можно заменить элементарным поступательным перемещением вместе с какой-либо точкой тела и элементарным поворотом вокруг мгновенной оси, проходящей через эту точку, осуществляемыми за то же время, что и истинное перемещение, тела.
Любое движение свободного твердого тела, таким образом, можно заменить совокупностью поступательных движений вместе с какой-либо точкой тела и вращений вокруг этой точки, совершаемых за то же время, что и истинное движение. Поступательное движение вместе с точкой тела и подвижной системой координат 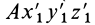 является переносным движением, а движение тела относительно этой подвижной системы координат, являющееся в каждый момент времени вращением вокруг своей мгновенной оси, проходящей через эту подвижную точку тела, есть относительное движение.
является переносным движением, а движение тела относительно этой подвижной системы координат, являющееся в каждый момент времени вращением вокруг своей мгновенной оси, проходящей через эту подвижную точку тела, есть относительное движение.
Итак, любое движение свободного твердого тела можно составить из поступательного движения вместе с подвижной системой координат и сферического движения относительно этой системы координат. Для относительного сферического движения можно ввести угловую скорость 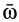 и угловое ускорение
и угловое ускорение 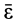 , которое является первой производной по времени от
, которое является первой производной по времени от 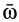 , как в случае вращения тела вокруг неподвижной точки.
, как в случае вращения тела вокруг неподвижной точки.
Угловую скорость и угловое ускорение относительного вращательного движения вокруг какой-либо точки тела называют в общем случае угловой скоростью и угловым ускорением свободного твердого тела. Эти величины не зависят от выбора точки тела. От выбора точки тела зависит только переносное поступательное движение тела.
Уравнения движения свободного твердого тела
В общем случае для определения положения свободного твердого тела относительно системы координат 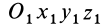 достаточно задать относительно этой системы координат положение другой системы координат
достаточно задать относительно этой системы координат положение другой системы координат 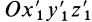 , движущейся поступательно относительно первой системы вместе с ка-кой-либо точкой
, движущейся поступательно относительно первой системы вместе с ка-кой-либо точкой 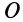 рассматриваемого тела, и углы Эйлера, определяющие положение системы координат
рассматриваемого тела, и углы Эйлера, определяющие положение системы координат 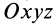 , скрепленной с движущимся телом, относительно системы координат
, скрепленной с движущимся телом, относительно системы координат 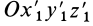 (рис. 83).
(рис. 83).
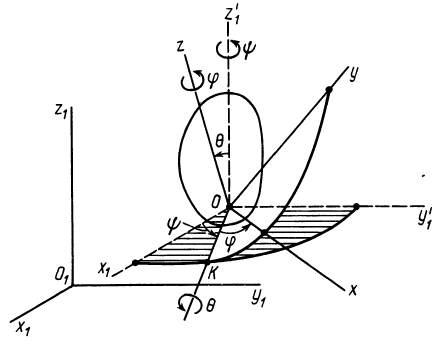
Рис. 83
Для простоты предположим, что оси 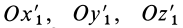 соответственно параллельны осям
соответственно параллельны осям 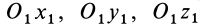 . Таким образом, положение свободного твердого тела относительно системы координат
. Таким образом, положение свободного твердого тела относительно системы координат 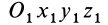 полностью определяется, если относительно этой системы задать координаты точки
полностью определяется, если относительно этой системы задать координаты точки  тела как однозначные функции времени и углы Эйлера подвижной системы координат
тела как однозначные функции времени и углы Эйлера подвижной системы координат 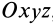 , скрепленной с движущимся телом, относительно системы координат
, скрепленной с движущимся телом, относительно системы координат 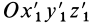 , поступательно движущейся вместе с точкой
, поступательно движущейся вместе с точкой  тела:
тела:
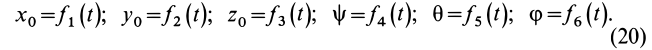
Уравнения (20) являются кинематическими уравнениями движения свободного твердого тела в общем случае его движения. Этих уравнений шесть, т. е. столько, сколько степеней свободы у свободного твердого тела. Первые три уравнения (20) определяют переносное движение тела вместе с точкой  О, вторые три уравнения определяют вращательное движение вокруг этой точки.
О, вторые три уравнения определяют вращательное движение вокруг этой точки.
Первые три уравнения для рассматриваемого движения свободного твердого тела зависят от выбора точки  тела; последние три уравнения (углы Эйлера) не зависят от выбора точки
тела; последние три уравнения (углы Эйлера) не зависят от выбора точки  , вокруг которой рассматривается вращение тела.
, вокруг которой рассматривается вращение тела.
Скорости и ускорения точек свободного твердого тела в общем случае
Так как движение свободного твердого тела в общем случае можно представить как сложное движение, то и скорость, и ускорение какой-либо точки 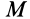 этого тела можно вычислить соответственно по теоремам сложения скоростей и ускорений (рис. 84). Так, для скорости
этого тела можно вычислить соответственно по теоремам сложения скоростей и ускорений (рис. 84). Так, для скорости 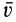 точки
точки 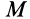
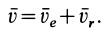
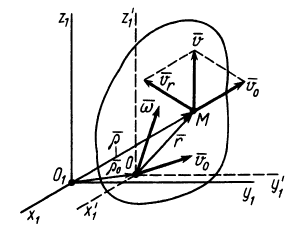
Рис. 84
Переносным движением является поступательное движение тела вместе с точкой О этого тела. Следовательно, скорости поступательного переносного движения одинаковы у всех точек тела и равны скорости 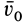 точки
точки  . Относительное движение есть вращение вокруг точки
. Относительное движение есть вращение вокруг точки  , и, следовательно, скорость относительного движения можно вычислить по векторной формуле Эйлера:
, и, следовательно, скорость относительного движения можно вычислить по векторной формуле Эйлера:
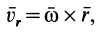
где 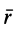 — радиус-вектор точки
— радиус-вектор точки 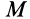 , проведенный из точки
, проведенный из точки  ;
; 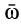 —угловая скорость вращения тела вокруг точки
—угловая скорость вращения тела вокруг точки  или подвижной мгновенной оси, проходящей через точку
или подвижной мгновенной оси, проходящей через точку  .
.
Рис. 85
Окончательно для скорости точки 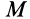 получим следующую формулу:
получим следующую формулу:
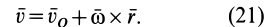
Формулу (21) можно получить непосредственным дифференцированием векторного равенства
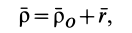
справедливого для любого момента времени. Возьмем полные производные по времени от обеих частей равенства, учитывая изменения векторов относительно неподвижной системы координат 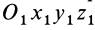 . Имеем
. Имеем
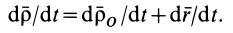
Здесь 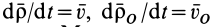 — скорости точек тела
— скорости точек тела 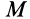 и
и  соответственно. Модуль вектора
соответственно. Модуль вектора 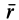 как отрезка, соединяющего две точки тела, не изменяется при движении этого тела. Следовательно, по формуле производной по времени от вектора постоянного модуля получаем
как отрезка, соединяющего две точки тела, не изменяется при движении этого тела. Следовательно, по формуле производной по времени от вектора постоянного модуля получаем
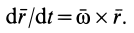
Объединяя результаты, получаем формулу (21):
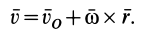
Так же как и при плоском движении твердого тела, часть скорости 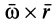 можно истолковать как скорость от вращения тела вокруг точки
можно истолковать как скорость от вращения тела вокруг точки  .
.
Ускорение а точки 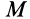 (рис. 85) в частном случае, когда переносное движение является поступательным, определяем по формуле
(рис. 85) в частном случае, когда переносное движение является поступательным, определяем по формуле
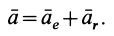
Ускорения переносного движения всех точек тела равны ускорению 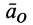 точки
точки  , так как за поступательное переносное движение принимается движение вместе с точкой
, так как за поступательное переносное движение принимается движение вместе с точкой  .
.
Ускорение относительного движения, как и при вращении тела вокруг неподвижной точки, состоит из вращательной и осестремительной составляющих, т. е.
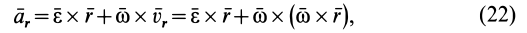
где 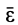 — угловое ускорение тела.
— угловое ускорение тела.
Окончательная формула для ускорения точки 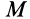 свободного тела в общем случае его движения имеет вид
свободного тела в общем случае его движения имеет вид
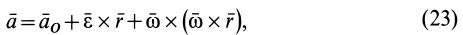
или на основании формулы Ривальса

где
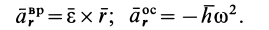
Формулу (23) можно получить непосредственным дифференцированием векторного равенства для скоростей (21), справедливого в любой момент времени. Вычисляя полные производные по времени, при определении которых учитываются изменения векторов относительно неподвижной системы координат, получаем
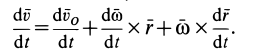
Здесь 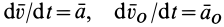 — ускорения точек
— ускорения точек 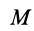 и
и 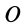 ;
; 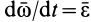 — угловое ускорение.
— угловое ускорение.
Учитывая, что вектор 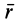 является вектором постоянного модуля, имеем
является вектором постоянного модуля, имеем
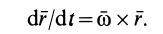
Окончательный результат выразится в форме
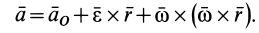
Заметим, что если в кинематике свободного твердого тела в качестве точки 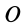 можно брать любую точку тела, то в динамике в качестве такой точки оказывается выгодным выбирать центр масс тела.
можно брать любую точку тела, то в динамике в качестве такой точки оказывается выгодным выбирать центр масс тела.
При выборе различных точек тела в качестве полюса изменяются скорость и ускорение полюса. Угловая скорость и угловое ускорение при этом не изменяются. Докажем это для угловой скорости, используя (21).
Пусть 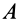 и
и 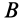 — две точки свободного твердого тела (рис. 86). Приняв за полюс точку
— две точки свободного твердого тела (рис. 86). Приняв за полюс точку 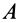 , для скорости точки
, для скорости точки 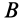 имеем
имеем
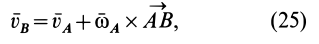
где 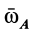 — угловая скорость вращения тела вокруг точки
— угловая скорость вращения тела вокруг точки 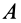 . Аналогично, приняв за полюс точку
. Аналогично, приняв за полюс точку 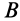 , для скорости точки
, для скорости точки 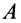 получим
получим
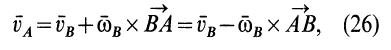
где 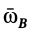 — угловая скорость вращения тела вокруг точки
— угловая скорость вращения тела вокруг точки 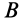 . Из (25) и (26) имеем
. Из (25) и (26) имеем
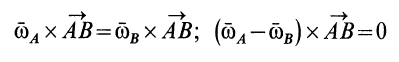
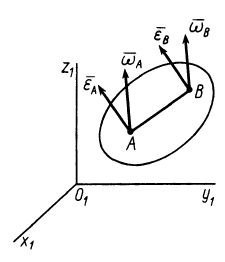
Рис. 86
для любых двух точек свободного твердого тела. Эти точки можно выбрать так, чтобы 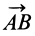 не было параллельно вектору
не было параллельно вектору 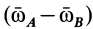 . Тогда получаем
. Тогда получаем
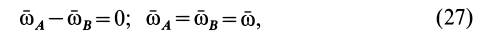
т. е. угловая скорость свободного твердого тела не зависит от выбора полюса. Она инвариантна по отношению к выбору полюса.
Так как равенство (27) справедливо для любого момента времени, то, дифференцируя его по времени, получим
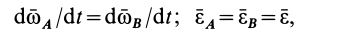
т. е. вектор углового ускорения свободного твердого тела тоже не зависит от выбора полюса.
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
- Плоское движение твердого тела
- Мгновенный центр скоростей
- Мгновенный центр ускорений
- Мгновенный центр вращения
Задачи на тему «теорема Штейнера».
Сначала давайте соберем в «кучку» все формулы моментов инерции для часто встречающихся тел.
Момент инерции тонкого кольца (ось вращения перпендикулярна плоскости кольца и проходит через центр)
Момент инерции полого тонкостенного цилиндра (ось вращения совпадает с осью цилиндра)
Момент инерции сплошного цилиндра (ось вращения совпадает с осью цилиндра)
Момент инерции полого толстостенного цилиндра (ось вращения совпадает с осью цилиндра)
Момент инерции диска (ось вращения совпадает с осью диска)
Момент инерции диска (ось вращения совпадает с диаметром диска)
Момент инерции шара (ось вращения совпадает с центром)
Момент инерции полой тонкостенной сферы (ось вращения совпадает с центром)
Момент инерции тонкого стержня (ось вращения совпадает с центром)
Напоминаю теорему Штейнера: момент инерции тела относительно любой оси вращения равен моменту его инерции относительно параллельной оси, проходящей через центр масс тела, плюс произведение массы тела на квадрат расстояния между осями.

Теорема Штейнера
Теперь можно решить пару задач.
Задача 1.
Найти момент инерции обруча массой и радиусом
относительно оси, проходящей через его край перпендикулярно обручу.
Решение:

К задаче 1
По таблице определим момент инерции обруча (кольца), и прибавим произведение массы тела на квадрат расстояния между осями, а это – радиус кольца. Тогда
Ответ:
Задача 2. Найти момент инерции тонкого стержня массой и длиной
относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на одну треть его длины.
Решение.

К задаче 2
Расстояние между осями
Согласно таблице момент инерции стержня равен , тогда по теореме Штейнера
Ответ:
Задача 3.
Два шара радиусами см и массой
г каждый скреплены тонким стержнем массой
г и длиной
см. Найти момент инерции системы относительно оси, перпендикулярной стержню и проходящей через центр тяжести, а также относительно оси, перпендикулярной стержню и проходящей в
от его конца.

К задаче 3
Решение:
- Сначала найдем момент инерции системы относительно ее центра масс.
Здесь – момент инерции стержня,
– момент инерции одного из шаров.
Момент инерции стержня определим по таблице, так как очевидно, что его центр является центром масс системы и ось вращения будет проходить через центр масс стержня.
Определим момент инерции одного из шаров по теореме Штейнера:
Тогда ответом на пункт а) будет
б) Теперь пусть ось проходит на расстоянии четверти длины стержня от его конца. Тогда момент инерции стержня будет равен по теореме Штейнера
Момент инерции шара, ближнего к оси вращения:
Момент инерции шара, дальнего от оси вращения:
Тогда ответом на пункт б) будет
Ответ: а) кг
м
, б)
кг
м
.
Задача 4.
Имеется диск диаметром см и массой
г. В диске вырезали круглое отверстие диаметром 8 см, центр которого находится на расстоянии
от центра диска. Найти момент инерции
фигуры относительно оси, проходящей через центр диска и перпендикулярной его плоскости.

К задаче 4
Решение:
– момент инерции диска,
– вырезанная часть.
– масса вырезанной части. Массу вырезанной части найдем как
,
– поверхностная плотность диска.
Если – площадь диска, а
– площадь вырезанной части, то
Тогда момент инерции вырезанной части
И момент инерции фигуры
Ответ: кг
м
.
В прошлый раз мы поговорили о такой величине, как статические моменты. Теперь можем двигаться дальше: сегодня на повестке моменты инерции.
Внимательный читатель уже может возмутиться:
“И зачем мы изучаем эти моменты? Какой в этом прок?
Причём же тут инерция, если сопромат — по сути статика?»
На первый вопрос у меня есть два ответа — краткий и не очень. Пока ограничусь кратким:
Статические моменты и моменты инерции широко используются для определения нормальных и касательных напряжений, определении прогибов и деформаций конструкций. Читая о том, как все это вычислить, вы будете сталкиваться с геометрическими характеристиками постоянно. Поэтому лучше сразу понимать, о чем идёт речь, а, при необходимости, подсматривать тут.
В изгибаемом элементе от момента сил возникают напряжения, для определения которых нам и нужен момент инерции (хотя и опосредованно. Впрочем, если вы читали статью про моменты, то это уже знаете). При этом сам элемент деформируется, и величина этих деформаций (прогибов) также определяется с помощью момента инерции.
Для ответа на второй вопрос перейдем уже к моментам инерции.
Что такое момент инерции
Суть и смысл моментов инерции в общем случае походит на статические моменты, однако корни нужно искать в описании вращения тела. Для вращательного движения одного только значения массы тела недостаточно, требуется еще знать распределение этой массы в теле. Рассмотрим вращающееся тело, как совокупность точек с предельно малыми размером и массой, которые находятся на расстояниях Ri (от нуля до R):
T — кинетическая энергия;
J — момент инерции;
m — масса;
v — скорость;
w — угловая скорость;
R — радиус;
Тут видно, что также, как в формуле кинетической энергии при линейном движении мера инертности — масса, при вращательном движении мера инертности — момент инерции. Впрочем, я немного забегаю вперёд.
Угловая скорость вращающегося тела — угол поворота, пройденный за единицу времени
Тут начальный угол поворота φ0 может быть равен нулю, если мы рассматриваем начало движения.
Линейная скорость тела:
Ускорение вращающегося тела (а нас интересует нормальное) тогда:
Я не буду затрагивать динамику вращающегося тела, и расскажу только о жизненно необходимом.
Сила (которая по второму закону Ньютона — произведение массы на ускорение):
и момент:
И вот тут вспомним уже третий закон Ньютона — действию всегда есть равное и противоположное противодействие, а значит действию найденного нами момента будет сопротивляться — момент инерции.
Вспомним также, что, как и со статическими моментами, на разные точки тела, удаленные от оси вращения на разные расстояния будет действовать разный момент, а общий момент можно получить их просуммировав:
При этом значения вращающего момента и момента инерции будут равны, а сами моменты направлены в противоположные стороны. При постоянной угловой скорости вращения, например w = 1, основными величинами, характеризующими вращающий момент или момент инерции будут масса материальных точек, составляющих тело, и расстояния от этих точек до оси вращения. Но, как я уже показал, рассказывая про статические моменты, массу точек для изотропных (в данном случае имеющих одинаковую плотность) объектов можно выносить за скобки и рассматривать исключительно геометрию. Формула момента инерции примет следующий вид:
Почему Iр? Потому что мы с вами оперировали радиусом и углом поворота (в формуле угловой скорости) — т.е. использовали полярную систему отсчета (что и демонстрирует индекс p).
Таким образом момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении.
Как найти момент инерции
Чтобы немного упростить себе операции со всеми этими величинами перейдем к родной и понятной системе отсчета: перпендикулярным осям X и Y. Возьмем случайное сечение стержня и рассмотрим интегралы, как мы уже делали со статическими моментами:
Первые два интеграла называются осевыми моментами инерции относительно осей x и y, а третий — центробежным моментом инерции сечения относительно осей x, y. Теперь рассмотрим случай параллельного переноса осей , не вдаваясь глубоко в вычисление интегралов.
Для осей x1=x+a, y1=y+b моменты инерции будут равны:
Если вы, как и часть прочитавших эту статью перед публикацией, не имеете черного пояса и седьмого дана в интегральных преобразованиях, то:
т.к.
и
Тут первый интеграл — Ix1, второй интеграл — Sx1, а третий раскрывается в площадь при нулевом свободном члене.
Надеюсь, понятно, что при параллельном переносе по y изменяется только ось (буква).
В последнем случае мы рассматриваем перенос по обеим осям сразу.
Где:
Ix — очевидно, момент инерции относительно оси x
Sx — статический момент сечения относительно оси y
F — площадь сечения
А теперь предположим, что некие оси x1 и y1 являются центральными, тогда и выражения упрощаются и принимают вид:
Немного проясню обозначение осей:
Центральными называются оси, проходящие через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю.
Главными называются оси, в которых центробежный момент инерции (Ixy) равен нулю. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью.
Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения называются главными осями. Если эти оси являются также и центральными, то они называются главными центральными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции.
И теперь можно уже коснуться практики: речь о моментах инерции простых сечений.
Момент инерции прямоугольника
Определим осевые моменты инерции прямоугольника со сторонами b и h относительно осей x и y, проходящих через его центр тяжести. В качестве элементарной площадки dA возьмем полоску шириной b и высотой . Тогда будем иметь:
Не прибегая к вычислениям, замечу, что для момента инерции относительно оси Y изменится только положение сторон b и h. Следовательно:
Момент инерции квадрата
Прямоугольник со сторонами b=h=a. Следовательно:
Момент инерции круга
Тут воспользуемся полярным моментом инерции относительно центра круга. Определим его, как сумму колец с толщиной dp:

Момент инерции кольца
А здесь – явная аналогия с моментом инерции круга:
Как мы видим, момент инерции кольца это разность моментов инерции большего и меньшего кругов.
Пример нахождения момента инерции тавра
Найдём осевые моменты инерции тавра (рисунок 5), приведенного на рисунке, относительно центральных осей xc и yc.
Рисунок 8. Тавр, положение осей
Так как оси x1 и x2 являются центральными осями для простых фигур в виде прямоугольников, для определения момента инерции фигуры относительно оси xc воспользуемся формулой.
Момент инерции относительно оси yc получим путем сложения моментов инерции простых фигур относительно этой же оси, так как ось yc является общей центральной осью для простых фигур и для всей фигуры.
Центробежный момент инерции относительно осей xc и yc равен нулю, так как ось инерции yc является главной осью (осью симметрии фигуры).
Обобщение и подведение итогов
Момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении. В статике момент инерции применяется в определении прогибов, расчетах конструкций на касательные и нормальные напряжения. Момент инерции также, как и статические моменты, характеризует положение осей относительно сечения элемента. Так у нас появляются:
Центральные оси, проходящие через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю.
Главные оси, в которых центробежный момент инерции (Ixy) равен нулю, а осевые моменты инерции — максимальны. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью.
При этом главные и центральные оси могут совпадать!
Список использованных источников
- Александров А.В. Сопротивление материалов: Учеб. для ВУЗов/ А.В. Александров, В.Д. Потапов, Б.П. Державин; под ред. А.В. Александрова – 3-е изд. испр. – М.: Высш. шк., 2003. – 560 с.: ил. ISBN 5-06-003732-0
- Дарков А.В., Шпиро Г.С. Сопротивление материалов – Учеб. для техн. вузов – 5-е изд. перераб. и дополн. – М.: Высш. шк., 1989 – 624 с. ил.
- Г.И. Беликов. Геометрические характеристики поперечных сечений стержней. Учебно-практическое пособие. — Волгоград: ВолгГАСУ, 2015. — 56 с. — ISBN 978-5-98276-752-3
Автор: Марк Ершов
Редактор, факт-чекер: К.А.Овчинников
5 349
