Рассмотрение движения твёрдого тела является непростой задачей. Однако часто ситуация сильно упрощается за счёт использования понятия кинематических связей. В данной статье будет рассмотрено плоское движение твёрдого тела (такое движение, при котором все точки тела движутся параллельно одной плоскости). Для этого необходимо сначала напомнить, что в механике считается твёрдым телом.
Определение. Твёрдое тело — это неизменяемая система материальных точек, то есть такая идеализированная система, при любых движениях которой взаимные расстояния между материальными точками системы остаются неизменными.

Плоское движение твёрдого тела удобно тем, что, не теряя общности, можно считать само тело плоским, а движение — происходящим в плоскости тела. Из определения твёрдого тела следует, что положение плоского тела однозначно определяется заданием положения каких-либо двух его точек (для объёмного тела это не так, так как не учитывается вращение вокруг оси, проходящей через эти две точки).
Рассмотрим вращение твёрдого тела вокруг неподвижной оси. Чтобы получить представление о распределении скоростей в нём, достаточно рассмотреть движение точек тела, лежащих в какой-либо одной плоскости, перпендикулярной к оси вращения. Таким образом, мы приходим к модели плоского движения твёрдого тела. Все точки тела будут двигаться по окружностям с центром в точке O и их скорости будут пропорциональны радиусам соответствующих окружностей (см. рис. 1).
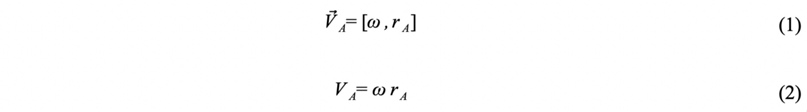

Рассмотрим теперь более общее движение плоского твёрдого тела. Плоскость вращения совпадает с плоскостью самого тела. В общем случае никакой неподвижной оси, вокруг которой происходило бы вращение тела, не предполагается.
Пусть А и B — две произвольные точки твёрдого тела. По определению твёрдого тела, расстояние между этими точками в процессе движения не меняется.

Продифференцировав это выражение, получим:

Допустим, что в рассматриваемый момент времени в теле существует точка, скорость которой в этот момент времени равна нулю. Стоит заметить, что такая точка существует для произвольного плоского движения тела. Это восходит к тому, что к твёрдому телу всегда можно мысленно добавить точку, положение которой относительно этого тела не меняется, и считать её частью твёрдого тела. Несложно убедиться, что это не идёт в противоречие с определением. Примем точку A за названную точку. Тогда формула (4) примет вид:

Это выражение будет верно для любого положения точки B. Используя понятие скалярного произведения, получаем:


Можно сделать вывод, что скорость точки B перпендикулярна к линии, соединяющей точки A и B. При движении твёрдого тела всякая прямая остаётся прямой. Это справедливо и для AB. Соответственно, поскольку в рассматриваемый момент точка А покоится, то величина скорости точки B в этот момент пропорциональна расстоянию AB (см. рис. 2). Таким образом, можно сделать вывод, что распределение скоростей в теле в рассматриваемый момент времени будет в точности таким же, как и при вращении вокруг неподвижной оси, проходящей через точку A. Движение тела в данном случае называется мгновенным вращением.
Определение. Мгновенная ось вращения — это прямая, проходящая через точки тела, скорости которых в рассматриваемый момент времени равны нулю.
Под словом «мгновенная» подразумевается, что это понятие служит для описания распределения скоростей только в какой-то заданный момент времени. В отличие от рассмотренной выше неподвижной оси, сохраняющей своё положение в теле и пространстве, мгновенная ось, вообще говоря, перемещается как в теле, так и в пространстве.
Резюмируя всё вышесказанное, можно сделать вывод, что использование мгновенной оси вращения является удобным инструментом для нахождения скоростей точек твёрдого тела в данный момент времени.
Стоит также заметить, что той же осью нельзя пользоваться для описания мгновенного распределения ускорений. Дело в том, что для определения ускорений недостаточно знать распределение скоростей только в рассматриваемый момент времени. Необходимо знать также распределение скоростей в бесконечно близкий момент времени.
Далее рассмотрим алгоритм поиска точки, принадлежащей мгновенной оси вращения. В соответствии со сказанным выше для описания движения твёрдого тела достаточно рассмотреть движение двух точек этого тела.
Случай 1. (Пусть точки не лежат на одной прямой с искомой точкой) В этом случае из каждой точки нужно построить перпендикуляры к направлениям их скоростей. Пересечение этих перпендикуляров и будет точкой, принадлежащей мгновенной оси вращения тела.
Случай 2. (Пусть точки лежат на одной прямой с искомой точкой) Если попробовать повторить алгоритм, рассмотренный в случае 1, то мы неминуемо столкнёмся с противоречием, так как сможем определить только прямую, на которой будет лежать искомая точка. На этот раз нужно провести прямую через концы векторов скоростей обеих точек. Пересечение этой прямой с линией, на которой лежат эти точки, и даст искомую точку.
Рассмотрим задачу по механике, при решении которой можно использовать понятие мгновенной оси вращения.

Задача. Пусть есть система, изображённая на рис. 3. Она состоит из стержней АВ и BC, шарнирно закреплённых друг с другом под прямым углом. Точка А также шарнирно закреплена с плоскостью опоры. Стержень АB начинает вращаться вокруг точки А с угловой скоростью ω. Длины стержней равны l. Какова будет скорость точки С?
Решение. Так как стержень АВ вращается вокруг неподвижной оси, проходящей через точку А, то скорость точки В будет сонаправлена с ВС, а модуль скорости будет вычисляться по формуле (2):


Далее рассмотрим движение точки С. Так как она не может отрываться от плоскости опоры, то её скорость направлена вдоль горизонтальной оси. Применим алгоритм нахождения мгновенного центра вращения, описанный для случая 1 выше. Иллюстрацию применения метода можно видеть на рис. 4.
Из геометрии построения видно, что
По определению мгновенной оси вращения:
![]()
Таким образом:
![]()
Ответ:

Надеюсь, после прочтения этой статьи вы стали лучше понимать кинематику твёрдого тела. Для закрепления материала рекомендую решить предложенные ниже задачи.
Задачи
Задача 1. а) Пусть диск катится по горизонтальной плоскости без проскальзывания со скоростью V. Найти мгновенную ось вращения и угловую скорость вращения относительно неё.
б) Пусть теперь диск катится по конвейеру без проскальзывания с такой же скоростью. Конвейер начинает двигаться со скоростью диска в направлении его движения. Вопрос тот же.

Задача 2. (Савченко О. Я. Сборник «Задачи по физике». № 1.5.7)
а) Скорость точки А твердого тела равна v и образует угол 45° с направлением прямой АВ. Скорость точки В этого тела равна u. Определите проекцию скорости точки В на направление АВ.
б) Скорости точек А и В твердого тела равны v. Скорость точки С, находящейся в плоскости прямой АВ и вектора v, равна u > v. Найдите проекцию скорости точки С на ось, перпендикулярную указанной плоскости.
Ответы
- а) В точке касания с горизонтальной осью. V/R, где R — радиус диска.
- б) На радиус ниже точки касания. Угловая скорость та же.
2. а) UAB = U/√2.
2. б) U₁ = √(u² – v²).
Список использованной литературы
- Сивухин Д. В. Курс общей физики. Том 1. М., 2000.
- Савченко О. Я. Задачи по физике. Новосибирск, 2008.
Автор: Артём Васюков
Содержание:
Вращение твердого тела вокруг неподвижной точки:
Вращением твердого тела вокруг неподвижной точки называют такое движение, при котором одна точка тела остается все время неподвижной. Это вращение часто называют сферическим движением твердого тела в связи с тем, что траектории всех точек тела при таком движении располагаются на поверхностях сфер, описанных из неподвижной точки. Тело, совершающее вращение вокруг неподвижной точки, имеет три степени свободы, так как закрепление одной точки тела уменьшает число степеней свободы на три единицы, а свободное тело имеет шесть степеней свободы. Одной из главных задач при изучении вращения тела вокруг неподвижной точки является установление величин, характеризующих это движение, т. е. углов Эйлера, угловой скорости, углового ускорения, и вывод формул для вычисления скоростей и ускорений точек тела.
Уравнения вращения твердого тела вокруг неподвижной точки (Углы Эйлера)
Три степени свободы, которые имеет тело при вращении вокруг неподвижной точки, требуют для задания положения тела относительно какой-либо системы координат трех независимых величин. Эти три величины, или параметра, можно задать различными способами. В теоретической механике наибольшее применение получили так называемые углы Эйлера, рассмотренные ниже.
Через неподвижную точку 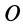
Первый из этих углов—угол прецессии 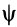 — определяет положение линии узлов
— определяет положение линии узлов  , которая является линией пересечения координатных плоскостей
, которая является линией пересечения координатных плоскостей 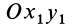 и
и 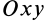 относительно неподвижной координатной оси
относительно неподвижной координатной оси 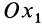 . Для изменения этого угла тело должно вращаться вокруг координатной оси
. Для изменения этого угла тело должно вращаться вокруг координатной оси 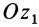 , которую называют осью прецессии. Положение линии узлов при движении тела изменяется как относительно неподвижной системы координат
, которую называют осью прецессии. Положение линии узлов при движении тела изменяется как относительно неподвижной системы координат 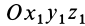 , так и относительно движущегося тела, т. е. подвижной системы координат
, так и относительно движущегося тела, т. е. подвижной системы координат 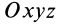 . Угол
. Угол 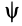 от положительной части оси
от положительной части оси 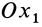 до положительного направления линии узлов
до положительного направления линии узлов  считается положительным, когда он отсчитывается против часовой стрелки, если смотреть с положительного направления оси
считается положительным, когда он отсчитывается против часовой стрелки, если смотреть с положительного направления оси 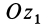 . За положительное направление на линии узлов
. За положительное направление на линии узлов  выбираем то ее направление, с которого поворот оси
выбираем то ее направление, с которого поворот оси 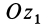 к оси
к оси 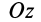 на наименьший угол виден происходящим против часовой стрелки.
на наименьший угол виден происходящим против часовой стрелки.
Вторым углом Эйлера является угол между координатными плоскостями 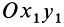 и
и 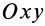 . Его измеряют углом
. Его измеряют углом 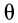 между перпендикулярами к этим координатным плоскостям, которыми являются оси
между перпендикулярами к этим координатным плоскостям, которыми являются оси 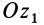 и
и 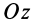 . Угол
. Угол 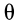 отсчитывают от оси
отсчитывают от оси 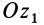 до оси
до оси 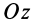 в положительном направлении, если направление поворота оси
в положительном направлении, если направление поворота оси 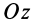 с положительного направления линии узлов
с положительного направления линии узлов  происходит против часовой стрелки.
происходит против часовой стрелки.
Угол 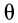 называют углом нутации, а ось
называют углом нутации, а ось  , вокруг которой вращается тело при изменении угла
, вокруг которой вращается тело при изменении угла 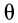 , соответственно называют осью нутации или линией узлов.
, соответственно называют осью нутации или линией узлов.
Для полного определения положения рассматриваемого тела относительно системы координат 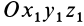 нужно задать угол между подвижной осью координат
нужно задать угол между подвижной осью координат 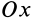 и положительным направлением линии узлов
и положительным направлением линии узлов  —угол собственного вращения
—угол собственного вращения 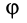 . Угол
. Угол 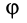 от линии узлов
от линии узлов  до оси
до оси 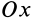 считается положительным, если вокруг оси
считается положительным, если вокруг оси 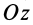 поворот оси
поворот оси 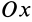 от линии
от линии  виден происходящим против часовой стрелки.
виден происходящим против часовой стрелки.
При изменении угла 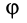 тело вращается вокруг так называемой оси собственного вращения
тело вращается вокруг так называемой оси собственного вращения 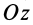 , перпендикулярной плоскости, в которой лежат прямые
, перпендикулярной плоскости, в которой лежат прямые  и
и 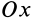 , образующие этот угол. Таким образом, угол
, образующие этот угол. Таким образом, угол 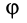 определяет положение подвижной координатной оси
определяет положение подвижной координатной оси 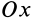 относительно линии узлов
относительно линии узлов  .
.
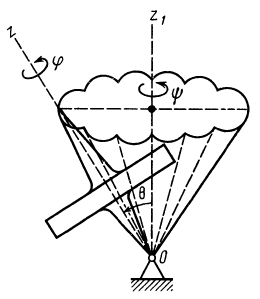
Рис. 74
Углы Эйлера широко применяются в теории гироскопов. Движение гироскопа, т. е. симметричного тела, имеющего неподвижную точку на оси симметрии и быстро вращающегося вокруг этой оси, в общем случае можно представить состоящим из трех движений (рис. 74): вращения с большой угловой скоростью вокруг оси симметрии, или оси собственного вращения, при котором изменяется угол собственного вращения (р; вращения гироскопа вместе со своей осью симметрии вокруг неподвижной оси 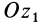 , при котором изменяется угол прецессии
, при котором изменяется угол прецессии 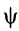 . Третье движение совершает ось симметрии, которая, участвуя в прецессионном движении, описывает коническую поверхность с вершиной в неподвижной точке, а вследствие изменения угла нутации
. Третье движение совершает ось симметрии, которая, участвуя в прецессионном движении, описывает коническую поверхность с вершиной в неподвижной точке, а вследствие изменения угла нутации 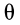 описывает в общем случае волнистую поверхность.
описывает в общем случае волнистую поверхность.
Если угол 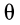 не изменяется, то коническая поверхность является круговым конусом. Если коническую поверхность пересечь плоскостью, перпендикулярной оси прецессии, то получится кривая линия, на которой возможны узловые точки, или точки возврата. Известно, например, что земной шар кроме собственного вращения вокруг своей оси еще прецессирует и совершает нутационное движение.
не изменяется, то коническая поверхность является круговым конусом. Если коническую поверхность пересечь плоскостью, перпендикулярной оси прецессии, то получится кривая линия, на которой возможны узловые точки, или точки возврата. Известно, например, что земной шар кроме собственного вращения вокруг своей оси еще прецессирует и совершает нутационное движение.
В технике особенно важное значение имеет так называемая регулярная прецессия, когда угловые скорости вращения вокруг оси собственного вращения и вокруг неподвижной оси прецессии постоянны и угол между этими осями (угол нутации) остается тоже постоянным.
При вращении тела вокруг неподвижной точки в общем случае изменяются все три угла Эйлера: 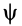 ,
, 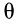 и
и 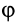 . Углы Эйлера являются независимыми параметрами, или обобщенными координатами, характеризующими положение тела с одной неподвижной точкой относительно неподвижной системы координат. Задание трех углов Эйлера для тела, вращающегося вокруг неподвижной точки, как функций времени является необходимым и достаточным для полного описания такого движения тела.
. Углы Эйлера являются независимыми параметрами, или обобщенными координатами, характеризующими положение тела с одной неподвижной точкой относительно неподвижной системы координат. Задание трех углов Эйлера для тела, вращающегося вокруг неподвижной точки, как функций времени является необходимым и достаточным для полного описания такого движения тела.
Итак, для определения положения тела с одной неподвижной точкой в любой момент времени надо задать углы Эйлера как однозначные функции времени, т. е.
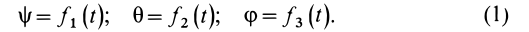
Уравнения (1) являются уравнениями вращения твердого тела вокруг неподвижной точки. Если эти уравнения заданы, то в любой момент времени известно положение твердого тела относительно системы координат 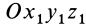 .
.
Отметим, что углы Эйлера не являются единственной комбинацией трех независимых углов для тела, имеющего одну неподвижную точку. Существуют и другие комбинации углов, определяющих положение одной системы координат относительно другой.
Теорема о конечном перемещении твердого тела, имеющего одну неподвижную точку
Тело, имеющее одну неподвижную точку, из одного положения в любое другое можно перевести одним поворотом вокруг оси, проходящей через неподвижную точку. Эту ось называют осью конечного вращения.
Положение тела с неподвижной точкой относительно некоторой системы отсчета можно полностью определить, если задать на какой-либо неподвижной сфере, описанной из неподвижной точки тела, положение сферической фигуры, скрепленной с этим телом. За сферическую фигуру можно принять любую часть поверхности сферы таким же радиусом, что и радиус неподвижной сферы, который обычно принимают равным единице. За сферическую фигуру можно принять также всю сферу единичного радиуса.
При движении тела вокруг неподвижной точки скрепленная с движущимся телом сфера единичного радиуса движется по неподвижной сфере того же радиуса. Положение сферы полностью определяется заданием на этой сфере дуги большого круга, крепленной со сферой.
Пусть положение 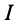 тела характеризуется дугой большого круга
тела характеризуется дугой большого круга 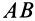 , описанной из неподвижной точки тела, а в положении
, описанной из неподвижной точки тела, а в положении 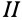 —той же дугой, но в другом положении на сфере
—той же дугой, но в другом положении на сфере 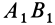 (рис. 75). Аналогично тому, как находится центр конечного вращения для плоской фигуры при плоском перемещении, найдем точку
(рис. 75). Аналогично тому, как находится центр конечного вращения для плоской фигуры при плоском перемещении, найдем точку 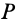 на сфере в случае тела, имеющего одну неподвижную точку. Для этого соединяем точки
на сфере в случае тела, имеющего одну неподвижную точку. Для этого соединяем точки 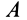 с
с 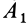 и
и 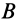 с
с 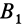 дугами большого круга, проведенными из неподвижной точки тела и целиком лежащими на неподвижной сфере. В серединах дуг
дугами большого круга, проведенными из неподвижной точки тела и целиком лежащими на неподвижной сфере. В серединах дуг 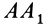
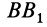 из точек
из точек 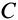 и
и 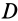 проводим сферические перпендикуляры, т. е. дуги большого круга
проводим сферические перпендикуляры, т. е. дуги большого круга 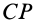 и
и 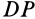 касательные к которым перпендикулярны в точках
касательные к которым перпендикулярны в точках 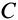 и
и 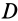 соответственно касательным дуг
соответственно касательным дуг 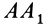 и
и 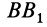 .
.
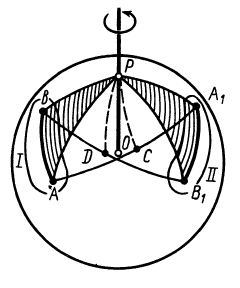
Рис. 75
Эти перпендикуляры, лежащие на сфере, пересекутся в точке 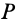 . Из равенства прямоугольных сферических треугольников
. Из равенства прямоугольных сферических треугольников 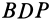 и
и 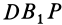 , имеющих общий катет
, имеющих общий катет 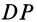 и равные катеты
и равные катеты 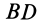 и
и 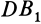 , следует, что гипотенузы этих сферических треугольников тоже равны, т. е. точки 5 и й, равноудалены от точки Р.
, следует, что гипотенузы этих сферических треугольников тоже равны, т. е. точки 5 и й, равноудалены от точки Р.
Аналогично доказывается, что точки 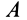 и
и 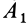 тоже одинаково удалены от точки
тоже одинаково удалены от точки 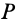 . Если повернуть заштрихованный сферический треугольник
. Если повернуть заштрихованный сферический треугольник 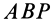 вокруг оси, проходящей через точку
вокруг оси, проходящей через точку 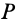 и неподвижную точку
и неподвижную точку 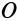 , то этот треугольник, перемещаясь по сфере, совпадет всеми своими точками с равным ему по трем сторонам сферическим треугольником
, то этот треугольник, перемещаясь по сфере, совпадет всеми своими точками с равным ему по трем сторонам сферическим треугольником 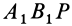 , так как сферический угол на сфере, на который надо повернуть вокруг
, так как сферический угол на сфере, на который надо повернуть вокруг 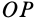 дугу
дугу 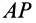 до совпадения с дугой
до совпадения с дугой 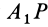 , равен сферическому углу на той же сфере, на который надо повернуть дугу
, равен сферическому углу на той же сфере, на который надо повернуть дугу 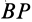 до совпадения с дугой
до совпадения с дугой 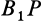 .
.
Итак, путем поворота вокруг оси, перпендикулярной поверхности сферы и проходящей через точку 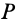 и, следовательно, проходящей также и через центр сферы, где расположена неподвижная точка, тело можно переместить из одного положения в любое другое. Для каждых двух положений тела получаются соответствующая точка
и, следовательно, проходящей также и через центр сферы, где расположена неподвижная точка, тело можно переместить из одного положения в любое другое. Для каждых двух положений тела получаются соответствующая точка 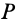 и, следовательно, соответствующая ось конечного вращения, проходящая через эту точку и неподвижную точку тела.
и, следовательно, соответствующая ось конечного вращения, проходящая через эту точку и неподвижную точку тела.
Мгновенная ось вращения (Аксоиды)
Ось, вокруг которой следует вращать тело, имеющее одну неподвижную точку, для перевода его из одного положения в другое, бесконечно близкое первому, называют мгновенной осью вращения (или мгновенной осью) для данного момента времени.
Любое движение тела вокруг неподвижной точки можно заменить последовательностью вращений вокруг совокупности мгновенных осей. Геометрическое место мгновенных осей относительно неподвижных осей координат, по отношению к которым рассматривается движение тела, называется неподвижным аксоидом. Неподвижный аксоид является конической поверхностью с вершиной в неподвижной точке тела, так как все мгновенные оси проходят через неподвижную точку.
Геометрическое место мгновенных осей в движущемся теле представляет подвижный аксоид, являющийся также конической поверхностью. Для каждого движения твердого тела вокруг неподвижной точки имеется пара аксоидов. При этом, когда тело совершает вращение вокруг неподвижной точки, подвижный аксоид катится по неподвижному без скольжения, так как общая образующая этих аксоидов в каждый момент времени служит мгновенной осью, вокруг которой вращается тело, и, следовательно, все точки оси в рассматриваемый момент времени неподвижны. Если подвижный аксоид катится без скольжения по неподвижному аксоиду, то осуществляется движение тела вокруг неподвижной точки.
Очевидно, что при плоском движении твердого тела конические аксоиды являются цилиндрическими поверхностями, которые в пересечении с плоскостью движения плоской фигуры образуют центроиды для этой фигуры.
Практически понятие аксоидов используется для классификации видов прецессионных движений гироскопов.
Угловая скорость и угловое ускорение при вращении тела вокруг неподвижной точки
Так как движение тела, имеющего одну неподвижную точку, в каждый момент времени можно считать вращением вокруг мгновенной оси, то в качестве величин, характеризующих это движение, можно ввести мгновенную угловую скорость и мгновенное угловое ускорение вращения твердого тела вокруг неподвижной точки. Очевидно, вводимая угловая скорость является векторной величиной, направленной в каждый момент времени по соответствующей мгновенной оси, и при использовании правой системы координат вектор угловой скорости 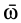 направлен по мгновенной оси так, что с направления этого вектора видно вращение тела вокруг мгновенной оси против часовой стрелки. Модуль вектора угловой скорости можно выразить через элементарный угол поворота
направлен по мгновенной оси так, что с направления этого вектора видно вращение тела вокруг мгновенной оси против часовой стрелки. Модуль вектора угловой скорости можно выразить через элементарный угол поворота 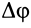 вокруг мгновенной оси за время
вокруг мгновенной оси за время 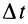 :
:
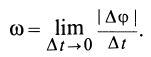
Элементарный угол поворота 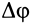 , аналогично случаю вращения тела вокруг неподвижной оси, следует рассматривать как угол между двумя положениями в моменты
, аналогично случаю вращения тела вокруг неподвижной оси, следует рассматривать как угол между двумя положениями в моменты 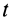 и
и 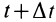 подвижной плоскости, скрепленной с телом и проходящей через мгновенную ось в момент времени
подвижной плоскости, скрепленной с телом и проходящей через мгновенную ось в момент времени 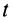 .
.
Введенный таким образом вектор угловой скорости 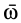 характеризует угловую скорость вращения вокруг мгновенной оси, направление мгновенной оси и направление вращения тела вокруг этой оси. Вектор угловой скорости
характеризует угловую скорость вращения вокруг мгновенной оси, направление мгновенной оси и направление вращения тела вокруг этой оси. Вектор угловой скорости 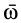 можно прикладывать в любой точке мгновенной оси (рис. 76).
можно прикладывать в любой точке мгновенной оси (рис. 76).
За вектор углового ускорения 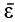 при вращении тела вокруг неподвижной точки принимают вектор, который характеризует изменение угловой скорости со в данный момент как по числовой величине, так и по направлению. Известно, что такой характеристикой является производная по времени от вектора угловой скорости
при вращении тела вокруг неподвижной точки принимают вектор, который характеризует изменение угловой скорости со в данный момент как по числовой величине, так и по направлению. Известно, что такой характеристикой является производная по времени от вектора угловой скорости 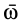 . Таким образом, угловое ускорение
. Таким образом, угловое ускорение
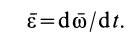
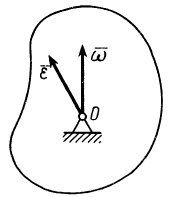
Рис. 76
Так как угловая скорость может изменяться по модулю и направлению, то в общем случае угловое ускорение не направлено по мгновенной оси, а имеет направление как производная по времени от вектора 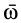 , параллельное касательной к годографу этого вектора. Условимся угловое ускорение
, параллельное касательной к годографу этого вектора. Условимся угловое ускорение 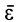 изображать в любой точке прямой, параллельной этой касательной годографа
изображать в любой точке прямой, параллельной этой касательной годографа 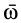 , но проходящей через неподвижную точку тела.
, но проходящей через неподвижную точку тела.
Скорости точек тела при вращательном движении вокруг неподвижной точки
При рассмотрении вращательного движения тела вокруг неподвижной оси получена векторная формула Эйлера, по которой скорости точек тела полностью характеризуются общей для всех точек тела угловой скоростью вращения и расположением точек тела относительно оси вращения.
Формула Эйлера справедлива и для случая вращения твердого тела вокруг неподвижной точки.
В этом случае в каждый момент времени тело вращается вокруг мгновенной оси, проходящей через неподвижную точку, с угловой скоростью со, направленной по мгновенной оси. Точки тела, лежащие на мгновенной оси, имеют скорости, равные нулю, как и в случае неподвижной оси вращения.
Следовательно, линейные скорости точек тела при вращении вокруг неподвижной точки можно вычислять также по векторной формуле Эйлера, как и в случае вращения вокруг неподвижной оси, только радиус-вектор каждой точки удобно проводить из неподвижной точки тела.
Итак, скорость 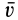 какой-либо точки
какой-либо точки 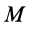 тела (рис. 77), по векторной формуле Эйлера,
тела (рис. 77), по векторной формуле Эйлера,

Модуль скорости
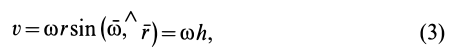
где 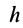 — кратчайшее расстояние от рассматриваемой точки до мгновенной оси.
— кратчайшее расстояние от рассматриваемой точки до мгновенной оси.
Таким образом, скорости точек тела пропорциональны расстояниям от этих точек до мгновенной оси. Направление скорости какой-либо точки тела перпендикулярно плоскости, в которой находятся векторы 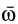 и
и 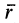 , а следовательно, перпендикулярно отрезку
, а следовательно, перпендикулярно отрезку 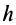 .
.
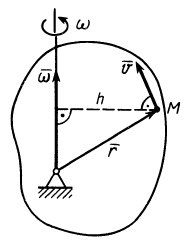
Рис. 77
Если требуется найти модуль угловой скорости тела в определенный момент времени, то для этого, согласно (3), достаточно разделить скорость какой-либо точки в этот же момент времени на кратчайшее расстояние от этой точки до мгновенной оси.
Мгновенную ось в конкретных задачах часто находят из механических условий задачи, т. е. в рассматриваемый момент времени она всегда проходит через две неподвижные точки тела. Так, если движущееся тело касается в какой-либо точке неподвижной поверхности другого тела и при этом нет скольжения, то мгновенная ось проходит через эту неподвижную в данный момент времени точку.
В случае качения без скольжения одного конуса по другому, неподвижному, конусу (рис. 78) мгновенной осью является та общая образующая этих конусов 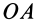 , вдоль которой в данный момент времени они касаются друг друга. Если, например, скорость
, вдоль которой в данный момент времени они касаются друг друга. Если, например, скорость 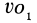 точки
точки 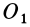 известна, то угловая скорость подвижного конуса
известна, то угловая скорость подвижного конуса
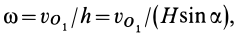
где 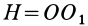 и
и 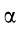 — угол полураствора подвижного конуса.
— угол полураствора подвижного конуса.
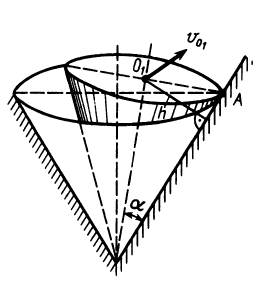
Рис. 78
Проекции угловой скорости тела 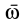 как на подвижные, так и неподвижные оси координат можно определить также через углы Эйлера как функции времени, характеризующие положение тела относительно неподвижной системы координат.
как на подвижные, так и неподвижные оси координат можно определить также через углы Эйлера как функции времени, характеризующие положение тела относительно неподвижной системы координат.
Если спроецировать правую и левую части (2) на координатные оси, то получим формулы Эйлера для проекций скоростей 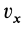 ,
, 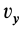 и
и 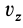 :
:
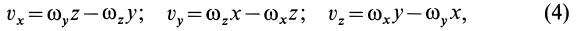
где 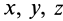 — координаты точек тела, скорости которых определяются.
— координаты точек тела, скорости которых определяются.
Если взять точки тела, лежащие на мгновенной оси в рассматриваемый момент времени, то для них скорости равны нулю, а следовательно, приняв равными нулю 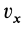 ,
, 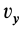 ,
,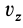 , из (4) получим следующие уравнения для координат этих точек:
, из (4) получим следующие уравнения для координат этих точек:
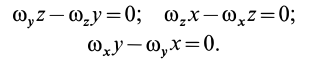
Эти уравнения можно представить в виде
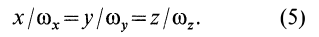
Для определенного момента времени формула (5) является уравнением мгновенной оси. Если же величины, входящие в (5), рассматривать как функции времени, то она будет представлять собой уравнения подвижного или неподвижного аксоида (в параметрической форме) в зависимости от того, в какой системе координат она составлена.
Если 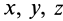 являются текущими координатами точки мгновенной оси относительно подвижных осей, скрепленных с движущимся телом, а
являются текущими координатами точки мгновенной оси относительно подвижных осей, скрепленных с движущимся телом, а 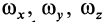 — проекции угловой скорости тела на эти оси, то формула (5) является уравнением подвижного аксоида.
— проекции угловой скорости тела на эти оси, то формула (5) является уравнением подвижного аксоида.
Если вместо подвижных осей координат взять неподвижные оси, относительно которых рассматривается движение тела, и проекции угловой скорости тоже взять на эти оси, то тогда формула (5) будет уравнением неподвижного аксоида.
Скорость какой-либо точки можно вычислить как первую производную по времени от радиуса-вектора 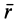 этой точки, проведенного из неподвижной точки. С другой стороны, скорость точки тела, вращающегося вокруг неподвижной точки, можно вычислить по векторной формуле Эйлера (2). Следовательно, производная по времени от радиуса-вектора любой точки твердого тела, вращающегося вокруг неподвижной точки, определится по формуле
этой точки, проведенного из неподвижной точки. С другой стороны, скорость точки тела, вращающегося вокруг неподвижной точки, можно вычислить по векторной формуле Эйлера (2). Следовательно, производная по времени от радиуса-вектора любой точки твердого тела, вращающегося вокруг неподвижной точки, определится по формуле

Длина радиуса-вектора 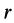 как расстояние между двумя точками твердого тела является постоянной величиной при движении этого тела. Следовательно, равенство (6) можно рассматривать как формулу для вычисления производной по времени от вектора, модуль которого постоянен, и изменение этого вектора происходит только вследствие вращения его с угловой скоростью со вместе с телом вокруг неподвижной точки.
как расстояние между двумя точками твердого тела является постоянной величиной при движении этого тела. Следовательно, равенство (6) можно рассматривать как формулу для вычисления производной по времени от вектора, модуль которого постоянен, и изменение этого вектора происходит только вследствие вращения его с угловой скоростью со вместе с телом вокруг неподвижной точки.
Если взять подвижную систему координат 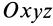 , скрепленную с телом, которое вращается вокруг неподвижной точки с угловой скоростью
, скрепленную с телом, которое вращается вокруг неподвижной точки с угловой скоростью 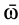 , то для единичных векторов
, то для единичных векторов 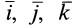 , направленных по этим осям координат, как для векторов, модули которых постоянны, на основании (6) имеем:
, направленных по этим осям координат, как для векторов, модули которых постоянны, на основании (6) имеем:
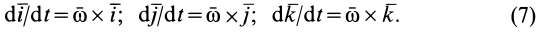
Формулы (7) называют формулами Пуассона.
Ускорения точек тела при вращении вокруг неподвижной точки
Формулу для ускорения какой-либо точки 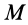 тела, вращающегося вокруг неподвижной точки, нельзя получить непосредственно используя формулу для ускорения при вращательном движении вокруг неподвижной оси, так как в рассматриваемом случае угловое ускорение в общем случае не направлено по оси вращения, а следовательно, и по а>. Во всем остальном формулы для ускорения в этих случаях полностью аналогичны.
тела, вращающегося вокруг неподвижной точки, нельзя получить непосредственно используя формулу для ускорения при вращательном движении вокруг неподвижной оси, так как в рассматриваемом случае угловое ускорение в общем случае не направлено по оси вращения, а следовательно, и по а>. Во всем остальном формулы для ускорения в этих случаях полностью аналогичны.
Формулу для ускорения какой-либо точки тела 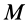 можно получить путем дифференцирования по времени вектора скорости, учитывая, что скорость вычисляют по формуле (2). Выполняя это дифференцирование, получаем
можно получить путем дифференцирования по времени вектора скорости, учитывая, что скорость вычисляют по формуле (2). Выполняя это дифференцирование, получаем
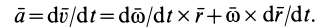
Так как
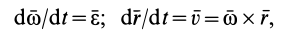
то

Формулу (8) часто называют формулой Ривальса. Часть общего ускорения точки

называют вращательным ускорением, а другую часть

— осестремительным ускорением. Следовательно, формула (8) примет вид

т. е. ускорение точки тела, вращающегося вокруг неподвижной точки, равно векторной сумме вращательного и осестремительного ускорений.
В общем случае вращательное и осестремительное ускорения не перпендикулярны; следовательно, модуль ускорения 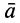 вычисляют как диагональ параллелограмма по формуле
вычисляют как диагональ параллелограмма по формуле
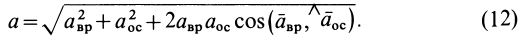
Рассмотрим вращательное и осестремительное ускорения по отдельности. Вращательное ускорение вычисляют по формуле (9), аналогичной формуле (2) для скорости точки. Только здесь вместо угловой скорости 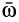 входит угловое ускорение
входит угловое ускорение 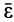 . Поэтому вращательное ускорение
. Поэтому вращательное ускорение 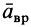 направлено аналогично скорости
направлено аналогично скорости 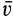 если тело вращается в рассматриваемый момент времени с угловой скоростью, равной угловому ускорению
если тело вращается в рассматриваемый момент времени с угловой скоростью, равной угловому ускорению 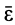 .
.
Модуль вращательного ускорения 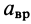 определяют аналогично модулю скорости
определяют аналогично модулю скорости 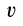 [см. формулу (3)]:
[см. формулу (3)]:

где 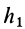 — кратчайшее расстояние от точки тела до линии, по которой направлено угловое ускорение
— кратчайшее расстояние от точки тела до линии, по которой направлено угловое ускорение 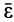 (рис. 79). Формула (13) для
(рис. 79). Формула (13) для 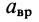 получается из (9):
получается из (9):
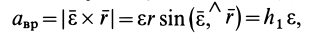
где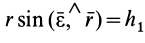 .
.
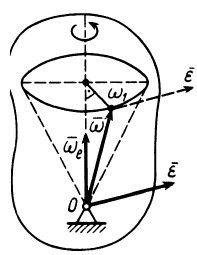
Рис. 79
Из (13) следует, что вектор углового ускорения 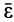 расположен на прямой линии, проходящей через неподвижную точку. В противном случае эта точка имела бы не равное нулю вращательное ускорение.
расположен на прямой линии, проходящей через неподвижную точку. В противном случае эта точка имела бы не равное нулю вращательное ускорение.
Модуль осестремительного ускорения 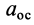 можно получить из формулы (10):
можно получить из формулы (10):
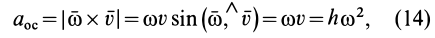
так как угловая скорость 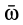 перпендикулярна скорости
перпендикулярна скорости 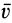 .
.
Осестремительное ускорение направлено по перпендикуляру к мгновенной оси, опущенному из точки, для которой оно вычисляется, т. е. по отрезку 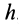 , так как, являясь векторным произведением
, так как, являясь векторным произведением 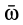 и
и 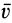 , оно перпендикулярно плоскости, где находятся эти векторы, и имеет направление вектора этого векторного произведения. Если ввести вектор
, оно перпендикулярно плоскости, где находятся эти векторы, и имеет направление вектора этого векторного произведения. Если ввести вектор 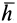 , направленный по перпендикуляру от мгновенной оси к рассматриваемой точке, то
, направленный по перпендикуляру от мгновенной оси к рассматриваемой точке, то

В случае вращения твердого тела вокруг неподвижной оси угловое ускорение и угловая скорость направлены по этой оси; тогда расстояния 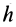 и
и 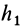 , равны. Следовательно, вращательное ускорение превращается в касательное ускорение, а осестремительное— в нормальное или центростремительное ускорение.
, равны. Следовательно, вращательное ускорение превращается в касательное ускорение, а осестремительное— в нормальное или центростремительное ускорение.
Таким образом, вращение тела вокруг неподвижной точки можно рассматривать как более общее движение, чем вращение тела вокруг неподвижной оси.
Вычисление углового ускорения
Для вычисления ускорения точек тела необходимо знать угловое ускорение 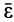 . Рассмотрим два основных способа его вычисления.
. Рассмотрим два основных способа его вычисления.
1. Если известны проекции угловой скорости на подвижные или неподвижные оси координат 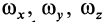 , то проекции углового ускорения на те же оси определяют по формулам
, то проекции углового ускорения на те же оси определяют по формулам
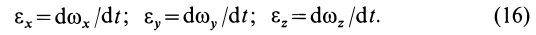
По проекциям легко найти модуль углового ускорения и косинусы его углов с осями координат.
2. Другой способ определения углового ускорения 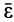 основан на его разложении на две взаимно перпендикулярные составляющие. Если ввести единичный вектор
основан на его разложении на две взаимно перпендикулярные составляющие. Если ввести единичный вектор 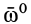 , направленный по
, направленный по 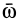 , то
, то
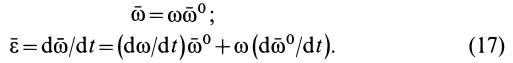
Составляющая 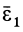 полного углового ускорения
полного углового ускорения 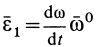 направлена по вектору
направлена по вектору 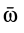 , когда
, когда 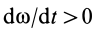 , и противоположно ему при
, и противоположно ему при 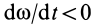 .
.
Составляющая 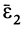 полного углового ускорения
полного углового ускорения 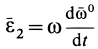 всегда перпендикулярна
всегда перпендикулярна 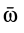 , так как производная по времени от единичного вектора
, так как производная по времени от единичного вектора 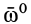 есть вектор, перпендикулярный дифференцируемому единичному вектору и, следовательно, перпендикулярный вектору
есть вектор, перпендикулярный дифференцируемому единичному вектору и, следовательно, перпендикулярный вектору 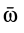 .
.
Составляющая углового ускорения 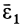 является полным угловым ускорением при вращении тела вокруг неподвижной оси, так как составляющая
является полным угловым ускорением при вращении тела вокруг неподвижной оси, так как составляющая 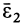 в этом случае равна нулю. Вычислим составляющую углового ускорения
в этом случае равна нулю. Вычислим составляющую углового ускорения 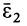 . Часто угловая скорость постоянна по модулю и изменяется только по направлению. В этом случае составляющая
. Часто угловая скорость постоянна по модулю и изменяется только по направлению. В этом случае составляющая 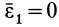 и полное угловое ускорение совпадает с
и полное угловое ускорение совпадает с 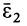 .
.
Если же угловое ускорение 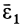 не равно нулю, то его можно вычислить отдельно и затем, сложив с составляющей
не равно нулю, то его можно вычислить отдельно и затем, сложив с составляющей 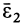 , определить полное угловое ускорение
, определить полное угловое ускорение 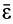 . Итак, если угловая скорость постоянна, то
. Итак, если угловая скорость постоянна, то
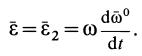
В этом случае воспользуемся определением углового ускорения через угловую скорость непосредственно:
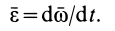
Учитывая, что 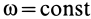 , и применяя формулу, аналогичную производной по времени от радиуса-вектора [см. формулу (6)], когда радиус-вектор постоянен по длине, будем иметь
, и применяя формулу, аналогичную производной по времени от радиуса-вектора [см. формулу (6)], когда радиус-вектор постоянен по длине, будем иметь

где 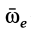 — угловая скорость вращения дифференцируемого по времени вектора
— угловая скорость вращения дифференцируемого по времени вектора 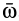 , т. е. угловая скорость вращения мгновенной оси, по которой направлен вектор
, т. е. угловая скорость вращения мгновенной оси, по которой направлен вектор 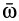 . Модуль углового ускорения можно найти аналогично скорости точки, т. е.
. Модуль углового ускорения можно найти аналогично скорости точки, т. е.

где расстоянием 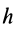 является
является 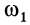 — кратчайшее расстояние от конца вектора
— кратчайшее расстояние от конца вектора 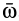 до оси, по которой направлена угловая скорость
до оси, по которой направлена угловая скорость 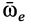 (рис. 80).
(рис. 80).
Вектор углового ускорения 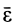 пройдет через неподвижную точку и будет параллелен касательной к годографу вектора
пройдет через неподвижную точку и будет параллелен касательной к годографу вектора 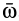 . Окончательно направление
. Окончательно направление 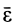 берут в соответствии с формулой (18), т. е. по направлению вращения мгновенной оси в зависимости от угловой скорости
берут в соответствии с формулой (18), т. е. по направлению вращения мгновенной оси в зависимости от угловой скорости 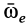 .
.
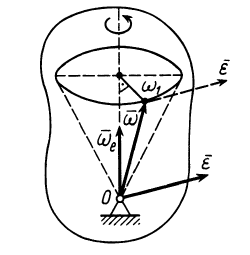
Рис. 80
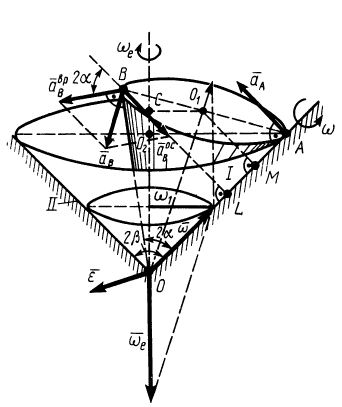
Рис. 81
Рассмотрим теперь пример на вычисление угловой скорости, углового ускорения и линейных скоростей и ускорений точек тела, вращающегося вокруг неподвижной точки.
- Заказать решение задач по теоретической механике
Пример с решением
Круговой конус I с углом раствора 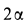 катится без скольжения по внутренней стороне неподвижного конуса II с углом раствора
катится без скольжения по внутренней стороне неподвижного конуса II с углом раствора 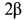 (рис. 81). Скорость точки
(рис. 81). Скорость точки 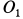 подвижного конуса постоянна и равна
подвижного конуса постоянна и равна 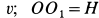 .
.
Определить угловую скорость и угловое ускорение подвижного конуса, а также скорости и ускорения точек 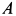 и
и 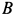 этого конуса.
этого конуса.
Решение. Мгновенной осью конуса I является образующая 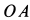 . Если скорость точки
. Если скорость точки 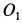 направлена от плоскости
направлена от плоскости 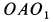 во внешнюю сторону, то угловая скорость конуса
во внешнюю сторону, то угловая скорость конуса 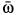 направлена по мгновенной оси от точки
направлена по мгновенной оси от точки 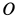 к точке
к точке 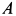 . Числовое значение угловой скорости
. Числовое значение угловой скорости
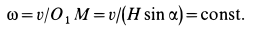
Скорость точки 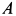 равна нулю, так как эта точка находится на мгновенной оси. Скорость точки
равна нулю, так как эта точка находится на мгновенной оси. Скорость точки 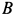 вычисляем по формуле
вычисляем по формуле
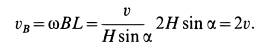
Скорость 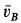 перпендикулярна плоскости
перпендикулярна плоскости 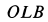 и направлена от нее во внешнюю сторону.
и направлена от нее во внешнюю сторону.
Угловое ускорение 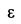 вычисляем по формуле (19):
вычисляем по формуле (19):
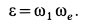
Годографом вектора 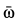 является окружность радиуса
является окружность радиуса 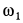 :
:
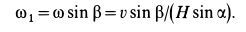
Если рассмотреть плоскость, в которой находятся мгновенная ось 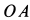 , ось подвижного конуса
, ось подвижного конуса 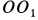 и ось неподвижного конуса
и ось неподвижного конуса 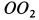 (плоскость рисунка), то при движении конуса I эта плоскость вращается вокруг оси неподвижного конуса
(плоскость рисунка), то при движении конуса I эта плоскость вращается вокруг оси неподвижного конуса 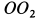 , расположенной в указанной плоскости, а следовательно, вокруг этой оси вращается и мгновенная ось
, расположенной в указанной плоскости, а следовательно, вокруг этой оси вращается и мгновенная ось 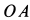 , находящаяся в этой плоскости. Угловую скорость этого вращения
, находящаяся в этой плоскости. Угловую скорость этого вращения 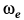 можно определить, если скорость какой-либо точки этой плоскости, участвующей только во вращении вокруг
можно определить, если скорость какой-либо точки этой плоскости, участвующей только во вращении вокруг 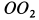 и не имеющей другого движения, разделить на кратчайшее расстояние от этой точки до оси
и не имеющей другого движения, разделить на кратчайшее расстояние от этой точки до оси 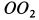 . Отмеченными выше свойствами обладают все точки, расположенные на оси подвижного конуса
. Отмеченными выше свойствами обладают все точки, расположенные на оси подвижного конуса 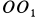 . Выбрав на этой оси точку
. Выбрав на этой оси точку 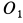 , имеем
, имеем
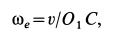
где 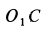 —кратчайшее расстояние от точки
—кратчайшее расстояние от точки 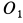 до
до 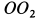 . Так как
. Так как
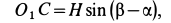
то
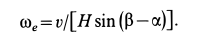
Таким образом,
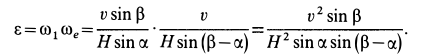
Так как скорость точки 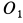 направлена во внешнюю сторону от рисунка, то мгновенная ось
направлена во внешнюю сторону от рисунка, то мгновенная ось 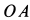 вращается вокруг
вращается вокруг 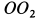 по часовой стрелке и, следовательно, угловое ускорение
по часовой стрелке и, следовательно, угловое ускорение 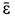 направлено перпендикулярно плоскости
направлено перпендикулярно плоскости 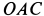 во внешнюю сторону.
во внешнюю сторону.
Ускорение какой-либо точки подвижного конуса можно определить по формуле
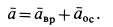
Для точки 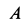 расстояние
расстояние 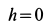 и поэтому
и поэтому 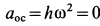 . Для вращательного ускорения имеем
. Для вращательного ускорения имеем
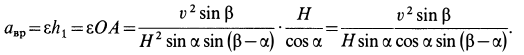
Ускорение 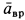 , а следовательно, и полное ускорение
, а следовательно, и полное ускорение 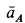 этой точки направлены перпендикулярно
этой точки направлены перпендикулярно 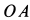 и находятся в плоскости
и находятся в плоскости 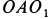 . С положительного направления вектора
. С положительного направления вектора 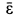 направление
направление 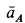 должно быть направлено как скорость при вращении против часовой стрелки вокруг
должно быть направлено как скорость при вращении против часовой стрелки вокруг 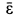 . Для точки
. Для точки 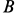
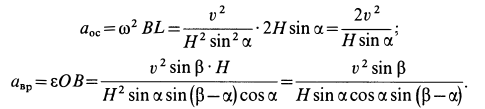
Ускорение 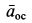 направлено по
направлено по 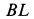 от точки
от точки 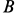 к точке
к точке 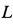 , а ускорение
, а ускорение 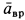 —перпендикулярно
—перпендикулярно 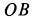 и расположено в плоскости
и расположено в плоскости 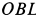 .
.
Полное ускорение точки 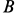 вычисляется как диагональ параллелограмма, построенного на ускорениях
вычисляется как диагональ параллелограмма, построенного на ускорениях 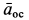 и
и 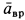 , т. е.
, т. е.
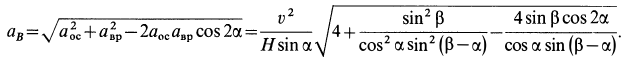
Отметим, что 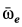 можно получить, если угловую скорость
можно получить, если угловую скорость 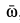 , направленную по мгновенной оси, разложить по правилу параллелограмма по осям подвижного и неподвижного конусов. Тогда составляющая по оси неподвижного конуса и будет угловой скоростью
, направленную по мгновенной оси, разложить по правилу параллелограмма по осям подвижного и неподвижного конусов. Тогда составляющая по оси неподвижного конуса и будет угловой скоростью 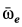 .
.
Общий случай движения свободного твердого тела
Разложение движения свободного твердого тела на поступательное и вращательное
Рассмотрим общий случай движения свободного твердого тела, т. е. тела, имеющего шесть степеней свободы. Покажем, что самое общее движение свободного твердого тела можно представить состоящим из поступательного движения вместе с какой-либо точкой тела и вращательного движения вокруг этой точки.
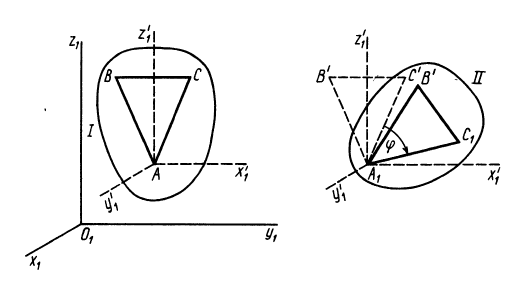
Рис. 82
Положение тела относительно какой-либо системы координат 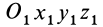 полностью определяется заданием трех точек тела, не лежащих на одной прямой, или заданием треугольника, скрепленного с телом (рис. 82). Треугольник
полностью определяется заданием трех точек тела, не лежащих на одной прямой, или заданием треугольника, скрепленного с телом (рис. 82). Треугольник 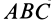 , а следовательно, и тело, скрепленное с ним, из одного положения I в любое другое положение II можно переместить одним поступательным перемещением вместе с какой-либо точкой тела (например, точкой
, а следовательно, и тело, скрепленное с ним, из одного положения I в любое другое положение II можно переместить одним поступательным перемещением вместе с какой-либо точкой тела (например, точкой 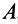 , когда подвижная система координат
, когда подвижная система координат 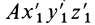 перемещается поступательно) и поворотом относительно подвижной системы координат
перемещается поступательно) и поворотом относительно подвижной системы координат 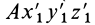 , т. е. вокруг оси, проходящей через эту точку.
, т. е. вокруг оси, проходящей через эту точку.
Поступательная часть перемещения тела зависит от выбора точки, вместе с которой перемещается тело, а вращательная часть перемещения вокруг оси или вокруг точки не зависит от выбора точки. Поступательную часть перемещения можно поменять местами с вращательной частью, и, наконец, их можно выполнять одновременно, т. е. пока тело совершает поступательное перемещение из одного положения в другое, за это же время можно осуществить и поворот тела вокруг точки на требующийся угол.
Если два положения тела бесконечно близки, то истинное элементарное перемещение свободного твердого тела можно заменить элементарным поступательным перемещением вместе с какой-либо точкой тела и элементарным поворотом вокруг мгновенной оси, проходящей через эту точку, осуществляемыми за то же время, что и истинное перемещение, тела.
Любое движение свободного твердого тела, таким образом, можно заменить совокупностью поступательных движений вместе с какой-либо точкой тела и вращений вокруг этой точки, совершаемых за то же время, что и истинное движение. Поступательное движение вместе с точкой тела и подвижной системой координат 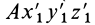 является переносным движением, а движение тела относительно этой подвижной системы координат, являющееся в каждый момент времени вращением вокруг своей мгновенной оси, проходящей через эту подвижную точку тела, есть относительное движение.
является переносным движением, а движение тела относительно этой подвижной системы координат, являющееся в каждый момент времени вращением вокруг своей мгновенной оси, проходящей через эту подвижную точку тела, есть относительное движение.
Итак, любое движение свободного твердого тела можно составить из поступательного движения вместе с подвижной системой координат и сферического движения относительно этой системы координат. Для относительного сферического движения можно ввести угловую скорость 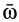 и угловое ускорение
и угловое ускорение 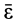 , которое является первой производной по времени от
, которое является первой производной по времени от 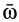 , как в случае вращения тела вокруг неподвижной точки.
, как в случае вращения тела вокруг неподвижной точки.
Угловую скорость и угловое ускорение относительного вращательного движения вокруг какой-либо точки тела называют в общем случае угловой скоростью и угловым ускорением свободного твердого тела. Эти величины не зависят от выбора точки тела. От выбора точки тела зависит только переносное поступательное движение тела.
Уравнения движения свободного твердого тела
В общем случае для определения положения свободного твердого тела относительно системы координат 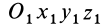 достаточно задать относительно этой системы координат положение другой системы координат
достаточно задать относительно этой системы координат положение другой системы координат 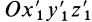 , движущейся поступательно относительно первой системы вместе с ка-кой-либо точкой
, движущейся поступательно относительно первой системы вместе с ка-кой-либо точкой 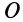 рассматриваемого тела, и углы Эйлера, определяющие положение системы координат
рассматриваемого тела, и углы Эйлера, определяющие положение системы координат 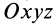 , скрепленной с движущимся телом, относительно системы координат
, скрепленной с движущимся телом, относительно системы координат 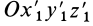 (рис. 83).
(рис. 83).
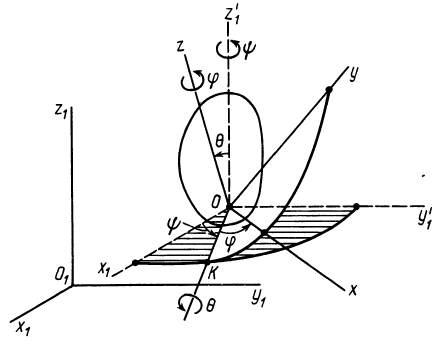
Рис. 83
Для простоты предположим, что оси 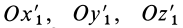 соответственно параллельны осям
соответственно параллельны осям 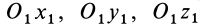 . Таким образом, положение свободного твердого тела относительно системы координат
. Таким образом, положение свободного твердого тела относительно системы координат 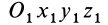 полностью определяется, если относительно этой системы задать координаты точки
полностью определяется, если относительно этой системы задать координаты точки  тела как однозначные функции времени и углы Эйлера подвижной системы координат
тела как однозначные функции времени и углы Эйлера подвижной системы координат 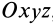 , скрепленной с движущимся телом, относительно системы координат
, скрепленной с движущимся телом, относительно системы координат 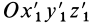 , поступательно движущейся вместе с точкой
, поступательно движущейся вместе с точкой  тела:
тела:
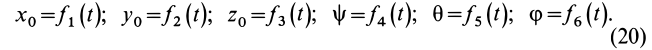
Уравнения (20) являются кинематическими уравнениями движения свободного твердого тела в общем случае его движения. Этих уравнений шесть, т. е. столько, сколько степеней свободы у свободного твердого тела. Первые три уравнения (20) определяют переносное движение тела вместе с точкой  О, вторые три уравнения определяют вращательное движение вокруг этой точки.
О, вторые три уравнения определяют вращательное движение вокруг этой точки.
Первые три уравнения для рассматриваемого движения свободного твердого тела зависят от выбора точки  тела; последние три уравнения (углы Эйлера) не зависят от выбора точки
тела; последние три уравнения (углы Эйлера) не зависят от выбора точки  , вокруг которой рассматривается вращение тела.
, вокруг которой рассматривается вращение тела.
Скорости и ускорения точек свободного твердого тела в общем случае
Так как движение свободного твердого тела в общем случае можно представить как сложное движение, то и скорость, и ускорение какой-либо точки 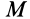 этого тела можно вычислить соответственно по теоремам сложения скоростей и ускорений (рис. 84). Так, для скорости
этого тела можно вычислить соответственно по теоремам сложения скоростей и ускорений (рис. 84). Так, для скорости 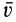 точки
точки 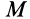
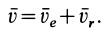
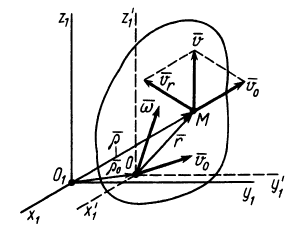
Рис. 84
Переносным движением является поступательное движение тела вместе с точкой О этого тела. Следовательно, скорости поступательного переносного движения одинаковы у всех точек тела и равны скорости 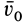 точки
точки  . Относительное движение есть вращение вокруг точки
. Относительное движение есть вращение вокруг точки  , и, следовательно, скорость относительного движения можно вычислить по векторной формуле Эйлера:
, и, следовательно, скорость относительного движения можно вычислить по векторной формуле Эйлера:
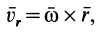
где 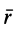 — радиус-вектор точки
— радиус-вектор точки 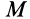 , проведенный из точки
, проведенный из точки  ;
; 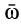 —угловая скорость вращения тела вокруг точки
—угловая скорость вращения тела вокруг точки  или подвижной мгновенной оси, проходящей через точку
или подвижной мгновенной оси, проходящей через точку  .
.
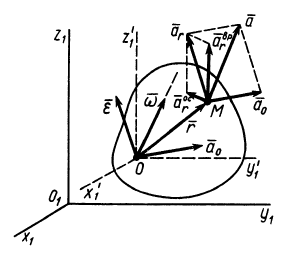
Рис. 85
Окончательно для скорости точки 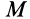 получим следующую формулу:
получим следующую формулу:
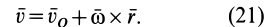
Формулу (21) можно получить непосредственным дифференцированием векторного равенства
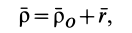
справедливого для любого момента времени. Возьмем полные производные по времени от обеих частей равенства, учитывая изменения векторов относительно неподвижной системы координат 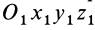 . Имеем
. Имеем
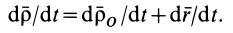
Здесь 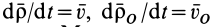 — скорости точек тела
— скорости точек тела 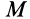 и
и  соответственно. Модуль вектора
соответственно. Модуль вектора 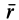 как отрезка, соединяющего две точки тела, не изменяется при движении этого тела. Следовательно, по формуле производной по времени от вектора постоянного модуля получаем
как отрезка, соединяющего две точки тела, не изменяется при движении этого тела. Следовательно, по формуле производной по времени от вектора постоянного модуля получаем
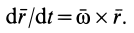
Объединяя результаты, получаем формулу (21):
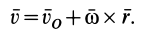
Так же как и при плоском движении твердого тела, часть скорости 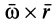 можно истолковать как скорость от вращения тела вокруг точки
можно истолковать как скорость от вращения тела вокруг точки  .
.
Ускорение а точки 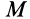 (рис. 85) в частном случае, когда переносное движение является поступательным, определяем по формуле
(рис. 85) в частном случае, когда переносное движение является поступательным, определяем по формуле
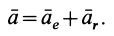
Ускорения переносного движения всех точек тела равны ускорению 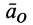 точки
точки  , так как за поступательное переносное движение принимается движение вместе с точкой
, так как за поступательное переносное движение принимается движение вместе с точкой  .
.
Ускорение относительного движения, как и при вращении тела вокруг неподвижной точки, состоит из вращательной и осестремительной составляющих, т. е.
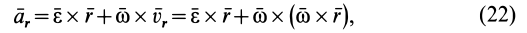
где 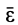 — угловое ускорение тела.
— угловое ускорение тела.
Окончательная формула для ускорения точки 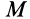 свободного тела в общем случае его движения имеет вид
свободного тела в общем случае его движения имеет вид
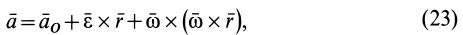
или на основании формулы Ривальса

где
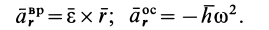
Формулу (23) можно получить непосредственным дифференцированием векторного равенства для скоростей (21), справедливого в любой момент времени. Вычисляя полные производные по времени, при определении которых учитываются изменения векторов относительно неподвижной системы координат, получаем
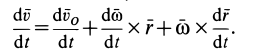
Здесь 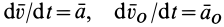 — ускорения точек
— ускорения точек 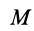 и
и 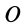 ;
; 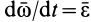 — угловое ускорение.
— угловое ускорение.
Учитывая, что вектор 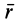 является вектором постоянного модуля, имеем
является вектором постоянного модуля, имеем
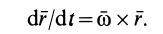
Окончательный результат выразится в форме
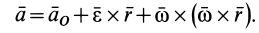
Заметим, что если в кинематике свободного твердого тела в качестве точки 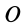 можно брать любую точку тела, то в динамике в качестве такой точки оказывается выгодным выбирать центр масс тела.
можно брать любую точку тела, то в динамике в качестве такой точки оказывается выгодным выбирать центр масс тела.
При выборе различных точек тела в качестве полюса изменяются скорость и ускорение полюса. Угловая скорость и угловое ускорение при этом не изменяются. Докажем это для угловой скорости, используя (21).
Пусть 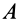 и
и 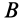 — две точки свободного твердого тела (рис. 86). Приняв за полюс точку
— две точки свободного твердого тела (рис. 86). Приняв за полюс точку 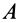 , для скорости точки
, для скорости точки 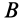 имеем
имеем
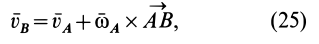
где 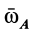 — угловая скорость вращения тела вокруг точки
— угловая скорость вращения тела вокруг точки 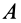 . Аналогично, приняв за полюс точку
. Аналогично, приняв за полюс точку 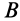 , для скорости точки
, для скорости точки 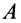 получим
получим
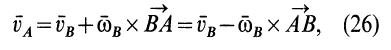
где 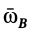 — угловая скорость вращения тела вокруг точки
— угловая скорость вращения тела вокруг точки 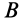 . Из (25) и (26) имеем
. Из (25) и (26) имеем
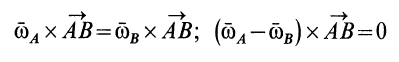
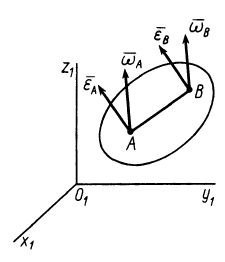
Рис. 86
для любых двух точек свободного твердого тела. Эти точки можно выбрать так, чтобы 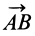 не было параллельно вектору
не было параллельно вектору 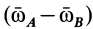 . Тогда получаем
. Тогда получаем
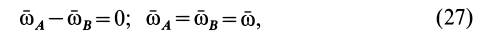
т. е. угловая скорость свободного твердого тела не зависит от выбора полюса. Она инвариантна по отношению к выбору полюса.
Так как равенство (27) справедливо для любого момента времени, то, дифференцируя его по времени, получим
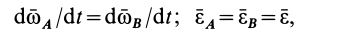
т. е. вектор углового ускорения свободного твердого тела тоже не зависит от выбора полюса.
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
- Плоское движение твердого тела
- Мгновенный центр скоростей
- Мгновенный центр ускорений
- Мгновенный центр вращения
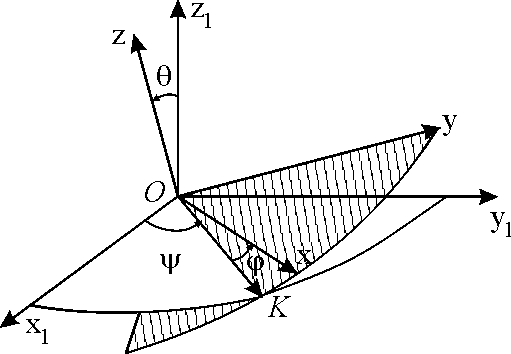
6.1. Задание движения. Углы Эйлера
Движение тела,
имеющего одну неподвижную точку, называют
сферическим движением или вращением
тела вокруг неподвижной точки.
|
Рис. 6.1. |
Твердое тело с |
Свяжем жестко с
телом подвижную систему координат Охуz,
выбрав начало координат в неподвижной
точке О (рис. 6.1). Координатная
плоскость хОу пересекается с
неподвижной плоскостью x1Oy1
вдоль прямой ОК, которая называется
линией узлов. Угол, составляемый
неподвижной осью Ox1
с линией узлов, называется углом прецессии
и обозначается буквой
![]()
.
Угол, составляемый линией узлов с
подвижной осью Ох, носит название
угла собственного вращения и
обозначается буквой
.
Угол между осями Oz1 и Оz
называется углом нутации и
обозначается буквой
![]()
.
Все углы отсчитываются соответственно
от осей Ox1,
ОК и Oz1 против хода
часовой стрелки, как показано на рис. 6.1.
Покажем, что, зная
три функции
![]()
,
![]()
и
![]()
,
можно всегда найти положение системы
координат Охуz, а
следовательно, и положение тела,
скрепленного с ней. Действительно,
откладывая от оси Ох1 угол
прецессии
,
мы найдем линию узлов ОК. Проведем
через точку О плоскость, перпендикулярную
линии узлов, и от оси Оz1
(эта ось должна лежать в построенной
плоскости) отложим угол нутации
.
Таким образом, будет определено
положительное направление оси Оz.
Через точку О проведем плоскость,
перпендикулярную оси Оz;
эта плоскость пройдет через линию узлов
ОК. Отложим теперь в построенной
плоскости от линии узлов угол собственного
вращения
и определим положительное направление
оси Ох. Ось Оу должна лежать в
той же плоскости и составлять вместе с
осями Ох и Оz
правую систему координат. Таким образом,
углы
![]()
и
полностью определяют положение осей
подвижной системы.
6.2. Распределение скоростей точек твердого тела, имеющего одну неподвижную точку. Мгновенная ось вращения. Мгновенная угловая скорость
|
Рис.6.2. |
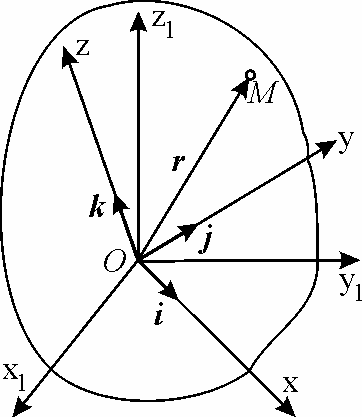
Пусть твердое |
радиусом-вектором
.
Если х, у и z – координаты
точки М в подвижной системе координат,
a i, j и k – единичные
векторы осей этой системы координат,
то радиус-вектор можно представить в
виде
![]()
. (6.1)
В подвижной системе
отсчета координаты х, у, z точки М
являются постоянными величинами, т.е.
,
,
,
а единичные векторы i, j, k будут
функциями времени, так как система
координат Охуz
движется вместе с твердым телом.
Дифференцируя
(6.1) по
,
получим скорость точки М
![]()
. (6.2)
Умножая обе части
равенства (6.2) скалярно на i, j и
k, получим
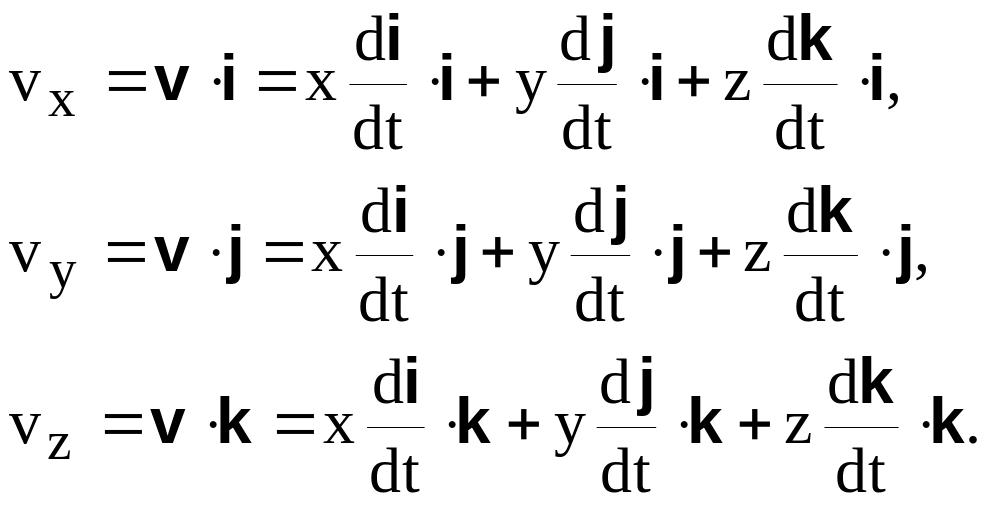
(6.3)
Так как векторы
i, j и k взаимно перпендикулярны,
то
![]()
(6.4)
Дифференцируя эти
равенства по времени, найдем две группы
формул:
![]()
(6.5)
![]()
(6.6)
Выражения (6.3) при
этом примут вид
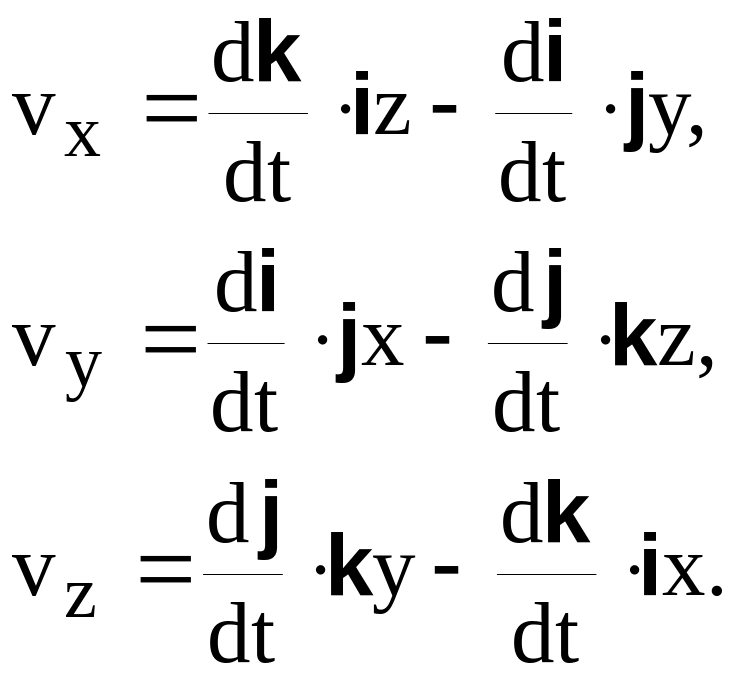
(6.7)
Формулы (6.7) содержат
три скалярные функции времени,
![]()
,
для которых введем
обозначения:
![]()
. (6.8)
Перепишем теперь
формулы (6.7) в виде
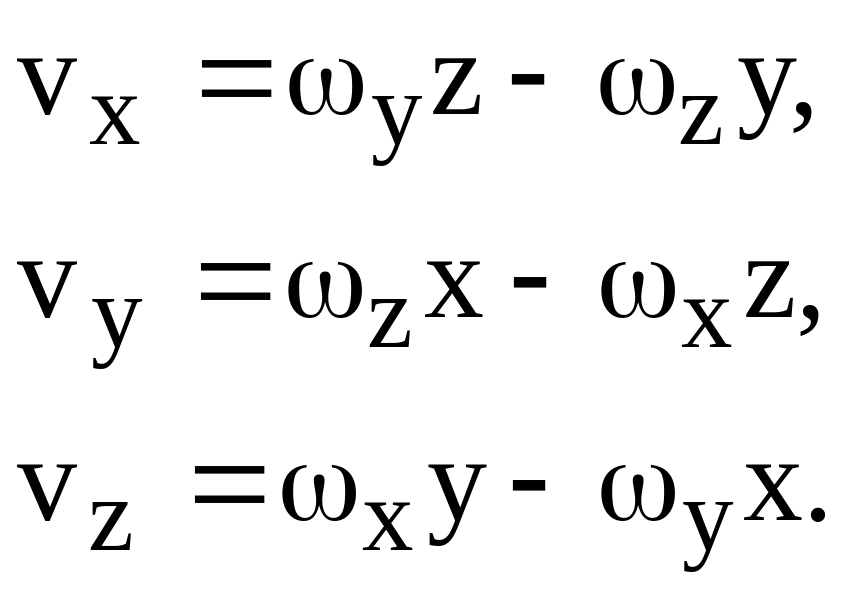
(6.9)
Так как ![]()
,
то, в соответствии
с выражением (6.9), имеем
![]()
.
Если теперь ввести
вектор
с проекциями
![]()
![]()
,
то скорость точки
можно представить векторным произведением
![]()
.
Итак, скорость
точки тела, совершающего сферическое
движение, определяется формулой
![]()
. (6.10)
Геометрическое
место точек, скорость которых равна
нулю, определяется из уравнения
![]()
, (6.11)
представляющего
собой условие коллинеарности векторов
и
.
Это векторное уравнение в системе
координат Охуz
можно записать в виде
![]()
. (6.12)
Уравнения (6.12)
определяют прямою линию, направляющие
косинусы которой пропорциональны
проекциям
![]()
вектора
.
В общем случае вектор
и его проекции
являются функциями времени, поэтому
положение прямой (6.12) изменяется как
относительно тела, так и относительно
неподвижной системы координат Ох1y1z1.
Прямая (6.12), в каждой
точке которой скорости точек тела в
данный момент равны нулю, называется
мгновенной осью вращения. (Она
также называется мгновенной осью
скоростей.)
Введенный нами
вектор
направлен по мгновенной оси вращения.
Как уже было
установлено, скорость любой точки М
тела определяется формулой (6.10),
совпадающей по своей форме с выражением
для скоростей точек твердого тела,
вращающегося вокруг неподвижной оси с
угловой скоростью
.
Следовательно, скорости точек твердого
тела, имеющего одну неподвижную точку,
распределяются так, как если бы тело
вращалось вокруг оси, совпадающей в
данный момент с мгновенной осью вращения.
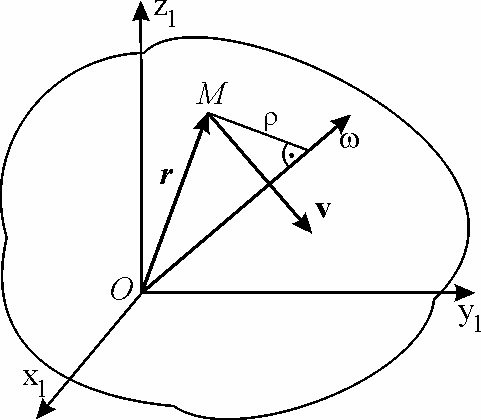
В частности, модуль скорости точки М
в данный момент определяется
равенством ![]()
,
где
– расстояние
от точки М до мгновенной оси вращения.
Скорость точки М направлена
перпендикулярно плоскости, проходящей
через ее радиус-вектор
и мгновенную ось вращений (рис. 6.3).
|
Рис. 6.3. |
По аналогии с вектором угловой скорости. представляет собой вектор, |
всегда направленный
по неподвижной оси вращения и
характеризующий изменение во времени
реального угла
поворота тела. Для тела, имеющего одну
неподвижную точку, выражение «угловая
скорость» имеет условный характер, т.к.
положение тела определяется не одним,
а тремя углами и, следовательно, нет
такого одного угла, скорость изменения
которого представил бы введенный вектор
.
Кроме того, этот вектор может меняться
и по модулю и по направлению. Проекции
этого вектора на координатные оси
являются функциями углов Эйлера и их
первых производных.
Отметим, что из
формул (6.8) для случая вращения твердого
тела вокруг неподвижной оси, например,
вокруг оси Oz, можно получить
![]()
,
т.к. ![]()
, ![]()
, ![]()
.
Если известны
направления скоростей двух точек тела,
то мгновенную ось вращения можно найти
графически. Как следует из картины
распределения скоростей точек тела в
данный момент времени, мгновенная ось
вращения лежит в плоскости, перпендикулярной
направлению скорости точки тела, и
проходит через неподвижную точку тела.
Следовательно, если через точки тела,
направления скоростей которых известны,
провести плоскости, перпендикулярные
этим скоростям, то линия пересечения
этих плоскостей и будет мгновенной осью
вращения.
Мгновенную ось
вращения можно определить и в том случае,
когда известна одна точка тела, скорость
которой в данный момент времени равна
нулю. Соединяя эту точку с неподвижной
точкой тела, найдем мгновенную ось
вращения.
Положение точки
М тела в неподвижной системе координат
определяется координатами х1,
y1, и z1
а вектор
имеет проекции
![]()
.
Тогда, в соответствии с формулой (6.10),
проекции скорости точки М на
неподвижные оси координат будут
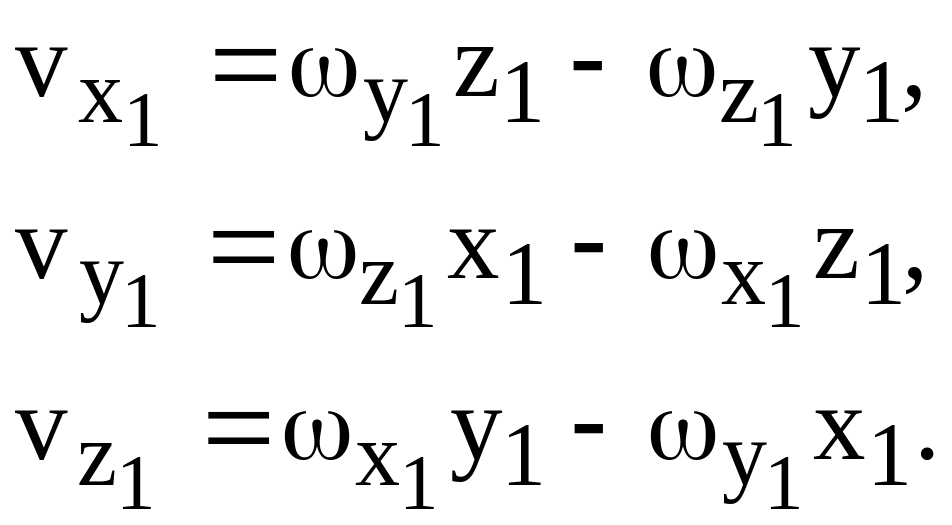
(6.13)
Уравнение мгновенной
оси вращения в неподвижной системе
координат имеет вид
![]()
. (6.14)
Геометрическое
место мгновенных осей вращений,
построенных в неподвижной системе
координат, называется неподвижным
аксоидом, а в подвижной системе
координат – подвижным аксоидом.
Из уравнений (6.14)
следует
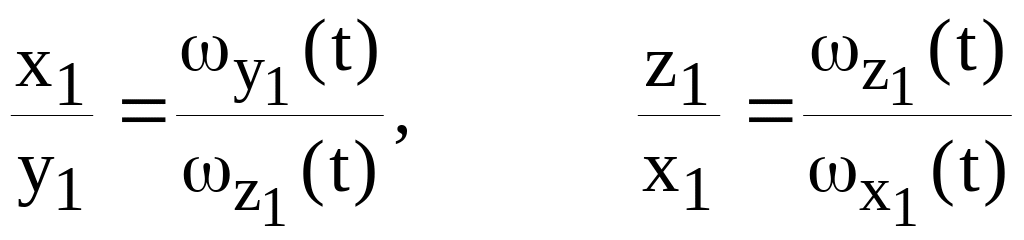
.
Полученные уравнения
дают уравнение неподвижного аксоида в
параметрическом виде; параметром служит
время t. Исключая из этих уравнений t,
можно получить уравнение конической
поверхности (неподвижного аксоида) ![]()
.
Аналогично, исключая
время t из уравнений
![]()
,
полученных из
формул (6.12), найдем уравнение подвижного
аксоида
![]()
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Сферическое движение твёрдого тела
- Исследование сферического движения твердого тела методом мгновенных осей
- Мгновенная ось вращения. Аксоиды
- Угловая скорость и угловое ускорение твердого тела во время сферического движения
- Вычисление углового ускорения тела
- Скорость и ускорение точек твердого тела во время сферического движения
- Исследование сферического движения твердого тела методом углов Эйлера
- Углы Эйлера. Уравнения сферического движения твердого тела
- Определение угловой скорости и углового ускорения тела по уравнениям его движения
- Аналитическое нахождения скоростей точек тела при сферическом движении. Уравнения мгновенной оси вращения
- Аналитическое нахождения ускоренний точек тела при сферическом движении
- Примеры решения задач на нахождение кинематических характеристик сферического движения тела
Сферическое движение (движение твёрдого тела вокруг неподвижной точки) — это движение абсолютно твёрдого тела, при котором оно имеет одну неподвижную точку.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Сферическое движение твёрдого тела
Если твердое тело движется так, что одна его точка остается все время неподвижной, то такое движение называется вращательным движением твердого тела вокруг неподвижной точки или сферическим движением. Название «сферический движение »следует из того, что траектории всех точек тела при таком движении размещены на поверхностях сфер, с центром в неподвижной точке.
Примером сферического движения тела может быть движение гироскопа в карданном подвесе или движение волчка, заостренный конец которой опирается на подставку и остается неподвижным.
При изучении кинематики сферического движения тела нужно установить основные характеристики этого движения, то есть уравнения движения, угловую скорость и угловое ускорение тела, и вывести формулы для вычисления скоростей и ускоренний точек тела. Ниже рассмотрим два основных метода исследования кинематики сферического движения: метод мгновенных осей и метод углов Эйлера.
Исследование сферического движения твердого тела методом мгновенных осей
Теорема Эйлера-Даламбера о конечном перемещении твердого тела во время сферического движения
Теорема. Твердое тело, имеющее одну неподвижную точку, можно переместить с одного положения в любое другое одним поворотом этого тела вокруг оси, проходящей через неподвижную точку.
Сформулированная теорема Эйлера-Даламбера является обобщением теоремы 2, доказанной в разделе 4 (см. § 4.2).
Доказательство. Положение свободного твердого тела в пространстве определяется
тремя его точками, которые не лежат на одной прямой. Во время сферического движения тела, когда одна точка является неподвижной, для определения его положения в пространстве достаточно знать положение двух его точек.
Для доказательства теоремы проведем сферическую поверхность произвольного радиуса с центром в неподвижной точке О. Будем считать, что эта сфера неизменно связана с телом S, что осуществляет сферическое движение, и поэтому положения сферы будет определять положение тела S в пространстве (Рис. 5.1).

Пусть положение  тела характеризуется дугой АВ большого круга, а положение II – этой же самой дугой
тела характеризуется дугой АВ большого круга, а положение II – этой же самой дугой  но во втором положении на сфере. аналогично том, как находится центр конечного вращения для плоской фигуры при движении ее в своей плоскости
но во втором положении на сфере. аналогично том, как находится центр конечного вращения для плоской фигуры при движении ее в своей плоскости
(Теорема 2 § 4.2), найдем точку Р на сфере в случае конечного перемещения тела с неподвижной точкой. Для этого соединим точки  с
с  и
и  с
с  дугами большого круга сферы. В серединах дуг
дугами большого круга сферы. В серединах дуг  и
и  из точек С и D проведем сферические перпендикуляры, то есть дуги большого круга СР и DР, касательные к которым перпендикулярны в точках
из точек С и D проведем сферические перпендикуляры, то есть дуги большого круга СР и DР, касательные к которым перпендикулярны в точках
С и D соответственно касательным к дугам и
и  . Эти перпендикуляры пересекаются в точке Р. С равенства прямоугольных сферических треугольников
. Эти перпендикуляры пересекаются в точке Р. С равенства прямоугольных сферических треугольников  и
и  которые имеют общий катет DP и равные катеты
которые имеют общий катет DP и равные катеты  и
и  следует, что гипотенузы этих сферических треугольников также равны между собой, то есть точки
следует, что гипотенузы этих сферических треугольников также равны между собой, то есть точки  и
и  равноудалены от точки Р.
равноудалены от точки Р.
Аналогично доказывается, что точки  и
и  также одинаково удалены от точки Р. Если вернуть заштрихованный сферический треугольник
также одинаково удалены от точки Р. Если вернуть заштрихованный сферический треугольник  вокруг оси
вокруг оси  то этот треугольник, двигаясь по сфере, совпадет всеми своими точками с равным ему (по трем сторонам
то этот треугольник, двигаясь по сфере, совпадет всеми своими точками с равным ему (по трем сторонам 
 сферическим треугольником
сферическим треугольником  Это следует из того, что сферический угол на сфере, на который нужно повернуть вокруг ОР дугу АР к совпадению с дугой
Это следует из того, что сферический угол на сфере, на который нужно повернуть вокруг ОР дугу АР к совпадению с дугой  равный сферическому углу на этой же сфере, в
равный сферическому углу на этой же сфере, в
который нужно вернуть дугу ВР до совпадения с дугой  то есть
то есть  (рис. 5.1). Итак, конечное перемещение тела при сферическом движении можно осуществить одним поворотом вокруг оси ОВ на угол
(рис. 5.1). Итак, конечное перемещение тела при сферическом движении можно осуществить одним поворотом вокруг оси ОВ на угол  Ось ОР называется осью конечного поворота. Теорема доказана.
Ось ОР называется осью конечного поворота. Теорема доказана.
Мгновенная ось вращения. Аксоиды
Очевидно, что перемещение твердого тела, имеющего неподвижную точку, с положения, которое оно занимает в момент времени t, в положение, соответствующее моменту времени  одним вращением вокруг оси конечного поворота на угол
одним вращением вокруг оси конечного поворота на угол  в целом не соответствует действительному движению тела за этот промежуток времени. Однако, чем меньше будет промежуток времени
в целом не соответствует действительному движению тела за этот промежуток времени. Однако, чем меньше будет промежуток времени  тем перемещения, которое осуществляется вращением вокруг оси конечного поворота на угол
тем перемещения, которое осуществляется вращением вокруг оси конечного поворота на угол  будет ближе к настоящему движению тела.
будет ближе к настоящему движению тела.
При приближении  к нулю второе положение тела приближается к первому, а ось конечного поворота ОР приближается к своему предельному положению
к нулю второе положение тела приближается к первому, а ось конечного поворота ОР приближается к своему предельному положению  и называется мгновенной осью вращения тела.
и называется мгновенной осью вращения тела.
Иначе говоря: ось, вокруг которой нужно вращать тело, имеющее одну неподвижную точку, при перемещении его с одного положения в другое, бесконечно близкое к первому, называется мгновенной осью вращения для конкретного момента времени.
Мгновенная ось вращения – это геометрическое место точек тела, скорости которых в конкретный момент равны нулю. Положение мгновенной оси вращения не остается неизменным за сферического движения тела, а со временем меняет свое положение в пространстве. Геометрическое место мгновенных осей относительно неподвижной системы отсчета, относительно которой рассматривается движение тела, называется недвижимым аксоидом (поверхность и на рис. 5.2).
Неподвижный аксоид является конической поверхностью с вершиной в неподвижной
точке О, поскольку все мгновенные оси вращения проходят через эту неподвижную точку.
Геометрическое место мгновенных осей в самом подвижном теле называется подвижным аксоидом (поверхность ИИ на рис. 5.2).

Движимый аксоид есть также конической поверхностью с вершиной в неподвижной точке О.Во время сферического движения тела движимый аксоид  катится без скольжения по неподвижному
катится без скольжения по неподвижному  Очевидно, что во время плоского движения твердого тела конические аксоиды есть цилиндрическими поверхностями, которые в пересечении с плоскостями движения плоской фигуры образуют центроиды для этой фигуры.
Очевидно, что во время плоского движения твердого тела конические аксоиды есть цилиндрическими поверхностями, которые в пересечении с плоскостями движения плоской фигуры образуют центроиды для этой фигуры.
Практически понятие аксоидов используется для классификации видов
прецессионного движения гироскопов.
Угловая скорость и угловое ускорение твердого тела во время сферического движения
Из теоремы Эйлера-Даламбера следует, что сферическое движение твердого тела в каждый момент времени является вращательным вокруг мгновенной оси, а потому
величинами, которые характеризуют сферическое движение тела в каждый момент
времени, будут мгновенная угловая скорость и мгновенное угловое ускорение тела.
Если за промежуток времени  тело вернулось вокруг мгновенной оси на угол
тело вернулось вокруг мгновенной оси на угол  то граница, к которой приближается отношение
то граница, к которой приближается отношение когда
когда  стремится к нулю, называется мгновенной угловой скоростью твердого тела в момент времени t
стремится к нулю, называется мгновенной угловой скоростью твердого тела в момент времени t

При этом нужно иметь в виду, что величина  не является производной от угла
не является производной от угла  по времени t, поскольку во время движения твердого тела вокруг неподвижной точки такого угла не существует. Поэтому мгновенную угловую скорость
по времени t, поскольку во время движения твердого тела вокруг неподвижной точки такого угла не существует. Поэтому мгновенную угловую скорость  нужно задать как функцию времени непосредственно или ее можно представить так, как это будет показано ниже, через углы Эйлера и их производные.
нужно задать как функцию времени непосредственно или ее можно представить так, как это будет показано ниже, через углы Эйлера и их производные.
Вектор мгновенной угловой скорости  направляется вдоль мгновенной оси вращения
направляется вдоль мгновенной оси вращения  в ту сторону, чтобы с конца этого вектора мгновенный поворот тела было видно против часовой стрелки (рис. 5.3).
в ту сторону, чтобы с конца этого вектора мгновенный поворот тела было видно против часовой стрелки (рис. 5.3).

Угловое ускорение тела во время сферического движения характеризует скорость изменения со временем вектора угловой скорости по величине и направлению. Вектор углового ускорения равен первой производной за временем от вектора угловой скорости

Вектор углового ускорения  направляется по касательной к годографу вектора угловой скорости в сторону движения конца вектора
направляется по касательной к годографу вектора угловой скорости в сторону движения конца вектора  (рис. 5.3).
(рис. 5.3).
Договоримся вектор углового ускорения  проводить с неподвижной точки О.
проводить с неподвижной точки О.
Вычисление углового ускорения тела
Существует два основных способа нахождения вектора углового ускорения тела во время сферического движения. Один из них – аналитический, который рассмотрим в § 5.2, базируется на углах Эйлера. В этом параграфе рассмотрим второй способ, который использует расписание вектора углового ускорения  на две взаимно перпендикулярные составляющие.
на две взаимно перпендикулярные составляющие.
Пусть тело совершает сферический движение и в заданный момент времени имеет угловую скорость  (рис. 5.4).
(рис. 5.4).
Если ввести единичный вектор направленный по
направленный по 
Тогда или
или
Составляющая  полного углового ускорения
полного углового ускорения  характеризует изменение вектора угловой скорости по величине. Вектор
характеризует изменение вектора угловой скорости по величине. Вектор  совпадает по направлению с вектором
совпадает по направлению с вектором  и противоположно направленный к нему при
и противоположно направленный к нему при
Составляющая  полного углового ускорения
полного углового ускорения  характеризует изменение вектора угловой скорости по направлению.
характеризует изменение вектора угловой скорости по направлению.
Производная  равна скорости конца вектора
равна скорости конца вектора  то есть линейной скорости точки А. Если допустить, что мгновенная ось вращается в заданный момент времени вокруг оси
то есть линейной скорости точки А. Если допустить, что мгновенная ось вращается в заданный момент времени вокруг оси  с угловой скоростью
с угловой скоростью  (рис. 5.4), то линейная скорость точки А по формуле Эйлера равна
(рис. 5.4), то линейная скорость точки А по формуле Эйлера равна


Составляющая углового ускорения  с учетом последнего равенства примет вид
с учетом последнего равенства примет вид

Вектор  напрямляеться согласно правилу векторного произведения векторов
напрямляеться согласно правилу векторного произведения векторов  и
и  и всегда будет перпендикулярен к вектору
и всегда будет перпендикулярен к вектору  Модуль вектора ускорения
Модуль вектора ускорения  равен
равен 
В частном случае, когда угловая скорость тела при сферическом движении постоянная по величине  то
то

Скорость и ускорение точек твердого тела во время сферического движения
Поскольку в каждый момент времени тело, которое движется вокруг неподвижной точки, имеет мгновенную ось вращения  вокруг которой проходит элементарный поворот с угловой скоростью
вокруг которой проходит элементарный поворот с угловой скоростью (рис. 5.5), то вектор скорости любой точки М тела будет определяться в этот момент по известной формуле Эйлера (3.17), т.е.
(рис. 5.5), то вектор скорости любой точки М тела будет определяться в этот момент по известной формуле Эйлера (3.17), т.е.

где  радиус-вектор, проведенный в точку М с неподвижной точки О. Направление вектора
радиус-вектор, проведенный в точку М с неподвижной точки О. Направление вектора  скорости точки М будет перпендикулярен плоскости
скорости точки М будет перпендикулярен плоскости  и направлен в сторону мгновенного вращения тела. модуль вектора скорости точки равен
и направлен в сторону мгновенного вращения тела. модуль вектора скорости точки равен



Размер  – это короткое расстояние от точки М к мгновенной оси вращения. Для определения ускорения произвольной точки тела в случае его сферического движения будем считать известными в заданный момент времени угловую скорость
– это короткое расстояние от точки М к мгновенной оси вращения. Для определения ускорения произвольной точки тела в случае его сферического движения будем считать известными в заданный момент времени угловую скорость  и угловое ускорение
и угловое ускорение  (Рис. 5.6). Ускорение точки равно первой производной по времени от вектора скорости, а потому, дифференцируя равенство (5.5), получим
(Рис. 5.6). Ускорение точки равно первой производной по времени от вектора скорости, а потому, дифференцируя равенство (5.5), получим

или с учетом, что получим выражение для нахождения
получим выражение для нахождения
ускорения точек тела в случае сферического движения:
Тут  вращательное ускорение точки;
вращательное ускорение точки;
 осевое ускорение точки.
осевое ускорение точки.
Итак,
Равенство (5.8) выражает теорему Ривальса об ускорении точки тела, осуществляет сферический движение, которая формулируется так: ускорение любой точки твердого тела в случае сферического движения равна векторной сумме вращательного и доосевого ускоренния.
Вектор вращательного ускорения напрямляеться согласно правилу векторного произведения, то есть перпендикулярно к плоскости, в которой лежат векторы
напрямляеться согласно правилу векторного произведения, то есть перпендикулярно к плоскости, в которой лежат векторы  и
и  в ту сторону, откуда кратчайший поворот вектора
в ту сторону, откуда кратчайший поворот вектора  вектору
вектору  видно против часовой стрелки. Модуль вращательного ускорения
видно против часовой стрелки. Модуль вращательного ускорения

где  короткое расстояние от точки М до прямой, вдоль которой направлен вектор углового ускорения
короткое расстояние от точки М до прямой, вдоль которой направлен вектор углового ускорения  (рис. 5.6).
(рис. 5.6).
Вектор доосевого ускорения  напрямляеться перпендикулярно векторам угловой скорости
напрямляеться перпендикулярно векторам угловой скорости  и линейной скорости
и линейной скорости  точки М, то есть вдоль перпендикуляра, опущенного из точки М на мгновенную ось
точки М, то есть вдоль перпендикуляра, опущенного из точки М на мгновенную ось в сторону этой оси (рис. 5.6).
в сторону этой оси (рис. 5.6).
Модуль доосевого ускорения

Модуль полного ускорения  вычисляется как диагональ параллелограмма по формуле
вычисляется как диагональ параллелограмма по формуле

Исследование сферического движения твердого тела методом углов Эйлера
В предыдущем параграфе исследованы движение твердого тела с неподвижной точкой геометрическим методом (методом мгновенной оси). Ниже рассмотрим аналитический метод исследования кинематики сферического движения тела, основанный на углах Эйлера.
Углы Эйлера. Уравнения сферического движения твердого тела
Как уже отмечалось в 5.1.1, положения твердого тела в пространстве определяется тремя точками, не лежащих на одной прямой, то есть девятью координатами этих точек. Положение всех остальных точек тела можно найти через заданные три точки. В твердом теле расстояние между отдельными точками тела не меняется, а потому координаты этих трех заданных точек должны удовлетворять трем уравнениям, которые выражают неизменность расстояний между отдельными точками тела. В случае свободного твердого тела остается шесть независимых координат, то есть свободное тело имеет шесть
степеней свободы.
В случае сферического движения тела одна точка закреплена, а следовательно, число независимых величин уменьшается до трех, то есть тело при таком движении имеет три степени свободы.
Три степени свободы, которыми тело в случае сферического движения, требуют для определения положения тела относительно произвольной системы координат трех независимых величин. Эти величины можно задать разными способами. В теоретической механике наибольшее применение получили углы Эйлера.
Через неподвижную точку О твердого тела проведем оси неподвижной декартовой системы координат по которой будем рассматривать движение тела (Рис. 5.7).
по которой будем рассматривать движение тела (Рис. 5.7).
Подвижную декартову систему координат неизменно свяжем с телом, которое вращается вокруг неподвижной точки О. Положение тела относительно неподвижной системы координат
неизменно свяжем с телом, которое вращается вокруг неподвижной точки О. Положение тела относительно неподвижной системы координат  определяется положением подвижной системы координат
определяется положением подвижной системы координат  относительно неподвижной.
относительно неподвижной.

Взаимное положение этих систем определяется углами Эйлера. Дадим определение углов
Эйлера.
Линия пересечения ON неподвижной плоскости  с подвижной плоскостью
с подвижной плоскостью  называется линией узлов. Угол
называется линией узлов. Угол  между неподвижной осью
между неподвижной осью  и линией узлов ОN называется углом прецессии.
и линией узлов ОN называется углом прецессии.
Для изменения этого угла тело должно вращаться вокруг оси  которая называется осью прецессии.
которая называется осью прецессии.
Следующим углом Эйлера является угол между координатными плоскостями  и
и  который измеряется линейным углом
который измеряется линейным углом  между перпендикулярами к этих координатным плоскостям, то есть углом между осями
между перпендикулярами к этих координатным плоскостям, то есть углом между осями  и
и  Угол
Угол  называется углом нутации, а линия узлов ON, вокруг которой вращается тело при изменении угла
называется углом нутации, а линия узлов ON, вокруг которой вращается тело при изменении угла  имеет еще название оси нутации.
имеет еще название оси нутации.
Для полного определения положения подвижной системы координат относительно неподвижной нужно задать угол между линией узлов и подвижной осью  Угол φ между линией узлов ON и осью
Угол φ между линией узлов ON и осью  называется углом собственного вращения. Для изменения угла φ тело должно вращаться вокруг оси
называется углом собственного вращения. Для изменения угла φ тело должно вращаться вокруг оси  которая носит название оси собственного вращения.
которая носит название оси собственного вращения.
Углы Эйлера положительные, когда они отложены по осям и ON против часовой стрелки, если смотреть с концов соответственно осей
и ON против часовой стрелки, если смотреть с концов соответственно осей 
 и
и  Положительные направления отчисления этих углов показаны на рис. 5.7 дуговыми стрелками.
Положительные направления отчисления этих углов показаны на рис. 5.7 дуговыми стрелками.
Во время движения тела с одной закрепленной точкой углы  непрерывно изменяются, то есть функциями времени
непрерывно изменяются, то есть функциями времени

Эти уравнения называются уравнениями сферического движения тела.
Заметим, что описанный вариант выбора углов  не единственный.
не единственный.
Существуют их модификации. Так при исследовании динамики кораблей и самолетов
используют углы Эйлера-Крылова.
Определение угловой скорости и углового ускорения тела по уравнениям его движения
Пусть сферическое движение тела описывается уравнениями (5.12). вычислим величину и направление угловой скорости тела в произвольный момент времени, как функцию углов Эйлера и их производных.
В случае изменения угла тело вращается вокруг оси
тело вращается вокруг оси  (прецессия) с угловой скоростью
(прецессия) с угловой скоростью при изменении угла
при изменении угла  – вокруг линии узлов ON (нутация) с угловой скоростью
– вокруг линии узлов ON (нутация) с угловой скоростью  и при изменении угла φ – вокруг оси
и при изменении угла φ – вокруг оси  (собственное вращение) с угловой скоростью
(собственное вращение) с угловой скоростью  Направления векторов
Направления векторов  показаны на рис. 5.8
показаны на рис. 5.8
Как будет показано в разделе 8, при вращении тела вокруг нескольких осей, пересекающихся результирующее движение будет мгновенно-вращательным с угловой скоростью, равной геометрической сумме составляющих угловых скоростей. В случае сферического движения тела вектор результирующей мгновенной угловой скорости равен

Для нахождения величины и направления вектора мгновенной угловой скорости определим его проекции на оси подвижной системы координат
определим его проекции на оси подвижной системы координат 
Проектируя обе части равенства (5.13) на оси  получим:
получим:

Проекции векторов  и
и  находим непосредственным проектированием (Рис. 5.8):
находим непосредственным проектированием (Рис. 5.8):

а для нахождения проекций вектора  проведем через оси
проведем через оси  и
и плоскость,которая пересекается с плоскостью
плоскость,которая пересекается с плоскостью  вдоль линии OL. Поскольку линия узлов ON перпендикулярна к плоскости
вдоль линии OL. Поскольку линия узлов ON перпендикулярна к плоскости  то она перпендикулярна и к линии
то она перпендикулярна и к линии  Тогда, проектируя вектор
Тогда, проектируя вектор  на линию OL, а полученную проекцию, в свою очередь, на оси
на линию OL, а полученную проекцию, в свою очередь, на оси  и
и получим:
получим:

Подставим полученные величины проекций в правые части равенств (5.14):
Аналогично, проектируя равенство (5.13) на оси неподвижной системы координат  найдем проекции вектора
найдем проекции вектора  на эти оси:
на эти оси:

Равенства (5.15) и (5.16) называются кинематическими уравнениями Эйлера. Эти уравнения дают возможность найти модуль мгновенной угловой скорости и направляющие косинусы вектора  с соответствующими осями координат:
с соответствующими осями координат:


Модуль и направляющие косинусы вектора углового ускорения также определим по его проекциями на неподвижные и подвижные оси координат.
Найдем проекции вектора углового ускорения на неподвижные оси координат  Раскладывая векторы угловой скорости
Раскладывая векторы угловой скорости  и углового ускорения
и углового ускорения  по ортах неподвижной системы координат, получим
по ортах неподвижной системы координат, получим

Дифференцируя первое равенство (5.18) с учетом, что векторы постоянные по величине и направлению, найдем
постоянные по величине и направлению, найдем

Сравнивая (5.19) с другим равенством (5.18), находим
то есть проекция углового ускорения на неподвижную ось декартовой системы координат равна производной по времени от проекции угловой скорости на соответствующую ось.
Определим проекции углового ускорения на движущиеся оси координат  связанные с твердым телом.
связанные с твердым телом.
Единичные векторы подвижной системы координат обозначим через
 (рис. 5.8). Эти орты меняются по направлению, то есть вращаются вместе с телом вокруг мгновенной оси с угловой скоростью
(рис. 5.8). Эти орты меняются по направлению, то есть вращаются вместе с телом вокруг мгновенной оси с угловой скоростью  Поэтому производные по времени от этих ортов являются скорости концов этих ортов, которые определяются по формулах.
Поэтому производные по времени от этих ортов являются скорости концов этих ортов, которые определяются по формулах.

Разложим векторы угловой скорости  и углового ускорения
и углового ускорения  по ортах
по ортах 

Вектор углового ускорения, как производная по времени от вектора угловой скорости, равна

Второе слагаемое полученной зависимости с учетом (5.21) преобразуется 
Угловое ускорение  с учетом последней тождества будет считаться равенством
с учетом последней тождества будет считаться равенством
Сравнивая выражения (5.22) и (5.23), находим проекции вектора углового ускорения на оси подвижной системы координат

то есть, проекции углового ускорения на движущиеся оси декартовой системы координат равны производным по времени от проекций угловой скорости на соответствующие подвижные оси. Модуль мгновенного углового ускорения и направляющие косинусы вектора  с соответствующими осями координат находятся по формулам
с соответствующими осями координат находятся по формулам

Аналитическое нахождения скоростей точек тела при сферическом движении. Уравнения мгновенной оси вращения
Пусть движение тела, имеющего одну неподвижную точку, задано уравнениями (5.12).
Найдем скорость произвольной точки М (рис. 5.8). если координаты точки  и проекции вектора угловой скорости
и проекции вектора угловой скорости  заданные в неподвижной системе координат, то скорость точки М, выражается по формуле (5.5), может также быть представлена определителем
заданные в неподвижной системе координат, то скорость точки М, выражается по формуле (5.5), может также быть представлена определителем
С другой стороны вектор скорости точки можно представить через его проекции на неподвижные оси координат

Приравнивая соответствующие компоненты в различных представлениях вектора
скорости  получим проекции вектора скорости точки тела во время сферического движения на оси неподвижной системы координат:
получим проекции вектора скорости точки тела во время сферического движения на оси неподвижной системы координат: 
Каждую из формул (5.26) можно получить из предыдущей циклической перестановкой букв  Формулы (5.26), как и формула (5.5), называются формулами Эйлера.
Формулы (5.26), как и формула (5.5), называются формулами Эйлера.
Если координаты точки  и проекции вектора угловой скорости
и проекции вектора угловой скорости  Заданные в подвижной системе координат
Заданные в подвижной системе координат  то, аналогично предыдущему, получим проекции вектора скорости точки и на оси подвижной системы координат:
то, аналогично предыдущему, получим проекции вектора скорости точки и на оси подвижной системы координат:

Модуль и направляющие косинусы вектора скорости произвольной точки тела во время сферического движения найдем по формулам:
По найденным проекциям скоростей точек тела во время его сферического движения можно найти уравнения мгновенной оси вращения.
Скорость каждой точки на мгновенной оси вращения в данный момент времени равна нулю, то есть  Учитывая это, из формул (5.26) получим
Учитывая это, из формул (5.26) получим

Откуда  или
или
Уравнение (5.29) является уравнением мгновенной оси вращения тела, имеющего одну
неподвижную точку, в неподвижной системе координат, то есть уравнением мгновенной
оси вращения тела во время сферического движения.
Аналогичным методом выводится уравнение мгновенной оси вращения в подвижной системе координат, которое будет иметь вид

Аналитическое нахождения ускоренний точек тела при сферическом движении
Согласно теореме Ривальса, ускорения произвольной точки тела в случае сферического движения определяется по формуле (5.8), то есть

Раскрывая второе слагаемое последнего равенства как двойное векторное произведение, то есть получим вектор ускорения точки в виде
получим вектор ускорения точки в виде
Найдем проекции вектора ускорения  на оси неподвижной и подвижной систем координат. Если ввести единичные орты неподвижной системы
на оси неподвижной и подвижной систем координат. Если ввести единичные орты неподвижной системы  а проекции вектора ускорения
а проекции вектора ускорения  обозначить через
обозначить через 
 то (5.31) можно представить следующим образом
то (5.31) можно представить следующим образом

Приравнивая соответствующие компоненты при  в полученной равенства слева и справа, получаем
в полученной равенства слева и справа, получаем

Формулы (5.32) определяют проекции вектора ускорения точки тела на оси неподвижной системы координат 
Аналогично находят проекции вектора ускорения  точки тела и на оси подвижной системы координат
точки тела и на оси подвижной системы координат 

Модуль вектора ускорения точки и его направляющие косинусы с соответствующими осями координат вычисляются по формулам:
Примеры решения задач на нахождение кинематических характеристик сферического движения тела
Задача 5.1. Конус с углом при вершине и радиусом основания
и радиусом основания  (рис. 5.9) катится по неподвижной горизонтальной плоскости без скольжения так, что его вершина В остается неподвижной, а центр основы С движется с постоянной скоростью
(рис. 5.9) катится по неподвижной горизонтальной плоскости без скольжения так, что его вершина В остается неподвижной, а центр основы С движется с постоянной скоростью  Определить угловую скорость и угловое ускорение конуса, скорость и ускорение точек А и B – концов диаметра АВ, которые занимают в заданный момент времени высокое и низкое положение.
Определить угловую скорость и угловое ускорение конуса, скорость и ускорение точек А и B – концов диаметра АВ, которые занимают в заданный момент времени высокое и низкое положение.

Решение. Конус находится в сферическом движении, поскольку точка О остается неподвижной. Для решения этой задачи можно использовать оба предложены методы исследования кинематики сферического движения тела. Проиллюстрируем их на этой задачи.
а) Метод мгновенных осей
По условию задачи конус катится без скольжения, поэтому мгновенной осью вращения  будет линия ОА контакта конуса с неподвижной плоскостью (рис. 5.10).
будет линия ОА контакта конуса с неподвижной плоскостью (рис. 5.10).

Скорость точки С можно найти по формуле (5.6)

С треугольника АСК

Тогда

Вектор угловой скорости  будет направлен по оси
будет направлен по оси  как показано на рисунке. Точка А лежит на мгновенной оси вращения, поэтому
как показано на рисунке. Точка А лежит на мгновенной оси вращения, поэтому 
Определим скорость точки В:

Поскольку центр конуса движется с постоянной линейной скоростью, то величина угловой скорости конуса  постоянна, и угловое ускорение
постоянна, и угловое ускорение  определяется по формуле (5.4)
определяется по формуле (5.4)
Найдем предварительно угловую скорость  вращения мгновенной оси
вращения мгновенной оси 
В случае качения конуса без скольжения мгновенная ось вращения  и собственная ось конуса ОС вращаются вокруг прямой ВО с одинаковой угловой скоростью
и собственная ось конуса ОС вращаются вокруг прямой ВО с одинаковой угловой скоростью  Вычисляя скорость точки С как вращательное вокруг оси
Вычисляя скорость точки С как вращательное вокруг оси  получим:
получим:

откуда
Вектор  направлен вдоль прямой ВО, как показано на рис. 5.10.
направлен вдоль прямой ВО, как показано на рис. 5.10.
Тогда

Вектор  перпендикулярен к векторам
перпендикулярен к векторам  и
и  и показан на рисунке 5.10.
и показан на рисунке 5.10.
Переходим к определению ускоренний точек А и В, воспользовавшись зависимостями (5.8), (5.9) и (5.10):


Векторы вращательного  и доосевого
и доосевого  ускоренний точки В показаны на рис. 5.10. Эти векторы взаимно перпендикулярны, а потому
ускоренний точки В показаны на рис. 5.10. Эти векторы взаимно перпендикулярны, а потому
б) Метод углов Эйлера
Для решения задачи этим методом нужно выбрать оси подвижной и неподвижной систем координат и вывести уравнение движения конуса. оси неподвижной системы координат  выбираем как показано на рис. 5.11.
выбираем как показано на рис. 5.11.
Исходное положение конуса выбираем так, чтобы диаметр АВ лежал в вертикальной плоскости  а точки А и В занимали соответственно низкое и высокое положение.
а точки А и В занимали соответственно низкое и высокое положение.
Подвижную ось  (ось собственного вращения) направим по оси конуса.
(ось собственного вращения) направим по оси конуса.
В начальный момент времени ось  совпадает с осью
совпадает с осью  а ось
а ось лежит в плоскости
лежит в плоскости  и перпендикулярна к осям
и перпендикулярна к осям  и
и
При выводе уравнений движения тела, вращающегося вокруг неподвижной точки, нужно иметь в виду, что Эйлеру углы независимые между собой тогда, когда тело имеет единую вязь в виде неподвижной точки О.

Если, кроме точечной связи, на тело наложены другие связи, то Эйлеру углы становятся зависимыми между собой.
В данной задачи конус катится по плоскости без скольжения. Поэтому дополнительными связями является плоскость, по которой катится конус, и условие движения без скольжения. При таком движения конуса угол нутации остается постоянным, а вращения тела вокруг собственной оси будет зависеть от его прецессионного движения. Свяжем угловые скорости прецессионного движения
остается постоянным, а вращения тела вокруг собственной оси будет зависеть от его прецессионного движения. Свяжем угловые скорости прецессионного движения  и собственного вращения
и собственного вращения  со скоростью центра конуса
со скоростью центра конуса При условии, что задано скорость центра основания конуса
При условии, что задано скорость центра основания конуса  можно найти эти угловые скорости и их направления, то есть направления вращения конуса вокруг оси прецессии
можно найти эти угловые скорости и их направления, то есть направления вращения конуса вокруг оси прецессии  и оси собственного вращения
и оси собственного вращения 
Точка С движется по кругу, а потому

Поскольку  то угловая скорость
то угловая скорость  Направление прецессионного движения показано на рис. 5.11. Как алгебраическая величина,
Направление прецессионного движения показано на рис. 5.11. Как алгебраическая величина, 
Скорость точки А, лежащей в данный момент времени в плоскости контакта, равна нулю. С другой стороны,
 откуда
откуда

Направление  показано на рис. 5.11. угловая скорость собственного вращения
показано на рис. 5.11. угловая скорость собственного вращения  также будет постоянной.
также будет постоянной.
Покажем тело в произвольный момент времени и установим закон его движения.
Из построения углов Эйлера следует, что линия узлов ON лежит в горизонтальной
плоскости и перпендикулярна осям  и
и  (рис. 5.12). Угол нутации
(рис. 5.12). Угол нутации  – это угол между
– это угол между
плоскостями  и
и  то есть угол между осями
то есть угол между осями  и
и  который в нашей задачи будет постоянным
который в нашей задачи будет постоянным
Направления изменения углов φ и ψ показаны на рис. 5.12 дуговыми стрелками.
По правилу выбора положительных направлений углов Эйлера (§ 5.2, 5.2.1) имеем
Как было отмечено выше, прецессионного движение и собственное вращение происходят с постоянными угловыми скоростями, поэтому:

Поскольку при (рис. 5.11), так и
(рис. 5.11), так и  а закон движения конуса приобретает вид:
а закон движения конуса приобретает вид:

По известным формулам (5.16), (5.17), (5.20), (5.25) находим проекции векторов угловой скорости и углового ускорения на оси неподвижной системы координат, а также их модули:

Векторы и
и  по величине не зависят от времени. Направление этих векторов найдем для начального положения конуса, то есть при
по величине не зависят от времени. Направление этих векторов найдем для начального положения конуса, то есть при (рис. 5.11).
(рис. 5.11).
При 

тогда 
Из результатов вычислений (г) видно, что вектор  перпендикулярен осям
перпендикулярен осям  и
и  и направлен вдоль положительного направления оси
и направлен вдоль положительного направления оси а вектор углового ускорения
а вектор углового ускорения 
перпендикулярно к осям  и
и  и направленный вдоль оси
и направленный вдоль оси (рис. 5.11).
(рис. 5.11).
Для определения скоростей точек А и В используем формулы (5.26) и (5.27). Находим координаты точек А и В при 
 или с учетом того, что
или с учетом того, что получим:
получим:
Тогда:

Следовательно, скорость точки А равна нулю.
Аналогично находим скорость точки В:

Скорость точки В равна  и вектор
и вектор  направлен вдоль положительного направления оси
направлен вдоль положительного направления оси  (рис. 5.11).
(рис. 5.11).
Для нахождения ускоренний точек А и В используем формулы (5.32), (5.33), (5.34) и известные величины (в) и (г).
Получим:

Ускорение точки А равно  и вектор этого ускорения направлен по положительном направлении оси
и вектор этого ускорения направлен по положительном направлении оси 
Аналогично находим ускорение точки В:

Вектор ускорения  точки В лежит в плоскости
точки В лежит в плоскости  и образует с положительными направлениями осей
и образует с положительными направлениями осей  и
и  одинаковые углы, равные
одинаковые углы, равные 
Результаты расчетов, полученные двумя методами, совпадают.
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Для кинематического описания процесса вращения твердого тела нужно ввести такие понятия как угловое перемещение Δφ, угловое ускорение ε и угловая скорость ω:
ω=∆φ∆t, (∆t→0),ε=∆φ∆t, (∆t→0).
Углы выражаются в радианах. За положительное направление вращения принимается направление против часовой стрелки.
Когда твердое тело вращается относительно неподвижной оси, все точки этого тела перемещаются с одинаковыми угловыми скоростями и ускорениями.
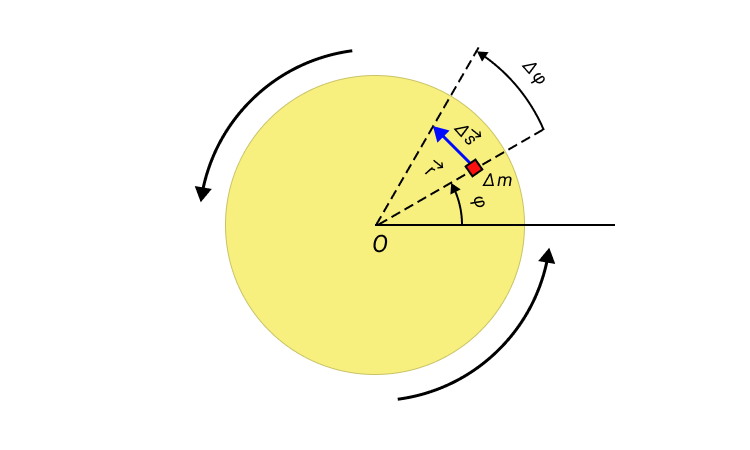
Рисунок 1. Вращение диска относительно оси, проходящей через его центр O.
Если угловое перемещение Δφ мало, то модуль вектора линейного перемещения ∆s→ некоторого элемента массы Δm вращающегося твердого тела можно выразить соотношением:
∆s=r∆ϕ,
в котором r – модуль радиус-вектора r→.
Между модулями угловой и линейной скоростей можно установить связь посредством равенства
v=rω.
Модули линейного и углового ускорения также взаимосвязаны:
a=aτ=rε.
Векторы v→ и a→=aτ→ направлены по касательной к окружности радиуса r.
Также нам необходимо учесть возникновение нормального или центростремительного ускорения, которое всегда возникает при движении тел по окружности.
Модуль ускорения выражается формулой:
an=v2r=ω2r.
Если разделить вращающееся тело на небольшие фрагменты Δmi, обозначить расстояние до оси вращения через ri, а модули линейных скоростей через vi, то запись формулы кинестетической энергии вращающегося тела будет иметь вид:
Ek=∑iνmvi22=∑i∆m(riω)22=ω22∑i∆miri2.
Физическая величина ∑i∆miri2 носит название момента инерции I тела относительно оси вращения. Она зависит от распределения масс вращающегося тела относительно оси вращения:
I=∑i∆miri2.
В пределе при Δm→0 эта сумма переходит в интеграл. Единица измерения момента инерции в СИ – килограмм–метр в квадрате (кг·м2). Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде:
Ek=Iω22.
В отличие от выражения, которое мы использовали для описания кинестетической энергии поступательно движущегося тела mv22, вместо массы m в формулу входит момент инерции I. Также мы принимаем во внимание вместо линейной скорости v угловую скорость ω.
Если для динамики поступательного движения основную роль играет масса тела, то в динамике вращательного движения имеет значение момент инерции. Но если масса – это свойство рассматриваемого твердого тела, которое не зависит от скорости движения и других факторов, то момент инерции зависит от того, вокруг какой оси вращается тело. Для одного и того же тела момент инерции будет определяться различными осями вращения.
В большинстве задач считается, что ось вращения твердого тела проходит через центр его массы.
Положение xC, yC центра масс для простого случая системы из двух частиц с массами m1 и m2, расположенными в плоскости XY в точках с координатами x1, y1 и x2, y2 определяется выражениями:
xC=m1x1+m2x2m1+m2, yC=m1y1+m2y2m1+m2.
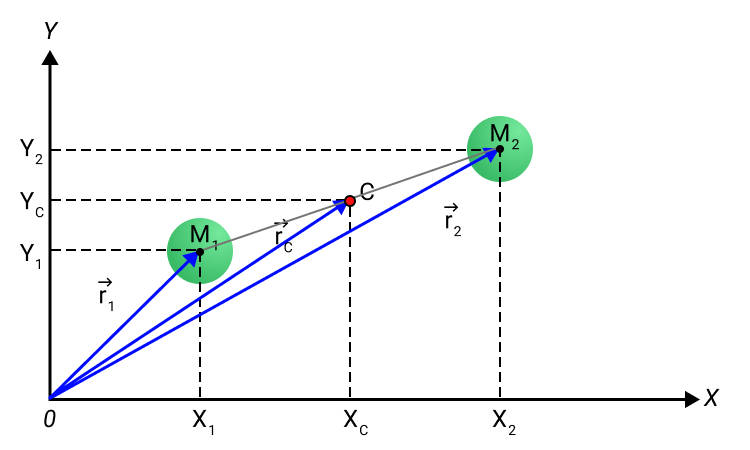
Рисунок 2. Центр масс C системы из двух частиц.
В векторной форме это соотношение принимает вид:
rC→=m1r1→+m2r2→m1+m2.
Аналогично, для системы из многих частиц радиус-вектор rC→ центра масс определяется выражением
rC→=∑miri→∑mi.
Если мы имеем дело с твердым телом, состоящим из одной части, то в приведенном выражении суммы для rC→ необходимо заменить интегралами.
Центр масс в однородном поле тяготения совпадает с центром тяжести. Это значит, что если мы возьмем тело сложной формы и подвесим его за центр масс, то в однородном поле тяготения это тело будет находиться в равновесии. Отсюда следует способ определения центра масс сложного тела на практике: его необходимо последовательно подвесить за несколько точек, одновременно отмечая по отвесу вертикальные линии.
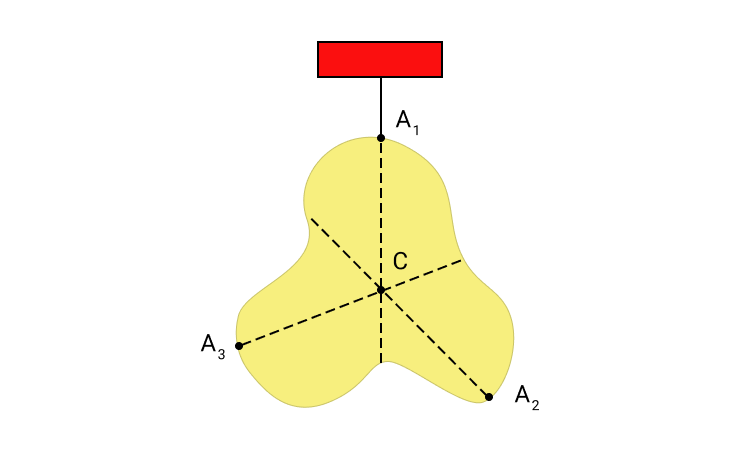
Рисунок 3. Определение положения центра масс C тела сложной формы. A1, A2, A3 точки подвеса.
На рисунке мы видим тело, которое подвешено за центр масс. Оно находится в состоянии безразличного равновесия. В однородном поле тяготения равнодействующая сил тяжести приложена к центру масс.
Мы можем представить любое движение твердого тела как сумму двух движений. Первое поступательное, которое производится со скоростью центра масс тела. Второе – это вращение относительно оси, которая проходит через центр масс.
Предположим. Что у нас есть колесо, которое катится по горизонтальной поверхности без проскальзывания. Все точки колеса во время движения перемещаются параллельно одной плоскости. Такое движение мы можем обозначить как плоское.
Теорема о движении центра масс
Кинестетическая энергия вращающегося твердого тела при плоском движении будет равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, которая проведена через центр масс и располагается перпендикулярно плоскостям, в которых движутся все точки тела:
Ek=mvC22+ICω22,
где m – полная масса тела, IC – момент инерции тела относительно оси, проходящей через центр масс.
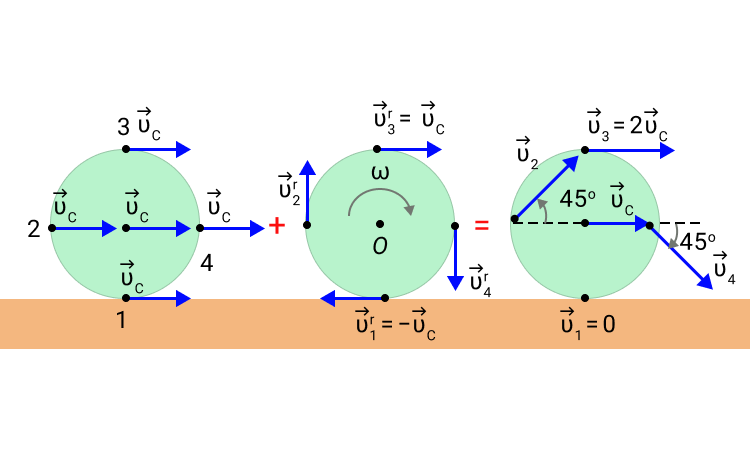
Рисунок 4. Качение колеса как сумма поступательного движения со скоростью vC→ и вращения с угловой скоростью ω=vCR относительно оси O, проходящей через центр масс.
В механике используется теорема о движении центра масс.
Любое тело или несколько взаимодействующих тел, которые представляют собой единую систему, обладают центром масс. Этот центр масс под воздействием внешних сил перемещается в пространстве как материальная точка, в которой сосредоточена вся масса системы.
На рисунке мы изобразили движение твердого тела, на которое действуют силы тяжести. Центр масс тела движется по траектории, которая близка к параболе, тогда как траектория остальных точек тела является более сложной.
Рисунок 5. Движение твердого тела под действием силы тяжести.
Теорема Штейнера о параллельном переносе оси вращения
Рассмотрим случай, когда твердое тело движется вокруг некоторой неподвижной оси. Момент инерции этого тела инерции I можно выразить через момент инерции IC этого тела относительно оси, проходящей через центр масс тела и параллельной первой.
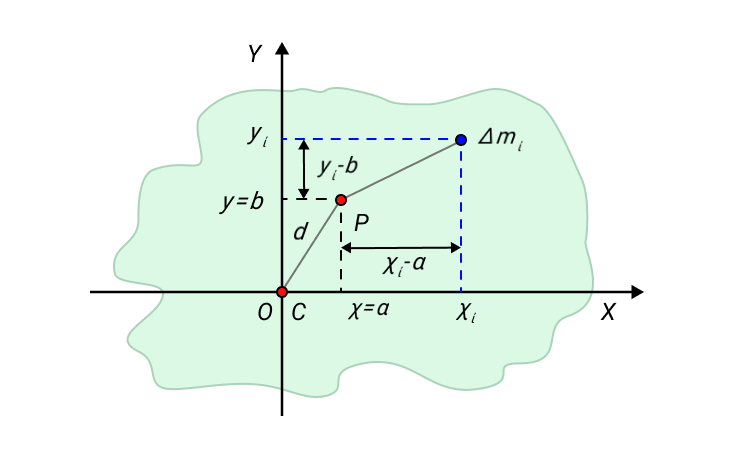
Рисунок 6. К доказательству теоремы о параллельном переносе оси вращения.
Для примера возьмем твердое тело, форма которого произвольна. Обозначим центр масс С. Выберем систему координат ХУ с началом координат 0. Совместим центр масс и начало координат.
Одна из осей проходит через центр масс С. Вторая ось пересекает произвольно выбранную точку Р, которая расположена на расстоянии d от начала координат. Выделим некоторый малый элемент массы данного твердого тела Δmi.
По определению момента инерции:
IC=∑∆mi(xi2+yi2),IP=∑mi(xi-a)2+yi-b2
Выражение для IP можно переписать в виде:
IP=∑∆mi(xi2+yi2)+∑∆mi(a2+b2)-2a∑∆mixi-2b∑∆miyi.
Два последних члена уравнения обращаются в нуль, так как начало координат в нашем случае совпадает с центром масс тела.
Так мы пришли к формуле теоремы Штейнера о параллельном переносе оси вращения.
Для тела, которое вращается относительно произвольной неподвижной оси, момент инерции, согласно теореме Штейнера, равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.
IP=IC+md2,
где m – полная масса тела.
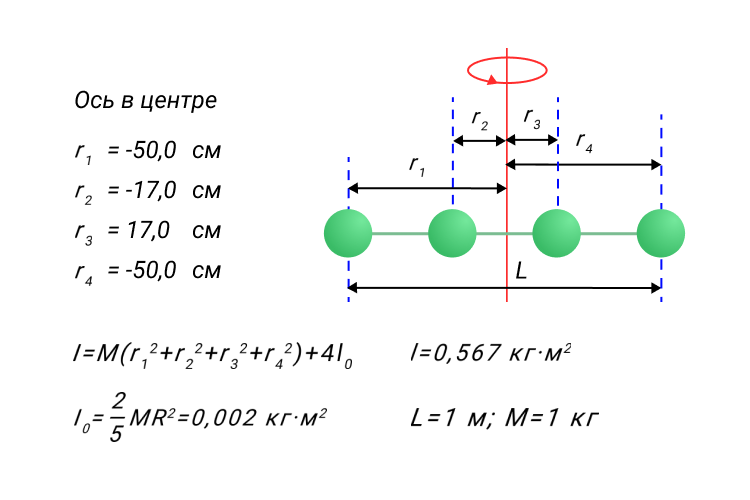
Рисунок 7. Модель момента инерции.
На рисунке ниже изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.
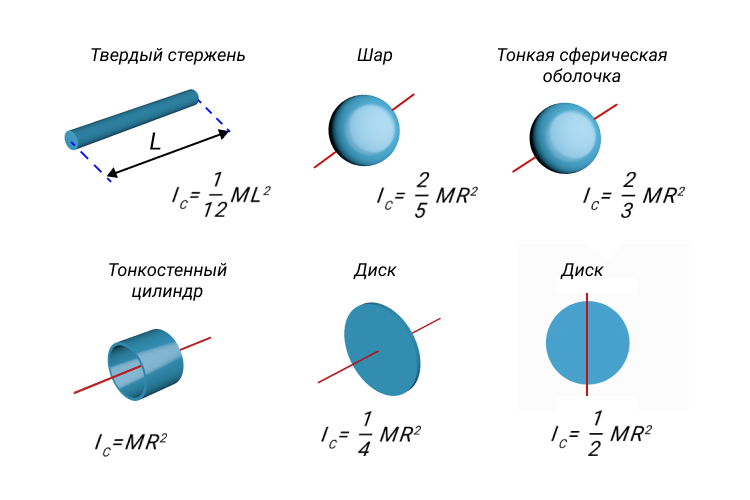
Рисунок 8. Моменты инерции IC некоторых однородных твердых тел.
Основное уравнение динамики вращательного движения твердого тела
В тех случаях, когда мы имеем дело с твердым телом, которое вращается относительно неподвижной оси, мы можем обобщить второй закон Ньютона. На рисунке ниже мы изобразили твердое тело произвольной формы, вращающееся относительно некоторой оси, проходящей через точку О. Ось вращения расположена перпендикулярно плоскости рисунка.
Δmi – это произвольный малый элемент массы, на который оказывают воздействие внешние и внутренние силы. Равнодействующая всех сил есть Fi→. Ее можно разложить на две составляющие: касательную составляющую Fiτ→ и радиальную Fir→. Радиальная составляющая Fir→ создает центростремительное ускорение an.
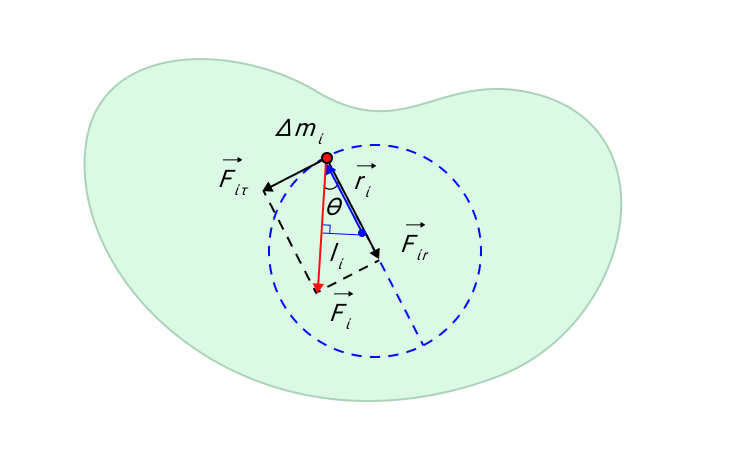
Рисунок 9. Касательная Fiτ→ и радиальная Fir→ составляющие силы Fi→ действующей на элемент Δmi твердого тела.
Касательная составляющая Fiτ→ вызывает тангенциальное ускорение aiτ→ массы Δmi. Второй закон Ньютона, записанный в скалярной форме, дает
∆miaiτ=Fiτsin θ или ∆miriε=Fisin θ,
где ε=aiτri – угловое ускорение всех точек твердого тела.
Если обе части написанного выше уравнения умножить на ri, то мы получим:
∆miri2ε=Firisin θ=Fili=Mi.
Здесь li – плечо силы, Fi,→Mi – момент силы.
Теперь нужно аналогичные соотношения записать для всех элементов массы Δmi вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:
∑∆miri2ε=∑Mi.
Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.
∑M=∑Miвнешн+∑Miвнутр.
Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M. Так мы получили основное уравнение динамики вращательного движения твердого тела.
Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими.
Iε=M
Обычно за положительное направление вращения принимают направление против часовой стрелки.
Возможна и векторная форма записи основного уравнения динамики вращательного движения, при которой величины ω→, ε→, M→ определяются как векторы, направленные по оси вращения.
Закон сохранения момента импульса
В разделе, посвященном поступательному движению тела, мы ввели понятие импульса тела p→. По аналогии с поступательным движением для вращательного движения мы вводим понятие момента импульса.
Момент импульса вращающегося тела – это физическая величина, которая равняется произведению момента инерции тела I на угловую скорость ω его вращения.
Для обозначения момента импульса используется латинская буква L.
L=lω
Поскольку ε=∆ω∆t; ∆t→0, уравнение вращательного движения можно представить в виде:
M=Iε=I∆ω∆t или M∆t=I∆ω=∆L.
Получаем:
M=∆L∆t; (∆t→0).
Мы получили это уравнение для случая, когда I = const. Но оно будет справедливо и тогда, когда момент инерции тела будет изменяться в процессе движения.
Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L=Iω относительно данной оси сохраняется: ∆L=0, если M=0.
Следовательно,
L=lω=const.
Так мы пришли к закону сохранения момента импульса.
В качестве примера приведем рисунок, на котором изображено неупругое вращательное столкновение дисков, которые насажены на общую для них ось.
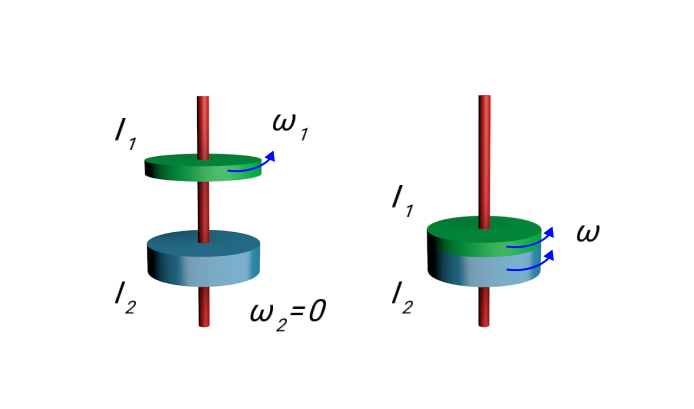
Рисунок 10. Неупругое вращательное столкновение двух дисков. Закон сохранения момента импульса: I1ω1=(I1+I2)ω.
Мы имеем дело с замкнутой системой. Для любой замкнутой системы закон сохранения момента импульса будет справедливым. Он выполняется и в условиях экспериментов по механике, и в условиях космоса, когда планеты движутся по своим орбитам вокруг звезды.
Мы можем записать уравнение динамики вращательного движения как для неподвижной оси, так и для оси, которая перемещается равномерно или с ускорением. Вид уравнения не изменится и в том случае, если ось движется ускоренно. Для этого должно выполняться два условия: ось должна проходить через центр массы тела, а ее направление в пространстве остается неизменным.
Предположим, что у нас есть тело (шар или цилиндр), которое катится по наклонной плоскости с некоторым трением.
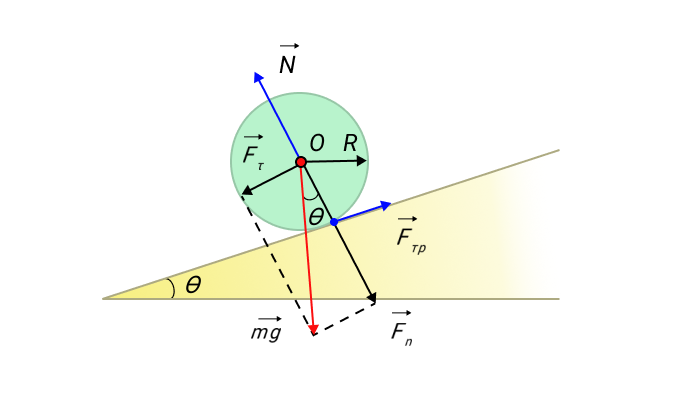
Рисунок 11. Качение симметричного тела по наклонной плоскости.
Ось вращения O проходит через центр масс тела. Моменты силы тяжести mg→ и силы реакции N→ относительно оси O равны нулю. Момент M создает только сила трения: M = FтрR.
Уравнение вращательного движения:
ICε=ICaR=M=FтрR,
где ε – угловое ускорение катящегося тела, a – линейное ускорение его центра масс, IC – момент инерции относительно оси O, проходящей через центр масс.
Второй закон Ньютона для поступательного движения центра масс записывается в виде:
ma=mg sin α-Fтр.
Исключая из этих уравнений Fтр, получим окончательно:
α=mg sin θICR2+m.
Из этого выражения видно, что быстрее будет скатываться с наклонной плоскости тело, обладающее меньшим моментом инерции. Например, у шара IC=25mR2, а у сплошного однородного цилиндра IC=12mR2. Следовательно, шар будет скатываться быстрее цилиндра.