Как найти осевой румб

Решение обратной геодезической задачи

Целью решения обратной геодезической задачи является вычисление длины линии и дирекционного угла линии по известным координатам её конечных точек. Т.е. при известных координатах точек А(X_A, Y_A) и В(X_B, Y_B) необходимо найти длину S_AB и направление линии АВ: осевой румб r_AB и дирекционный угол a_AB (рис. 10).

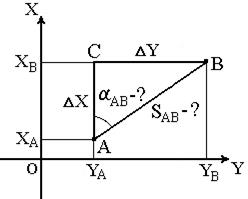Координаты точекА(X_A, Y_A) и В(X_B, Y_B) определяют при решении предыдущей задачи (см. п.1.4.2).

Данная задача решается следующим образом.

Сначала находим приращения координат

Рис. 10. Обратная геодезическая задача

Величину осевого румба r_AB определяем из отношения

.

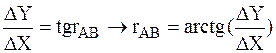По знакам приращений координат определяем четверть, в которой располагается румб, и её название (см. табл.1).

Знаки приращений координат ΔX и ΔY

Приращения координат	Четверть окружности, в которую направлена линия
I (СВ)	II (ЮВ)	III (ЮЗ)	IV (СЗ)
ΔX	+	–	–	+
ΔY	+	+	–	–

Используя зависимость между дирекционными углами и осевыми румбами (рис. 11), находим a_AB.

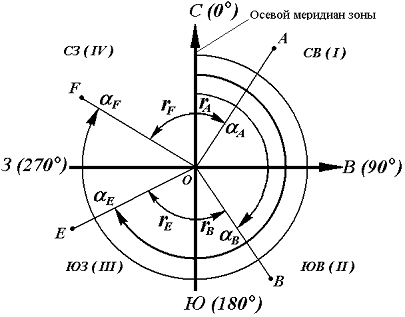
Рис. 11. Осевые румбы и дирекционные углы

Зависимость между дирекционными углами и румбами определяется для четвертей по следующим формулам:

I четверть (СВ) r = a ,

II четверть (ЮВ) r = 180° – a ,

III четверть (ЮЗ) r = a – 180° ,

IV четверть (СЗ) r = 360° – a .

Расстояние S_AB определяем по формуле

.

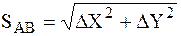Для контроля расстояние S_AB вычисляют дважды по формулам:

,

.

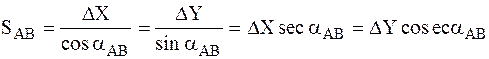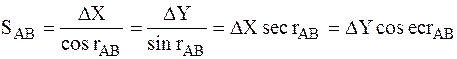Пример.Координаты точек:А(5998.650 км, 2396.750 км);

В(6000.150 км, 2395.250 км).

Вычисляем осевой румб r_AB из отношения

,

.

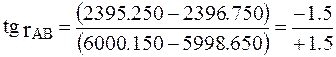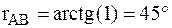По знакам приращений координат ΔX>0 и ΔY

Лучшие изречения:

80% успеха — это появиться в нужном месте в нужное время. © Вуди Аллен
==> читать все изречения. 167 — | 158 —

Источник

Решение обратной геодезической задачи

Основой решения является расчетная схема рис.1.5.

1. Выписать исходную информацию (расчетная схема соответствует рис.1.10).

2. Вычислить приращения координат по формулам (1.6).

3. На микрокалькуляторе вычислить румб и длину линии по формулам (1.7)-(1.8).

4. По знакам приращений определить название румба в соответствии с рис.1.6.

5. От румба перейти к дирекционному углу по формулам связи (рис.1.4).

6. Сравнить вычисленные значения с измеренными. Расхождения не должны превышать 2 мм в длине линии и 1 0 в дирекционном угле.

Задача решается на микрокалькуляторе. Но при этом непосредственно определить угол  по формуле:=arc tg(у/х), вытекающей из уравнений (1.4), невозможно из-за неоднозначного решения задачи. Так прих отрицательном,у положительном их положительном,у отрицательном получим одинаковые значения. Для контроля вычисления можно выполнить через радианы. Связь между градусами и радианами:

r рад =r 0 / 57.29578 ;r 0 =r рад 57.29578. (1.10)

2. Приращения координат: x=X_B -X_A=6064410 — 6065675 = -1265 м,y=У_В— У_А= -188318–(- 188030) = — 288 м.

3. Румб линии через градусы, установив программу DEG:

/r/ = arc tg ( Δу / Δх )=”288” : ” 1265” = ”2ndF» tg -1 ” = 12.826 0 = 12 0 50′ .

Длина линии (программа DEG):

d=x/Cosr=“12.826“Cos”2ndF“1/x”×”1265”=1297 м. Второе вычисление:d=y/Sinr=“12.826“Sin”2ndF“1/x”×”288” = 1297 м. Расхождений в вычислениях не должно быть.

4. В соответствии со знаками приращений румб r = ЮЗ:12 0 50′.

5. Дирекционный угол = 192 0 50′.

6. Расхождение в длине линии 3 м, в румбе 10′. Расхождения допустимы.

Пример вычисления румба через радианы. Программа RAD:

arctg(Δу/Δх )=”288”:”1265“=“2ndF»tg -1 ”=»×»57.2958″=12.826 0 =12 0 50′.

Вычисления следует выполнять по разным формулам. Так, решение прямой задачи выполняется через дирекционные углы по формулам (1.4) и через румбы по формулам (1.5), кроме первой четверти. В северо-восточной части r= , контроля не будет. В этом случае, как и при решении обратной задачи, вычисления следует вести через градусы и через радианы.

Определение отметок точек

Отметки точек определяют по правилам, см. фрагмент листа карты (рис.1.1).

1. Точка лежит на горизонтали. Отметка точки равна отметке горизонтали: Н₁=152.5 м.

2. Точка лежит между разноименными горизонталями. Отметка точки определяется графической интерполяцией на глаз: Н₂=150+2.5/3=150.8 м.

3. Седловина. Отметка точки равна отметке ближней горизонтали ± полсечения рельефа: Н₃=152.5+h/2=153.8 м или 155 – h/2 = 153.8 м.

4. Определяемая точка лежит между горизонталью и точкой с подписанной на карте отметкой. Отметка определяется графической интерполяцией: Н₄=155+(156.9–155)/2=155.7 м.

5. Точка лежит на полугоризонтали: Н₅ = 155 +h/ 2 = 156.2 м.

6 и 7. Отметки вершин: H₆ =155 +h/ 2 = 156.2 м;H₇ = 156.25 (полугоризонталь)+h/4=156.8 м.

Источник

Тема 3. Прямая и обратная геодезическая задача.

При производстве строительных работ создается разбивочная основа в виде строительной сетки. Пункт Государственной геодезической сети выносится на территорию строительства для обеспечения исходными данными всех геодезических работ. Решение прямой геодезической задачи позволяет определить координаты всех точек, расположенных в зоне строительства.

В геодезии принята система плос­ких прямоугольных координат, в которой относительно оси XX , совпадающей с направлением меридиана, и оси YY , перпендику­лярной к оси XX , определяют положение каждой точки, т. е. её координаты х и у; при этом счет четвертей идет по ходу часовой стрелки, согласно возрастанию азимутов и дирекционных углов .

При составлении планов ситуацию накладывают от опорных точек и линий, их соединяющих. Поэтому на бумагу сначала на­носят опорные точки по их координатам. Так как число этих точек весьма велико, то при геодезических работах часто решают прямую задачу на координаты. Она состоит в том, что по извест­ным координатам данной точки, а также дирекционному углу и горизонтальному проложению линии от этой точки до определяе­мой вычисляют координаты определяемой точки.

Решить прямую геодезическую задачу, т.е Пример

определить прямоугольные координаты точки 2 через координаты точки 1 по следующим данным:

Кординаты точки 1 — X, = 4250 м. У,=6730 м;

Расстояние между точками d =120,10 м; направление линии, т.е дирекционный угол 48°30′ =r.

Для определения координат точки 2 сначала нужно найти приращение координат –ΔХ и ΔУ,затем сами координаты Х₂;У_{2 .}

1.Определяем приращение координат ΔХ =d . cosr = 120,10 . 0,6626 =79,51 м

ΔУ= d . sinr =12,10 . 0,7490 =89,95 м

ΔУ

х₂ 2

r d

х₁ 1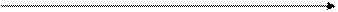

2. Определяем координаты точки 2

В практике прикладной геодезии для нужд проектирования и выноса проекта на местность приходиться определять значения дирекционного угла и длинны стороны по известным координатам её конечных точек. Это и составляет сущность решения обратной геодезической задачи.

Решение обратной геодезической задачи состоит в том, что, зная координаты опорных точек, можно вычислить дирекционный угол и расстояние между данными точками.

Пример.

Решить обратную геодезическую задачу, т.е. найти расстояниеd между точками и направление этой линии ( румб, азимут), если координаты точки1 Х₁= 320,5 м, У₁ = 780,2 м; координаты т очки 2 Х₂= 230,7 м, У₂ =900,1 м.

1. Определяем приращение координатΔХ = Х₂-Х₁ = 230,7 -320,5 = -89,8 м

ΔХ = У₂ –У₁ =900,1 – 780,2 = 119,9 м

Знаки приращений говорят, что линия расположена во второй четверти (ЮВ)

Знаки приращения координат можно определить по следующей схеме:

СЗ С х

З +ΔХ — ΔУ +ΔХ + ΔУ В

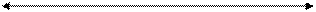
у -ΔХ — ΔУ -ΔХ + ΔУ у

Они зависят от четверти, в которой расположена линия.

2. Величина румба определяется по формуле

tg r= 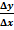= = 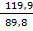1, 3352

ctgr = 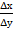= = 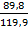0,74,89

По таблицам Брадиса находим величину румба — 53⁰ 10ʹ

3. Расстояние между точками найдем по теореме Пифагора:

d= 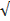ΔХ 2 + ΔУ 2 = 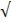89,8 2 + 119,9 2 = 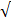22440,05 = 149,8 м

Контрольные вопросы:

1. Какие знаки у приращения координат ΔХ и ΔУ, если наименование румба ЮЗ?

а) –ΔХ, –ΔУ; б)+ ΔХ, +ΔУ; в)–ΔХ,+ΔУ; г))+ ΔХ,–ΔУ;

2. Найдите координаты точки 2, если координаты точки 1 Х= 10, У=5 и приращение ΔХ = 20, ΔУ =15.

а) 30, 20; б) 20, 30; в) 20, 40; г) 30, 40;

3. Решить обратную геодезическую задачу: найти расстояние между двумя точками и румб линии, если координаты начала и конца линии Х₁= 320,5 м, У₁ = 780,2 м; Х₂ 230,7 м,

а); 160,7 м, 60⁰ 20ʹ; б)149,8 м, 53⁰ 10ʹ; в) 120, 9 м, 58⁰ 45ʹ; г) 456,7м, 45⁰ 15ʹ;

4. Решить прямую геодезическую задачу: определить прямоугольные координаты точки 2 через координаты точки 1 по следующим данным: Х₁ = 4250м, У₁= 6730м, расстояние d – 120, 1 м, дирекционный угол — 48⁰30ʹ.

Какие слова нужно вставить в место точек в определении «Дирекционным углом лини называют угол, отсчитанный от. до данной прямой по направлению часовой стрелки?»

Азимут лини находится в пределах 90°-180 каково градусное значение румба?

Каково название румба линии и его величина , если азимут её определён по формуле А°-З60-r°

№	Вопросы (задания)	Ответы	Код
I	Осевого меридиана зоны	1
Ближайшего направления меридиана	2
Южного направления магнитного меридиана	3
Северного направления географического меридиана	4
II	Азимут лини находиться в пределах от 180°-270°	Сз	1
каково наименование румба?	Юв	2
Юз	3
Св	4
III	r°=А°	1
r°=180°-А°	2
r°=А°-180°	3
r°=360°-А°	4
IV	каково градусное значение азимута (А°) линии для ЮВ:r	А°=180°+r°	1
А о =360°-r°	2
А°=180°-r°	3
А°=r°	4
V	Сз:r°	1
Юз:r°	2
Юв:r°	3
Св:r°	4

Азимут лини находится в пределах 270°-360° каково градусное значение румба?

Каково название румба линии и его величина, если азимут её определён по формуле А°- 180°+r°

№	Вопросы (задания)	Ответы	Код
I	Какие слова нужно вставить в место точек в определении «Дирекционным углом лини называют угол, отсчитанный от. до данной прямой по направлению часовой стрелки?»	Северного направления географического меридиана	1
Осевого меридиана зоны	2
Южного	3
направления магнитного
меридиана
Ближайшего	4
направления меридиана
И	Азимут лини находиться в пределах от 0°-90° каково наименование румба?	Сз	1
Юв	2
Юз	3
Св	4
III	r°=А°	1
r°=180°-А°	2
r°=А°-180°	3
r°=360°-А°	4
IV	каково градусное значение азимута (А°) линии для Юз:ч°	А°=180°-r°	1
А°-360°-r°	2
A°=180W	3
А°=r°	4
V	Сз:r°	1
Юз:r°	2
Юв:r°	3
Св:r°	4

Азимут лини находится в пределах 180°-270° каково градусное значение румба?

Каково название румба линии и его величина , если азимут её определён по формуле А°-360°-r°

№	Вопросы (задания)	Ответы	Код
I	Какие слова нужно вставить в место точек в определении «Дирекционным углом лини называют угол, отсчитанный от. до данной прямой по направлению часовой стрелки?»	Северного направления географического меридиана	1
Южного
направления магнитного	2
меридиана
Ближайшего
направления меридиана	3
Осевого	4
меридиана зоны
И	Азимут лини находиться в пределах 90°-180 каково	Сз	8
наименование румба?	Юв	9
Юз	1
Св	2
III	r°=А°	3
r°=180°-А°	4
r°=А°-180°	5
r°=360°-А°	6
IV	каково градусное значение азимута (А°) линии для румба св: r°	А°=180°-r°	7
А°=360°-r°	8
А°=180°+r°	9
А°=r°	1
V	Сз:r°	2
Юз:r°	3
Юв:r°	4
Св:r°	5

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Источник

румбом
называется острый горизонтальный угол,
отсчитываемый от ближайшего направления
осевого меридиана (северного или южного)
до данной линии. Румбы обозначают буквой
r с индексом, указывающим четверть, в
которой находится румб.

Зависимость
между дирекционными углами и румбами
определяется для четвертей по следующим
формулам:

I
четверть (СВ) r = α

II
четверть (ЮВ) r = 180° – α

III
четверть (ЮЗ) r = α – 180°

IV
четверть (СЗ) r = 360° – α

Румб
в точке М направления ВС называется
прямым, а противоположного направления
СВ – обратным. Прямой и обратный румб
в одной и той же точке данной линии равны
по численному значению, но имеют индексы
противоположных четвертей.

19. Прямая геодезическая задача

В
геодезии часто приходится передавать
координаты с одной точки на другую.
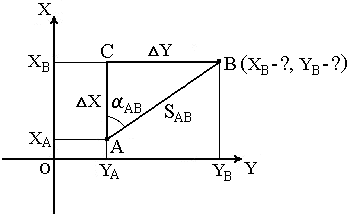
Например, зная исходные координаты
точки А (рис.23), горизонтальное расстояние
SAB от неё до точки В и направление линии,
соединяющей обе точки (дирекционный
угол αAB или румб rAB), можно определить
координаты точки В. В такой постановке
передача координат называется прямой
геодезической задачей.

Для
точек, расположенных на сфероиде, решение
данной задачи представляет значительные
трудности. Для точек на плоскости она
решается следующим образом.

Дано:
Точка А( XA, YA ), SAB и αAB. Найти: точку В( XB,
YB ).

Непосредственно
из рисунка имеем:

ΔX
= XB – XA ; ΔY = YB – YA .

Разности
ΔX и ΔY координат точек последующей и
предыдущей называются приращениями
координат. Они представляют собой
проекции отрезка АВ на соответствующие
оси координат. Их значения находим из
прямоугольного прямоугольника АВС:

ΔX
= SAB · cos αAB ;ΔY = SAB · sin αAB .

Так
как в этих формулах SAB всегда число
положительное, то знаки приращений
координат ΔX и ΔY зависят от знаков cos
αAB и sin αAB.

При
помощи румба приращения координат
вычисляют по формулам:

ΔX
= SAB · cos rAB ;ΔY
= SAB · sin rAB .

Знаки
приращениям дают в зависимости от
названия румба. Вычислив приращения
координат, находим искомые координаты
другой точки:

XB
= XA + ΔX ; YB = YA + ΔY .

Таким
образом можно найти координаты любого
числа точек по правилу: координаты
последующей точки равны координатам
предыдущей точки плюс соответствующие
приращения.

Контроль
вычислений координат выполняют по
формуле

20. Обратная геодезическая задача

Обратная
геодезическая задача – это вычисление
дирекционного угла α и длины S линии,
соединяющей два пункта с известными
координатами X1, Y1 и X2, Y2

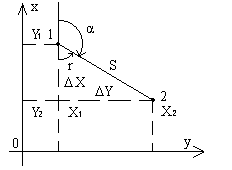
Построим
на отрезке 1-2 как на гипотенузе
прямоугольный треугольник с катетами,
параллельными осям координат. В этом
треугольнике гипотенуза равна S, катеты
равны приращениям координат точек 1 и
2 ( ΔX = X2 – X1, ΔY = Y2 – Y1 ), а один из острых
углов равен румбу r линии 1-2.

Если
Δ X 00 и Δ Y 00, то решаем треугольник по
известным формулам:

Для
данного рисунка направление линии 1-2
находится во второй четверти, поэтому
на основании (1.22) находим:

Общий
порядок нахождения дирекционного угла
линии 1-2 включает две операции:

*
определение номера четверти по знакам
приращений координат Δ>X и ΔY (рис.1.4-а),

*
вычисление α по формулам связи (1.22) в
соответствии с номером четверти.Контролем
правильности вычислений является
выполнение равенства:

Контроль:
d . cos α + XA = XB, d . sin α + YB = YB.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Перейти к содержанию

Азимуты

Азимут

Это направление, измеряемое в градусах по часовой стрелке от севера на азимутальной окружности. Азимутальный круг состоит из 360 градусов. Девяносто градусов соответствует востоку, 180 градусов — югу, 270 градусов — западу, а 360 градусов и 0 градусов — северу.

Слово «азимут» иногда используется как синоним азимута для обозначения направления (показания в градусах) от одного объекта к другому. Такое использование корректно только в первом (СВ) квадранте между 0° и 90°.

Азимуты также можно считывать с юга. Национальная геодезическая служба Национального управления океанических и атмосферных исследований (NOAA) (бывшая Береговая и геодезическая служба США) всегда использует юг в качестве нулевого направления. В пожарной службе дикой природы азимут всегда считывается с северной точки.

Направление ветра

Азимут часто используется для обозначения направления ветра. Традиционно направление ветра указывается как одна из восьми точек компаса (С, СВ, В, ЮВ, Ю, ЮЗ, З, СЗ). Однако графики направления ветра и скорости часто дают значение азимута, используя 0° и 360° для севера. Ветры называются по направлению, откуда они дуют. Например, западный ветер дует с запада (или 270°), а юго-восточный ветер дует с юго-востока (135°).

Обратный азимут и обратное визирование

Обратный азимут — это проекция азимута от начала координат до противоположной стороны азимутального круга. В азимутальном круге 360 градусов, поэтому противоположное направление будет 180 градусов (половина 360 градусов) от азимута.

Обратный азимут рассчитывается путем прибавления 180° к азимуту, если азимут меньше 180°, или вычитания 180° из азимута, если он больше 180°. Например, если азимут равен 320°, обратный азимут будет 320° – 180° = 140°. Если азимут равен 30°, обратный азимут будет равен 180° + 30° = 210°.

Обратное прицеливание — это метод прицеливания, в котором используется отсчет азимута, снятый в обратном направлении.

Компас – это инструмент, используемый для навигации и ориентации. Азимутальный компас градуирован/отмечен полным кругом в 360 градусов, который называется азимутальным кругом. Компоненты компаса включают магнитную стрелку, которая всегда указывает на магнитный север, градуированную окружность для откладывания углов от истинного севера и линию визирования для продолжения линии визирования при следовании курсу направления.

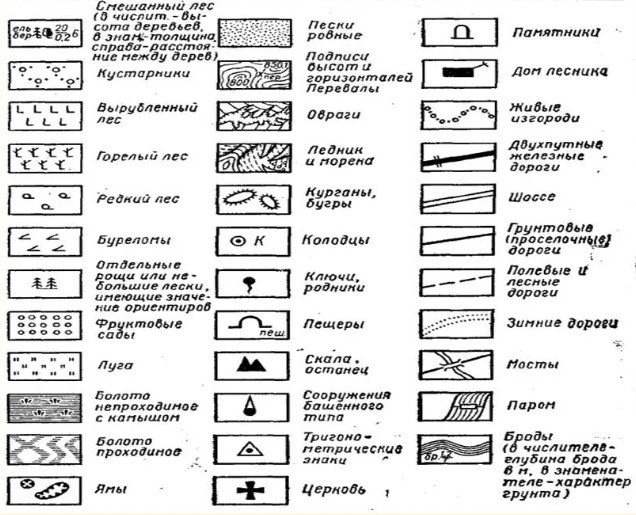
Условные знаки

Дирекционные углы и румбы

Дирекционные углы и румбы используются для ориентирования линий.

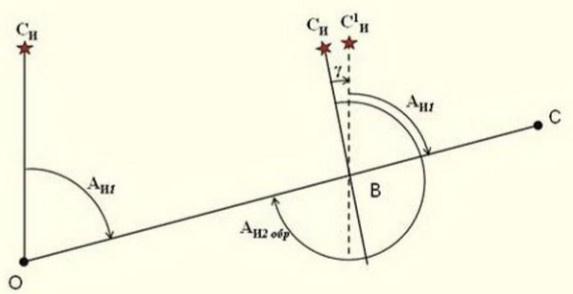
Дирекционным углом (α) линии называют угол, отсчитанный по ходу часовой стрелки от северного направления вертикальной линии километровой сетки (осевого меридиана зоны) до направления заданной линии. Пределы изменения дирекционного угла от 0º до 360º.

Румб (r)

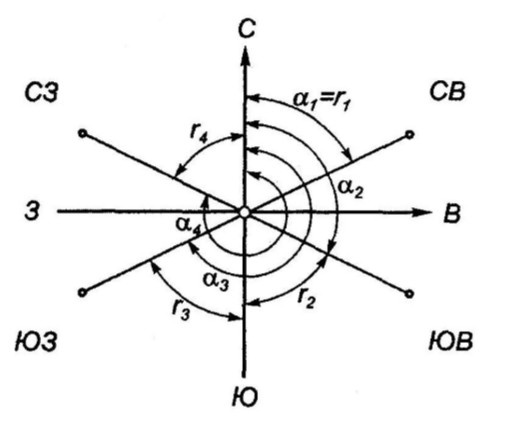
Это острый угол от ближайшего направления меридиана (северного или южного) до направления ориентирной линии. Пределы изменения румба от 0º до 90º.

Связь между дирекционными углами и румбами зависит от четверти, в которой находится заданное направление. Перевод дирекционных углов в румбы выполняется согласно таблице ниже.

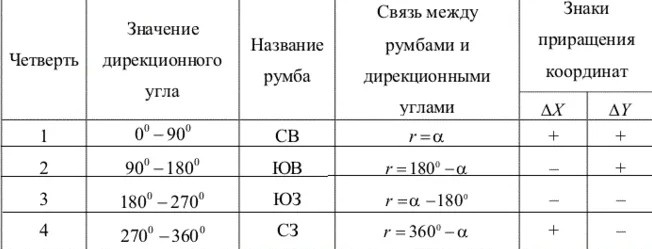
Пример перевода дирекционных углов в румбы

1. если дирекционный угол α равен 42°15′55″, тогда согласно таблице румб вычисляется по формуле r=α=42°15′55″, а название румба будет СВ;
2. если дирекционный угол α равен 100°45′11″, тогда согласно таблице румб вычисляется по формуле r=180°-α=180°-100°45′11″=79°14′49″, а название румба будет ЮВ;
3. если дирекционный угол α равен 210°17′42″, тогда согласно таблице румб вычисляется по формуле r=α-180°=210°17′42″-180°=30°17′42″, а название румба будет ЮЗ;
4. если дирекционный угол α равен 335°28′32″, тогда согласно таблице румб вычисляется по формуле r=360°-α=360°-335°28′32″=24°31′28″, а название румба будет СЗ.