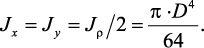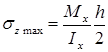Моменты сопротивления.
Осевой
момент сопротивления
— отношение момента инерции относительно
оси к расстоянию от нее до наиболее
удаленной точки сечения.
[см3,
м3]
Особенно
важны моменты сопротивления относительно
главных центральных осей:
прямоугольник:
;
круг:Wx=Wy=
,
трубчатое
сечение (кольцо): Wx=Wy=

где =
dН/dB.
Полярный
момент сопротивления — отношение
полярного момента инерции к расстоянию
от полюса до наиболее удаленной точки
сечения:
.
Для
круга Wр=
.
Кручение
Т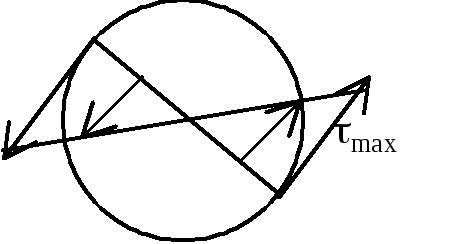
вид деформации, при котором в поперечных
сечениях возникает только одни крутящие
моменты — Мк.
Знак крутящего момента Мк
удобно определять по направлению
внешнего момента. Если при взгляде со
стороны сечения внешний момент направлен
против час.стр., то Мк>0
(встречается и обратное правило). При
кручении происходит поворот одного
сечения относительно другого на угол
закручивания
-.
При кручении круглого бруса (вала)
возникает напряженное состояние чистого
сдвига (нормальные напряжения отсутствуют),
возникают только касательные напряжения.
Принимается, что сечения плоские до
закручивания остаются плоскими и после
закручивания — закон
плоских сечений.
Касательные напряжения в точках сечения
изменяются пропорционально расстоянию
точек от оси. Из закона Гука при сдвиге:
=G,
G — модуль сдвига,
,
— полярный момент сопротивления круглого
сечения. Касательные напряжения в центре
равны нулю, чем дальше от центра, тем
они больше. Угол закручивания,GJp
— жесткость
сечения при кручении.
—относительный
угол закручивания.
Потенциальная энергия при кручении:
.
Условие прочности:,
[]
=,
для пластичного материала за пред
принимается предел текучести при сдвиге
т,
для хрупкого материала – в
– предел прочности, [n]
– коэффициент запаса прочности. Условие
жесткости при кручении: max[]
– допустимый угол закручивания.
Кручение бруса прямоугольного сечения
П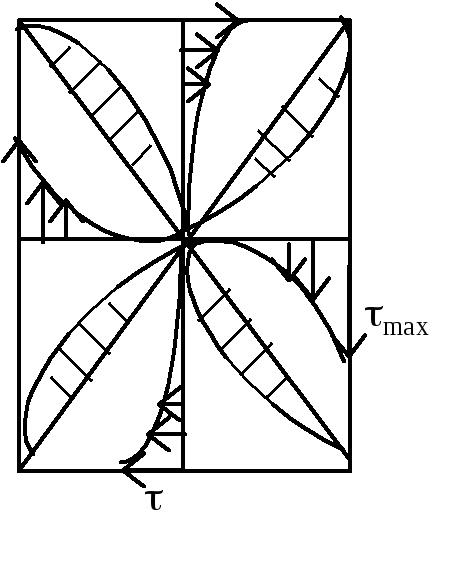
этом нарушается закон плоских сечений,
сечения некруглой формы при кручении
искривляются –депланация
поперечного сечения.
Э
касательных напряжений прямоугольного
сечения.
;
,Jk
и Wk
— условно называют моментом инерции и
моментом сопротивления при кручении.
Wk=
hb2,
Jk=
hb3,
Максимальные касательные напряжения
max
будут посредине длинной стороны,
напряжения по середине короткой стороны:
=
max,
коэффициенты: ,,
приводятся в справочниках в зависимости
от отношения h/b
(например, при h/b=2,
=0,246;
=0,229;
=0,795.
Изгиб
П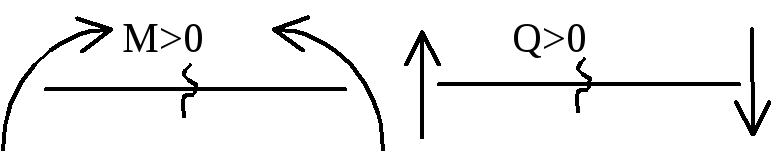
(прямой) изгиб
— когда изгибающий момент действует в
плоскости, проходящей через одну из
главных центральных осей инерции
сечения, т.е. все силы лежат в плоскости
симметрии балки. Основные
гипотезы
(допущения): гипотеза о не надавливании
продольных волокон: волокна, параллельные
оси балки, испытывают деформацию
растяжения – сжатия и не оказывают
давления друг на друга в поперечном
направлении; гипотеза плоских сечений:
сечение балки, плоское до деформации,
остается плоским и нормальным к
искривленной оси балки после деформации.
При плоском изгибе в общем случае
возникают внутренние
силовые факторы:
продольная сила N,
поперечная сила Q
и изгибающий момент М. N>0,
если продольная сила растягивающая;
при М>0 волокна сверху балки сжимаются,
снизу растягиваются.
.
С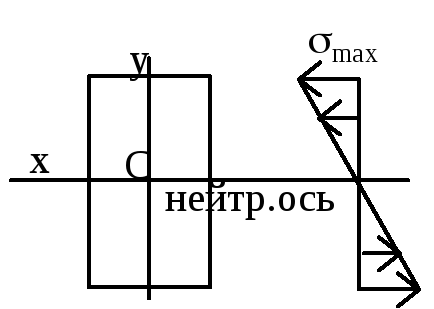
в котором отсутствуют удлинения,
называетсянейтральным
слоем (осью,
линией). При N=0
и Q=0,
имеем случай чистого
изгиба.
Нормальные напряжения:
,
— радиус кривизны нейтрального слоя,
y
— расстояние от некоторого волокна до
нейтрального слоя. Закон
Гука при изгибе:
,
откуда (формула Навье):,Jx
— момент инерции сечения относительно
главной центральной оси, перпендикулярной
плоскости изгибающего момента, EJx
— жесткость при изгибе,
— кривизна нейтрального слоя.
М
напряжения при изгибе возникают в
точках, наиболее удаленных от нейтрального
слоя:,Jx/ymax=Wx—момент
сопротивления сечения при изгибе,
.
Если сечение не имеет горизонтальной
оси симметрии, то эпюра нормальных
напряжений
не будет симметричной. Нейтральная ось
сечения проходит через центр тяжести
сечения. Формулы для определения
нормального напряжения для чистого
изгиба приближенно годятся и когда Q0.
Это случай поперечного
изгиба. При
поперечном изгибе, кроме изгибающего
момента М, действует поперечная сила
Q
и в сечении возникают не только нормальные
,
но и касательные
напряжения. Касательные напряжения
определяются формулой
Журавского:
,
гдеSx(y)
— статический момент относительно
нейтральной оси той части площади,
которая расположена ниже или выше слоя,
отстоящего на расстоянии “y”
от нейтральной оси; Jx
— момент инерции всего
поперечного сечения относительно
нейтральной оси, b(y)
— ширина сечения в слое, на котором
определяются касательные напряжения.
Д
прямоугольного сечения:,F=bh,
для круглого сечения:,F=R2,
для сечения любой формы
,
k—
коэфф., зависящий от формы сечения
(прямоугольник: k=
1,5; круг – k=
1,33).
M
и Qmax
определяются из эпюр изгибающих моментов
и поперечных сил. Для этого балка
разрезается на две части и рассматривается
одна из них. Действие отброшенной части
заменяется внутренними силовыми
факторами М и Q,
которые определяются из уравнений
равновесия. В некоторых вузах момент
М>0 откладывается вниз, т.е. эпюра
моментов строится на растянутых волокнах.
При Q=
0 имеем экстремум эпюры моментов.
Дифференциальные
зависимости между М,Q
и q:
q
— интенсивность распределенной нагрузки
[кН/м]
Главные
напряжения при поперечном изгибе:

Расчет
на прочность при изгибе:
два условия прочности, относящиеся к
различным точкам балки: а) по нормальным
напряжениям
,
(точки наиболее удаленные от С); б) по
касательным напряжениям,
(точки на нейтр.оси). Из а) определяют
размеры балки:,
которые проверяют по б). В сечениях балок
могут быть точки, где одновременно
большие нормальные и большие касательные
напряжения. Для этих точек находятся
эквивалентные напряжения, которые не
должны превышать допустимых. Условия
прочности проверяются по различным
теориям прочности
I-я:
;II-я:
(при коэфф.Пуассона=0,3);
— применяются редко.
III-я:,IV-я:
,
теория
Мора:
,
(используется для чугуна, у которого
допускаемое напряжение на растяжение
[р][с]
– на сжатие).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В предыдущей статье я рассказывал о моментах инерции, с которыми неразрывно связаны моменты сопротивления. Именно о них сейчас и пойдёт речь. Так что если читатель ещё не читал её — самое время!
А пока нам следует разобраться, что чему сопротивляется. И вообще, является ли организация своего протестного движения моментом сопротивления?
Что такое моменты сопротивления?
В статье про изгиб мы с вами разбирались в том, как найти максимальные напряжения в зоне чистого изгиба
Спойлер:

Где a — максимальное расстояние по интересующей нас оси.
Но чтобы упростить себе расчеты и допускать меньше ошибок, соотношение

Принято называть моментом сопротивления.
Тут может возникнуть вопрос: “Ну так а может не стоило вводить новую величину, а просто оперировать моментами инерции?”
На самом деле так действительно можно сделать, но столкнувшись с большим количеством расчетов читатель и сам наверняка начнет выписывать момент сопротивления. Упрощая алгоритм расчета, мы стремимся исключить возможные ошибки и ускорить сами расчеты. Ведь вместо трехэтажных дробей гораздо удобнее оперировать уже готовым значением.
То есть:
Осевой момент сопротивления – по сути отношение момента инерции к расстоянию до наиболее удаленной от этой оси точки:
По аналогии с полярным моментом инерции для расчетов круглых и близких к ним тел используется полярный момент сопротивления:
Момент сопротивления имеет размерность см3.
Как определить моменты сопротивления простых сечений?
1. Момент сопротивления прямоугольного сечения:
Где Ix:
2. Момент сопротивления квадратного сечения. Частный случай предыдущего пункта:
Где Ix:
3. Момент сопротивления сечения круга:
Где Ix:
4. Момент сопротивления сечения кольцо:
Расчет момента сопротивления сложного сечения
В качестве примера, определим момент инерции и момент сопротивления сечения, изображенного на рисунке ниже:d =20 см, a = 6 см.
1. Определим момент инерции сечения, как разность моментов инерции круга с диаметром d и квадрата со стороной a:
2. Определим момент сопротивления сечения:
3. А теперь давайте попробуем найти разность моментов сопротивления сечения. Будет ли она отличаться от ответа, полученного из двух предыдущих пунктов?
То есть момент сопротивления сечения определяется только через момент инерции! Напрямую складывая/вычитая моменты сопротивления вы получите неправильный ответ!
Подведем небольшой итог:
Момент сопротивления неразрывно связан с моментом инерции.
Моменты сопротивления упрощают расчет нормальных напряжений при изгибе (что особенно важно — максимальных нормальных напряжений), что делает прочностные расчёты при подборе сечения заметно легче и быстрее.
Информация о произведении
Автор: Марк Ершов
Редактор, факт-чекер: К.А.Овчинников
Условия использования: свободное некоммерческое использование при условии указания людей участвовавших в его создании и ссылку на первоисточник (статьи на действующем сайте интернет-журнала «Стройка Века»).
Для коммерческого использования — обращаться на почту:
buildxxvek@gmail.com
Список использованных источников
- Александров А.В. Сопротивление материалов: Учеб. для ВУЗов/ А.В. Александров, В.Д. Потапов, Б.П. Державин; под ред. А.В. Александрова – 3-е изд. испр. – М.: Высш. шк., 2003. – 560 с.: ил. ISBN 5-06-003732-0
- Дарков А.В., Шпиро Г.С. Сопротивление материалов – Учеб. для техн. вузов – 5-е изд. перераб. и дополн. – М.: Высш. шк., 1989 – 624 с. ил.
- Г.И. Беликов. Геометрические характеристики поперечных сечений стержней. Учебно-практическое пособие. — Волгоград: ВолгГАСУ, 2015. — 56 с. — ISBN 978-5-98276-752-3
4 804
Осевой момент сопротивления при изгибе
Формула осевого момента сопротивления при изгибе выводится просто. Когда поперечное сечение балки симметрично относительно нейтральной оси, нормальные напряжения в наиболее удаленных точках (при 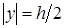
Геометрическую характеристику поперечного сечения балки, равную 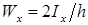
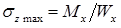
формула осевого момент сопротивления при изгибе для прямоугольного поперечного сечения: 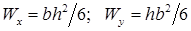
формула осевого момент сопротивления при изгибе для круглого поперечного сечения: 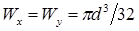
На этой странице ты можешь найти формулы для расчёта осевых моментов сопротивления простых сечений (фигур).
Формулы для расчёта моментов сопротивления
Моменты сопротивления обозначаются буквой – W.
Моменты сопротивления квадрата


Моменты сопротивления круга


Моменты сопротивления прямоугольника


Моменты сопротивления кольца


На проекте ssopromat.ru, ты также можешь найти другие справочные материалы здесь.
Лекция 4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ СТЕРЖНЯ
Математические определения геометрических характеристик плоских
фигур: статические моменты, осевые моменты инерции и центробежный,
полярный момент инерции. Центральные оси. Главные оси. Определение
положения центра тяжести элементарных сечений и составленного из
элементарных фигур. Нахождение геометрических характеристик сечений
относительно центральных осей.
Различают следующие характеристики сечений: площадь А, статические
моменты площади, моменты инерции площади, центробежный момент инерции
площади.
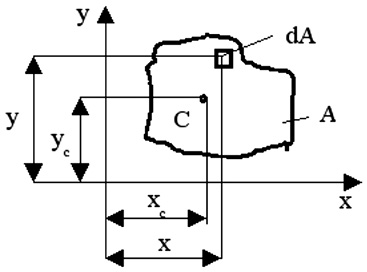
Рис. 10. Площадь А в системе координат х, у
Под статическим моментом площади относительно некоторой оси
понимается сумма произведений площадей элементарных площадок на
расстояния от их центра тяжести до соответствующей оси:
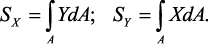
Определение центра тяжести сечения. Статические моменты сечения
относительно осей проходящих через центр тяжести равны нулю, поэтому их
используют для определения координат центров тяжести сечения. Для этого
проводят вспомогательные оси x и y и координаты центра тяжести сечения
определяют по зависимостям:
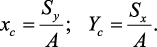
Моменты инерции сечения. Осевым моментом инерции сечения I
называется интеграл по площади произведения элементарной площадки на
квадрат расстояния до оси. Осевые моменты инерции сечения относительно
осей x и y будут соответственно равны
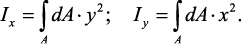
Полярным моментом инерции сечения Iρ называется интеграл по
площади произведения элементарной площадки на квадрат расстояния до
начало координат.
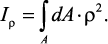
Учитывая, что ρ2 = x2 + y2, получаем Iρ = Ix + Iy.
Полярный момент инерции сечения равен сумме осевых моментов инерции сечения.
Оси, относительно которых центробежный момент инерции равен нулю,
называются главными центральными осями, осевые моменты инерции
относительно их принимают свои экстремальные значения (максимум
и минимум).
Полярный момент инерции
Jρ = Jx + Jy;, (6)
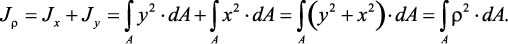
Полярный момент инерции относительно данной точки – сумма
произведений элементарных площадей dA на квадраты их расстояний
(ρ2 = y2 + z2) до этой точки, взятая по всей площади сечения А.
Моменты сопротивления. Осевой момент сопротивления относительно
рассматриваемой оси – величина равная моменту инерции относительно той
же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки
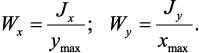
Полярный момент сопротивления
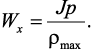
Осевой и полярный моменты сопротивления имеют размерность м3.
Радиус инерции
Радиусом инерции сечения относительно некоторой оси, называется величина, определяемая из соотношения:
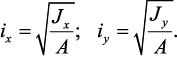
Вычисление геометрических характеристик простых фигур.
Прямоугольное сечение.
Определим осевой момент инерции прямоугольника относительно оси х.
Разобьем площадь прямоугольника на элементарные площадки
с размерами b (ширина) и dy (высота) (рис. 11). Тогда площадь такого
элементарного прямоугольника (заштрихована)равна dA = b•dy. Подставляя
значение dA в формулу для определения осевого момента инерции, получим:
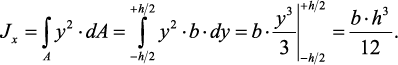
По аналогии запишем
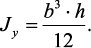
Круглое сечение
Вначале целесообразно найти полярный момент инерции. Затем,
учитывая, что для круга Jx = Jy, а Jρ = Jx + Jy, найдем Jx = Jy = Jρ/2.
Разобьем круг на бесконечно малые кольца толщиной dρ и радиусом ρ
(рис. 12); площадь такого кольца 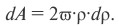
площади кольца в выражение для Jρ и интегрируя, получим:
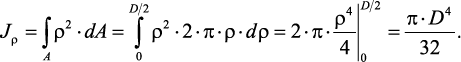
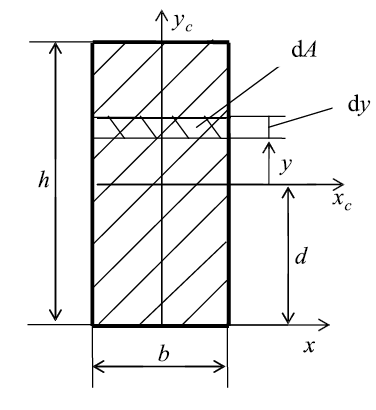
Рис. 11. Прямоугольник
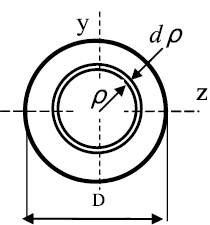
Рис. 12. Круг
Тогда