-
Виды ошибок регулирования и методы их снижения.
Прямые показатели качества подразделяются
на показатели качества динамического
и установившегося режимов.
Показателями качества динамических
режимов определяются из графика
переходного процесса и основными из
них являются (рис.1.42):
–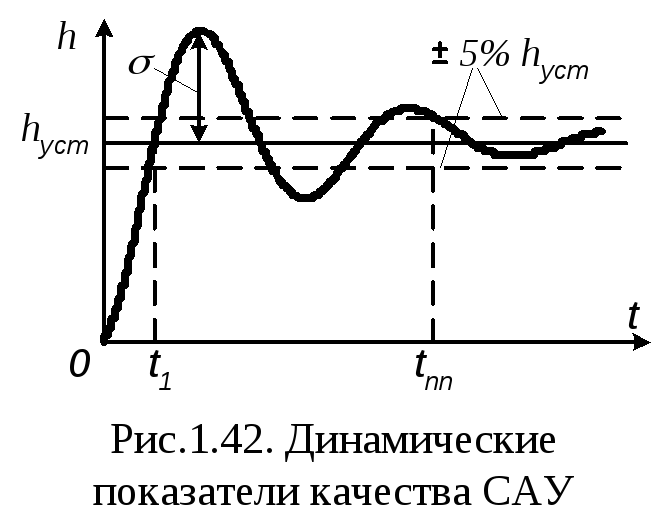 перерегулирование или забросσ,
перерегулирование или забросσ,
равный максимуму отклонения значения
переходного процесса относительно
установившегося значения процессаhycm;
– время первой установки t1,
определяемое моментом первого пересечения
графиком переходного процесса
установившегося значенияhycm;
– время переходного процесса tПП,
определяемое момент окончательного
входа графика переходного процесса в
зону допуска, равную±5%от
установившегося значения процессаhycm.
Для всех названных динамических
показателей качества невозможно в общем
случае получить формулы для их расчета.
Это является существенным препятствием
для решения задач анализа и синтеза
САУ.
Показателями качества установившихся
режимов являются ошибки регулирования,
равные абсолютной величине разности
между заданным и фактическим значениями
сигналов САУ и которые в зависимости
от вида входного сигнала САУ подразделяются
на статические (εСТ) и
скоростные ошибки (εСК) и
ошибки (εm)
при отработке гармонического входного
сигнала.
Д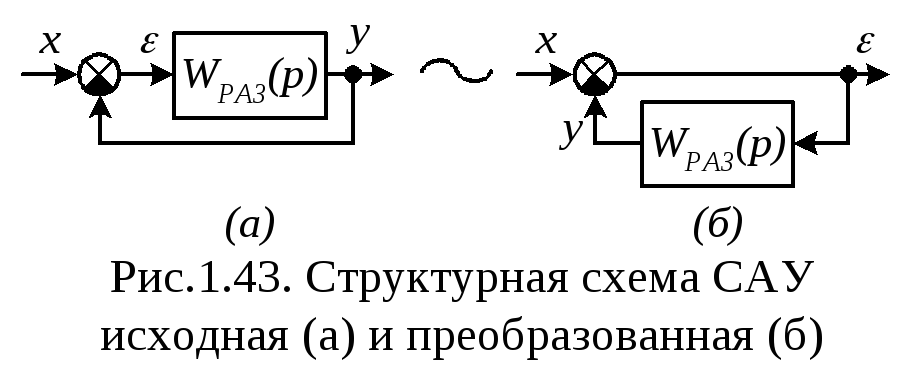 ля
ля
всех названных ошибок регулирования
можно в общем случае получить формулы
их расчета.
Из структурной схемы замкнутой САУ
(рис.1.43) следуют выражения передаточной
функции САУ Wε(p)по ошибке и изображенияε(р)ошибки
регулирования:
![]()
Расчет ошибки εmотработки гармонического входного
сигналаx=Xmsinωt
производится по формуле
![]()
где
![]() – модуль комплексного числа
– модуль комплексного числа![]() .
.
Статическая (εСТ) и
скоростная (εСК) ошибки
равны установившимся значениям оригинала![]() и
и![]() ,
,
или в общем виде, по формуле![]() .
.
Значение![]() вычисляют через изображениеε(р)
вычисляют через изображениеε(р)
по доказываемой в теории операционного
исчисления формуле предельного перехода,
![]() (1.54)
(1.54)
Выражение передаточной функции
разомкнутой САУ в общем случае может
быть приведено к виду:
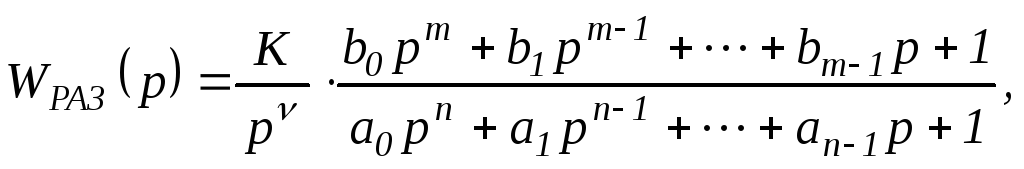 (1.55)
(1.55)
где К– общий коэффициент усиления
разомкнутой САУ:
ν– порядок астатизма САУ, причемνявляется целым неотрицательным
числом.
Для удобства вычислений по формуле
(1.54) подставим в нее выражение WРАЗ(р)из (1.55) и выполним предельный переход:
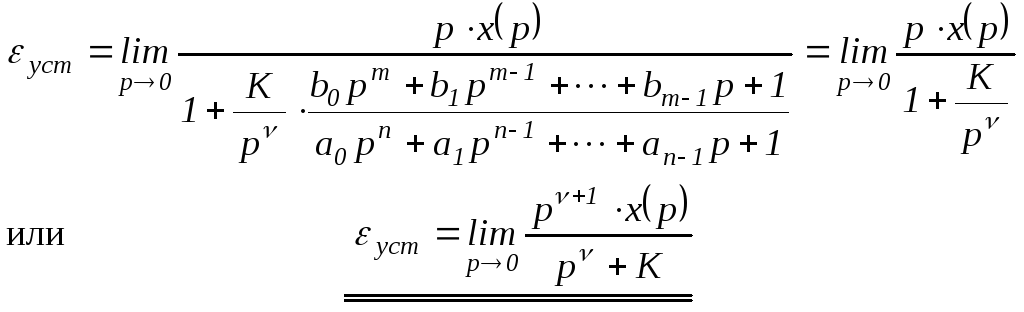 (1.56)
(1.56)
Статическая ошибка регулирования εСТрассчитывается при постоянном входном
сигналеx(t)=X=const,
а скоростнаяεСК– при
входном сигналеx=Vt,
изменяющемуся во времени с постоянной
скоростьюV=const.
Далее расчеты статической (εСТ)
и скоростной (εСК) ошибок
выполним раздельно.
Расчеты статической ошибки εСт регулирования
Входной сигнал x(t)=X=constи изображением его является![]() .
.
В соответствии с (1.56) статическую ошибкуεСТследует вычислять по
формуле
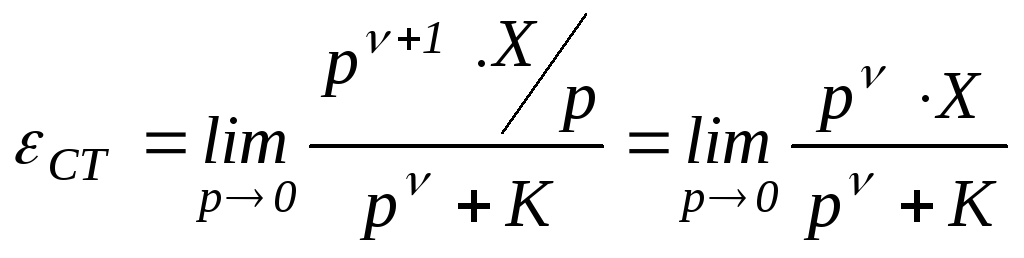 (1.57)
(1.57)
1). Пусть в (1.57) значение порядка νастатизма САУ равно нулю:ν=0. Такая
САУ называется статической. Тогда
статическая ошибкаεСТбудет равна
![]()
В статической САУ имеется статическая
ошибка εСТ, которую можно
только уменьшить путем увеличения
общего коэффициента усиленияКразомкнутой САУ, но обратить в ноль ее
нельзя.
2). Пусть в (1.57) значение порядка νастатизма САУ равно 1:ν=1. Такая САУ
называется астатической 1-го порядка.
Тогда статическая ошибкаεСТбудет равна
![]()
В астатической САУ 1-го порядка статическая
ошибка εСТравна нулю,
т.е САУ является абсолютно точной. Можно
проверить, что при астатизме САУ выше1, статическая ошибка регулирования
всегда будет нулевой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вместо введения
Системы автоматического управления (САУ) предназначены для автоматического изменения одного или нескольких параметров объекта управления с целью установления требуемого режима его работы. САУ обеспечивает поддержание постоянства заданных значений регулируемых параметров или их изменение по заданному закону либо оптимизирует определенные критерии качества управления. Например, к таким системам относятся:
- системы стабилизации,
- системы программного управления,
- следящие системы
Это достаточно широкий класс систем, которые можно найти где угодно. Но какое это отношение имеет к Unity3D и вероятно к играм в частности? В принципе прямое: в любой игре так или иначе использующей симуляцию как элемент геймплея реализуются САУ, к таким играм относятся, например, Kerbal Space Programm, Digital Combat Simulator (бывший Lock On), Strike Suit Zero и т.д. (кто знает еще примеры — пишите в комментариях). В принципе любая игра, моделирующая реальные физические процессы, в том числе и просто кинематику с динамикой движения, может реализовывать те или иные САУ — этот подход проще, естественнее, а у разработчика уже есть есть набор готовых инструментов, предоставленных всякими Вышнеградскими, Ляпуновыми, Калманами, Чебышевами и прочими Коломогоровами, поэтому можно обойтись без изобретения велосипеда, т.к. его уже изобрели, да так, что получилась отдельная наука: Теория автоматического управления. Главное тут не переусердствовать. Одна тут только проблема: рассказывают про ТАУ не везде, не всем, зачастую мало и не очень понятно.
Немножко теории
Классическая система автоматического управления представленная на следующем рисунке:
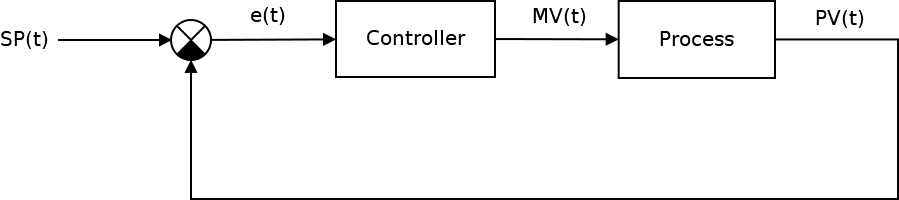
Ключевым элементом любой САУ является регулятор представляющий из себя устройство, которое следит за состоянием объекта управления и обеспечивает требуемый закон управления. Процесс управления включает в себя: вычисление ошибки управления или сигнала рассогласования e(t) как разницы между желаемой уставкой (set point или SP) и текущей величиной процесса (process value или PV), после чего регулятор вырабатывает управляющие сигналы (manipulated value или MV).
Одной из разновидностью регуляторов является пропорционально-интегрально-дифференцирующий (ПИД) регулятор, который формирует управляющий сигнал, являющийся суммой трёх слагаемых: пропорционального, интегрального и дифференциального.
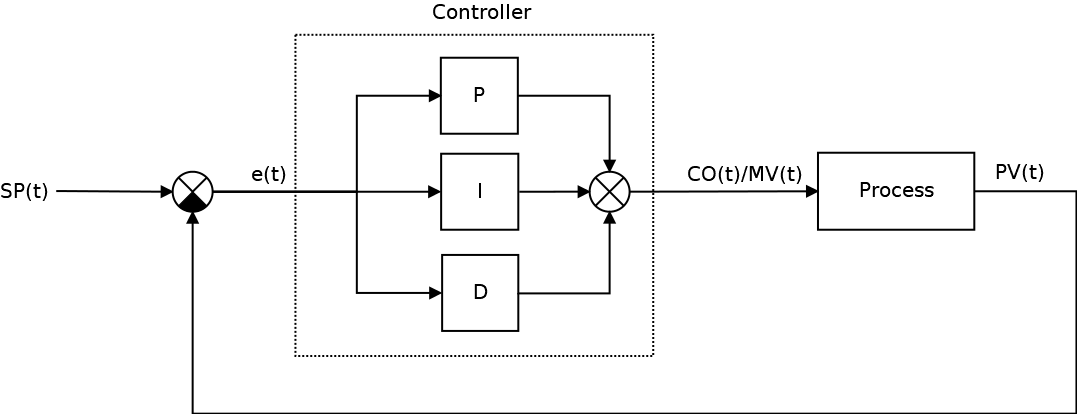
Где, ошибка рассогласования, а также,
— пропорциональная,
— интегральная,
— дифференциальная составляющие (термы) закона управления, который в итоговом виде описывается следующими формулами
Пропорциональная составляющая P — отвечает за т.н. пропорциональное управление, смысл которого в том, что выходной сигнал регулятора, противодействует отклонению регулируемой величины (ошибки рассогласования или еще это называют невязкой) от заданного значения. Чем больше ошибка рассогласования, тем больше командное отклонение регулятора. Это самый простой и очевидный закон управления. Недостаток пропорционального закона управления заключается в том, что регулятор никогда не стабилизируется в заданном значении, а увеличение коэффициента пропорциональности всегда приводит к автоколебаниям. Именно поэтому в довесок к пропорциональному закону управления приходиться использовать интегральный и дифференциальный.
Интегральная составляющая I накапливает (интегрирует) ошибку регулирования, что позволяет ПИД-регулятору устранять статическую ошибку (установившуюся ошибку, остаточное рассогласование). Или другими словами: интегральное звено всегда вносит некоторое смещение и если система подвержена некоторыми постоянным ошибкам, то оно их компенсирует (за счет своего смещения). А вот если же этих ошибок нет или они пренебрежительно малы, то эффект будет обратным — интегральная составляющая сама будет вносить ошибку смещения. Именно по этой причине её не используют, например, в задачах сверхточного позиционирования. Ключевым недостатком интегрального закона управления является эффект насыщения интегратора (Integrator windup).
Дифференциальная составляющая D пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Примечательно то, что дифференциальная компонента устраняет затухающие колебания. Дифференциальное регулирование особенно эффективно для процессов, которые имеют большие запаздывания. Недостатком дифференциального закона управления является его неустойчивость к воздействую шумов (Differentiation noise).
Таким образом, в зависимости от ситуации могут применятся П-, ПД-, ПИ- и ПИД-регуляторы, но основным законом управления в основном является пропорциональный (хотя в некоторых специфических задачах и могут использоваться исключительно только звенья дифференциаторов и интеграторов).
Казалось бы, вопрос реализации ПИД-регуляторов уже давно избит и здесь на Хабре есть парочка неплохих статей на эту тему в том числе и на Unity3D, также есть неплохая статья PID Without a PhD (перевод) и цикл статей в журнале «Современные технологии автоматизации» в двух частях: первая и вторая. Также к вашим услугам статья на Википедии (наиболее полную читайте в английском варианте). А на форумах коммьюнити Unity3D нет-нет, да и всплывет PID controller как и на gamedev.stackexchange
При вопрос по реализации ПИД-регуляторов несколько глубже чем и кажется. Настолько, что юных самоделкиных, решивших, реализовать такую схему регулирования ждет немало открытий чудных, а тема актуальная. Так что надеюсь сей опус, кому-нибудь да пригодиться, поэтому приступим.
Попытка номер раз
В качестве примера попытаемся реализовать схему регулирования на примере управления поворотом в простенькой космической 2D-аркаде, по шагам, начиная с самого начала (не забыли, что это туториал?).
Почему не 3D? Потому что реализация не измениться, за исключением того, что придется воротить ПИД-регулятор для контроля тангажа, рысканья и крена. Хотя вопрос корректного применения ПИД-регулирования вместе с кватернионами действительно интересный, возможно в будущем его и освящу, но даже в NASA предпочитают углы Эйлера вместо кватернионов, так что обойдемся простенькой моделью на двухмерной плоскости.
Для начала создадим сам объект игровой объект космического корабля, который будет состоять из собственно самого объекта корабля на верхнем уровне иерархии, прикрепим к нему дочерний объект Engine (чисто спецэффектов ради). Вот как это выглядит у меня:
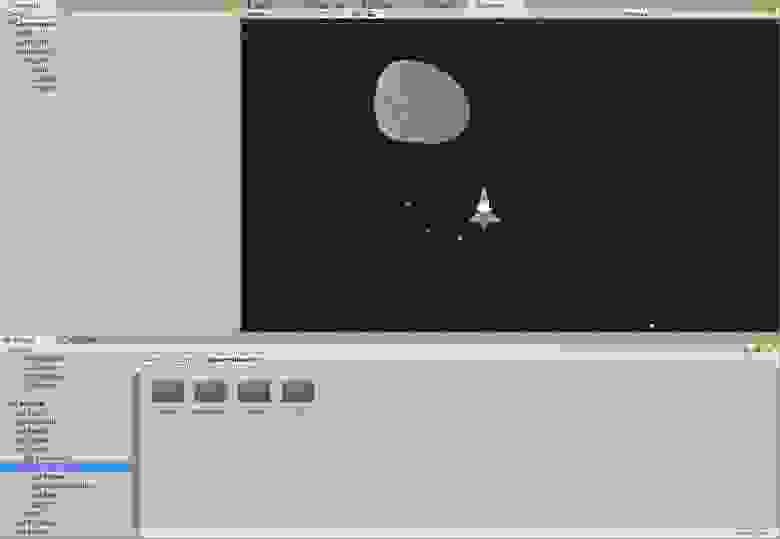
А на сам объект космического корабля накидаем в инспекторе всяческих компонент. Забегая вперед, приведу скрин того, как он будет выглядеть в конце:
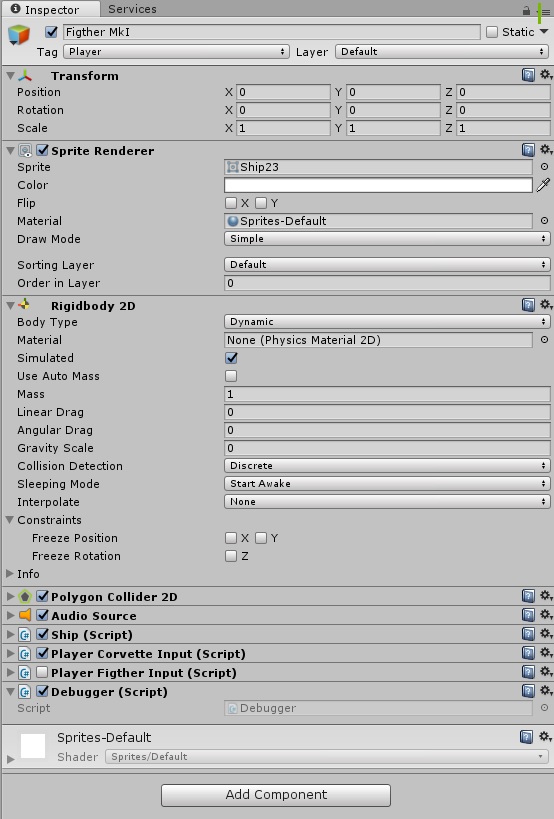
Но это потом, а пока в нем еще нет никаких скриптов, только стандартный джентльменский набор: Sprite Render, RigidBody2D, Polygon Collider, Audio Source (зачем?).
Собственно физика у нас сейчас самое главное и управление будет осуществляться исключительно через неё, в противном случае, применение ПИД-регулятора потеряло бы смысл. Масса нашего космического корабля оставим также в 1 кг, а все коэффициенты трения и гравитации равны нулю — в космосе же.
Т.к. помимо самого космического корабля есть куча других, менее умных космических объектов, то сначала опишем родительский класс BaseBody, который в себе будет содержать ссылки на на наши компоненты, методы инициализации и уничтожения, а также ряд дополнительных полей и методов, например для реализации небесной механики:
BaseBody.cs
using UnityEngine;
using System.Collections;
using System.Collections.Generic;
namespace Assets.Scripts.SpaceShooter.Bodies
{
[RequireComponent(typeof(SpriteRenderer))]
[RequireComponent(typeof(AudioSource))]
[RequireComponent(typeof(Rigidbody2D))]
[RequireComponent(typeof(Collider2D))]
public class BaseBody : MonoBehaviour
{
readonly float _deafultTimeDelay = 0.05f;
[HideInInspector]
public static List<BaseBody> _bodies = new List<BaseBody>();
#region RigidBody
[HideInInspector]
public Rigidbody2D _rb2d;
[HideInInspector]
public Collider2D[] _c2d;
#endregion
#region References
[HideInInspector]
public Transform _myTransform;
[HideInInspector]
public GameObject _myObject;
/// <summary>
/// Объект, который появляется при уничтожении
/// </summary>
public GameObject _explodePrefab;
#endregion
#region Audio
public AudioSource _audioSource;
/// <summary>
/// Звуки, которые проигрываются при получении повреждения
/// </summary>
public AudioClip[] _hitSounds;
/// <summary>
/// Звуки, которые проигрываются при появлении объекта
/// </summary>
public AudioClip[] _awakeSounds;
/// <summary>
/// Звуки, которые воспроизводятся перед смертью
/// </summary>
public AudioClip[] _deadSounds;
#endregion
#region External Force Variables
/// <summary>
/// Внешние силы воздйствующие на объект
/// </summary>
[HideInInspector]
public Vector2 _ExternalForces = new Vector2();
/// <summary>
/// Текущий вектор скорости
/// </summary>
[HideInInspector]
public Vector2 _V = new Vector2();
/// <summary>
/// Текущий вектор силы гравитации
/// </summary>
[HideInInspector]
public Vector2 _G = new Vector2();
#endregion
public virtual void Awake()
{
Init();
}
public virtual void Start()
{
}
public virtual void Init()
{
_myTransform = this.transform;
_myObject = gameObject;
_rb2d = GetComponent<Rigidbody2D>();
_c2d = GetComponentsInChildren<Collider2D>();
_audioSource = GetComponent<AudioSource>();
PlayRandomSound(_awakeSounds);
BaseBody bb = GetComponent<BaseBody>();
_bodies.Add(bb);
}
/// <summary>
/// Уничтожение персонажа
/// </summary>
public virtual void Destroy()
{
_bodies.Remove(this);
for (int i = 0; i < _c2d.Length; i++)
{
_c2d[i].enabled = false;
}
float _t = PlayRandomSound(_deadSounds);
StartCoroutine(WaitAndDestroy(_t));
}
/// <summary>
/// Ждем некоторое время перед уничтожением
/// </summary>
/// <param name="waitTime">Время ожидания</param>
/// <returns></returns>
public IEnumerator WaitAndDestroy(float waitTime)
{
yield return new WaitForSeconds(waitTime);
if (_explodePrefab)
{
Instantiate(_explodePrefab, transform.position, Quaternion.identity);
}
Destroy(gameObject, _deafultTimeDelay);
}
/// <summary>
/// Проигрывание случайного звука
/// </summary>
/// <param name="audioClip">Массив звуков</param>
/// <returns>Длительность проигрываемого звука</returns>
public float PlayRandomSound(AudioClip[] audioClip)
{
float _t = 0;
if (audioClip.Length > 0)
{
int _i = UnityEngine.Random.Range(0, audioClip.Length - 1);
AudioClip _audioClip = audioClip[_i];
_t = _audioClip.length;
_audioSource.PlayOneShot(_audioClip);
}
return _t;
}
/// <summary>
/// Получение урона
/// </summary>
/// <param name="damage">Уровень урона</param>
public virtual void Damage(float damage)
{
PlayRandomSound(_hitSounds);
}
}
}Вроде описали все что надо, даже больше чем нужно (в рамках этой статьи). Теперь отнаследуем от него класс корабля Ship, который должен уметь двигаться и поворачивать:
SpaceShip.cs
using UnityEngine;
using System.Collections;
using System.Collections.Generic;
namespace Assets.Scripts.SpaceShooter.Bodies
{
public class Ship : BaseBody
{
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
public float _rotation = 0f;
public void FixedUpdate()
{
float torque = ControlRotate(_rotation);
Vector2 force = ControlForce(_movement);
_rb2d.AddTorque(torque);
_rb2d.AddRelativeForce(force);
}
public float ControlRotate(Vector2 rotate)
{
float result = 0f;
return result;
}
public Vector2 ControlForce(Vector2 movement)
{
Vector2 result = new Vector2();
return result;
}
}
}Пока в нем нет ничего интересно, на текущий момент это просто класс-заглушка.
Также опишем базовый(абстрактный) класс для всех контроллеров ввода BaseInputController:
BaseInputController.cs
using UnityEngine;
using Assets.Scripts.SpaceShooter.Bodies;
namespace Assets.Scripts.SpaceShooter.InputController
{
public enum eSpriteRotation
{
Rigth = 0,
Up = -90,
Left = -180,
Down = -270
}
public abstract class BaseInputController : MonoBehaviour
{
public GameObject _agentObject;
public Ship _agentBody; // Ссылка на компонент логики корабля
public eSpriteRotation _spriteOrientation = eSpriteRotation.Up; //Это связано с нестандартной
// ориентации спрайта "вверх" вместо "вправо"
public abstract void ControlRotate(float dt);
public abstract void ControlForce(float dt);
public virtual void Start()
{
_agentObject = gameObject;
_agentBody = gameObject.GetComponent<Ship>();
}
public virtual void FixedUpdate()
{
float dt = Time.fixedDeltaTime;
ControlRotate(dt);
ControlForce(dt);
}
public virtual void Update()
{
//TO DO
}
}
}И наконец, класс контроллера игрока PlayerFigtherInput:
PlayerInput.cs
using UnityEngine;
using Assets.Scripts.SpaceShooter.Bodies;
namespace Assets.Scripts.SpaceShooter.InputController
{
public class PlayerFigtherInput : BaseInputController
{
public override void ControlRotate(float dt)
{
// Определяем позицию мыши относительно игрока
Vector3 worldPos = Input.mousePosition;
worldPos = Camera.main.ScreenToWorldPoint(worldPos);
// Сохраняем координаты указателя мыши
float dx = -this.transform.position.x + worldPos.x;
float dy = -this.transform.position.y + worldPos.y;
//Передаем направление
Vector2 target = new Vector2(dx, dy);
_agentBody._target = target;
//Вычисляем поворот в соответствии с нажатием клавиш
float targetAngle = Mathf.Atan2(dy, dx) * Mathf.Rad2Deg;
_agentBody._targetAngle = targetAngle + (float)_spriteOrientation;
}
public override void ControlForce(float dt)
{
//Передаем movement
_agentBody._movement = Input.GetAxis("Vertical") * Vector2.up
+ Input.GetAxis("Horizontal") * Vector2.right;
}
}
}Вроде бы закончили, теперь наконец можно перейти к тому, ради чего все это затевалось, т.е. ПИД-регуляторам (не забыли надеюсь?). Его реализация кажется простой до безобразия:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace Assets.Scripts.Regulator
{
[System.Serializable] // Этот атрибут необходим для того что бы поля регулятора
// отображались в инспекторе и сериализовывались
public class SimplePID
{
public float Kp, Ki, Kd;
private float lastError;
private float P, I, D;
public SimplePID()
{
Kp = 1f;
Ki = 0;
Kd = 0.2f;
}
public SimplePID(float pFactor, float iFactor, float dFactor)
{
this.Kp = pFactor;
this.Ki = iFactor;
this.Kd = dFactor;
}
public float Update(float error, float dt)
{
P = error;
I += error * dt;
D = (error - lastError) / dt;
lastError = error;
float CO = P * Kp + I * Ki + D * Kd;
return CO;
}
}
}Значения коэффициентов по умолчанию возьмем с потолка: это будет тривиальный единичный коэффициент пропорционального закона управления Kp = 1, небольшое значение коэффициента для дифференциального закона управления Kd = 0.2, который должен устранить ожидаемые колебания и нулевое значение для Ki, которое выбрано потому, что в нашей программной модели нет никаких статичных ошибок (но вы всегда можете их внести, а потом героически побороться с помощью интегратора).
Теперь вернемся к нашему классу SpaceShip и попробуем заюзать наше творение в качестве регулятора поворота космического корабля в методе ControlRotate:
public float ControlRotate(Vector2 rotate)
{
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
MV = _angleController.Update(angleError, dt);
return MV;
}ПИД-регулятор будет осуществлять точное угловое позиционировая космического корабля только за счет крутящего момента. Все честно, физика и САУ, почти как в реальной жизни.
И без этих ваших Quaternion.Lerp
if (!_rb2d.freezeRotation)
rb2d.freezeRotation = true;
float deltaAngle = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
float T = dt * Mathf.Abs( _rotationSpeed / deltaAngle);
// Трансформируем угол в вектор
Quaternion rot = Quaternion.Lerp(
_myTransform.rotation,
Quaternion.Euler(new Vector3(0, 0, targetAngle)),
T);
// Изменяем поворот объекта
_myTransform.rotation = rot;Получившейся исходный код Ship.cs под спойлером
using UnityEngine;
using Assets.Scripts.Regulator;
namespace Assets.Scripts.SpaceShooter.Bodies
{
public class Ship : BaseBody
{
public GameObject _flame;
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
public float _targetAngle = 0f;
public float _angle = 0f;
[Header("PID")]
public SimplePID _angleController = new SimplePID();
public void FixedUpdate()
{
float torque = ControlRotate(_targetAngle);
Vector2 force = ControlForce(_movement);
_rb2d.AddTorque(torque);
_rb2d.AddRelativeForce(force);
}
public float ControlRotate(float rotate)
{
float MV = 0f;
float dt = Time.fixedDeltaTime;
_angle = _myTransform.eulerAngles.z;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_angle, rotate);
//Получаем корректирующее ускорение
MV = _angleController.Update(angleError, dt);
return MV;
}
public Vector2 ControlForce(Vector2 movement)
{
Vector2 MV = new Vector2();
//Кусок кода спецэффекта работающего двигателя ради
if (movement != Vector2.zero)
{
if (_flame != null)
{
_flame.SetActive(true);
}
}
else
{
if (_flame != null)
{
_flame.SetActive(false);
}
}
MV = movement;
return MV;
}
}
}
Все? Расходимся по домам?
WTF! Что происходит? Почему корабль поворачивается как-то странно? И почему он так резко отскакивает от других объектов? Неужели этот глупый ПИД-регулятор не работает?
Без паники! Давайте попробуем разобраться что происходит.
В момент получения нового значения SP, происходит резкий (ступенчатый) скачок рассогласования ошибки, которая, как мы помним, вычисляется вот так: соответственно происходит резкий скачок производной ошибки
, которую мы вычисляем в этой строчке кода:
D = (error - lastError) / dt;Можно, конечно, попробовать другие схемы дифференцирования, например, трехточечную, или пятиточечную, или… но все равно это не поможет. Ну вот не любят производные резких скачков — в таких точках функция не является дифференцируемой. Однако поэкспериментировать с разными схемами дифференцирования и интегрирования стоит, но потом и не в этой статье.
Думаю что настал момент построить графики переходного процесса: ступенчатое воздействие от S(t) = 0 в SP(t) = 90 градусов для тела массой в 1 кг, длинной плеча силы в 1 метр и шагом сетки дифференцирования 0.02 с — прям как в нашем примере на Unity3D (на самом деле не совсем, при построении этих графиков не учитывалось, что момент инерции зависит от геометрии твердого тела, поэтому переходный процесс будет немножко другой, но все же достаточно похожий для демонстрации). Все величены на грифике приведены в абсолютных значениях:
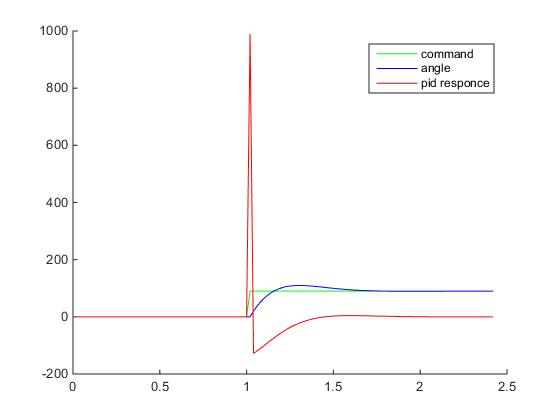
Хм, что здесь происходит? Куда улетел отклик ПИД-регулятора?
Поздравляю, мы только что столкнулись с таким явлением как «удар» (kick). Очевидно, что в момент времени, когда процесс еще PV = 0, а уставка уже SP = 90, то при численном дифференцировании получим значение производной порядка 4500, которое умножится на Kd=0.2 и сложится с пропорциональным теромом, так что на выходе мы получим значение углового ускорения 990, а это уже форменное надругательство над физической моделью Unity3D (угловые скорости будут достигать 18000 град/с… я думаю это предельное значение угловой скорости для RigidBody2D).
- Может стоит подобрать коэффициенты ручками, так чтобы скачок был не таким сильным?
- Нет! Самое лучше чего мы таким образом сможем добиться — небольшая амплитуда скачка производной, однако сам скачок как был так и останется, при этом можно докрутиться до полной неэффективности дифференциальной составляющей.
Впрочем можете поэкспериментировать.
Попытка номер два. Сатурация
Логично, что привод (в нашем случае виртуальные маневровые двигатели SpaceShip), не может отрабатывать сколько угодно большие значения которые может выдать наш безумный регулятор. Так что первое что мы сделаем — сатурируем выход регулятора:
public float ControlRotate(Vector2 rotate, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
CO = _angleController.Update(angleError, dt);
//Сатурируем
MV = CO;
if (MV > thrust) MV = thrust;
if (MV< -thrust) MV = -thrust;
return MV;
}А очередной раз переписанный класс Ship полностью выглядит так
namespace Assets.Scripts.SpaceShooter.Bodies
{
public class Ship : BaseBody
{
public GameObject _flame;
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
public float _targetAngle = 0f;
public float _angle = 0f;
public float _thrust = 1f;
[Header("PID")]
public SimplePID _angleController = new SimplePID(0.1f,0f,0.05f);
public void FixedUpdate()
{
_torque = ControlRotate(_targetAngle, _thrust);
_force = ControlForce(_movement);
_rb2d.AddTorque(_torque);
_rb2d.AddRelativeForce(_force);
}
public float ControlRotate(float targetAngle, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
CO = _angleController.Update(angleError, dt);
//Сатурируем
MV = CO;
if (MV > thrust) MV = thrust;
if (MV< -thrust) MV = -thrust;
return MV;
}
public Vector2 ControlForce(Vector2 movement)
{
Vector2 MV = new Vector2();
if (movement != Vector2.zero)
{
if (_flame != null)
{
_flame.SetActive(true);
}
}
else
{
if (_flame != null)
{
_flame.SetActive(false);
}
}
MV = movement * _thrust;
return MV;
}
public void Update()
{
}
}
}Итоговая схема нашего САУ тогда станет уже вот такой
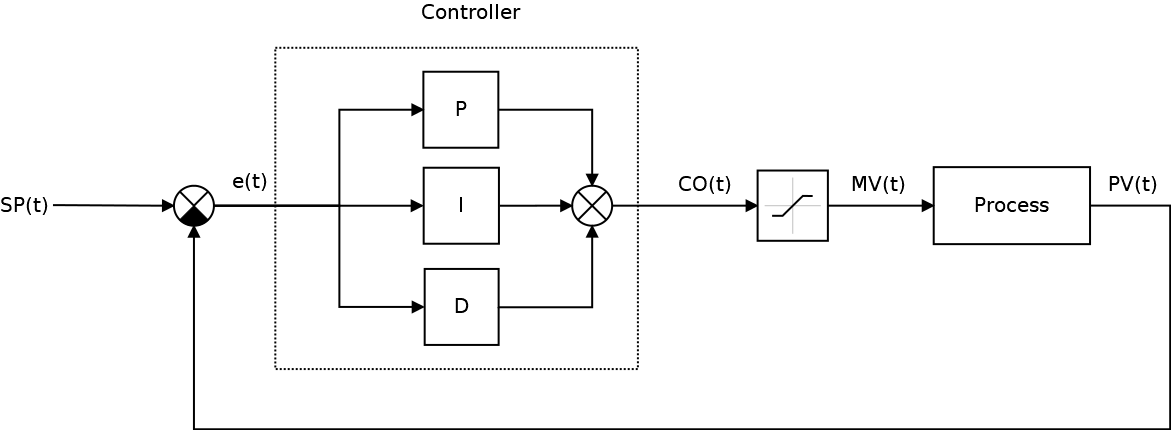
При этом уже становится понятно, что выход контроллера CO(t) немного не одно и тоже, что управляемая величина процесса MV(t).
Собственно с этого места можно уже добавлять новую игровую сущность — привод, через которую и будет осуществляться управление процессом, логика работы которой может быть более сложной, чем просто Mathf.Clamp(), например, можно ввести дискретизацию значений (дабы не перегружать игровую физику величинами идущими шестыми после запятой), мертвую зону (опять таки не имеет смысл перегружать физику сверхмалыми реакциями), ввести задержку в упраление и нелинейность (например, сигмоиду) привода, после чего посмотреть, что из этого получится.
Запустив игру, мы обнаружим, что космический корабль стал наконец управляемым:
Если построить графики, то можно увидеть, что реакция контроллера стала уже вот такой:
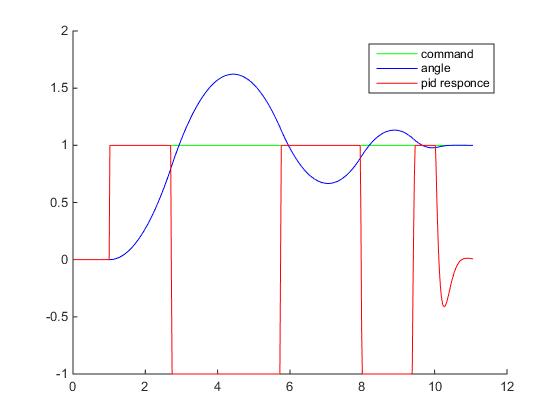
Здесь уже используются нормированные величены, углы поделены на значение SP, а выход контроллера отнормирован относительно максимального значения на котором уже происходит сатурация.
Теперь на графике видно наличие ошибки перерегулирования (overshooting) и затухающие колебания. Уменьшая Kp и увеличивая Kd можно добиться уменьшения колебаний, но зато увеличится время реакции контроллера (скорость поворота корабля). И наоборот, увеличивая Kp и уменьшая Kd — можно добиться увеличения скорости реакции контроллера, но появятся паразитные колебания, которые при определенных (критических) значениях, перестанут быть затухающими.
Ниже приведена известна таблица влияния увеличения параметров ПИД-регулятора (как уменьшить шрифт, а то таблица безе переносов не лезет?):
А общий алгоритм ручной настройки ПИД-регулятора следующий:
- Подбираем пропорциональный коэффициенты при отключенных дифференциальных и интегральных звеньях до тех пор пока не начнутся автоколебания.
- Постепенно увеличивая дифференциальную составляющую избавляемся от автоколебаний
- Если наблюдается остаточная ошибка регулирования (смещение), то устраняем её за счет интегральной составляющей.
Каких-то общих значений параметров ПИД-регулятора нет: конкретные значения зависят исключительно от параметров процесса (его передаточной характеристики): ПИД-регулятор отлично работающий с одним объектом управления окажется неработоспособным с другим. Более того, коэффициенты при пропорциональной, интегральной и дифференциальной составляющих еще и взаимозависимы.
В общем не будем о грустном, дальше нас ждет самое интересное…
Попытка номер три. Еще раз производные
Приделав костыль в виде ограничения значений выхода контроллера мы так и не решили самую главную проблему нашего регулятора — дифференциальная составляющая плохо себя чувствует при ступенчатом изменении ошибки на входе регуляторе. На самом деле есть множество других костылей, например, в момент скачкообразного изменения SP «отключать» дифференциальную составляющую или же поставить фильтры нижних частот между SP(t) и операцией за счет которого будет происходить плавное нарастание ошибки, а можно совсем развернуться и впендюрить самый настоящий фильтр Калмана для сглаживания входных данных. В общем костылей много, и добавить наблюдателя конечно хотелось бы, но не в этот раз.
Поэтому снова вернемся к производной ошибки рассогласования и внимательно на неё посмотрим:
Ничего не заметили? Если хорошенько присмотреться, то можно обнаружить, что вообще-то SP(t), не меняется во времени (за исключением моментов ступенчатого изменения, когда регулятор получает новую команду), т.е. её производная равна нулю:
тогда
Иными словами, вместо производной ошибки, которая дифференцируема не везде мы можем использовать производную от процесса, который в мире классической механики как правило непрерывен и дифференцируем везде, а схема нашей САУ уже приобретет следующий вид:
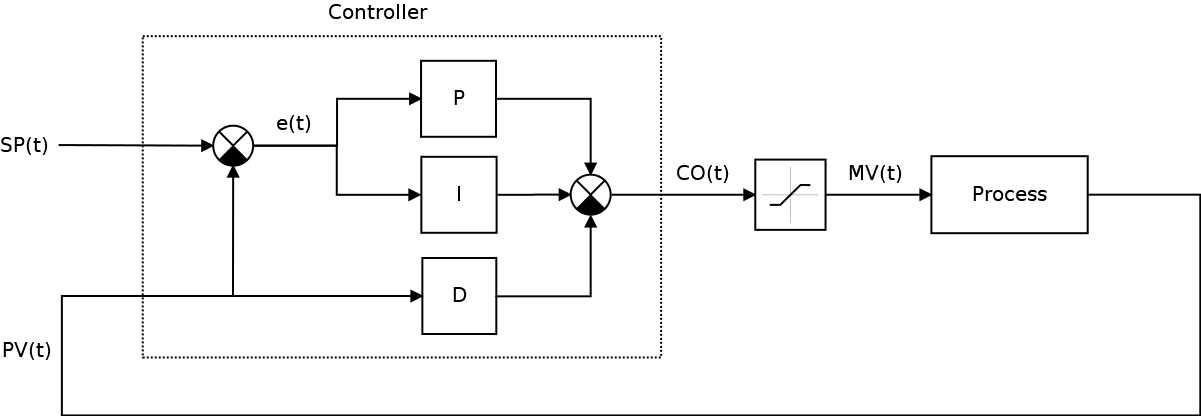
Модифицируем код регулятора:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace Assets.Scripts.Regulator
{
[System.Serializable]
public class SimplePID
{
public float Kp, Ki, Kd;
private float P, I, D;
private float lastPV = 0f;
public SimplePID()
{
Kp = 1f;
Ki = 0f;
Kd = 0.2f;
}
public SimplePID(float pFactor, float iFactor, float dFactor)
{
this.Kp = pFactor;
this.Ki = iFactor;
this.Kd = dFactor;
}
public float Update(float error, float PV, float dt)
{
P = error;
I += error * dt;
D = -(PV - lastPV) / dt;
lastPV = PV;
float CO = Kp * P + Ki * I + Kd * D;
return CO;
}
}
}И немного изменим метод ControlRotate:
public float ControlRotate(Vector2 rotate, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
CO = _angleController.Update(angleError, _myTransform.eulerAngles.z, dt);
//Сатурируем
MV = CO;
if (CO > thrust) MV = thrust;
if (CO < -thrust) MV = -thrust;
return MV;
}И-и-и-и… если запустить игру, то обнаружиться, что на самом деле ничего ничего не изменилось с последней попытки, что и требовалось доказать. Однако, если убрать сатурацию, то график реакции регулятора будет выглядеть вот так:
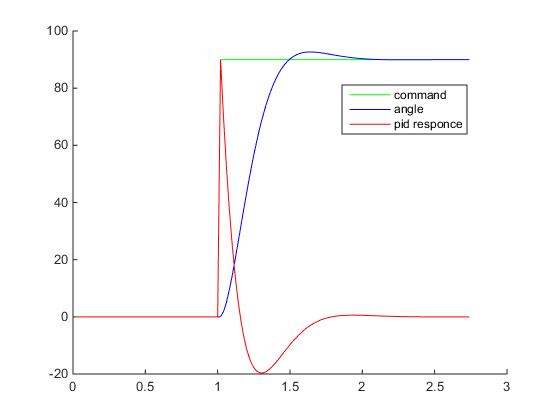
Скачок CO(t) по прежнему присутствует, однако он уже не такой большой как был в самом начале, а самое главное — он стал предсказуемым, т.к. обеспечивается исключительно пропорциональной составляющей, и ограничен максимально возможной ошибкой рассогласования и пропорциональным коэффициентом ПИД-регулятора (а это уже намекает на то, что Kp имеет смысл выбрать все же меньше единицы, например, 1/90f), но не зависит от шага сетки дифференцирования (т.е. dt). В общем, я настоятельно рекомендую использовать именно производную процесса, а не ошибки.
Думаю теперь никого не удивит, но таким же макаром можно заменить на
, однако останавливаться на этом мы не будем, можете сами поэкспериментировать и рассказать в комментариях, что из этого получилось (самому интересно)
Попытка номер четыре. Альтернативные реализации ПИД-регулятор
Помимо описанного выше идеального представления ПИД-регулятора, на практике часто применяется стандартная форма, без коэффициентов Ki и Kd, вместо которых используются временные постоянные.
Такой подход связан с тем, что ряд методик настройки ПИД-регулятора основан на частотных характеристиках ПИД-регулятора и процесса. Собственно вся ТАУ и крутится вокруг частотных характеристик процессов, поэтому для желающих углубиться, и, внезапно, столкнувшихся с альтернативной номенклатурой, приведу пример т.н. стандартной формы ПИД-регулятора:
где, — постоянная дифференцирования, влияющая на прогнозирование состояния системы регулятором,
— постоянная интегрирования, влияющая на интервал усреднения ошибки интегральным звеном.
Основные принципы настройки ПИД-регулятора в стандартной форме аналогичны идеализированному ПИД-регулятору:
- увеличение пропорционального коэффициента увеличивает быстродействие и снижает запас устойчивости;
- с уменьшением интегральной составляющей ошибка регулирования с течением времени уменьшается быстрее;
- уменьшение постоянной интегрирования уменьшает запас устойчивости;
- увеличение дифференциальной составляющей увеличивает запас устойчивости и быстродействие
Исходный код стандартной формы, вы можете найти под спойлером
namespace Assets.Scripts.Regulator
{
[System.Serializable]
public class StandartPID
{
public float Kp, Ti, Td;
public float error, CO;
public float P, I, D;
private float lastPV = 0f;
public StandartPID()
{
Kp = 0.1f;
Ti = 10000f;
Td = 0.5f;
bias = 0f;
}
public StandartPID(float Kp, float Ti, float Td)
{
this.Kp = Kp;
this.Ti = Ti;
this.Td = Td;
}
public float Update(float error, float PV, float dt)
{
this.error = error;
P = error;
I += (1 / Ti) * error * dt;
D = -Td * (PV - lastPV) / dt;
CO = Kp * (P + I + D);
lastPV = PV;
return CO;
}
}
}В качестве значений по умолчанию, выбраны Kp = 0.01, Ti = 10000, Td = 0.5 — при таких значениях корабль поворачивается достаточно быстро и обладает некоторым запасом устойчивости.
Помимо такой формы ПИД-регулятора, часто используется т.н. реккурентная форма:
Не будем на ней останавливаться, т.к. она актуальна прежде всего для хардверных программистов, работающих с FPGA и микроконтроллерами, где такая реализация значительно удобнее и эффективнее. В нашем же случае — давайте что-нибудь сваям на Unity3D — это просто еще одна реализация ПИД-контроллера, которая ни чем не лучше других и даже менее понятная, так что еще раз дружно порадуемся как хорошо программировать в уютненьком C#, а не в жутком и страшном VHDL, например.
Вместо заключения. Куда бы еще присобачить ПИД-регулятор
Теперь попробуем немного усложнить управление корабля используя двухконтурное управление: один ПИД-регулятор, уже знакомый нам _angleController, отвечает по прежнему за угловое позиционирование, а вот второй — новый, _angularVelocityController — контролирует скорость поворота:
public float ControlRotate(float targetAngle, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
_angle = _myTransform.eulerAngles.z;
//Контроллер угла поворота
float angleError = Mathf.DeltaAngle(_angle, targetAngle);
float torqueCorrectionForAngle =
_angleController.Update(angleError, _angle, dt);
//Контроллер стабилизации скорости
float angularVelocityError = -_rb2d.angularVelocity;
float torqueCorrectionForAngularVelocity =
_angularVelocityController.Update(angularVelocityError, -angularVelocityError, dt);
//Суммарный выход контроллера
CO = torqueCorrectionForAngle + torqueCorrectionForAngularVelocity;
//Дискретизируем с шагом 100
CO = Mathf.Round(100f * CO) / 100f;
//Сатурируем
MV = CO;
if (CO > thrust) MV = thrust;
if (CO < -thrust) MV = -thrust;
return MV;
}Назначение второго регулятора — гашение избыточных угловых скоростей, за счет изменения крутящего момента — это сродни наличию углового трения, которое мы отключили еще при создании игрового объекта. Такая схема управления [возможно] позволит получить более стабильное поведение корабля, и даже обойтись только пропорциональными коэффициентами управления — второй регулятор будет гасить все колебания, выполняя функцию, аналогичную дифференциальной составляющей первого регулятора.
Помимо этого, добавим новый класс ввода игрока — PlayerInputCorvette, в котором повороты буду осуществляться уже за счет нажатия клавиш «вправо-влево», а целеуказание с помощью мыши мы оставим для чего-нибудь более полезного, например, для управления турелью. Заодно у нас теперь появился такой параметр как _turnRate — отвечающий за скорость/отзывчивость поворота (не понятно только куда его поместить лучше в InputCOntroller или все же Ship).
public class PlayerCorvetteInput : BaseInputController
{
public float _turnSpeed = 90f;
public override void ControlRotate()
{
// Находим указатель мыши
Vector3 worldPos = Input.mousePosition;
worldPos = Camera.main.ScreenToWorldPoint(worldPos);
// Сохраняем относительные координаты указателя мыши
float dx = -this.transform.position.x + worldPos.x;
float dy = -this.transform.position.y + worldPos.y;
//Передаем направление указателя мыши
Vector2 target = new Vector2(dx, dy);
_agentBody._target = target;
//Вычисляем поворот в соответствии с нажатием клавиш
_agentBody._rotation -= Input.GetAxis("Horizontal") * _turnSpeed * Time.deltaTime;
}
public override void ControlForce()
{
//Передаем movement
_agentBody._movement = Input.GetAxis("Vertical") * Vector2.up;
}
}Также для наглядности накидаем на коленках скрипт для отображения отладочной информации
namespace Assets.Scripts.SpaceShooter.UI
{
[RequireComponent(typeof(Ship))]
[RequireComponent(typeof(BaseInputController))]
public class Debugger : MonoBehaviour
{
Ship _ship;
BaseInputController _controller;
List<SimplePID> _pids = new List<SimplePID>();
List<string> _names = new List<string>();
Vector2 _orientation = new Vector2();
// Use this for initialization
void Start()
{
_ship = GetComponent<Ship>();
_controller = GetComponent<BaseInputController>();
_pids.Add(_ship._angleController);
_names.Add("Angle controller");
_pids.Add(_ship._angularVelocityController);
_names.Add("Angular velocity controller");
}
// Update is called once per frame
void Update()
{
DrawDebug();
}
Vector3 GetDiretion(eSpriteRotation spriteRotation)
{
switch (_controller._spriteOrientation)
{
case eSpriteRotation.Rigth:
return transform.right;
case eSpriteRotation.Up:
return transform.up;
case eSpriteRotation.Left:
return -transform.right;
case eSpriteRotation.Down:
return -transform.up;
}
return Vector3.zero;
}
void DrawDebug()
{
//Направление поворота
Vector3 vectorToTarget = transform.position
+ 5f * new Vector3(-Mathf.Sin(_ship._targetAngle * Mathf.Deg2Rad),
Mathf.Cos(_ship._targetAngle * Mathf.Deg2Rad), 0f);
// Текущее направление
Vector3 heading = transform.position + 4f * GetDiretion(_controller._spriteOrientation);
//Угловое ускорение
Vector3 torque = heading - transform.right * _ship._Torque;
Debug.DrawLine(transform.position, vectorToTarget, Color.white);
Debug.DrawLine(transform.position, heading, Color.green);
Debug.DrawLine(heading, torque, Color.red);
}
void OnGUI()
{
float x0 = 10;
float y0 = 100;
float dx = 200;
float dy = 40;
float SliderKpMax = 1;
float SliderKpMin = 0;
float SliderKiMax = .5f;
float SliderKiMin = -.5f;
float SliderKdMax = .5f;
float SliderKdMin = 0;
int i = 0;
foreach (SimplePID pid in _pids)
{
y0 += 2 * dy;
GUI.Box(new Rect(25 + x0, 5 + y0, dx, dy), "");
pid.Kp = GUI.HorizontalSlider(new Rect(25 + x0, 5 + y0, 200, 10),
pid.Kp,
SliderKpMin,
SliderKpMax);
pid.Ki = GUI.HorizontalSlider(new Rect(25 + x0, 20 + y0, 200, 10),
pid.Ki,
SliderKiMin,
SliderKiMax);
pid.Kd = GUI.HorizontalSlider(new Rect(25 + x0, 35 + y0, 200, 10),
pid.Kd,
SliderKdMin,
SliderKdMax);
GUIStyle style1 = new GUIStyle();
style1.alignment = TextAnchor.MiddleRight;
style1.fontStyle = FontStyle.Bold;
style1.normal.textColor = Color.yellow;
style1.fontSize = 9;
GUI.Label(new Rect(0 + x0, 5 + y0, 20, 10), "Kp", style1);
GUI.Label(new Rect(0 + x0, 20 + y0, 20, 10), "Ki", style1);
GUI.Label(new Rect(0 + x0, 35 + y0, 20, 10), "Kd", style1);
GUIStyle style2 = new GUIStyle();
style2.alignment = TextAnchor.MiddleLeft;
style2.fontStyle = FontStyle.Bold;
style2.normal.textColor = Color.yellow;
style2.fontSize = 9;
GUI.TextField(new Rect(235 + x0, 5 + y0, 60, 10), pid.Kp.ToString(), style2);
GUI.TextField(new Rect(235 + x0, 20 + y0, 60, 10), pid.Ki.ToString(), style2);
GUI.TextField(new Rect(235 + x0, 35 + y0, 60, 10), pid.Kd.ToString(), style2);
GUI.Label(new Rect(0 + x0, -8 + y0, 200, 10), _names[i++], style2);
}
}
}
}Класс Ship также претерпел необратимые мутации и теперь должен выглядеть вот так:
namespace Assets.Scripts.SpaceShooter.Bodies
{
public class Ship : BaseBody
{
public GameObject _flame;
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
public float _targetAngle = 0f;
public float _angle = 0f;
public float _thrust = 1f;
[Header("PID")]
public SimplePID _angleController = new SimplePID(0.1f,0f,0.05f);
public SimplePID _angularVelocityController = new SimplePID(0f,0f,0f);
private float _torque = 0f;
public float _Torque
{
get
{
return _torque;
}
}
private Vector2 _force = new Vector2();
public Vector2 _Force
{
get
{
return _force;
}
}
public void FixedUpdate()
{
_torque = ControlRotate(_targetAngle, _thrust);
_force = ControlForce(_movement, _thrust);
_rb2d.AddTorque(_torque);
_rb2d.AddRelativeForce(_force);
}
public float ControlRotate(float targetAngle, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
_angle = _myTransform.eulerAngles.z;
//Контроллер угла поворота
float angleError = Mathf.DeltaAngle(_angle, targetAngle);
float torqueCorrectionForAngle =
_angleController.Update(angleError, _angle, dt);
//Контроллер стабилизации скорости
float angularVelocityError = -_rb2d.angularVelocity;
float torqueCorrectionForAngularVelocity =
_angularVelocityController.Update(angularVelocityError, -angularVelocityError, dt);
//Суммарный выход контроллера
CO = torqueCorrectionForAngle + torqueCorrectionForAngularVelocity;
//Дискретизируем с шагом 100
CO = Mathf.Round(100f * CO) / 100f;
//Сатурируем
MV = CO;
if (CO > thrust) MV = thrust;
if (CO < -thrust) MV = -thrust;
return MV;
}
public Vector2 ControlForce(Vector2 movement, float thrust)
{
Vector2 MV = new Vector2();
if (movement != Vector2.zero)
{
if (_flame != null)
{
_flame.SetActive(true);
}
}
else
{
if (_flame != null)
{
_flame.SetActive(false);
}
}
MV = movement * thrust;
return MV;
}
public void Update()
{
}
}
}А вот, собственно заключительное видео того, что должно получиться:
К сожалению получилось охватить не все, что хотелось бы, в частности почти не затронут вопрос настройки ПИД-регулятора и практически не освящена интегральная составляющая — фактически приведен пример только для ПД-регулятора. Собственно изначально планировалось несколько больше примеров (круиз-контроль, вращение турели и компенсация вращательного момента), но статья итак уже разбухла, да и вообще:

Немного ссылок
- Годная статья на английской вики
- PID tutorial
- ПИД-регуляторы: вопросы реализации. Часть 1
- ПИД-регуляторы: вопросы реализации. Часть 2
- PID Without a PhD
- PID Without a PhD. Перевод
- Derivative Action and PID Control
- Control System Lab: PID
- ПИД-регулятор своими руками
- Корректная реализация разностной схемы ПИД регулятора
- Программируем квадрокоптер на Arduino (часть 1)
- Виртуальный квадрокоптер на Unity + OpenCV (Часть 1)
- Поляков К.Ю. Теория автоматического управления для чайников
- PID control system analysis, design, and technology
- Aidan O’Dwyer. Handbook of PI and PID Controller Tuning Rules (3rd ed.)
- PID process control, a “Cruise Control” example
- https://www.mathworks.com/discovery/pid-control.html
- http://scilab.ninja/study-modules/scilab-control-engineering-basics/module-4-pid-control/
- https://sourceforge.net/p/octave/control/ci/default/tree/inst/optiPID.m
Еще немного ссылок на другие примеры
http://luminaryapps.com/blog/use-a-pid-loop-to-control-unity-game-objects/
http://www.habrador.com/tutorials/pid-controller/3-stabilize-quadcopter/
https://www.gamedev.net/articles/programming/math-and-physics/pid-control-of-physics-bodies-r3885/
https://ksp-kos.github.io/KOS/tutorials/pidloops.html
Часть 2
Расчёт параметров регулятора
Перед тем как рассчитывать параметры регулятора, необходимо
сформулировать цель и критерии качества регулирования, а также ограничения на
величины и скорости изменения переменных в системе. Традиционно основные
качественные показатели формулируются исходя из требований к форме реакции
замкнутой системы на ступенчатое изменение уставки. Однако такой критерий очень
ограничен. В частности, он ничего не говорит о величине ослабления шумов
измерений или влияния внешних возмущений, может дать ошибочное представление о
робастности системы.
Поэтому для полного описания или тестирования системы с ПИД-регулятором нужен ряд дополнительных показателей качества, о
которых речь пойдёт дальше.
В общем случае выбор показателей
качества не может быть формализован полностью и должен осуществляться, исходя
из смысла решаемой задачи.
Качество регулирования
Выбор критерия качества
регулирования зависит от цели, для которой используется регулятор. Целью может
быть:
-
поддержание
постоянного значения параметра (например, температуры); -
слежение
за изменением уставки или программное управление; -
управление
демпфером в резервуаре с жидкостью и т.д.
Для той или иной задачи наиболее
важным фактором может быть:
-
форма
отклика на внешние возмущения (время установления, перерегулирование, время
отклика и др.); -
форма
отклика на шумы измерений; -
форма
отклика на сигнал уставки; -
робастность
по отношению к разбросу параметров объекта управления; -
экономия
энергии в управляемой системе; -
минимизация
шумов измерений.
Для классического ПИД-регулятора параметры, которые являются наилучшими для
слежения за уставкой, в общем случае отличаются от параметров, наилучших для
ослабления влияния внешних возмущений. Для того чтобы оба параметра
одновременно были оптимальными, необходимо использовать
ПИД-регуляторы с двумя степенями свободы [1].
Точное слежение за изменением уставки
необходимо в системах управления движением, в робототехнике; в системах
управления технологическими процессами, где уставка обычно остаётся длительное
время без изменений, требуется максимальное ослабление влияния нагрузки (внешних возмущений); в системах управления резервуарами
с жидкостью требуется обеспечение ламинарности потока (минимизация дисперсии
выходной переменной регулятора) и т.д.
Ослабление влияния внешних
возмущений
Как было показано в подразделе
«Функции чувствительности» (часть 1), обратная связь ослабляет влияние внешних
возмущений в |S(jω)| раз за исключением тех
частот, на которых |S(jω)|>1. Внешние возмущения могут быть приложены к объекту в самых
разных его частях, однако, когда конкретное место
неизвестно, считают, что возмущение воздействует на вход объекта. В этом случае
отклик системы на внешние возмущения определяется передаточной функцией со
входа внешних возмущений на выход системы:
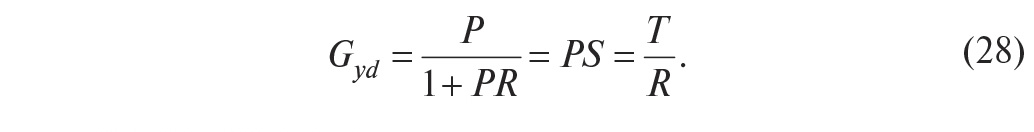
Поскольку внешние возмущения обычно
лежат в низкочастотной части спектра, где |S(jω)|<1 и, следовательно, T ≈1, то выражение
(28) можно упростить:
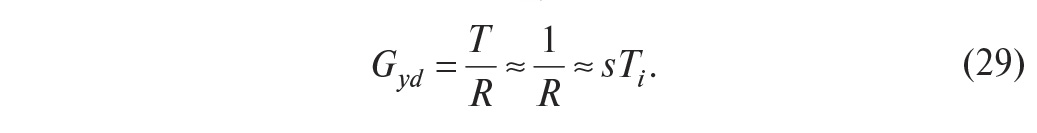
Таким образом, для ослабления
влияния внешних возмущений (в частности, влияния нагрузки) можно уменьшить
постоянную интегрирований Ti.
Во временной области реакцию на
внешние возмущения оценивают по отклику на единичный скачок d(t).
Ослабление влияния шумов измерений
Передаточная функция от точки
приложения шума на выход системы имеет вид [1]:
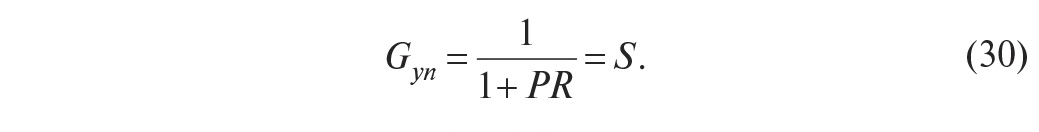
Благодаря спаду АЧХ объекта на
высоких частотах функция чувствительности стремится к 1 (рис. 16). Поэтому
ослабить влияние шумов измерений с помощью обратной связи невозможно. Однако
эти шумы легко устраняются применением фильтров нижних частот, а также правильным экранированием и заземлением [3, 4].
Робастность к вариации параметров
объекта
Замкнутая система остаётся
устойчивой при изменении параметров объекта на величину ∆P(jω), если
выполняется условие (18).
Критерии качества во временной
области
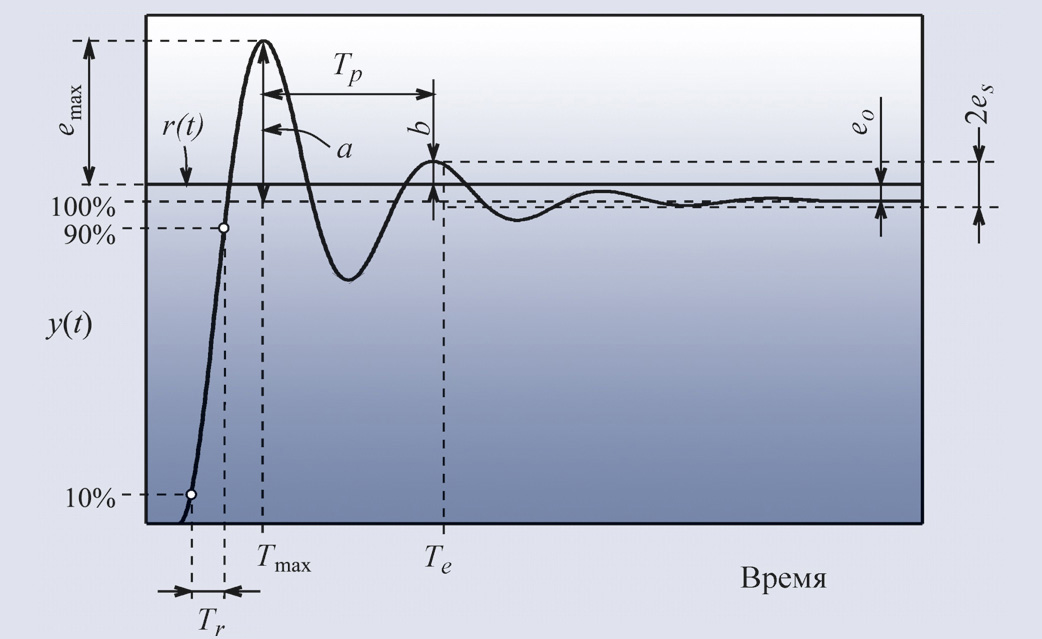
Для оценки качества регулирования в
замкнутой системе с ПИД-регулятором обычно используют
ступенчатое входное воздействие и ряд критериев для описания формы переходного
процесса (рис. 19):
-
максимум
ошибки регулирования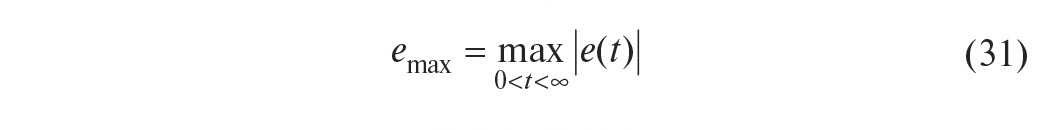
и
момент времени Tmax, при котором ошибка достигает
этого максимума; -
интегрированная
абсолютная ошибка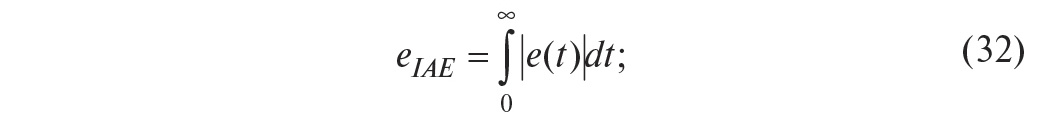
-
интеграл
от квадрата ошибки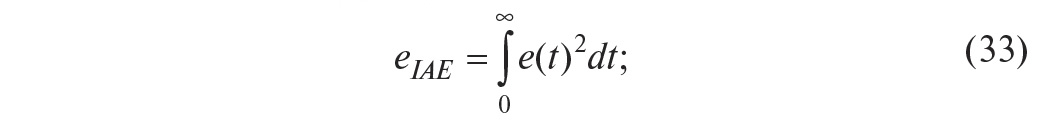
-
декремент
затухания d (это отношение первого максимума ко второму, типовое значение d=4 и
более)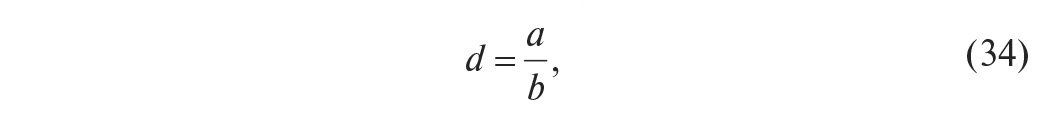
отметим,
что в литературе встречаются и другие определения декремента затухания, в
частности, как b/a или как коэффициент в показателе степени экспоненты, описывающей
огибающую затухающих колебаний; -
статическая
ошибка eo (это постоянная ошибка в равновесном, то есть в установившемся, или
статическом, режиме системы); -
время
установления Te с заданной погрешностью es (это время, по истечении которого
погрешность регулирования не превышает заданного значения es; обычно es = 1%,
реже 2% или 5% – соответственно время установления обозначают T0,01, T0,02,
T0,05); -
перерегулирование
emax (это превышение первого выброса над установившимся значением переменной,
обычно выражается в процентах от установившегося значения); -
время
нарастания Tr (это интервал времени, в
течение которого выходная переменная нарастает от 10 до 90% от своего
установившегося значения); -
период
затухающих колебаний Tcl (строго говоря, затухающие колебания не являются
периодическими, поэтому здесь под периодом понимается расстояние между двумя
соседними максимумами переходной характеристики).
Для систем управления движением в
качестве тестового сигнала чаще используют не функцию скачка, а линейно
нарастающий сигнал, поскольку электромеханические системы обычно имеют
ограниченную скорость нарастания выходной величины.
Приведённые критерии используются
для оценки качества реакции как на изменение уставки, так и на воздействие
внешних возмущений и шумов измерений.
Частотные критерии качества
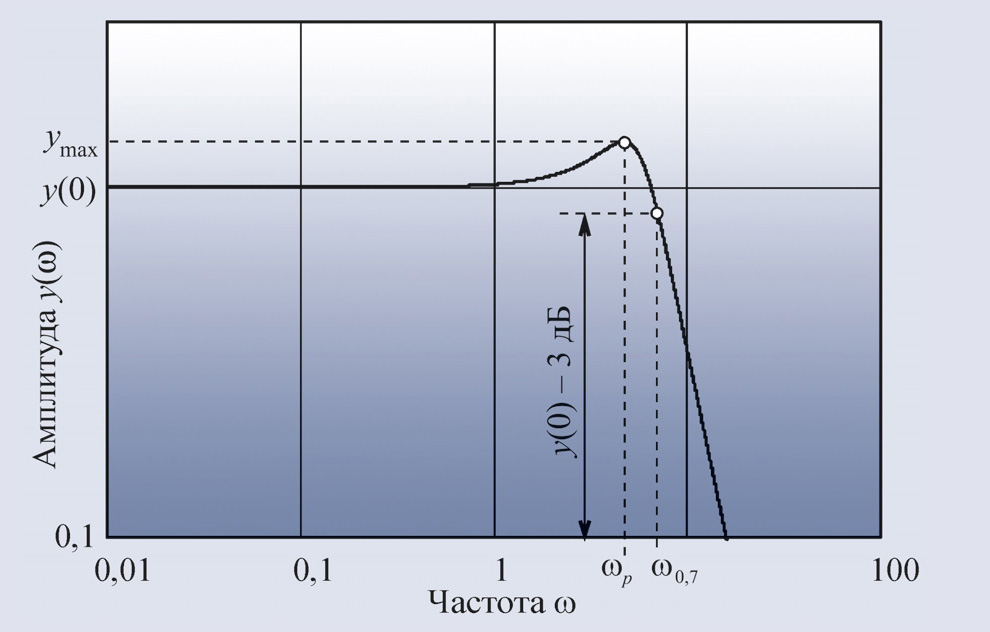
В частотной области обычно
используются следующие критерии, получаемые из графика амплитудно-частотной характеристики замкнутой системы y(ω) (рис. 20):
-
полоса
пропускания ω–3дБ (или ω0,7) по уровню –3 дБ (или по уровню 1/√2 = 0,7) – полоса
частот от 0 до ω–3дБ = ω0,7, в пределах которой кривая АЧХ снижается не более
чем на 3 дБ относительно её значения на нулевой частоте y(0); -
колебательность
М – отношение максимального (пикового) значения АЧХ ymax к её значению на
нулевой частоте y(0), то есть в установившемся режиме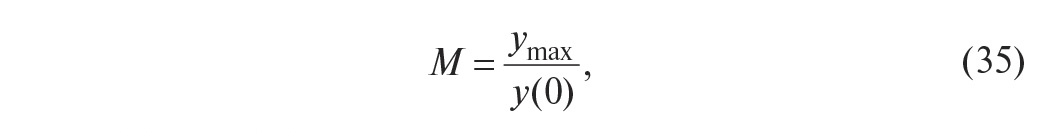
типовыми
значениями являются М = 1,5…1,6; -
резонансная
частота системы ωp – частота, на которой АЧХ достигает максимума ymax = y(ωp).
Частотные критерии у реальных
регуляторов не могут быть однозначно связаны с временными критериями из-за нелинейностей (обычно это нелинейности типа «ограничение»)
и алгоритмов устранения эффекта интегрального насыщения. Однако приближённо
можно установить следующие зависимости между критериями в частотной и временной
областях:
-
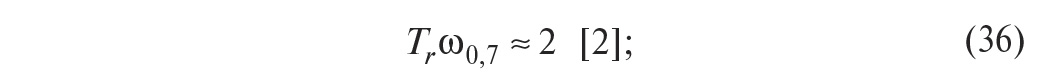
-
частота
максимума передаточной характеристики замкнутой системы приблизительно
соответствует периоду затухающих колебаний отклика на ступенчатое входное
воздействие – ωз ≈ 2π/Tp -
чем
медленнее затухают колебания, тем больше показатель колебательности М.
Выбор параметров регулятора
В общей теории автоматического
управления структура регулятора выбирается исходя из модели объекта управления.
При этом более сложным объектам управления соответствуют более сложные
регуляторы. В нашем же случае структура регулятора уже задана – мы рассматриваем ПИД-регулятор. Эта структура
очень простая, поэтому ПИД-регулятор не всегда может
дать хорошее качество регулирования, хотя в подавляющем большинстве приложений
в промышленности применяются именно ПИД-регуляторы.
Впервые методику расчёта параметров
ПИД-регуляторов предложили Зиглер и Никольс в 1942 году
[8]. Эта методика очень проста и даёт не очень хорошие результаты. Тем не менее
она до сих пор часто используется на практике, хотя до настоящего времени
появилось множество более точных методов.
После расчёта параметров регулятора
обычно требуется его ручная подстройка для улучшения качества регулирования.
Для этого используется ряд правил, хорошо обоснованных теоретически.
Для настройки ПИД-регуляторов
можно использовать и общие методы теории автоматического управления, такие как
метод назначения полюсов и алгебраические методы. В литературе опубликовано и
множество других методов, которые имеют преимущества в конкретных применениях. Мы приведём только самые распространённые из них.
Все аналитические (формульные)
методы настройки регуляторов основаны на аппроксимации динамики объекта моделью
первого или второго порядка с задержкой. Причиной этого является невозможность
аналитического решения систем уравнений, которое необходимо при использовании моделей более высокого порядка. В последние годы
в связи с появлением мощных контроллеров и персональных компьютеров получили
развитие и распространение численные методы оптимизации. Они являются гибким
инструментом для оптимальной настройки параметров
регулятора для моделей любой сложности и легко учитывают нелинейности объекта управления
и требования к робастности.
Настройка параметров регулятора по
методу Зиглера и Никольса
Зиглер и Никольс предложили два
метода настройки ПИД-регуляторов [8]. Один из них
основан на параметрах отклика объекта на единичный скачок, второй – на частотных
характеристиках объекта управления.
Для расчёта параметров ПИД-регулятора по первому методу Зиглера-Никольса
используются всего два параметра: a и L (рис. 21 и пояснения к нему в тексте).
Формулы для расчёта коэффициентов ПИД-регулятора
сведены в табл. 1.

В качестве примера на рис. 22
приведён отклик на единичный скачок системы с объектом второго порядка и ПИД-регулятором, настроенным по табл. 1, и переходная
характеристика самого объекта управления. Из характеристики объекта получены
значения a = 0,135 и L = 0,135 c. По
табл. 1 для этих значений a и L можно найти коэффициенты ПИД-регулятора:
K = 8,9, Ti = 0,00796 c, Td = 0,156 c.
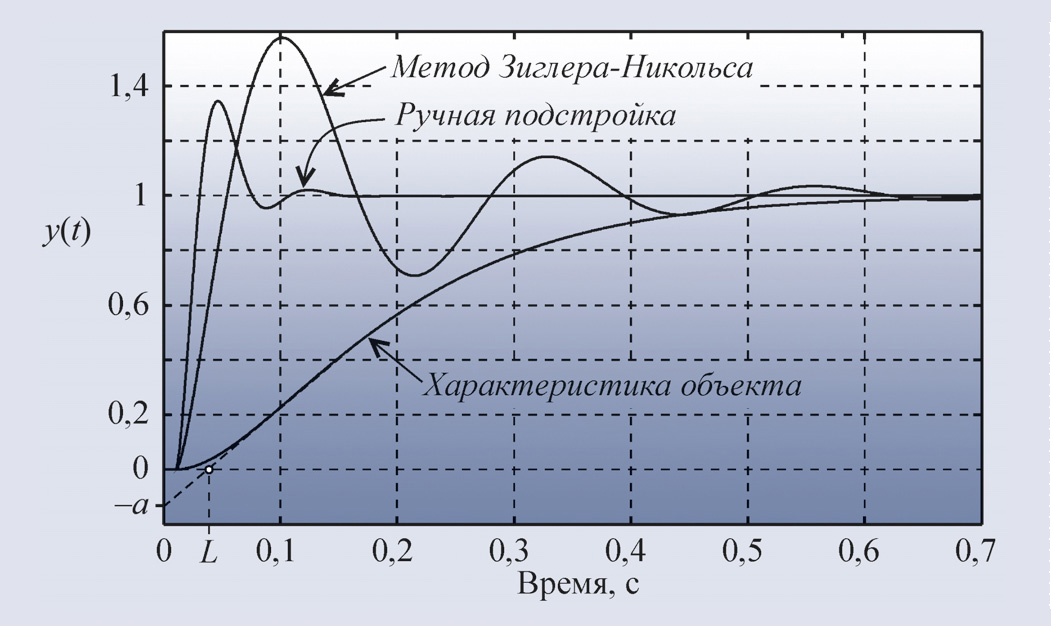
На рис. 22 приведён также отклик на
единичный скачок той же системы при параметрах K =15, Ti = 0,013 c, Td = 0,525 c, полученных путём ручной подстройки. Как видим,
метод Зиглера-Никольса даёт параметры, далёкие от
оптимальных. Это объясняется не только упрощённостью самого метода (он
использует только 2 параметра для описания объекта), но и тем, что параметры регулятора в этом методе определялись Зиглером и
Никольсом, исходя из требования к декременту затухания, равному 4, что и даёт
медленное затухание процесса колебаний.
Метод Зиглера-Никольса
никак не учитывает требования к запасу устойчивости системы, что является вторым
его недостатком. Судя по медленному затуханию переходного процесса в системе,
этот метод даёт слишком малый запас устойчивости.
Второй метод Зиглера-Никольса (частотный метод) в качестве исходных данных для
расчёта использует частоту ω180, на которой сдвиг фаз в разомкнутом контуре
достигает 180°, и модуль коэффициента петлевого усиления на этой частоте K180.
Зная параметр ω180, сначала находят период собственных
колебаний системы T180 = 2π/ω180, а затем по табл. 1
определяют параметры регулятора. Точность настройки регулятора и недостатки
обоих методов Зиглера-Никольса одинаковы.
Метод CHR
В отличие от Зиглера и Никольса,
которые использовали в качестве критерия качества настройки декремент
затухания, равный 4, Chien, Hrones и Reswick (CHR) [9] использовали критерий максимальной
скорости нарастания при отсутствии перерегулирования или при наличии не более чем 20-процентного
перерегулирования. Такой критерий позволяет получить больший запас
устойчивости, чем в методе Зиглера-Никольса.

Метод CHR даёт две разные системы
параметров регулятора. Одна из них получена при наблюдении отклика на изменение
уставки (табл. 2), вторая – при наблюдении отклика на внешние возмущения (табл.
3).

Какую систему параметров выбирать, зависит от того, что важнее
для конкретного регулятора: качество регулирования при изменении уставки или
ослабление внешних воздействий. Если же важно и то и другое, то необходимо
использовать регуляторы с двумя степенями свободы [1].
Метод CHR использует аппроксимацию
объекта моделью первого порядка с задержкой (1).
В CHR используются те же исходные
параметры a и L, что и в методе Зиглера-Никольса.
Обратим внимание, что
пропорциональный коэффициент в методе CHR меньше, чем в методе Зиглера-Никольса.
Ручная настройка ПИД-регулятора, основанная на правилах
Расчёт параметров по формулам не
может дать оптимальной настройки регулятора, поскольку аналитически полученные
результаты основываются на сильно упрощённых моделях объекта. В частности, в
них не учитывается всегда присутствующая нелинейность типа «ограничение» для управляющего воздействия (см. раздел «Интегральное
насыщение»). Кроме того, модели используют параметры, идентифицированные с
некоторой погрешностью. Поэтому после расчёта параметров регулятора желательно
сделать его подстройку. Подстройку можно выполнить на
основе правил, которые используются для ручной настройки. Эти правила получены
из опыта, теоретического анализа и численных экспериментов. Они сводятся к
следующему [2]:
-
увеличение
пропорционального коэффициента увеличивает быстродействие и снижает запас
устойчивости; -
с
уменьшением интегральной составляющей ошибка регулирования с течением времени
уменьшается быстрее; -
уменьшение
постоянной интегрирования уменьшает запас устойчивости; -
увеличение
дифференциальной составляющей увеличивает запас устойчивости и быстродействие.
Перечисленные правила применяются
также для регуляторов, использующих методы экспертных систем и нечёткой логики.
Ручную настройку с помощью правил
удобно выполнять с применением интерактивного программного обеспечения на
компьютере, временно включённом в контур управления. Для оценки реакции системы
на изменение уставки, внешние воздействия или шумы измерений подают искусственные воздействия и наблюдают реакцию на них. После
выполнения настройки значения коэффициентов регулятора записывают в память ПИД-контроллера, а компьютер удаляют.
Отметим, что применение правил
возможно только после предварительной настройки регулятора по формулам. Попытки
настроить регулятор без начального приближённого расчёта коэффициентов могут
быть безуспешными.
При регулировке тепловых процессов
настройка по правилам может занять недопустимо много времени.
Сформулированные правила справедливы
только в окрестности оптимальной настройки регулятора. Вдали от неё эффекты
могут быть иными.
Численные методы оптимизации для настройки ПИД-регуляторов
Методы оптимизации для нахождения
параметров регулятора концептуально очень просты. Выбирается критерий
минимизации, в качестве которого может быть один из показателей качества (см.
подразделы «Критерии качества во временной области» и «Частотные критерии качества») или комплексный критерий, составленный из
нескольких показателей с разными весовыми коэффициентами. К критерию
добавляются ограничения, накладываемые требованиями робастности. Таким путём
получается критериальная функция, зависящая от параметров ПИД-регулятора.
Далее используются численные методы минимизации критериальной функции с заданными
ограничениями, которые и позволяют найти искомые параметры ПИД-регулятора.
Методы, основанные на оптимизации,
имеют следующие достоинства:
-
позволяют
получить оптимальные значения параметров, не требующие дальнейшей подстройки; -
не
требуют упрощения модели объекта, модель может быть как угодно сложной; -
позволяют
быстро достичь конечного результата (избежать процедуры длительной подстройки
параметров).
Однако реализация данного подхода
связана с большими проблемами, которые не один десяток лет являются предметом
научных исследований. К этим проблемам относятся:
-
длительность
процесса поиска минимума; -
низкая
надёжность метода (во многих случаях вычислительный процесс может расходиться и
искомые коэффициенты не будут найдены); -
низкая
скорость поиска минимума для овражных функций и функций с несколькими
минимумами.
Тем не менее методы оптимизации
являются мощным средством настройки ПИД-регуляторов с
помощью специально разработанных для этого компьютерных программ (см. раздел
«Программные средства для настройки ПИД-регуляторов»).
Автоматическая настройка и адаптация
Естественным направлением развития
коммерческих ПИД-регуляторов является разработка
методов, позволяющих снизить затраты человеческого труда на инсталляцию,
настройку и обслуживание. Несмотря на то что многие методы автоматической
настройки и адаптации ПИД-регуляторов, используемые в
настоящее время, были разработаны ещё в 60-х годах XX
века [10], в промышленных контроллерах адаптивная техника начала использоваться
только с середины 80-х. Это связано с технической
сложностью реализации адаптивных алгоритмов на элементной базе, которая
существовала до появления микроконтроллеров.
Настройка может выполняться вручную
или автоматически, без участия человека (автонастройка).
Автонастройка может выполняться
полностью автоматически и по требованию, когда человек является инициатором
настройки. Полностью автоматическая настройка может инициироваться при
наступлении заранее заданного условия (например, при изменении нагрузки, при изменении внешних воздействий, при изменении погрешности
регулирования) или непрерывно во времени. Автоматическая настройка,
инициируемая без участия человека, называется адаптацией. Примером адаптации
может быть автонастройка при изменении числа яиц в инкубаторе или
при изменении нагрузки на валу двигателя. Иногда термин «адаптация» трактуют
более широко, как приспособление регулятора к реальному объекту на стадии ввода
системы в эксплуатацию [10].
Разновидностью адаптации является
разомкнутое управление параметрами регулятора (табличная автонастройка), когда
заранее найденные параметры регулятора для разных условий работы системы
заносятся в таблицу, из которой они извлекаются при наступлении условий, по которым инициируется адаптация.
Отметим, что адаптация в принципе
является медленным процессом, поэтому её нельзя рассматривать как непрерывное
слежение параметров регулятора за изменяющимися параметрами объекта.
Отметим, что регуляторы, настроенные
в автоматическом режиме, чаще настроены хуже, чем настроенные в ручном режиме
[11]. Объясняется это философским умозаключением, что компьютер не может
выполнять сложные и плохо формализуемые задачи лучше человека.
В настоящий момент отсутствуют
простые, надёжные и общепринятые методы автоматической настройки.
Основные принципы
Все виды автоматической настройки
используют три принципиально важных этапа: идентификация, расчёт параметров
регулятора, настройка регулятора [7]. Часто конечный этап включает этап
подстройки (заключительная оптимизация настройки). Оптимизация настройки необходима в связи с тем, что методы расчёта параметров
регулятора по формулам не учитывают нелинейности объекта, в частности, всегда
присутствующую нелинейность типа «ограничение», а идентификация параметров
объекта выполняется с некоторой погрешностью. Подстройка
регулятора может быть поисковой (без идентификации объекта, путём поиска
оптимальных параметров) и беспоисковой (с идентификацией). Поисковая
идентификация базируется обычно на правилах (см. раздел «Ручная настройки ПИД-регулятора, основанная на правилах»)
или на итерационных алгоритмах поиска минимума критериальной функции. Наиболее
распространён поиск оптимальных параметров с помощью градиентного метода:
находят производные от критериальной функции по параметрам ПИД-регулятора, которые являются компонентами
вектора градиента, а далее производится изменение параметров в соответствии с
направлением градиента.
Важно подчеркнуть, что несмотря на
наличие автоматической подстройки, контроллер может не дать требуемого качества
регулирования по причинам, не зависящим от качества заложенных в него
алгоритмов. Например, объект управления может быть плохо спроектирован
(зависимые контуры регулирования, большая задержка, высокий порядок объекта);
объект может быть нелинейным; датчики могут быть расположены не в том месте,
где нужно, и иметь плохой контакт с объектом, уровень помех в канале измерения
может быть недопустимо большим; разрешающая способность датчика может быть
недостаточно высокой; источник входного воздействия на объект может иметь
слишком большую инерционность или гистерезис; могут быть также ошибки в монтаже
системы, плохое заземление, обрывы проводников и т.д.
Поэтому, прежде чем начинать автоматическую настройку, необходимо убедиться в
отсутствии перечисленных проблем. Например, если вследствие износа механической
системы появился непредусмотренный проектом гистерезис и поэтому система
находится в режиме колебаний, подстройка регулятора
может не дать желаемого результата, пока не устранена причина проблемы.
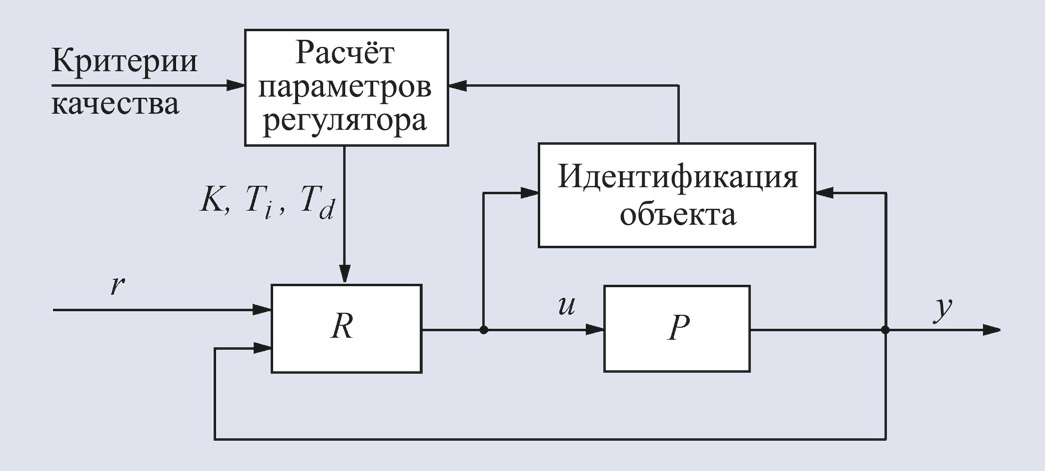
Структурная схема
самонастраивающейся системы приведена на рис. 23. Автонастройка практически не
имеет никаких особенностей по сравнению с описанными ранее методами, за
исключением того, что она выполняется в автоматическом режиме. Основным этапом
автоматической настройки и адаптации является
идентификация модели объекта. Она выполняется в автоматическом режиме обычными
методами идентификации параметров моделей объектов управления [7, 10].
Автоматическая настройка может выполняться и без идентификации объекта, основываясь на правилах (см. раздел «Ручная настройки ПИД-регулятора, основанная на правилах») или поисковых методах.
Идентификация объекта управления
Для выполнения качественного
регулирования, в том числе после автоматической настройки ПИД-регулятора,
необходимы знания о динамическом поведении объекта управления. Процесс
получения (синтеза) математического описания объекта на основе экспериментально
полученных сигналов на его входе и выходе называется
идентификацией объекта. Математическое описание может быть представлено в
табличной форме или в форме уравнений. Идентификация может быть структурной,
когда ищется структура математического описания объекта,
или параметрической, когда для известной структуры находят величины параметров,
входящих в уравнения модели. Когда ищутся параметры модели с известной
структурой, то говорят об идентификации параметров модели, а не объекта.
Результатом идентификации может быть
импульсная или переходная характеристика объекта, а также соответствующие им
спектральные характеристики, которые могут быть представлены в виде таблицы
(массива), а не в форме математических зависимостей. Табличные характеристики могут использоваться в дальнейшем для структурной
и параметрической идентификации математической модели объекта регулирования или
непосредственно для определения параметров ПИД-регулятора
(как, например, в методе Зиглера-Никольса, см.
подраздел «Настройка параметров регулятора по методу Зиглера и Никольса»).
Несмотря на разнообразие и сложность
реальных объектов управления, в ПИД-регуляторах
используются, как правило, только две структуры математических моделей: модель
первого порядка с задержкой и модель второго порядка с задержкой (см. подраздел
«Модели объектов управления»). Гораздо реже
используются модели более высоких порядков, хотя они могут более точно
соответствовать объекту. Существуют две причины, ограничивающие применение
точных моделей. Первой из них является невозможность аналитического решения системы уравнений, описывающих ПИД-регулятор
с моделью высокого порядка (а именно аналитические решения получили наибольшее
распространение в ПИД-регуляторах с автоматической
настройкой). Вторая причина состоит в том, что при большом числе параметров и
высоком уровне шума измерений количество информации,
полученной в эксперименте, оказывается недостаточным для идентификации тонких
особенностей поведения объекта.
Выбор оптимальной модели обычно
основан на критерии достаточности качества регулирования при минимальной
сложности модели. Для нелинейных процессов и при повышенных требованиях к
качеству регулирования разрабатывают модели с индивидуальной структурой, основываясь на физике процессов, протекающих в объекте
управления.
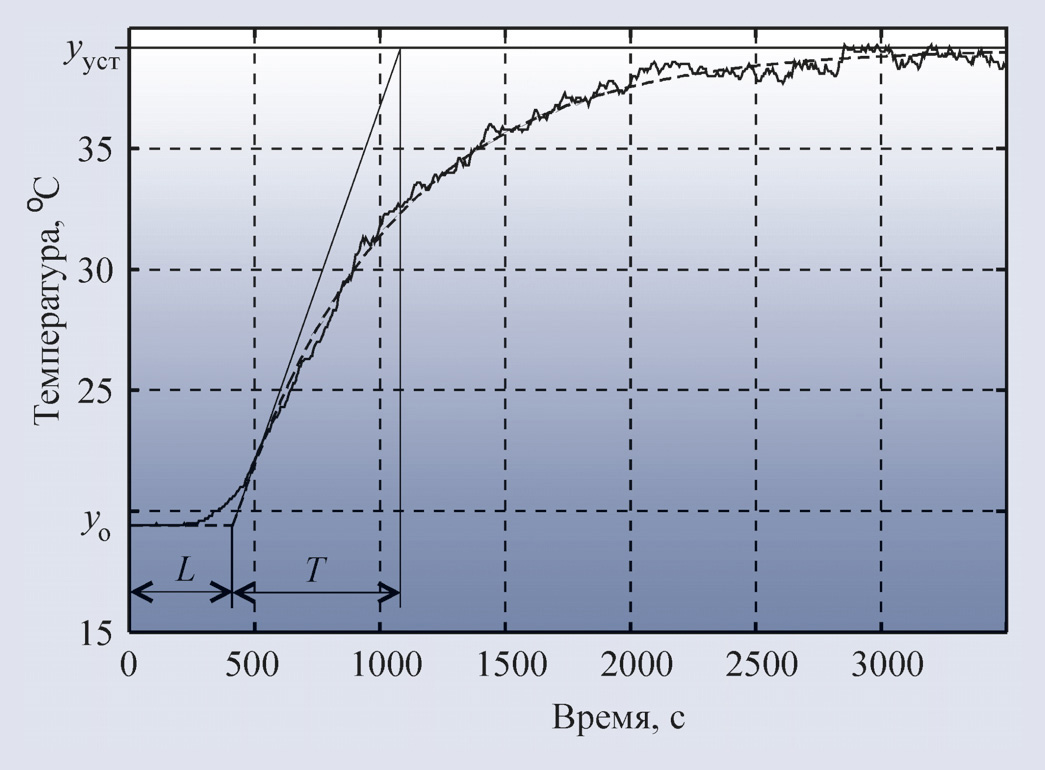
Если процесс любой сложности
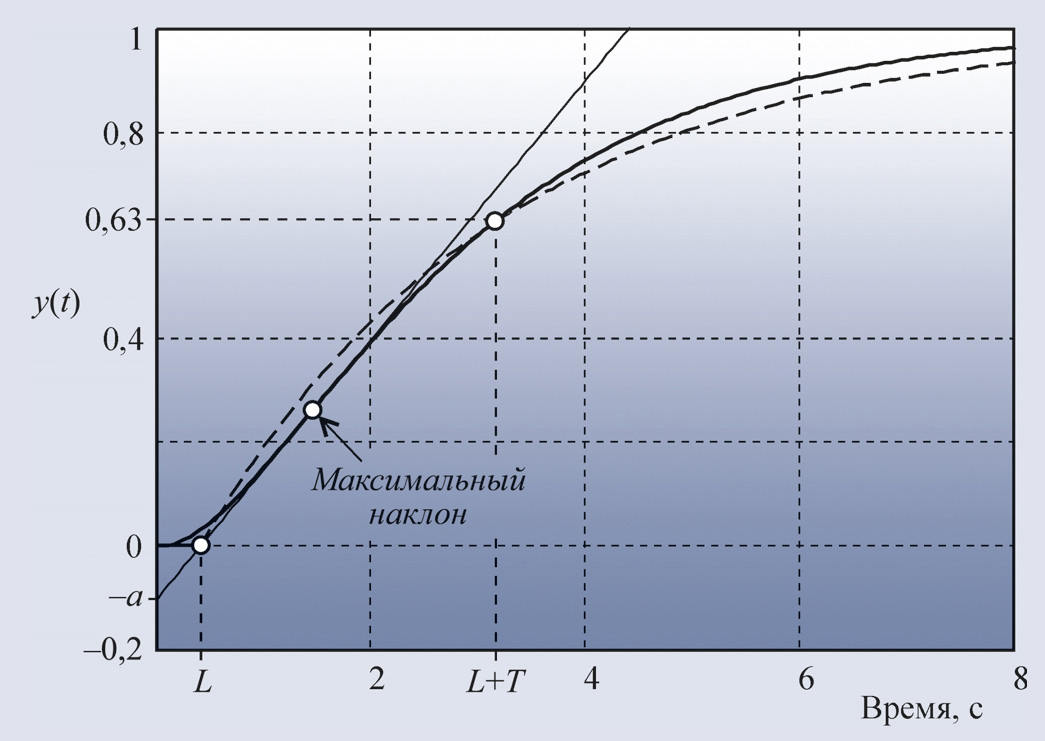
аппроксимировать моделью первого порядка с транспортной задержкой (рис. 24), то
полученные таким способом постоянная времени Т и задержка L называются соответственно эффективной
постоянной времени и эффективной задержкой.
Идентификация может выполняться с
участием оператора или в автоматическом режиме, а также непрерывно (в реальном
времени) – в адаптивных регуляторах либо по требованию оператора – в
регуляторах с самонастройкой.
Теория ПИД-регуляторов
хорошо развита для линейных объектов управления. Однако практически все
реальные объекты имеют нелинейность типа «ограничение управляющего
воздействия». Ограничение может быть связано, например, с ограниченной
мощностью нагревателя при регулировании тепловых
процессов, с ограничением площади сечения перепускного клапана, с ограничением
скорости потока жидкости и т.п. Ограничение «снизу» в тепловых системах связано
с тем, что источник тепла не может, как правило, работать в режиме холодильника, когда этого требует закон регулирования.
Для минимизации нелинейных эффектов
при идентификации объекта в рабочей точке («в малом») используют малые
изменения управляющего воздействия, когда нелинейности системы можно не
учитывать. При этом процесс вывода системы в зону линейности является предметом отдельного рассмотрения.
Идентификацию можно выполнять в
замкнутом контуре с обратной связью или в разомкнутом. Идентификация в
замкнутом контуре может быть косвенной и прямой. При косвенной идентификации
измеряется тестовый сигнал и отклик на него системы с обратной связью, затем
путём вычислений по уравнениям системы находится передаточная функция объекта
управления. При прямой идентификации передаточная функция объекта находится по
измерениям сигналов непосредственно на его входе и выходе.
Различают активную идентификацию (с
помощью воздействия на систему, которое подаётся специально с целью
идентификации) и пассивную (в качестве воздействий используют сигналы,
имеющиеся в системе в процессе её нормального функционирования). В пассивном
эксперименте производят только наблюдение за поведением
системы в нормальном режиме её функционирования, пытаясь извлечь из этого
наблюдения информацию, достаточную для настройки регулятора.
Модели объектов управления
Существуют два способа получения
модели объекта управления: формальный и физический. При формальном подходе
используют модель типа «чёрный ящик», в которой не содержится информация о
физических процессах, происходящих в объекте, или о его структуре. Синтез
формальной модели сводится к выбору одной из небольшого числа моделей,
описываемых далее, и идентификации её параметров.
Модель первого порядка. Наиболее
распространёнными объектами управления являются системы, описываемые
уравнениями тепломассопереноса. Реакция таких объектов (при условии, что они
являются линейными по входному воздействию) на ступенчатое входное воздействие имеет задержку L и точку перегиба (рис. 24). Точное решение
этих уравнений осуществляется численными методами и в теории автоматического
управления не используется. Используют достаточно простое выражение
передаточной функции объекта управления (модель первого порядка с транспортной
задержкой) [6]:
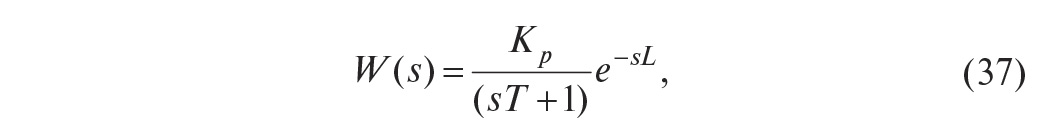
где s – комплексная частота, Kp – коэффициент передачи в
установившемся режиме, T – постоянная времени, L – транспортная задержка. Как
видим, модель первого порядка описывается тремя параметрами: Kp, T, L, которые
должны быть найдены в процессе идентификации. На рис. 24 приведена переходная
характеристика реального объекта, измеренная в производственном цехе с помощью
модуля NL-4RTD серии RealLab! (НИЛ АП), датчика ТСМ-50, OPC-сервера
NLopc и программы MS Excel. Погрешность измерений составляет 1 градус, разрешающая способность – 0,01 градуса. Экспериментально снятые
точки (несколько тысяч) образуют сплошную линию, кривая аппроксимирующей модели
показана штриховой линией.
Модель второго порядка. Если
описанная модель первого порядка оказывается слишком грубой, используют модель
второго порядка:
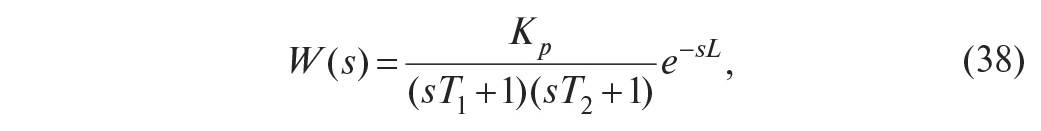
где T1, T2 — две постоянные времени
объекта управления. Модель второго порядка имеет характерную точку перегиба на
передаточной характеристике.
Модели интегрирующих процессов.
Выходная величина некоторых объектов управления при подаче на вход ступенчатого
воздействия не стремится к установившемуся значению, как на рис. 24, а
продолжает изменяться в установившемся режиме. Такие переходные процессы называют интегрирующими. Пример интегрирующего процесса
приведён на рис. 25.
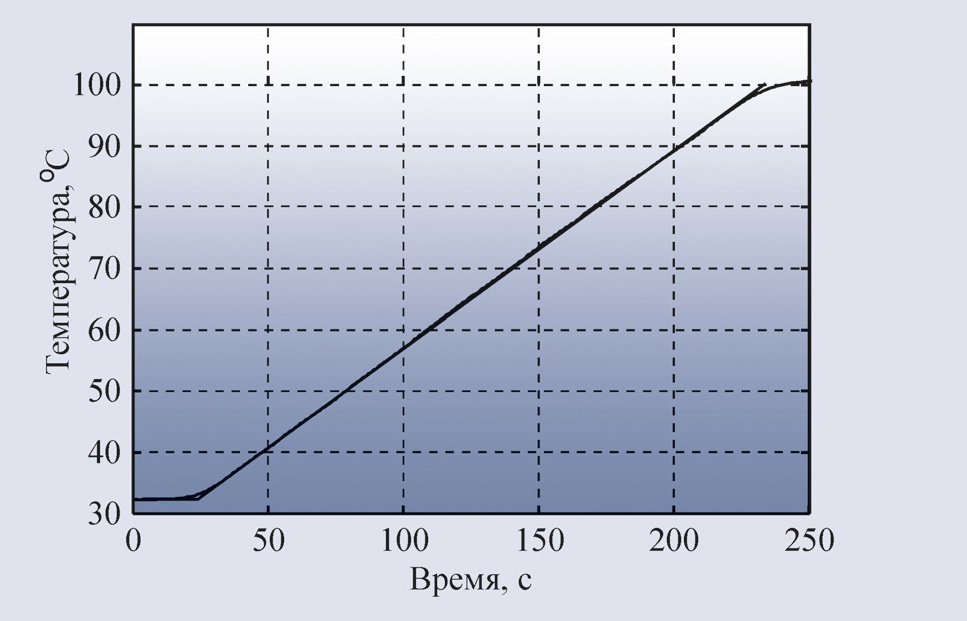
Это зависимость температуры в чайнике мощностью 2 кВт от
времени после включения нагрева. Поскольку мощность нагревателя очень высока,
то чайник успевает закипеть за время t<<T Передаточная функция такого процесса имеет вид:
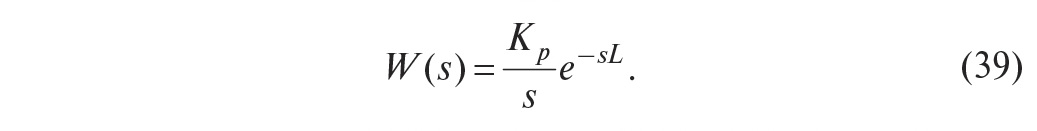
Другими примерами интегрирующих
процессов могут быть перемещение ленты транспортёра, поворот оси двигателя,
налив жидкости в ёмкость, рост давления в замкнутом сосуде.
Применение более сложных моделей
позволяет улучшить качество регулирования, однако делает невозможным простой
аналитический расчёт параметров регулятора на основании параметров модели. Для
сложных моделей качество регулирования ограничивается не точностью модели, а возможностями ПИД-регулятора.
Поэтому наибольшее распространение в ПИД-регуляторах
нашли простейшие линейные модели первого и второго порядка.
Выбор тестовых сигналов и измерение
динамических характеристик
Для идентификации объекта управления
необходимо измерять сигнал на его входе u(t) и реакцию y(t) на выходе.
Идентификацию можно выполнить не только путём подачи тестового сигнала на вход
системы, но и посредством изменения нагрузки (например, нагрузки на валу двигателя), а также параметров объекта (например,
количества яиц в инкубаторе).
Идентификация в пассивном
эксперименте привлекательна тем, что не вносит погрешность в нормальное течение
технологического процесса, однако её достоверность крайне низка в принципе [6]
и может привести не к настройке, а расстройке ПИД-регулятора.
Тем не менее, число патентов по ПИД-регуляторам
с пассивной идентификацией равно числу патентов с активной идентификацией [12].
При проведении активного
эксперимента возникает задача выбора формы тестового воздействия. Используют
сигналы в форме ступеньки (скачка), в форме прямоугольного импульса, линейно
нарастающего сигнала, треугольного импульса, псевдослучайного двоичного сигнала (ПСДС), шума, синусоидальных воздействий (частотный
метод). Наиболее часто для настройки ПИД-регуляторов
используют скачок и двойной прямоугольный импульс (первый импульс – вверх,
второй – вниз относительно установившегося значения).
Тестовое воздействие должно иметь
достаточно малую амплитуду, чтобы переходный процесс в объекте оставался в
границах линейности. В то же время оно должно быть достаточно большим, чтобы
увеличить отношение сигнала к шуму и внешним возмущениям.
Объект должен находиться в
установившемся состоянии перед подачей тестового сигнала и быть устойчивым.
Граничная частота спектра тестового
сигнала должна быть выше наибольшего по абсолютной величине полюса передаточной
функции объекта [10]. Точнее, выше, чем частота единичного усиления ω1
разомкнутого контура с обратной связью. До настройки регулятора, когда частота ω1 ещё неизвестна, верхнюю граничную частоту
спектра тестового сигнала выбирают выше частоты ω180, на которой фазовый сдвиг
выходного синусоидального сигнала объекта относительно входного составляет
–180°. Указанный диапазон частот важен потому, что
именно на частоте ω180 возникают колебания, когда объект находится на границе
устойчивости в замкнутом контуре с релейным регулятором или П-регулятором.
В контуре с ПИ-регулятором частота затухающих колебаний
может быть ниже и соответствовать точке, где сдвиг фаз
в объекте составляет около –145° [2] вследствие дополнительного фазового
сдвига, вносимого интегратором. В ПИД-регуляторах
дифференцирующее звено может скомпенсировать этот фазовый сдвиг, и колебания
возникнут на частоте ω180.
Нижняя граница диапазона, в котором
необходимо достаточно точно идентифицировать передаточную функцию, должна быть
примерно в 10 раз ниже частоты единичного усиления ω1. Более точно нижнюю
границу диапазона можно определить только после настройки ПИД-регулятора.
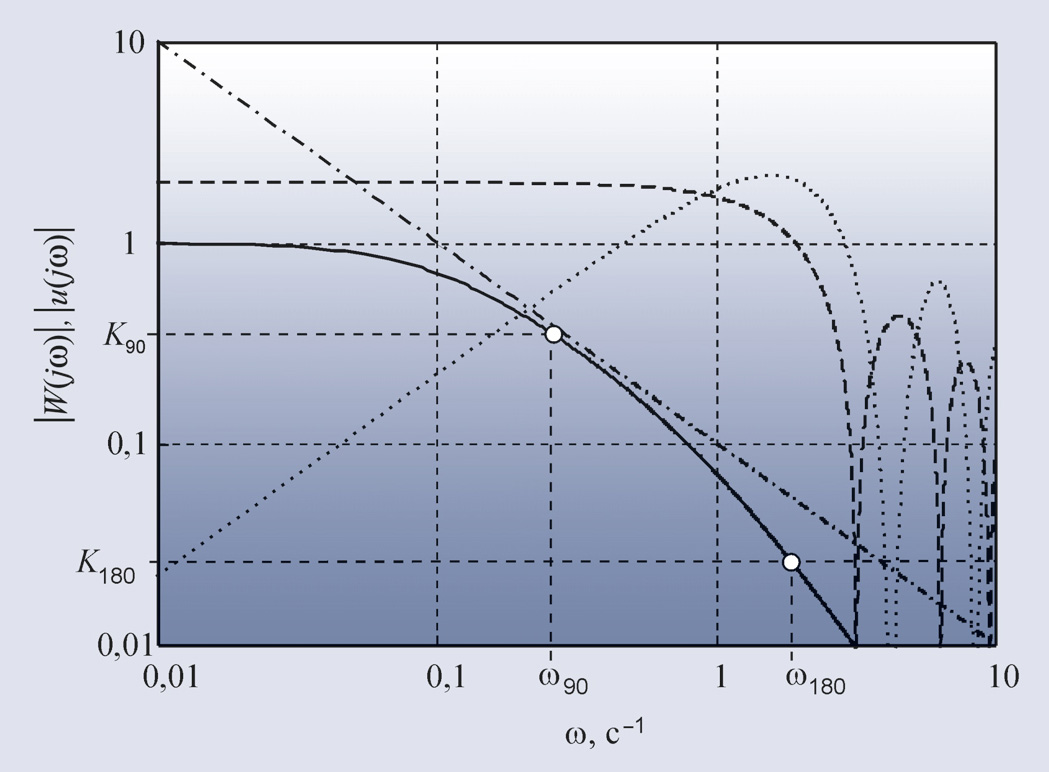
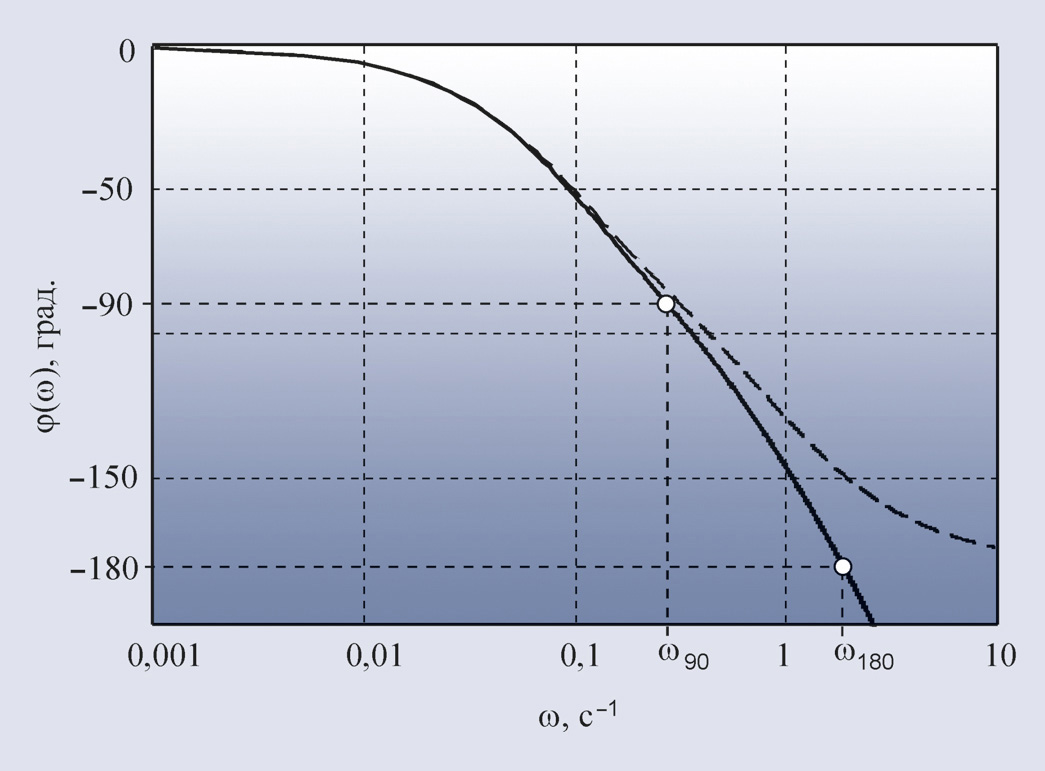
В качестве иллюстрации к сказанному на рис. 26 и рис. 27
сплошной жирной линией показаны амплитудно-частотная и
фазочастотная характеристики объекта с передаточной функцией:
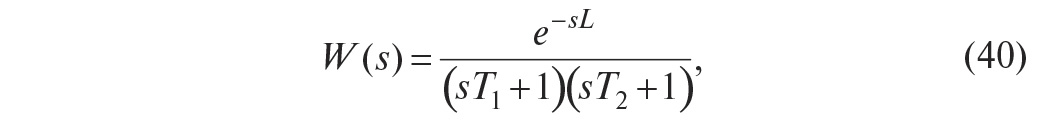
где s = jω, T1 = 1, T2 = 10, L =
0,3. Для получения хорошего отношения сигнал/шум зависимость модуля
спектральной функции тестового воздействия от частоты не должна иметь сильных
провалов в интересующей области частот, чтобы обеспечить достаточно большое отношение сигнал/шум. Этому условию, в частности,
удовлетворяют сигналы, показанные штриховой и пунктирной линиями на рис. 26.
Желательно также, чтобы порядок функции, описывающей спектральную функцию
тестового сигнала (то есть порядок многочлена в знаменателе
функции), был не ниже порядка объекта управления, поскольку крутизна спада АЧХ
в области верхних частот увеличивается с ростом порядка.
Ширина спектра и мощность тестового
сигнала существенно влияют на точность идентификации. В общем случае более
мощные и широкополосные сигналы позволяют определить большее число параметров
передаточной функции.
Если идентификация выполняется без
остановки технологического процесса (а это наиболее важный для практики
случай), то могут существовать ограничения на максимальную мощность,
длительность или энергию тестового сигнала, чтобы не нарушать нормальный ход
технологического процесса. Например, в инкубаторе допускается
подать импульс, кратковременно (на 5 минут) повышающий температуру до 50°С,
однако повышение температуры даже на 1°С в течение нескольких часов приводит к
гибели зародыша. Поэтому возникает задача выбора
тестового сигнала с требуемым спектром при ограничении, накладываемом на его
мощность, длительность или энергию.
Наилучшую спектральную
характеристику можно получить, усложняя форму сигнала и увеличивая общее время
идентификации. Для идентификации быстрых процессов (например, в
электромеханических системах) получил широкое распространение псевдослучайный
двоичный сигнал, имеющий равномерный спектр в
ограниченной полосе частот. Однако при управлении тепловыми процессами для ПИД-регуляторов наиболее критическим параметром является быстрота
идентификации. Поэтому здесь чаще используют простые сигналы, которые, кроме
быстроты идентификации, позволяют использовать простые
расчёты по формулам вместо численных методов минимизации функционала ошибки.
Конечно, достоверность результата при этом падает.
Даже тщательно выполненная
идентификация может не дать положительного результата, если окажется, что
объект существенно нелинеен. Для тестирования на линейность объект возбуждают
серией тестовых воздействий разной амплитуды. Полученные реакции объекта нормируют на амплитуду тестового сигнала и сравнивают между
собой. Для линейных объектов полученные кривые должны совпадать. Если различие
между кривыми существенно превышает оценку погрешности идентификации, то объект
следует рассматривать как нелинейный и использовать для
него методы теории автоматического управления нелинейными системами.
Частотная идентификация в режиме
релейного регулирования
Идентификация с помощью
широкополосных сигналов, к которым относятся единичный скачок и прямоугольный
импульс, не позволяет получить достаточно достоверные результаты в условиях
сильных шумов и жёстких ограничений, накладываемых на энергию сигнала. Гораздо
более высокую точность при малой амплитуде позволяет получить воздействие
узкополосным сигналом, в качестве которого используют отрезок синусоидального
сигнала. С ростом числа периодов сужается ширина спектра и растёт спектральная
плотность такого сигнала на частоте колебаний. Благодаря этому появляется
возможность использовать узкополосный фильтр для выделения сигнала на фоне
помех, что резко повышает достоверность идентификации. Однако при использовании
фильтра перед измерением необходимо дождаться окончания
переходного процесса, который тем длиннее, чем выше добротность фильтра. Это
существенно увеличивает время идентификации. Идентификацию выполняют для
нескольких разных частот. Для ускорения процесса можно использовать тестовое
воздействие в виде суммы гармонических колебаний с разными частотами, которые
затем выделяют несколькими узкополосными фильтрами.
Существенным недостатком этого
метода является большое время идентификации. Поэтому его чаще используют только
для измерения коэффициента передачи и фазового сдвига на частоте ω180, а для
идентификации других параметров объекта используют широкополосные тестовые сигналы.
Метод частотной (релейной)
идентификации в замкнутом контуре с релейным регулятором является самым
распространённым в коммерческих ПИД-регуляторах с
автонастройкой [2, 13]. Этот метод очень давно известен в микроэлектронике как
метод кольцевого генератора. Он использует свойство замкнутой динамической
системы с отрицательной обратной связью генерировать незатухающие колебания на
частоте фазового сдвига –180° при петлевом усилении K180 ≥1.
Основная идея метода. Рассмотрим
систему с отрицательной обратной связью, состоящую из релейного регулятора R и
объекта управления P (рис. 28).
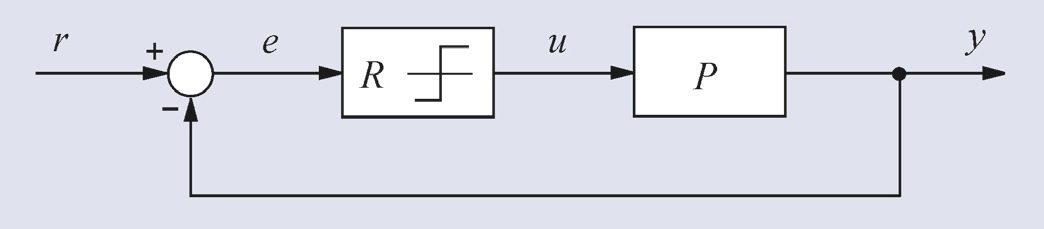
Здесь регулятор R имеет два значения выходной
величины u:

Гармонический сигнал, проходя через
объект управления, изменяет свою амплитуду и фазу (рис. 26 и 27). Поскольку на
входе объекта присутствует шум, в его спектре всегда найдутся такие
гармонические составляющие с частотой ω180, которые, пройдя через объект управления, появятся на его выходе с той же частотой ω180, но
с отставанием по фазе на 180° от соответствующей входной составляющей. Если
этот сигнал с выхода объекта опять подать на его вход с помощью отрицательной
обратной связи, то общий фазовый сдвиг в петле с обратной связью составит уже
360°, то есть на частоте ω180 обратная связь в системе из отрицательной
превращается в положительную. Это приводит к нарастанию циркулирующего по петле
сигнала при петлевом усилении Kn > 1 или к его затуханию при Kn < 1. Нарастание
сигнала в некоторый момент начинает ограничиваться, например, нелинейностью
типа «насыщение», и тогда в системе устанавливаются стационарные колебания. При
этом эффективный коэффициент усиления, найденный по первой гармонике колебаний
на частоте ω180, становится равным единице Kn = 1 (так
как после установления стационарных колебаний сигнал больше не усиливается).
Таким образом, в рассмотренной
системе возникают незатухающие колебания, когда усиление по контуру с обратной
связью (петлевое усиление) равно единице на частоте фазового сдвига в объекте
180°. В нелинейной системе петлевое усиление на малом сигнале может быть больше единицы до момента, когда колебания установятся.
В контуре регулирования с идеальным релейным регулятором (рис. 28) усиление до
начала колебаний равно бесконечности. Поэтому, если фазочастотная
характеристика включает в себя точку со сдвигом фазы
180°, возникают колебания. С увеличением порядка объекта (рис. 29) сдвиг по
фазе становится более 180° и условия для возникновения колебаний выполняются
всегда.
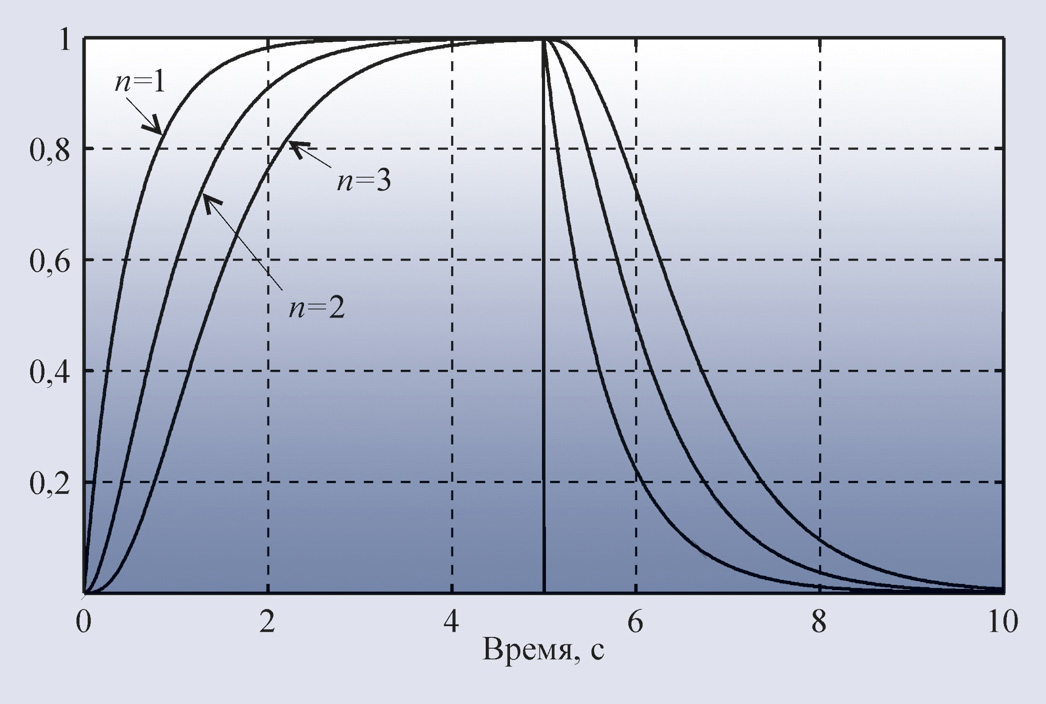
Обычно АЧХ строят в логарифмическом
масштабе по обеим координатным осям и называют диаграммами Боде. При этом
наклон линейных участков АЧХ измеряют в децибелах на декаду (дБ/дек.).
Например, объект первого порядка (1) имеет наклон АЧХ –20 дБ/дек. (рис. 30), и
при L = 0 этому наклону взаимно однозначно соответствует максимальный фазовый
сдвиг –90° при ω → ∞ (рис. 31, пунктирная линия). Объект второго порядка (2)
имеет наклон АЧХ –40 дБ/дек., и ему соответствует максимальный фазовый сдвиг –180°
при ω → ∞ (рис. 26). Для объекта третьего порядка наклон АЧХ равен –60 дБ/дек.,
и фазовый сдвиг составляет –270°.
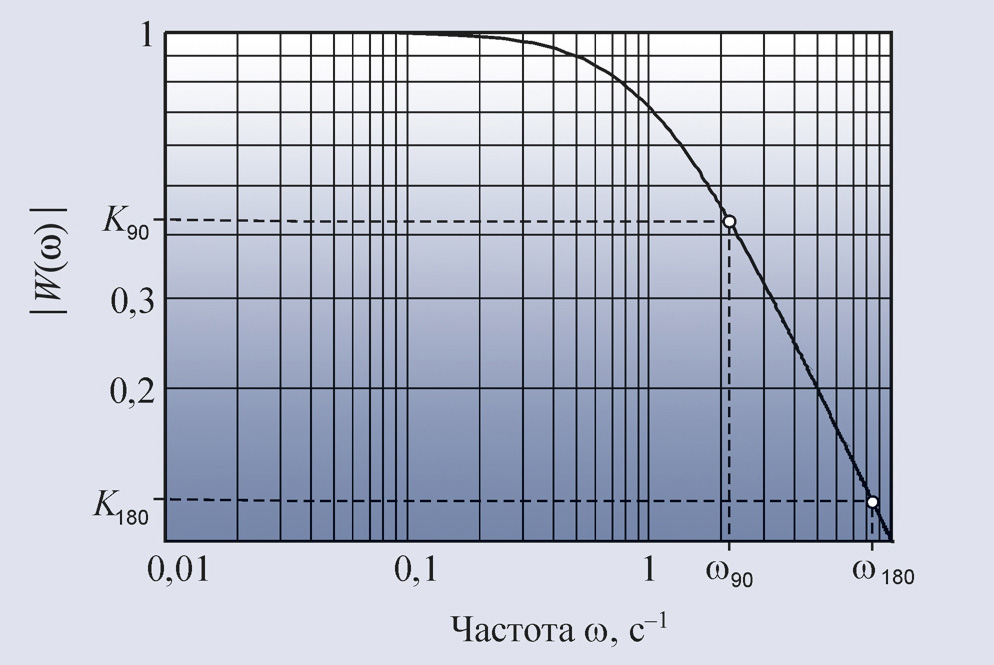
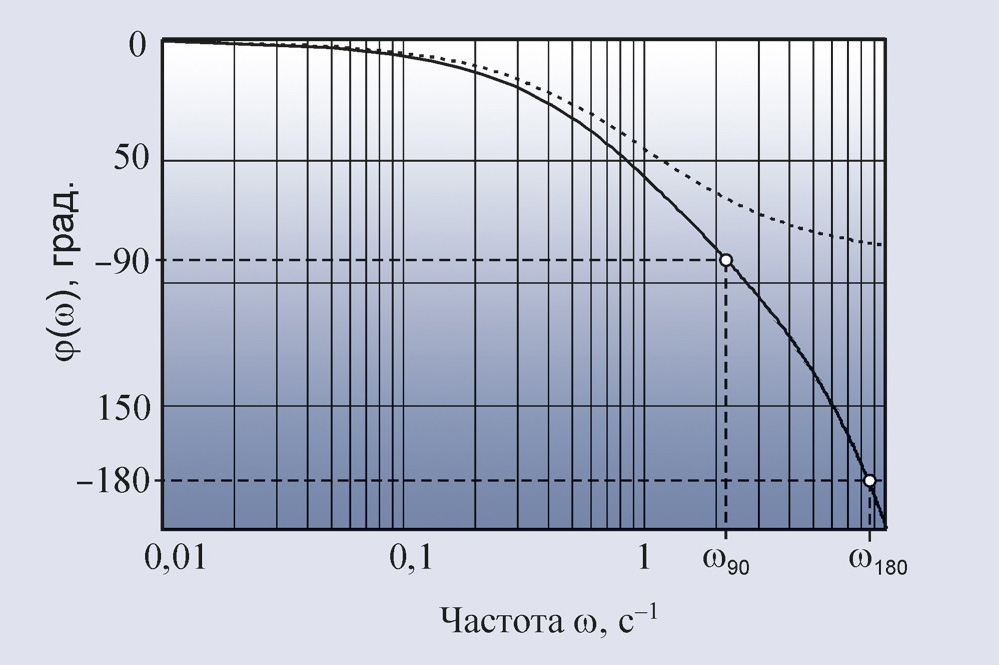
Из изложенного следует, что система
регулирования с объектом первого порядка без транспортной задержки всегда
устойчива, даже в контуре с релейным регулятором. Система с объектом второго
порядка может быть неустойчивой при ω → ∞. Система с объектом третьего порядка и система любого порядка с транспортной задержкой в
контуре с релейным регулятором всегда находится в режиме автоколебаний.
Поэтому качество системы управления
в первую очередь нужно обеспечивать путём проектирования объекта управления с
минимальным порядком (если это возможно), и только после этого проектировать
регулятор для него. Например, некоторые системы термостатирования используют
нагревательный элемент в виде тонкой проволочки, через которую продувается
воздух. Такая система имеет первый порядок передаточной функции, и даже
релейный регулятор для неё даёт хорошее качество регулирования.
Система с объектом первого порядка
перестаёт быть устойчивой, если в передаточную функцию добавляется транспортная
задержка. При этом объект перестаёт быть минимально-фазовым
и, несмотря на то что наклон АЧХ остаётся равным –20 дБ/дек. (рис. 30), в
системе возникают колебания, поскольку фазовый сдвиг транспортной задержки ϕ =
Lω растёт неограниченно с ростом частоты ω и на частоте ω180 достигает –180°
(рис. 31, сплошная линия).
Поскольку в реальном объекте
вследствие его пространственной протяжённости всегда появляется небольшая
транспортная задержка, в любой системе с релейным регулятором возникают
колебания, однако их амплитуда на выходе объекта может быть пренебрежимо малой
вследствие резкого снижения коэффициента передачи
объекта с ростом частоты (рис. 30).
Таким образом, замкнутый контур с
объектом управления и релейным регулятором позволяет найти частоту ω180. Найдём
теперь коэффициент передачи объекта на этой частоте. К сожалению, его можно
найти только приближённо, поскольку на вход объекта в системе с релейным регулятором воздействует последовательность
прямоугольных импульсов, которая получается после прохождения сигнала обратной
связи y(t) через релейный регулятор.
Приближённый метод расчёта основан на разложении входной последовательности
прямоугольных импульсов в ряд Фурье с отбрасыванием
всех гармоник, кроме первой. Возможность замены последовательности
прямоугольных импульсов их первой гармоникой основана на том, что объекты с
передаточными функциями вида (2) являются фильтрами, ослабляющими высшие гармоники. Серия прямоугольных импульсов, пройдя через такой
объект, становится очень близкой к синусоидальному сигналу (рис. 32). Поэтому
после разложения входного сигнала в ряд Фурье можно считать, что через объект
проходит только первая гармоника, а остальные
подавляются.
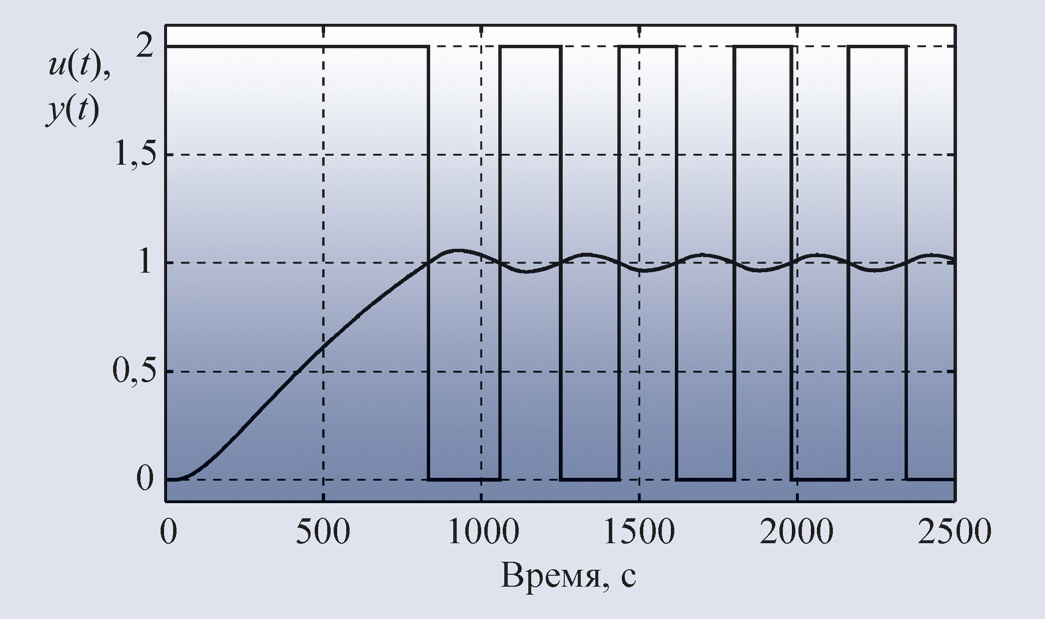
Если размах прямоугольных импульсов
на входе объекта равен 2Umax, то амплитуда первой гармоники этих импульсов, как
известно из курса радиотехники, равна 4Umax/π. Если обозначить амплитуду первой
гармоники сигнала на выходе объекта через Ymax, то искомый коэффициент
передачи системы на частоте ω180 будет равен отношению амплитуды на выходе к
амплитуде на входе:
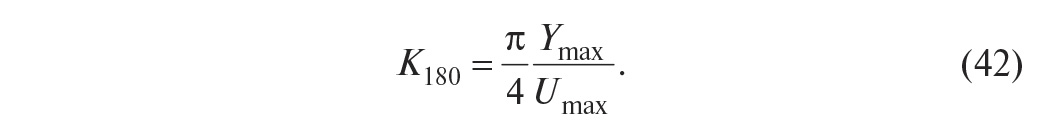
Пример. Рассмотрим АЧХ (рис. 26) и
ФЧХ (рис. 27) объекта второго порядка вида (40). Из графика на рис. 27 можно
найти частоту ω180 = 1,84, а по рис. 26 – коэффициент передачи объекта на этой
частоте K180 = 0,026. То есть при включении такого объекта в контур с релейным регулятором получим колебания с частотой ω180 =
1,84 при усилении K180 = 0,026.
Примерно эти же значения можно
получить из эксперимента с релейным регулятором по формуле (42), если из
графиков на рис. 32 найти значения амплитуды на выходе Ymax = 0,035 и входе
Umax = 1, а затем по формуле (42) рассчитать значение K180 = 0,027. Значение
частоты ω180 = 1,8 можно найти непосредственно по графику на рис. 32. Таким
образом, приближённая формула в данном случае даёт достаточно низкую
погрешность (около 4%).
Для объекта первого порядка с
транспортной задержкой L = 0,2 и постоянной времени T = 1 (ω = 2π/Τ) из рис. 31
можно найти ω180 = 8,44, а из рис. 30 определить K180 = 0,118. Форма колебаний
в системе с релейным регулятором показана на рис. 33 (штриховая линия).
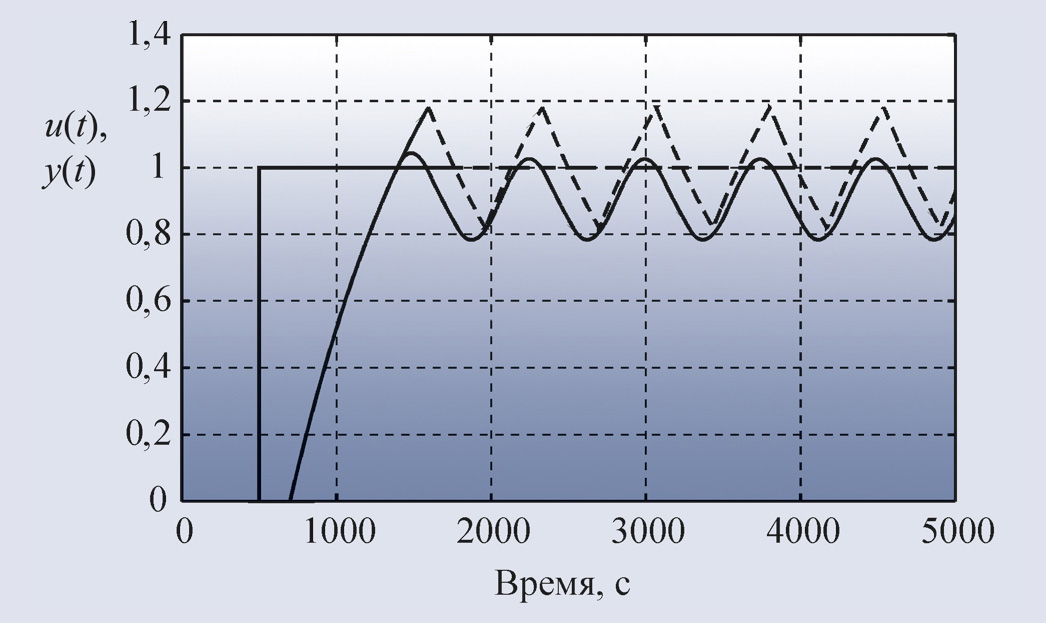
Особенностью объекта первого порядка является
существенное отличие формы колебаний от синусоидальной, что делает слишком
грубым её аппроксимацию первой гармоникой ряда Фурье, которая была использована
при получении формулы (42). Для устранения этой проблемы
вместо релейного регулятора можно использовать линейный усилитель, чтобы не
искажать форму сигнала в системе. Тогда форма колебаний становится близкой к
синусоидальной (сплошная линия на рис. 33). Такая колебательная система даёт
довольно точные значения ω180 = 8,49 и K180 = 0,096.
Однако для обеспечения режима, близкого к линейному, петлевое усиление должно
быть равно 1, то есть усилитель должен обеспечить усиление в 1/K180 раз, где
параметр K180 априори неизвестен. Это является основным недостатком метода
колебаний в линейном режиме.
Важным условием, которое нужно
соблюдать при использовании идентификации в режиме релейного регулирования,
является симметричность уровней umax и umin относительно уровня сигнала ur, при
котором y = r, то есть должно выполняться условие:
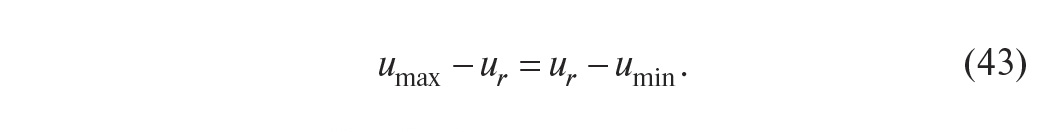
В противном случае скорости
нарастания сигнала выше уставки и спада ниже неё будут сильно различаться, а
форма колебаний в системе будет существенно отличаться от синусоидальной (рис.
34), что приведёт к высокой погрешности данного метода.
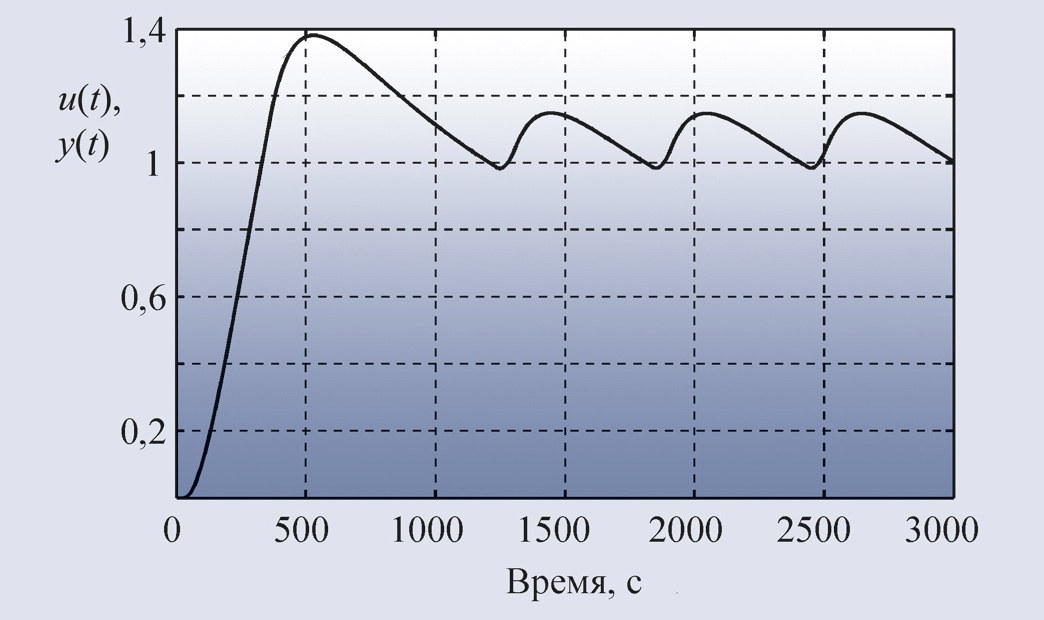
Аналогичный эффект возникает и в
системах более высокого порядка, если транспортная задержка превышает наибольшую
постоянную времени. С ростом задержки колебания становятся сначала
треугольными, затем приближаются к трапецеидальным и прямоугольным. Это объясняется тем, что с ростом транспортной задержки реакция
объекта на каждый из фронтов сигнала на выходе реле приближается к форме
реакции на функцию единичного скачка (рис. 29). В частотной области указанный
эффект объясняется тем, что с ростом задержки точка
ω180 (рис. 30 и 31) смещается влево, то есть фильтрующие свойства объекта
ухудшаются, и он транслирует прямоугольный входной сигнал на свой выход с
меньшими искажениями.
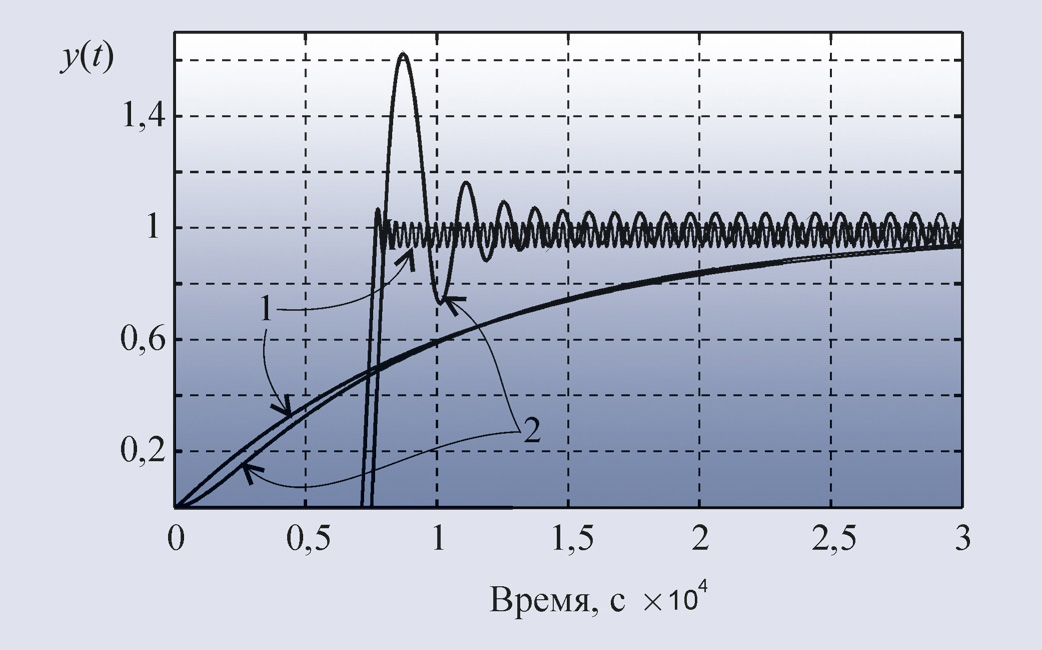
Для иллюстрации высокой разрешающей
способности описанного метода на рис. 35 приведены процессы в двух моделях, у
которых переходные характеристики различаются слабо, однако частоты колебаний в
контуре с релейным регулятором отличаются в 4 раза. Благодаря узкой
полосе сигнала он может быть эффективно выделен на фоне шумов, например,
методом наименьших квадратов.
Описанный метод позволяет получить
только одну точку передаточной функции объекта, то есть два параметра, которых
недостаточно для нахождения трёх параметров ПИД-регулятора.
Поэтому используют дополнительное соотношение Ti = 4Td/K2 которое позволяет найти третий
параметр.
Чтобы получить и другие точки АЧХ,
можно использовать реле с гистерезисом или фильтры, сдвигающие точку ω180 в
сторону более низких частот.
Описанный метод релейной
идентификации является в настоящее время самым распространённым в ПИД-регуляторах с автоматической настройкой. Это объясняется
следующими достоинствами метода:
-
всегда
даёт результат; -
имеет
высокую разрешающую способность; -
не
требует сложных вычислений; -
даёт
результат в рабочей точке.
Метод обладает следующими
недостатками:
-
не
справедлив для большой задержки, когда метод расчёта коэффициента передачи даёт
большую ошибку; -
самостоятельно
может использоваться только для очень грубой настройки, в общем случае должен
комбинироваться с другими методами идентификации.
Табличное управление
Наиболее простым методом адаптации
ПИД-регулятора к изменяющимся свойствам объекта
управления является табличное управление коэффициентами регулятора. Он может
быть использован не только для адаптивного управления, но и для управления
нелинейными объектами, нестационарными процессами, при необходимости изменять
параметры в зависимости от некоторых условий.
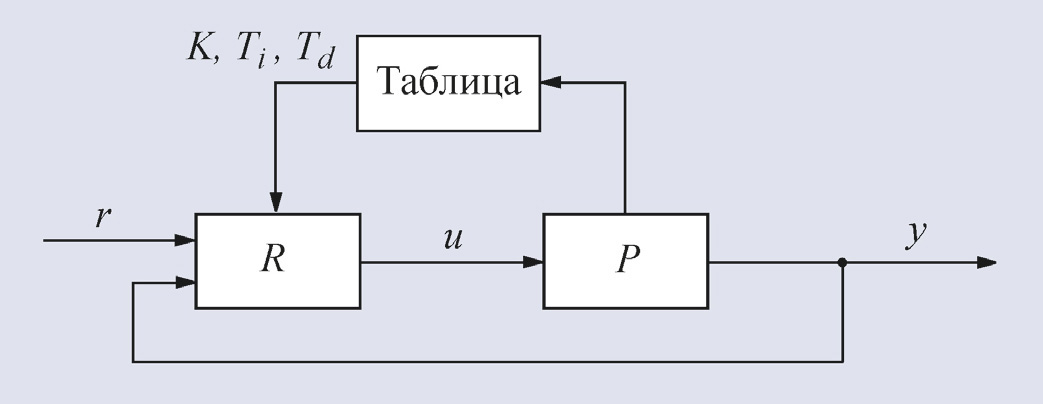
Принцип табличного управления очень
прост (рис. 36). Зная заранее возможные изменения режима работы системы
(например, возможные варианты загрузки инкубатора яйцами), выполняют
идентификацию объекта для нескольких разных режимов и для каждого из них находят параметры регулятора. Значения этих параметров записывают в
таблицу. В процессе функционирования системы измеряют величину, которая характеризует
режим работы системы (например, вес яиц с помощью датчика веса или уровень
жидкости в автоклаве с помощью датчика уровня), и в
зависимости от её значений выбирают из таблицы значения коэффициентов ПИД-регулятора.
Описанную систему можно рассматривать
как систему с двумя контурами регулирования. Однако контур, служащий для
адаптации (в нашем примере с весом яиц в инкубаторе или уровнем жидкости в
автоклаве), является разомкнутым. По этой причине табличное управление
характеризуется высоким быстродействием, отсутствием ложного срабатывания или
расхождения алгоритмов адаптации.
В общем случае таблица может быть
многомерной; для снижения необходимой размерности таблицы можно использовать
интерполяцию данных с помощью сплайна.
Недостатком этого метода являются
большие затраты на предварительную идентификацию, необходимую для составления
таблицы. Однако эту проблему частично можно решить посредством применения
специальных программ для автоматической идентификации и адаптации регулятора, после выполнения которых полученные параметры
заносятся в таблицу.
Табличное управление коэффициентами
регулятора целесообразно использовать в тех случаях, когда заранее известны
виды и величины дестабилизирующих факторов, которые к тому же можно измерить.
Программные средства для на стройки ПИД-регуляторов
Типовая система для настройки ПИД-регуляторов состоит из компьютера с программным обеспечением
под Windows, комплекта модулей ввода-вывода и
соединительных кабелей. Объект включается в контур регулирования, система
настраивается желаемым способом, затем полученные
коэффициенты регулятора записываются в ПИД-контроллер.
Благодаря удобному пользовательскому интерфейсу, большой производительности
компьютера и отсутствию ограничений на алгоритмы идентификации системы удаётся
получить параметры регулятора, близкие к оптимальным.
В настоящее время имеется около
полусотни коммерческих продуктов [12] для настройки ПИД-регуляторов.
Среди аналитических методов
настройки в этих программах наиболее распространены Lambda-тьюнинг
[2] или метод регулятора с внутренней моделью [1]. Подавляющее большинство
программ использует модель первого порядка с задержкой для описания объекта
регулирования.
Связь с оборудованием выполняется с
применением OPC-сервера, DDE-, COM- или DCOM-
технологий, среди которых только OPC-сервер является
средством, основанным на международном стандарте.
Развитие описываемых средств идёт в
направлении расширения диапазона поддерживаемых ПИД-регуляторов,
применения методов искусственного интеллекта и методов диагностики, развития
пользовательского интерфейса. Современные средства настройки позволяют анализировать износ клапанов, делать оценку робастности,
автоматически генерировать отчёт с параметрами контура регулирования, строить
графики спектральной плотности мощности и функций авто- и взаимной корреляции,
делать оптимизацию инверсной модели объекта управления
и т.п.
В качестве примера рассмотрим один
из коммерческих продуктов – систему для настройки ПИД-регуляторов
Protuner (см. Application
manual на сайте www.protuner.com) фирмы Techmation Inc. Система
отображает графики переходного процесса, выполняет преобразование
экспериментальных характеристик из временной области в частотную и вычисляет
параметры регулятора, используя несколько различных методов настройки.
Перед началом работы системы
пользователю предлагается меню для ввода априорной информации об объекте
регулирования:
-
диапазон
изменения входного и выходного сигналов объекта; -
тип
процесса в объекте управления (интегрирующий или нет); -
желаемые
единицы измерения; -
структура
контроллера (идеальная, последовательная или параллельная); -
частота
дискретизации; -
постоянная
времени фильтра в измерительном канале.
Идентификация выполняется с помощью
анализа реакции на входной скачок в замкнутом или разомкнутом контуре (по
выбору пользователя). Рекомендуется вариант в разомкнутом контуре. После того
как пользователь нажимает кнопку «Старт», входной и выходной сигнал отображаются на экране компьютера.
Имеются некоторые возможности
предварительной обработки собранных данных. К ним относятся удаление грубых
ошибок измерений и выбросов, связанных с импульсными помехами, а также цифровая
фильтрация. Это позволяет выполнять эксперименты в реальных условиях индустриального окружения.
После предварительной обработки
данных Protuner выполняет расчёт частотной характеристики объекта, которая
может быть отображена в виде диаграммы Боде, Найквиста или Никольса.
Отображаются также статический коэффициент передачи, постоянные времени и
транспортная задержка, частота ω180 и период T180.
Параметры ПИД-регулятора
вычисляются по частотным характеристикам. Сначала вычисляются постоянная
интегрирования и постоянная дифференцирования, затем на основе заданного запаса
по фазе и усилению вычисляется пропорциональный коэффициент регулятора.
Качество регулирования задаётся в
виде понятий «сильно демпфированная» переходная характеристика, «слабо
демпфированная» и «быстрая» (с коэффициентом затухания 1/0,38).
Protuner даёт разные коэффициенты регулятора для реакции на
изменение уставки и нагрузки.
Имеются средства для моделирования
системы до записи параметров в ПИД-контроллер. Могут
быть также построены частотные характеристики замкнутой системы, которые
позволяют оценить полученный запас по фазе и усилению.
Заключение
Дифференциальный член в ПИД-регуляторах всегда реализуется совместно с фильтром, иначе
вместо производной на выходе дифференциатора получаются только шумы.
Интегральное насыщение является одной из причин ухудшения качества переходного
процесса, сильно отличающегося от расчёта по линейной
модели регулятора. Запас устойчивости и робастность являются параметрами, о
которых часто забывают, однако построение регулятора для ответственных
применений невозможно без детального анализа этих параметров, что можно выполнить с помощью коммерческих программных пакетов для
настройки ПИД-регуляторов.
При формулировании критериев
настройки ПИД-регулятора необходимо принимать во
внимание реакцию не только на изменение уставки, но и на внешние возмущения.
Выбор критериев качества регулирования должен исходить из смысла решаемой
задачи. Несмотря на давность разработки, множество недостатков и наличие
большого количества новых методов настройки, по-прежнему
наиболее популярным является метод Зиглера-Никольса.
Однако часто он используется только для генерации начальных приближений
параметров, которые затем уточняются методами
оптимизации и с помощью нечётких правил.
Автоматическая настройка и адаптация
являются самыми актуальными задачами при построении ПИД-регуляторов.
Несмотря на большое количество коммерческих продуктов, остаётся много нерешённых
проблем, связанных с качеством настройки, влиянием нелинейностей объекта управления и внешних возмущений в процессе идентификации.
При автоматической настройке и адаптации используются те же методы
идентификации и расчёта параметров регулятора, что и при ручной настройке,
однако они выполняются в автоматическом режиме. Наиболее
эффективны методы автоматической настройки с применением компьютера, временно
включённого в контур регулирования. Благодаря большой мощности процессора и
отсутствию ограничений на объём программы появляется возможность создания
программного средства с широкими сервисными свойствами и качественной
математической обработкой.
Обзор публикаций
Методы оценки запаса устойчивости и
робастности для нескольких наиболее популярных методик настройки ПИД-регуляторов с объектом первого порядка с задержкой описаны в
работе [14]; в [15, 16] предложен метод расчёта параметров для объекта
произвольного порядка при заданной робастности системы;
в [17] использованы генетические алгоритмы для расчёта параметров ПИД-регулятора при заданных робастности и запасе устойчивости. В
[18] дан обзор методов, а в [19] – новый метод предотвращения интегрального
насыщения; в работе [20] исследована причина плохой робастности предиктора
Смита к разбросу транспортной задержки и предложены методы её улучшения.
Методика настройки ПИД-регулятора для системы второго порядка с помощью методов
оптимизации и с учётом ограничений в виде заданной робастности и полосы
пропускания системы предложена в работе [21]. В [22] предложен метод расчёта
параметров ПИД-регулятора как
для устойчивых, так и для неустойчивых объектов после идентификации в
разомкнутом контуре, а в [23] – для регулятора с внутренней моделью. В [18]
также дана классификация методов настройки и получен новый метод для систем с
транспортной задержкой. В [24] изложен новый метод настройки ПИД-регулятора, в котором вместо модели объекта управления
используется интеграл Боде, при настройке учитывается запас по фазе и усилению.
Большинство методов настройки ПИД-регуляторов описаны в работах по адаптивным и
самонастраивающимся регуляторам.
Программные средства настройки ПИД-регуляторов с помощью компьютера описаны в следующих работах:
в [25] – программа для идентификации линейных систем, которая включает в себя
обработку сигналов, построение графиков и идентификацию; в [26, 27] – системы
для идентификации моделей и настройки параметров ПИД-регулятора,
включающие устройства ввода-вывода и компьютер; в [13]
дан обзор коммерческих программных продуктов. На упомянутом в статье сайте
www.protuner.com в Application manual описана система для автоматической настройки ПИД-регуляторов.
Большое число публикаций посвящено
методам автоматической настройки ПИД-регуляторов. В
работе [28] предложен процесс автоматической настройки, нацеленный на получение
эффективного ослабления внешних возмущений; в [29] – метод автонастройки для
нелинейных систем, основанный на запоминании истории
процесса и построении локальных моделей на основе накопленных данных о сигналах
на входе и выходе системы.
Некоторые методы используют
автоматическую настройку с идентификацией в замкнутом контуре регулирования в
процессе нормального функционирования системы [30, 31]. В [32] предложен
итерационный метод для автоматической настройки ПИД-регулятора,
не требующий идентификации модели. В работах [33, 34]
для автоматической настройки используются методы оптимизации.
Адаптивная настройка предиктора
Смита описана в работе [35]; с применением базы нечётких правил – в [36], а для
систем с неизвестной транспортной задержкой – в [37]. Большое количество
методов автоматической настройки использует нечёткую логику, нейронные сети и генетические алгоритмы, они представлены в [38, 35,
39]. ●
Литература
8. Ziegler J.G., Nichols N.B. Optimum
settings for automatic controllers // Trans. ASME. 1942. Vol. 64. P. 759-768.
9. Chien K.L., Hrones J.A., Reswick
J.B. On automatic control of generalized passive systems // Trans. ASME.
1952. Vol. 74. P. 175-185.
10. Справочник
по теории автоматического управления / Под ред. А.А. Красовского. – М. : Наука,
1987. – 712 с.
11. O’Dwyer A. PID compensation of time
delayed processes 1998-2002:
a survey // Proceedings of the American Control Conference, 4-6 June 2003. Vol. 2. P. 1494-1499.
12. Li Y., Ang K.H., Chong G.C.Y. Patents,
Software, and Hardware for PID control: an overview and analysis of the current
art // IEEE Control Systems Magazine. Feb. 2006. P. 42-54.
13. Ang K.H., Chong G., Li Y. PID control
system analysis, design, and technology // IEEE Trans. on Control Systems
Technology. July 2005. Vol. 13. No. 4. P. 559-576.
14. Silva G.J., Datta A., Bhattacharyya
S.P. On the stability and controller robustness of some popular PID tuning
rules // IEEE Trans. on Automatic Control. Sept. 2003. Vol. 48. No. 9. P. 1638-1641.
15. Ho M.-T., Lin C.-Y. PID controller design for robust performance
// IEEE Trans. on Automatic Control. Aug. 2003. Vol. 48. No. 8. P. 1404-1409.
16. Keel L.H., Rego J.I., Bhattacharyya
S.P. A new approach to digital PID controller design // IEEE Trans. on
Automatic Control. April 2003. Vol. 48. No. 4. P. 687-692.
17. Obika M., Yamamoto T. An evolutionary
design of robust PID controllers // Mechatronics and Automation, 2005 IEEE International
Conference, 29 July – 1
Aug. 2005. Vol. 1. P. 101-106.
18. Moradi M.H. New techniques for PID
controller design // Proceedings of 2003 IEEE Conference on Control
Applications (CCA 2003), 23-25 June 2003. Vol. 2. P. 903-908.
19. Hodel A.S., Hall C.E. Variable-structure PID control to prevent
integrator windup // IEEE Trans. on Industrial Electronics. 2001. Vol. 48. No.
2. P. 442-451.
20. Shouli W., Watanabe K., Muramatsu E.,
Ariga Y., Endo S. Robust stability of approximate Smith predictor control systems
// SICE 2004 Annual Conference, 4-6 Aug. 2004. Vol. 2. P. 1522-1527.
21. Jing-Chung Shen, Huann-Keng Chiang. PID tuning rules for second order
systems // Control Conference, 2004 (5th Asian), 20-23 July 2004. Vol. 1. P. 472-477.
22. Silva G.J., Datta A., Bhattacharyya
S.P. New results on the synthesis of PID controllers // IEEE Trans. on
Automatic Control. Feb. 2002. Vol. 47. No. 2. P. 241-252.
23. Skoczowski S., Domek S., Pietrusewicz
K., Broel-Plater B. A
method for improving the robustness of PID control // IEEE Trans. on Industrial
Electronics. Dec. 2005. Vol. 52. No. 6. P. 1669-1676.
24. Karimi A., Garcia D., Longchamp R. PID
controller tuning using Bode’s integrals // IEEE Trans. on Control Systems
Technology. Nov. 2003. Vol. 11. No. 6. P. 812-821.
25. Sanchez-Gasca J.J., Clark K., Miller N.W., Okamoto H.,
Kurita A., Chow J.H. Identifying linear models from time domain simulations //
IEEE Computer Applications in Power. Apr. 1997. Vol. 10. No. 2. P. 26-30.
26. Hemerly E.E. PC-based packages for identification,
optimization, and adaptive control // IEEE Control Systems Magazine. Feb. 1991.
Vol. 11. Issue 2. P. 37-43.
27. Oviedo J.J.E., Boelen T., van
Overschee P. Robust advanced PID control (RaPID): PID tuning based on engineering
specifications // IEEE Control Systems Magazine. Feb. 2006. Vol. 26. Issue 1.
P. 15-19.
28. Leva A. Autotuning process controller
with enhanced load disturbance rejection // American Control Conference, 30
June – 2 July 2004.
Proceedings. Vol. 2. P. 1400-1405.
29. Takao K., Yamamoto T., Hinamoto T.
Design of a memory-based
self-timing PID
controller // 43rd IEEE Conference on Decision and Control (CDC 2004), 14-17 Dec. 2004. Vol. 2. P. 1598-1603.
30. Qiwen Yang, Yuncan Xue, Jiao Huang.
Simultaneous PID self-tuning
and control // Proceedings of the 2004 IEEE International Symposium on
Intelligent Control, 2-4
Sept. 2004. P. 363-367.
31. Ho H.F., Wong Y.K., Rad A.B. Adaptive
PID controller for nonlinear system with H∞ Physics and Control, 2003
International Conference, 20-22 Aug. 2003. Proceedings. Vol. 4. P. 1315-1319.
32. Calcev G., Gorez R. Iterative
technique for PID controller tuning // Proceedings of the 34th IEEE Conference
on Decision and Control, 13-15 Dec. 1995. Vol. 3. P. 3209-3210.
33. Glickman S., Kulessky R., Nudelman G.
Identification-based
PID control tuning for power station processes // IEEE Trans. on Control System
Technology. 2004. Vol. 12. No. 1. P. 123-132.
34. Rad A.B., Lo W.L., Tsang K.M. Self-tuning PID controller using Newton-Raphson search method // IEEE Trans.
on Industrial Electronics. Oct. 1997. Vol. 44. No. 5. P. 717-725.
35. Jih-Jenn Huang, DeBra D.B. Automatic Smith-predictor tuning using optimal
parameter mismatch // IEEE Trans. on Control Systems Technology. May 2002. Vol.
10. No. 3. P. 447-459.
36. Ivanova E., Hadjiski M. Rules based
adaptation of Smith predictor // Intelligent Systems, First International IEEE
Symposium, 2002. Proceedings. Vol. 3. P. 26-30.
37. Ren X.M., Rad A.B., Lo W.L., Chan P.T.
Adaptive H/sub 2/ optimal control based on Smith predictor for continuous-time systems with unknown time delay
// International Conference on Control and Automation (ICCA ‘05), 26-29 June 2005. Vol. 1. P. 159-164.
38. Hsuan-Ming Feng. A self-tuning fuzzy control system design // IFSA
World Congress and 20th NAFIPS International Conference, 25-28 July 2001. Vol. 1. P. 209-214.
39. Pin-Yan Tsai, Huang-Chu Huang, Shang-Jen Chuang, Yu-Ju Chen, Rey-Chue Hwang. The model reference control by
adaptive PID-like fuzzy-neural controller // IEEE
International Conference on Systems, Man and Cybernetics, 10-12 Oct. 2005. Vol. 1. P. 239-244
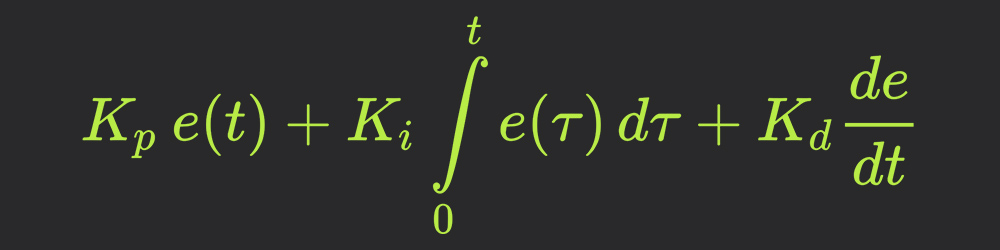
ПИД регулятор – один из самых распространенных автоматических регуляторов. Он настолько универсален, что применяется практически везде, где нужно автоматическое управление. Например температурой: специальные печи, холодильники, инкубаторы, паяльники, сопло и стол 3D принтера, ИК паяльные станции и прочее. Поддержание частоты оборотов мотора, например для станков. Всевозможные балансирующие штуки, гироскутеры, сигвеи, левитирующие магнитные платформы, и конечно же квадрокоптеры и самолёты с автопилотом. Это всё ПИД регулятор. Почему именно ПИД? Существуют и другие регуляторы, превосходящие ПИД по адаптивности к управляемой системе и стабильности, например линейно квадратичный. Но, чтобы грамотно синтезировать такой регулятор, нужно быть гораздо больше чем “семи пядей” во лбу, а настройка ПИД регулятора дело хоть и неприятное, но фактически очень простое и под силу любому, а сам ПИД регулятор универсален для почти любого процесса.
Система управления
Прежде чем переходить непосредственно к пиду, очень важно понять и запомнить несколько базовых понятий, из которых состоит автоматическая система. В первую очередь это регулятор, который всем заправляет и находится в центре системы. Регулятор в данном понимании – математический алгоритм или часть программы, которая крутится на микроконтроллере. Регулятор, как алгоритм, работает с обычными числами. Объект управления – это девайс, которым мы управляем, например печка или мотор. Для этого у нас есть управляющее устройство, например диммируемый тен или драйвер мотора. Управляющее устройство получает от регулятора управляющий сигнал, то есть конкретное число. Это может быть заполнение шим сигнала, от 0 до 255, а может быть угол поворота сервомашинки от 0 до 180, потому что регулятору без разницы чем управлять. В объекте управления у нас стоит датчик, с которого регулятор получает управляемую величину, то есть текущий сигнал с датчика. Это – обратная связь, которая и даёт возможность системе ирчно поддержать заданное значение. В случае с печкой это температура, а с мотором – частота оборотов. Ну и наконец регулятор получает установку (уставку), то есть число, к которому он должен привести текущее значение с датчика. Установка может задаваться каким угодно образом: крутилкой, ползунком, энкодером, кнопками, да хоть смской или голосовым вводом. Регулятору это неважно, для него это просто цифра. Задача регулятора состоит в том, чтобы сравнивать текущее значение с установкой и выдавать управляющий сигнал на управляющее устройство. То есть в программе это будет выглядеть условно так: регулятор получил установку, регулятор получил значение с датчика, регулятор выполнил вычисления и выдал нам управляющий сигнал, опять же число. Если это шим – мы его подаём через функцию генерации шим. Есть ещё один момент – регулятор должен делать расчёты и применять управляющий сигнал через равные промежутки времени, то есть с равным периодом или частотой. Эта частота называется частотой дискретизации системы, а период обозначается как dt, прямо как период интегрирования. 
Под капотом у ПИД регулятора
ПИД регулятор состоит из трёх составляющих: пропорциональной P, интегрирующей I и дифференциирующей D, формируется просто как сумма трёх значений, умноженных каждая на свой коэффициент. Эта сумма после вычислений становится управляющим сигналом, который подаётся на управляющее устройство, обозначим его как out.
out = P*kP + I*kI + D*kD
kP, kI и kD это и есть те самые коэффициенты, которые нужно настроить для работы ПИДа. Значения тут могут быть самые разные, от 0.001 то десятков и тысяч, это зависит от конкретной системы. Тут есть ещё один момент: любой коэффициент может быть равен нулю, и в таком случае обнуляется вся его компонента. То есть регулятор можно превратить в П, ПИ, ПД, и прочие сочетания. Разные системы требуют разного подхода, именно поэтому ПИД регулятор такой универсальный. В дальнейшем будем пользоваться следующими названиями переменных:
- out – выход с регулятора (управляющий сигнал)
- setpoint – установка (заданное значение)
- input – вход (значение с датчика)
- err – ошибка регулирования
- dt – период вычисления и регулирования
P составляющая
Пропорциональная составляющая предоставляет собой разность текущего значения с датчика и установки.
P = setpoint - input
Данная разность называется ошибкой регулирования, то есть насколько далеко находится система от заданного значения. Получается чем больше ошибка, тем больше будет управляющий сигнал и тем быстрее система будет приводить управляемую величину к заданному значению. Коэффициент kP тут влияет роль усиления ошибки и настраивается вручную. Но в то же время, если система пришла к заданной величине, ошибка станет равной нулю, и управляющий сигнал тоже! Другими словами, п регулятор никогда не сможет привести к заданному значению, всегда будет некая ошибка. П составляющая является основной в ПИД регуляторе и так сказать тянет самую большую лямку, регулятор может неплохо работать только лишь на ней одной. P составляющая исправляет ошибку в текущий момент времени.
I составляющая
Интегральная составляющая просто суммирует в саму себя ту же самую ошибку, разность текущего и заданного значения, умноженную на период дискретизации системы, то есть на время, прошедшее с предыдущего расчёта dt – фактически берёт интеграл от ошибки по времени.
I = I + (setpoint - input) * dt
В самом регуляторе это ещё умножается на коэффициент kI, которым настраивается резкость данной составляющей. В интегральной составляющей буквально копится ошибка, что позволяет регулятору с течением времени полностью её устранить, то есть привести систему ровно к заданному значению с максимальной точностью. I составляющая исправляет прошлые, накопившиеся ошибки.
D составляющая
Дифференциальная составляющая представляет собой разность текущей и предыдущей ошибки, поделенную на время между измерениями, то есть на ту же dt, которая общий период регулятора. Иными словами – это производная от ошибки по времени.
err = setpoint - input D = (err - prevErr) / dt prevErr = err
Фактически D составляющая реагирует на изменение сигнала с датчика, и чем сильнее происходит это изменение, тем большее значение прибавляется к общей сумме. Иными словами, D позволяет компенсировать резкие изменения в системе и при правильной настройке предотвратить сильное перерегулирование и уменьшить раскачку. Коэффициент д позволяет настроить вес, или резкость данной компенсации, как и остальные коэффициенты регулируют свои составляющие. D составляющая в первую очередь нужна для быстрых систем, то есть для систем с резкими изменениями, такие как квадрокоптер или шпиндель станка под переменной нагрузкой. D составляющая исправляет возможные будущие ошибки, анализируя скорость.
Настройка регулятора
Для настройки регулятора нужно варьировать коэффициенты:
- При увеличении kP увеличивается скорость выхода на установленное значение, увеличивается управляющий сигнал. Чисто математически система не может прийти ровно к заданному значению, так как при приближении к установке П составляющая пропорционально уменьшается. При дальнейшем увеличении kP реальная система теряет устойчивость и начинаются колебания.
- При увеличении kI растёт скорость компенсации накопившейся ошибки, что позволяет вывести систему точно к заданному значению с течением времени. Если система медленная, а kI слишком большой – интегральная сумма сильно вырастет и произойдёт перерегулирование, которое может иметь характер незатухающих колебаний с большим периодом. Поэтому интегральную сумму в алгоритме регулятора часто ограничивают, чтобы она не могла увеличиваться и уменьшаться до бесконечности.
- При увеличении kD растёт стабильность системы, она не даёт системе меняться слишком быстро. В то же время kD может стать причиной неадекватного поведения системы и постоянных скачков управляющего сигнала, если значение с датчика шумит. На каждое резкое изменение сигнала с датчика Д составляющая будет реагировать изменением управляющего сигнала, поэтому сигнал с датчика нужно фильтровать (читай урок по фильтрам).
Вот так выглядит процесс стабилизации при изменении коэффициентов: 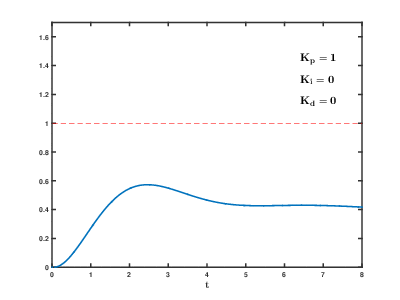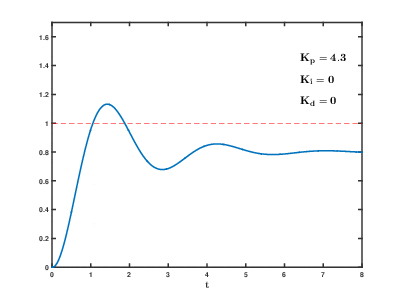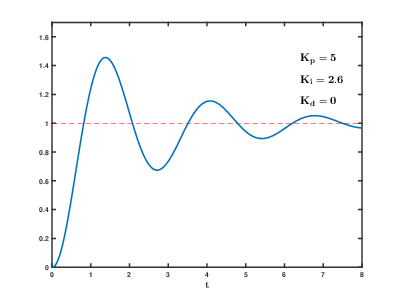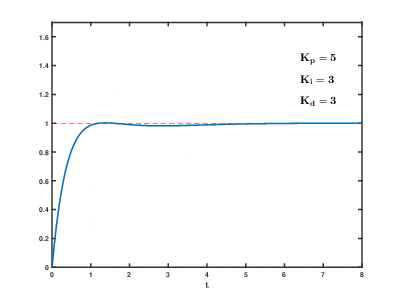 Настройка регулятора – дело не очень простое. Начальные коэффициенты для подбора можно получить по следующему алгоритму: сначала выставляем все коэффициенты в 0. Плавно увеличиваем kP до появления незатухающих колебаний. Значение kP, при котором они появились, запишем и обозначим как kP1. Далее замеряем период колебаний системы в секундах, обозначим как T. Итоговые коэффициенты получим так:
Настройка регулятора – дело не очень простое. Начальные коэффициенты для подбора можно получить по следующему алгоритму: сначала выставляем все коэффициенты в 0. Плавно увеличиваем kP до появления незатухающих колебаний. Значение kP, при котором они появились, запишем и обозначим как kP1. Далее замеряем период колебаний системы в секундах, обозначим как T. Итоговые коэффициенты получим так:
- kP = 0.6 * kP1
- kI = kP / T * 2 * dt
- kD = kP * T / 8 / dt
Например, незатухающие колебания появились при kP 20, период колебаний составил 3 секунды. Период dt в системе будет 50 мс (0.05 с). Считаем:
- kP: 0.6*20=12
- kI: 12/3*2*0.05=0.4
- kD: 12*2/8/0.05=60
На полученных коэффициентах должны более-менее работать большинство систем, но не все. Также можно воспользоваться автоматическим тюнером коэффициентов, например два разных алгоритма встроены в библиотеку GyverPID.
Реализация на C++
Соединяя все рассмотренные выше уравнения, получим:
// (вход, установка, п, и, д, период в секундах, мин.выход, макс. выход)
int computePID(float input, float setpoint, float kp, float ki, float kd, float dt, int minOut, int maxOut) {
float err = setpoint - input;
static float integral = 0, prevErr = 0;
integral = constrain(integral + (float)err * dt * ki, minOut, maxOut);
float D = (err - prevErr) / dt;
prevErr = err;
return constrain(err * kp + integral + D * kd, minOut, maxOut);
}
Это готовая функция, которая принимает значение с датчика, установку, три коэффициента и время, а также ограничение выхода с регулятора. Как пользоваться этой функцией: функция должна вызываться с некоторым периодом, причем длительность этого периода нужно будет передать в функцию в секундах. Если попроще, можно использовать задержку. Но делать так не рекомендуется, лучше сделать таймер на миллис и работать с ним. Функция возвращает управляющий сигнал, то есть можно подать его например как ШИМ. Период dt имеет такой смысл: чем инерционнее у нас система, тем реже можно вычислять пид. Например для обогрева комнаты период можно поставить 1 секунду или больше, а для контроля за оборотами двигателя надо будет поставить пару десятков миллисекунд, то есть около сотни раз в секунду.
Библиотеки
- GyverPID – моя библиотека со встроенным тюнером коэффициентов
- QuickPID – хорошая библиотека с интересными возможностями (оптимизация интегральной суммы, смешанный режим пропорционально ошибке/измерению)
- sTune – тюнер коэффициентов, несколько алгоритмов
Видео
Полезные страницы
- Набор GyverKIT – большой стартовый набор Arduino моей разработки, продаётся в России
- Каталог ссылок на дешёвые Ардуины, датчики, модули и прочие железки с AliExpress у проверенных продавцов
- Подборка библиотек для Arduino, самых интересных и полезных, официальных и не очень
- Полная документация по языку Ардуино, все встроенные функции и макросы, все доступные типы данных
- Сборник полезных алгоритмов для написания скетчей: структура кода, таймеры, фильтры, парсинг данных
- Видео уроки по программированию Arduino с канала “Заметки Ардуинщика” – одни из самых подробных в рунете
- Поддержать автора за работу над уроками
- Обратная связь – сообщить об ошибке в уроке или предложить дополнение по тексту ([email protected])
Данная статья посвящена исследованию методов настройки непрерывных ПИД-регуляторов на примере объектов первого и второго порядка и второго порядка с запаздыванием, а также выбору оптимальной настройки регулятора путем сравнения полученных результатов.
Сразу оговорюсь, что это не статья, а скорее реферат, то есть информация, собранная из разных источников с некой оценкой полезности и эффективности/применимости каждого метода.
Начнем с того, что с настройкой ПИД регулятора можно столкнуться где угодно, например, на преобразователе частоты, и хорошо, если это будет регулятор давления, они настраиваются достаточно просто, если не считать особенностей настройки ПИД, чтобы ПЧ гарантировано “уходил в сон”, то есть если отсутствует расход воды, частоник может снизить обороты до указанных минимальных, а дальше просто остановить двигатель и ждать, когда ошибка регулирования не превысит какую-то тоже настроенную величину. В термоконтроллерах чаще всего есть автонастройка, но не всегда она дает приемлемые показатели работы. На сервоприводах контур положения часто тоже имеет ПИ регулятор, он хоть и представляет из себя только часть от ПИД-регулятора, но общие принципы настройки тоже присутствуют, тк имеются основные канал пропорциональный и интегральный.
А что если регулятор не имеет автонастройки и регулируемый объект достаточно сложен, например, чтобы вывести в автонастройку агрегат мощностью 100кВт требуется ее прогрев и работа, а это может составить десятки минут (а иногда и часы, а время- деньги, особенно если это время работы энергоемкого прибора) не говоря уже о себестоимости материала. Тут стоит для начала разобраться в особенностях самого ПИД, чтобы подобрать во-первых подходящий метод, а во-вторых, понять где и как стоит добиваться устойчивости в первую очередь, а где и как можно и потом делать тонкую настройку.
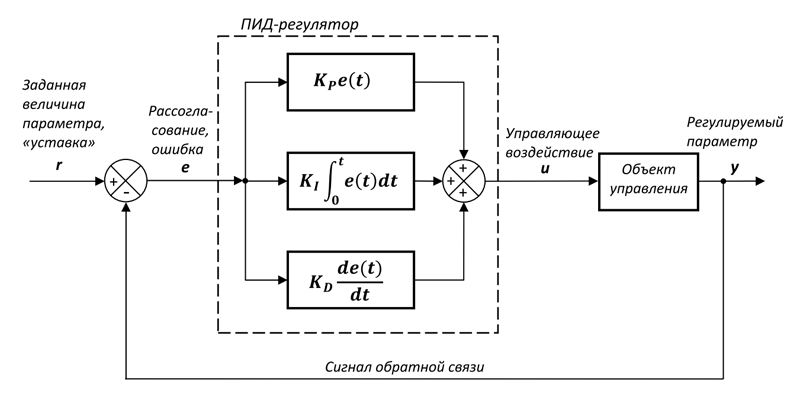
Структура регулятора по классике приведена на картинке, хотя существуют варианты, когда коэффициенты объединяются, это конечно усложняет работу, но общий принцип остается один, главное вовремя заметить, что изменение коэффициента пропорционального влияет например на интегральный канал.
- Пропорциональный канал выдает величину выходного сигнала, который рассчитывается как ошибка (разница, рассогласование) e(t) сигнала обратной связи (ОС) и сигнала задания r, умноженная на коэффициент Kp, который опять же может быть выражен и как 1/Tp – постоянная времени пропорционального канала регулятора. Если убрать (обнулив коэффициенты) остальные составляющий ПИД-регулятора, то результат такого регулятора будет иметь статическую ошибку, тк пропорциональный канал может только компенсировать часть рассогласования. Дальнейшее увеличение значение коэффициента в попытках увеличить эффективность, приведет к перерегулированию (превышению величины над уставкой, иногда многократному и повторяющемуся, в худшем случае в виде автоколебаний) при появлении большого рассогласования (например пуск или резкое изменение параметра). Данный канал отвечает за быстродействие регулятора в целом и наибольшую часть работы (компенсация большей части рассогласования).
- Интегральный канал в общем тоже берет за основу ошибку регулирования, но при этом выход интегрирует эту ошибку, умноженную на коэффициент Ki (1/Ti). Это дает возможность компенсации статической ошибки, если система не испытывает внешних возмущений (со временем конечно, если процесс не устойчивый, это событие может и не наступить), но не избавляет от динамической. Попытки уменьшить динамическую ошибку или как-то уменьшить время, за которое регулятор компенсирует ошибку, приведут к тому, что тоже появится перерегулирование и почти гарантировано автоколебания (ну как минимум несколько затухающих даже на фоне отсутствия перерегулирования в целом, если пропорциональный канал имеет слабое значение).
- Дифференциальный канал подает на выход скорость изменения ошибки de/dt, умноженную на коэффициент Kd (1/Td), что дает возможность как бы предугадать описанное выше резкое изменение рассогласования (пуск или резкое изменение параметра) и тем самым помочь своим более медленным братьям компенсировать величину ошибки. В дальнейшем, когда вступят в дело каналы пропорциональный и интегральный, роль дифференциального канала должна затухать. Конечно отыграют и электрические составляющие, и задержка расчета, и механика с инерцией, которая часто является самой долгой в перечне задержек, но что-то все же можно получить и от этого канала. Дифференциальный канал чувствителен к ВЧ-помехам. Поэтому, при построении системы регулирования, необходимо принять меры для защиты от помех. Кстати в теории дифференциальный канал может уменьшить значение перерегулирования, полученного при настройки пропорционального и интегрального канала за счет более быстрого уменьшения ошибки регулирования до вмешательства других каналов.
Итак теперь перейдем непосредственно к методам настройки
Ручная настройка или метод настройки “по графикам”.
Часто можно услышать о простейшем подходе к настройке (сейчас говорим о ручной), когда вручную настраивают сперва Kp, предварительно обнулив остальные каналы, потом Ki, а последним Kd, оценивая результат работы чисто по графикам процессе (так называемый эмпирический и эвристический методы), либо пользуясь ТАУ (нахождение частоты устойчивости и отступ от нее на 2-4 лога), такая инструкция встречается практически для всех ПЧ и даже сервоприводов, возможно это оправдано тем, что процесс быстрый и графики можно получить без особых затрат просто перебирая коэффициенты по логарифмической шкале, но для температуры так будет настраивать неудобно. Да-да если коэффициент равный двум слишком мал, а введение в коэффициент цифры 4 не дало необходимого изменения, нет смысла вводить K=6, нужно вводить 8, а потом 16, смысл в том, что мы тем самым ищем нужную нам частоту среза, а она как многие помнят из ТАУ у нас на логарифмической шкале выложена, и если она далеко, то перебор по обычной шкале сильно удлинит время поиска.
Важное замечание: даже для одного и того же объекта процедуру настройки ПИД регулятора следует повторять, если изменились параметры объекта (например, загрузка печи) или значительно изменилась рабочая температура (остывание и соответственно отток мощности зависит от градиента температур).
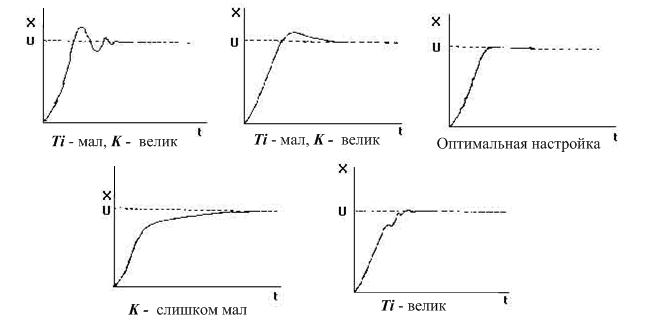
Второй вариант больше подходит для долгих процессов (температура) – предварительно нужно вывести систему на границу устойчивости. Для этого нужно вывести регуляторы И и Д (записать нули), оставив только П (пропорциональный), устойчивость необходимо проверять на той температуре, которая близка к рабочей, то есть эксперименты с большим Кр нужно проводить уже после выхода на установившийся процесс, до этого лучше постараться выбрать коэффициент поменьше, либо уменьшить его уже когда перескочили уставку. На установившемся процессе добиваемся увеличением Кп коэффициента появления заметных колебаний, либо если колебания уже есть, то уменьшаем Кр до их исчезновения, полученный коэффициент Кркр запомним. Что делать с полученной частотой среза (частота, на которой настройка теряет устойчивость)? Переведем ее в период колебаний τ (хотя можно сразу измерить именно период колебаний τ). Далее для термоконтроллеров Термодат предлагает следующую таблицу.
| Тип регулирования | Пропорциональный коэффициент Kp |
Интегральный коэффициент Ki |
Дифференциальный коэффициент Kd |
| Только P | 2*Кркр | Выключено | Выключено |
| P+I | 2.2*Кркр | 0.8* τ | Выключено |
| P+I+D | 1.7*Кркр | 0.5*τ | 0.12*τ |
Для других применений думаю лучше пользоваться методом “по графикам” для ручной настройки.
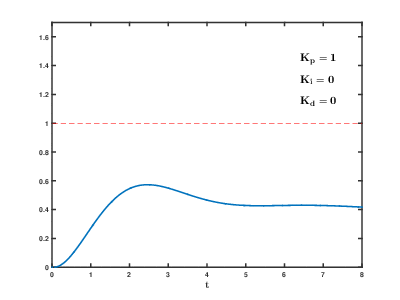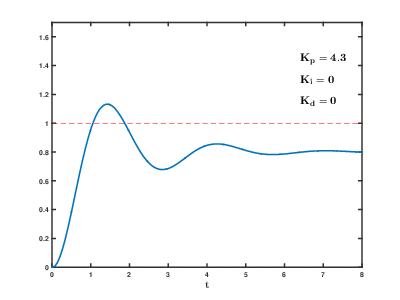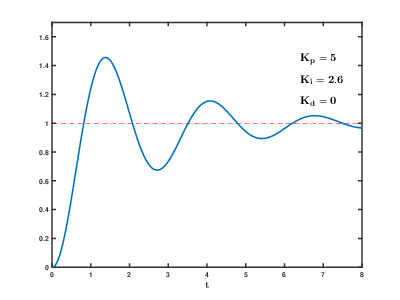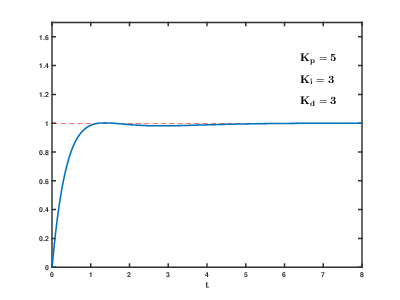
Тангенциальный метод настройки ПИД-регулятора (первый метод Зиглера-Никольса).
Следующий метод, который предлагается опять же для настройки ПИД регулировки температуры, это Тангенциальный метод.
В тангенциальном методе для нахождения ПИД коэффициентов используется переходная характеристика объекта, в случае терморегулирования кривая разогрева объекта.
Для начала опишу метод, который предлагается производителем приборов Термодат (коэффициенты соответственно могут отличаться у разных производителей).
В режиме ручного управления контроллера задается некоторое значение мощности на нагрузке. Значение мощности должно быть таким, чтобы установившаяся температура не превысила допустимого значения. Нужно дождаться установления температуры Т1, в этом режиме и в некоторый момент времени скачком изменить значение мощности (например: на 5%). Записать процесс изменения температуры (на компьютере, на самописце или по точкам, вручную) до установления нового устоявшегося значения температуры Т2.
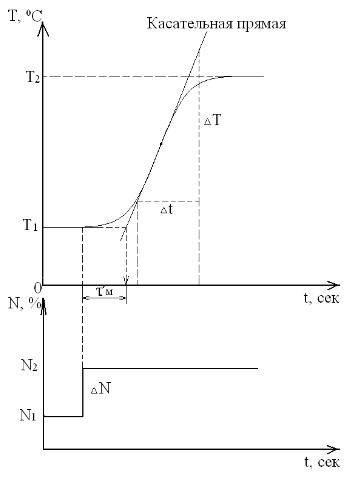
Провести касательную к полученной кривой в точке, где наклон касательной будет максимален.
Определить «мёртвое» время процесса как промежуток времени, прошедший с момента изменения мощности до момента времени, определяемого точкой пересечения касательной и средней линии температуры первого устойчивого состояния Т1 (до изменения мощности нагрева).
Определить величину относительного наклона касательной по формуле:
К = (∆T/∆t)/∆N.
∆T – изменение температуры в °С,
∆t – соответствующее изменение времени в секундах,
∆N – изменение мощности в %.
Установите значения коэффициентов Kp, Ki, Kd в соответствии с таблицей.
| Тип регулирования | Пропорциональный коэффициент Kp |
Интегральный коэффициент Ki |
Дифференциальный коэффициент Kd |
| Только P | 100*τм*К | Выключено | Выключено |
| P+I | 111*τм*К | 3.3*τм | Выключено |
| P+I+D | 83*τм*К | 2*τм | 0.25*τм |
К сожалению данный метод имеет еще пару трактовок, посему приведу обе, а решать какая лучше подойдет вам. Оба используют только два параметра для описания объекта, проводится линия по участку, соответствующему максимальному наклону графика переходной характеристики.
Первый вариант основан на поиске мертвого времени и длительности переходного процесса.
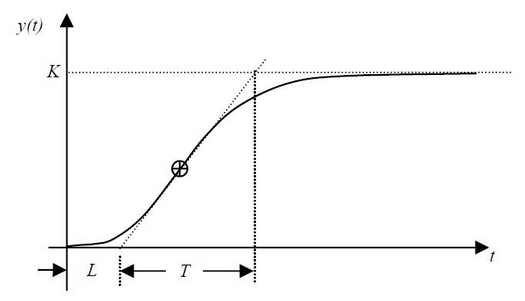
В первом случае ищется пересечение с осью времени и с мнимой линией максимального задания, значения параметров L и T, используются в расчете, формулы приведены в таблице:
| Тип регулирования | Пропорциональный коэффициент Kp |
Интегральный коэффициент Ti=Kp/Ki |
Дифференциальный коэффициент Td=Kd/Kp |
| Только P | T/L | Выключено | Выключено |
| P+I | 0.9*T/L | L/0.3 | Выключено |
| P+I+D | 1.2*T/L | 2*L | 0.5*L |
Второй вариант использует: a и L, которые определяются по графику переходной характеристике объекта управления так:
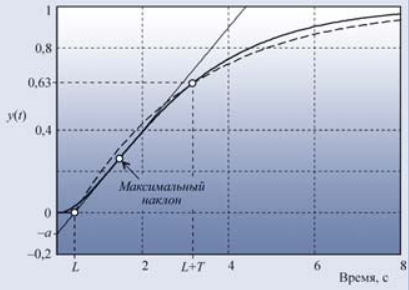
Формулы для расчета коэффициентов сведены в следующую таблицу:
| Тип регулирования | Пропорциональный коэффициент Kp |
Интегральный коэффициент Ti |
Дифференциальный коэффициент Td |
| Только P | 1/a | Выключено | Выключено |
| P+I | 0,9/a | 3*L/Kp | Выключено |
| P+I+D | 1,2/a | 0,9*L/Kp | 0.5*L/Kp |
Замечание: метод Зиглера-Никольса даёт параметры, далёкие от оптимальных. Это объясняется не только упрощённостью самого метода (он использует только 2 параметра для описания объекта), но и тем, что параметры регулятора в этом методе определялись Зиглером и Никольсом, исходя из требования к декременту затухания, равному 4, что и даёт медленное затухание процесса колебаний.
Метод Зиглера-Никольса никак не учитывает требования к запасу устойчивости системы, что является вторым его недостатком. Судя по медленному затуханию переходного процесса в системе, этот метод даёт слишком малый запас устойчивости. Но все же для начальной настройки вполне пойдет.
Метод колебаний (или второй частотный метод Зиглера-Никольса)
Данный метод основан на поиске частоты устойчивости, на которой сдвиг по фазе в разомкнутом контуре равен 180°.
Назначить уставку Тус, равной температуре регулирования (или 0.7Тус, если перегрев во время настройки нежелателен, а он может быть значительным).
Тоже существует два варианта, первый упрощенный от Термодата:
Включить позиционный (пороговый) режим регулирования.
В установившемся режиме колебаний температуры измерить период τ колебаний температуры (время между соседними максимальными или минимальными значениями температуры). Измерить также полный размах колебаний температуры ΔТ=Тmax-Тmin (разность максимального и минимального значений температуры).
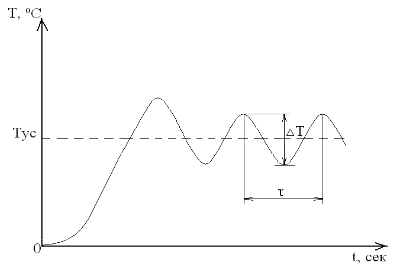
Установите значения коэффициентов Kp, Ki, Kd в соответствии с таблицей. Параметр «Ограничение ПИД» или «Зона» (если он есть в приборе) сделать равным Kp.
| Тип регулирования | Пропорциональный коэффициент Kp |
Интегральный коэффициент Ki |
Дифференциальный коэффициент Kd |
| Только P | 1.4*∆Т | Выключено | Выключено |
| P+I | 1.6*∆Т | 2.4*τ | Выключено |
| P+I+D | 1.2*∆Т | 1.5*τ | 0.2*τ |
Второй вариант такой:
Настройка пропорциональной компоненты (Kp)
1.Перед настройкой зоны пропорциональности интегральная и дифференциальная компоненты отключаются (Kи =0, Kд = 0) и задаем некоторое целевое значение регулируемого параметра (например, температуры):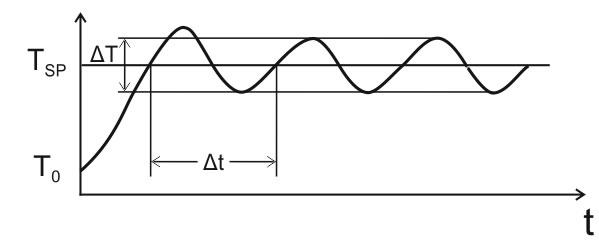
Тο — начальная температура в системе;
Тsp — заданная температура (уставка);
∆T — размах колебаний температуры (в расчетах не участвует);
∆t — период колебаний температуры.
2.Меняем значение пропорциональной составляющей Kp от минимума (можно от 0) до момента, пока не появятся устойчивые колебания системы с периодом ∆t. Фиксируем это значение как Kуст, а также период колебаний системы ∆t. Система должна находится в постоянном колебательном процессе, притом колебательный процесс незатухающий, колебания должны быть одинаковы относительно Тsp.
После получения данной кривой на нашем объекте, засекаем время периода колебаний ∆t – полный период. Данное время есть характеристика системы, оборудования.
3.На этом практическая часть метода заканчивается. Из полученных значений рассчитываем коэффициенты ПИД:
Kp=0.6⋅Kуст
Ki=(2⋅Kp)/∆t
Kd=(Kp⋅∆t)/8
Здесь Kуст – тот самый коэффициент пропорциональной составляющей, при котором возникли колебания, а ∆t – период этих колебаний.
Второй вариант, когда надо найти постоянные времени Ti и Td
Используя полученные параметры рассчитываем Ти и Тд по таблице.
| Пропорциональный коэффициент Kp |
Интегральный коэффициент Ti |
Дифференциальный коэффициент Td |
|
| П-регулятор | 0.5*Kуст | ||
| ПИ-регулятор | 0.4*Kуст | 0.8*∆t/Kp | |
| ПИД-регулятор | 0.6*Kуст | 0.5*∆t/Kp | 0.125*∆t/Kp |
Хочется сказать, что данный метод не несет за собой никаких улучшений, просто он построен на другом способе поиска, недостатки те же, что и у метода Зиглера-Никольса первого.
Метод CHR (Chien, Hrones и Reswick) или Чина-Хронеса-Ресвика, если по-русски
Этот метод предполагает предварительное определение времени задержки L и времени выравнивания T по переходной характеристике объекта. Ну это мы делали и для Зиглера-Никольса, но в отличие от Зиглера и Никольса, которые использовали в качестве критерия качества настройки декремент затухания, равный 4, Chien, Hrones и Reswick (CHR) использовали критерий максимальной скорости нарастания при отсутствии перерегулирования или при наличии не более чем 20 процентного перерегулирования. Такой критерий позволяет получить больший запас устойчивости, чем в методе Зиглера-Никольса. Метод CHR даёт две разные системы параметров регулятора. Одна из них получена при наблюдении отклика на изменение уставки (таблица), вторая – при наблюдении отклика на внешние возмущения (не представлена). Какую систему параметров выбирать, зависит от того, что важнее для конкретного регулятора: качество регулирования при изменении уставки или ослабление внешних воздействий (в жизни изменение уставки вызывает намного более существенные процессы в регулятора, потому лучше настраивать по этой таблице, будет настройка не “в малом”, а “в большом”). Если же важно и то и другое, то необходимо использовать регуляторы с двумя степенями свободы. Метод CHR использует аппроксимацию объекта моделью первого порядка с задержкой. В CHR используются те же исходные параметры a и L, что и в методе Зиглера-Никольса. Обратим внимание, что пропорциональный коэффициент в методе CHR меньше, чем в методе Зиглера-Никольса.
Формулы для определения коэффициентов приведены в таблице:
| Без перерегулирования | С 20% перерегулированием | |||||
| Пропорциональный коэффициент Kp |
Интегральный коэффициент Ti |
Дифференциальный коэффициент Td |
Пропорциональный коэффициент Kp |
Интегральный коэффициент Ti |
Дифференциальный коэффициент Td |
|
| П-регулятор | 0.3/a | 0.7/a | ||||
| ПИ-регулятор | 0.35/a | 1.2*L/Kp | 0.6/a | L/Kp | ||
| ПИД-регулятор | 0.6/a | L/Kp | 0.5*L/Kp | 0.95/a | 1.4*L/Kp | 0.47*L/Kp |
Остальные методы, а именно Спектральный метод, метод Куна, метод Стогестада, метод Шеделя требуют уже больших знаний ТАУ и самое главное требуют либо реальной переходной характеристики, которую придется искать методом интерполяции и аппроксимации, либо вовсе моделирования объекта управления. Если вкратце, то суть методов можно описать парой предложений.
Спектральный метод
Спектральный метод предполагает компенсацию нулями регулятора нежелательных полюсов объекта.
На основе полюсов объекта {p1, p2} определяются компенсирующие значения постоянных времени интегрального и дифференцирующего каналов:
Tи = |1/p1|, Tд = |1/p2|.
и коэффициенты регулятора Kp и Kd в виде:
Kp = Ki(Tи + Tд), Kd = Ki*Tи*Tд/(Tи + Tд).
Метод Куна
Параметром, характеризующим быстродействие любых рассматриваемых объектов, является суммарная постоянная времени. Метод настройки Куна (или метод «Т-правило») основан на аппроксимации объекта звеном третьего порядка. Параметры ПИД-регулятора Ti и Td выбирают, таким образом, чтобы компенсировать два полюса. Расчетные значения для регулятора даны в таблице, но я здесь ее приводить не стану.
Метод Стогестада
По идентифицированным параметрам модели ОУ находят необходимые параметры настройки регулятора. Принцип синтеза ПИД-регулятора с использованием метода Стогестада заключается в следующем: задание желаемого вида переходной характеристики замкнутой САУ (желаемый вид описывается инерционным звеном первого порядка) путем выбора постоянной времени.
Для апериодического звена второго порядка с транспортным запаздыванием параметры ПИД-регулятора могут быть найдены по следующим формулам:
kp = T1/k*(Tc+τ), Ti=min[T1;c(Tc+τ)],Td=T2.
где T1, T2, k и τ–параметры объекта; с–параметр, который рекомендуют принимать равным 4, для обеспечения апериодического вида переходного процесса на выходе системы управления (например пароперегревателем котла).
Метод Шеделя
Метод Шеделя основан на принципе каскадного коэффициента демпфирования. В методе обобщается понятие коэффициента демпфирования на случай системы 3-го порядка. Параметры ПИД-регулятора должны быть выбраны таким образом, чтобы коэффициенты демпфирования системы принимали определенные значения. Их если будет интересно лучше поискать в справочниках.
