Загрузить PDF
Загрузить PDF
Магические квадраты обрели популярность наряду с появлением математических игр, таких как судоку. Магический квадрат — это таблица, заполненная целыми числами таким образом, чтобы сумма чисел по горизонтали, вертикали и диагонали была одинакова (так называемая магическая константа). Эта статья расскажет вам, как построить квадрат нечетного порядка, квадрат порядка одинарной четности и квадрат порядка двойной четности.
-
1
Вычислите магическую константу.[1]
Это можно сделать при помощи простой математической формулы [n * (n2 + 1)] / 2, где n – количество строк или столбцов в квадрате. Например, в квадрате 3×3 n=3, а его магическая константа:- Магическая константа = [3 * (32 + 1)] / 2
- Магическая константа = [3 * (9 + 1)] / 2
- Магическая константа = (3 * 10) / 2
- Магическая константа = 30/2
- Магическая константа квадрата 3х3 равна 15.
- Сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
-
2
Напишите 1 в центральной ячейке верхней строки. Строить любой нечетный квадрат нужно именно с этой ячейки. Например, в квадрате 3х3 напишите 1 во второй ячейке верхней строки, а в квадрате 15х15 напишите 1 в восьмой ячейке верхней строки.
-
3
Следующие числа (2,3,4 и так далее по возрастанию) записывайте в ячейки по правилу: одна строка – вверх, один столбец – вправо. Но, например, чтобы записать 2, нужно “выйти” за пределы квадрата, поэтому существуют три исключения из данного правила:
- Если вы вылезли за верхний предел квадрата, напишите цифру в самой нижней ячейке соответствующего столбца.
- Если вы вылезли за правый предел квадрата, напишите цифру в самой дальней (левой) ячейке соответствующей строки.
- Если вы попали на ячейку, которая занята другой цифрой, напишите цифру непосредственно под предыдущей записанной цифрой.
Реклама
-
1
Существуют различные методики для построения квадратов порядка одинарной четности и двойной четности.
- Число строк или столбцов в квадрате порядка одинарной четности делится на 2, но не на 4.[2]
- Наименьшим квадратом порядка одинарной четности является квадрат 6х6 (квадрат 2×2 построить нельзя).
- Число строк или столбцов в квадрате порядка одинарной четности делится на 2, но не на 4.[2]
-
2
Вычислите магическую константу. Это можно сделать при помощи простой математической формулы [n * (n2 + 1)] / 2, где n – количество строк или столбцов в квадрате. Например, в квадрате 6×6 n=6, а его магическая константа:
- Магическая константа = [6 * (62 + 1)] / 2
- Магическая константа = [6 * (36 + 1)] / 2
- Магическая константа = (6 * 37) / 2
- Магическая константа = 222/2
- Магическая константа квадрата 6х6 равна 111.
- Сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
-
3
Разделите магический квадрат на четыре квадранта одинакового размера. Обозначьте квадранты через А (сверху слева), C (сверху справа), D (снизу слева) и B (снизу справа). Чтобы выяснить размер каждого квадранта, разделите n на 2.
- Таким образом, в квадрате 6х6 размер каждого квадранта равен 3×3.
-
4
В квадранте А напишите четвертую часть всех чисел; в квадранте В напишите следующую четвертую часть всех чисел; в квадранте С напишите следующую четвертую часть всех чисел; в квадранте D напишите заключительную четвертую часть всех чисел.
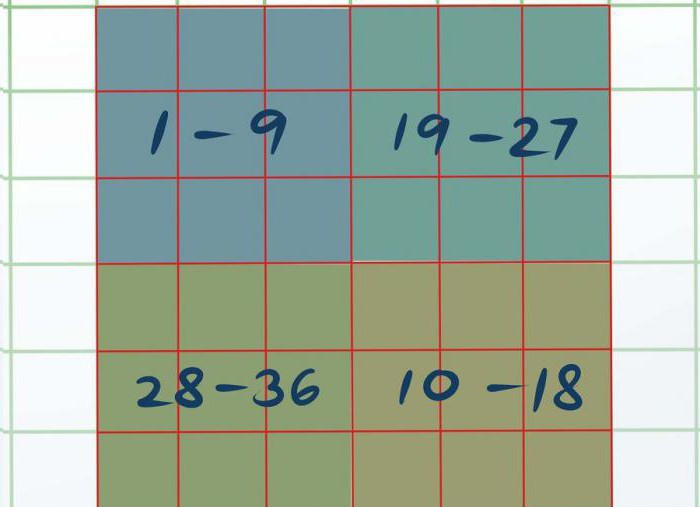
- В нашем примере квадрата 6х6 в квадранте А напишите числа 1-9; в квадранте В – числа 10-18; в квадранте С – числа 19-27; в квадранте D – числа 28-36.
-
5
Числа в каждом квадранте записывайте так, как вы строили нечетный квадрат. В нашем примере квадрант А начните заполнять числами с 1, а квадранты С, B, D – с 10, 19, 28, соответственно.
- Число, с которого вы начинаете заполнение каждого квадранта, всегда пишите в центральной ячейке верхней строки определенного квадранта.
- Заполняйте каждый квадрант числами так, как будто это отдельный магический квадрат. Если при заполнении квадранта доступна пустая ячейка из другого квадранта, игнорируйте этот факт и пользуйтесь исключениями из правила заполнения нечетных квадратов.
-
6
Выделите определенные числа в квадрантах А и D.[3]
На данном этапе сумма чисел в столбцах, строках и по диагонали не будет равна магической константе. Поэтому вы должны поменять местами числа в определенных ячейках верхнего левого и нижнего левого квадрантов.- Начиная с первой ячейки верхней строки квадранта А, выделите количество ячеек, равное медиане количества ячеек во всей строке. Таким образом, в квадрате 6×6 выделите только первую ячейку верхней строки квадранта А (в этой ячейке написано число 8); в квадрате 10х10 вам нужно выделить первые две ячейки верхней строки квадранта А (в этих ячейках написаны числа 17 и 24).
- Образуйте промежуточный квадрат из выделенных ячеек. Так как в квадрате 6х6 вы выделили только одну ячейку, то промежуточный квадрат будет состоять из одной ячейки. Назовем этот промежуточный квадрат как A-1.
- В квадрате 10х10 вы выделили две ячейки верхней строки, поэтому необходимо выделить две первые ячейки второй строки, чтобы образовать промежуточный квадрат 2х2, состоящий из четырех ячеек.
- В следующей строке пропустите число в первой ячейке, а затем выделите столько чисел, сколько вы выделили в промежуточном квадрате A-1. Полученный промежуточный квадрат назовем A-2.
- Получение промежуточного квадрата А-3 аналогично получению промежуточного квадрата A-1.
- Промежуточные квадраты А-1, А-2, А-3 образуют выделенную область А.
- Повторите описанный процесс в квадранте D: создайте промежуточные квадраты, которые образуют выделенную область D.
-
7
Поменяйте местами числа из выделенных областей А и D (числа из первой строки квадранта А с числами из первой строки квадранта D и так далее). Теперь сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
Реклама
-
1
Число строк или столбцов в квадрате порядка двойной четности делится на 4.[4]
- Наименьшим квадратом порядка двойной четности является квадрат 4х4.
-
2
Вычислите магическую константу. Это можно сделать при помощи простой математической формулы [n * (n2 + 1)] / 2, где n – количество строк или столбцов в квадрате. Например, в квадрате 4×4 n=4, а его магическая константа:
- Магическая константа = [4 * (42 + 1)] / 2
- Магическая константа = [4 * (16 + 1)] / 2
- Магическая константа = (4 * 17) / 2
- Магическая константа = 68/2
- Магическая константа квадрата 4х4 равна 34.
- Сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
-
3
Создайте промежуточные квадраты А-D. В каждом углу магического квадрата выделите промежуточный квадрат размером n/4, где n – количество строк или столбцов в магическом квадрате.[5]
Обозначьте промежуточные квадраты как A, B, C, D (в направлении против часовой стрелки).- В квадрате 4×4 промежуточные квадраты будут состоять из угловых ячеек (по одной в каждом промежуточном квадрате).
- В квадрате 8х8 промежуточные квадраты будут иметь размер 2×2.
- В квадрате 12х12 промежуточные квадраты будут иметь размер 3×3 (и так далее).
-
4
Создайте центральный промежуточный квадрат. В центре магического квадрата выделите промежуточный квадрат размером n/2, где n – количество строк или столбцов в магическом квадрате. Центральный промежуточный квадрат не должен пересекаться с угловыми промежуточными квадратами, но должен касаться их углов.
- В квадрате 4×4 центральный промежуточный квадрат имеет размер 2×2.
- В квадрате 8×8 центральный промежуточный квадрат имеет размер 4×4 (и так далее).
-
5
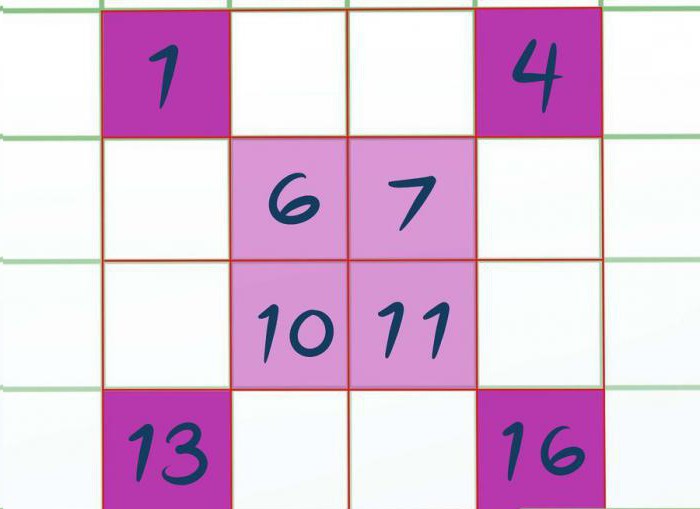
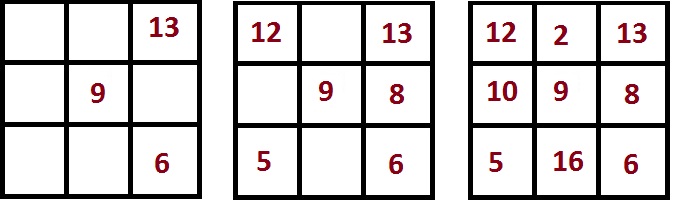
Начните строить магический квадрат (слева направо), но числа записывайте только в ячейки, расположенные в выделенных промежуточных квадратах. Например, квадрат 4×4 вы заполните так:
- Напишите 1 в первой строке первом столбце; напишите 4 в первой строке четвертом столбце.
- Напишите 6 и 7 в центре второй строки.
- Напишите 10 и 11 в центре третьей строки.
- Напишите 13 в четвертой строке первого столбца; напишите 16 в четвертой строке четвертого столбца.
-
6
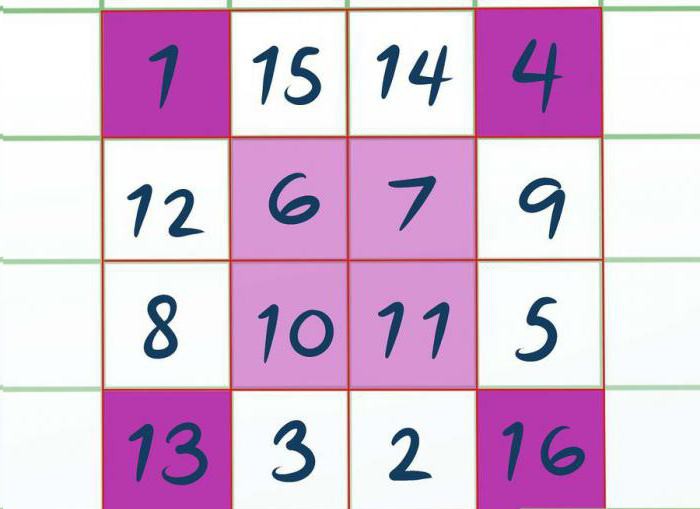
Оставшиеся ячейки квадрата заполняются аналогичным образом (слева направо), но числа нужно записывать в порядке убывания и только в ячейки, расположенные вне выделенных промежуточных квадратов. Например, квадрат 4×4 вы заполните так:
- Напишите 15 и 14 в центре первой строки.
- Напишите 12 во второй строке первого столбца; напишите 9 во второй строке четвертого столбца.
- Напишите 8 в третьей строке первого столбца; напишите 5 в третьей строке четвертого столбца.
- Напишите 3 и 2 в центре четвертой строки.
- Теперь сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
Реклама
Советы
- Воспользуйтесь описанными методами и найдите свой способ решения магических квадратов.
Реклама
Что вам понадобится
- Карандаш
- Бумага
- Ластик
Похожие статьи
Об этой статье
Эту страницу просматривали 352 161 раз.
Была ли эта статья полезной?
Математических загадок существует невообразимое количество. Каждые из них уникальны по-своему, но их прелесть заключается в том, что для решения неизбежно нужно приходить к формулам. Конечно же, можно попытаться решить их, как говорится, методом тыка, но это будет очень долго и практически безуспешно.
В данной статье будет говориться об одной из таких загадок, а чтобы быть точнее — о магическом квадрате. Мы детально разберем, как решить магический квадрат. 3 класс общеобразовательной программы, конечно, это проходит, но возможно не каждый понял или вовсе не помнит.
Что это за загадка?
Магический квадрат, или, как его еще называют, волшебный, — это таблица, в которой число столбцов и строк одинаково, и все они заполнены разными цифрами. Главная задача, чтобы эти цифры в сумме по вертикали, горизонтали и диагонали давали одинаковое значение.
Помимо магического квадрата, есть еще и полумагический. Он подразумевает то, что сумма чисел одинакова лишь по вертикали и горизонтали. Магический квадрат «нормальный» только в том случае, если для заполнения использовались натуральные числа от единицы.
Еще есть такое понятие, как симметричный магический квадрат — это когда значение суммы двух цифр равно, в то время, когда они располагаются симметрично по отношению к центру.
Важно также знать, что квадраты могут быть любой величины помимо 2 на 2. Квадрат 1 на 1 также считается магическим, так как все условия выполняются, хотя и состоит он из одного-единственного числа.
Итак, с определением мы ознакомились, теперь поговорим про то, как решить магический квадрат. 3 класс школьной программы вряд ли все так детально разъяснит, как эта статья.
Какие есть решения
Те люди, которые знают, как решить магический квадрат (3 класс точно знает), сразу же скажут, что решения только три, и каждое из них подходит для разных квадратов, но все же нельзя обойти стороной и четвертое решение, а именно «наугад». Ведь в какой-то мере есть вероятность того, что незнающий человек все же сможет решить данную задачку. Но данный способ мы отбросим в длинный ящик и перейдем непосредственно к формулам и методикам.
Первый способ. Когда квадрат нечетный
Данный способ подходит только для решения такого квадрата, у которого количество ячеек нечетное, например, 3 на 3 или 5 на 5.
Итак, в любом случае изначально необходимо найти магическую константу. Это число, которое получится при сумме цифр по диагонали, вертикали и горизонтали. Вычисляется она с помощью формулы:
В данном примере мы рассмотрим квадрат три на три, поэтому формула будет выглядеть так (n — число столбцов):
Итак, перед нами квадрат. Первое, что надо сделать — это вписать цифру один в центре первой строки сверху. Все последующие цифры необходимо располагать на одну клетку правей по диагонали.
Но тут сразу встает вопрос, как решить магический квадрат? 3 класс вряд ли использовал данный метод, да и у большинства появится проблема, как это сделать таким способом, если данной клетки нет? Чтобы сделать все правильно, необходимо включить воображение и дорисовать аналогичный магический квадрат сверху и получится так, что число 2 будет находиться в нем в нижней правой клетке. Значит, и в наш квадрат мы вписываем двойку в то же место. Это означает, что нам необходимо вписать цифры так, чтобы в сумме они давали значение 15.
Последующие цифры вписываются точно так же. То есть 3 будет находиться в центре первого столбца. А вот 4 по такому принципу вписать не удастся, так как на ее месте уже стоит единица. В таком случае цифру 4 располагаем под 3, и продолжаем. Пятерка — в центре квадрата, 6 — в правом верхнем углу, 7 — под 6, 8 — в верхний левый и 9 — по центру нижней строки.
Вы теперь знаете, как решить магический квадрат. 3 класс Демидова проходил, но у этого автора были чуть попроще задания, однако, зная данный способ, удастся разгадать любую подобную задачу. Но это, если число столбцов нечетное. А что же делать, если у нас, например, квадрат 4 на 4? Об этом дальше по тексту.
Второй способ. Для квадрата двойной четности
Квадратом двойной четности называют тот, у которого количество столбцов можно разделить и на 2, и на 4. Сейчас мы рассмотри квадрат 4 на 4.
Итак, как решить магический квадрат (3 класс, Демидова, Козлова, Тонких – задание в учебнике математики), когда количество его столбцов равно 4? А очень просто. Проще, чем в примере до этого.
В первую очередь находим магическую константу по той же формуле, что приводилась в прошлый раз. В данном примере число равно 34. Теперь надо выстроить цифры так, чтобы сумма по вертикали, горизонтали и диагонали была одинаковой.
В первую очередь надо закрасить некоторые ячейки, сделать это вы можете карандашом или же в воображении. Закрашиваем все углы, то есть верхнюю левую клеточку и верхнюю правую, нижнюю левую и нижнюю правую. Если квадрат был бы 8 на 8, то закрашивать надо не одну клеточку в углу, а четыре, размером 2 на 2.
Теперь необходимо закрасить центр этого квадрата, так, чтобы его углы касались углов уже закрашенных клеточек. В данном примере у нас получится квадрат по центру 2 на 2.
Приступаем к заполнению. Заполнять будем слева направо, в том порядке, в котором расположены ячейки, только вписывать значение будем в закрашенные клетки. Получается, что в верхний левый угол вписываем 1, в правый — 4. Потом центральный заполняем 6, 7 и дальше 10, 11. Нижний левый 13 и правый — 16. Думаем, порядок заполнения понятен.
Остальные ячейки заполняем точно так же, только в порядке убывания. То есть так как последняя вписанная цифра была 16, то вверху квадрата пишем 15. Далее 14. Потом 12, 9 и так далее, как показано на картинке.
Теперь вы знаете второй способ, как решить магический квадрат. 3 класс согласится, что квадрат двойной четности намного легче решается, чем другие. Ну а мы переходим к последнему способу.
Третий способ. Для квадрата одинарной четности
Квадратом одинарной четности называется, тот квадрат, число столбцов которого можно разделить на два, но нельзя на четыре. В данном случае это квадрат 6 на 6.
Итак, вычисляем магическую константу. Она равна 111.
Теперь нужно наш квадрат визуально поделить на четыре разных квадрата 3 на 3. Получится четыре маленьких квадрата размером 3 на 3 в одном большом 6 на 6. Верхний левый назовем А, нижний правый — В, верхний правый — С и нижний левый — D.
Теперь необходимо каждый маленький квадрат решить, используя самый первый способ, что приведен в этой статье. Получится так, что в квадрате А будут числа от 1 до 9, в В — от 10 до 18, в С — от 19 до 27 и D — от 28 до 36.
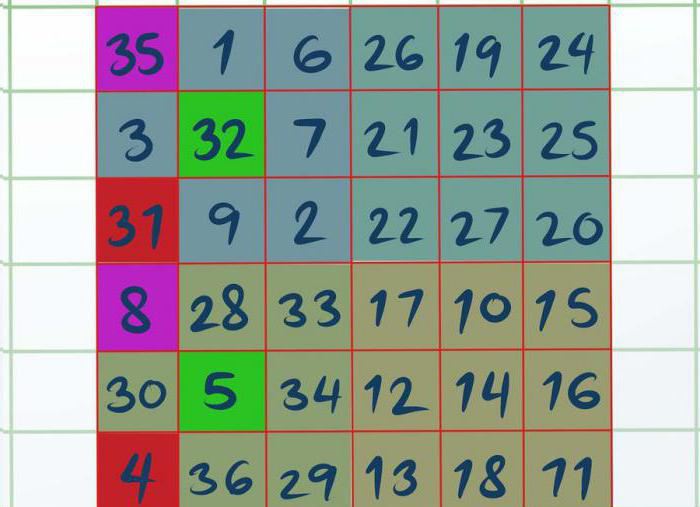
Как только вы решили все четыре квадрата, работа начнется над А и D. Необходимо в квадрате А визуально или при помощи карандаша выделить три ячейки, а именно: верхнюю левую, центральную и нижнюю левую. Получится так, что выделенные цифры — это 8, 5 и 4. Точно так же надо выделить и квадрат D (35, 33, 31). Все, что остается сделать, это поменять местами выделенные цифры из квадрата D в А.
Теперь вы знаете последний способ, как можно решить магический квадрат. 3 класс квадрат одинарной четности не любит больше всего. И это неудивительно, из всех представленных он самый сложный.
Вывод
Прочтя данную статью, вы узнали, как решить магический квадрат. 3 класс (Моро – автор учебника) предлагает подобные задачи только с несколькими заполненными ячейками. Рассматривать его примеры нет смысла, так как зная все три способа, вы с легкостью решите и все предлагаемые задачи.
Магическая константа M – сумма чисел в каждой строке, столбце и на диагоналях.
Для квадрата любой размерности n∙n минимальная магическая константа вычисляется по следующей формуле:
M = n(n2 + 1)/2
I. Магический квадрат 3×3
Для квадрата размера 3×3 минимально возможная магическая константа будет равна:
3(32 + 1)/2 = 3(9 + 1)/2 = 15
Подчеркнём, что 15 – это не единственно возможная магическая константа для квадрата 3×3, а константа, меньше которой других констант для этого квадрата быть не может.
Важное правило, которое вам пригодится при построении магического квадрата 3×3:
Число в центре квадрата 3×3 всегда в три раза меньше магической константы.
То есть, если у нас магическая константа M = 15, то в центре квадрата 3×3 будет стоять
15:3 = 5.
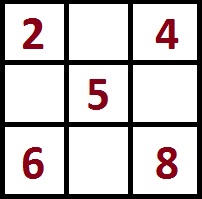
Для дальнейшего составления магического квадрата с магической константой M=15 расставьте по углам чётные числа 2,4,8,6.
Как видим, по сумма чисел на диагоналях квадрата равна 15, то есть магической константе.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Зная магическую константу и по два числа в ряду и столбце, мы можем вписать третье число в ряд и столбец. Определить это число очень просто – надо из магической константы вычесть два числа из ряда или столбца.
Применив этот метод, мы получим полностью заполненный магический квадрат:
Ещё одно важное правило построения магических квадратов:
Если у нас есть один магический квадрат, и мы все числа этого квадрата увеличим на одно и то же число или умножим на одно и то же число, то у нас опять получится квадрат. Это правило достаточно очевидно.
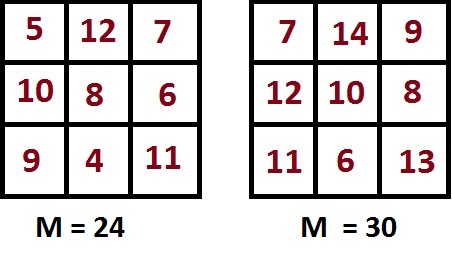
Пример 1. К числам в нашем магическом квадрате с M=15 прибавим 3 и 5
Как видим, у первого квадрата сумма чисел по вертикали, горизонтали и диагонали одинакова и составляет 24 (это и есть его магическая константа), а у второго квадрата магическая константа равна 30.
У этих двух квадратов число в центре по прежнему в три раза меньше, чем магическая константа (8 у первого квадрата и 10 у второго).
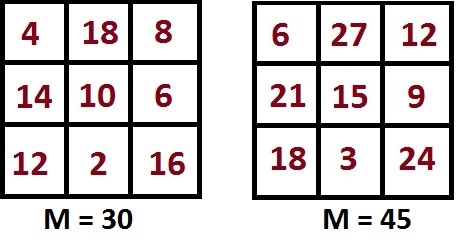
Пример 2. Числа нашего магического квадрата с M=15 умножим на 2 и на 3
Как видим, в первом случае, после умножения чисел на два, мы получили квадрат с магической константой 30 – та же самая константа, что и после того, как в первом примере мы увеличили все числа на 5. Но при этом, несмотря на то, что у этих двух магических квадратах одинаковые магические константы, числа при этом в клетках разные – а вот число в центральном квадрате одно и то же – это 10.
Так и должно быть, ведь, как было сказано выше, в магическом квадрате 3×3 число в центральной клетке должно быть в три раза меньше магической константы. Т.к. магическая константа у обеих магических квадратов одинаковая, то и центральное число одно и то же.
Задача 1.
Постройте магический квадрат с магической константой 39.
Зная магическую константу, мы легко найдём число, которое должно быть в центральной клетке – нужно магическую константу разделить на 3. 39:3 = 13.
Далее можно или подбирать числа (помня о том, что сумма чисел по диагонали, по горизонтали и по вертикали должна быть равна магической константе) или, для ускорения процесса, воспользоваться знанием чисел магического квадрата с минимальной магической константой M = 15.
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
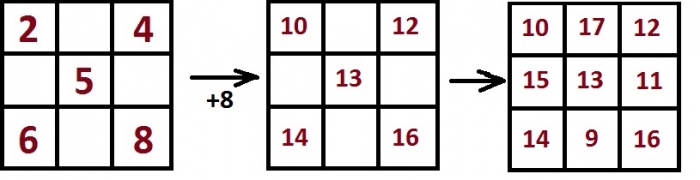
Напомним этот квадрат:
В центре этого квадрата – число 5. В центре того квадрата, который мы должны построить – число 13.
Разница между этими числами составляет 8. И, как следует из правила, которое мы написали выше, если все числа одного магического квадрата увеличить на одно и то же число, то получится другой магический квадрат.
Достаточно запомнить, что в центре минимального магического квадрата – 5, а по углам – чётные числа 2, 4, 6, 8. Таким образом, нам надо увеличить эти числа на 8. Далее будет легко заполнить оставшиеся клетки (числа в них вычисляются как магическая константа минус числа в ряду или столбце).
В итоге получится вот такой квадрат:
Задача 2.
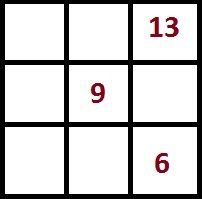
Достройте магический квадрат
В этом квадрате мы знаем число в центральной клетке (9), а, значит, мы знаем магическую константу, которая в 3 раза больше и равна 27. Ну а зная магическую константу и три первоначальных числа, вписать оставшиеся числа в клетки не составит труда.
Решение:
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
II. Магический квадрат 4×4
Мы не будем подробно останавливаться на магических квадратах 4×4 – они почти не встречаются на математических олимпиадах и вступительных экзаменах в физматшколы, но общее представление о них дадим.
Минимально возможная магическая константа вычисляется всё по той же формуле:
M = n(n2 + 1)/2
M = 4(42 + 1)/2 = 34.
У квадрата 4×4 обе стороны чётные, а это значит, что центральной клетки, в отличие от квадрата 3×3, у него нет, и нет соответствующей закономерности, с ним связанной.
Однако, у этого квадрата есть другие закономерности:
Помимо того, что у магического квадрата 4×4 равна сумма числе по диагонали, вертикали и горизонтали, у него сумма чисел в угловых квадратах 2×2 равна магической константе M, сумма чисел в центральном квадрате 2×2 также равна M, и сумма чисел в углах квадрата тоже равна M.
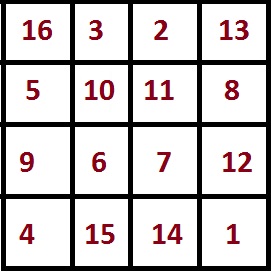
Сумма чисел в левом верхнем квадрате 2×2: 16+3+5+10 = 34. В трёх других угловых квадратах 2×2 сумма также равна магической константе, о чём и сказано выше.
Сумма чисел в центральном квадрате 2×2 также равна магической константе 34: 10+11+6+7 = 34.
Сумма чисел в углах магического квадрата тоже равна магической константе: 16+13+4+1 = 34
Download Article
What makes magic squares special and how to fill them in
Download Article
- What is a magic square?
- Solving a 3 x 3
- Solving a 4 x 4
- Singly Even Magic Square
- Video
- Q&A
|
|
|
|
|
If you’re a fan of math and logic puzzles like Sudoku or Kenken, then trying to solve a magic square is the perfect little challenge to try out. A magic square is a grid of numbers where each row, column, and diagonal add up to the same sum. How you solve your magic square depends on the size of the puzzle, but they each have easy instructions for filling them in. Keep reading and we’ll walk through our solving strategies step by step to finish any odd- or even-numbered magic square.
Things You Should Know
- A magic square is a square grid of numbers where each row, column, and diagonal add up to the same total.
- Find the “magic constant” sum of each row, column, and diagonal with
where n is the number of squares in each row.
- Use a solving technique based on the size of the magic square and how many boxes are in each row or column.
-
Magic squares have rows, columns, and diagonals that total the same sum. Each number in a magic square fits into a cell on a grid. The number of rows or columns determines the order, so an “order 3” magic square is one with a 3 x 3 grid. When you add up the numbers in a column, the value is called the “magic constant,” and all the other columns, rows, and diagonals will add up to that number.[1]
- A normal magic square has consecutive numbers from 1 to
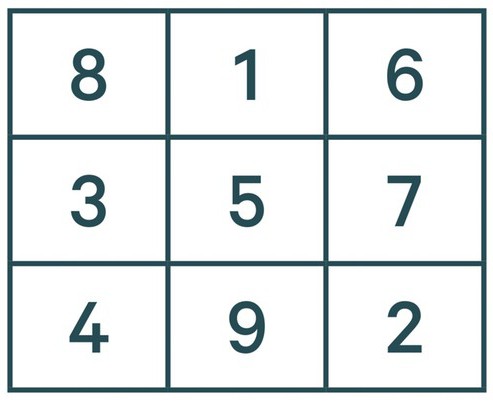
(where n equals the order). A normal order 3 magic square with a magic constant of 15 would be:
8 – 1 – 6
3 – 5 – 7
4 – 9 – 2 - On a non-normal magic square, the lowest number may be higher than 1. A non-normal order 4 magic square with a magic constant of 87 could be:
21 – 24 – 28 – 14
27 – 15 – 20 – 25
16 – 30 – 22 – 19
23 – 18 – 17 – 29
- A normal magic square has consecutive numbers from 1 to
Advertisement
-
1
Calculate the magic constant. To find the magic constant (S) for a normal magic square use the formula
where
equals the order, or number of rows, in the magic square. So for a 3×3 magic square, the formula would be:[2]
-
2
Place the number 1 in the center box on the top row. The placement is the same for any normal magic square with an odd number of columns or rows. Find the center square in the top row and write down the number 1 to get started.[3]
- Example: If you have a 3 x 3 magic square, put 1 in the second box in the top row.
- Example: For a 15 x 15 magic square, put the 1 in the eighth box of the row.
-
3
Follow an up-one, right-one pattern to fill in the remaining numbers. Start at the middle box in the top row where you placed the 1. Move up one row and to the right one column and write in the next number sequentially. Whenever a move takes you above the top row (like the first move will), go to the bottom row instead. If you need to move a square to the right but are already in the rightmost column, move to the leftmost column instead. Continue filling in the square following the pattern until it’s complete.[4]
- Example: In a normal 3 x 3 square, the 2 goes in the bottom right corner and the 3 goes in the left column in the center row.
- If the movement takes you to a box that is already occupied, go back to the last box that has been filled in, and place the next number directly below it. For example, when you place the 4 in a 3 x 3 magic square, it fits in the bottom left corner below the 3. Then, following the same up-one, right-one pattern, place the 5 in the center of the puzzle to continue.
Advertisement
-
1
Recognize a doubly even square if the sides are divisible by 4. Count the number of squares in a single row or column of your magic square. If the magic square is an order 4 square or the number is evenly divisible by 4 (8, 12, 16, etc.), then you’re working with a doubly even square.[5]
-
2
Calculate the magic constant. Use the formula
, where
equals the order, or the number of boxes per row in your magic square. So, for a 4 x 4 square, the magic constant calculation becomes:[6]
-
3
Create Highlights A–D in the corners of the magic square. Form a mini square in each corner that has a length of
on each side, where
is the magic square’s order. Start in the top left corner and label the mini squares A, B, C, and D going clockwise around the magic square.[7]
- In a 4 x 4 square, only mark the 4 corner boxes as your highlights.
- For an 8 x 8 magic square, the Highlights become 2 x 2 mini squares in the corners.
- In a 12 x 12 square, each Highlight is a 3 x 3 area.
-
4
Create the Central Highlight. Mark all the boxes in the center of the magic square in a square area of length
, where
is the magic square’s order. The Central highlight will touch a 1 corner each from Highlights A–D, but it shouldn’t overlap them at all.[8]
- In a 4 x 4 square, the Central Highlight would be a 2 x 2 area in the center.
- In an 8 x 8 square, the Central Highlight would be a 4 x 4 area in the center.
-
5
Fill in the highlighted areas of your magic square. Start in the top left corner of your magic square. Place 1 in the top left corner and count the boxes across the top row. If a box is highlighted, fill it in with the number. Work down the entire magic square until all the highlighted areas are filled in. In an order 4 magic square, the boxes and their numbers are:[9]
- 1 in the top-left box and 4 in the top-right box
- 6 and 7 in the second and third boxes in Row 2
- 10 and 11 in the second and third boxes of Row 3
- 13 in the bottom-left box and 16 in the bottom-right box
-
6
Fill in the rest of the magic square by counting backward. Begin again with the top left box, but skip over all the boxes that you already filled in. Count down from the highest number in the magic square as you work across the row, and add the number to any empty box. Once you finish, your magic square is complete. In a 4×4 magic square, the boxes you fill in are:[10]
- 15 and 14 in the second and third boxes in Row 1
- 12 in the leftmost box and 9 in the rightmost box in Row 2
- 8 in the leftmost box and 5 in the rightmost box in Row 3
- 3 and 2 in the second and third boxes in Row 4
Advertisement
-
1
Check if the square’s sides are divisible by 2, but not 4. Singly even magic squares have an even number of boxes in their rows and columns. If you divide the magic square’s order by 2 and get an odd number as the result, you’re working with a singly even square.[11]
- The smallest possible singly even magic square is 6 x 6 since 2 x 2 magic squares are impossible to make.
-
2
Calculate the magic constant. Use the formula
, where n equals the magic square’s order, or the number of boxes per side. For a 6 x 6 square, your formula would look like:[12]
-
3
Divide the magic square into four quadrants of equal size. Divide the magic square’s order by 2 to find out how many boxes each side of the quadrant should be. Draw lines to separate the quadrants and label them A (top left), C (top right), D (bottom left), and B (bottom right).[13]
- For a 6 x 6 square, each quadrant is 3 x 3 boxes.
-
4
Assign each quadrant a number range. Count the number of boxes in a single quadrant to know how many numbers are in each section. Assign Quadrant A the first quarter of numbers, Quadrant B the second quarter, Quadrant C the third quarter, and Quadrant D the final quarter. That way, you know which numbers are going into specific quadrants without accidentally reusing them.[14]
- In a 6 x 6 square, Quadrant A contains the numbers 1-9, Quadrant B has 10-18, Quadrant C has 19-27, and Quadrant D ends with 28-36.
-
5
Solve each quadrant using a one-up, one-right pattern. In each quadrant, put the lowest value in the center box in the top row. Move up one row and to the right one column to place your next number. If you go above the top row of the quadrant, then move to the bottom row instead. When you go past the rightmost column, add the number to the leftmost column. If there’s already a number in the next square, put the next number directly below the last one.[15]
-
6
Create Highlights A and D. In Quadrant A, mark all the squares in the top row to the left of the quadrant’s center square. In the second row, skip the first column and highlight the center square and remaining boxes to the left of it. Then, mark the squares in the bottom row that share a column with the boxes in the top row to finish the A highlights. Then, repeat the same process in Quadrant D for the D highlights.[16]
- In a 6 x 6 square, Highlight A-1 is the top right box, Highlight A-2 is the center box in the middle row, and Highlight A-3 is the bottom right corner of Quadrant A. The D highlights are in the same position in Quadrant D.
- If you tried to add up your columns, rows, and diagonals right now, the square isn’t considered magic since they don’t add up to the same magic constant yet.
-
7
Swap the positions of Highlights A and D. Simply take the number from one square and swap it with the corresponding box between Quadrant A and Quadrant D. Once you’ve done this, all the rows, columns, and diagonals in a 6 x 6 magic square will add up to the magic constant you calculated.[17]
- Example: In a 6 x 6 magic square, 8 swaps positions with 35, 5 swaps with 32, and 4 swaps with 31.
-
8
Swap the right columns in B and C for magic squares larger than 6 x 6. Count the highlighted columns in the top row of Quadrant A and subtract 1. Count that number of columns in from the right side of Quadrants B and C and highlight all the squares. Move the values in Quadrant C into the corresponding squares in Quadrant B, and vice-versa to complete your magic square.[18]
- For a 10 x 10 magic square, only swap the rightmost column in quadrants B and C.
- For a 14 x 14 magic square, swap the 2 rightmost columns instead.
Advertisement
Add New Question
-
Question
How do you solve a 7×7 magic square?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
Place the first number of the magic square in the center box of the top row. Then, use an up-one, right-one pattern to add the numbers.
-
Question
How do I solve a magic square with no known sum?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
Magic squares with numbers that start at 1 and are in consecutive order always have the same sum. A 3 x 3 magic square always has the sum of 15 and a 4 x 4 has a sum of 34.
-
Question
How do you make a 4 x 4 magic square using only 0-9 digits?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
Typically, you can’t repeat digits in a magic square so making a 4 x 4 with the digits 0-9 isn’t possible unless you repeat them.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
References
About This Article
Article SummaryX
To solve an odd-numbered magic square, start by using the formula n[(n^2+1)/2] to calculate the magic constant, or the number that all rows, columns, and diagonals must add up to. For example, in a 3 by 3 square where n=3, the magic constant is 15. Next, start your square by placing the number 1 in the center box of the top row. Then, arrange the rest of the numbers sequentially by moving up 1 row, then 1 column to the right. To learn more, including how to solve singly even magic squares and doubly even magic squares, read on.
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,004,692 times.
Did this article help you?
Проект выполнила ученица
7в класса Копчук Роксолана
Аннотация
Цель данной
работы – выяснить различные варианты
составления магических квадратов, изучив которые можно заполнить квадрат любого размера, а так же рассмотреть
возможные области их применения.
В ходе работы
были использованы следующие методы:
- поисковый метод (использование
справочной и учебной литературы, а также информационных ресурсов глобальной сети Интернет); - практический метод (составление
магических квадратов на основе полученных знаний); - исследовательский метод (составление
психологического портрета личности по квадрату Пифагора).
В работе
исследуется происхождение и формулируется определение магических квадратов,
рассмотрены различные виды квадратов, способы их составления, а так же показана
область применения этих загадочных фигур.
В ходе работы над
проектом, я не только расширила свои знания по данной теме и повысила свои
вычислительные навыки, но и научилась составлять
магический квадрат Пифагора, с помощью которого
можно
познать характер человека, состояние его здоровья, потенциальные возможности,
раскрыть достоинства и недостатки.
Во время
летних каникул мне часто приходилось решать кроссворды. В одном журнале меня
заинтересовала задача на логическое мышление – заполнение магического квадрата.
Необходимо было заполнить квадрат числами
от 1 до 9 так, чтобы сумма чисел по
столбцам, по строкам и по диагоналям была одинакова.
Как это
сделать, я не знала, поэтому решила обратиться за помощью к папе. Мы перебирали
различные варианты, и, наконец, задача решена. И вот мой квадрат заполнен. Но метод перебора мне не понравился: он
отнимает много времени, хотя и позволяет тренировать свои вычислительные
навыки. Я предположила, что существует
специальный прием, который помогает быстро заполнить магический квадрат. Это и
побудило меня заняться данным проектом.
История
появления магических квадратов.
Магический квадрат – квадратная
таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого
столбца и любой из двух главных диагоналей равны одному и тому же числу.
Страна, в которой
был впервые придуман магический квадрат, точно неизвестна, неизвестен век, даже
тысячелетие нельзя установить точно. Первые упоминания о магических квадратах
были у древних китайцев. И, вероятно, самым старым из дошедших до нас
магических квадратов является таблица Ло Шу. Она имеет размер 3*3 и заполнена
натуральными числами от 1 до 9. В этом магическом квадрате сумма чисел в каждой
строке, столбце и диагонали равна 15. Согласно одной из легенд прообразом Ло Шу
стал узор из связанных черных и белых точек, украшавший панцирь огромной
священной черепахи, всплывшей из вод реки Хуанхэ.


Из Китая магические квадраты распространились сначала в
Индию, а затем и в другие страны. В начале XVI века
знаменитый немецкий художник Альбрехт Дюрер увековечил магический
квадрат в искусстве, изобразив его на гравюре «Меланхолия». Дата создания
гравюры (1514 год) указана числами, стоящими в двух центральных клетках нижней
строки.
В IX веке. интерес к магическим квадратам
вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры. Получение
магических квадратов считалось популярным развлечением среди математиков. Ими
создавались огромные квадраты, например, 45*45, содержащий числа от 1 до 2025, Были придуманы способы построения
магических квадратов любого размера, однако до сих пор не найдена формула, по
которой можно было бы найти количество магических квадратов данного размера.
В наше время магические квадраты продолжают привлекать к
себе внимание не только специалистов, но и любителей математических игр и
развлечений. За последнее столетие
значительно возросло число книг по занимательной математике, в которых
содержатся головоломки и задачки, связанные с необычными квадратами.
Виды
магических квадратов и способы их заполнения.
В ходе своей работы, я пришла к выводу,
что магических квадратов 2*2 не существует. Квадрат размером 2*2 должен был бы
состоять из чисел 1,2,3,4, а его постоянная была бы равна 5. У такого квадрата
по две строки, столбца и диагонали. Чтобы квадрат стал магическим, надо
представить число 5 в виде суммы двух данных чисел шестью различными способами,
но это сделать не возможно! Ведь таких комбинаций всего две: 1+ 4 и 2+3. Как ни
расставляй числа в клетках таблицы, их сумма будет равна 5 либо в каждой
строке, либо в обоих столбцах, либо по диагоналям, но никак не одновременно.
Существует
единственный магический квадрат 3*3, так как остальные магические
квадраты 3*3 получаются из него либо перестановкой строк или
столбцов либо путем поворота исходного квадрата на 900 или на 1800
Общий метод построения квадратов неизвестен.
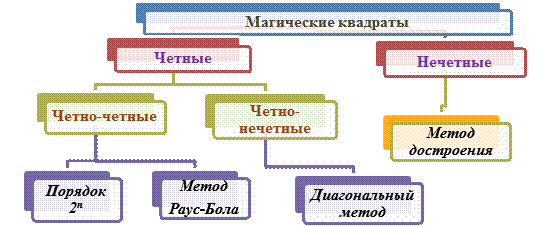
Правила построения магических квадратов делятся на три
категории в зависимости от того, каков порядок квадрата.
Квадраты могут быть:
– нечетными, то есть состоять из нечетного
числа клеток,
– четно-четные, то есть порядок равен
удвоенному четному;
– четно-нечетные, то есть порядок равен
удвоенному нечетному.
Магические квадраты нечетного порядка.
|
1. Метод достроения. Рассмотрю на примере квадрата |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1) Построю квадрат |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2) В полученной фигуре |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3). Каждое |
1 – вниз 2 – вниз 6 – вниз 21 – 22 – 16 – |
5 – влево 4 – влево 10-влево 25 – вверх 24 – вверх 20 – вверх |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4) Таким |
|
Магические квадраты четно-четного порядка.
|
1. Порядок 2n . Этот |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2) Отмеченные Сумма чисел по |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1) Квадрат заполняется слева направо и сверху вниз числами от 1 до n2 в их естественном порядке. Разделить заполненный числами от 1 до 64 квадрат на четыре равных квадрата порядка 4. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2) В каждой строке и столбце верхнего левого |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3) Для |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4) Содержимое каждой из |
|
Магические квадраты четно-нечетного
порядка.
|
Диагональный метод. Для примера возьму квадрат 10*10. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1) Разделить |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2) В левом верхнем квадрате закрашу разным цветом три группы |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3) Клетки, симметричные |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4) Число, стоящее в каждой из отмеченных в пункте 2 клеток, |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
6) Содержимое каждой клетки третьей группы обменяю |
|
Применение магических квадратов.
Когда я рассмотрела способы составления магических квадратов, меня
заинтересовала область их применения. Она показалась
мне довольно таки интересной. Сегодня очень актуальным становится вопрос о
защите информации. Например, на уроке информатики мы изучали тему кодирование.
С помощью магических квадратов так же можно закодировать информацию. Например,
зашифровать текст. Расположив буквы согласно числам магического квадрата,
получаем фразу «БУДУ В СЕМЬ» или «КЛЮЧИ ПОД КОВРИКОМ».
Так же очень популярна японская головоломка
судоку, прародителем которой можно считать Магический квадрат. Она помогает нам
развивать логическое мышление и вычислительные навыки. В настоящее время много газет печатают эти головоломки вместе с
кроссвордами и другими логическими задачами. Не меньшую популярность завоевали
судоку и в сети Интернет.
Англичане используют площадку для игры в
шаффлборд, размеченную в виде магического квадрата.
Ну, и, конечно же, в нумерологии. Еще великий
ученый Пифагор, считал, что всем на свете управляют числа. Поэтому сущность
человека заключается тоже в числе – дате его рождения. Он создал метод
построения квадрата, по которому можно познать характер человека, состояние его
здоровья и его потенциальные возможности, раскрыть достоинства и недостатки и
тем самым выявить, что следует предпринять для его совершенствования. Во
времена Пифагора магические квадраты на каждого человека создавались
индивидуально. Сейчас есть специальная программа, где вводится дата рождения
человека, а на экран выводится готовый магический квадрат. Составлю
магический квадрат для себя.
Я родилась 28
июля 1998 года.
1) Складываем числа дня месяца и года рождения, получаем
первое рабочее число 44.
2) Далее складываем цифры первого рабочего числа и
получаем второе рабочее число 8.
3) Из первого
рабочего числа вычитаем удвоенную первую цифру дня рождения, так получается
третье рабочее число: 44-(2+2)=40
4) четвертое
рабочее число получаем из суммы цифр третьего рабочего числа: 4+0=4
Теперь выпишу два ряда цифр. Первый
состоит из цифр даты рождения: 28.07.1998. Второй – рабочих чисел: 44.8.40.4. Запишу
их в квадрат.
«1» – стремлюсь из любого положения
извлечь максимальную выгоду, «2» – я
человек чувствительный к изменениям в атмосфере, «4444»– у меня отличное здоровье, «7»– для того, чтобы достичь желаемого, я должна много трудиться, «888» – означает, что в жизни, я
добьюсь выдающихся результатов, «99»– умна от рождения, знания даются легко.
Чтобы быть
более уверенной я использую данный квадрат в качестве талисмана.
Безусловно, не
следует слепо верить всему магическому. Возможно, некоторые черты характера и
заложены в дате рождения человека, но человек всегда может найти способы что-то
изменить в своей судьбе.
















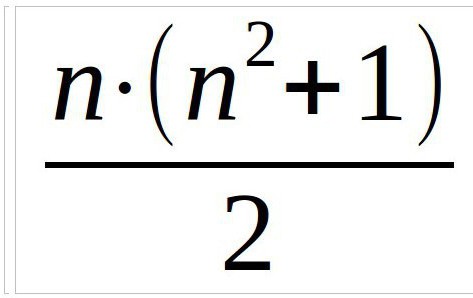
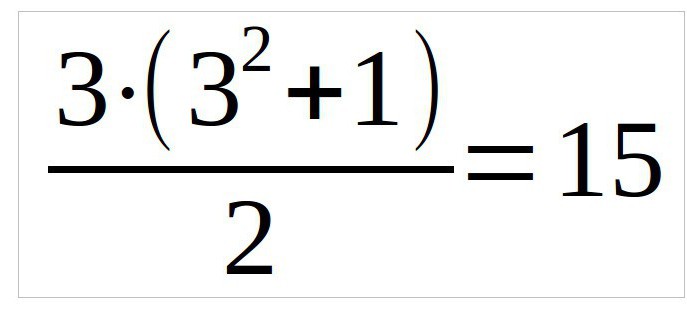



![{displaystyle S=n[(n^{2}+1)/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6645cd02ee35be03b0fc03e0e9c3dd8b3295d96)








![{displaystyle S=[n(n^{2}+1)]/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d5a367b0a5dbe975df34131a0b5bd57332d05d5)