Как найти основание числа в информатике

Система счисления – это способ записи чисел. Обычно, числа записываются с помощью специальных знаков – цифр (хотя и не всегда). Если вы никогда не изучали данный вопрос, то, по крайней мере, вам должны быть известны две системы счисления – это арабская и римская. В первой используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и это позиционная система счисления. А во второй – I, V, X, L, C, D, M и это непозиционная система счисления.

Подробная инструкция, как быстро научиться считать в двоичной и шестнадцатеричной системах приведена на сайте https://itvdn.com/ru/blog/article/binary-hexadecimal-system.

В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, а в непозиционных – нет. Например:

11 – здесь первая единица обозначает десять, а вторая – 1.
II – здесь обе единицы обозначают единицу.

345, 259, 521 – здесь цифра 5 в первом случае обозначает 5, во втором – 50, а в третьем – 500.

XXV, XVI, VII – здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.

Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, чем в непозиционных, т.к. математические операции осуществляются по несложным алгоритмам (например, умножение в столбик, сравнение двух чисел).

В мире наиболее распространены позиционные системы счисления. Помимо знакомой всем с детства десятичной (где используется десять цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная и шестнадцатеричная.

Следует отметить, важную роль нуля. «Открытие» этой цифры в истории человечества сыграло большую роль в формировании позиционных систем счисления.

Основание системы счисления – это количество знаков, которое используется для записи цифр.

Разряд – это позиция цифры в числе. Разрядность числа – количество цифр, из которых состоит число (например, 264 – трехразрядное число, 00010101 – восьмиразрядное число). Разряды нумеруются справа на лево (например, в числе 598 восьмерка занимает первый разряд, а пятерка – третий).

Итак, в позиционной системе счисления числа записываются таким образом, что каждый следующий (движение справа на лево) разряд больше другого на степень основания системы счисления. (придумать схему)

Одно и тоже число (значение) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.

Двоичная система счисления

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)

Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.

В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.

Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.

Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.
Перевод чисел из двоичной системы счисления в десятичную

Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:

1476 = 1000 + 400 + 70 + 6

Можно пойти еще дальше и разложить так:

1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100

Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 – это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.

Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

10001001 = 1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:

1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:

10001001₂ = 13710
Почему двоичная система счисления так распространена?

Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Перевод десятичного числа в двоичное

Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:

77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)

Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:

1001101 = 1*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 1*2 2 + 0*2 1 + 1*2 0 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

Восьмеричная система счисления

Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.

В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:

000 – 0
001 – 1
010 – 2
011 – 3
100 – 4
101 – 5
110 – 6
111 – 7

Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки и заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями. Например:

1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135

Т.е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 1011101₂ = 1358.

Обратный перевод. Допустим, требуется перевести число 1008 (не заблуждайтесь! 100 в восьмеричной системе – это не 100 в десятичной) в двоичную систему счисления.

100₈ = 1 0 0 = 001 000 000 = 001000000 = 10000002

Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:

6728 = 6 * 8 2 + 7 * 8 1 + 2 * 8 0 = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 44210
1008 = 1 * 8 2 + 0 * 8 1 + 0 * 8 0 = 6410

Шестнадцатеричная система счисления

Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел. При шестнадцатеричной записи числа получаются более компактными.

В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15).

При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления:

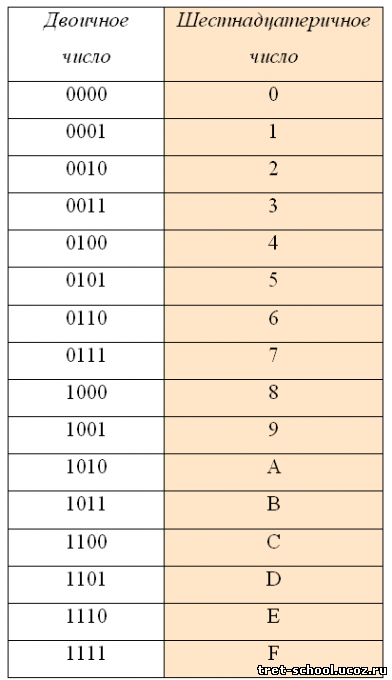
Например:
10001100101 = 0100 1100 0101 = 4 C 5 = 4C5

Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):

4C5 = 4 * 162 + 12 * 161 + 5 * 160 = 4 * 256 + 192 + 5 = 1221

Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи – это FF.

FF = 15 * 161 + 15 * 160 = 240 + 15 = 255

255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние

118924 в 10 системе счисления = 350214 в х системе счисления, как найти х? если можно то попродобнее

5 ответов 5

Это ж всё брутфорс, это ж несерьезно 🙂

На самом деле, конечно, перебор здесь вполне подходит, и можно дать ему границы сразу — по количеству цифр, по максимальной цифре. Но есть же и аналитический метод.

Это означает, что

3x 5 + 5x 4 + 2x 2 + x – 118920 = 0

Классический многочлен пятой степени. И теперь нужно просто решить полиномиальное уравнение. По основной теореме алгебры у него будет пять комплексных корней, нас, правда, интересует только действительный, хорошо бы положительный, и хорошо бы целый 🙂

Из теоремы Абеля-Руффини известно, что аналитически мы такое уравнение не решим в общем случае, но я бы даже и пробовать не стал: на то придуманы численные методы, которых всяких есть многатыщ — выбрать можно по вкусу, начиная хоть с метода товарища Ньютона. Решаем, и получаем:

x = 8

Хорошо и красиво. Ну можете еще добить преподавателя комплексными корнями, сказав, что это же число записывается точно так же в системе счисления с основанием (-7.07949 – 4.865i) 🙂

1) если нужно проверить может ли быть такое число a в данной системе счисления с основанием b, проверьте что все цифры a меньше основания b

т.е. 2358 не может являться числом в 4-ной СС

2)если вы перевели число a из десятичной СС в p-ичную, то для того, чтобы проверить, верно ли вы это сделали, просто переведите ее обратно в десятичную, и проверьте, получится ли то же число а.

Для того чтобы перевести число из p-ичной СС в десятичную, умножьте первую справа цифру на 1, вторую справа на p, третью на p², и т.д. умножая на степени p, а потом найдите сумму всего этого

1. Порядковый счет в различных системах счисления.

В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».

Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.

Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.

Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):

0	0	0	0
1	1	1	1
2	10	2	2
3	11	10	3
4	100	11	4
5	101	12	10
6	110	20	11
7	111	21	12
8	1000	22	13
9	1001	100	14
10	1010	101	20
11	1011	102	21
12	1100	110	22
13	1101	111	23
14	1110	112	24
15	1111	120	30

Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):

0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10
11
12	10
13	11
14	12
15	13

 
2.Перевод из десятичной системы счисления в любую другую.

Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.

Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

3. Перевод из любой системы счисления в десятичную.

Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.

Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:

Это и есть десятичная запись нашего числа, т.е.

Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.

Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.

4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).

Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.

Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:

Таблицу соответствия мы научились строить в п.1.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7

Т.е.

Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.

Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.

Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.

Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:

Это ж всё брутфорс, это ж несерьезно 🙂

На самом деле, конечно, перебор здесь вполне подходит, и можно дать ему границы сразу — по количеству цифр, по максимальной цифре. Но есть же и аналитический метод.

350214_х = 118924₁₀

Это означает, что

3x⁵ + 5x⁴ + 0x³ + 2x² + 1x + 4 = 118924₁₀

или

3x⁵ + 5x⁴ + 2x² + x – 118920 = 0

Классический многочлен пятой степени. И теперь нужно просто решить полиномиальное уравнение. По основной теореме алгебры у него будет пять комплексных корней, нас, правда, интересует только действительный, хорошо бы положительный, и хорошо бы целый 🙂

Из теоремы Абеля-Руффини известно, что аналитически мы такое уравнение не решим в общем случае, но я бы даже и пробовать не стал: на то придуманы численные методы, которых всяких есть многатыщ — выбрать можно по вкусу, начиная хоть с метода товарища Ньютона. Решаем, и получаем:

x = 8

Хорошо и красиво. Ну можете еще добить преподавателя комплексными корнями, сказав, что это же число записывается точно так же в системе счисления с основанием (-7.07949 – 4.865i) 🙂

Системы счисления

• Двоичная, восьмеричная и шестнадцатеричная
• Калькулятор перевода чисел

Система счисления — это способ записи (представление) чисел с помощью определённого набора письменных знаков, называемых цифрами.

Основание системы счисления — это количество цифр, которые используются в данной системе счисления для записи чисел.

Системы счисления делятся на позиционные и непозиционные.

Позиционными называются такие системы счисления, в которых значение цифры зависит от её расположения в записи числа. В качестве примера позиционной системы счисления можно привести привычную для нас десятичную систему счисления. Например, в записи числа  2222  одна и та же цифра —  2  означает (последовательно справа налево) количество — единиц, десятков, сотен, тысяч.

Непозиционными называются такие системы счисления, в которых значение цифры не зависит от её расположения в записи числа. В качестве примера непозиционной системы счисления можно привести достаточно широко применяемую в настоящее время, римскую систему. Например, в записи числа  CCC  (триста) символ  C  в любом месте означает число сто.

Двоичная, восьмеричная и шестнадцатеричная

В двоичной системе счисления основание равно  2,  то есть для записи чисел используется всего  2  цифры —  0  и  1.

В восьмеричной системе основание равно  8,  используется  8  цифр — от  0  до  7.

В шестнадцатеричной системе основание равно  16,  используется  16  цифр — от  0  до  15.  Цифры от  10  до  15  условились обозначать латинскими буквами в алфавитном порядке:  A  (10),  B  (11),  C  (12),  D  (13),  E  (14),  F  (15).

Калькулятор перевода чисел

Для быстрого перевода числа из одной системы счисления в другую (кроме римской) вы можете воспользоваться калькулятором: