Десятичный логарифм — логарифм по основанию 10. Другими словами, десятичный логарифм числа 
есть решение уравнения 
Вещественный десятичный логарифм числа существует, если 
(комплексный десятичный логарифм существует для всех 
). Международный стандарт ISO 31-11 обозначает его 
. Примеры:
В зарубежной литературе, а также на клавиатуре калькуляторов встречаются и другие обозначения десятичного логарифма: 
, причём следует иметь в виду, что первые 2 варианта могут относиться и к натуральному логарифму.
Алгебраические свойства[править | править код]
В нижеследующей таблице предполагается, что все значения положительны[1]:
| Формула | Пример | |
|---|---|---|
| Произведение |  |
|
| Частное от деления |  |
|
| Степень |  |
|
| Корень | ![{displaystyle lg {sqrt[{p}]{x}}={frac {lg(x)}{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e97e52fca667f88ed4136deba0fbf70161ffa88) |
|
Существует очевидное обобщение приведённых формул на случай, когда допускаются отрицательные переменные, например:
Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:
Вышеописанные свойства объясняют, почему применение логарифмов (до изобретения калькуляторов) существенно облегчало вычисления. Например, умножение многозначных чисел 
с помощью логарифмических таблиц[⇨] производилось по следующему алгоритму:
- Найти в таблицах логарифмы чисел
. - Сложить эти логарифмы, получая (согласно первому свойству) логарифм произведения .
- По логарифму произведения найти в таблицах само произведение.
Деление, которое без помощи логарифмов намного более трудоёмко, чем умножение, выполнялось по тому же алгоритму, лишь с заменой сложения логарифмов на вычитание. Аналогично производились возведение в степень и извлечение корня.
Связь десятичного и натурального логарифмов[2]:
Знак логарифма зависит от логарифмируемого числа: если оно больше 1, логарифм положителен, если оно между 0 и 1, то отрицателен. Пример:
Чтобы унифицировать действия с положительными и отрицательными логарифмами, у последних целая часть (характеристика) надчёркивалась сверху:
Мантисса логарифма, выбираемая из таблиц, при таком подходе всегда положительна.
Функция десятичного логарифма[править | править код]
Если рассматривать логарифмируемое число как переменную, мы получим функцию десятичного логарифма: 
Она определена при всех 
Область значений: 
. График этой кривой часто называется логарифмикой[3].
Функция монотонно возрастает, непрерывна и дифференцируема всюду, где она определена. Производная для неё даётся формулой:
Ось ординат 
является вертикальной асимптотой, поскольку:
Применение[править | править код]
Логарифмы по основанию 10 до изобретения в 1970-е годы компактных электронных калькуляторов широко применялись для вычислений. Как и любые другие логарифмы, они позволяли многократно упростить и облегчить трудоёмкие расчёты, заменяя умножение на сложение, а деление на вычитание; аналогично упрощались возведение в степень и извлечение корня. Но десятичные логарифмы обладали преимуществом перед логарифмами с иным основанием: целую часть логарифма числа 
(характеристику логарифма) ![{displaystyle [lg x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95dba0944686ae335cc4855187bf6270ee6c856d)
легко определить.
Кроме того, при переносе десятичной запятой в числе на 
разрядов значение десятичного логарифма этого числа изменяется на 
Например:
Отсюда следует, что для вычисления десятичных логарифмов достаточно составить таблицу логарифмов для чисел в диапазоне от 
до 
[4]. Такие таблицы, начиная с XVII века, выпускались большим тиражом и служили незаменимым расчётным инструментом учёных и инженеров.
Поскольку применение логарифмов для расчётов с появлением вычислительной техники почти прекратилось, в наши дни десятичный логарифм в значительной степени вытеснен натуральным[5]. Он сохраняется в основном в тех математических моделях, где исторически укоренился — например, при построении логарифмических шкал.
| Число | Логарифм | Характеристика | Мантисса | Запись |
|---|---|---|---|---|
| n | lg(n) | C | M = lg(n) − C | |
| 5 000 000 | 6.698 970… | 6 | 0.698 970… | 6.698 970… |
| 50 | 1.698 970… | 1 | 0.698 970… | 1.698 970… |
| 5 | 0.698 970… | 0 | 0.698 970… | 0.698 970… |
| 0.5 | −0.301 029… | −1 | 0.698 970… | 1.698 970… |
| 0.000 005 | −5.301 029… | −6 | 0.698 970… | 6.698 970… |
Обратите внимание, что у всех приведенных в таблице чисел одна и та же мантисса 
, поскольку:
- ,
где 
— значащая часть числа .
История[править | править код]
Первые таблицы десятичных логарифмов опубликовал в 1617 году оксфордский профессор математики Генри Бригс для чисел от 1 до 1000, с восемью (позже — с четырнадцатью) знаками. Поэтому за рубежом десятичные логарифмы часто называют бригсовыми. Но в этих и в последующих изданиях таблиц обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги (1783) появилось только в 1852 году в Берлине (таблицы Бремикера)[6].
В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого[7]. В СССР выпускались несколько сборников таблиц логарифмов[8]:
- Брадис В. М. Четырехзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Таблицы Брадиса, издаваемые с 1921 года, использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
- Вега Г. Таблицы семизначных логарифмов, 4-е издание, М.: Недра, 1971. Профессиональный сборник для точных вычислений.
Литература[править | править код]
- Теория логарифмов
- Выгодский М. Я. Справочник по элементарной математике. — изд. 25-е. — М.: Наука, 1978. — ISBN 5-17-009554-6.
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — 680 с.
- История логарифмов
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- Клейн Ф. Элементарная математика с точки зрения высшей. — М.: Наука, 1987. — Т. I. Арифметика. Алгебра. Анализ. — 432 с.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
- Успенский Я. В. Очерк истории логарифмов. — Петроград: Научное книгоиздательство, 1923. — 78 с.
Ссылки[править | править код]
- Десятичные (бригсовы) логарифмы. (англ.)
Примечания[править | править код]
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 187..
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 189..
- ↑ Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Элементарная математика, 1976, с. 94—100.
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 406..
- ↑ История математики, том II, 1970, с. 62..
- ↑ Гнеденко Б. В. Очерки по истории математики в России, издание 2-е. — М.: КомКнига, 2005. — С. 66.. — 296 с. — ISBN 5-484-00123-4.
- ↑ Логарифмические таблицы // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
Результатом вычисления логарифма числа является показатель степени, в которую необходимо возвести одно число для получения другого.
- Определение десятичного логарифма
- Свойства десятичного логарифма
- Таблица десятичных логарифмов
- График десятичного логарифма
Определение десятичного логарифма
Десятичный логарифм — это логарифм, основанием которого является число 10. Обозначается как lg и пишется следующим образом:
lg y = log10 y = x, при y>0
lg y является решением уравнения y = 10 x. Другими словами, в какую степень (x) необходимо возвести число 10, чтобы получить y.
Связь с натуральным логарифмом
lg x ≈ 0,43429 ln x
Данное соотношение получено путем перехода к новому основанию:
т.к. ln 10 ≈ 2,30259.
Свойства десятичного логарифма
Таблица десятичных логарифмов
| x | lg x | x | lg x | x | lg x | x | lg x |
| 1 | 0 | 26 | 1,41497 | 51 | 1,70757 | 76 | 1,88081 |
| 2 | 0,30103 | 27 | 1,43136 | 52 | 1,716 | 77 | 1,88649 |
| 3 | 0,47712 | 28 | 1,44716 | 53 | 1,72428 | 78 | 1,89209 |
| 4 | 0,60206 | 29 | 1,4624 | 54 | 1,73239 | 79 | 1,89763 |
| 5 | 0,69897 | 30 | 1,47712 | 55 | 1,74036 | 80 | 1,90309 |
| 6 | 0,77815 | 31 | 1,49136 | 56 | 1,74819 | 81 | 1,90849 |
| 7 | 0,8451 | 32 | 1,50515 | 57 | 1,75587 | 82 | 1,91381 |
| 8 | 0,90309 | 33 | 1,51851 | 58 | 1,76343 | 83 | 1,91908 |
| 9 | 0,95424 | 34 | 1,53148 | 59 | 1,77085 | 84 | 1,92428 |
| 10 | 1 | 35 | 1,54407 | 60 | 1,77815 | 85 | 1,92942 |
| 11 | 1,04139 | 36 | 1,5563 | 61 | 1,78533 | 86 | 1,9345 |
| 12 | 1,07918 | 37 | 1,5682 | 62 | 1,79239 | 87 | 1,93952 |
| 13 | 1,11394 | 38 | 1,57978 | 63 | 1,79934 | 88 | 1,94448 |
| 14 | 1,14613 | 39 | 1,59106 | 64 | 1,80618 | 89 | 1,94939 |
| 15 | 1,17609 | 40 | 1,60206 | 65 | 1,81291 | 90 | 1,95424 |
| 16 | 1,20412 | 41 | 1,61278 | 66 | 1,81954 | 91 | 1,95904 |
| 17 | 1,23045 | 42 | 1,62325 | 67 | 1,82607 | 92 | 1,96379 |
| 18 | 1,25527 | 43 | 1,63347 | 68 | 1,83251 | 93 | 1,96848 |
| 19 | 1,27875 | 44 | 1,64345 | 69 | 1,83885 | 94 | 1,97313 |
| 20 | 1,30103 | 45 | 1,65321 | 70 | 1,8451 | 95 | 1,97772 |
| 21 | 1,32222 | 46 | 1,66276 | 71 | 1,85126 | 96 | 1,98227 |
| 22 | 1,34242 | 47 | 1,6721 | 72 | 1,85733 | 97 | 1,98677 |
| 23 | 1,36173 | 48 | 1,68124 | 73 | 1,86332 | 98 | 1,99123 |
| 24 | 1,38021 | 49 | 1,6902 | 74 | 1,86923 | 99 | 1,99564 |
| 25 | 1,39794 | 50 | 1,69897 | 75 | 1,87506 | 100 | 2 |
microexcel.ru
| lg x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| x | 10 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 1010 |
microexcel.ru
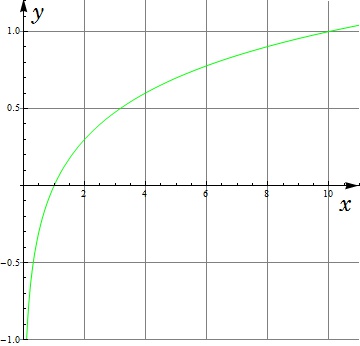
График десятичного логарифма
Функция десятичного логарифма задается как y = lg x. Существует только при неотрицательных значениях переменной x. График выглядит так:
Десятичный логарифм
Навигация по странице:
- Определение
- Калькулятор
- Свойства
- Примеры
Определение. Логарифмом числа b по основанию a, где a > 0, a ≠ 1, b > 0, называется показатель степени, в которую нужно возвести основание a, чтоб получить число b.
Определение. Десятичный логарифм — логарифм по основанию 10.
Другими словами, десятичный логарифм числа b является решением уравнения 10x = b.
Обозначение. Десятичный логарифм обозначается lg x или log x.
Калькулятор десятичных логарифмов
lg 2
Свойства десятичного логарифмов
Для любых x > 0 и y > 0 выполняются следующие свойства десятичных логарифмов.
-
lg x = log10 x – так как основание десятичного логарифма равно 10.
-
10lg b = b.
-
lg 1 = 0
-
lg 10 = 1
-
lg 10n = n
-
lg(x · y) = lg x + lg y
-
lg xy = lg x – lg y
-
lg xn = n lg x
-
График функции y = lg x
-
(lg x)′ = 1x ln 10
-
∫ lg x dx = x lg x – xln 10 + C
Пример 1. Найти значения десятичного логарифма от чисел 100, 1000, 0.1, 0.01, 0.001.
lg 100 = lg 102 = 2
lg 1000 = lg 103 = 3
lg 0.1 = lg 10-1 = -1
lg 0.01 = lg 10-2 = -2
lg 0.001 = lg 10-3 = -3
Пример 2.
Доказать равенство: a lg b = b lg a.
Запишем очевидное равенство:
lg b · lg a = lg a · lg ab
Возведем 10 в соответствующие степени
10lg b · lg a = 10lg a · lg b
(10lg b)lg a = (10lg a)lg b
blg a = alg b
Равенство доказано.
Пример 3.
Зная, что lg 2 = a, lg 3 = b, lg 5 = c, выразить lg 6; lg 30; lg 16 через a, b, c.
Используем формулы логарифма произведения и степени получим:
lg 6 = lg (2·3)= lg 2 + lg 3 = a + b;
lg 30 = lg (5·2·3)= lg 5 + lg 2 + lg 3 = a + b + c;
lg 16 = lg 24= 4 · lg 2 = 4a.
Пример 4.
Вычислить log9 5 · log25 27.
Перейдем к основе 10:
log9 5 · log25 27 = lg 5lg 9 · lg 27lg 25
Используем свойство логарифма степени lg xn = n lg x:
lg 5lg 9 · lg 27lg 25 = lg 5lg 32 · lg 33lg 52 = lg 52 lg 3 · 3 lg 32 lg 5 = 34
Пример 5.
Вычислить log30 8, если lg 5 = a, lg 3 = b.
Перейдем к основе 10:
log 30 8 = lg 8lg 30 = lg 23lg (3 · 10) =
Используем свойство логарифма степени, произведения, частного и то что 2= 105:
= 3 lg 2lg 3 + lg 10 = 3 lg 2lg 3 + 1 = 3 lg 105lg 3 + 1 = 3(lg 10 – lg 5)lg 3 + 1 = 3(1 – lg 5)lg 3 + 1 =
Подставим lg 5 = a, lg 3 = b:
= 3(1 – a)b + 1
Ответ:
log30 8 = 3(1 – a)b + 1
Десятичные и натуральные логарифмы
- Десятичный логарифм и его свойства
- Натуральный логарифм и его свойства
- Примеры
п.1. Десятичный логарифм и его свойства
Логарифмы чисел по основанию 10 называют десятичными.
Для десятичных логарифмов принято специальное обозначение: begin{gather*} log_{10}xoverset{def}{=}lg x end{gather*}
Основание десятичных логарифмов (10gt 1), поэтому они обладают всеми свойствами логарифмов с основанием больше единицы (см. §30 данного справочника).
Но у десятичных логарифмов есть также целых ряд дополнительных свойств, благодаря которым в докомпьютерную эпоху они широко использовались для трудоемких вычислений. Роль калькулятора тогда выполняли логарифмическая таблица и логарифмическая линейка.
Целая часть десятичного логарифма ([lg x]) называется характеристикой, а дробная часть (left{lg xright}) – мантиссой.
Для числа (b), записанного в стандартном виде (b=acdot 10^n)
характеристика равна порядку числа ([lg b]=n), мантисса (left{lg bright}=lg a)
О стандартном виде числа, см. §41 справочника для 8 класса.
Например:
| Число b |
Стандартный вид |
Характеристика | Мантисса b |
Унифицированная запись |
Логарифм числа (lg b) |
| 420 | 4,2·102 | 2 | 0,623 | 2,623 | 2,623 |
| 42 | 4,2·101 | 1 | 0,623 | 1,623 | 1,623 |
| 4,2 | 4,2 | 2 | 0 | 0,623 | 0,623 |
| 0,42 | 4,2·10–1 | –1 | 0,623 | (overline{1},623) | –0,377 |
| 0,042 | 4,2·10–2 | –2 | 0,623 | (overline{2},623) | –1,377 |
(lg 4,2approx 0.623)
Если использовать унифицированную запись, как в представленной таблице, то мантисса всегда лежит в промежутке (0lt lg alt 1). У чисел, отличающихся только порядком, мантисса одинакова. Можно составить таблицы мантисс и пользоваться ими для умножения и деления, «разбавляя» их несложным сложением и вычитанием целых характеристик по необходимости.
Первые таблицы логарифмов были изданы в 1617 году оксфордским математиком Бригсом. Таблицы пересчитывались, дополнялись и переиздавались вплоть до 70-х гг. ХХ века, когда на столах стали появляться калькуляторы.
Таблицы Брадиса, которыми по традиции пользуются наши школьники с 1921 года, издаются до сих пор и постепенно перекочевывают в Интернет.
Непосредственная связь десятичных логарифмов с десятичной системой исчисления делает их удобным инструментом для оценки порядка числа и сравнения чисел.
В практике приближенных вычислений используется следующая оценочная таблица:
(lg 1)
(lg 2)
(lg 3)
(lg 4)
(lg 5)
(lg 8)
Относительная погрешность этих приближений (кроме (lg 3)) (deltasim 0,5text{%})
Например:
Сравним (log_23) и (log_58)
Сравнивая с помощью оценки, получаем: begin{gather*} log_23=frac{lg 3}{lg 2}approxfrac{0,5}{0,3}=frac53, log_58=frac{lg 8}{lg 5}approxfrac{0,9}{0,7}=frac97\ frac{35}{21}gt frac{27}{21}Rightarrow frac53gt frac97Rightarrowlog_23gtlog_58 end{gather*}
п.2. Натуральный логарифм и его свойства
Логарифмы чисел по основанию e называют натуральными.
Для натуральных логарифмов принято специальное обозначение: begin{gather*} log_{e}xoverset{def}{=}ln x end{gather*}
Число e≈2,71828… – это математическая константа, число иррациональное и трансцендентное, которое появляется при описании моделей нашего мира ничуть не реже числа (pi). Мы познакомимся с ним подробней, изучая пределы и производные.
Основание натуральных логарифмов e>1, поэтому они обладают всеми свойствами логарифмов с основанием больше единицы (см. §30 данного справочника).
Для приближенного вычисления значения натурального логарифма используется «ряд Меркатора»:
$$ ln(1+x)=x-frac{x^2}{2}+frac{x^3}{3}-frac{x^4}{4}+…, -1lt xleq 1 $$
Например:
С точностью до первого слагаемого: (ln 1,3=ln(1+0,3)approx 0,3)
До второго слагаемого: (ln 0,3approx 0,3-frac{0,3^2}{2}=0,255)
До третьего слагаемого: (ln 0,3approx 0,3-frac{0,3^2}{2}+frac{0,3^3}{3}=0,264) и т.д.
Натуральные логарифмы настолько распространены в различных областях научных исследований, что когда вообще речь заходит «логарифмах», по умолчанию подразумевают именно их. Если же у вас в работе какие-то другие «логарифмы» (по основанию 2 или 10, например), это нужно уточнять.
п.3. Примеры
Пример 1. Найдите (x):
a) ( lg x=2lg a+lg 7 )
(lg x=lg a^2+lg 7=lg(7a^2))
(x=7a^2)
б) ( lg x=2lg(a+c)-3lg(a-c) )
(lg x =lg(a+c)^2-lg(a-c)^3=lgfrac{(a+c)^2}{(a-c)^3})
(x=frac{(a+c)^2}{(a-c)^3})
в) ( lg x=frac13lg 54+lg 5-frac13lg 16 ) ( lg x=lg 54^{frac13}+lg 5-lg 16^{frac13}=lgfrac{54^{frac13}cdot 5}{16^3}= lgfrac{(27cdot 2)^{frac13}cdot 5}{(2^4)^{frac13}} = lgfrac{3cdot 2^{frac13}cdot 5}{2^{frac43}} = lgfrac{15}{2} =lg 7,5 )
(x=7,5)
г) ( lg x=lgsqrt[{3}]{2-sqrt{3}}+lgsqrt[6]{7+4sqrt{3}} )
(lgleft(sqrt[{3}]{2-sqrt{3}}cdot sqrt[6]{7+4sqrt{3}}right))
Преобразуем выражение в скобках: begin{gather*} sqrt[{3}]{2-sqrt{3}}cdot sqrt[6]{7+4sqrt{3}} = sqrt[6]{(2-sqrt{3})^2(7+4sqrt{3})} = sqrt[6]{(4-4sqrt{3}+3)(7+4sqrt{3})} = \ =sqrt[6]{(7-4sqrt{3})(7+4sqrt{3})} = sqrt[6]{7^2-(4sqrt{3})^2}=sqrt[6]{49-48}=1 end{gather*} (lg x=lg 1)
(x=1)
Пример 2. Прологарифмируйте по основанию 10:
a) (x=frac{3a^2sqrt[3]{b^7}}{c^5(a-b)}) begin{gather*} lg x=lgfrac{3a^2sqrt[3]{b^7}}{c^5(a-b)}=lg 3+lg a^2+lgsqrt[3]{b^7}-lg c^5-lg(a-b)=\ =lg 3+2lg a+frac73lg b-5lg c-lg(a-b) end{gather*}
б*) (x=frac{sqrt[3]{100sqrt{10asqrt[4]{0,1a^2}}}}{10sqrt{0,1a}}) begin{gather*} lg x=lgfrac{sqrt[3]{100sqrt{10asqrt[4]{0,1a^2}}}}{10sqrt{0,1a}} = lgsqrt[3]{100sqrt{10asqrt[4]{0,1a^2}}} – lg 10sqrt{0,1a}=\ =frac13lgleft(100sqrt{10asqrt[4]{0,1a^2}}right)-(lg 10+lgsqrt{0,1a})=frac13left(lg 100+lgsqrt{10asqrt[4]{0,1a^2}}right)-\ -left(1+frac12lg(0,1a)right)=frac13left(2+frac12lg(10asqrt[4]{0,1a^2})right)-left(1+frac12(lg 0,1+lg a)right)=\ =frac23+frac32left(lg 10+lg a+lgsqrt[4]{0,1a^2}right)-1-frac12cdot(-1)-frac12lg a=\ =left(frac23+frac32-1+frac12right)+left(frac32-frac12right)lg a+frac32cdot frac14(lg 0,1+lg a^2)=\ =frac53+lg a+frac38cdot(-1)+frac38cdot 2lg a=left(frac53-frac38right) + left(1+frac34right)lg a=frac{31}{24}+frac74lg a end{gather*} Заметим, что попутно мы получили упрощенное выражение для (x=10^{frac{31}{24}}cdot a^{frac74}.)
Логарифмирование удобно для ‘сборки» запутанных степеней.
Пример 3. Найдите значение выражения:
a) (log_{sqrt{sqrt{3}+2}}(4sqrt{3}+7)^{frac13})
Заметим, что ((sqrt{3}+2)^2=3+4sqrt{3}+4=4sqrt{3}+7)
Тогда (sqrt{sqrt{3}+2}=(sqrt{3}+2)^{frac12}=left(sqrt{4sqrt{3}+7}right)^{frac12}=(4sqrt{3}+7)^{frac14})
Перейдем к десятичному основанию: begin{gather*} log_{sqrt{sqrt{3}+2}}(4sqrt{3}+7)^{frac13} = frac{lg(4sqrt{3}+7)^{frac13}}{lgsqrt{sqrt{3}+2}} = frac{frac13lg(4sqrt{3}+7)}{lg(4sqrt{3}+7)^{frac14}} = frac{frac13lg(4sqrt{3}+7)}{frac14lg(4sqrt{3}+7)}=frac43 end{gather*} Ответ: (frac43)
б) (log_{sqrt{2}+1}(5sqrt{2}-7))
Заметим, что: ((sqrt{2}-1)^3=2sqrt{2}-3cdot 2+3sqrt{2}-1=5sqrt{2}-7) $$ (sqrt{2}+1)(sqrt{2}-1)=2-1=1Rightarrow sqrt{2}+1=frac{1}{sqrt{2}-1}=(sqrt{2}-1)^{-1} $$ Перейдем к десятичному основанию: $$ log_{sqrt{2}+1}(5sqrt{2}-7)=lgfrac{(5sqrt{2}-7)}{lg(sqrt{2}+1)}=frac{lg(sqrt{2}-1)^3}{lg(sqrt{2}-1)^{-1}}= frac{3lg(sqrt{2}-1)-1}{-lg(sqrt{2}-1)}=-3 $$ Ответ: -3
Заметим, что переход к десятичному основанию в этих примерах не обязателен.
Но он значительно упрощает запись и облегчает решение.
Пример 4*. Постройте (с помощью какого-либо математического приложения или собственной программы) в одной системе координат для (-1lt xleq 1) график (y=ln(1+x)) и его приближения по ряду Меркатора: $$ y=x, y=x-frac{x^2}{2}, y=x-frac{x^2}{2}+frac{x^3}{3} $$ Сделайте выводы.
Чем больше слагаемых в ряду, тем ближе соответствующая кривая к графику логарифма, тем точнее результат. В данном случае ближе всего к кривой (y=ln(1+x)) расположена кубическая парабола (y=x-frac{x^2}{2}+frac{x^3}{3}).
Чем меньше модуль (|x|), тем точнее приближение. Визуально, уже в окрестности (|x|lt 0,2) квадратичная и кубическая парабола дают хорошую точность приближения.
Приближение 1-го порядка ((ln(1+x)approx x)) довольно грубое, но может использоваться для предварительной оценки.
Расчет относительной погрешности приближения на границах окрестностей (|x|lt 0,1) и (|x|lt 0,2) представлен в таблице:
| x=0,1 | x=0,2 | |||
| y(x) | δ, % | y(x) | δ, % | |
| (y=x) | 0,1 | 4,92% | 0,2 | 9,70% |
| (y=x-frac{x^2}{2}) | 0,095 | 0,33% | 0,18 | 1,27% |
| (y=x-frac{x^2}{2}+frac{x^3}{3}) | 0,095333 | 0,02% | 0,182667 | 0,19% |
| (y=ln(1+x)) | 0,095310 | 0,182322 |
Десятичный логарифм
оксана николаевна кузнецова
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Десятичный логарифм
Определение 1
Десятичным логарифмом называют логарифм, который имеет в основании число $10$.
Десятичный логарифм вматематике принято обозначать $lg$:
$lg a=log_{10}a$.
Название десятичного логарифма происходит именно от его основания, которое равняется десяти.
Иногда можно встретить следующее обозначение десятичного логарифма:
$log a$.
Замечание 1
Согласно определению логарифма можно сделать вывод, что десятичный логарифм $lg a$ является решением показательного уравнения $10^b=a$.
Свойства десятичного логарифма
-
Т.к. логарифм по любому основанию от $1$ равен $0$, то и десятичный логарифм единицы равен $0$:
$lg 1=0$.
-
Десятичный логарифм от числа $10$ равен единице:
$lg 10=1$.
-
Десятичный логарифм произведения двух чисел равен сумме десятичных логарифмов от этих чисел:
$lg (ab)=lg a+lg b$.
-
Десятичный логарифм частного двух чисел равен разнице десятичных логарифмов этих чисел:
$lg frac{a}{b}=lg a-lg b$.
-
Десятичный логарифм степени числа может быть представлен в виде произведения показателя степени на десятичный логарифм подлогарифмического числа:
$lg a^s=s cdot lg a$.
Пример 1
Упростить выражение $frac{2 lg 40-lg 16}{lg 50-frac{1}{2} lg 25}$.
Решение.
Применим к первому логарифму в числителе и в знаменателе свойство логарифма произведения, а ко второму логарифму числителя и знаменателя – свойство логарифма степени:
$frac{2 lg 40-lg 16}{lg 50-frac{1}{2} lg 25}=frac{2(lg 4+lg 10 )-lg 4^2}{lg 5+lg 10-frac{1}{2} lg 5^2}=$
откроем скобки и приведем подобные слагаемые, а также применим свойство $lg 10=1$:
$=frac{2 lg 4+2-2 lg 4}{lg 5+1-frac{1}{2} cdot 2 lg 5}=frac{2}{lg 5+1-lg 5}=2$.
Ответ: $frac{2 lg 40-lg 16}{lg 50-frac{1}{2} ln 25}=2$.
Пример 2
Вычислить значение логарифмического выражения $lg 200+lg frac{1}{20}$.
Решение.
Применим формулу суммы логарифмов:
$lg 200+lg frac{1}{20}=lg (200 cdot frac{1}{20})=lg 10=1$.
Ответ: $lg 200+lg frac{1}{20}=1$.
«Десятичный логарифм» 👇
Пример 3
Вычислить значение логарифмического выражения $2 ln frac{1}{e^2}+3 lg 10000$.
Решение.
Применим свойство логарифма степени:
$2 ln frac{1}{e^2}+3 lg 10000=2 ln e^{-2}+3 lg 10^4=2 cdot (-2) ln e+3 cdot 4 lg 10=-4 ln e+12 lg 10=$
теперь применим свойство логарифма, у которого основание равно подлогарифмическому числу:
$=-4 cdot 1+12 cdot 1=8$.
Ответ: $2 ln frac{1}{e^2}+3 lg 10000=8$.
Пример 4
Упростить логарифмическое выражение $lg frac{1}{8}-3 lg 4$.
Решение.
Применим свойство логарифма степени:
$lg frac{1}{8}-3 lg 4=lg 2^{-3}-3 lg 2^2=-3 lg 2-3 cdot 2 lg 2=-9 lg 2$.
Ответ: $lg frac{1}{8}-3 lg 4=-9 lg 2$.
Пример 5
Вычислить значение логарифмического выражения $3 lg 0,09-2 lg 27$.
Решение.
Применим к обоим логарифмам свойство логарифма степени:
$3 lg frac{9}{10^2}-2 lg 27=3 lg (frac{3}{10})^2-2 lg 3^3=3 cdot 2 lg frac{3}{10}-2 cdot 3 lg 3=6 lg frac{3}{10}-6 lg 3=$
применим к первому логарифму свойство логарифма частного:
$=6(lg 3-lg 10 )-6 lg 3=$
откроем скобки и приведем подобные слагаемые:
$=6 lg 3-6 lg 10-6 lg 3=-6$.
Ответ: $3 lg 0,09-2 lg 27=-6$.
Пример 6
Упростить логарифмическое выражение $lg 0,81-2 lg 9$.
Решение.
Применим ко второму логарифму свойство логарифма степени, внеся число $2$ под знак логарифма:
$lg 0,81-lg 9^2=lg 0,81-lg 81=$
применим формулу разности логарифмов:
$=lg frac{0,81}{81}=lg 0,01=$
запишем число под знаком логарифма как $10$ в степени:
$=lg 10^{-2}=$
применим формулу логарифма степени:
$=-2 lg 10=-2$.
Ответ: $lg 0,81-2 lg 9=-2$.
Пример 7
Вычислить значение логарифмического выражения $frac{2 lg 2-lg 16}{lg 4+lg 16}$.
Решение.
Внесем число $2$ в числителе под знак логарифма:
$frac{2 lg 2-lg 16}{lg 4+lg 16}=frac{lg 2^2-lg 16}{lg 4+lg 16}=$
применим формулы разности и суммы логарифмов:
$=frac{lg frac{4}{16}}{lg (4 cdot 16)} =frac{lg frac{1}{4}}{lg 64} =$
применим формулу логарифма степени, записав число под знаком логарифма как число $4$ в степени:
$=frac{lg 4^{-1}}{lg 4^3} =frac{-lg 4}{3 lg 4}=-frac{1}{3}$.
Ответ: $frac{2 lg 2-lg 16}{lg 4+lg 16} =-frac{1}{3}$.
Пример 8
Преобразовать логарифмическое выражение $lg frac{100}{e}$.
Решение.
Применим формулу логарифма частного:
$lg frac{100}{e}=lg 100-lg e=$
к первому логарифму применим формулу логарифма степени:
$=lg 10^2-lg e=2 lg 10-lg e=$
применив свойство значения логарифма с одинаковым основанием и подлогарифмическим числом, получим:
$=2 cdot 1-lg e=2-lg e$.
Ответ: $lg frac{100}{e}=2-lg e$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 20.07.2022
