Теория множеств
- Истоки
- Аксиомы теории множеств
- Теория трансфинитных ординальных и кардинальных чисел
- Универсум всех множеств V
- Теория множеств как основание математики
- Теория множеств континуума
- Конструктивный универсум Гёделя
- Вынуждение
- Поиск новых аксиом
- Большие кардинальные числа
- Аксиомы вынуждения
- Библиография
Впервые опубликовано 8 октября 2014; содержательно переработано 12 февраля 2019
Теория множеств — это математическая теория о вполне определенных совокупностях, называемых множествами, содержащиеся в них объекты называются членами или элементами множества. Чистая теория множеств работает исключительно со множествами, то есть она рассматривает только те множества, элементы которых также представляют собой множества. Теория наследственно конечных множеств — чьи элементы также являются конечными множествами, которые также состоят из конечных элементов и т.д. — формально эквивалентна арифметике. Таким образом, суть теории множеств состоит в изучении бесконечных множеств, следовательно, ее можно определить как математическую теорию об актуально бесконечном (в противовес потенциально бесконечному).
Понятие множества настолько простое, что обычно его определяют неформальным образом и считают чем-то само собой разумеющимся. Однако в теории множеств, как это часто происходит в математике, множества задаются аксиоматически, поэтому их существование и базовые свойства постулируются при помощи соответствующих формальных аксиом. Аксиомы теории множеств предполагают существование настолько богатого теоретико-множественного универсума, что все математические объекты можно представить в виде множеств. Кроме того, формальный язык чистой теории множеств позволяет формализовать все математические понятия и аргументы. Таким образом, теория множеств становится стандартным основанием математики, поскольку всякий математический объект можно рассматривать в виде множества и всякую математическую теорему можно логически вывести в исчислении предикатов из аксиом теории множеств.
Оба аспекта теории множеств, а именно, теория множеств как математическое исследование бесконечности и как основание математики, обладают философской значимостью.
Теория множеств как отдельная математическая дисциплина берет свое начало в работах Георга Кантора. Можно сказать, что теория множеств появилась на свет в 1873 году, когда он совершил потрясающее открытие, установив, что линейный континуум, то есть вещественная прямая, несчетен — иными словами, что входящие в прямую точки нельзя посчитать с помощью натуральных чисел. Так, даже если и множество натуральных чисел, и множество действительных чисел являются бесконечными, действительных чисел больше, чем натуральных — и осознание этого факта послужило толчком для возникновения идеи множеств с различными объемами бесконечности (см. обсуждение истоков идей теории множества и их использования различными математиками и философами до Кантора и в его время в статье о ранних этапах развития теории множеств).
Согласно Кантору, два множества A и В обладают одинаковым объемом, или кардинальностью, если элементы множества А можно поставить во взаимно-однозначное соответствие элементам множества В. Таким образом, множество N натуральных чисел и множество R действительных чисел характеризуются различной кардинальностью. В 1878 году Кантор сформулировал знаменитую континуум-гипотезу (CH), в которой утверждается, что всякое конечное множество действительных чисел является одинаково счетным — то есть характеризуется той же кардинальностью, что и N, либо той же кардинальностью, что R. Иными словами, существуют только два возможных объема бесконечных множеств действительных чисел. CH представляет наиболее известную проблему теории множеств. Сам Кантор приложил немало усилий для ее развития — как и многие другие крупнейшие математики первой половины XX века, в частности Гильберт — расположивший CH в начало своего знаменитого списка из 23 неразрешенных проблем математики, представленных в 1900 году во время Второго Международного Конгресса Математиков в Париже.
Попытки доказать СН привели к крупным открытиям в теории множеств, таким как теория конструктивных множеств, а также метод вынуждения, благодаря которому удалось доказать, что СН невозможно ни доказать, ни отпровергнуть исходя из стандартных аксиом теории множеств.
Вплоть до сегодняшнего дня проблема СН остается открытой.
Уже на раннем этапе понятия так называемой наивной теории множеств порождали всякие противоречия и парадоксы; в частности, парадоксы возникают из, казалось бы, естественного допущения о том, что всякое свойство задает множество, а именно — множество объектов, обладающих данным свойством. Известным примером служит так называемый парадокс Рассела, также известный Цермело:
Представим свойство множеств, не являющихся элементами самих себя. Если данное свойство задает множество — назовем его множество А — тогда А является элементом самого себя, если и только если А не является элементом самого себя.
Таким образом, некоторые совокупности, подобно совокупности всех множеств, совокупности всех ординальных чисел или совокупности всех кардинальных чисел, не являются множествами. Такие совокупности называются собственными классами.
Для того, чтобы избежать парадоксов и найти твердое основание для теории множеств, необходимо задать для нее систему аксиом. Первую попытку аксиоматизации теории множеств предпринял Цермело (Zermelo 1908); к этому его подтолкнула необходимость установления базовых теоретико-множественных принципов, на которые опиралось бы его доказательство канторовского принципа вполне упорядоченного множества. Аксиоматизация Цермело позволяет избежать парадокса Рассела с помощью аксиомы выделения, которая формулируется как количественная оценка свойств множеств — то есть она представляет собой высказывание второго порядка.
Дальнейшая работа, проведенная Скулемом и Френкелем, привела к формализации аксиомы выделения с помощью формул первого порядка, заменивших неформальное понятие свойства, а также к введению аксиомы преобразования, которая также была сформулирована в виде схемы аксиом для формул первого порядка (см. следующий раздел). Аксиома преобразования необходима для правильного развития теории трансфинитных ординальных и кардинальных чисел с использованием трансфинитной рекурсии (см. раздел 3).
Было также необходимо доказать существование такого простого множества, как множество наследственно конечных множеств, т.е. таких конечных множеств, которые состоят из конечного числа элементов, элементы которых также конечны и т.д.; или доказать базовые теоретико-множественные утверждения, например то, что всякое множество содержится в транзитивном множестве — то есть множестве, содержащем все элементы, входящие в состав элементов данного множества (о погрешностях теории множеств Цермело см. Mathias 2001). Дальнейшее появление аксиомы регулярности, предложенное фон Нейманом, привело к установлению стандартной аксиоматической системы теории множеств, известной как аксиомы Цермело — Френкеля с добавлением аксиомы выбора, или ZFC.
Прочие аксиоматизации теории множеств (например, аксиоматизация фон Неймана —Бернайса — Гёделя или Морза — Келли) также позволяют нам проводить формальный анализ собственных классов.
Аксиомы Цермело — Френкеля с добавлением аксиомы выбора (ZFC) — это системы аксиом, сформулированных в первопорядковой логике с равенством и единственным символом бинарного отношения ∈, обозначающим принадлежность. Так, запись A∈B означает, что А является элементом множества В. Ниже мы приводим неформализованную запись аксиом ZFC.
Аксиомы ZFC
● Аксиома объемности: Если элементы двух множеств А и В совпадают, то эти множества равны.
● Аксиома пустого множества: Существует множество, обозначаемое как ∅ и называемое пустым множеством, в которое не входят никакие элементы.
● Аксиома пары: Для любых множеств А и В существует множество, обозначаемое {A,B}, которое содержит А и В в качестве своих единственных элементов. Также существует множество {А}, которое содержит А в качестве единственного элемента.
● Аксиома множества подмножеств (аксиома булеана): Для любого множества А существует множество, обозначаемое Р(А) и называемое множеством подмножеств А, элементами которого являются все подмножества А.
● Аксиома объединения: Для любого множества А существует множество, обозначаемое ⋃A, которое называется объединением А, и элементами которого являются все элементы, входящие в состав хотя бы одного из множеств элементов А.
● Аксиома бесконечности: Существует некоторое бесконечное множество. Существует множество Z, которое содержит ∅, так что если A∈Z, то ⋃{A,{A}}∈Z.
● Аксиома выделения: для всякого множества А и всякого заданного свойства существует множество, содержащее все элементы А, обладающие данным свойством. Свойство задается формулой φ первопорядкового языка теории множеств.
Таким образом, аксиома выделения — это не одна аксиома, а схема аксиом, то есть бесконечный список аксиом — по одной для каждой формулы φ.
● Аксиома преобразования: Для всякой определенной функции, область определения которой задает множество А, существует множество, элементами которого являются все значения данной функции. Аксиома преобразования также представляет собой схему аксиом, поскольку определенные функции задаются формулами.
● Аксиома регулярности: Всякое непустое множество А содержит минимальное подмножество, то есть такое подмножество, которому не принадлежит никакой другой элемент множества А.
Так выглядят аксиомы теории множеств Цермело — Френкеля (ZF). Аксиомы пустого множества или пары выводятся из других аксиом ZF, так что их можно опустить. Кроме того, из аксиомы преобразования выводится аксиома выделения.
Наконец, существует аксиома выбора (АС):
● Аксиома выбора: Для всякого множества А попарно непересекающихся непустых множеств существует множество, содержащее ровно один элемент из каждого подмножества А.
Долгое время АС считалась противоречивой аксиомой. С одной стороны, она очень полезна и широко используется в математике. С другой стороны, ее следствия контринтуитивны; таковым является например, парадокс Банаха — Тарского, который гласит, что один шар можно разделить на конечное множество частей, из которых затем можно собрать два шара. Возражения против данной аксиомы произрастают из того факта, что в ней утверждается существование множеств, которые невозможно эксплицитно определить. Однако приведенное Гёделем в 1938 году доказательство ее непротиворечивости — относительно непротиворечивости ZF — позволило отбросить все сомнения, остававшиеся в связи с этой аксиомой.
Аксиома выбора эквивалентна (по модулю ZF) принципу вполне упорядоченного множества, который гласит, что всякое множество можно представить как вполне упорядоченное — то есть линейно упорядочить его таким образом, что всякое непустое подмножество этого множества содержало минимальный элемент.
Хотя формально это и не является необходимым, помимо символа ∈, как правило, для обозначения принадлежности используются другие специальные символы. Например, выражение А⊆B означает, что А является подмножеством В, то есть всякий член А является членом В. Прочие символы используются для обозначения множеств, полученных при применении базовых операций, например, A∪B обозначает объединение множеств А и В — множество, элементами которого являются элементы А и В; или A∩B обозначает пересечение А и В — множество, элементы которого являются общими для А и В. Упорядоченная пара (А,В) определяется как множество {{А},{А,В}}. Таким образом, две упорядоченные пары (А,В) и (С,D) равны, если и только если А=С и В=D. Декартово произведение (или прямое произведение)) A×B определяется как множество упорядоченных пар (С,D), таких что C∈A и D∈B. Для любой формулы φ(x,y1,…,yn) и множеств A,B1,…,Bn можно сформировать множество всех элементов А, которые удовлетворяют формуле φ(x,B1,…,Bn). Это множество обозначается так: {a∈A:φ(a,B1,…,Bn)}. В ZF можно легко доказать, что все эти множества существуют.
В ZFC можно развить канторову теорию трансфинитных (то есть бесконечных) ординальных и кардинальных чисел. Согласно определению, данному фон Нейманом в начале 1920-х годов, ординальные числа, или ординалы, мы получаем, производя две операции над элементами множества, начиная с пустого множества: берем следующий за ним элемент и переходим к предельному. Так, первым ординальным числом является ∅. Если существует ординал α, то непосредственно следующий за ним элемент, обозначаемый α+1, составляет множество α∪{α}. И если мы возьмем непустое множество Х ординалов, таких что для всякого α∈X следующий за ним α+1 также входит в Х, то мы получим предельный ординал ⋃X. Всякий ординал (строго говоря) вполне упорядочен за счет ∈, т.е. он линейно упорядочен за счет ∈ и не существует бесконечной ∈-нисходящей последовательности. Кроме того, любое вполне упорядоченное множество изоморфно единственному ординалу, называемому его порядковым типом.
Отметим, что всякий ординал равен множеству предшествующих ему элементов. Однако класс ON всех ординалов не составляет множество. Иными словами, ON был бы ординалом, превосходящим все ординалы, а это невозможно. Первый бесконечный ординал, который является множеством всех конечных ординалов, обозначается греческой буквой омега (ω). В ZFC конечные ординалы отождествляются с натуральными числами. Тогда ∅=0, {∅}=1, {∅,{∅}}=2 и т.д., следовательно, ω является просто множеством N натуральных чисел.
Список этих операций можно расширить, прибавив к нему умножение натуральных чисел на все ординалы. Например, ординал α+β является порядковым типом вполне упорядоченного множества, полученного за счет объединения вполне упорядоченного множества порядкового типа α и вполне упорядоченного множества порядкового типа β. Начало последовательности ординалов, вполне упорядоченных с помощью операции ∈, выглядит так:
0, 1, 2, …, n, …, ω, ω+1, ω+2, …, ω+ω, …, n⋅ω, …, ω⋅ω, …, ωn, …, ωω, …
Ординалы удовлетворяют принципу трансфинитной индукции: предположим, что С является классом ординалов таким, что, если С содержит все ординалы β, меньшие, чем некоторый ординал α, то α также содержится в С. Тогда класс С будет содержать все ординалы. Используя трансфинитную индукцию, можно доказать важнейший принцип трансфинитной рекурсии в ZFC (для этого понадобится схема преобразования), который гласит, что для произвольной функции класса G:V→V можно определить функцию класса F:ON→V такую, что F(α) является значением функции G, примененным к функции F, ограниченной до α. Можно использовать трансфинитную рекурсию, например, для того, чтобы определить свойство арифметических операций сложения, умножения и возведения в степень на ординалах.
Не будем забывать, что бесконечное множество счетно, если его можно поставить во взаимно-однозначное соответствие с ω. Все приведенные выше ординалы являются либо конечными, либо счетными. Но множество всех конечных и счетных ординалов также является ординалом, называемым ω1, и он не является счетным. Аналогичным образом, множество всех ординалов, которые можно привести во взаимно-однозначное соответствие некоторому ординалу, меньшему или равному ω1, также является ординалом, называемым ω2, причем его нельзя привести во взаимно-однозначное соответствие с ω1, и т.д.
Кардинальные числа
Кардинальное число — это ординал, который нельзя привести во взаимно-однозначное соответствие меньшему ординалу. Таким образом, всякий конечный ординал является кардинальным числом, и ω, ω1, ω2 и т.д. также являются кардинальными числами. Бесконечные кардинальные числа обозначаются буквой алеф (ﭏ) ивритского алфавита, и их последовательность индексируется ординалами: ℵ0, ℵ1, ℵ2, …, ℵω, ℵω+1, …, ℵω+ω, …, ℵω2, …, ℵωω, …, ℵω1, …, ℵω2, …
Таким образом, ω=ℵ0, ω1=ℵ1, ω2=ℵ2 и т.д. Для всякого кардинального числа существует превосходящее его кардинальное число, и пределом возрастающей последовательности кардинальных чисел также является кардинальное число. Таким образом, класс всех кардинальных чисел не составляет множество, но является собственным классом.
Бесконечное кардинальное число κ также называется регулярным, если оно не является объединением меньшего, чем κ числа меньших кардинальных чисел. Тогда ℵ0 является регулярным, и таковыми же являются все бесконечные последующие кардиналы, например ℵ1. Нерегулярные бесконечные кардинальные числа называют сингулярными. Первым сингулярным кардинальным числом является ℵω, так как оно представляет собой объединение счетной последовательности меньших кардинальных чисел — т.е. ℵω=⋃n<ωℵn.
Конфинальностью кардинального числа κ, обозначаемого как cf(κ), является наименьшее кардинальное число λ такое, что κ является объединением λ меньших ординалов. Тогда cf(ℵω)=ℵ0.
Согласно аксиоме выбора (в виде принципа вполне упорядоченных множеств), всякое множество А может быть вполне упорядоченным, так как его элементы можно привести во взаимно-однозначное соответствие с единственным кардинальным числом, называемым кардинальностью А. Для кардинальных чисел κ и λ сумма κ+λ будет определяться как кардинальность множества, состоящего из объединения любых двух равномощных множеств (между которыми можно установить взаимно-однозначное соответствие), при этом кардинальностью одного множества будет κ, а другого — λ. Произведение κ⋅λ определяется как кардинальность декартова произведения κ×λ. Операции сложения и умножения бесконечных кардинальных чисел тривиальны, ибо если κ и λ — бесконечные кардинальные числа, тогда κ+λ=κ⋅λ=maximum{κ,λ}.
Напротив, возведение в степень кардинальных чисел — крайней нетривиальная операция, ибо даже значение простейших нетривиальных бесконечных степеней — 2ℵ0 — неизвестно и не может быть определено в ZFC (см. ниже). Кардинальное число κλ определяется как кардинальность декартова λ-кратного произведения κ; таким же образом определяется кардинальность множество всех функций от λ до κ. Согласно теореме Кёнига, κcf(κ)>κ, а это значит, что конфинальность кардинального числа 2ℵ0, каким бы оно ни было, должна быть несчетной. В сущности, это все, что можно сказать о значении степени 2ℵ0 исходя из ZFC.
В случае возведения в степень сингулярных кардинальных чисел ZFC позволяет нам сказать гораздо больше. В 1989 году Сахарону Шелаху удалось прийти к важному выводу, что если ℵω является строгим пределом, т.е. 2ℵn<ℵω для любого n<ω, тогда 2ℵω<ℵω4 (см. Shelah 1994). Технику доказательства этой теоремы и аналогичных ей теорем в ZFC, разработанную Шелахом, называют теорией pfc (possible confinalities — теория возможных конфинальностей). Эта теория нашла множество применений и в других разделах математики.
Апостериори аксиомы ZF — помимо аксиомы объемности, не требующей обоснования, поскольку в ней просто утверждается некоторое свойство множеств — можно обосновать через их использование в построении кумулятивной иерархии множеств. То есть в ZFC мы определяем использование трансфинитных рекурсий функций класса, предписывающих каждому ординалу α множество Vα, заданное следующим образом:
● V0=∅
● Vα+1=P(Vα)
● Vα=⋃β<αVβ, всегда, когда α — предельный ординал.
Аксиома булеана используется для того, чтобы получить Vα+1 из Vα. Схемы преобразования и объединения позволяют построить Vα для α предельного ординала. Действительно, представим функцию, предписывающую каждому β<α множество Vβ. По схеме преобразования, совокупность всех Vβ для β<α является множеством, следовательно, аксиома объединения, примененная к этому множеству, дает Vα. Аксиома бесконечности необходима для доказательства существования ω, а следовательно — и трансфинитной последовательности ординалов. Наконец, аксиома регулярности, исходя из остальных аксиом, равнозначна утверждению, что всякое множество принадлежит некоторому универсуму Vα с некоторым ординалом α. Таким образом, ZF доказывает, что теоретико-множественный универсум, называемый V, представляет собой объединение всех Vα, если α — ординал.
Собственный класс V вкупе с отношением ∈ удовлетворяет всем аксиомам ZFC, а следовательно — и модели ZFC. Он является предполагаемой моделью ZFC; можно сказать, что ZFC задает описание V. Впрочем, как мы увидим далее, это описание весьма неполное.
Одним из важных свойств V является так называемый принцип рефлексивности. То есть для всякой формулы φ(x1,…,xn) ZFC доказывает, что существует некоторый универсум Vα, который ее отражает, иными словами, что для всякого a1, …, an∈Vα, φ(a1,…,an) выполняется в V, если и только если φ(a1,…,an) выполняется в Vα.
Таким образом, V нельзя охарактеризовать никаким высказыванием, поскольку всякое высказывание, которое является истинным в V, также должно быть истинным в некотором исходном сегменте Vα. В частности, ZFC нельзя аксиоматизировать окончательно, в противном случае ZFC доказывала бы, что для неограниченного набора ординалов α Vα является моделью ZFC — а это противоречит второй теореме Гёделя о неполноте (см. раздел 2).
Принцип рефлексивности воплощает сущность теории множеств ZF, ведь, как показал Леви (Levy 1960), аксиомы объемности, выделения и регулярности вкупе с принципом рефлексивности, сформулированным в качестве схемы аксиом, утверждающей, что всякую формулу отображает некоторое множество, содержащее все элементы и все подмножества его элементов (отметим, что Vα таковым является), — всё это равнозначно ZF.
Всякий математический объект можно рассматривать как множество. Например, натуральные числа отождествляются с конечными ординалами: N=ω. Множество целых чисел Z можно определить как множество эквивалентных классов пар натуральных чисел, выполняющих условие (n,m)≡(n′,m′) если и только если n+m′=m+n′. Отождествляя всякое натуральное число n с эквивалентным классом пар (n,0), можно легко перенести правила сложения и произведения натуральных чисел на Z (подробнее см. в Enderton 1977; альтернативное построение см. в Levy 1979). Далее можно определить рациональные числа Q как множества эквивалентных классов пар (n,m) целых чисел, где m≠0 при выполнении равенства (n,m)≡(n′,m′), если и только если n⋅m′=m⋅n′. Опять же, операции сложения и произведения на Z можно естественным образом перенести на Q. Кроме того, упорядочение ≤Q на дроби задается следующим образом: r≤Qs, если и только если существует t∈Q такое, что s=r+t Действительные числа можно определить как дедекиндовы сечения Q: действительное число задается парой (А,В) непустых равномощных множеств, так что A∪B=Q и a≤Qb для всех a∈A и b∈B. Тогда мы можем, опять же, перенести операции сложения и умножения на Q, а также упорядочение ≤Q на множество действительных чисел R.
Подчеркнем, что здесь не утверждается, что, скажем, действительные числа являются дедекиндовыми сечениями рациональных чисел, ведь их также можно представить с помощью последовательности Коши или как-то иначе. Что важно с точки зрения обоснования, так это то, что теоретико-множественная версия R вкупе с обычными алгебраическими операциями удовлетворяет основополагающим аксиомам, которым удовлетворяют действительные числа, а именно аксиомам полного упорядоченного поля. Метафизический вопрос о том, чем на самом деле являются действительные числа, здесь роли не играет.
Алгебраические структуры можно также рассматривать как множества, раз всякое n-арное отношение элементов множества А можно представить как множества из n элементов (a1, …, an) элементов А. И всякую n-арную функцию f на А, область значения которой составляет множество В, можно представить в виде множества из n+1 элементов ((a1, …, an),b) такое, что b является значением f на (a1, …, am). Таким образом, например, группа представляет собой простую тройку (А,+,0), где А — непустое множество, + является бинарной функцией на А (т.е. ассоциативной), 0 — элемент А такой, что а+0=0+а=а для всех а∈А, и для всех а∈А существует элемент А, обозначаемый –а, такой что a+(−a)=(−a)+a=0. Кроме того, топологическое пространство представляет собой просто множество Х вкупе с топологией τ на этом множестве, то есть τ является подмножеством Р(Х), содержащим Х и ∅, замкнутым относительно произвольных объединений и конечных пересечений.
Любой математический объект — абсолютно любой — можно представить в виде множества или собственного класса. Свойства объекта можно выразить с помощью языка теории множеств.
Всякое математическое утверждение можно формализовать при помощи языка теории множеств, и всякую математическую теорему можно вывести из аксиом ZFC или некоторых следствий из ZFC, используя исчисление логики первого порядка. Именно в этом смысле теория множеств служит основанием математики.
Хотя роль обоснования математики является безусловно значимой для теории множеств, тем не менее это далеко не единственная причина, по которой ее стоит изучать. Идеи и техники, разработанные в рамках теории множеств, например, комбинаторика, метод вынуждения или теория больших кардиналов — все это превратило ее в глубокую и захватывающую математическую теорию, которая достойна изучения сама по себе и может находить важные применения практически во всех разделах математики.
Метаматематика
Благодаря тому примечательному факту, что практически всю математику можно формализовать в ZFC, возможно исследование самой математики при помощи математических средств. Так, любой вопрос, связанный с существованием математического объекта или доказуемостью допущения или гипотезы, можно представить в строгой математической формулировке. Благодаря этому и возможна метаматематика — математическое исследование самой математики. Таким образом, вопрос о доказуемости или недоказуемости любого математического утверждения становится осмысленной математической проблемой. Сталкиваясь с открытой математической проблемой или гипотезой, имеет смысл задаться вопросом о ее доказуемости или недоказуемости в рамках формальной системы ZFC. К сожалению, ответ может отсылать к чему-то третьему, поскольку даже если ZFC действительно непротиворечива, все же она неполна.
Феномен неполноты
Из теоремы Гёделя о неполноте для логики первого порядка следует, что ZFC непротиворечива — то есть что из нее нельзя вывести противоречие — если и только если у нее есть модель. Моделью ZFC является пара (М,Е), где М — непустое множество, а Е — бинарное отношение на М, такое что все аксиомы ZFC будут истинны, если интерпретировать их в (М,Е), то есть если фигурирующие в аксиомах переменные пробегают элементы М и ∈ интерпретируется как Е. Таким образом, если φ — выражение языка теории множеств и можно найти модель ZFC, в которой φ истинно, то его отрицание, ¬φ, невозможно доказать в ZFC. Следовательно, если мы можем найти модель φ, а также модель ¬φ, то невозможно доказать ни истинность, ни ложность φ в рамках ZFC, и в таком случае мы должны сказать, что φ неразрешимо или независимо от ZFC.
В 1931 году Гёдель заявил о своих поразительных теоремах о неполноте, в которых утверждалось, что любые формальные системы для математики непременно должны быть неполными. В частности, если ZFC непротиворечива, то в ZFC должны существовать неразрешимые утверждения. Кроме того, вторая теорема Гёделя о неполноте предполагает, что формальное (арифметическое) выражение CON(ZFC), утверждающее, что даже если ZFC действительно непротиворечива, утверждение о ее непротиворечивости невозможно доказать в самой ZFC. И также невозможно доказать обратное. Таким образом, CON(ZFC) неразрешима в ZFC.
Если ZFC непротиворечива, тогда в ней нельзя доказать существование модели ZFC, ведь в противном случае ZFC доказывала бы свою непротиворечивость. Таким образом, доказательство непротиворечивости или неразрешимости данного высказывания φ всегда будет лишь относительно непротиворечивым. То есть мы заключаем, что ZFC непротиворечива, поскольку у нее есть модель, и затем мы строим другую модель ZFC, в которой φ истинно. В последующих разделах мы рассмотрим несколько примеров.
Со времен Кантора и примерно до 1940 года теория множеств в основном развивалась в связи с проблемой континуума, то есть действительной линии R. Главным предметом исследования были так называемые свойства регулярности, а также другие структурные свойства легко определяемых множеств действительных чисел — этот раздел математики известен под названием дескриптивной теории множеств.
Дескриптивная теория множеств
Дескриптивная теория множеств — это исследование свойств и структур определенных множеств действительных чисел и, в более общем виде, определенных подмножеств Rn и прочих польских пространств (топологических пространств, которые гомеоморфны отдельным полным метрическим пространствам), например, бэровского пространства N всех функций f:N→N, пространства комплексных чисел, гильбертова пространства и отдельных банаховых пространств. Простейшие множества действительных чисел являются базовыми открытыми множествами (открытыми интервалами с конечными точками, заданными рациональными числами) и их дополнениями. Множества, которые можно получить в результате конечного числа шагов, начиная с базовых открытых множеств, применяя операции дополнения и составления счетного объединения ранее полученных множеств — это борелевские множества. Все борелевские множества являются регулярными, то есть они пользуются всеми классическими свойствами регулярности. Одним из примеров регулярного свойства является измеримость Лебега: ко множеству действительных чисел применима мера Лебега, если оно отлично от борелевского множества за счет пустого множества, то есть множества, которое можно покрыть множествами с базовыми открытыми интервалами сколь угодно малой длины. Таким образом, проще говоря, ко всякому борелевскому множеству применима мера Лебега, однако более сложные множества, чем борелевское, могут быть неизмеримы. Другими классическими свойствами регулярности являются бэровское свойство (множество, состоящее из действительных чисел, обладает бэровским свойством, если оно отличается от открытого множества за счет остаточного множества, а именно множества, представляющего собой счетное объединение множеств, которые не являются плотными ни на одном интервале), а также свойство совершенного множества (множество, состоящее из действительных чисел, обладает свойством совершенного множества, либо если оно счетно, либо если оно содержит совершенное множество, то есть непустое замкнутое множество без изолированных точек). В ZFC можно доказать существование нерегулярных множеств, состоящих из действительных чисел, однако для этого необходима АС (Solovay 1970).
Аналитические множества, также называемые Σ11, являются непрерывными образами борелевских множеств; а коаналитические множества (или Π11) являются дополнениями аналитических множеств.
Исходя из аналитических (или коаналитических) множеств и применяя операцию проекции (из произведения пространства R×N на R) и дополнения, мы получим проективные множества. Проективные множества образуют иерархию возрастающей сложности. Например, если A⊆R×N является коаналитическим, тогда проекция {x∈R:∃y∈N((x,y)∈A)} является проективным множеством уровня сложности, следующего за коаналитическими множествами. Такие множества называются Σ12, а их дополнения называются Π12.
Проективные множества довольно часто встречаются в математической практике, ведь множество А, состоящее из действительных чисел, является проективным, если и только если его можно определить в структуре
R=(R,+,⋅,Z).
То есть существует формула первого порядка φ(x,y1,…,yn) в языке для такой структуры, что для некоторого r1,…,rn∈R будет верно A={x∈R:R⊨φ(x,r1,…,rn)}.
ZFC доказывает, что всякое аналитическое множество, а следовательно, и всякое коаналитическое множество поддаются мере Лебега и обладают бэровским свойством. Она также доказывает, что всякое аналитическое множество обладает свойством совершенного множества. Однако свойство совершенного множества для коаналитических множеств предполагает, что первое несчетное кардинальное число ℵ1 является большим кардинальным числом в построенном универсуме L (см. раздел 7) —так называемым недостижимым кардинальным числом (см. раздел 10), которое предполагает, что в ZFC невозможно доказать, что любое коаналитическое множество обладает свойством совершенного множества.
Теория проективных множеств более высокой сложности, чем коаналитические, полностью не определена ZFC. Например, в L существует множество Σ12, которое является неизмеримым и не обладает бэровским свойством, в то время как, если аксиома Мартина верна (см. раздел 11), всякое такое множество обладает такими свойствами регулярности. Но все же есть аксиома, называемая аксиомой проективной детерминированности (PD), которая совместима с ZFC, что означает непротиворечивость некоторых больших кардинальных чисел (по сути, это следует из самого существования некоторых больших кардинальных чисел), и которая предполагает, что все проективные множества являются регулярными. Кроме того, PD позволяет разрешить большинство вопросов, связанных с проективными множествами. Подробнее см. статью о больших кардинальных числах и детерминированности.
Детерминированность
Свойство регулярности множеств, включающее все прочие классические свойства регулярности, — это свойство детерминированности. Для простоты мы будем работать с бэровским пространством N. Мы помним, что элементами N являются функции f:N→N, то есть последовательности натуральных чисел с длиной ω. Пространство N топологически эквивалентно (то есть гомеоморфно) множеству иррациональных точек R. Таким образом, поскольку нас интересуют свойства регулярности подмножеств R и поскольку счетными множествами, такими как множество рациональных чисел, можно пренебречь в плане этих свойств, мы также можем работать с N вместо R.
При данном A⊆N пусть будет игра, связанная с А; обозначим ее как GA. В ней участвуют двое игроков, Игрок 1 и Игрок 2, которые по очереди делают ход ni∈N: Игрок 1 делает ход n0, затем Игрок 2 делает ход n1, затем Игрок 1 делает ход n2 и т.д. Так, на шаге 2k Игрок 1 совершает ход n2k, а на шаге 2k+1 Игрок 2 ходит n2k+1. Можно наглядно представить последовательность этой игры следующим образом:
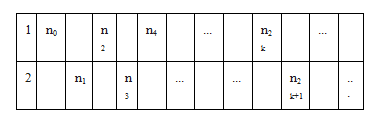
После бесконечного числа шагов два игрока производят бесконечную последовательность натуральных чисел. Игрок 1 выигрывает игру, если последовательность принадлежит А. В противном случае побеждает Игрок 2.
Игра GA является детерминированной, если существует победная стратегия для одного из игроков. Победная стратегия для одного из игроков, скажем, для Игрока 2 — это отображение σ из множества конечных последовательностей натуральных чисел в N такое, что, если игрок действует согласно этой функции, то есть играет σ(n0,…,n2k) на ходу k, он всегда будет побеждать в игре, что бы при этом ни делал другой игрок.
Мы будем говорить, что подмножество А множества N является детерминированным, если и только если игра GA является детерминированной.
В ZFC (при этом необходимо применение АС) можно доказать, что существуют недетерминированные множества. Таким образом, аксиома детерминированности (AD), которая гласит, что все подмножества N являются детерминированными, несовместима с АС. Однако Дональду Мартину удалось доказать в рамках ZFC, что всякое борелевское множество является детерминированным. Кроме того, он показал, что если существует большое кардинальное число, называемое измеримым (см. раздел 10), то даже аналитические множества являются детерминированными. Аксиома проективной детерминированности (PD) утверждает, что всякое проективное множество является детерминированным. Выходит, что, согласно PD, все проективные множества действительных чисел являются регулярными. Вудин показал, что в некотором смысле PD позволяет разрешить практически все проблемы, связанные с проективными множествами. Более того, по-видимому, PD для этого просто необходима. Другая аксиома, ADL(R), утверждает, что AD истинна в L(R) — в наименьшем транзитивном классе, содержащем все ординалы и все действительные числа, и удовлетворяющем аксиомам ZF (см. раздел 7). Таким образом, ADL(R) подразумевает, что любое множество, состоящее из действительных чисел, которое принадлежит L(R), является регулярным. Кроме того, так как ADL(R) содержит все проективные множества, то из ADL(R) следует PD.
Континуум-гипотеза
В континуум-гипотезе (СН). сформулированной Кантором в 1878 году, говорится о том, что кардинальность всякого бесконечного множества, состоящего из действительных чисел, будет либо ℵ0, либо она будет равна кардинальности всего множества R. Таким образом, СН равнозначна 2ℵ0=ℵ1.
Кантор доказал в 1883 году, что замкнутые множества действительных чисел обладают свойством совершенного множества, из чего следует, что всякое несчетное замкнутое множество, состоящее из действительных чисел, характеризуется той же кардинальностью, что R. Таким образом, СН истинна для замкнутых множеств. Более 30 лет назад Павел Александров расширил этот результат до всех борелевских множеств, а затем Михаил Суслин доказал, что СН истинна для всех аналитических множеств. Следовательно, все аналитические множества удовлетворяют СН. Однако попытки доказать, что все коаналитические множества удовлетворяют СН, не увенчаются успехом, поскольку это невозможно доказать в рамках ZFC.
В 1938 году Гёдель доказал непротиворечивость СН и ZFC. Исходя из предположительной непротиворечивости ZFC, он выстраивает модель ZFC, известную как конструктивный универсум, в котором СН истинна. Так, доказательство показывает, что если ZF непротиворечива, то непротиворечивы ZF и АС, а также ZF и СН. Следовательно, если мы допускаем непротиворечивость ZF, то АС невозможно будет опровергнуть в ZF — и СН также будет невозможно опровергнуть в ZF.
Обзор текущих дискуссий вокруг данной проблемы, включая недавние результаты, полученные Вудином, см. в статье, посвященной континуум-гипотезе.
Конструктивный универсум Гёделя, обозначаемый как L, задается с помощью трансфинитной рекурсии на ординалах, подобно V, но на последующих ступенях вместо того, чтобы получить множество Vα+1 из множества Vα, нам требуются только те подмножества Lα, которые можно определить в Lα, если использовать элементы Lα в качестве параметров. Таким образом, если PDef(X) обозначает множество всех подмножеств Х, определимых в структуре (Х,∈) за счет формул языка теории множеств, используя элементы Х в качестве параметров определения, мы получаем
● L0=∅
● Lα+1=PDef(Lα)
● Lλ=⋃α<λLα, если λ — предельный ординал.
Тогда L — совокупность всех Lα, где α — ординал, то есть L=Uα∈ONLα.
Гёдель показал, что L удовлетворяет всем аксиомам, а также удовлетворяет СН. Действительно, он удовлетворяет обобщенной континуум-гипотезе (GCH), то есть 2ℵα=ℵα+1 для всякого ординала α.
Высказывание V=L, называемое аксиомой конструктивности, утверждает, что всякое множество принадлежит L. Это утверждение истинно в L, так как оно не противоречит ZFC, и из него следует как AC, так и GCH.
Собственный класс L вкупе с отношением ∈, ограниченным до L, является внутренней моделью ZFC, то есть он является транзитивным (содержащим все элементы, входящие в его элементы) классом, который содержит все ординалы и удовлетворяет всем аксиомам ZFC. По сути, это наименьшая внутренняя модель ZFC, поскольку она содержится в любой другой внутренней модели.
В более общем виде, располагая произвольным множеством А, мы можем построить наименьшую транзитивную модель ZF, содержащую А и все ординалы, так же как и L, но теперь начиная с транзитивного замыкания {A}, наименьшего транзитивного множества, содержащего А, вместо ∅. Полученная в результате модель L(A), однако, необязательно должна быть моделью АС. Одной очень важной такой моделью является L(R) — наименьшая транзитивная модель ZF, содержащая все ординалы и все действительные числа.
Развитие теории конструктивных множеств многим обязано трудам Рональда Дженсена. Он развил так называемую теорию тонкой структуры L и выделил некоторые комбинаторные принципы — такие как ♢ и □, — которые можно использовать для того, чтобы вывести сложные конструкции неисчислимых математических объектов. Теория тонкой структуры также играет очень важную роль в анализе больших L-образных моделей, таких как L(R) или внутренних моделей для больших кардиналов (см. раздел 10.1).
В 1963 году, спустя двадцать пять лет после гёделевского доказательства непротиворечивости СН и АС относительно ZF, Пол Коэн (1969) доказал непротиворечивость отрицания СН, а также отрицания АС относительно непротиворечивости ZF. Таким образом, если ZF непротиворечива, тогда СН неразрешима в ZFC, а АС неразрешима в ZF. Чтобы достичь этого результата, Коген применил новую и чрезвычайно действенную технику, называемую вынуждением или форсингом (forcing), для расширения счетных транзитивных моделей ZF.
Так как из аксиомы V=L следует АС и СН, то любая модель отрицания АС или СН должна противоречить V=L. Давайте же проиллюстрируем идею вынуждения в случае построения модели для отрицания V=L. Мы начнем с транзитивной модели М для ZFC, которая, как мы можем допустить, не теряя степени обобщенности, является моделью V=L. Чтобы прийти в противоречие с V=L, нам нужно расширить М за счет прибавления нового множества r таким образом, чтобы в рамках расширенной модели r было неконструктивным множеством. Так как все наследственно конечные множества являются конструктивными, мы должны прибавить бесконечное множество натуральных чисел.
Первая проблема, с которой мы сталкиваемся, состоит в том, что М может уже содержать все подмножества ω. К счастью, по теореме Лёвенгейма — Скулема для первопорядковой логики, М характеризуется элементарной подмоделью N. Таким образом, поскольку нас интересуют только утверждения, истинное в М, а не М как таковая, мы также можем допустить, что сама М является счетной. Тогда, коль скоро P(ω) несчетно, то существует огромное число подмножеств ω, не принадлежащих М. Однако, к сожалению, мы не можем просто взять любое бесконечное множество r или ω, не принадлежащее М, и добавить его в М, поскольку r может содержать много информации, так что, если добавить его в М, М перестанет быть моделью ZFC или же будет оставаться моделью V=L. Чтобы этого избежать, нам нужно тщательно подобрать r. Идея состоит в том, чтобы r было родовым для М, то есть чтобы r выстраивалось из конечных аппроксимаций таким образом, чтобы оно не обладало никаким свойством, которое было бы определимым в М и которое можно избежать. Например, если мы рассматриваем r как бесконечную последовательность натуральных чисел, расположенную в возрастающем порядке, свойство r, содержащего только конечный ряд четных чисел, можно избежать, потому что при любой конечной аппроксимации r — то есть при всяком конечном увеличении последовательности натуральных чисел — мы всегда можем расширить это множество, добавив еще четных чисел, так что в конце конструирования r будет содержать бесконечно много четных чисел; хотя и нельзя будет избежать свойства содержания числа 7, ведь когда конечная аппроксимация к r содержит число 7, тогда оно будет присутствовать, каким бы образом мы ни проводили построение r. Так как М счетно, то такие родовые r существуют. Тогда расширенная модель M[r], которая включает М и содержит новое множество r, будет называться родовым расширением М. Коль скоро мы допускаем, что М — транзитивная модель V=L, то модель M[r] является просто Lα(r), где α — супремум ординалов М. Тогда при помощи принудительного отношения между конечными аппроксимациями к r и формулами в языке теории множеств, расширенной за счет так называемых имен для множеств в родовых расширениях, мы можем показать, что М[r] является моделью ZFC и что r невозможно построить в M[r], а следовательно, аксиома конструктивности V=L будет опровержена.
В общем и целом, вынужденное расширение модели М достигается за счет прибавления к М родового подмножества G некоторого частично упорядоченного множества Р, принадлежащего М. В приведенном выше примере Р было бы множеством всех конечных возрастающих последовательностей натуральных чисел, рассматриваемых как конечных аппроксимации к бесконечным последовательностям r, упорядоченным при помощи ⊆; а G было бы множеством всех конечных исходных сегментов r.
В случае непротиворечивого доказательства отрицания СН мы начинаем с модели М и прибавляем ℵ2 новых подмножеств ω, так что в родовом расширении СН опровергается. В таком случае нам необходимо использовать соответствующее частичное упорядочение Р, так чтобы ℵ2, содержащееся в М, не схлопнулось, то есть чтобы оно совпадало с ℵ2 родового расширения, и таким образом родовое расширение М[G] будет удовлетворять утверждению, согласно которому существует ℵ2 действительных чисел.
Другие применения метода вынуждения
Помимо СН, техника вынуждения используется во многих других математических задачах и проблемах, связанных с континуумом и прочими бесконечными математическими объектами, которые оказались неразрешимыми в ZFC.
Один из наиболее важных примеров представляет гипотеза Суслина (SH). Кантор доказал, что всякое линейно упорядоченное множество S без крайних точек, которое является плотным (между любыми двумя различными элементами S можно указать еще один элемент), полным (у всякого ограниченного сверху подмножества S есть супремум) и обладает плотным счетным подмножеством, будет изоморфно вещественной прямой. Суслин предположил, что это также будет верно, если смягчить требование о содержании плотного счетного множества, сказав, что всякая совокупность попарно-равномощных интервалов является счетной. В начале 1970-х годов Томас Жеч придумал последовательный контрпример с использованием техники вынуждения, а Рональд Дженсен доказал, что данный контрпример существует в L. Примерно в это же время Роберт Соловей и Стэнли Тенненбаум (Solovey and Tennenbaum 1971) разработали и впервые применили итерированную технику вынуждения, чтобы построить модель, в которой бы выполнялась SH, тем самым показывая ее независимость от ZFC. Чтобы убедиться в том, что SH выполняется в родовом расширении, необходимо опровергнуть все контрпримеры, однако опровергнув один конкретный контрпример, мы можем случайно произвести другие, так что нам придется использовать технику вынуждения вновь и вновь; в сущности, нам пришлось бы продолжать эту операцию по меньшей мере на протяжении ω2 шагов. Именно поэтому нам необходима итерация вынуждения.
Среди прочих известных математических проблем, неразрешимость которых в ZFC удалось доказать, благодаря технике вынуждения, в частности за счет применения итерированного вынуждения, иногда в сочетании с большими кардинальными числами, можно назвать проблему измерения и гипотезу Бореля в связи с мерой множества, гипотезу Капланского об алгебре Банаха, а также проблему теории групп Уайтхеда.
По итогам разработок последних пятидесяти лет, связанных с техникой вынуждения и ее применением ко множеству открытых проблем в математике, в настоящий момент существуют буквально тысячи вопросов — практически во всех разделах математики — которые, как было доказано, являются независимыми от ZFC. Сюда входят практически все вопросы относительно структуры несчетных множеств. Можно сказать, что феномен неразрешимости настолько вездесущий, что исследование несчетных множеств оказывается практически невозможным только в рамках ZFC (впрочем, существуют весьма примечательные исключения; см. Shelah 1994).
Это подводит нас к вопросу об истинностном значении высказываний, которые оказываются неразрешимыми в ZFC. Должны ли мы удовлетвориться тем, что они неразрешимы? Имеет ли смысл задаваться вопросом об их истинностном значении? Существует несколько возможных позиций на этот счет. Одна из них — позиция скептика: насчет высказываний, неразрешимых в ZFC, не существует окончательного ответа, они также могут оказаться, по существу, пустыми. Другая позиция весьма широко распространена среди математиков, ее также придерживался Гёдель: неразрешимость всего лишь показывает, что система ZFC слишком слабая, чтобы в ней можно было дать ответ на эти вопросы, а следовательно, нам нужно искать новые аксиомы, и когда мы дополним ими ZFC, то сможем найти ответы на эти вопросы. Такой поиск новых аксиом получил название Программы Гёделя (философские аспекты программы Гёделя см. в Hauser 2006; обзор философских проблем обоснования новых аксиом теории множеств см. в статье о больших кардинальных числах и детерминированности).
Центральный мотив теории множеств, таким образом, связан с поиском и классифицированием новых аксиом. Последние в настоящий момент подпадают под два типа: аксиомы больших кардинальных чисел и аксиомы вынуждения.
В рамках ZFC невозможно доказать существование регулярного предельного кардинального κ, поскольку если κ является таким кардинальным числом, тогда Lκ будет моделью ZFC и тогда ZFC доказывала бы собственную непротиворечивость, тем самым противореча второй теореме Гёделя о неполноте. Таким образом, существование регулярного предельного кардинального числа необходимо постулировать в качестве новой аксиомы. Такое кардинальное число называют слабо недостижимым. Если, кроме того, κ является сильным пределом, то есть 2λ<κ для любого кардинального числа λ<κ, тогда κ называют сильно недостижимым. Кардинальное число κ является сильно недостижимым, если и только если оно регулярно и Vκ является моделью ZFC. Если GCH выполняется, тогда всякое слабо недостижимое кардинальное число должно быть сильно недостижимым.
Большие кардинальные числа — это несчетные кардинальные числа, удовлетворяющие некоторым свойствам, которые делают их очень большими, и их существование недоказуемо в ZFC. Первое слабо недостижимое кардинальное число является наименьшим из всех больших кардинальных чисел. Помимо недостижимых кардинальных чисел существует богатое и сложное разнообразие больших кардинальных чисел, формирующих линейную иерархию по принципу наибольшей непротиворечивости, а зачастую – и по принципу наиболее непосредственной выводимости (подробнее см. статью о независимости и больших кардинальных числах).
Чтобы образовать следующее, более мощное свойство больших кардинальных чисел, скажем, что подмножество С бесконечного кардинального числа κ является замкнутым, если всякий предел элементов С также находится в С; и С является неограниченным, если для всякого α<κ существует β∈C больше, чем α. Например, множество предельных ординалов меньших, чем κ, является замкнутым и неограниченным. Кроме того, подмножество S из κ называется стационарным, если оно пересекается с каждым замкнутым незамкнутым подмножеством, входящим в κ. Если κ — регулярное и несчетное множество, тогда множество всех ординалов, меньших, чем κ с конфинальностью ω, является примером стационарного множества. Регулярное кардинальное число называется кардинальным числом Мало (Mahlo), если множество сильно недостижимых кардиналов, меньших, чем κ, является стационарным. Таким образом, первое кардинальное число Мало гораздо больше, чем первое сильно недостижимое кардинальное число, так как существует κ сильно недостижимых кардинальных чисел, меньших, чем κ.
Более мощные свойства больших кардиналов возникают из анализа свойств сильной рефлексивности. Как мы помним, принцип рефлексивности (см. раздел 4), который можно доказать в ZFC, утверждает, что всякое истинное высказывание (то есть всякое высказывание, которое является истинным в V) будет истинным в некотором Vα. Если мы усилим этот принцип за счет его преобразования в высказывание второго порядка, мы получим некоторые большие кардиналы. Например, κ — сильно недостижимое кардинальное число, если и только если всякое высказывание Σ11 (утверждение о существовании второго порядка в языке теории множеств, в котором содержится один дополнительный предикативный символ), истинное в любом структуре вида (Vκ,∈,A), где A⊆Vκ, является истинным в некотором (Vα,∈,A∩Vα), при α<κ. Тот же самый тип рефлексивности, но теперь уже для высказываний Π11 (универсальных высказываний второго порядка), дает куда более мощное свойство большого кардинального числа κ, называемое слабой компактностью. Всякое слабо компактное кардинальное число κ является кардинальным числом Мало, и множество кардинальных чисел Мало, меньших, чем κ, является стационарным. Допуская рефлексию для более сложных высказываний второго или более высокого порядка, мы получаем большие кардинальные числа, которые являются более мощными, чем слабая компактность.
Наиболее известные большие кардинальные числа, которые называют измеримыми, были открыты Станиславом Уламом в 1930 году в ходе решения проблемы меры множества. Мерой множества (двузначной) или ультрафильтром на кардинальном числе κ является подмножество U∈Р(κ), обладающее следующими свойствами: (1) пересечение любых двух элементов U содержится в U; (2) если Х∈U и Y является подмножеством κ, таким что X⊆Y, тогда Y∈U; и (3) для всякого X∈κ, выполняется строгая дизъюнкция: либо X∈U, либо κ–X∈U. Мера множества U называется κ-полной, если всякое пересечение элементов, число которых меньше, чем κ элементов, принадлежащих U, также содержится в U. И мера множества называется непринципиальной, если не существует α<κ, которое принадлежит ко всем элементам U. Кардинальное число κ называется измеримым, если существует мера множества на κ, которая является κ-полной и непринципиальной.
Измеримые кардинальные числа можно описать с помощью элементарного вложения универсума V в некоторый транзитивный класс М. Когда говорят, что такое вложение j:V→M является элементарным, это означает, что j сохраняет истинность, то есть для любой формулы φ(x1,…,xn) языка теории множеств и любой последовательности a1,…,an, высказывание φ(a1,…,an) будет истинным в V, если и только если φ(j(a1),…,j(an)) истинно в М. Получается, что кардинальное число κ измеримо, если и только если существует элементарное вложение j:V→M, причем М — транзитивно, так что κ будет первым ординалом, сдвинутым j, то есть первым ординалом, таким что j(κ)≠κ. Мы будем говорить, что κ — критическая точка на j, и записывать это следующим образом: crit(j)=κ. Вложение j можно вывести из κ-полной непринципиальной меры на κ, используя так называемое построение ультрастепени. И напротив, если j:V→M является элементарным вложением, М — транзитивно и κ=crit(j), тогда множество U={X⊆κ:κ∈j(X)} является κ-полным непринципиальным ультрафильтром на κ. Полученная из j таким образом мера U называется нормальной.
Всякое измеримое кардинальное число κ является слабо компактным, и существует множество слабо компактных кардинальных чисел, меньших чем κ. В действительности, помимо κ существует множество полностью неописуемых кардинальных чисел — это значит, что они отражают все высказывания любой сложности, в языке любого порядка.
Если κ измеримо и j:V→M задается ультрастепенным построением, тогда Vκ⊆M и всякое высказывание меньшей длины, чем κ элементов из М, или равной ей, будет принадлежать М. Таким образом, М во многом схоже с V, но они не могут совпадать. Действительно, знаменитая теорема Кеннета Кунена доказывает, что не существует никакого элементарного вложения j:V→V, помимо тривиального — то есть тождества. Во всех известных доказательствах этого положения используется аксиома выбора, и вопрос о необходимости ее применения является исключительно важным. Благодаря требованию близкого сходства М и V теорема Кунена открывает возможность образования более мощных свойств больших кардинальных чисел, чем измеримость.
Например, κ называют сильным, если для всякого ординала α существует элементарное вложение j:V→M, для некоторого транзитивного М, так что κ=crit(j) и Vα⊆M.
Другое важное и гораздо более мощное свойство кардинальных чисел — это суперкомпактность. Кардинальное число κ называют суперкомпактным, если для всякого α существует элементарное вложение j:V→M с транзитивным М и критической точкой κ, такое что j(κ)>α и всякая последовательность элементов М длиной α принадлежит М.
Кардинальные числа Вудина располагаются между сильными и суперкомпактными. Всякое суперкомпактное кардинальное число является кардинальным числом Вудина, и если δ является кардинальным числом Вудина, тогда Vδ является моделью ZFC, в которой существует собственный класс сильных кардинальных чисел. Таким образом, хотя кардинальное число Вудина δ необязательно должно быть очень сильным само по себе (первое кардинальное число Вудина даже не является слабо компактным), это подразумевает, что в Vδ существует много больших кардинальных чисел.
Помимо суперкомпактных кардинальных чисел мы также находим кардинальные числа Райнхардта, огромные, сверхогромные кардинальные числа и т.д.
Теорема Кунена о несуществовании нетривиального элементарного вложения j:V→V, по сути, показывает, что для любого λ невозможно произвести элементарное вложение j:Vλ+2→Vλ+2, отличное от тождества.
Самые сильные свойства кардинальных чисел, которые, по всей видимости, не противоречат ZFC, формулируются следующим образом:
● Существует элементарное вложение j:Vλ+1→Vλ+1, отличное от тождества.
● Существует элементарное вложение j:L(Vλ+1)→L(Vλ+1), отличное от тождества.
Большие кардиналы образуют линейную иерархию по принципу большей непротиворечивости. В действительности они представляют собой основание иерархии интерпретируемых математических теорий (подробнее см. в статье о независимости и больших кардинальных числах). Для любого высказывания φ выполняется ровно одно из следующих трех положений касательно ZFC и φ:
● ZFC и φ вместе противоречивы.
● ZFC и φ равнонепротиворечиво ZFC.
● ZFC и φ равнонепротиворечиво ZFC и существованию некоторого большого кардинального числа.
Таким образом, большие кардинальные числа могут использоваться для доказательства того, что из данного высказывания φ не выводится другое высказывание Ψ, равное ZFC, за счет доказательства того, что из ZFC вместе с Ψ следует непротиворечивость некоторых больших кардинальных чисел, в то время как из ZFC и φ составляют непротиворечивую систему, если мы допускаем существование меньшее большого кардинального числа или только допускаем, что ZFC непротиворечива. Иными словами, Ψ более непротиворечива, чем φ, равное ZFC. Тогда, согласно второй теореме Гёделя о неполноте, исходя из ZFC и φ нельзя доказать ψ, если мы допускаем, что ZFC и φ составляют непротиворечивую систему.
Как уже было отмечено, в ZFC невозможно доказать существование больших кардинальных чисел. Однако все указывает на то, что их существование не только нельзя опровергнуть, но, в сущности, допущение их существования является весьма обоснованной аксиомой теории множеств. Во-первых, существует множество свидетельств в пользу их непротиворечивости, в частности, для тех больших кардинальных чисел, для которых возможно построить внутреннюю модель.
Внутренние модели больших кардинальных чисел
Внутренняя модель ZFC является транзитивным собственным классом, который содержит все ординалы и удовлетворяет всем аксиомам ZFC. Таким образом, L является наименьшей внутренней моделью, а V — наибольшей. Некоторые большие кардинальные числа, например, недостижимые, слабо компактные или кардинальные числа Мало, могут существовать в L. То есть, если κ обладает одним из таких свойств больших кардинальных чисел, тогда оно также будет обладает этим свойством в L. Однако некоторые большие кардинальные числа не существуют в L. Действительно, Скотт (Scott 1961) показал, что, если существует измеримое кардинальное число κ, тогда V≠L. Важно отметить, что κ не принадлежит L, так как L содержит все ординалы, но оно неизмеримо в L, так как κ-полная непринципиальная мера множества на κ не может существовать в L.
Если κ — измеримое кардинальное число, тогда мы можем построить L-образную модель, в которой κ будет измеримым, за счет применения κ-полной непринципиальной и нормальной меры множества U, примененной к κ, продолжив далее, как в определении L, но теперь используя U в качестве дополнительного предиката. Полученная модель, называемая L[U], будет внутренней моделью ZFC, в которой κ измеримо, причем κ будет единственным измеримым кардинальным числом. Модель является каноничной в том же смысле, что и любая другая нормальная мера множества, свидетельствующая об измеримости κ, производила бы ту же самую модель; она также обладает многими свойствами L. Например, она характеризуется проективной вполне упорядоченностью и удовлетворяет GCH.
Куда сложнее построить аналогичные L-образные модели для более сильных больших кардинальных чисел, таких как сильные кардинальные числа или кардинальные числа Вудина. Это модели вида L[E], где Е — последовательность расширенных систем (extenders), каждая из которых представляет собой систему мер множеств, задающих соответствующие элементарные вложения.
Наибольшие L-образные модели для больших кардинальных чисел, которые были получены на данный момент, могут содержать вудиновы пределы кардинальных чисел Вудина (Neeman 2002). Однако, построение L-образной модели для суперкомпактного кардинального числа все еще проблематично. Граница суперкомпактности, по-видимому, играет ключевую роль, поскольку Вудин смог доказать, что для L-образного типа моделей суперкомпактных кардинальных чисел, которые он называет Ultimate-L, все более сильные большие кардинальные числа, которые могут существовать в V (расширимые, огромные, I1 и т.д.), также будут существовать в этой модели. Построение Ultimate-L пока не доведено до конца, и все еще неясно, будет ли оно завершено, поскольку оно основано на некоторых технических гипотезах, которые нуждаются в подтверждении.
Следствия из существования больших кардинальных чисел
Существование больших кардинальных чисел имеет очень важные следствия, даже для легко определяемых малых множеств, таких как проективные множества, состоящие из действительных чисел. Например, Соловей (Solovay 1970) исходя из допущения о существовании измеримых кардинальных чисел доказал, что все множества Σ12 действительных чисел поддаются мере Лебега и обладают бэровским свойством, что невозможно доказать в ZFC. А Шелах и Вудин (Shelah and Woodin 1990) доказали, что из существования собственного класса кардинальных чисел Вудина следует, что теорию L(R), даже с действительными числами в качестве параметров, невозможно изменить при помощи техники вынуждения, а значит, все множества действительных чисел, принадлежащие L(R), являются регулярными. Далее, в соответствии с более слабой гипотезой о больших кардинальных числах, а именно гипотезой о существовании бесконечного числа кардиналов Вудина, Мартин и Стил (Martin and Steel 1989) смогли доказать, что всякое проективное множество действительных чисел является детерминированным, то есть аксиома PD будет выполняться, следовательно, все проективные множества являются регулярными. Более того, Вудин показал, что из существования бесконечного числа кардиналов Вудина, над которыми стоит измеримое кардинальное число, следует, что любое множество действительных чисел в L(R) является определенным, то есть аксиома ADL(R) будет выполняться, следовательно, все множества действительных чисел, принадлежащие L(R) — а значит, и все проективные множества — являются регулярными. Он также доказал, что кардинальные числа Вудина позволяют сделать оптимальные допущения о больших кардинальных числах, приведя доказательство следующих утверждений:
1. Существует бесконечно много кардинальных чисел Вудина.
2. ADL(R) являются равнонепротиворечивыми, т.е. ZFC + 1 непротиворечиво, если и только если ZFC + 2 непротиворечиво. Подробнее см. в статье о больших кардинальных числах и детерминированности.
Другая область, в которой большие кардинальные числа играют важную роль, связана с возведением в степень сингулярных кардинальных чисел. Так называемая гипотеза сингулярных кардиналов (SCH) полностью детерминирует поведение степеней сингулярных кардинальных чисел по показателям степеней регулярных кардинальных чисел. SCH следует из GCH, а следовательно, выполняется в L. Следствием из SCH является то, что, если 2ℵn<ℵω для всех конечных n, то 2ℵω=ℵω+1. Таким образом, если GCH выполняется для кардинальных чисел, меньших, чем ℵω, тогда она также выполняется для ℵω. SCH выполняется для первого суперкомпактного кардинального числа (Solovay). Но Магидор (Magidor 1977) доказал примечательный факт, что, благодаря допущению существования больших кардинальных чисел, возможно построить такую модель ZFC, в которой GCH не выполняется для ℵω, а следовательно, SCH также не будет выполняться. Для этого требуются большие кардинальные числа, более сильные, чем измеримые. С другой стороны, ZFC достаточно для доказательства того, что если SCH истинна для всех кардинальных чисел, меньших, чем ℵω1, то она также истинна и для ℵω1. Кроме того, если SCH истинна для всех сингулярных кардинальных чисел счетной конфинальности, тогда она будет истинна для всех сингулярных кардинальных чисел (Силвер).
Аксиомы вынуждения — это аксиомы теории множеств, которые утверждают, что некоторые утверждения о существовании теоретико-множественных объектов являются абсолютными между универсумом V всех множеств и его (идеальных) расширений, произведенных за счет процедуры вынуждения, то есть некоторые утверждения о существовании, которые являются истинными для некоторых расширений универсума V, истинны в самом универсуме V. Первая аксиома вынуждения была сформулирована Дональдом Мартином как следствие доказательства непротиворечивости гипотезы Суслина Соловеем и Тенненбаумом; ныне эта аксиома известна как аксиома Мартина (МА). Перед тем как сформулировать ее, скажем, что частичное упорядочение является непустым множеством Р вкупе с бинарным отношением ≤ на Р, которое является рефлексивным и транзитивным. Два элемента множества Р, p и q, называют совместимыми, если существует r∈P, такой что r≤p и r≤q. Антицепь Р является подмножеством Р, элементы которого попарно несовместимы. Частичное упорядочение Р называют ссс, если всякая антицепь Р является счетной. Непустое подмножество G, входящее в Р, называют фильтром, если (1) любые два элемента G совместимы, и (2) если p∈G и p≤q, то q∈G. Наконец, подмножество D, входящее в Р, называют плотным, если для всякого p∈P существует q∈D такое, что q≤p.
МА утверждает следующее:
Для всякого ссс частичного упорядочения Р и любого множества {Dα:α<ω1} плотных подмножеств Р существует фильтр G⊆P, который является родовым для этого множества, то есть G∩Dα≠∅ для всех α<ω1.
Мартин и Соловей (Martin and Solovay 1970) доказали непротиворечивость МА и ZFC применяя видоизмененную технику вынуждения к свойству ссс. На первый взгляд, МА не выглядит как аксиома, то есть не кажется очевидным или по крайней мере вполне обоснованным утверждением о множествах, но, скорее, она напоминает техническое утверждение о ссс частичных упорядочениях. МА, тем не менее, выглядит более естественно, если ее выразить в топологических терминах, ведь она представляет собой простое обобщение хорошо известной теоремы о категории Бэра, в которой говорится, что во всяком компактном хаусдорфовом топологическом пространстве пересечение открытых плотных счетных множеств будет непустым. Действительно, МА равнозначна следующему утверждению:
В любом компактном хаусдорфовом топологическом пространстве ссс пересечение открытых ℵ1-численных плотных множеств будет непустым.
Существует много разных равнозначных формулировок МА; эта аксиома весьма успешно использовалась для разрешения большого числа открытых проблем, существующих в других разделах математики. Например, из нее вытекает гипотеза Суслина и то, что всякое Σ12 множество действительных чисел поддается мере Лебега и обладает бэровским свойством. Из нее также следует, что СН неверна и что 2ℵ0 — регулярное кардинальное число, но невозможно определить исходя из МА, какое это кардинальное число (прочие следствия из МА и ее равнозначных формулировок см. в Fremlin 1984). Несмотря на это, статус МА в качестве аксиомы теории множеств все еще не вполне утвержден. Вероятно, наиболее естественной формулировкой МА, с точки зрения обоснованности, будет формулировка в терминах рефлексивности. МА равнозначна следующему утверждению (где НС обозначает множество наследственно счетных множеств — то есть счетных множеств, элементы которых являются счетными, и элементы подмножеств этих множеств также являются счетными и т.д.):
Для всякого ссс частичного упорядочивания Р, если утверждение о существовании относительно НС истинно в (идеальном) родовом расширении V, достижимом за счет процедуры вынуждения на Р, тогда это утверждение будет истинным, то есть оно будет выполняться в V. Иными словами, если множество, обладающее свойством, которое зависит только от множеств в НС, существует в некотором (идеальном) родовом расширении V, полученным благодаря процедуре вынуждения с ссс частичным упорядочением, тогда множество, обладающее таким свойством, уже существует в V.
Понятие идеального родового расширения V можно уточнить в терминах так называемых булево-значных моделей, которые дают альтернативный способ вынуждения.
Гораздо более сильные аксиомы вынуждения, чем МА, были введены в 1980-е годы, например, аксиома собственного вынуждения Баумгартена (Proper Forcing Axiom, PFA) и более сильный максимум Мартина (ММ) Формана, Магидора и Шелаха (Foreman, Magidor, and Shelah 1988), который, по сути, является наиболее сильной из всех возможных аксиом вынуждения. И PFА, и ММ не противоречат существованию суперкомпактного кардинального числа. PFA утверждает то же, что МА, но для частичного упорядочения, которое обладает более слабым свойством, чем ссс, называемым собственностью (properness; понятие ввел Шелах). ММ выдвигает то же утверждение для более широкого класса частичных упорядочений, которые не разрушают стационарные подмножества ω1 при процедуре вынуждения.
Из сильных аксиом вынуждения, таких как PFA и ММ, вытекает, что все проективные множества действительных чисел являются детерминированными (PD); они также дают множество других важных следствий для бесконечной комбинаторики. В частности, из них следует, что кардинальность континуума равна | | 2.
● Коэн, П. Дж., 1969 [1966], Теория множеств и континуум-гипотеза, Москва: Мир.
● Bagaria, J., 2008, “Set Theory”, in The Princeton Companion to Mathematics, edited by Timothy Gowers; June Barrow-Green and Imre Leader, associate editors. Princeton: Princeton University Press.
● Enderton, H.B., 1977, Elements of Set Theory, New York: Academic Press.
● Ferreirós, J., 2007, Labyrinth of Thought: A History of Set Theory and its Role in Modern Mathematics, Second revised edition, Basel: Birkhäuser.
● Foreman, M., M. Magidor, and S. Shelah, 1988, “Martin’s maximum, saturated ideals and non-regular ultrafilters”, Part I, Annals of Mathematics, 127: 1–47.
● Fremlin, D.H., 1984, “Consequences of Martin’s Axiom”, Cambridge tracts in Mathematics #84. Cambridge: Cambridge University Press.
● Gödel, K., 1931, “Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I,” Monatshefte für Mathematik Physik, 38: 173–198. English translation in Gödel 1986, 144–195.
● –––, 1938, “The consistency of the axiom of choice and of the generalized continuum hypothesis”, Proceedings of the National Academy of Sciences, U.S.A. 24: 556–557.
● –––, 1986, Collected Works I. Publications 1929–1936, S. Feferman et al. (eds.), Oxford: Oxford University Press.
● Hauser, K., 2006, “Gödel’s program revisited, Part I: The turn to phenomenology”, Bulletin of Symbolic Logic, 12(4): 529–590.
● Jech, T., 2003, Set theory, 3d Edition, New York: Springer.
● Jensen, R.B., 1972, “The fine structure of the constructible hierarchy”, Annals of Mathematical Logic, 4(3): 229–308.
● Kanamori, A., 2003, The Higher Infinite, Second Edition. Springer Monographs in Mathematics, New York: Springer.
● Kechris, A.S., 1995, Classical Descriptive Set Theory, Graduate Texts in Mathematics, New York: Springer Verlag.
● Kunen, K., 1980, Set Theory, An Introduction to Independence Proofs, Amsterdam: North-Holland.
● Levy, A., 1960, “Axiom schemata of strong infinity in axiomatic set theory”, Pacific Journal of Mathematics, 10: 223–238.
● –––, 1979, Basic Set Theory, New York: Springer.
● Magidor, M., 1977, “On the singular cardinals problem, II”, Annals of Mathematics, 106: 514–547.
● Martin, D.A. and R. Solovay, 1970, “Internal Cohen Extensions”, Annals of Mathematical Logic, 2: 143–178.
● Martin, D.A. and J.R. Steel, 1989, “A proof of projective determinacy”, Journal of the American Mathematical Society, 2(1): 71–125.
● Mathias, A.R.D., 2001, “Slim models of Zermelo Set Theory”, Journal of Symbolic Logic, 66: 487–496.
● Neeman, I., 2002, “Inner models in the region of a Woodin limit of Woodin cardinals”, Annals of Pure and Applied Logic, 116: 67–155.
● Scott, D., 1961, “Measurable cardinals and constructible sets”, Bulletin de l’Académie Polonaise des Sciences. Série des Sciences Mathématiques, Astronomiques et Physiques, 9: 521–524.
● Shelah, S., 1994, “Cardinal Arithmetic”, Oxford Logic Guides, 29, New York: The Clarendon Press, Oxford University Press.
● –––, 1998, Proper and improper forcing, 2nd Edition, New York: Springer-Verlag.
● Shelah, S. and W.H. Woodin, 1990, “Large cardinals imply that every reasonably definable set of reals is Lebesgue measurable”, Israel Journal of Mathematics, 70(3): 381–394.
● Solovay, R., 1970, “A model of set theory in which every set of reals is Lebesgue measurable”, Annals of Mathematics, 92: 1–56.
● Solovay, R. and S. Tennenbaum, 1971, “Iterated Cohen extensions and Souslin’s problem”, Annals of Mathematics (2), 94: 201–245.
● Todorcevic, S., 1989, “Partition Problems in Topology”, Contemporary Mathematics, Volume 84. American Mathematical Society.
● Ulam, S., 1930, ‘Zur Masstheorie in der allgemeinen Mengenlehre’, Fundamenta Mathematicae, 16: 140–150.
● Woodin, W.H., 1999, The Axiom of Determinacy, Forcing Axioms, and the Nonstationary Ideal, De Gruyter Series in Logic and Its Applications 1, Berlin-New York: Walter de Gruyter.
● –––, 2001, “The Continuum Hypothesis, Part I”, Notices of the AMS, 48(6): 567–576, and “The Continuum Hypothesis, Part II”, Notices of the AMS 48(7): 681–690.
● Zeman, M., 2001, Inner Models and Large Cardinals, De Gruyter Series in Logic and Its Applications 5, Berlin-New York: Walter de Gruyter.
● Zermelo, E., 1908, “Untersuchungen über die Grundlagen der Mengenlehre, I”, Mathematische Annalen 65: 261–281. Reprinted in Zermelo 2010: 189–228, with a facing-page English translation, and an Introduction by Ulrich Felgner (2010). English translation also in van Heijenoort 1967: 201–215.
Содержание:
Основные понятия:
Множество – одно из важнейших понятий математики. Вводится аксиоматически и не может быть определено через какие-либо элементарные понятия.
Кантор описывает множество следующим образом:
Множество S есть любое собрание определенных и различимых между собой объектов пашей интуиции и интеллекта, мыслимое как единое целое. Эти объекты называются элементами множества S
Термин «множество» характеризует совокупность, объединение некоторых объектов произвольной природы – элементов множества, которые обладают каким-либо общим для них свойством (признаком). Этот общий признак содержится в самом названии (задании) множества. Множество состоит из элементов и считается заданным, если о каждом из рассматриваемых объектов известно, входит он во множество или нет. Множество может быть задано либо перечислением его элементов, либо описанием свойств его элементов. Символическая запись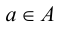
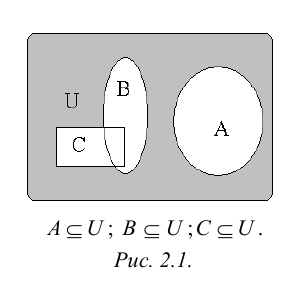
Рис. 2.1. Множество А называют подмножеством другого множества U или множество А включено во множество U, если каждый элемент множества А является одновременно элементом множества U. Это обозначается 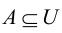 . Выделение подмножеств из множеств можно провести по различным признакам. В результате могут получиться как непересекающиеся подмножества (например, А и В ) так и подмножества, имеющие общие элементы ( В и С). Если множество состоит из конечного числа элементов, оно называется конечным. При этом число элементов множества может быть очень велико или вообще неизвестно. Множество может состоять также из бесконечного количества элементов, тогда оно называется бесконечным.
. Выделение подмножеств из множеств можно провести по различным признакам. В результате могут получиться как непересекающиеся подмножества (например, А и В ) так и подмножества, имеющие общие элементы ( В и С). Если множество состоит из конечного числа элементов, оно называется конечным. При этом число элементов множества может быть очень велико или вообще неизвестно. Множество может состоять также из бесконечного количества элементов, тогда оно называется бесконечным.
Свойства включения:
- Каждое множество есть подмножество самого себя
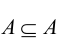 ;
; - Если
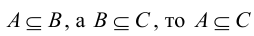 ;
; 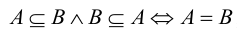 , т.е. множества А и В равны тогда и только тогда, когда эти множества состоят из одних и тех же элементов;
, т.е. множества А и В равны тогда и только тогда, когда эти множества состоят из одних и тех же элементов;- Каждый элемент множества А определяет некоторое подмножество множества А:
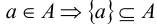
Множество, не содержащее ни одного элемента, называется пустым и обозначается 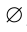 .
.
- Любое множество содержит
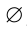 в качестве подмножества.
в качестве подмножества. - Каждое множество
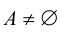 имеет, по крайней мере, два различных подмножества:
имеет, по крайней мере, два различных подмножества: 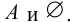 .
.
Множество 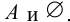 называют несобственными подмножествами множества А. Все остальные подмножества множества А называются собственными или истинными. В этом случае, когда
называют несобственными подмножествами множества А. Все остальные подмножества множества А называются собственными или истинными. В этом случае, когда 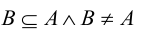 говорят, что В строго включено в А (обозначается
говорят, что В строго включено в А (обозначается 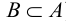 ):
):
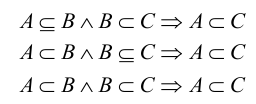
Множество всех подмножеств множества А называется множеством-степенью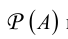 множества А.
множества А.
Если А не содержит элементов, т.е. 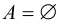 , то его единственным подмножеством является
, то его единственным подмножеством является 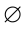 .
.
Если А – одноэлементное множество, т.е. 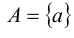 , то его подмножествами являются А и
, то его подмножествами являются А и 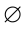 . Число этих подмножеств равно 2.
. Число этих подмножеств равно 2.
Если А – двухэлементное множество, т.е. 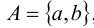 , то его подмножествами являются
, то его подмножествами являются 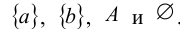 Число этих подмножеств равно 4.
Число этих подмножеств равно 4.
Несложно убедиться в том, что множество-степень 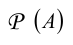 конечного n-элементного множества (А) состоит из 2″ подмножеств.
конечного n-элементного множества (А) состоит из 2″ подмножеств.
Основные операции над множествами
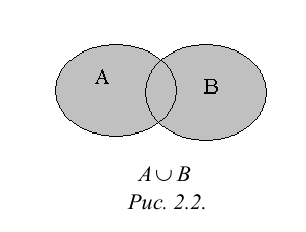
Суммой или объединением двух или произвольного (даже бесконечного) числа заданных множеств называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из заданных множеств. Эта операция над множествами обозначается знаком 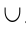 .
.
Произведением или пересечением двух или произвольного (даже бесконечного) числа заданных множеств называется множество, состоящее из всех элементов, принадлежащих каждому из заданных множеств. Эта операция над множествами обозначается знаком  . Если
. Если 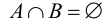 , то множества А и В называются непересекающимися.
, то множества А и В называются непересекающимися.
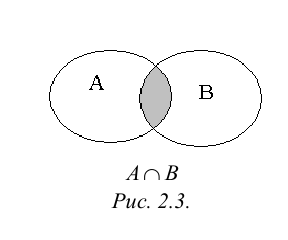
Два множества называются непересекающимися (или расчлененными) если 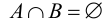 . Практический интерес представляют разбиения множества на взаимно непересекающиеся подмножества (эту задачу иногда называются классификацией). Разбиением множества А называется такая расчлененная система непустых подмножеств множества А, что каждый элемент множества А является элементом некоторого единственного множества этой системы. Возможность разбиения множества на непересекающиеся подмножества зависит от признака, по которому производится разбиение.
. Практический интерес представляют разбиения множества на взаимно непересекающиеся подмножества (эту задачу иногда называются классификацией). Разбиением множества А называется такая расчлененная система непустых подмножеств множества А, что каждый элемент множества А является элементом некоторого единственного множества этой системы. Возможность разбиения множества на непересекающиеся подмножества зависит от признака, по которому производится разбиение.
Разностью множеств А и В или дополнением В до А называется множество, состоящее только из тех элементов А, которые не входят в В. Эта операция над множествами обозначается знаком .
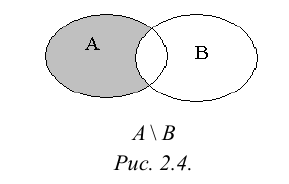
А В Рис. 2.4.
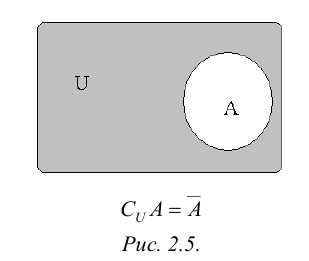
Часто все рассматриваемые множества считают подмножествами одного основного множества U. В таком случае разность U А (дополнение А до U) обозначают, как , а операцию называют взятием дополнения.
, а операцию называют взятием дополнения.
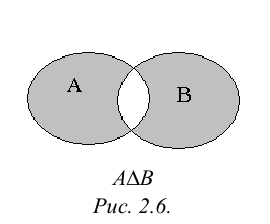
Симметрической разностью множеств А и В называется множество С: 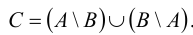 .
.
Обозначается симметрическая разность: 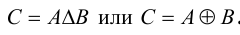 .
.
Для подмножеств данного множества U выполняются следующие законы:
Закон коммутативности (переместительный закон):
Закон ассоциативности (сочетательный закон) для любой тройки множеств А, В и С:
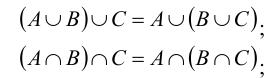
Закон дистрибутивности (распределительный закон) для любой тройки множеств А, В и С:
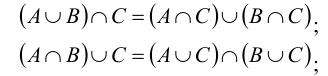
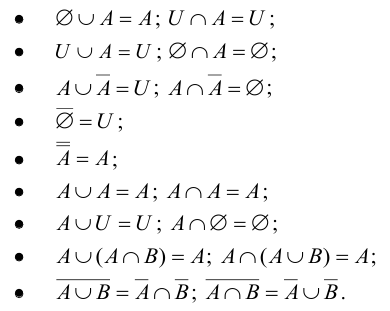
Если операции объединения множеств поставить в соответствие операцию сложения чисел, операции пересечения множеств – операцию умножения, универсальному множеству U – единицу, а пустому множеству – ноль, то возникает аналогия между множествами и числами. Операции объединения и пересечения множеств, как и действия над действительными числами, подчиняются законам коммутативности, ассоциативности и дистрибутивности. Можно также провести аналогию между свойствами логических операций, где логической эквивалентности соответствует операция равенства, а операциям конъюнкции и дизъюнкции – операции объединения и пересечения.
Свойства фигурируют попарно таким образом, что каждое получается из соседнего заменой на
на  , U на
, U на 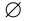 и наоборот. Такие выражения называются двойственными друг другу.
и наоборот. Такие выражения называются двойственными друг другу.
Принцип двойственности. Для любого тождества множеств двойственное ему выражение также является тождеством.
Очевидно, что операция разность не обладает свойствами коммутативности и ассоциативности, в то же время операция симметрическая разность и коммутативна, и ассоциативна.
Большое значение в современной математике имеет множественная операция декартово произведение. Если заданы два множества А и то из их элементов можно составить упорядоченные пары, взяв сначала какой-либо элемент первого множества, а затем -элемент второго множества. Декартовым произведением двух исходных множеств А и В называется множество С, составленное из упорядоченных пар (а,b). Декартово произведение множеств А и В обозначается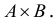 .
.
Очевидно, что  и
и 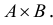 – различные множества, т.е. операция декартова произведения не коммутативна, но, в то же время, она обладает свойством ассоциативности.
– различные множества, т.е. операция декартова произведения не коммутативна, но, в то же время, она обладает свойством ассоциативности.
Отображения
Отображение – одно из основных понятий математики. Отображение есть какое-либо правило или закон соответствия множеств. Пусть X и Y – произвольные непустые множества. Говорят, что задано отображение 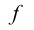 множества X на множество Y (запись:
множества X на множество Y (запись: 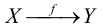 или
или 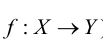 ) если каждому элементу х множества
) если каждому элементу х множества 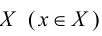 поставлен соответствие единственный, однозначно определенный элемент
поставлен соответствие единственный, однозначно определенный элемент 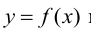 множества
множества  .
.
Элемент 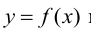 называется образом элемента х при отображении
называется образом элемента х при отображении 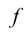 , а элемент
, а элемент 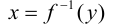 называется прообразом элемента у при этом отображении. Образом множества X элементов х при отображении
называется прообразом элемента у при этом отображении. Образом множества X элементов х при отображении называется множество всех элементов вида
называется множество всех элементов вида , принадлежащих области значений Y. Множество X всех элементов
, принадлежащих области значений Y. Множество X всех элементов , образы которых
, образы которых 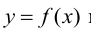 составляют область значений Y называется прообразом множества Y элементов
составляют область значений Y называется прообразом множества Y элементов  . Множество X называется областью определения отображения
. Множество X называется областью определения отображения  .
.
Отображение  называется сюръективным, когда каждый элемент y множества
называется сюръективным, когда каждый элемент y множества 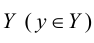 имеет хотя бы один прообраз х множества
имеет хотя бы один прообраз х множества 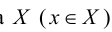 , т.е.
, т.е. 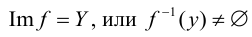 .
.
Отображение 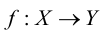 называется инъективным, когда каждый элемент
называется инъективным, когда каждый элемент 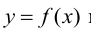 множества
множества 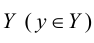 является образом лишь одного элемента х множества
является образом лишь одного элемента х множества 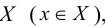 , т.е. образы любых двух различных элементов множества X различны, т.е. из
, т.е. образы любых двух различных элементов множества X различны, т.е. из 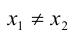 следует
следует 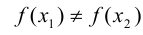 .
.
Отображение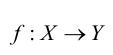 называется биективным или взаимно однозначным, когда оно одновременно ипъективно и сюръективно, т.е. каждый элемент множества Y является образом одного и только одного элемента множества X.
называется биективным или взаимно однозначным, когда оно одновременно ипъективно и сюръективно, т.е. каждый элемент множества Y является образом одного и только одного элемента множества X.
Равенство двух отображений 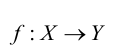 и
и 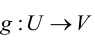 означает по определению, что их соответствующие области совпадают (X = U и Y= V), причем
означает по определению, что их соответствующие области совпадают (X = U и Y= V), причем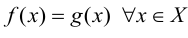 .
.
Произведение двух отображений 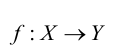 и
и 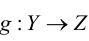 можно определить как отображение
можно определить как отображение 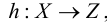 , которое каждому элементу х множества
, которое каждому элементу х множества 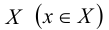 ставит в соответствие элемент
ставит в соответствие элемент 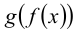 множества
множества 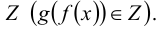 .
.
Отображение 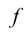 множества X на множество Y иначе называется функцией на множестве X со значениями во множестве Y. Если множества X и Y совпадают, то биективное отображение множества X на себя
множества X на множество Y иначе называется функцией на множестве X со значениями во множестве Y. Если множества X и Y совпадают, то биективное отображение множества X на себя 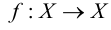 называется преобразованием множества X. Простейшее преобразование множества X – тождественное
называется преобразованием множества X. Простейшее преобразование множества X – тождественное 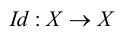 – определяется так:
– определяется так: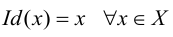 . Тождественное отображение
. Тождественное отображение 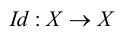 , переводящее каждый элемент
, переводящее каждый элемент 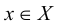 в себя, также называют единичным преобразованием. Если заданы преобразования
в себя, также называют единичным преобразованием. Если заданы преобразования 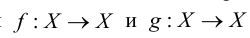 , то преобразование
, то преобразование 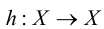 , являющееся результатом последовательного выполнения сначала преобразования
, являющееся результатом последовательного выполнения сначала преобразования 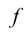 , а затем и преобразования g, называется произведением преобразований
, а затем и преобразования g, называется произведением преобразований 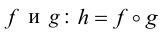 .
.
Для преобразований  одного и того же множества X справедливы следующие законы:
одного и того же множества X справедливы следующие законы:
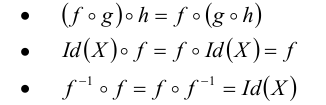
Коммутативный закон для произведения преобразований в общем случае не выполняется, т.е. 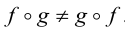 .
.
Если между двумя множествами можно задать биективное отображение (установить взаимно однозначное соответствие между их элементами), то такие множества называются эквивалентными или равномощными. Конечные множества равномощны только в том случае, когда число их элементов одинаково.
Бесконечные множества также можно сравнивать между собой.
Два множества имеют одинаковую мощность или называются эквивалентными (обозначение А = В), если между их элементами можно установить взаимно однозначное соответствие, т.е. если можно указать некоторое правило, в соответствии с которым каждому элементу одного из множеств соотносится один и только один элемент другого множества.
Если же подобное отображение невозможно, то множества имеют различную мощность; при этом оказывается, что в последнем случае, каким бы образом мы не пытались привести в соответствие элементы обоих множеств, всегда останутся лишние элементы и притом всегда от одного и того же множества, которому приписывается более высокое значение кардинального числа или говорят, что это множество имеет большую мощность.
Бесконечное множество и некоторое его подмножество могут быть эквивалентными.
Множество, эквивалентное множеству натуральных чисел, называется счетным множеством. Для того чтобы множество А было счетным, необходимо и достаточно, чтобы каждому элементу а множества А был поставлен в соответствие его порядковый номер 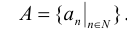 „ Из всякого бесконечного множества можно выделить счетное подмножество. Всякое подмножество счетного множества является счетным или конечным. Счетное множество является наиболее примитивно организованным бесконечным множеством. Декартово произведение двух счетных множеств является счетным. Объединение конечного или бесконечного числа конечных или счетных множеств является конечным или счетным множеством.
„ Из всякого бесконечного множества можно выделить счетное подмножество. Всякое подмножество счетного множества является счетным или конечным. Счетное множество является наиболее примитивно организованным бесконечным множеством. Декартово произведение двух счетных множеств является счетным. Объединение конечного или бесконечного числа конечных или счетных множеств является конечным или счетным множеством.
Отношения эквивалентности и упорядоченности
В математике понятие отношения используется для обозначения какой-либо связи между объектами. Отношение есть некоторое множество упорядоченных пар {х,у), где 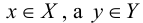 .
.
Часто приходится рассматривать несколько элементов множества как эквивалентные, потому что по определенным признакам один элемент может быть заменен другим. Так, например, по признаку величины дроби  эквивалентны. Отношение эквивалентности рефлексивно, симметрично и транзитивно. Понятие эквивалентности подразумевает выполнение следующих условий:
эквивалентны. Отношение эквивалентности рефлексивно, симметрично и транзитивно. Понятие эквивалентности подразумевает выполнение следующих условий:
- каждый элемент эквивалентен самому себе;
- высказывание, что два элемента являются эквивалентными, не требует уточнения, какой из элементов рассматривается первым;
- два элемента, эквивалентные первому, эквивалентны между собой.
Пусть А – множество, в котором определено отношение эквивалентности. Подмножество элементов, эквивалентных элементу а, называется классом эквивалентности: все элементы этого класса эквивалентны между собой и всякий элемент а из А находится в одном и только в одном классе (если элементов, эквивалентных а, не существует, то а может быть и единственным элементом класса). Отношение эквивалентности в А определяет на А разбиение на классы эквивалентности, т.е. А становится объединением непересекающихся классов.
Особенности природы элементов множества в большинстве случаев позволяют установить между ними отношения полного (или совершенного) порядка. Это отношение по определению обладает следующими свойствами:
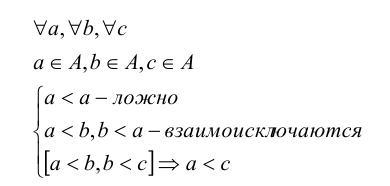
Если между элементами множества определено также и отношение эквивалентности, то между элементами устанавливается отношение неполного или нестрогого порядка:
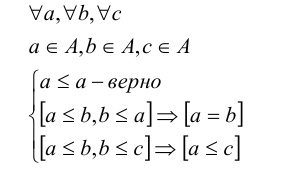
Возможны случаи, когда некоторые элементы множества не сравнимы. Такие множества называются частично упорядоченными.
Способы задания множеств
Как в повседневной, так и в научной жизни часто говорят о чертах какого-либо коллектива, совокупности некоторых объектов. Так, например, можно говорить о студентах группы некоторого института, о совокупности точек внутри некоторого круга и т.д.
Понятие множества в математике выведено из понятия совокупностей, образуемых из предметов, сведенных в одно целое. Предметы, собранные во множество, называются элементами множества. Понятие множество и элемент считаются основным понятиями и не сведены к другим понятиям путем применения формального определения. Таким образом, под множеством, мы будем понимать любое объединение в одно целое М определенных вполне различимых объектов m из нашего восприятия или мысли, которые называются элементами М
Каждое множество считается самостоятельной осмысленной вещыо, как бы осмысленной оболочкой его элементов. Множество
считается известным, если заданы его элементы; множество определяется раз и навсегда заданием его элементов; множества не зависят or времени.
Следовательно, множество однозначно определяется его элементами.
Множество, у которого ни один предмет не является элементом, называется пустым множеством. Пустое множество обозначается символом  .
.
Для обозначения множеств обычно применяются заглавные латинские буквы. Выражение 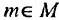 обозначает, что объект m является элементом М (читается: «m является элементом М или m принадлежит М»).
обозначает, что объект m является элементом М (читается: «m является элементом М или m принадлежит М»).
Выражение 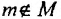 : «m не является элементом М или m не принадлежит М». Элементами множества могут быть и множссгва.
: «m не является элементом М или m не принадлежит М». Элементами множества могут быть и множссгва.
Справедлива следующая
Теорема 1.1.1. Два множества тождественны (равны) тогда и только тогда. если их элементы одинаковы.
Доказательство. Если два множества тождественны (равны), то на основе понятия тождественности элементы обоих множеств одинаковы.
С другой стороны, если о двух множествах нам известно, что их элементы тождественны, то эти два множссгва тождественны, так как множество однозначно определяется его элементами. 
В определениях, касающихся геометрических мест, всегда присутствует отождествление множеств, заданных двумя разнымиопределениями.
Например. Перпендикулярная липия, пересекающая отрезок прямой, является геометрическим местом точек, расположенных на одинаковом расстоянии от двух концов озрезка. Это означает следующее: В плоскости множество точек перпендикулярной линии, пересекающей в середине отрезок прямой, тождественно множеству точек, расположенных на одинаковом расстоянии от обоих концов отрезка.
Множество часто задается в следующем виде: элементы множества заключаются внутри фигурных скобок: {…}. Подобной записью может быть конкретное перечисление элементов множества или задание такого определения, которым элементы множества однозначно задаются.
Например:
- а) {гласные звуки слова «МАТЕМАТИКА»} – множество задано путем определения;
- б) {E, О, И, Я, О, Е}, {О, А, Е} – множество задано путем перечисления элементов.
Заметим, что один предмет в одном множестве является элементом только один раз, даже если предмет повторяется несколько раз.
Тождественные множества связываются знаком равенства (=):
{А, А, Е, Е|={А, Е}.
Множество А считается подмножеством В, если каждый элемент А является и элементом В, что обозначается выражением 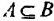 .
.
Понятие части (подмножества) в теории множеств отличается от обычного понятия части. В обычном понимании часть всегда меньше целого. А по понятию части в теории множеств целое также входит в понятие части, т.е. каждое множество является элементом самого себя, гак как каждый элемент А является элементом А, значит 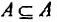 . Пустое множество является частью каждого множества.
. Пустое множество является частью каждого множества.
Множество А является действительным подмножеством множества B, если А является частью В, но не тождественно с ним, что обозначается 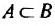 .
.
Примеры:
- Множество N неотрицательных целых чисел является действительной частью множества Z произвольных целых чисел:
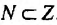 .
. - Множество Z действительная часть множества Q рациональных чисел:
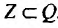
- Множество Q действительная часть множества R вещественных чисел
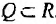
- Множество R действительная часть множества С комплексных чисел:
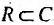
Не существует никакого ограничения в отношении того, насколько много (или мало) элементов может быть в одном множеств: в одном множестве может быть любое, даже бесконечное количество элементов.
Сравнивать множества можно, используя понятие взаимно однозначного соответствия между элементами.
Если каждому элементу множества А по некоторому закону ставится в соответствие определенный элемент множества В и если при этом каждый элемент множества В оказывается поставленным в соответствие одному и только одному элементу множества А, то говорят, что между А и В установлено взаимно однозначное соответствие.
Если между множествами А и В установить взаимно однозначное соответствие, то такие множества называются равиомощны-ми. Множество А называется бесконечным, если оно имеет ту же мощность, что и хотя бы одно из его действительных подмножеств, в противном случае А – конечное множество. Бесконечное множество А счётно, если можно установить взаимно однозначное соответствие между ним и множеством натуральных чисел.
Например, множество всех действительных чисел R и множество натуральных чисел N имеют разные мощности. Первое множество имеет мощность континуума, а второе – счетное множество.
Особую роль в теории множеств играет универсальное множество, которое часто называют просчранством. Это некоторое множество, фиксированное в рамках данной математической теории и содержащее в качестве элементов все объекты, рассматриваемые в этой теории.
Алгебраические операции над множествами
Определим операции, выполняемые над множествами.
а) Пересечением множеств Ми N называется множество, которое будет обозначаться М 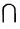 N, состоящее из элементов, принадлежащих как М, так и N, т.е. М
N, состоящее из элементов, принадлежащих как М, так и N, т.е. М 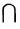 N =
N = 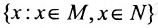 .
.
Эта запись означает, что пересечение M N двух множеств состоит из элементов х, одновременно принадлежащих как М, так и
N двух множеств состоит из элементов х, одновременно принадлежащих как М, так и
N. Например, если М = {0,1,2,3}, а N = {1,4,3,6}, то М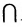 N = {1,3}. Основные тождества этой операции состоят в следующем:
N = {1,3}. Основные тождества этой операции состоят в следующем:
Если А 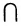 В = А, то действительны следующие соотношения:
В = А, то действительны следующие соотношения: 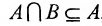 ,
,
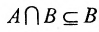 ,
,
А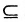 В.
В.
Вели 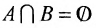 , т.е. если А и В не имеют общих элементов, то
, т.е. если А и В не имеют общих элементов, то
А и Б называются посторонними множествами.
Если есть совокупность множеств  ,то пересечение всех множеств
,то пересечение всех множеств  есть множество
есть множество  , которое состоит из элементов,
, которое состоит из элементов,
принадлежащих одновременно всем множествам совокупности 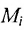 .
.
6) Объединением двух множеств А и В называется множество A  В, состоящее из элементов, по крайней мере, одного из множеств А и В, т. е.
В, состоящее из элементов, по крайней мере, одного из множеств А и В, т. е.
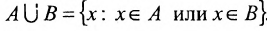 .
.
Эта запись означает, что объединение A 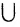 В двух множеств А и В состоит из элементов х, принадлежащих множеству А или множеству В, или множеством А и В одновременно. Например, если A={0,1,2,3} а B={4,5,6,}, то A
В двух множеств А и В состоит из элементов х, принадлежащих множеству А или множеству В, или множеством А и В одновременно. Например, если A={0,1,2,3} а B={4,5,6,}, то A  B = {0,1,2,3,4,5,6}.
B = {0,1,2,3,4,5,6}.
Легко увидеть, что если А и В являются ограниченными множествами без общих элементов, то количество элементов A B = (количество элементов А) + (количество элементов В). На основе этих соотношений операция объединения часто называется суммированием множеств. Для операции объединения справедливы следующие тождества:
B = (количество элементов А) + (количество элементов В). На основе этих соотношений операция объединения часто называется суммированием множеств. Для операции объединения справедливы следующие тождества:
- A
 В = В
В = В  А (коммутативность).
А (коммутативность). - A
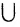 А = А (идемпотснция).
А = А (идемпотснция). - A
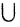
 = А.
= А. - (A
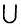 B)
B)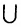 C = A
C = A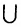 (B
(B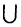 C) (ассоциативность).
C) (ассоциативность).
Так же действительны соотношения: 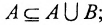
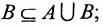
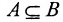 , тогда и только тогда, если A
, тогда и только тогда, если A 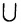 В=В.
В=В.
В общем случае, когда имеется совокупность множеств 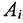 ,то объединение всех множеств
,то объединение всех множеств 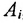 есть множество
есть множество 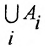 , которое состоит из элементов, принадлежащих хотя бы одному из множеств совокупности
, которое состоит из элементов, принадлежащих хотя бы одному из множеств совокупности 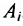 .
.
в) Множество элементов Е, не принадлежащих некоторой его части А, называется дополнением (разностью) к А в Е и обозначается через 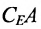 или СА или ЕА, т.е.
или СА или ЕА, т.е. 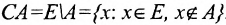 .
.
Например. Если областью существования функции  является А, а множество ее корней – В, то область существования функции
является А, а множество ее корней – В, то область существования функции -множество АВ.
-множество АВ.
Для операции разности справедливы следующие соотношения:
- 1°.
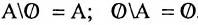 .
. - 2°.
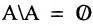 .
. - 3°.
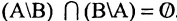 .
. - 4°.
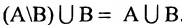 .
. - 5°.
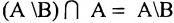 .
. - 6°.
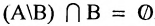 .
. - 7°.
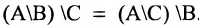 .
. - 8°.
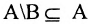 .
.
Два любых предмета а и b представляют собой упорядоченную пару, если предварительно задано, какой из них считается первым и какой вторым. Упорядоченные пары обозначаются символом (a, b), где а – первый элемент, b – второй {а и b могут быть тождественны).
г) Произведением А х В двух множеств А и В называется множество всевозможных упорядоченных пар (а, Ь), образованных из элементов а множества А и элементов b множества В, т.е. 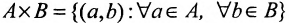 .
.
Пары (а, b) и (b, а) с 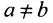 считаются различными. Это особенно важно иметь в виду, когда множества Aw В совпадают.
считаются различными. Это особенно важно иметь в виду, когда множества Aw В совпадают.
Пример:
Если А ={a,е,i}, а В={b,с}, то
А х В = {(a,b), (а,с), (e,b), (e,c), (i,b), (i,с)},
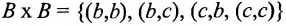 .
.
В координатной геометрии точки плоскости характеризуются парами чисел, а точки пространства – тремя числами. Это означает, что если R обозначает множество точек числовой оси, то R х R -множество точек плоскости, а (RxR)xR- множество точек пространства. Отсюда возникло обозначение  для произведения n множеств, идентичных множеству R всех вещественных чисел. Точка из
для произведения n множеств, идентичных множеству R всех вещественных чисел. Точка из  является, следовательно, упорядоченной системой произвольных вещественных чисел
является, следовательно, упорядоченной системой произвольных вещественных чисел 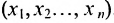 .
.
Справедливы следующие операции для декартового произведения множеств:
- 1°.
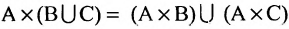 .
. - 2°.
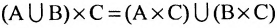 .
. - 3°.
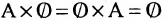 , т.к. пустое множество не имеет элементов.
, т.к. пустое множество не имеет элементов.
Понятие множества широко используется в экономических исследованиях. Так при изучении системы производства одного предприятия или нескольких, которые потребляют продукты: сырьё, энергию и трудовые ресурсы и производят в соответствии с некоторой технологией другие продукты-изделия, составляется математическая модель, где используется множество
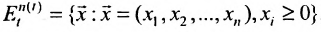 , которое характеризует производственный процесс. Элементами этого множества являются векторы
, которое характеризует производственный процесс. Элементами этого множества являются векторы 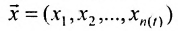 описывающие количество любого продукта, находящегося в системе.
описывающие количество любого продукта, находящегося в системе.
- Заказать решение задач по высшей математике
Выпуклые множества. Пересечение выпуклых множеств
В первом пункте мы определили множество, указали способы его задания. Теперь мы укажем некоторые дополнительные свойства множеств. Для этого введем ряд определений.
Окрестностью точки  называется множество
называется множество
точек  удовлетворяющих условию:
удовлетворяющих условию: 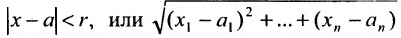 или
или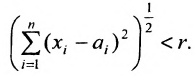
Таким образом, окрестность образуют все точки х, удаленные от точки а на расстояние меньшее r.
Точка 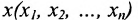 некоторого множества называется внутренней точкой этого множества, если она принадлежит множеству вместе с некоторой её окрестностью.
некоторого множества называется внутренней точкой этого множества, если она принадлежит множеству вместе с некоторой её окрестностью.
Точка пространства называется внешней по отношению к некоторому множеству точек, если она с некоторой окрестностью не принадлежит этому множеству.
Точка пространства называется граничной, если в любой её окрестности имеются точки как принадлежащие множеству так и не принадлежащие ему. Множество, содержащее все граничные точки, называется замкнутым.
Например, отрезок является замкнутым множеством.
Множество (тело) называется выпуклым, если оно вместе со своими двумя любыми точками Р и Q содержит все точки отрезка  .
.
Примером выпуклого множества может служить отрезок. Из геометрии известны фигуры: треугольник, квадрат, прямоугольник, ромб, круг, эллипс. Множества точек, ограниченные эти фигурами, являются выпуклыми. В пространстве выпуклыми множествами являются: шар, эллипсоид, конус, цилиндр и другие.
Для выпуклых множеств, справедлива следующая теорема.
Теорема 1.3.1. Пересечение выпуклых множеств (тел) есть выпуклое множество, если оно не пусто.
Доказательство. Пусть имеется не пустое пересечение выпуклых множеств. Возьмём две произвольные точки Р u Q, принадлежащие этому пересечению. По определению пересечения эти точки принадлежат каждому из множеств, а так как эти множества выпуклы, то вместе с точками Р и Q им принадлежат и все точки отрезка PQ. Следовательно, все точки отрезка PQ принадлежат и пересечению, что и доказывает его выпуклость. 
Точка множество называется крайней, если она не является внутренней ни для какого отрезка, целиком принадлежащего множеству.
Так у выпуклого многоугольника крайними точками являются его вершины. Их конечное число. В пространстве многогранником называется множество с конечным числом крайних точек. Следовательно. выпуклый многогранник является замкнутым выпуклым множеством.
Высказывание
Математическая логика является современной формой так называемой формальной логики, применяющей математические методы для исследования своего предмета. В формальной логике и, соответственно, математической логике, собраны результаты законов структуры правильных выводов. Вывод является таким мыслительным процессом, в результате которого появляются новые открытия на основании уже имеющихся, без практических исследований. Рассмотрим пример вывода:
Предпосылки: Если будет раздача премии, то мы выполним план.
Будет раздача премии.
Окончательные выводы: Мы выполним план.
Если принять правильность предпосылок, то следует принять и правильность окончательного вывода. Обычно вместо предложений могут быть записаны любые такие изъявительные предложения, значения которых может быть правильно или ложно; следует оставить неизменённым только расположение слов «если» и «то» и расположение предложений, то есть структуру вывода. Структуру вывода можно выразить следующей схемой:
Если А, то В.
Путем изменения условий могут быть построены различные теории логики. Важнейшими главами математической логики является калькуляция высказываний и калькуляция предикатов.
Определение 1.4.1. Под термином высказывания подразумевается такое изъявительное предложение, которое является однозначно или правильным, или ложным.
Высказывание удовлетворяет условиям:
- а) оно не может быть одновременно и правильным и ложным (принцип непротиворечивости);
- б) исключено, чтобы оно было и неправильным и нсложным (принцип исключения третьей возможности).
Следовательно, каждое высказывание имеет значение 1 (истинно) или 0 (ложно).
В выводах могут фигурировать высказывания (либо в виде предпосылок, либо как окончательный вывод), возникшие из одного или нескольких высказываний, путем применения некоторого грамматического метода; они называются сложными высказываниями.
Определение 1.4.2. Под термином калькуляция высказываний подразумевается такой метод, с помощью которого из одного или нескольких высказываний получается такое высказывание, правильность или ложность которого однозначно определяется правильностью или ложсностью членов.
Операции над высказываниями
Отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность
Простейшими примерами операций калькуляции высказываний является отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность и т.д.
Определение 1.5.1. Под отрицанием высказывания А подразумевается высказывание «Неправильно, что А» или некоторая грамматически преобразованая форма данного высказывания.
По значению выражения «неправильно» отрицание А правильно тогда и только тогда, если самоё А неправильно; следовательно, отрицание действительно есть операция калькуляции высказываний.
Например: отрицание предложения «мотор работает» является предложение «мотор не работает».
Отрицание является (унарной) одночленной операцией. Отрицание А обозначается символом 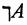 (читается «не А»). Таблица истинности для операции отрицания имеет вид: Таблица 1
(читается «не А»). Таблица истинности для операции отрицания имеет вид: Таблица 1
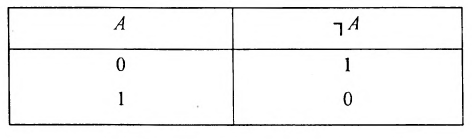
Закон двойного отрицания:  .
.
Здесь и в дальнейшем свойство высказываний «правильное» и «ложное» называется логическими значениями и обозначается 1 и О (п. и л.). Тогда операции, проводимые на логических значениях, называются логическими операциями. Для выражения любых логических значений вводятся логические переменные; они обозначаются символами  .
.
Следовательно, логические переменные могут принимать два значения 1 или 0. При использовании нескольких операций последовательно порядок выполнения отдельных операций обозначается скобками.
В общем случае, n-члснной логической операцией называется каждая такая функция, областью существования которой является упорядоченное множество всех выражений, образуемых из логических значений 1 и 0 с длиной выражения n, а значением её является одно из двух логических значений 1 и 0.
Определение 1.5.2. Под конъюнкцией двух высказываний А и В подразумевается высказывание «А и В».
По значению союза «и» конъюнкция является правильной тогда и только тогда, если оба её члена правильны, т.е. используя логические переменные можно записать:
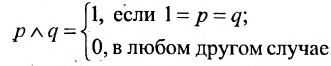
Таблица значений конъюнкции имеет вид:
Таблица 2
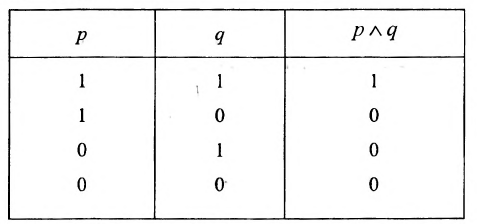
Справедлива следующая
Теорема 1.5.1. Любая логическая операция может быть выражена через операции отрицания и конъюнкции.
В области логических операций для контроля любого тождества составляется общая таблица операций, представленных по обеим сторонам знака =. Результат операций указывается в столбцах.
Пример:
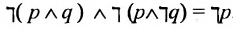 .
.
Решение:
Доказательство данного равенства проведём в табл. 3:
Таблица 3
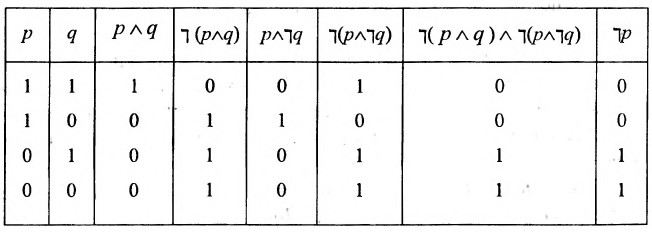
Определение 7.5.3. Под дизъюнкцией двух высказываний А и В подразумевается высказывание «А или В».
По значению союза «или» дизъюнкция является ложной, если оба её члена ложны, т.е. используя логические переменные можно записать:
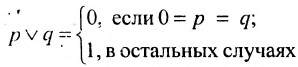 .
.
Дизъюнкция выражается с помощью операции конъюнкции и отрицания б следующей форме: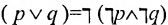
Таблица значений дизъюнкции имеет следующий вид:
Таблица 4
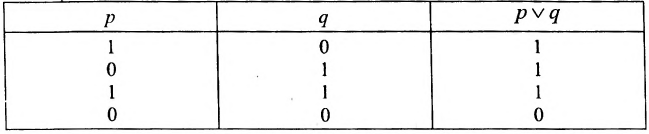
По аналогии с теоремой 3 можно сформулировать следующую теорему
Теорему 1.5.2. Каждая логическая операция может быть выражена с помощью только операций дизъюнкции и отрицания.
Например, операция конъюнкции выражается с помощью операций дизъюнкции и отрицания в виде: 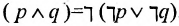 .
.
Определение 1.5.4. Операция, обозначаемая 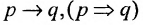 ,
,
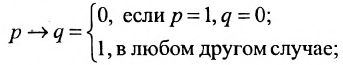
называется импликацией (с предварительным членом р и с последующим q).
Иначе её обозначение 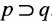 . Она выражается в следующем виде:
. Она выражается в следующем виде:
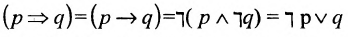 и читается: если р, то q из p следует q.
и читается: если р, то q из p следует q.
Таблица значений импликации имеет следующий вид: Таблица 5
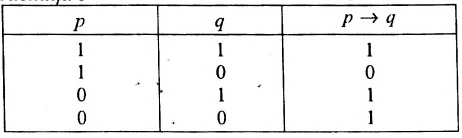
И конъюнкция, и дизъюнкция выражаются с помощью операций импликации и отрицания: 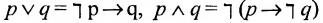 ,
,
Поэтому любая логическая операция может быть выражена ( помощью операций импликации и отрицания.
Выражения вида: «если А, то В», «неправильно, что: А и не В» «В если только А», «только тогда А, если В», «Достаточным условием В является А», «Необходимым условием А является В» соответственно обозначаются А 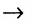 В или А
В или А  В.
В.
Определение 1.5.5. Операция, обозначаемая ,
,
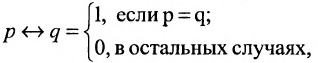
называется эквивалентностью (читается р эквивалентно q). Выражениями данной операции являются следующие: 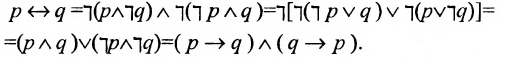
Так как высказывание 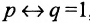 тогда и только тогда, когда
тогда и только тогда, когда
p=q, то данная логическая операция соответствует образованию
сложного предложения вида «А тогда и только тогда, когда В». Таблица значений эквивалентности имеет вид:
Таблица 6
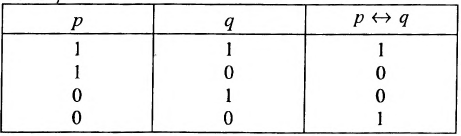
Рассматриваются ещё:
операция Шеффера – отрицание операции конъюнкции 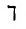
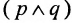 , обозначаемая
, обозначаемая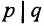 (р штрих q).
(р штрих q).
1) операция взаимоисключающего или (р или же q): 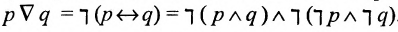 . Например, или ты вылечишься до завтрашнего дня, или мы тебя отвезём в больницу;
. Например, или ты вылечишься до завтрашнего дня, или мы тебя отвезём в больницу;
2) операция «ни-ни» (обозначается 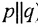 ) «ни А ни В»:
) «ни А ни В»: 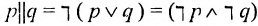 .
.
Предикаты и кванторы
Мри анализе вывода следует отмстить, что применяемые высказывания могут быть приведены из так называемых открытых предложений или предикатов, примерами которых служат: … является неделимым числом; … является столицей; … купил … за … рублей.
Если в эти схемы предложений вставить названия соответственно подобранных предметов (вместо пунктира), то получатся замкнутые предложения, высказывания. Такие предикаты выражаются однозначно в некоторых случаях, если вместо пунктира записываются буквы: x, у,z, … .
Кроме заполнения оставленных свободных мест названиями имеется и другой способ образования высказываний из предикатов: квантификация. Например, из открытого предложения «если х представляет собой дифференцируемую функцию, то функция х-непрерывная функция», подставив перед предложением «Для каждого л», получим следующее: Для каждого х, если х представляет собой дифференцируемую функцию, то x представляет собой непрерывную функцию. Текст «Для каждого x» обозначается символом 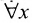 и называется универсальным квантором.
и называется универсальным квантором.
Существует ещё экзистенциальный квантор, который заменят текст «Имеется такое х» или «Существует такое х» и обозначается 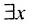 .
.
Для точного анализа вводятся следующие понятия:
Определение 1.6.1. n-мерным предикатом 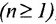 , определённым на непустом множестве H, называется такая функция, областью существования которой является множество упорядоченных n – членных знаков, образованных из элементов множества H, а значениями – логические значения.
, определённым на непустом множестве H, называется такая функция, областью существования которой является множество упорядоченных n – членных знаков, образованных из элементов множества H, а значениями – логические значения.
Предикаты обозначаются символами 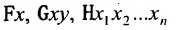 и т.д.
и т.д.
Жирными буквами обозначаются предикаты, а строчными буквами- аргументы предиката как функции; количеством последних определяется размерность предиката.
Например. Пусть Н- множество натуральных чисел, тогда предикат неделимого числа Fx определяется следующим образом:

Множества, операции над ними
Понятие множества является одним из основных в математике. Оно принадлежит к числу первичных, не определяемых через более простые.
Под множеством будем понимать совокупность объектов, объединенных по какому-либо признаку. Слова «совокупность», «набор», «система», «объединение» и другие являются синонимами слова «множество». Например, можно говорить о множестве студентов в институте, множестве букв в алфавите, множестве целых чисел и т. д. Из приведенных примеров следует, что множество может содержать как конечное, так и бесконечное число объектов некоторой природы. Объекты, из которых состоит множество, называются его элементами или точками. Принадлежность элемента 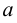 множеству
множеству  обозначают следующим образом:
обозначают следующим образом: 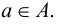 Если
Если 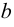 не является элементом множества
не является элементом множества 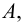 то пишут:
то пишут: 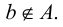 Если
Если 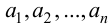 – некоторые элементы, то запись
– некоторые элементы, то запись 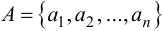 означает, что множество
означает, что множество 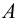 состоит из элементов
состоит из элементов 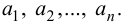
Два множества 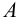 и
и 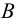 называют равными, если они состоят из одних и тех же элементов (обозначение:
называют равными, если они состоят из одних и тех же элементов (обозначение: 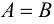 ). Множество
). Множество  называется подмножеством множества
называется подмножеством множества 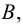 если все элементы множества
если все элементы множества 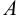 являются одновременно и элементами множества
являются одновременно и элементами множества 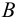 (обозначение:
(обозначение: 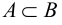 («множество
(«множество 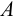 содержится в множестве
содержится в множестве 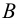 ») или
») или 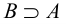 («множество
(«множество 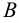 содержит множество
содержит множество 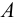 »). Например, так как всякое натуральное число
»). Например, так как всякое натуральное число 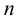 является целым, то
является целым, то 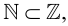 где
где 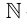 – множество натуральных чисел,
– множество натуральных чисел, 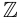 – множество целых чисел.
– множество целых чисел.
Множество, не содержащее ни одного элемента, будет называться пустым множеством и обозначаться 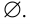 Это множество является подмножеством любого множества. Пусть
Это множество является подмножеством любого множества. Пусть 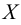 – множество, а
– множество, а 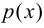 – какое-либо свойство элементов этого множества. Тогда запись
– какое-либо свойство элементов этого множества. Тогда запись 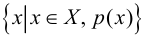 означает совокупность тех элементов множества
означает совокупность тех элементов множества 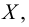 которые обладают свойством
которые обладают свойством 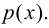 Например, если
Например, если  и
и 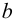 – два числа и
– два числа и 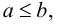 то встречавшиеся в элементарной математике отрезок, интервал и полуинтервалы можно записать в следующем виде:
то встречавшиеся в элементарной математике отрезок, интервал и полуинтервалы можно записать в следующем виде: 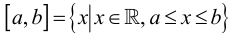 – отрезок;
– отрезок; 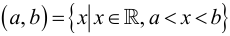 – интервал;
– интервал;
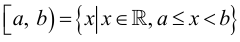 и
и 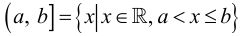 – полуинтервалы. Здесь
– полуинтервалы. Здесь 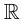 – множество действительных (вещественных) чисел.
– множество действительных (вещественных) чисел.
Множество  всех чисел называется также числовой прямой или числовой осью, а любое число – точкой этой прямой.
всех чисел называется также числовой прямой или числовой осью, а любое число – точкой этой прямой.
Пересечением множеств 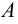 и
и 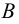 называется множество
называется множество 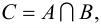 состоящее из всех элементов, одновременно принадлежащих как
состоящее из всех элементов, одновременно принадлежащих как 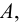 так и
так и  т.е.
т.е. 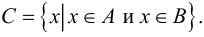
Объединением множеств  и
и 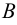 называется множество
называется множество 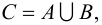 состоящее из всех элементов, принадлежащих хотя бы одному из двух данных множеств, т. е.
состоящее из всех элементов, принадлежащих хотя бы одному из двух данных множеств, т. е. 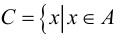 или
или 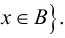
Разностью множеств 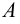 и
и 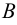 называется множество
называется множество 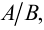 состоящее из тех элементов множества
состоящее из тех элементов множества 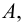 которые не принадлежат множеству
которые не принадлежат множеству 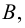 т.е.
т.е. 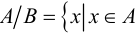 и
и 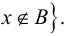
Пусть  – некоторое основное множество, тогда дополнением множества
– некоторое основное множество, тогда дополнением множества 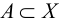 называется множество
называется множество 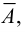 состоящее из всех элементов
состоящее из всех элементов 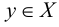 и не принадлежащих
и не принадлежащих 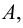 т. е.
т. е.
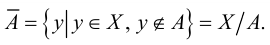
Таким образом, все элементы, которые не принадлежат множеству 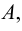 образуют множество
образуют множество 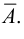 Следовательно,
Следовательно, 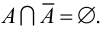
Логические символы
Многие математические понятия удобно записывать, пользуясь логической символикой. Так, символ  называемый квантором общности, используется вместо слов «для любого», «для всех», «для каждого», «какого бы ни было» и т. д., символ
называемый квантором общности, используется вместо слов «для любого», «для всех», «для каждого», «какого бы ни было» и т. д., символ 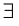 – квантор существования – вместо слов «существует», «найдется», «имеется» и т. д.
– квантор существования – вместо слов «существует», «найдется», «имеется» и т. д.
Часто используются также логические символы следствия 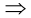 и равносильности
и равносильности 
Грани числовых множеств
Говорят, что множество 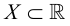 ограничено сверху (снизу), если существует такое число
ограничено сверху (снизу), если существует такое число 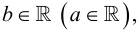 что
что 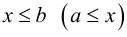 для любого
для любого 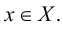 Число
Число 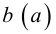 в этом случае называется верхней (нижней) гранью множества
в этом случае называется верхней (нижней) гранью множества 
Множество, ограниченное и сверху, и снизу, называется ограниченным, т. е. существуют два числа 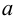 и
и 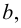 такие, что
такие, что 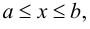
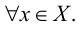 Эти неравенства показывают, что множество
Эти неравенства показывают, что множество 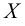 ограничено в том и только в том случае, если оно расположено на некотором конечном отрезке числовой прямой. Очевидно, что множество
ограничено в том и только в том случае, если оно расположено на некотором конечном отрезке числовой прямой. Очевидно, что множество 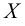 ограничено тогда и только тогда, когда существует положительное число
ограничено тогда и только тогда, когда существует положительное число  такое, что
такое, что
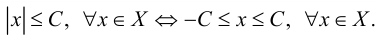
Множество, не ограниченное сверху или снизу, называется неограниченным.
Если число 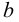 является верхней гранью множества
является верхней гранью множества 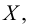 то и любое число больше
то и любое число больше 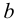 тоже является верхней гранью, и, если число
тоже является верхней гранью, и, если число 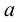 -нижняя грань множества
-нижняя грань множества 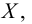 то всякое число, меньше
то всякое число, меньше 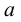 будет нижней гранью
будет нижней гранью 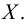
Наименьшая (наибольшая) из всех верхних (нижних) граней называется точной верхней (нижней) гранью множества и обозначается символом 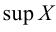 («супремум
(«супремум 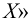 ) (
) (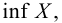 «инфимум
«инфимум 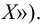
Точные верхняя и нижняя грани множества могут принадлежать или не принадлежать этому множеству. Если множество 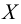 не ограничено сверху (снизу), то иногда используют обозначение
не ограничено сверху (снизу), то иногда используют обозначение 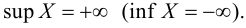
Теорема 1*. Всякое ограниченное сверху (снизу) числовое множество имеет точную верхнюю (нижнюю) грань.
Предельные точки числового множества. Открытые и замкнутые множества
Множество вещественных чисел 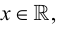 удовлетворяющих неравенству
удовлетворяющих неравенству 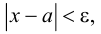 т.е.
т.е. 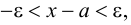 называется
называется 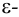 окрестностью точки
окрестностью точки 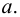
Множество вещественных чисел 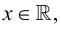 удовлетворяющих неравенству
удовлетворяющих неравенству 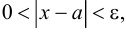 называется проколотой
называется проколотой 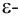 окрестностью точки
окрестностью точки 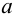 (точка
(точка 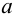 исключена из своей
исключена из своей  окрестности).
окрестности).
Геометрически 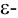 окрестность точки
окрестность точки 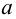 есть интервал
есть интервал 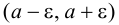 длиной
длиной 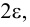 серединой которого является точка
серединой которого является точка 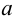 числовой прямой.
числовой прямой.
Точка 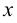 называется предельной точкой множества
называется предельной точкой множества 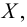 если в любой
если в любой  окрестности точки
окрестности точки 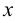 находятся точки из
находятся точки из 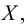 отличные от
отличные от 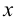 . Предельная точка может как принадлежать, так и не принадлежать множеству
. Предельная точка может как принадлежать, так и не принадлежать множеству 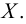
Точка 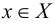 называется изолированной точкой этого множества, если в достаточно малой ее
называется изолированной точкой этого множества, если в достаточно малой ее  окрестности нет точек из
окрестности нет точек из 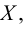 отличных от
отличных от 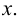
Точка 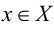 называется внутренней, если существует некоторая
называется внутренней, если существует некоторая 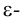 окрестность этой точки, целиком содержащаяся в множестве
окрестность этой точки, целиком содержащаяся в множестве 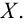
Множество, все точки которого являются внутренними, называется открытым; множество, содержащее все свои предельные точки, называется замкнутым. Открытым множеством является, например, интервал 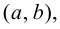 замкнутым множеством – отрезок
замкнутым множеством – отрезок 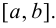
Точка 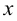 называется граничной точкой множества
называется граничной точкой множества 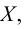 если любая
если любая 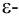 окрестность этой точки содержит точки, как принадлежащие множеству
окрестность этой точки содержит точки, как принадлежащие множеству 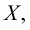 так и не принадлежащие ему. Множество всех граничных точек множества
так и не принадлежащие ему. Множество всех граничных точек множества 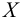 называется границей этого множества. Например, если
называется границей этого множества. Например, если 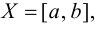 то все точки интервала
то все точки интервала 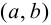 являются внутренними точками множества
являются внутренними точками множества 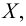 а граница этого множества состоит из двух точек:
а граница этого множества состоит из двух точек: 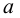 и
и 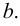
Если множество  представляет собой область (открытое множество), то множество
представляет собой область (открытое множество), то множество  полученное присоединением к
полученное присоединением к  всех граничных точек этого множества, называется замкнутой областью.
всех граничных точек этого множества, называется замкнутой областью.
- Числовые множества
- Вектор – определение и основные понятия
- Прямая – понятие, виды и её свойства
- Плоскость – определение, виды и правила
- Степень с рациональным показателем
- Степень с действительным показателем
- Логарифм – формулы, свойства и примеры
- Корень из числа – нахождение и вычисление
Мно́жество — одно из ключевых понятий математики, представляющее собой набор, совоку́пность каких-либо (вообще говоря любых) объектов — элеме́нтов этого множества[1]. Два множества равны тогда и только тогда, когда содержат в точности одинаковые элементы[2].
Изучением общих свойств множеств занимаются теория множеств, а также смежные разделы математики и математической логики. Примеры: множество жителей заданного города, множество непрерывных функций, множество решений заданного уравнения. Множество может быть пустым и непустым, упорядоченным и неупорядоченным, конечным и бесконечным. Бесконечное множество может быть счётным или несчётным. Более того, как в наивной, так и в аксиоматической теориях множеств любой объект обычно считается множеством. Понятие множества позволяет практически всем разделам математики использовать общую идеологию и терминологию.
История понятия[править | править код]
Основы теории конечных и бесконечных множеств были заложены Бернардом Больцано, который сформулировал некоторые из её принципов[3][4][5].
С 1872 года по 1897 год (главным образом в 1872—1884 годы) Георг Кантор опубликовал ряд работ, в которых были систематически изложены основные разделы теории множеств, включая теорию точечных множеств и теорию трансфинитных чисел (кардинальных и порядковых)[6]. В этих работах он не только ввёл основные понятия теории множеств, но и обогатил математику рассуждениями нового типа, которые применил для доказательства теорем теории множеств, в частности впервые к бесконечным множествам. Поэтому общепризнано, что теорию множеств создал Георг Кантор. В частности, он определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством», и назвал эти объекты элементами множества.
Множество всех объектов, обладающих свойством 




Несмотря на доброкачественность этого определения, концепция Кантора привела к парадоксам — в частности, к парадоксу Рассела.
Так как теория множеств фактически используется как основание и язык всех современных математических теорий, в 1908 году теория множеств была аксиоматизирована независимо Бертраном Расселом и Эрнстом Цермело. В дальнейшем обе системы пересматривались и изменялись, но в основном сохранили их характер. Они известны как теория типов Рассела и теория множеств Цермело. Впоследствии теорию множеств Кантора стала называться наивной теорией множеств, а теорию (в частности, Рассела и Цермело), перепостроенную после Кантора, — аксиоматической теорией множеств.
В практике, сложившейся с середины XX века, множество определяется как модель, удовлетворяющая аксиомам ZFC (аксиомы Цермело — Френкеля с аксиомой выбора). Однако при таком подходе в некоторых математических теориях возникают совокупности объектов, которые не являются множествами. Такие совокупности называются классами (различных порядков).
Элемент множества[править | править код]
Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают заглавными буквами латинского алфавита, их элементы — строчными. Если 









Если всякий элемент множества 








Таким образом, порядок записи элементов множества не влияет на само множество, то есть 



Задание множества[править | править код]
Существуют два основных способа задания множеств: перечислением элементов и их описанием.
Перечисление[править | править код]
Первый способ требует задать (перечислить) все элементы, входящие в множество. Например, множество 

Описание[править | править код]
Второй способ применяется, когда множество нельзя или затруднительно задать перечислением (например, если множество содержит бесконечное число элементов). В таком случае его можно описать свойствами принадлежащих ему элементов.
Множество 




Например, график функции 
где 
Отношения между множествами[править | править код]
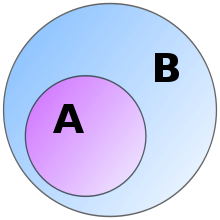
Для множеств 

Иногда различают строгое включение (


Операции над множествами[править | править код]


Для наглядного представления операций часто используются диаграммы Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.
Основные операции[править | править код]
Пересечение (множество общих точек):
.
Объединение (множество всех точек):
.
Объединение непересекающихся 



Разность (множество точек первого без второго):
.
Симметрическая разность:
;
Дополнение для 


.
Булеан 
.
Для операций над множествами также справедливы законы де Моргана:
,
.
Приоритет операций[править | править код]
Последовательность выполнения операций над множествами, как и обычно, может быть задана скобками. При отсутствии скобок сначала выполняются унарные операции (дополнение), затем — пересечения, затем — объединения, разности и симметрической разности[источник не указан 1326 дней]. Операции одного приоритета выполняются слева направо. При этом надо иметь в виду, что в отличие от арифметических сложения и вычитания, для которых, в частности, верно, что 





Декартово произведение[править | править код]
Декартовым произведением множеств 



Удобно представить, что элементы декартова произведения заполняют таблицу элементов, столбцы которой описывают все элементы одного множества, а строки, соответственно, другого.
Мощность[править | править код]
Мощность множества — характеристика множества, обобщающая понятие о количестве элементов конечного множества таким образом, чтобы множества, между которыми возможно установление биекции, были равномощны. Обозначается 





Наименьшая бесконечная мощность обозначается 





Некоторые виды множеств и сходных объектов[править | править код]
Специальные множества
- Пустое множество — множество, не содержащее ни одного элемента.
- Одноэлементное множество — множество, состоящее из одного элемента.
- Универсальное множество (универсум) — множество, содержащее все мыслимые объекты. В связи с парадоксом Рассела данное понятие трактуется в настоящее время более узко как «множество, включающее все множества и объекты, участвующие в рассматриваемой задаче».
Сходные объекты[править | править код]
- Кортеж (в частности, упорядоченная пара) — упорядоченная совокупность конечного числа именованных объектов. Записывается внутри круглых или угловых скобок, а элементы могут повторяться.
- Мультимножество (в теории сетей Петри называется «комплект») — множество с кратными элементами.
- Пространство — множество с некоторой дополнительной структурой.
- Вектор — элемент линейного пространства, содержащий конечное число элементов некоторого поля в качестве координат. Порядок имеет значение, элементы могут повторяться.
- Последовательность — функция одного натурального переменного. Представляется как бесконечный набор элементов (не обязательно различных), порядок которых имеет значение.
- Нечёткое множество — математический объект, подобный множеству, принадлежность которому задаётся не отношением, а функцией. Иными словами, относительно элементов нечёткого множества можно говорить «в какой мере» они в него входят, а не просто, входят они в него или нет.
По иерархии[править | править код]
- Система множеств (множество множеств) — множество, все элементы которого также являются множествами, обычно схожего происхождения (например, все они могут быть подмножествами некоторого другого множества)[7].
- Алгебра множеств, кольцо множеств — примеры типов структур, являющихся системами множеств.
- Булеан — множество всех подмножеств данного множества.
- Семейство множеств — индексированный аналог системы множеств.
- Подмножество
- Надмножество
Примечания[править | править код]
- ↑ Множество // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3. — С. 762.
- ↑ Stoll, Robert. Sets, Logic and Axiomatic Theories. — W. H. Freeman and Company, 1974. — P. 5.
- ↑ Steve Russ. The Mathematical Works of Bernard Bolzano. — OUP Oxford, 9 December 2004. — ISBN 978-0-19-151370-1. Архивная копия от 27 апреля 2022 на Wayback Machine
- ↑ William Ewald. From Kant to Hilbert Volume 1: A Source Book in the Foundations of Mathematics / William Ewald, William Bragg Ewald. — OUP Oxford, 1996. — P. 249. — ISBN 978-0-19-850535-8. Архивная копия от 22 апреля 2022 на Wayback Machine
- ↑ Paul Rusnock. Bernard Bolzano: His Life and Work / Paul Rusnock, Jan Sebestík. — OUP Oxford, 25 April 2019. — P. 430. — ISBN 978-0-19-255683-7. Архивная копия от 17 апреля 2022 на Wayback Machine
- ↑ «Eine Menge, ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens — welche Elemente der Menge genannt werden — zu einem Ganzen.» Archived copy. Дата обращения: 22 апреля 2011. Архивировано 10 июня 2011 года.
- ↑ Студопедия — Теория множеств. Дата обращения: 2 мая 2020. Архивировано 25 ноября 2020 года.
Литература[править | править код]
- К. Куратовский, А. Мостовский. Теория множеств / Перевод с английского М. И. Кратко под редакцией А. Д. Тайманова. — М.: Мир, 1970. — 416 с.
- Столл Р. Р. Множества. Логика. Аксиоматические теории. / Перевод с английского Ю. А. Гастева и И. Х. Шмаина под редакцией Ю. А. Шихановича. — М.: Просвещение, 1968. — 232 с.
Элементы теории множеств
I. Основные понятия и аксиомы теории множеств
За тысячи лет своего существования от простейших представлений о числе и фигуре математики пришла к образованию многих новых понятий и методов. Она превратилась в мощное средство изучения природы и гибкое орудие практики. XX век принес математике новые идеи, теории, расширилась сфера её применения. Математика занимает особое положение в системе наук – её нельзя отнести ни к гуманитарным, ни к естественным наукам. Но она ввела те основные понятия, которые используются в них. Таким понятием является понятие «множество», которое впервые возникло в математике и в настоящее время является общенаучным.
Первый набросок теории множеств принадлежит Бернарду Больцано («Парадоксы бесконечного», 1850). В этой работе рассматриваются произвольные (числовые) множества, и для их сравнения определено понятие взаимно-однозначного соответствия.
В конце 19 века Георг Кантор, немецкий математик, основоположник теории множеств, дал интуитивное определение понятию «множеству» так: «Множество есть многое, мыслимое как единое целое» [1]. Такое определение множества потребовало введения трех символов.
Первый из них должен представлять множество как нечто «единое», т.е. являться представителем самого множества. В качестве такого символа принято применять любую прописную букву какого-либо алфавита: например, обозначать множества прописными буквами латинского алфавита А, В, …, Х или какого-либо другого по соглашению.
Второй символ должен представлять «многое», то есть рассматриваться как элемент множества. В качестве этого символа принято использовать строчные буквы этого же алфавита: a, b, …, z.
Третий символ должен однозначно соотнести элемент множеству. В качестве соответствующего символа определен знак ![]() , который происходит от первой буквы греческого слова (быть). Запись определяет отношение: х есть элемент Х. Для того чтобы указать, что х не есть элемент Х, пишут
, который происходит от первой буквы греческого слова (быть). Запись определяет отношение: х есть элемент Х. Для того чтобы указать, что х не есть элемент Х, пишут![]() .
.
Стоит отметить, что такое определение понятия множества приводит к ряду внутренних противоречий теории – так называемым парадоксам.
Например, рассмотрим парадокс Рассела. Парикмахер
(элемент х), проживающий в некоторой деревне, которые не бреются сами (пусть Х – множество всех тех и только тех жителей данной деревни, которые не бреются сами). Бреет ли парикмахер самого себя? То есть ![]() или
или ![]() ? Ответить на вопрос невозможно, поскольку полагая, например, что
? Ответить на вопрос невозможно, поскольку полагая, например, что ![]() , сразу приходим к противоречию:
, сразу приходим к противоречию:![]() , и обратно.
, и обратно.
В школьном курсе математики учащимися рассматривается понятие множества, как неопределяемое понятие, под которым понимается совокупность объектов окружающей нас действительности, мыслимую как единое целое. А каждый объект этой совокупности называют элементом данного множества.
На настоящее время существует несколько аксиоматических систем теории множеств:
-Система аксиом Цермело. К этой системе аксиом часто добавляют аксиому выбора, и называют системой Цермело — Френкеля с аксиомой выбора (ZFC).
-Аксиомы теории NBG. Данная система аксиом, предложенная фон Нейманом, впоследствии пересмотренная и упрощенная Робинсоном, Бернайсом и Геделем.
Система Цермело (Z-система) состоит из 7 аксиом. Опишем данные аксиомы в тех рамках, в которых они используются в школьном курсе математики.
Аксиома объемности (Z1). Если все элементы множества А принадлежат множеству В, а все элементы множества В принадлежат также множеству А, то А=В.
Для пояснения данной аксиомы нам необходимо использовать термин «подмножество»: Если каждый элемент множества A является элементом множества Z, то говорят, что А – подмножество Z, и пишут![]() . Символ
. Символ ![]() именуется «включение». Если не исключается возможность ситуации, когда Z=A, то для того чтобы акцентировать на этом внимание, пишут
именуется «включение». Если не исключается возможность ситуации, когда Z=A, то для того чтобы акцентировать на этом внимание, пишут ![]() .
.
Введя термин «подмножество», сформулируем аксиому 1 в символьном виде:![]() .
.
Аксиома пары (Z2). Для произвольных a и b существует множество, единственными элементами которого являются {a,b}.
Данная аксиома используется при пояснении декартова произведения множеств, где первоначальным понятием является «упорядоченная пара». Под упорядоченной парой понимают совокупность двух элементов, каждый из которых занимает в записи определенное место. Обозначают упорядоченную пару так: (а,b).
Аксиома суммы (Z3). Для произвольных множеств А и В существует единственное множество С, элементами которого являются все элементы множества А и все элементы множества В и которое никаких других элементов больше не содержит.
В символьном виде аксиому Z3 можно записать так: ![]() . На основании данной аксиомы и вытекающих из неё теорем [6] указываются свойства операций множеств, описание которых будут изложены в пункте 3. Аксиомы Z1 и Z2 позволяют нам ввести понятие операции объединения, пересечения, дополнение, разности множеств.
. На основании данной аксиомы и вытекающих из неё теорем [6] указываются свойства операций множеств, описание которых будут изложены в пункте 3. Аксиомы Z1 и Z2 позволяют нам ввести понятие операции объединения, пересечения, дополнение, разности множеств.
Аксиома степени (Z4). Для любого множества Х существует множество всех его подмножеств Р(Х).
Аксиома бесконечности (Z6). Существует, по крайней мере, одно бесконечное множество – натуральный ряд чисел.
Аксиома выбора (Z7). Для всякого семейства непустых множеств существует функция, которая каждому множеству семейства сопоставляет один из элементов этого множества. Функция называется функцией выбора для заданного семейства.
Стоит отметить важность соответствующих аксиом, так как множества и отношения между ними являются предметом изучения любой математической дисциплины.
Укажем ещё одно важное открытие в теории множеств – изображение отношений между подмножествами, для наглядного представления [4]. Одним из первых, кто пользовался этим методом, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц. Затем этот метод довольно основательно развил и Леонард Эйлер. После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано. Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов Эйлера пользовался и немецкий математик Эрнест Шредер. Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна, а в некоторых книгах их называют также диаграммами Эйлера-Венна [4]. Диаграммы Эйлера-Венна используются не только в математике и логике, но и в менеджменте и других прикладных направлениях.
II. Отношения между множествами и способы их задания
Итак, под множествами понимается совокупность любых объектов, мыслимая как единое целое. Множества могут состоять их объектов самой различной природы. Их элементами могут быть буквы, атомы, числа, уравнения, точки, углы и т. д. Именно этим объясняется чрезвычайная широта теории множеств и ее приложение к самым разнообразным областям знания (математике, физике, экономике, лингвистике и т. д.).
Считают, что множество определяется своими элементами, то есть множество задано, если о любом объекте можно сказать, принадлежит он этому множеству или не принадлежит. Различают два способа задания множеств.
- Множество можно задать с помощью перечисления элементов.
Например, если множество А состоит из элементов а, b, с, то пишут: А = {a, b, c}.
Не каждое множество можно задать с помощью перечисления элементов. Множества, все элементы которых можно перечислить называют конечными. Множества, все элементы которых нельзя перечислить называют бесконечными. Их нельзя задать с помощью перечисления элементов. Исключение составляют бесконечные множества, в которых ясен порядок образование каждого следующего элемента на основе предыдущего. Например, множество натуральных чисел – бесконечное множество. Но известно, что в нем каждое следующее число, начиная со второго, на 1 больше предыдущего. Поэтому можно задать так N = {1, 2, 3, 4, …}.
- Множество можно задать с помощью указания характеристического свойства.
Характеристическим свойством данного множества называется свойство, которым обладают все элементы этого множества и не обладают ни один, не принадлежащий ему элемент. Обозначается: А = {x|…}, где после вертикальной черты записывается характеристическое свойство элементов данного множества.
Например, В={1,2,3}. Нетрудно заметить, что каждый элемент множества В – натуральное число, меньшее 4. Именно это свойство элементов множества В является для него характеристическим. В этом случае пишут: ![]() и читают: «Множество В состоит из таких элементов х, что х принадлежит множеству натуральных чисел и х меньше четырех» или множество В состоит из натуральных чисел, меньших 4. Множество В можно задать и по – другому:
и читают: «Множество В состоит из таких элементов х, что х принадлежит множеству натуральных чисел и х меньше четырех» или множество В состоит из натуральных чисел, меньших 4. Множество В можно задать и по – другому: ![]() или
или ![]() , и т.д.
, и т.д.
При этом, если элемент не подчиняется характеристическому свойству множества, то он данному множеству и не принадлежит. Существуют множества, которые можно задать только с помощью указания характеристического свойства, например,![]() .
.
Особую важность в школьном курсе математике имеют числовые множества, т.е. множества, элементами которого являются числа [2]. Для названия числовых множеств в математике приняты специальные обозначения:
N = {1, 2, 3, 4, …} – множество натуральных чисел;
Z = {…,-4, -3, -2, -1, 0, 1, 2, 3, 4, …} – множество целых чисел (содержит все натуральные числа и числа, им противоположные);
Q = {x | x=p/q, где p∈Z, q∈N} – множество рациональных чисел (состоит из чисел, допускающих представление в виде обыкновенной дроби);
J – множество иррациональных чисел (множество, состоящее из бесконечных десятичных непериодических дробей, например: 1,23456342…;![]() ,
, ![]() и др.)
и др.)
R = (-∞; +∞) – множество действительных чисел.
Множество всех действительных чисел Л. Эйлер изобразил с помощью кругов. (Рис. 1)

Cтоит отметить, что все любые числовые множества можно задать с помощью числового промежутка. (Рис. 2)
Типы числовых промежутков

Множество С, рассмотренное выше, это числовое множество и его можно указать с помощью числового промежутка (Рис. 3)

Рисунок 3 – Числовой промежуток
Укажем еще одно важное правило для задания числовых множеств: Конечные числовые множества изображаются на числовой прямой отдельными точками.
В математике иногда приходится рассматривать множества, содержащие только один элемент, и даже множества, не имеющие ни одного элемента. Множество, не содержащее ни одного элемента, называют пустым. Его обозначают знаком ∅. Например, дано множество A={x|x∈N∧-2<x<0}. Это множество задано своим характеристическим свойством, но оно является пустым, так как в нем нет ни одного элемента, удовлетворяющее данному свойству [3]. Или, например, пусть множество В – это множество всех прямоугольников с неравными диагоналями. То, что свойство «быть прямоугольником с неравными диагоналями» задает пустое множество, составляет утверждение геометрической теоремы: «Во всяком прямоугольнике диагонали равны».
Стоит отметить, когда речь идет о двух и более множествах, то между ними могут быть какие-либо отношения или нет. Если множества находятся в каких-либо отношениях, то речь идет или об отношении равенства или отношении включении.
Множество А включается во множество В, если каждый элемент множества А принадлежит множеству В. Обозначается данное отношение так: A⊂B. Или, по-другому говорят, что множество А является подмножеством множества В.
Множества А и В называются равными, тогда и только тогда, когда каждый элемент множества А принадлежит множеству В и вместе с этим каждый элемент множества В принадлежит множеству А. Обозначается данное отношение так: А=В
Например:
1) A={a,b,c,d} и B={b,d}, эти множества находятся в отношении включения B⊂A, т.к. каждый элемент множества В принадлежит множеству А.
2) M={x|x∈R∧x<6}=(-∞;6) и K{x|x∈R∧x≤8}=(-∞;8], эти множества находятся в отношении включения M⊂K, т.к. каждый элемент множества M принадлежит множеству K (Рис. 4)

Рисунок 4 – Числовой промежуток
3) A={x|x∈N∧x:2}={2,4,6,8,10,…} и B={x|x∈N∧x:3}={3,6,9,12,…}, эти два множества не находятся ни в каких отношениях A⊄B, так как во множестве А есть элемент 2, не принадлежащий множеству В
и B⊄A, т.к. во множестве В есть элемент 3, не принадлежащий множеству А.
Следовательно, данные множества не находятся ни в каких отношениях.
III. Операции и свойства операций над множествами
Опр.1.Пересечением множеств А и В называется операция, результатом которой является множество, состоящее из тех и только тех элементов, которые принадлежат и А и В одновременно.
A∩B={x|x∈A∧x∈B}
Опр.2. Объединением множеств А и В называется операция, результатом которой является множество, состоящее из тех и только тех элементов, которые принадлежат множеству А или множеству В (т.е. хотя бы одному из этих множеств).
A∪B={x|x∈A∨x∈B}
Опр.3. Разностью множеств А и В называется операция, результатом которой является множество, состоящее из тех и только тех элементов, которые принадлежат А и не принадлежат В одновременно.
А В ={x∈A∧x∉B}
Опр.4. Дополнением множества А до универсального множества называется множество, каждый элемент которого принадлежит универсальному и не принадлежит А.
![]()
Выражения с множествами
Из множеств, знаков операций над ними и, может быть, скобок можно составлять выражения. Например, А∩ВС.
Необходимо знать порядок выполнения операций в таких выражениях и уметь их читать.
Порядок выполнения операций
-
если нет скобок, то в первую очередь выполняется дополнение до универсального множества простого множества, затем пересечение и объединение (они равноправны между собой), в последнюю очередь – разность;
-
если в выражении есть скобки, то сначала выполняют операции в скобках по порядку, приведенному в пункте 1), а затем все операции за скобками.
Например, а) А∩ВС; б) А∩(ВС); в) А∩(ВС)’ .
Чтение выражения начинается с результата последней операции. Например, выражение а) читается так: разность двух множеств, первое из которых пересечение множеств А и В, а второе – множество С.
Круги Эйлера
Операции над множествами и отношения между ними можно изобразить с помощью кругов Эйлера. Это специальные чертежи, на которых обычные множества изображаются кругами, универсальное множество – прямоугольником

Задача. Изобразить с помощью кругов Эйлера множество (А∪В)’∩С.

Решение. Расставим порядок выполнения операций в данном выражении: (А∪В)’∩С. Заштрихуем результаты операций согласно порядку их выполнения

Свойства операции над множествами (рис.5)
Свойства I – 8 и 10 – 80 связаны между собой гак называемым принципом двойственности:
если в любом из двух столбиков свойств поменять знаки ∩→∪, ∪→∩, ∅→U, U→∅, то получится другой столбик свойств.

IV. Разбиение множества на классы
Считают, что множество Х разбито на попарно непересекающиеся подмножества или классы, если выполнены следующие условия:
1) пересечение любых двух подмножеств пусто;
2) объединение всех подмножеств совпадает с множеством Х.
Разбиение множества на классы называют классификацией.
V. Декартово произведение множеств
Декартовым произведением множеств А и В называется множество пар, первая компонента каждой из которых принадлежит множеству А, а вторая — множеству В Декартово произведение множеств А и В обозначают А х В. Таким образом, А×В={(x,y)|x∈A˄y∈B}. Операцию нахождения декартова произведения множеств А и В называют декартовым умножением этих множеств. Если А и В — числовые множества, то элементами декартова произведения этих множеств будут упорядоченные пары чисел.
VI. Правила суммы и произведения
Обозначим число элементов конечного множества A символом n(A). Если множества А и В не пересекаются, то n(AUВ)= n(А) +n (В). Если множества А и В пересекаются, то n(А U В) = n (A) + n (В) — n (A ∩ В).
Число элементов декартова произведения множеств A и В подсчитывается по формуле n (А X В) = n (A) • n (В).
Правило подсчета числа элементов объединения непересекающихся конечных множеств в комбинаторике носит название правила суммы, если элемент х можно выбрать k способами, а элемент у — m способами, причем ни один из способов выбора элемента х не совпадает со способом выбора элемента у, то выбор «х или у» можно осуществить k + m способами.
Правило подсчета числа элементов декартова произведения конечных множеств в комбинаторике носит название правила произведения: если элемент х можно выбрать k способами, а элемент y – m способами, то пару (х,y) можно выбрать km способами.
VII. Список использованных источников
-
Асеев Г.Г. Абрамов О.М., Ситников Д.Э. Дискретная математика: Учебное пособие. – Ростов н/Д: «Феникс», Харьков: «Торсинг», 2003, -144с.
-
Виленкин Н. Я. Алгебра. Учебное пособие для IX – X классов средних школ с математической специализацией, 1968
-
Виленкин Н.Я. Рассказы о множествах. М.: Изд-во «Наука». – 1965. – 128с
-
Диаграммы Эйлера – Венна.URL:http://studopedia.net/1_5573_diagrammi-eylera-venna.html
-
Киреенко С.Г., Гриншпон И. Э. Элементы теории множеств (учебное пособие). – Томск, 2003. – 42 с.
-
Куратовский К., Мостовский А. Теория множеств. – М.: Мир, 1970, – 416с.
Введение в теорию множеств
Время на прочтение
12 мин
Количество просмотров 94K
Концепция бесконечности идеологически далека от обычной математической терминологии — ни одна другая тема не выходит за пределы математики так, что превращается из практического, аналитического инструмента в явление мифического порядка. Понятие бесконечности на короткой ноге с такими культурными темами, как религия и философия, и окутана загадочной аурой божественности.
Когда-то давным давно во всех академических дисциплинах было заложено фундаментальное убеждение — существует единственная бесконечность.
Но 1874 году довольно малоизвестный математик провёл серию революционных наблюдений, подвергавших сомнению это всеми принятое и глубоко укоренившееся убеждение. Георг Кантор в своей (теперь уже ставшей легендарной) публикации On a Property of the Collection of All Real Algebraic Numbers доказал, что множество вещественных чисел «более многочисленно», чем множество алгебраических чисел. Так он впервые показал, что существуют бесконечные множества разных размеров (не волнуйтесь — для прояснения этого мы вскоре подробно изучим его статью).

«Множество — это большое количество, которое позволяет воспринимать себя как одно» — Георг Кантор
С 1874 по 1897 год Кантор неистово публиковал статью за статьёй, разворачивая свою теорию абстрактных множеств в расцветающую дисциплину. Однако она была встречена упорным сопротивлением и критикой; многие педанты считали, что его теории перешли в область философии и нарушили принцип религии.
Однако когда начали находиться практические применения математического анализа, отношение к теории изменилось, а идеи и результаты Кантора начали получать признание. К первому десятилению 20-го века его наблюдения, теории и публикации достигли своей кульминации — признания современной теории множеств новой, совершенно уникальной областью математики:
Теория множеств — это математическая теория о точно определённых наборах (множествах) отдельных объектов, называемых членами или элементами множества.
Сколько чисел есть между 0 и 1?
Первая публикация Кантора, состоящая из четырёх с половиной страниц, является великолепным примером краткости. Она разделена на два отдельных доказательства, совместно приводящих к выводу о существовании по крайней мере двух уникальных видов множеств.
В первой части теории исследуется множество вещественных алгебраических чисел и доказывается, что это бесконечное счётное множество. Здесь не стоит путать — «счётное» не обязательно значит, что счёт ведётся строго в целых числах; в контексте теории множеств «счётное» означает, что множество, пусть даже состоящее из бесконечного числа элементов, можно описать повторяющимся рядом, например упорядоченной многочленной функцией. Кантор назвал это свойство бесконечного набора чисел соответствия «один к одному» с рядом, наличием взаимно однозначного соответствия.
Если говорить вкратце, то набор, или множество всех вещественных алгебраических чисел можно вывести с помощью какого-то теоретического ряда многочленов с различными степенями и коэффициентами; следовательно, множество всех вещественных алгебраических чисел является бесконечным счётным множеством.
Во второй части труда Кантора анализируется роль вещественных комплексных чисел, также называющихся трансцендентными числами. Транцендентные числа (лучшие примеры которых — это пи и e) имеют любопытное свойство: математически невозможно вывести их с помощью многочленной функции — они не являются алгебраическими. Вне зависимости от величин, количества частей, степеней или коэффициентов, никакой ряд никогда не может посчитать пи в своём наборе бесконечного счётного множества.
Затем Кантор указывает, что в любом замкнутом интервале [a,b] существует хотя бы одно транцендентное число, которое никогда нельзя будет подсчитать в бесконечном счётном множестве. Поскольку одно такое число существует, то предполагается, что в семействе вещественных чисел существует бесконечное количество транцендентных чисел.
Таким образом он доказал очень чёткое различие между множеством непрерывных, идущих потоком несчётных чисел и набора счётных чисел, которые можно представить как ряд, например, всех вещественных алгебраических чисел.
Далее: запись и операции
Первая публикация Кантора завершилась на этом потрясающем подтверждении существования по крайней мере двух разных видов бесконечности. После его первой статьи появился шквал дополнений, медленно, но верно прокладывавших путь к современной теории множеств.
Стоит также поделиться интересным наблюдением: большинство людей, использующих теорию множеств на практике, ценят скорее не эту конкретную теорему, а заданный ею обобщённый язык. Благодаря своей абстрактной природе теория множеств скрытно влияет на множество областей математики. В математическом анализе, который требует дифференциального и интегрального исчисления, необходимо понимание пределов и непрерывности функций, окончательно закреплённых в теории множеств. В алгебре логики логические операции «и», «или» и «не» соответствуют операциям пересечения, объединения и разности в теории множеств. И последнее, но не менее важное — теория множеств закладывает основы топологии — исследования геометрических свойств и пространственных отношений.
Вооружившись базовым пониманием истории множеств и совершив кратковременное погружение в глубины его влияния, мы можем приступать к знакомству с основами системы обозначений теории множеств.

Часть вторая. Краткий обзор операций, обозначений и диаграмм Венна.
Как сказано в предыдущей части, одно из фундаментальных преимуществ теории множеств произрастает не из какой-то конкретной теории, а из созданного ею языка. Именно поэтому основная часть этого раздела будет посвящена обозначениям, операциям и визуальному представлению теории множеств. Давайте начнём с объяснения базовых символов обозначения множества — соответствующих ему элементов. В таблице ниже показан пример одного множества A с тремя элементами:

A — это множество с элементами «1», «2» и «3»
«1» — элемент множества A
В первой строке показано множество A с тремя отдельными элементами (A = {1,2,3}); во второй строке показан правильный способ обозначения отдельного конкретного элемента 1, принадлежащего множеству A. Пока всё довольно просто, но теория множеств становится существенно интереснее, когда мы добавляем второе множество — начинается путешествие по стандартным операциям.
Для показанной выше таблицы давайте введём два дополнительных множества B и C, содержащие следующие элементы: B = {3,A,B,C,D,E}, C = {1,2}. Хоть мы и создали три множества (A,B и C), в показанных ниже примерах операции выполняются одновременно только с двумя множествами, поэтому внимательно следите за тем, какие множества указаны в самом левом столбце. В показанной ниже таблице представлено пять самых распространённых операндов множеств:

Операции: пересечение (intersection) — множество элементов, принадлежащих множеству A и множеству B;
объединение (union) — множество элементов, принадлежащих множеству A или множеству B;
подмножество (subset) — C является подмножеством A, множество C включено во множество A;
собственное (истинное) подмножество — C является подмножеством A, но C не равно A;
относительное дополнение (relative complement) — множество элементов, принадлежащих к A и не к B.
Вот и они, самые распространённые операции в теории множеств; они довольно популярны и в областях за пределами чистой математики. На самом деле, высока вероятность того, что вы уже видели подобные типы операций в прошлом, хоть и не совсем с такой терминологией, и даже пользовались ими. Хорошая иллюстрация: попросите любого студента описать диаграмму Венна из двух пересекающихся групп, и он интуитивно придёт к правильному результату.
Ещё раз взгляните на последнюю строку, относительное дополнение — какое необычное сочетание слов, правда? Относительное к чему? Если относительное дополнение A — B определяется как A и не B, то как нам обозначить всё, что не является B?
Универсальное множество — пустое множество
Оказывается, если мы хотим получить значимый ответ, то для начала нужно предоставить генеральной совокупности нашей задачи множеств некий контекст. Он часто явным образом задаётся в начале задачи, когда допустимые элементы множества ограничиваются некоторым фиксированным классом объектов, в котором существует универсальное множество, являющееся общим множеством, содержащим все элементы для этой конкретной задачи. Например, если мы хотели бы работать со множествами только из букв английского алфавита, то наше универсальное множество U состояло бы из 26 букв алфавита.
Для любого подмножества A множества U дополнение множества A (обозначаемое A′ или U − A) определяется как множество всех элементов в генеральной совокупности U, которое не находится в A. Если вернуться к поставленному выше вопросу, то дополнением множества B является всё в пределах универсального множества, что не принадлежит B, в том числе и A.
Прежде чем мы двинемся дальше, надо упомянуть ещё одно принципиальное множество, которое достаточно важно для базового понимания: нулевое или пустое множество. Учтите, что существует единственное пустое множество, поэтому никогда не говорят «пустые множества». Хотя мы не будем рассматривать в этой статье эквивалентность, основная теория гласит, что два множества эквивалентны, если они имеют одинаковые элементы; следовательно, может быть только одно множество без элементов. Поэтому существует единственное пустое множество.
Диаграммы Венна и остальное
Диаграммы Венна, официально изобретённые в 1880 году Джоном Венном, являются именно тем, что вы и представляете, хотя их научное определение звучит примерно так:
Схематичное изображение всех возможных отношений нескольких множеств
Ниже показано изображение шести самых распространённых диаграмм Венна, и почти во всех показаны недавно изученные нами операнды:
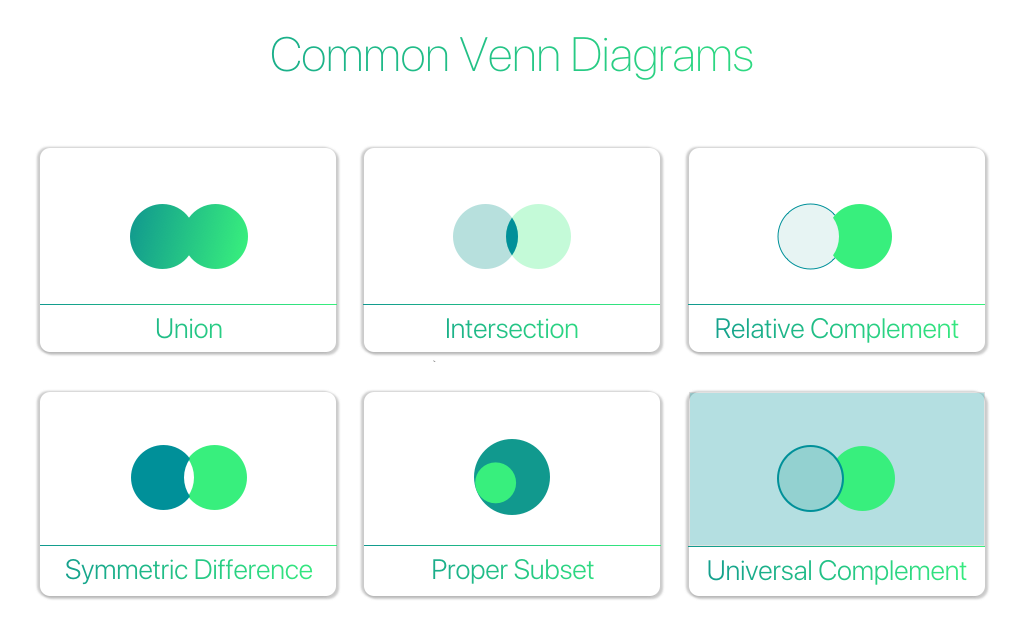
Объединение (union), пересечение (intersection), относительное дополнение (relative complement), симметрическая разность (symmetric difference), собственное множество (proper subset), абсолютное дополнение (universal дополнение).
Начав с очень простых обозначений множества и его элементов, мы узнали затем о базовых операциях, позволивших нарисовать эту визуальную подсказку. Мы рассмотрели все операции, за исключением симметрической разности (внизу слева). Чтобы не оставлять пробелов в знаниях, скажем, что симметрическая разность, также называемая дизъюнктивным объединением — это просто множество элементов, которые находятся в любом из множеств, но не входят в их пересечение.
Закончим мы этот раздел введением понятия мощности (кардинального числа). Мощность множества, обозначаемая символом абсолютного значения — это просто количество уникальных элементов, содержащихся в определённом множестве. Для показанного выше примера мощность трёх множеств равна: |A| = 3, |B| =6, |C| = 2.
Прежде чем двигаться дальше, дам вам пищу для размышлений — какова связь между мощностью и количеством возможных подмножеств?

Часть 3. Мощность и показательные множества
В предыдущих двух частях мы разобрались с основами теории множеств. В третьей части мы укрепим своё понимание, сосредоточившись на самом важном свойстве любого множества: общем количестве содержащихся в нём уникальных элементов.
Количество уникальных элементов во множестве, также известное как мощность, предоставляет нам фундаментальную опорную точку для дальнейшего, более глубокого анализа этого множества. Во-первых, мощность — это первое из рассматриваемых нами уникальных свойств, позволяющее нам объективно сравнивать различные виды множеств, проверяя, существует ли биекция (это, с небольшими оговорками, просто более изысканный термин для function ) одного множества на другое. Ещё один способ применения мощности, а также тема этой части статьи — мощность позволяет оценить все возможные подмножества, существующие в данном множестве. Что достаточно буквально можно применять в повседневных задачах распределения решений, будь то планирование бюджета на поездку в продуктовый магазин или оптимизация портфеля акций.

Примеры мощности множеств
Например, в таблице выше показаны пять отдельных множеств с их указанной справа мощностью. Как мы уже говорили, символ мощности напоминает символ абсолютного значения — значение, заключённое между двумя вертикальными линиями. Все примеры понятны, за исключением, возможно, последней строки, которая подчёркивает тот факт, что на мощность влияют только уникальные элементы множества.
Помните подмножества из предыдущей части статьи? Оказывается, что мощность некоторого множества A и количество возможных подмножеств множества A имеют удивительную связь. Ниже показано, что количество подмножеств, которые можно составить из некоторого подмножества, увеличивается с порядком мощности на предсказуемую величину:
Количество возможных подмножеств в C= 2|C|
Давайте подробно рассмотрим показанный ниже пример. Однако для начала поразмыслим над формулой. Представим мощность как общее количество «позиций», которое представляет множество. При создании некоторого подмножества для каждой возможной позиции принимается булево решение (да/нет). Это означает, что каждый уникальный элемент, добавляемый к множеству (то есть увеличивающий мощность на единицу) увеличивает количество возможных подмножеств на множитель два. Если вы программист или учёный, то можете уяснить эту логику немного глубже, если поймёте, что все подмножества множества можно вычислить с помощью таблицы двоичных чисел.
Показательное множество (булеан)
Прежде чем мы вычислим все подмножества для примера множества C, я хотел бы ввести последнее понятие — булеан.
Булеан обозначается заглавной буквой S, за которой в скобках указывается исходное множество S(С). Булеан — это множество всех подмножеств C, включая пустое множество и само множество C. В таблице ниже показан булеан S(С) со всеми перестановками возможных подмножеств для множества C, содержащихся в одном большом множестве.

Для удобства форматирования я убрал запятые между множествами***
Чем может быть полезен булеан? На самом деле, вы скорее всего много раз интуитивно использовали булеаны, даже об этом не догадываясь. Каждый раз, когда вы выбираете подмножество элементов из более крупного множества, вы выбираете элемент булеана. Например ребёнок внимательно изучающий кондитерский магазин с купюрой в 5 долларов — какой элемент булеана множества всех доступных сладостей он выберет? Или если взять более технический пример: вам, как разработчику ПО может потребоваться запросить всех возможных пользователей базы данных, также обладающих свойством X и Y — ещё один случай, в котором одно подмножество выбирается из всех возможных подмножеств.
Эквивалентность и биективная функция
Теперь мы понимаем, что такое мощность множества, почему оно важно, и его связь с булеаном. Поэтому вернёмся ненадолго к тому, что упоминали в самом начале: что конкретно определяет эквивалентность в теории множеств?
Очевидно, что два множества с одинаковой мощностью имеют некое общее свойство, но на этом сходства заканчиваются — что если в одном из множеств есть многократно повторяющийся элемент? Что если два множества имеют одинаковую мощность и количество элементов? Нельзя отрицать, что они в какой-то степени «эквивалентны», но даже в этом случае всё равно есть возможность различий, потому что каждое множество может иметь разные элементы, повторяющиеся одинаковое количество раз. Смысл здесь в том, что концепция эквивалентности в теории множеств немного чужда другим областям математики. Установление эквивалентности в этом мире требует знакомства с этой концепцией и нового языка. В последней части этой статьи мы введём понятие эквивалентности, а также таких базисных свойств, как инъективные, биективные и сюръективные функции.

Часть 4. Функции.
В этой части мы подробнее расскажем о функциях в пределах теории множеств. Как и в случае с предыдущими понятиями, терминология стандартных функций в теории множеств слегка отличается от других областей математики, а потому требует объяснения. Терминологии довольно много, так что давайте сразу приступим к делу! В первой таблице внизу отражены понятия области определения, области значений и значения функции:

Функция в мире теории множеств — это просто соответствие некоторых (или всех) элементов из Множества A некоторым (или всем) элементам Множества B. В показанном выше примере набор всех возможных элементов A называется областью определения; элементы A, используемые в качестве входных значений, в частности называются аргументами. Справа набор всех возможных выходных значений (называющихся в других областях математики «областью значений»), называется кообластью; набор настоящих выходных элементов B, соответствующих A, называется образом.
Пока особо ничего сложного, только новый способ задания параметров функций. Далее мы расскажем о том, как описывать поведения этих функций соответствия при помощи обычных типов функций.
Инъекции, сюръекции и биекции
В теории множеств для классификации соответствия множеств обычно используются три понятия: инъекция, сюръекция и биекция. К сожалению, эти понятия имеют несколько разных названий, усиливающих неразбериху, поэтому мы сначала рассмотрим каждое определение, а затем изучим визуальные примеры. Все три термина описывают способ, которым отображаются аргументы на образы:
- Функция является инъективной (или «один к одному»), если каждый элемент в кообласти отображается не более чем на один элемент в области определения.
- Функция является сюръективной, если каждый элемент в кообласти отображается не менее чем на один элемент в области определения. (то есть образ и кообласть функции эквивалентны.)
- Функция является биективной, если каждый элемент кообласти отображается ровно на один элемент области определения.
Вишенкой на торте этих сложных определений стали возможные дополнительные значения слов «инъективный», «сюръективный» и «биективный». Когда они используются для описания функции (соответствия), верным будет представленное выше значение; однако также верно будет идентифицировать функции (соответствия) исключительно по этим характеристикам. То есть функция с инъективным поведением называется инъекцией, функция с сюръективным поведением — сюръекцией, а функция с биективным поведением — биекцией.
Прочитайте заново представленный выше список пунктов. Биекция — это просто функция, удовлетворяющая обоим предыдущим требованиям; то есть, функция инъективна и сюръективна. Инъективная функция не должна быть сюръективной, а сюръективная — инъективной. Ниже показан визуальный пример, в котором эти три классификации привели к созданию функций множеств, определяемых четырьмя возможными комбинациями инъективных и сюръективных свойств:

Биекция (инъекция + сюръекция), инъекция (инъекция + не-сюръекция), сюръекция (не-инъекция + сюръеция), без классификации (не-инъекция + не-сюръекция)
Вот и всё! Теперь мы обладаем элементарным пониманием самых часто встречаемых соотношений, встречающихся в мире множеств. Однако это ни в коем случае не конец нашего пути: напротив, это самое начало.
Фундаментальные основы теории множеств — ключ к пониманию более высокоуровневых областей математики. Чтобы продолжить наше движение вверх, к этим различным областям, далее нужно будет, пользуясь своими знаниями о теории множеств, уяснить одну из самых революционных теорий в истории математики: систему аксиом Цермело-Френкеля.

