Нахождение основания системы счисления
В какой системе счисления число (3375_{10}) будет выглядеть как (1000_{?})?
Стоить заметить, что любое десятичное число A в n-ой степени можно записать как единицу и n нулей в системе счисления с основанием A: (A^{n}_{10}=1underbrace{000…000}_{n}) (_{A})
Тогда (3375_{10}=15^3_{10}), значит в системе счисления с основанием 15 будет выглядеть как (1000_{15}).
Ответ: 15
В какой системе счисления число (121_{10}) будет выглядеть как (100_{?})?
Стоить заметить, что любое десятичное число A в n-ой степени можно записать как единицу и n нулей в системе счисления с основанием A: (A^{n}_{10}=1underbrace{000…000}_{n}) (_{A})
Тогда (121_{10}=11^2_{10}), значит в системе счисления с основанием 11 будет выглядеть как (100_{11}).
Ответ: 11
В какой системе счисления число (2744_{10}) будет выглядеть как (1000_{?})?
Стоить заметить, что любое десятичное число A в n-ой степени можно записать как единицу и n нулей в системе счисления с основанием A: (A^{n}_{10}=1underbrace{000…000}_{n}) (_{A})
Тогда (2744_{10}=14^3_{10}), значит в системе счисления с основанием 14 будет выглядеть как (1000_{14}).
Ответ: 14
В какой системе счисления число (1331_{10}) будет выглядеть как (1000_{?})?
Стоить заметить, что любое десятичное число A в n-ой степени можно записать как единицу и n нулей в системе счисления с основанием A: (A^{n}_{10}=1underbrace{000…000}_{n}) (_{A})
Тогда (1331_{10}=11^3_{10}), значит в системе счисления с основанием 11 будет выглядеть как (1000_{11}).
Ответ: 11
В какой системе счисления число (1024_{10}) будет выглядеть как (100000_{?})?
Стоить заметить, что любое десятичное число A в n-ой степени можно записать как единицу и n нулей в системе счисления с основанием A: (A^{n}_{10}=1underbrace{000…000}_{n}) (_{A})
Тогда (1024_{10}=4^5_{10}), значит в четверичной системе счисления будет выглядеть как (100000_{4}).
Ответ: 4
В какой системе счисления число (6561_{10}) будет выглядеть как (100000000_{?})?
Стоить заметить, что любое десятичное число A в n-ой степени можно записать как единицу и n нулей в системе счисления с основанием A: (A^{n}_{10}=1underbrace{000…000}_{n}) (_{A})
Тогда (6561_{10}=3^8_{10}), значит в троичной системе счисления будет выглядеть как (100000000_{3}).
Ответ: 3
В какой системе счисления число (4096_{10}) будет выглядеть как (10000_{?})?
Стоить заметить, что любое десятичное число A в n-ой степени можно записать как единицу и n нулей в системе счисления с основанием A: (A^{n}_{10}=1underbrace{000…000}_{n}) (_{A})
Тогда (4096_{10}=8^4_{10}), значит в восмеричной системе счисления будет выглядеть как (10000_{8}).
Ответ: 8
На этой странице вы узнаете
- В каких случаях 10 не равно 10?
- Как купить шоколадку у инопланетянина?
Привычная нам система счисления называется десятичной, потому что нам с детства удобно считать 10 пальцев на руках. Но так было не всегда: раньше людям было удобнее считать до 12, по количеству фаланг на пальцах одной руки. Для них и для нас число 10 имеет совершенно разное значение.
Виды систем счисления
Система счисления — это модель, которая позволяет записывать числа по определенным правилам.
Основных типов систем счисления две:
- позиционные,
- непозиционные.
Непозиционные системы счисления основываются на том, что значение цифр никак не зависит от того, на какой позиции в числе они находятся.
Возьмем фермера и его овец. Какой способ записать количество овец — самый удобный? Самый простой пример — подсчет с помощью одной насечки. Тогда мы подсчитываем овец в своем стаде поштучно, обозначая при записи каждую отдельной засечкой.

Очевидно, что это неудобно. В наших интересах размножать овец. Но чем их больше, тем менее читаема такая запись. Когда мы добьемся невиданных высот в скотоводстве, и у нас станет 2796 голов, их подсчет с помощью одной засечки будет невозможен.
Римская система счисления — еще один известный пример непозиционной системы счисления. В ней уже появляются символы для обозначения отдельных чисел. Но в какой бы позиции символ ни стоял, он все еще значит только самого себя:
- I — 1;
- V — 5;
- X — 10 и так далее.
Римская система счисления упрощает запись чисел, но не решает проблему неудобства чтения полностью. Например, число 2796 в римской записи будет выглядеть как MMDCCXCVI. Уже неприятно.
В позиционных системах счисления значение цифры зависит от того, на какой позиции она стоит.
На примере нашей родной десятичной системы счисления, мы с вами понимаем, что в числе 1234:
- 1 — количество тысяч, и обозначает не 1, а 1000;
- 2 обозначает количество сотен и понимается как 200;
- 3 отвечает за количество десятков и означает 30;
- 4 стоит на самой последней позиции и означает количество единиц, поэтому в данном случае 4 — это 4.
Это сильно упрощает чтение чисел любого размера, так как меняется сам принцип их чтения:
- В непозиционной системе счисления (на примере римской): СХХIII = 100 + 10 + 10 + 1 + 1 + 1 = 123.
- В позиционной: 123 = 100 + 20 + 3.
Именно позиционную систему счисления выберет грамотный фермер, чтобы подсчитать количество овечек.
Основание позиционной системы счисления
Позиционная система счисления характеризуется ее основанием — количеством цифр, которые она использует для записи чисел.
- Десятичная система счисления (10сс) использует 10 цифр — от 0 до 9, с ней мы знакомы с детства.
- Компьютеру роднее двоичная система счисления (2сс), которая использует 2 цифры — 1 и 0.
- В двенадцатеричной системе счисления (12сс) помимо цифр 0–9 необходимы еще два символа. Для удобства заменим их буквами: A = 10, B = 11. Теперь имеем 12 символов от 0 до B.
- Также небезызвестная система счисления — шестнадцатеричная. Для нее кроме цифр 0–9 нужно еще больше символов, чтобы обозначить все цифры. Происходит это по аналогии — каждая новая буква отвечает за большее значение: A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Мы используем числа тогда, когда кончаются цифры. Привычная нам система счисления называется десятичной, потому что использует 10 цифр — от 0 до 9. Для записи значений больше 9, мы начинаем строить числа из цифр. Первое такое число — 10.
Если бы мы использовали другое количество цифр, всё выглядело бы иначе. При использовании цифр от 0 до 6, нам пришлось бы строить числа уже для записи значений, больше 6. В таком случае 10 будет равно 7, но эти значения будут записаны в разных системах счисления.
Построение числа в непривычных нам системах счисления происходит точно так же, как и в 10сс:
- Увеличиваем значения единиц, используя доступные цифры.
- Как только цифры закончились, значение единиц обнуляется. Появляется новый разряд десятков, который также увеличивается от 1 до предела системы счисления.
- Когда любой разряд числа принимает значение максимальной цифры — разряд выше увеличивается на 1, а текущий разряд обнуляется.
Например:
- В 10сс число 88 будет увеличиваться так:
88 → 89 → 90 → 91 → 92 → … 99 → 100;
- В 2сс разряды будут появляться быстрее из-за маленького количества цифр:
1 → 10 → 11 → 100 → 101 → 110 → 111 → 1000;
- В 12сс чуть медленнее, так как цифр больше:
8 → 9 → A → B → 10 → 11 → … 18 → 19 → 1A → 1B → 20 → … 99 → 9A → 9B → A0 → A1 → … AA → AB → B0 → B1 → … BA → BB → 100.
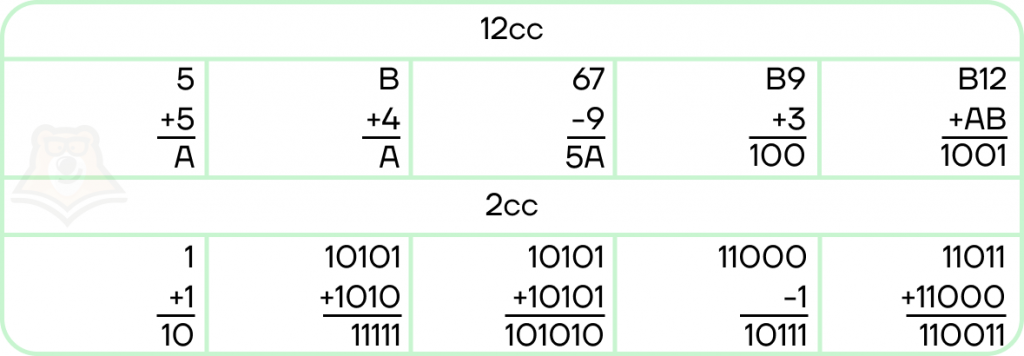
Арифметика, как и построение числа, во всех системах счисления одинакова:
- Изменение разрядов происходит с единиц.
- При сложении избыток суммы увеличивает разряд выше (то самое “6 пишем, 1 в уме”).
- В вычитании при необходимости занимаем значение из старшего разряда, уменьшая его на 1.
Расширенная запись числа и перевод из Nсс в 10сс
Уметь переводить числа из 10сс в другие и обратно важно для того, чтобы торговать с инопланетянами.
Однажды мы, вероятно, достучимся до внеземных цивилизаций. Но у них может оказаться не 10 пальцев на руках, а 7, 12 или любое другое количество. Если их представления о математике шли путем, подобному нашему, какую систему счисления придумали они?
Когда мы захотим купить инопланетный сникерс за 2256 межгалактических юнитов, вполне может оказаться, что наши представления о числах сильно отличаются.

Подсчитав количество пальцев на руках продавца шоколадок, важно научиться переводить числа из одной системы счисления в другую.
Полная запись числа a1a2a3…ai, где ai — цифра числа под номером i, состоящей из k символов и с основанием системы счисления n, будет выглядеть как:
a1a2a3…ai…ak = a1 * nk — 1 + a2 * nk — 2 + … + ai * nk — i + … + ak * n0.
На примерах:
- 123 в 10сс расписывается как: 1 * 102 + 2 * 101 + 3 * 100;
- 1010 в 2сс: 1 * 23 + 0 * 22 + 1 * 21 + 0 * 20;
- A9B в 12сс: 10 * 122 + 9 * 121 + 11 * 120.
Такой записи числа достаточно, чтобы перевести значение числа из любой системы счисления в 10сс — нужно посчитать значение составленной записи:
- 10102 = 1 * 23 + 0 * 22 + 1 * 21 + 0 * 20 = 8 + 0 +2 + 0 = 1010;
- 5259 = 5 * 92 + 2 * 91 + 5 * 90 = 5 * 81 + 2 * 9 + 5 * 1 = 42810;
- A9B12 = 10 * 122 + 9 * 121 + 11 * 120 = 10 * 144 + 9 * 12 + 11 * 1 = 155910.
Перевод из 10сс в Ncc
Принцип деления с остатком поможет переводить числа в другую сторону — из 10сс в любую другую систему счисления.
Алгоритм перевода следующий:
1. Делим исходное число на основание новой системы счисления.
2. Остаток от деления — новая найденная цифра числа.
3. Целую часть от деления снова делим на основание. Записываем остаток как новую цифру искомой записи, а целую часть от деления — как цель следующего деления. Снова делим целую часть на основание.
4. Деление происходит до тех пор, пока целая часть от деления не станет равна 0.
5. Полученные в качестве остатков от деления цифры нового числа читаются в обратном порядке.
Для примера давайте переведем число 2589 в 7сс:
- На первом шаге делим исходное число на 7, записывая остаток от деления как новую цифру и целую часть как оставшееся значение.

- На втором шаге делаем то же самое, но с целой частью предыдущего деления — теперь делим ее на 7.

- И так до тех пор, пока целая часть от деления не будет равна 0.



Интересующее нас значение находится в самом правом столбце и читается снизу вверх.
258910 = 103567
Перевод в системы счисления с основанием, больше 10, происходит так же. Просто надо не забывать, что цифры больше 9, будут обозначаться соответствующими буквами.
Например, таблица перевода десятичного числа 48406 в 16сс будет выглядеть следующим образом:

И искомое значение будет BD16.
Лайфхак или как быстрее закодировать геном
Представим, что нам нужно написать программу для биологов, которую они будут применять в исследованиях ДНК и нам надо реализовать хранение ДНК в памяти компьютера.
В ДНК встречается четыре вида азотистых оснований: аденин (A), гуанин (G), тимин (T) и цитозин (C). Всю ДНК можно записать как последовательность этих 4 символов. Но можно же записать тогда эту последовательность букв как число в 4сс, сопоставив цифры символам, например, код A – 0, C – 1, G – 2, T – 3. Тогда кусок ДНК GGT будет записан в 4сс как 223.
Но чтобы закодировать геном в компьютере, его надо перевести из 4сс в 2сс. Делать это делением может оказаться очень долго, ведь геном может быть очень длинным и делить его просто неэффективно. К счастью, есть выход!
Между 2сс и системами счисления, в основании которых стоит степень двойки (4сс, 8сс, 16сс), есть связь, которую можно использовать для быстрого перевода из 2сс в них и обратно. Для этого используется следующая таблица:
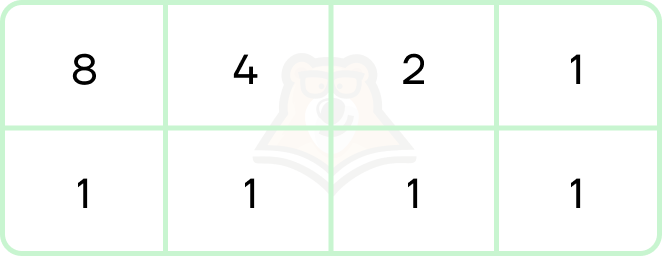
Алгоритм перевода состоит в следующем:
1. Вычисляется степень, в которую нужно возвести 2, чтобы получить основание необходимой системы счисления.
2. Используется количество столбцов таблицы, равное этой степени. Отсчет ведем с правого столбца.
3. При переводе из 2сс весь код разбивается на кодовые слова длиной, равной степени — при необходимости в начало записи добавляются нули. Отдельные кодовые слова подставляются в нижнюю строку таблицы. Цифра записи числа в новой системе счисления будет равна сумме цифр верхней строки, под которыми стоит 1 кодового слова.
4. При переводе в 2сс каждая цифра представляется как сумма цифр верхней строки таблицы. Цифрам, которые используются в сумме, соответствуют 1 кодового слова 2сс, а не использующимся — 0.
На примере:
- Для перевода между 2сс и 4сс используется часть таблицы:
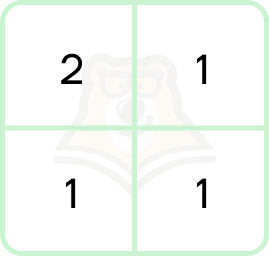
- Перевод из 2сс в 4сс:
110001 = 11.00.01 = (2 + 1).(0 + 0).(0 + 1) = 3.0.1 = 301
- Перевод из 4сс в 2сс:
103 = 1.0.3 = (0 + 1).(0 + 0).(2 + 1) = 01.00.11 = 10011
- Для перевода между 2сс и 8сс используется часть таблицы:
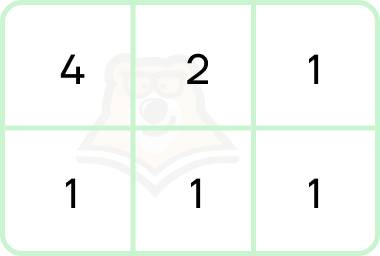
- Перевод из 2сс в 8сс:
10101011100 = 010.101.011.100 = (0 + 2 + 0).(4 + 0 + 1).(0 + 2 + 1).(4 + 0 + 0) = 2.5.3.4 = 2534
- Перевод из 8сс в 2сс:
1753 = 1.7.5.3 = (0 + 0 + 1).(4 + 2 + 1).(4 + 0 + 1).(0 + 2 + 1) = 001.111.101.011 = 1111101011
- Для перевода между 2сс и 16сс используется вся таблица:
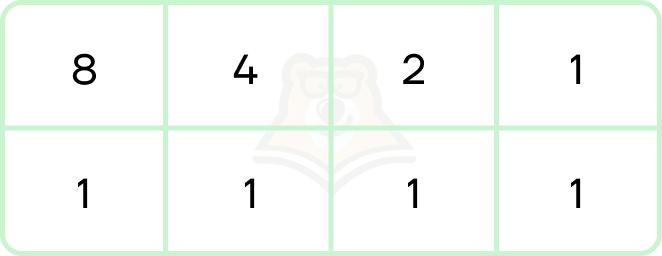
- Перевод из 2сс в 16сс:
101101111000001 = 0101.1011.1100.0001 = (0 + 4 + 0 + 1).(8 + 0 + 2 + 1).(8 + 4 + 0 + 0).(0 + 0 + 0 + 1) = 5.11.12.1 = 5BC1
- Перевод из 16сс в 2сс:
F87A = 15.8.7.10 = (8 + 4 + 2 + 1).(8 + 0 + 0 + 0).(0 + 4 + 2 + 1).(8 + 0 + 2 + 0) = 1111.1000.0111.1010 = 1111100001111010
Перевод между системами счисления на Python
Перевод больших чисел между системами счисления вручную неудобен и может занимать много времени. Иногда выгоднее было бы написать программу.
Перевод из 10сс в другие будем выполнять по описанному выше алгоритму. Пока исходное число больше 0, делим его на основание системы счисления. Записываем остаток от деления как новую цифру числа. Искомое число — остатки от деления, записанные в обратном порядке.
- Основным циклом программы будет while, который работает, пока исходное число больше 0.
- Новую цифру числа берем как остаток от деления исходного числа на основание новой системы счисления с помощью оператора %. Новые цифры будем записывать в новую строку, в которой и будет храниться искомая запись. Чтобы не переворачивать число в конце, можем сразу заносить каждую новую цифру не в конец, а в начало строки.
- Уменьшаем само число, деля его нацело на основание с помощью оператора //.
Например, перевод числа 258936 в 5сс.
number = 258936
n = 5
new_number = ""
while number > 0:
d = number % n
new_number = str(d) + new_number
number //= n
print(new_number)
_____________________________________________________________________
Вывод: 31241221Перевод в 10сс из других систем счисления будем производить по описанной выше формуле:
a1a2a3…ai…ak = a1 * nk — 1 + a2 * nk — 2 + … + ai * nk — i + … + ak * n0.
- Главный цикл программы — for. Он будет перебирать цифры исходного числа, а точнее, их индексы, с помощью диапазона range по длине исходного числа.
- На каждом шаге цикла цифру ai числа будем умножать на основание системы счисления этого числа n в степени, равной разности длины числа k и порядкового номера текущей цифры i — ai*nk — i . Не забываем, что индексация строки начинается с 0, а не с 1, поэтому порядковый номер цифры — на 1 больше ее индекса.
Например, переведем число 31241221 из 5сс обратно в 10сс.
number = "31241221"
n = 5
new_number = 0
k = len(number)
for i in range(k):
new_number += int(number[i]) * n ** (k - i - 1)
print(new_number)
_____________________________________________________________________
Вывод: 258936Лайфхаки по переводу между системами счисления программой:
- для перевода числа из 10сс в 2сс, 8сс и 16сс есть встроенные команды: bin, oct и hex соответственно
- bin(123) — “0b1111011”
- oct(123) — “0o173”
- hex(123) — “0x7b”
Важно заметить, что первые два символа в записи числа окажутся лишними в нашем случае — они будут обозначать идентификатор системы счисления, в которую мы перевели число.
Чтобы сразу от него избавиться, при переводе можно использовать срез, который будет учитывать все число без этого идентификатора:
- bin(123)[2:] — “1111011”
- oct(123)[2:] — “173”
- hex(123)[2:] — “7b”
- перевести число из любой системы счисления в 10сс можно с помощью команды int. Ей необходимо передать два параметра: исходное число в виде строки и основание его системы счисления:
- int(«31241221», 5) — 258936
- int(«7b», 16) — 123
Хорошо. А зачем всё это, если мы не генетики и не торгуем с инопланетянами?
Системы счисления — одно из базовых понятий информатики и оттого используются в большом количестве заданий на ЕГЭ. С применением различных систем счисления придется столкнуться при решении задачи 14, при построении большинства алгоритмов задачи 5, в заданиях на расчет объема информации в номере 7. Также, хотя это не упоминается в условиях заданий явно, в задаче 22 немалая часть алгоритмов связана с переводом числа из одной системы в другую.
Фактчек
- В позиционных системах счисления, в отличие от непозиционных, значение цифры зависит от ее положения в числе.
- Основание позиционной системы счисления определяет количество используемых в ней цифр для записи чисел.
- Для перевода из 10сс в любую другую: берем остаток от деления на основание новой системы счисления в качестве цифр нового числа и записываем их в обратном порядке.
- Для перевода из любой системы счисления в 10сс: умножаем каждую цифру числа на основание его системы счисления, возведенную в степень разности длины числа и порядкового номера данной цифры.
Проверь себя
Задание 1.
Какая цифра не может использоваться в 8сс?
- 0
- 3
- 7
- 8
Задание 2.
Для записи цифр 10-15 в 16сс используются …
- буквы A-F
- буквы А-Д
- буквы U-Z
- любые символы по договоренности
Задание 3.
Десятичное число 101 в 2сс будет выглядеть как…
- 101
- 101101
- 1100101
- 1010011
Задание 4.
Шестнадцатеричное число FBA000 в 10сс будет выглядеть как …
- 16490496
- 69409461
- 61400900
- Это некорректная запись числа в 16сс
Задание 5.
Что сделает запись на языке Python — int(“777”, 8)?
- Переведет число 777 из 10сс в 8сс
- Переведет число 8 из 10сс в 777сс
- Переведет число 777 из 8сс в 10сс
Ответы: 1. — 4; 2. — 1; 3. — 3; 4. — 1; 5. — 3.
Позиционная систе́ма счисле́ния (позиционная, поме́стная нумерация) — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда) относительно десятичного разделителя. Позиционные системы по сравнению с другими позволяют существенно упростить алгоритмы выполнения арифметических операций и ускорить вычисления. Их создание и распространение сыграли большую роль в развитии точных наук — математики, астрономии и физики.
| Системы счисления в культуре | |
|---|---|
| Индо-арабская | |
| Арабская Тамильская Бирманская |
Кхмерская Лаосская Монгольская Тайская |
| Восточноазиатские | |
| Китайская Японская Сучжоу Корейская |
Вьетнамская Счётные палочки |
| Алфавитные | |
| Абджадия Армянская Ариабхата Кириллическая Греческая |
Грузинская Эфиопская Еврейская Акшара-санкхья |
| Другие | |
| Вавилонская Египетская Этрусская Римская Дунайская |
Аттическая Кипу Майяская Эгейская Символы КППУ |
| Позиционные | |
| 2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60 | |
| Нега-позиционная | |
| Симметричная | |
| Смешанные системы | |
| Фибоначчиева | |
| Непозиционные | |
| Единичная (унарная) |
История[править | править код]
Исторически первое изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам. Независимо от евразийских цивилизаций двадцатеричную позиционную систему счисления изобрели индейцы майя. В более поздний период такая нумерация была развита индусами и имела неоценимые последствия в истории цивилизации. К числу таких систем относится десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у арабов.
Определения[править | править код]
Позиционная система счисления определяется целым числом 


Целое число без знака 


, где
— это целые числа, называемые цифрами, удовлетворяющие неравенству
Каждый базисный элемент 

С помощью 




Запись чисел[править | править код]
Если не возникает разночтений (например, когда все цифры представляются в виде уникальных письменных знаков), число 

В ненулевых числах 
Для записи чисел в системах счисления с основанием до 36 включительно в качестве цифр (знаков) используются арабские цифры (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и, затем, буквы латинского алфавита (a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z). При этом, a = 10, b = 11 и т. д., иногда x = 10.
При одновременной работе с несколькими системами счисления для их различения основание системы обычно указывается в виде нижнего индекса, который записывается в десятичной системе:
— это число 123 в десятичной системе счисления;
— то же число в восьмеричной системе счисления;
— то же число, но в двоичной системе счисления;
— то же число, но в десятичной системе счисления с двоичным кодированием десятичных цифр (BCD);
— то же число, но в несимметричной троичной системе счисления;
— то же число, но в симметричной троичной системе счисления, знаки «i», «7», «2» и «−» обозначают «−1», знаки «1» и «+» обозначают «+1».
В некоторых специальных областях применяются особые правила указания основания. Например, в программировании шестнадцатеричная система обозначается:
- в ассемблере и записях общего рода, не привязанных к конкретному языку, буквой h (от hexadecimal) в конце числа (синтаксис Intel);
- в Паскале знаком «$» в начале числа;
- в Си и многих других языках комбинацией 0x или 0X (от hexadecimal) в начале.
В некоторых диалектах языка Си по аналогии с «0x» используется префикс «0b» для обозначения двоичных чисел (обозначение «0b» не входит в стандарт ANSI C).
В русских счётах для записи чисел в десятичной показательной позиционной системе счисления применяется унарнодесятичная система записи (представления) десятичных цифр с одной избыточной унарнодесятичной цифрой «1111111111» = 10_10 на каждый разряд.
Примеры[править | править код]
- 2 — двоичная (в дискретной математике, информатике, программировании)
- 3 — троичная система счисления
- 4 — четверичная система счисления
- 7 — семеричная (в музыке для обозначения названий нот)[2]
- 8 — восьмеричная (в программировании)
- 10 — десятичная система счисления
- 12 — двенадцатеричная (широко использовалась в древности, в некоторых частных областях используется и сейчас)
- 16 — шестнадцатеричная (наиболее распространена в программировании, а также в шрифтах)
- 20 — двадцатеричная (использовалась у майя и ацтеков)
- 40 — сорокаичная система счисления (применялась в древности: в частности, «сорок сороков» = 1600)
- 60 — шестидесятеричная (использовалась в древнем Вавилоне, а впоследствии древнегреческими астрономами для измерения угловых координат звёзд (долготы и широты) и для измерения времени). И сегодня используется в измерении времени суток.
Свойства[править | править код]
Позиционная система счисления обладает рядом свойств:
- Таким образом, естественный порядок на числах соответствует лексикографическому порядку на их записях в позиционной системе счисления при условии, что эти записи дополнены ведущими нулями до одинаковой длины.
- Арифметические операции над числами. Позиционная система счисления позволяет без труда выполнять сложение, вычитание, умножение, деление и деление с остатком чисел, зная только таблицу сложения однозначных чисел, а для трёх последних операций ещё и таблицу умножения в соответствующей системе (см., например, деление столбиком).
Экономичность[править | править код]
В цифровой технике система счисления с основанием 








Экономичность системы счисления — немаловажное обстоятельство с точки зрения её использования в вычислительной машине. Поэтому, хотя применение в вычислительной машине троичной системы вместо двоичной влечёт некоторые конструктивные трудности (при этом нужно пользоваться элементами, каждый из которых может находиться не в двух, а в трёх устойчивых состояниях), эта система уже была использована[4] в некоторых реально существующих вычислительных устройствах.[1]С. В. Фомин
Эквивалентное описание экономичности системы счисления можно получить, используя понятие информационной энтропии. При условии равновероятности появления каждой из цифр в записи числа информационная энтропия записи n-разрядного числа в системе счисления с основанием b принимает значение 

Переход к другому основанию[править | править код]
Перевод в десятичную систему счисления[править | править код]
Если целое число в 
то для перевода в десятичную систему вычисляем следующую сумму:[5]
или в виде схемы Горнера:
Например:
Аналогичные действия имеют место также для дробной части:
Перевод из десятичной системы счисления[править | править код]
- Целая часть
- Последовательно (итеративно) делить с остатком целую часть десятичного числа на основание, пока десятичное число (частное) не станет равно нулю.
- Полученные при делении остатки являются цифрами нужного числа. Число в новой системе записывают, начиная с последнего остатка.[5][6]
- Дробная часть
- Дробную часть десятичного числа умножаем на основание системы, в которую требуется перевести, и отделяем целую часть. Продолжаем умножать дробную часть на основание новой системы и отделять целую часть, пока число не станет равным 0 точно.
- Цифры дробной части в новой системе счисления — это целые части, полученные в первом шаге, которые, убывая по старшинству с самого старшего разряда дробной части, идут в порядке, в каком были они и были получены.
Примечание. Иногда при переводе дробного рационального числа из десятичной системы по таким алгоритмам может получиться бесконечная периодическая дробь: например, 
- Примеры

44 делим на 2. частное 22, остаток 0 22 делим на 2. частное 11, остаток 0 11 делим на 2. частное 5, остаток 1 5 делим на 2. частное 2, остаток 1 2 делим на 2. частное 1, остаток 0 1 делим на 2. частное 0, остаток 1
Частное равно нулю — деление закончено. Теперь, записав все остатки снизу вверх, получим число 
Для дробной части алгоритм выглядит так:
0,625 умножаем на 2. Дробная часть 0,250. Целая часть 1. 0,250 умножаем на 2. Дробная часть 0,500. Целая часть 0. 0,500 умножаем на 2. Дробная часть 0,000. Целая часть 1.
Таким образом, 
Перевод из двоичной в восьмеричную и шестнадцатеричную системы[править | править код]
Для этого типа операций существует упрощённый алгоритм.[8]
Целая часть[править | править код]
Для восьмеричной — разбиваем переводимое число на количество цифр, равное степени 2 (2 возводится в ту степень, которая требуется, чтобы получить основание системы, в которую требуется перевести (2³=8), в данном случае 3, то есть триад). Преобразуем триады по таблице триад:
000 — 0; 100 — 4; 001 — 1; 101 — 5; 010 — 2; 110 — 6; 011 — 3; 111 — 7.
Для шестнадцатеричной — разбиваем переводимое число на количество цифр, равное степени 2 (2 возводится в ту степень, которая требуется, чтобы получить основание системы, в которую требуется перевести (24=16), в данном случае 4, то есть тетрад). Преобразуем тетрады по таблице тетрад:
0000 — 0; 0100 — 4; 1000 — 8; 1100 — C; 0001 — 1; 0101 — 5; 1001 — 9; 1101 — D; 0010 — 2; 0110 — 6; 1010 — A; 1110 — E; 0011 — 3; 0111 — 7; 1011 — B; 1111 — F.
Пример:
преобразуем 1011002 восьмеричная — 101 100 → 548 шестнадцатеричная — 0010 1100 → 2C16
Дробная часть[править | править код]
Перевод дробной части из двоичной системы счисления в системы счисления с основаниями 8 и 16 осуществляется точно так же, как и для целых частей числа, за тем лишь исключением, что разбивка на октавы и тетрады идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа. Например, рассмотренное выше число 1100,0112 будет выглядеть как 14,38 или C,616.
Перевод из восьмеричной и шестнадцатеричной систем в двоичную[8][править | править код]
Для этого типа операций также существует упрощённый алгоритм, обратный вышенаписанному алгоритму.
Для восьмеричной — преобразуем по таблице в триплеты:
0 000 4 100 1 001 5 101 2 010 6 110 3 011 7 111
Для шестнадцатеричной — преобразуем по таблице в квартеты:
0 0000 4 0100 8 1000 C 1100 1 0001 5 0101 9 1001 D 1101 2 0010 6 0110 A 1010 E 1110 3 0011 7 0111 B 1011 F 1111
Пример:
преобразуем 548 → 101 1002 2C16 → 0010 11002
Вариации и обобщения[править | править код]
Запись рациональных чисел[править | править код]
Рациональное число 


где 


Конечной записью в 




где 




Рациональные числа, не представимые в виде 
Симметричные системы счисления[править | править код]
Симметричные (уравновешенные, знакоразрядные) системы счисления по основанию 




Чаще всего используется симметричная троичная система счисления с цифрами 
Отрицательные основания[править | править код]
Существуют позиционные системы с отрицательными основаниями, называемые нега-позиционными:
- −2 — нега-двоичная система счисления;
- −3 — нега-троичная система счисления;
- −10 — нега-десятичная система счисления.
Нецелочисленные основания[править | править код]
Иногда также рассматривают позиционные системы счисления с нецелочисленными основаниями: рациональными, иррациональными, трансцендентными.
Примерами таких систем счисления являются:
- при b = φ = 1,61… — система счисления Бергмана с иррациональным основанием, равным «золотому сечению».[10]
Комплексные основания[править | править код]
Основаниями позиционных систем счисления могут быть также комплексные[11][12] числа. При этом цифры в них принимают значения из некоторого конечного множества, удовлетворяющего условиям, которые позволяют выполнять арифметические операции непосредственно с представлениями чисел в этих системах счисления.
В частности, среди позиционных систем счисления с комплексными основаниями можно выделить двоичные, в которых используются лишь две цифры 0 и 1.
- Примеры
Далее будем записывать позиционную систему счисления в следующем виде 

Примерами систем счисления с комплексными основаниями являются (далее j — мнимая единица):
- Двоичные комплексные системы счисления
Ниже перечислены основания двоичных позиционных систем счисления и представления чисел 2, −2 и −1 в них:
:
(система счисления с натуральным основанием);
:
,
,
(нега-позиционная система счисления);
:
,
,
(система счисления с комплексным основанием);
:
,
,
(система счисления с комплексным основанием);
:
,
,
(система счисления с комплексным основанием);
:
,
,
(система счисления с комплексным основанием).
Непоказательные системы счисления[править | править код]
Показательные системы счисления являются частным случаем позиционных систем счисления с показательной зависимостью. Вместо показательной зависимости могут быть другие зависимости. Например, гипероператорная позиционная система счисления
позволяет записывать бо́льшие диапазоны чисел тем же числом знаков.
Примечания[править | править код]
- ↑ 1 2 3 4 С. В. Фомин. Системы счисления. — М.: Наука, 1987. — 48 с. — (Популярные лекции по математике). (альтернативная ссылка Архивная копия от 2 июня 2013 на Wayback Machine)
- ↑ Битюков Сергей. 13 звуков и интервалов. Их восприятие и обозначение. Лады отклонения и модуляции (рус.). Хабр (7 августа 2021). Дата обращения: 26 августа 2021. Архивировано 12 августа 2021 года.
- ↑ Hayes, Brian. Third base (англ.) // American Scientist (англ.) (рус. : magazine. — 2001. — Vol. 89, no. 6. — P. 490—494. — doi:10.1511/2001.40.3268.
- ↑ См. Троичный компьютер.
- ↑ 1 2 Перевод чисел из одной системы счисления в другую онлайн. matworld.ru. Дата обращения: 8 мая 2021. Архивировано 9 мая 2021 года.
- ↑ Глава 4 — Арифметические основы компьютеров. mif.vspu.ru. Дата обращения: 8 мая 2021. Архивировано 19 февраля 2020 года.
- ↑ Перевод дробных чисел из одной системы счисления в другую — урок. Информатика, 11 класс. www.yaklass.ru. Дата обращения: 8 мая 2021. Архивировано 8 мая 2021 года.
- ↑ 1 2 Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно. www.5byte.ru. Дата обращения: 8 мая 2021. Архивировано 15 мая 2021 года.
- ↑ С. Б. Гашков. Системы счисления и их применение. — 2004. — 52 с. — (Библиотека «Математическое просвещение»). — ISBN 5-94057-146-8. Архивированная копия. Дата обращения: 8 марта 2008. Архивировано из оригинала 12 января 2014 года.
- ↑ А. В. Никитин Система Бергмана Архивная копия от 5 мая 2009 на Wayback Machine.
- ↑ 1 2 Хмельник С. И. Специализированная ЦВМ для операций с комплексными числами // Вопросы радиоэлектроники. — 1964. — Т. XII, вып. 2. (недоступная ссылка)
- ↑ 1 2 Knuth D. E. An Imaginary Number System // Communication of the ACM. — 1960. — Т. 3, № 4. — С. 245—247. — doi:10.1145/367177.367233.
- ↑ 1 2 Хмельник С. И. Кодирование комплексных чисел и векторов. — Mathematics in Computers. — Израиль, 2004. — ISBN 978-0-557-74692-7.
- ↑ Хмельник С. И. Позиционное кодирование комплексных чисел // Вопросы радиоэлектроники. — 1966. — Т. XII, вып. 9. (недоступная ссылка)
- ↑ Khmelnik S.I. Method and system for processing complex numbers. — Patent USA, US2003154226 (A1). — 2001.
Ссылки[править | править код]
- И. Яглом. Системы счисления // Квант. — 1970. — № 6. — С. 2—10.
- Позиционные системы счисления. Перевод чисел из одной позиционной системы счисления в другую. Арифметические операции с числами в позиционных системах счисления // Введение в информатику. Лабораторные работы / Авт.-сост. А. П. Шестаков. — Пермь: Перм. ун-т., 1999.
- Поспелов Д. А. Арифметические основы вычислительных машин дискретного действия. — Высшая школа. — 1970.
Автор – Лада Борисовна Есакова.
Перед тем, как приступить к решению задач, нам нужно понять несколько несложных моментов.
Рассмотрим десятичное число 875. Последняя цифра числа (5) – это остаток от деления числа 875 на 10. Последние две цифры образуют число 75 – это остаток от деления числа 875 на 100. Аналогичные утверждения справедливы для любой системы счисления:
Последняя цифра числа – это остаток от деления этого числа на основание системы счисления.
Последние две цифры числа – это остаток от деления числа на основание системы счисления в квадрате.
Например, . Разделим 23 на основание системы 3, получим 7 и 2 в остатке (2 – это последняя цифра числа в троичной системе). Разделим 23 на 9 (основание в квадрате), получим 18 и 5 в остатке (5 =
).
Вернемся опять к привычной десятичной системе. Число = 100000. Т.е. 10 в степени k– это единица и k нулей.
Аналогичное утверждение справедливо для любой системы счисления:
Основание системы счисления в степени k в этой системе счисления записывается как единица и k нулей.
Например, .
1. Поиск основания системы счисления
Пример 1.
В системе счисления с некоторым основанием десятичное число 27 записывается в виде 30. Укажите это основание.
Решение:
Обозначим искомое основание x. Тогда .Т.е. x = 9.
Ответ: 9
Пример 2.
В системе счисления с некоторым основанием десятичное число 13 записывается в виде 111. Укажите это основание.
Решение:
Обозначим искомое основание x. Тогда
Решаем квадратное уравнение, получаем корни 3 и -4. Поскольку основание системы счисления не может быть отрицательным, ответ 3.
Ответ: 3
Пример 3
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.
Решение:
Если в некоторой системе число 29 оканчивается на 5, то уменьшенное на 5 число (29-5=24) оканчивается на 0. Ранее мы уже говорили, что число оканчивается на 0 в том случае, когда оно без остатка делится на основание системы. Т.е. нам нужно найти все такие числа, которые являются делителями числа 24. Эти числа: 2, 3, 4, 6, 8, 12, 24. Заметим, что в системах счисления с основанием 2, 3, 4 нет числа 5 (а в формулировке задачи число 29 оканчивается на 5), значит остаются системы с основаниями: 6, 8, 12,
Ответ: 6, 8, 12, 24
Пример 4
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 71 оканчивается на 13.
Решение:
Если в некоторой системе число оканчивается на 13, то основание этой системы не меньше 4 (иначе там нет цифры 3).
Уменьшенное на 3 число (71-3=68) оканчивается на 10. Т.е. 68 нацело делится на искомое основание системы, а частное от этого при делении на основание системы дает в остатке 0.
Выпишем все целые делители числа 68: 2, 4, 17, 34, 68.
2 не подходит, т.к. основание не меньше 4. Остальные делители проверим:
68:4 = 17; 17:4 = 4 (ост 1) – подходит
68:17 = 4; 4:17 = 0 (ост 4) – не подходит
68:34 = 2; 2:17 = 0 (ост 2) – не подходит
68:68 = 1; 1:68 = 0 (ост 1) – подходит
Ответ: 4, 68
2. Поиск чисел по условиям
Пример 5
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?
Решение:
Для начала выясним, как выглядит число 25 в системе счисления с основанием 4.
. Т.е. нам нужно найти все числа, не больше
, запись которых оканчивается на 11. По правилу последовательного счета в системе с основанием 4,
получаем числа и
. Переводим их в десятичную систему счисления:
Ответ: 5, 21
3. Решение уравнений
Пример 6
Решите уравнение:
Ответ запишите в троичной системе (основание системы счисления в ответе писать не нужно).
Решение:
Переведем все числа в десятичную систему счисления:
Квадратное уравнение имеет корни -8 и 6. (т.к. основание системы не может быть отрицательным).
.
Ответ: 20
4. Подсчет количества единиц (нулей) в двоичной записи значения выражения
Для решения этого типа задач нам нужно вспомнить, как происходит сложение и вычитание «в столбик»:
При сложении происходит поразрядное суммирование записанных друг под другом цифр, начиная с младших разрядов. В случае, если полученная сумма двух цифр больше или равна основанию системы счисления, под суммируемыми цифрами записывается остаток от деления этой суммы на основание системы, а целая часть от деления этой суммы на основание системы прибавляется к сумме следующих разрядов.
При вычитании происходит поразрядное вычитание записанных друг под другом цифр, начиная с младших разрядов. В случае, если первая цифра меньше второй, мы «занимаем» у соседнего (большего) разряда единицу. Занимаемая единица в текущем разряде равна основанию системы счисления. В десятичной системе это 10, в двоичной 2, в троичной 3 и т.д.
Пример 7
Сколько единиц содержится в двоичной записи значения выражения: ?
Решение:
Представим все числа выражения, как степени двойки:
В двоичной записи двойка в степени n выглядит, как 1 и n нулей. Тогда суммируя и
, получим число, содержащее 2 единицы:
Теперь вычтем из получившегося числа 10000. По правилам вычитания занимаем у следующего разряда.
Теперь прибавляем к получившемуся числу 1:
Видим, что у результата 2013+1+1=2015 единиц.
Ответ: 2015.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задача №16. Поиск основания системы по окончанию числа, уравнения и различные кодировки, арифметические действия в различных системах.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Основы систем счисления
Время на прочтение
11 мин
Количество просмотров 502K
Изучая кодировки, я понял, что недостаточно хорошо понимаю системы счислений. Тем не менее, часто использовал 2-, 8-, 10-, 16-ю системы, переводил одну в другую, но делалось все на “автомате”. Прочитав множество публикаций, я был удивлен отсутствием единой, написанной простым языком, статьи по столь базовому материалу. Именно поэтому решил написать свою, в которой постарался доступно и по порядку изложить основы систем счисления.
Введение
Система счисления — это способ записи (представления) чисел.
Что под этим подразумевается? Например, вы видите перед собой несколько деревьев. Ваша задача — их посчитать. Для этого можно — загибать пальцы, делать зарубки на камне (одно дерево — один палецзарубка) или сопоставить 10 деревьям какой-нибудь предмет, например, камень, а единичному экземпляру — палочку и выкладывать их на землю по мере подсчета. В первом случае число представляется, как строка из загнутых пальцев или зарубок, во втором — композиция камней и палочек, где слева — камни, а справа — палочки
Системы счисления подразделяются на позиционные и непозиционные, а позиционные, в свою очередь, — на однородные и смешанные.
Непозиционная — самая древняя, в ней каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет.
Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе. Например, привычная для нас 10-я система счисления — позиционная. Рассмотрим число 453. Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — кол-во десяток и аналогично значению 50, а 3 — единиц и значению 3. Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453.
Однородная система — для всех разрядов (позиций) числа набор допустимых символов (цифр) одинаков. В качестве примера возьмем упоминавшуюся ранее 10-ю систему. При записи числа в однородной 10-й системе вы можете использовать в каждом разряде исключительно одну цифру от 0 до 9, таким образом, допускается число 450 (1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, поскольку символ F не входит в набор цифр от 0 до 9.
Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может отличаться от наборов других разрядов. Яркий пример — система измерения времени. В разряде секунд и минут возможно 60 различных символов (от «00» до «59»), в разряде часов – 24 разных символа (от «00» до «23»), в разряде суток – 365 и т. д.
Непозиционные системы
Как только люди научились считать — возникла потребность записи чисел. В начале все было просто — зарубка или черточка на какой-нибудь поверхности соответствовала одному предмету, например, одному фрукту. Так появилась первая система счисления — единичная.
Единичная система счисления
Число в этой системе счисления представляет собой строку из черточек (палочек), количество которых равно значению данного числа. Таким образом, урожай из 100 фиников будет равен числу, состоящему из 100 черточек.
Но эта система обладает явными неудобствами — чем больше число — тем длиннее строка из палочек. Помимо этого, можно легко ошибиться при записи числа, добавив случайно лишнюю палочку или, наоборот, не дописав.
Для удобства, люди стали группировать палочки по 3, 5, 10 штук. При этом, каждой группе соответствовал определенный знак или предмет. Изначально для подсчета использовались пальцы рук, поэтому первые знаки появились для групп из 5 и 10 штук (единиц). Все это позволило создать более удобные системы записи чисел.
Древнеегипетская десятичная система
В Древнем Египте использовались специальные символы (цифры) для обозначения чисел 1, 10, 102, 103, 104, 105, 106, 107. Вот некоторые из них:
Почему она называется десятичной? Как писалось выше — люди стали группировать символы. В Египте — выбрали группировку по 10, оставив без изменений цифру “1”. В данном случае, число 10 называется основанием десятичной системы счисления, а каждый символ — представление числа 10 в какой-то степени.
Числа в древнеегипетской системе счисления записывались, как комбинация этих
символов, каждый из которых повторялся не более девяти раз. Итоговое значение равнялось сумме элементов числа. Стоит отметить, что такой способ получения значения свойственен каждой непозиционной системе счисления. Примером может служить число 345:
Вавилонская шестидесятеричная система
В отличии от египетской, в вавилонской системе использовалось всего 2 символа: “прямой” клин — для обозначения единиц и “лежачий” — для десятков. Чтобы определить значение числа необходимо изображение числа разбить на разряды справа налево. Новый разряд начинается с появления прямого клина после лежачего. В качестве примера возьмем число 32:
Число 60 и все его степени так же обозначаются прямым клином, что и “1”. Поэтому вавилонская система счисления получила название шестидесятеричной.
Все числа от 1 до 59 вавилоняне записывали в десятичной непозиционной системе, а большие значения — в позиционной с основанием 60. Число 92:
Запись числа была неоднозначной, поскольку не существовало цифры обозначающей ноль. Представление числа 92 могло обозначать не только 92=60+32, но и, например, 3632=3600+32. Для определения абсолютного значения числа был введен специальный символ для обозначения пропущенного шестидесятеричного разряда, что соответствует появлению цифры 0 в записи десятичного числа:
Теперь число 3632 следует записывать, как:
Шестидесятеричная вавилонская система — первая система счисления, частично основанная на позиционном принципе. Данная система счисления используется и сегодня, например, при определении времени — час состоит из 60 минут, а минута из 60 секунд.
Римская система
Римская система не сильно отличается от египетской. В ней для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используются заглавные латинские буквы I, V, X, L, C, D и M соответственно. Число в римской системе счисления — это набор стоящих подряд цифр.
Методы определения значения числа:
- Значение числа равно сумме значений его цифр. Например, число 32 в римской системе счисления имеет вид XXXII=(X+X+X)+(I+I)=30+2=32
- Если слева от большей цифры стоит меньшая, то значение равно разности между большей и меньшей цифрами. При этом, левая цифра может быть меньше правой максимум на один порядок: так, перед L(50) и С(100) из «младших» может стоять только X(10), перед D(500) и M(1000) — только C(100), перед V(5) — только I(1); число 444 в рассматриваемой системе счисления будет записано в виде CDXLIV = (D-C)+(L-X)+(V-I) = 400+40+4=444.
- Значение равно сумме значений групп и цифр, не подходящих под 1 и 2 пункты.
Помимо цифирных, существуют и буквенные (алфавитные) системы счисления, вот некоторые из них:
1) Славянская
2) Греческая (ионийская)
Позиционные системы счисления
Как упоминалось выше — первые предпосылки к появлению позиционной системы возникли в древнем Вавилоне. В Индии система приняла форму позиционной десятичной нумерации с применением нуля, а у индусов эту систему чисел заимствовали арабы, от которых её переняли европейцы. По каким-то причинам, в Европе за этой системой закрепилось название “арабская”.
Десятичная система счисления
Это одна из самых распространенных систем счисления. Именно её мы используем, когда называем цену товара и произносим номер автобуса. В каждом разряде (позиции) может использоваться только одна цифра из диапазона от 0 до 9. Основанием системы является число 10.
Для примера возьмем число 503. Если бы это число было записано в непозиционной системе, то его значение равнялось 5+0+3 = 8. Но у нас — позиционная система и значит каждую цифру числа необходимо умножить на основание системы, в данном случае число “10”, возведенное в степень, равную номеру разряда. Получается, значение равно 5*102 + 0*101 + 3*100 = 500+0+3 = 503. Чтобы избежать путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса. Таким образом, 503 = 50310.
Помимо десятичной системы, отдельного внимания заслуживают 2-, 8-, 16-ая системы.
Двоичная система счисления
Эта система, в основном, используется в вычислительной технике. Почему не стали использовать привычную нам 10-ю? Первую вычислительную машину создал Блез Паскаль, использовавший в ней десятичную систему, которая оказалась неудобной в современных электронных машинах, поскольку требовалось производство устройств, способных работать в 10 состояниях, что увеличивало их цену и итоговые размеры машины. Этих недостатков лишены элементы, работающие в 2-ой системе. Тем не менее, рассматриваемая система была создана за долго до изобретения вычислительных машин и уходит “корнями” в цивилизацию Инков, где использовались кипу — сложные верёвочные сплетения и узелки.
Двоичная позиционная система счисления имеет основание 2 и использует для записи числа 2 символа (цифры): 0 и 1. В каждом разряде допустима только одна цифра — либо 0, либо 1.
Примером может служить число 101. Оно аналогично числу 5 в десятичной системе счисления. Для того, чтобы перевести из 2-й в 10-ю необходимо умножить каждую цифру двоичного числа на основание “2”, возведенное в степень, равную разряду. Таким образом, число 1012 = 1*22 + 0*21 + 1*20 = 4+0+1 = 510.
Хорошо, для машин 2-я система счисления удобнее, но мы ведь часто видим, используем на компьютере числа в 10-й системе. Как же тогда машина определяет какую цифру вводит пользователь? Как переводит число из одной системы в другую, ведь в её распоряжении всего 2 символа — 0 и 1?
Чтобы компьютер мог работать с двоичными числами (кодами), необходимо чтобы они где-то хранились. Для хранения каждой отдельной цифры применяется триггер, представляющий собой электронную схему. Он может находится в 2-х состояниях, одно из которых соответствует нулю, другое — единице. Для запоминания отдельного числа используется регистр — группа триггеров, число которых соответствует количеству разрядов в двоичном числе. А совокупность регистров — это оперативная память. Число, содержащееся в регистре — машинное слово. Арифметические и логические операции со словами осуществляет арифметико-логическое устройство (АЛУ). Для упрощения доступа к регистрам их нумеруют. Номер называется адресом регистра. Например, если необходимо сложить 2 числа — достаточно указать номера ячеек (регистров), в которых они находятся, а не сами числа. Адреса записываются в 8- и 16-ричной системах (о них будет рассказано ниже), поскольку переход от них к двоичной системе и обратно осуществляется достаточно просто. Для перевода из 2-й в 8-ю число необходимо разбить на группы по 3 разряда справа налево, а для перехода к 16-ой — по 4. Если в крайней левой группе цифр не достает разрядов, то они заполняются слева нулями, которые называются ведущими. В качестве примера возьмем число 1011002. В восьмеричной — это 101 100 = 548, а в шестнадцатеричной — 0010 1100 = 2С16. Отлично, но почему на экране мы видим десятичные числа и буквы? При нажатии на клавишу в компьютер передаётся определённая последовательность электрических импульсов, причём каждому символу соответствует своя последовательность электрических импульсов (нулей и единиц). Программа драйвер клавиатуры и экрана обращается к кодовой таблице символов (например, Unicode, позволяющая закодировать 65536 символов), определяет какому символу соответствует полученный код и отображает его на экране. Таким образом, тексты и числа хранятся в памяти компьютера в двоичном коде, а программным способом преобразуются в изображения на экране.
Восьмеричная система счисления
8-я система счисления, как и двоичная, часто применяется в цифровой технике. Имеет основание 8 и использует для записи числа цифры от 0 до 7.
Пример восьмеричного числа: 254. Для перевода в 10-ю систему необходимо каждый разряд исходного числа умножить на 8n, где n — это номер разряда. Получается, что 2548 = 2*82 + 5*81 + 4*80 = 128+40+4 = 17210.
Шестнадцатеричная система счисления
Шестнадцатеричная система широко используется в современных компьютерах, например при помощи неё указывается цвет: #FFFFFF — белый цвет. Рассматриваемая система имеет основание 16 и использует для записи числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. C, D, E, F, где буквы равны 10, 11, 12, 13, 14, 15 соответственно.
В качестве примера возьмем число 4F516. Для перевода в восьмеричную систему — сначала преобразуем шестнадцатеричное число в двоичное, а затем, разбив на группы по 3 разряда, в восьмеричное. Чтобы преобразовать число в 2-е необходимо каждую цифру представить в виде 4-х разрядного двоичного числа. 4F516 = (100 1111 101)2. Но в 1 и 3 группах не достает разряда, поэтому заполним каждый ведущими нулями: 0100 1111 0101. Теперь необходимо разделить полученное число на группы по 3 цифры справа налево: 0100 1111 0101 = 010 011 110 101. Переведем каждую двоичную группу в восьмеричную систему, умножив каждый разряд на 2n, где n — номер разряда: (0*22+1*21+0*20) (0*22+1*21+1*20) (1*22+1*21+0*20) (1*22+0*21+1*20) = 23658.
Помимо рассмотренных позиционных систем счисления, существуют и другие, например:
1) Троичная
2) Четверичная
3) Двенадцатеричная
Позиционные системы подразделяются на однородные и смешанные.
Однородные позиционные системы счисления
Определение, данное в начале статьи, достаточно полно описывает однородные системы, поэтому уточнение — излишне.
Смешанные системы счисления
К уже приведенному определению можно добавить теорему: “если P=Qn (P,Q,n – целые положительные числа, при этом P и Q — основания), то запись любого числа в смешанной (P-Q)-ой системе счисления тождественно совпадает с записью этого же числа в системе счисления с основанием Q.”
Опираясь на теорему, можно сформулировать правила перевода из P-й в Q-ю системы и наоборот:
- Для перевода из Q-й в P-ю, необходимо число в Q-й системе, разбить на группы по n цифр, начиная с правой цифры, и каждую группу заменить одной цифрой в P-й системе.
- Для перевода из P-й в Q-ю, необходимо каждую цифру числа в P-й системе перевести в Q-ю и заполнить недостающие разряды ведущими нулями, за исключением левого, так, чтобы каждое число в системе с основанием Q состояло из n цифр.
Яркий пример — перевод из двоичной системы счисления в восьмеричную. Возьмем двоичное число 100111102, для перевода в восьмеричное — разобьем его справа налево на группы по 3 цифры: 010 011 110, теперь умножим каждый разряд на 2n, где n — номер разряда, 010 011 110 = (0*22+1*21+0*20) (0*22+1*21+1*20) (1*22+1*21+0*20) = 2368. Получается, что 100111102 = 2368. Для однозначности изображения двоично-восьмеричного числа его разбивают на тройки: 2368 = (10 011 110)2-8.
Смешанными системами счисления также являются, например:
1) Факториальная
2) Фибоначчиева
Перевод из одной системы счисления в другую
Иногда требуется преобразовать число из одной системы счисления в другую, поэтому рассмотрим способы перевода между различными системами.
Преобразование в десятичную систему счисления
Имеется число a1a2a3 в системе счисления с основанием b. Для перевода в 10-ю систему необходимо каждый разряд числа умножить на bn, где n — номер разряда. Таким образом, (a1a2a3)b = (a1*b2 + a2*b1 + a3*b0)10.
Пример: 1012 = 1*22 + 0*21 + 1*20 = 4+0+1 = 510
Преобразование из десятичной системы счисления в другие
Целая часть:
- Последовательно делим целую часть десятичного числа на основание системы, в которую переводим, пока десятичное число не станет равно нулю.
- Полученные при делении остатки являются цифрами искомого числа. Число в новой системе записывают, начиная с последнего остатка.
Дробная часть:
- Дробную часть десятичного числа умножаем на основание системы, в которую требуется перевести. Отделяем целую часть. Продолжаем умножать дробную часть на основание новой системы, пока она не станет равной 0.
- Число в новой системе составляют целые части результатов умножения в порядке, соответствующем их получению.
Пример: переведем 1510 в восьмеричную:
158 = 1, остаток 7
18 = 0, остаток 1
Записав все остатки снизу вверх, получаем итоговое число 17. Следовательно, 1510 = 178.
Преобразование из двоичной в восьмеричную и шестнадцатеричную системы
Для перевода в восьмеричную — разбиваем двоичное число на группы по 3 цифры справа налево, а недостающие крайние разряды заполняем ведущими нулями. Далее преобразуем каждую группу, умножая последовательно разряды на 2n, где n — номер разряда.
В качестве примера возьмем число 10012: 10012 = 001 001 = (0*22 + 0*21 + 1*20) (0*22 + 0*21 + 1*20) = (0+0+1) (0+0+1) = 118
Для перевода в шестнадцатеричную — разбиваем двоичное число на группы по 4 цифры справа налево, затем — аналогично преобразованию из 2-й в 8-ю.
Преобразование из восьмеричной и шестнадцатеричной систем в двоичную
Перевод из восьмеричной в двоичную — преобразуем каждый разряд восьмеричного числа в двоичное 3-х разрядное число делением на 2 (более подробно о делении см. выше пункт “Преобразование из десятичной системы счисления в другие”), недостающие крайние разряды заполним ведущими нулями.
Для примера рассмотрим число 458: 45 = (100) (101) = 1001012
Перевод из 16-ой в 2-ю — преобразуем каждый разряд шестнадцатеричного числа в двоичное 4-х разрядное число делением на 2, недостающие крайние разряды заполняем ведущими нулями.
Преобразование дробной части любой системы счисления в десятичную
Преобразование осуществляется также, как и для целых частей, за исключением того, что цифры числа умножаются на основание в степени “-n”, где n начинается от 1.
Пример: 101,0112 = (1*22 + 0*21 + 1*20), (0*2-1 + 1*2-2 + 1*2-3) = (5), (0 + 0,25 + 0,125) = 5,37510
Преобразование дробной части двоичной системы в 8- и 16-ую
Перевод дробной части осуществляется также, как и для целых частей числа, за тем лишь исключением, что разбивка на группы по 3 и 4 цифры идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа.
Пример: 1001,012 = 001 001, 010 = (0*22 + 0*21 + 1*20) (0*22 + 0*21 + 1*20), (0*22 + 1*21 + 0*20) = (0+0+1) (0+0+1), (0+2+0) = 11,28
Преобразование дробной части десятичной системы в любую другую
Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в ноль и начать умножение получившегося числа на основание системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в ноль, предварительно запомнив (записав) значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль.
Для примера переведем 10,62510 в двоичную систему:
0,625*2 = 1,25
0,250*2 = 0,5
0,5*2 = 1,0
Записав все остатки сверху вниз, получаем 10,62510 = (1010), (101) = 1010,1012