Основание треугольника – уравнение
Основание треугольника – это такая же сторона, как и две других. Основание редко имеет особое значение, но из-за визуальной обособленности от других сторон, ученики часто путаются и допускают ошибки. Разберем подробнее, как сторона треугольника может считаться основанием, и в каких случаях это действительно имеет значение

Стороны треугольника
У треугольника всегда три стороны. Одна из них считается основанием. Как правило, основание выделяется только построением, т.е. нижняя сторона треугольника, и приниматься за основание.
Иногда в решении указывают углы при основании произвольного треугольника. Это не совсем верно, поскольку в произвольном треугольнике все углы равнозначны, а значит не имеет смысла выделять углы при основании. Выделяются только углы при основании равнобедренного треугольника.

Рис. 1. Углы произвольного треугольника.
Нужно учитывать, что любой произвольный треугольник можно условно перевернуть, т.е. перечертить фигуру таким образом, чтобы основанием стала другая сторона. По этому разделять понятие боковых сторон и основания у произвольного треугольника не имеет смысла – это только добавит путаницы в решение задачи.
Уравнение основания треугольника, так же, как и уравнение любой из сторон треугольника, является уравнением прямой линии.
Равнобедренный треугольник
Равнобедренный треугольник – это единственный подвид треугольника, где основание имеет реальное практическое значение. Равнобедренным треугольником называется треугольник, у которого две стороны равны между собой. Равные стороны зовутся боковыми, а третья сторона считается основанием.
Существует две теоремы об основании равнобедренного треугольника. Это:
- Теорема о равенстве углов: в равнобедренном треугольнике углы при основании равны.
- Теорема о равенстве медианы, биссектрисы и высоты, проведенной к основанию. Теорема особенно подчеркивает, что из трех возможных медиан, высот и биссектрис, только проведенные к основанию окажутся равными между собой.
В равнобедренном треугольнике основание определяется значением сторон: равные стороны – боковые, неравная – основание.

Рис. 2. Равнобедренный треугольник.
По ходу решения задачи может получится так, что основание окажется сбоку, не нужно этого пугаться. Стоит или привыкнуть к такому построению равнобедренного треугольника или каждый раз перечерчивать чертеж, разворачивая треугольник в нужную сторону.
Равносторонний треугольник
Равносторонний треугольник – это частный случай равнобедренного. У равнобедренного треугольника равны две стороны, а у равностороннего все три. Но именно из-за этого свойства значение основания равнобедренного треугольника теряется.
В равностороннем треугольнике какую сторону не выбери: две другие всегда будут равны между собой, а значит любая сторона может считаться основанием.

Рис. 3. Равносторонний треугольник.
Существует формула, где часто упоминается слово основание. Это формула площади, которая равна половине произведения основания треугольника на высоту, проведенную к этому основанию. Но в качестве основания может быть принята любая сторона, главное, чтобы именно на нее падала высота. Поэтому и в этом случае выбор стороны треугольника, которую можно считать основанием, некритичен.
Что мы узнали?
Мы узнали, что такое основание треугольника. Поговорили о ситуациях, когда стоит выделять основание среди других сторон треугольника, а когда это окажется напрасной тратой времени. Обсудили значимость основания равнобедренного треугольника.
Как найти основание треугольника
Для того, чтобы найти основание треугольника, можно воспользоваться одной из формул, обязательно должны быть заданы для этой формулы площадь и высота. Вообще, в геометрии и тригонометрии нет четкого обозначения того, какая именно сторона является основанием, так как его можно перевернуть на любую из них. Чтобы найти основание треугольника, его для начала нужно обозначить, а именно выделить ту сторону, на противоположном от которой углу расположена высота. Это перпендикуляр по отношению к основанию, и в зависимости от типа треугольника, он может делить основание пополам.
Есть ряд основных формул, по которым можно найти основание треугольника, в том числе и равнобедренного. Основная формула выглядит так:
- S – площадь треугольника;
- С – длина основания треугольника, которую надо найти;
- h – высота треугольника.
Исходя из тех данных, которые у нас есть, можно найти основание треугольника, если дана площадь и высота.
Как найти основание равнобедренного треугольника
По этой же формуле можно найти основание равнобедренного треугольника. Если известна одна сторона и значение угла напротив основания, то можно вывести по формуле высоту треугольника и потом найти основание по общей формуле.
Как найти основание равностороннего треугольника через косинус
Если известны боковая сторона и величина противоположного основанию угла, можно найти основание треугольника через формулу, где используется значение косинуса.
- С – величина противоположного основанию угла равностороннего треугольника;
- А – длина боковой стороны треугольника;
- с – длина основания.
Эта формула для того, чтобы найти основание треугольника, основана на теореме косинусов и имеет более известную и более простую для применения формулу с=2*а*sin(B/2).
А еще интересно знать, стоит ли покупать евро, так как валюта постоянно дорожает.
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c – стороны произвольного треугольника
α , β , γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b – катеты
c – гипотенуза
α , β – острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
4. Найти длину высоты треугольника
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
H – высота треугольника
a – сторона, основание
b, c – стороны
β , γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
[spoiler title=”источники:”]
http://www-formula.ru/2011-10-09-11-08-41
[/spoiler]
Как найти основание треугольника
Часто в задачах по планиметрии и тригонометрии требуется найти основание треугольника. Для этой операции существует даже несколько методов.

Вам понадобится
- Калькулятор
Инструкция
Строгого определения понятия «основание треугольника» в геометрии не существует. Как правило, этим термином обозначается, сторона треугольника, к которой из противоположной вершины проведен перпендикуляр (опущена высота). Также этим термином принято называть «неравную» сторону равностороннего треугольника. Поэтому выберем из всего многообразия примеров, известного в математике под понятием «решение треугольников», варианты, в которых встречаются высоты и равносторонние треугольники.
Если известны высота и площадь треугольника, то для того чтобы найти основание треугольника (длину стороны, на которую опущена высота), воспользуемся формулой нахождения площади треугольника, утверждающей, что площадь любого треугольника можно посчитать, умножив половину длины основания на длину высоты:
S=1/2*c*h, где:
S – площадь треугольника,
с – длина его основания,
h – длина высоты треугольника.
Из этой формулы находим:
с=2*S/h.
Например, если площадь треугольника равняется 20 кв.см., а длина высоты – 10 см, то основание треугольника будет:
с=2*20/10=4 (см).
Если известны боковая сторона и периметр равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=Р-2*а, где:
Р – периметр треугольника,
а – длина боковой стороны треугольника,
с – длина его основания.
Если известны боковая сторона и величина противоположного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=а*√(2*(1-cosC)), где:
C – величина противоположного основанию угла равностороннего треугольника,
а – длина боковой стороны треугольника.
с – длина его основания.
(Формула является прямым следствием теоремы косинусов)
Имеется и более компактная запись этой формулы:
с=2*а*sin(B/2)
Если известны боковая сторона и величина смежного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей легко запоминающейся формуле:
с=2*а*cosA
A – величина смежного основанию угла равностороннего треугольника,
а – длина боковой стороны треугольника.
с – длина его основания.
Эта формула является следствием теоремы о проекциях.
Если известен радиус описанной окружности и величина противоположного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=2*R*sinC, где:
C – величина противоположного основанию угла равностороннего треугольника,
R – радиус описанной вокруг треугольника окружности,
с – длина его основания.
Эта формула является прямым следствием теоремы синусов.
Обратите внимание
Для начала абстрагируемся от частностей и посмотрим, как найти основание треугольника, не являющегося ни равносторонним, ни равнобедренным, ни прямоугольным. Так как основанием в такой фигуре может служить любая сторона, для начала выберем какую-то грань и «обзовём» её основанием. Соответственно, повернём треугольник так, чтобы он на ней стоял, и будем искать её длину.
Полезный совет
Как найти основание равнобедренного треугольника? Смотря, что дано в данном треугольнике. Если в равнобедренном треугольнике дана сторона и угол, который находится напротив основания, то можете провести из этого угла высоту треугольника. В результате, по свойству равностороннего треугольника вы получите два равных прямоугольника.
Источники:
- Медианы, биссектрисы и высоты треугольника
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Провести высоту к основанию, она же будет биссектрисой и медианой. Ну а потом у Вас имеется прямоугольный треугольник: известна гипотенуза (4см) , угол прилежащего катета 40градусов – этот прилежащий катет равен половине искомого основания. находим его из уравнения косинуса угла 40градусов.
воспользоваться теоремой косинусов
по-моему проще теоремой синусов:
4/sin 40 = x/sin 100 => x = (sin 100)/(sin 40) *4
Как найти основание равнобедренного треугольника если боковые стороны равны 4см. а углы 40,40и 100градусов?
Поскольку треугольник равнобедренный, то бисектриса будет высотой и медианой. Тогда рассмотрим маленький трегольник в котором углы 50, 40, 90
Синус угла -это отношение противолежашего катета к гипотенузе
Тогда Синус 50=(х/2)/4 х/2- это потому что медиана делит пополам
Дальше по таблице синусов смотрим син. 50=0,766=х/8 х=8*0,766=6.128 приблизительно 6,1
Основание треугольника


4.7
Средняя оценка: 4.7
Всего получено оценок: 136.
4.7
Средняя оценка: 4.7
Всего получено оценок: 136.
Основание треугольника – это такая же сторона, как и две других. Основание редко имеет особое значение, но из-за визуальной обособленности от других сторон, ученики часто путаются и допускают ошибки. Разберем подробнее, как сторона треугольника может считаться основанием, и в каких случаях это действительно имеет значение
Стороны треугольника
У треугольника всегда три стороны. Одна из них считается основанием. Как правило, основание выделяется только построением, т.е. нижняя сторона треугольника, и приниматься за основание.
Иногда в решении указывают углы при основании произвольного треугольника. Это не совсем верно, поскольку в произвольном треугольнике все углы равнозначны, а значит не имеет смысла выделять углы при основании. Выделяются только углы при основании равнобедренного треугольника.
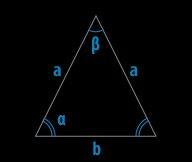
Нужно учитывать, что любой произвольный треугольник можно условно перевернуть, т.е. перечертить фигуру таким образом, чтобы основанием стала другая сторона. По этому разделять понятие боковых сторон и основания у произвольного треугольника не имеет смысла – это только добавит путаницы в решение задачи.
Уравнение основания треугольника, так же, как и уравнение любой из сторон треугольника, является уравнением прямой линии.
Равнобедренный треугольник
Равнобедренный треугольник – это единственный подвид треугольника, где основание имеет реальное практическое значение. Равнобедренным треугольником называется треугольник, у которого две стороны равны между собой. Равные стороны зовутся боковыми, а третья сторона считается основанием.
Существует две теоремы об основании равнобедренного треугольника. Это:
- Теорема о равенстве углов: в равнобедренном треугольнике углы при основании равны.
- Теорема о равенстве медианы, биссектрисы и высоты, проведенной к основанию. Теорема особенно подчеркивает, что из трех возможных медиан, высот и биссектрис, только проведенные к основанию окажутся равными между собой.
В равнобедренном треугольнике основание определяется значением сторон: равные стороны – боковые, неравная – основание.
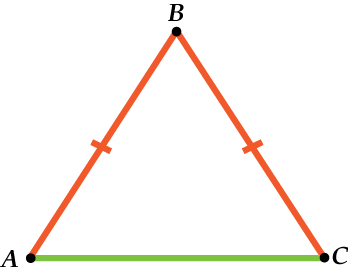
По ходу решения задачи может получится так, что основание окажется сбоку, не нужно этого пугаться. Стоит или привыкнуть к такому построению равнобедренного треугольника или каждый раз перечерчивать чертеж, разворачивая треугольник в нужную сторону.
Равносторонний треугольник
Равносторонний треугольник – это частный случай равнобедренного. У равнобедренного треугольника равны две стороны, а у равностороннего все три. Но именно из-за этого свойства значение основания равнобедренного треугольника теряется.
В равностороннем треугольнике какую сторону не выбери: две другие всегда будут равны между собой, а значит любая сторона может считаться основанием.
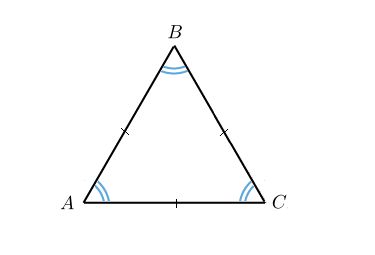
Существует формула, где часто упоминается слово основание. Это формула площади, которая равна половине произведения основания треугольника на высоту, проведенную к этому основанию. Но в качестве основания может быть принята любая сторона, главное, чтобы именно на нее падала высота. Поэтому и в этом случае выбор стороны треугольника, которую можно считать основанием, некритичен.

Что мы узнали?
Мы узнали, что такое основание треугольника. Поговорили о ситуациях, когда стоит выделять основание среди других сторон треугольника, а когда это окажется напрасной тратой времени. Обсудили значимость основания равнобедренного треугольника.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Елена Елемщикова
5/5
Оценка статьи
4.7
Средняя оценка: 4.7
Всего получено оценок: 136.
А какая ваша оценка?
Совет 1: Как обнаружить основание треугольника
Зачастую в задачах по планиметрии и тригонометрии требуется обнаружить основание треугольника. Для этой операции существует даже несколько способов.

Вам понадобится
- Калькулятор
Инструкция
1. Сурового определения представления «основание треугольника» в геометрии не существует. Как водится, этим термином обозначается, сторона треугольника, к которой из противоположной вершины проведен перпендикуляр (опущена высота). Также этим термином принято называть «неравную» сторону равностороннего треугольника. Следственно предпочтем из каждого разнообразия примеров, вестимого в математике под представлением «решение треугольников», варианты, в которых встречаются высоты и равносторонние треугольники.Если знамениты высота и площадь треугольника, то для того дабы обнаружить основание треугольника (длину стороны, на которую опущена высота), воспользуемся формулой нахождения площади треугольника, утверждающей, что площадь всякого треугольника дозволено посчитать, умножив половину длины основания на длину высоты: S=1/2*c*h, где: S – площадь треугольника,с – длина его основания,h – длина высоты треугольника.Из этой формулы находим:с=2*S/h.Скажем, если площадь треугольника равняется 20 кв.см., а длина высоты – 10 см, то основание треугольника будет:с=2*20/10=4 (см).
2. Если знамениты боковая сторона и периметр равностороннего треугольника, то длину основания дозволено посчитать по дальнейшей формуле:с=Р-2*а, где:Р – периметр треугольника,а – длина боковой стороны треугольника,с – длина его основания.
3. Если знамениты боковая сторона и величина противоположного основанию угла равностороннего треугольника, то длину основания дозволено посчитать по дальнейшей формуле:с=а*?(2*(1-cosC)), где:C – величина противоположного основанию угла равностороннего треугольника,а – длина боковой стороны треугольника.с – длина его основания.(Формула является прямым следствием теоремы косинусов)Имеется и больше суперкомпактная запись этой формулы:с=2*а*sin(B/2)
4. Если знамениты боковая сторона и величина смежного основанию угла равностороннего треугольника, то длину основания дозволено посчитать по дальнейшей легко запоминающейся формуле:с=2*а*cosA A – величина смежного основанию угла равностороннего треугольника,а – длина боковой стороны треугольника.с – длина его основания.Эта формула является следствием теоремы о проекциях.
5. Если знаменит радиус описанной окружности и величина противоположного основанию угла равностороннего треугольника, то длину основания дозволено посчитать по дальнейшей формуле:с=2*R*sinC, где:C – величина противоположного основанию угла равностороннего треугольника,R – радиус описанной вокруг треугольника окружности,с – длина его основания.Эта формула является прямым следствием теоремы синусов.
Совет 2: Как обнаружить площадь равностороннего треугольника
Равносторонним называют треугольник, имеющий три равные стороны и три идентичных угла. Такой треугольник еще называют положительным. Высота, проведенная из вершины к основанию, единовременно является биссектрисой и медианой, из чего следует, что эта линия делит угол вершины на два равных угла, а основание, на которую опускается, на два равных отрезка. Эти свойства треугольника помогут вычислить его площадь , равную половине произведения высоты на всякую из его сторон.
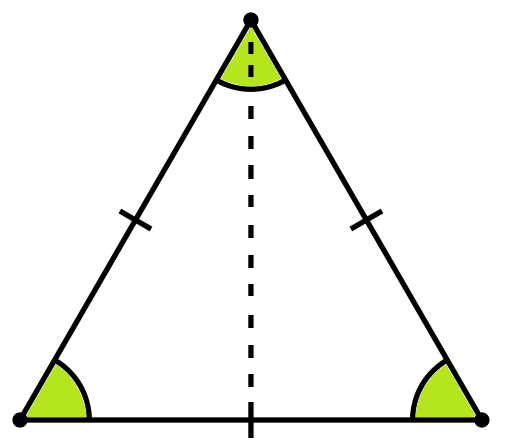
Вам понадобится
- – знать, что такое высота и ее свойства
- – знать, что такое прямоугольный треугольник
- – знать, что такое гипотенуза и катеты
- – уметь решать уравнения с одной переменной со скобками
Инструкция
1. Если в верном треугольнике знамениты правда бы одна сторона и его высота, то для определения площади фигуры умножьте высоту на длину стороны и поделите получившееся число на два.
2. Для вычисления площади треугольника при неведомой высоте и знаменитой стороне вначале обнаружьте высоту. Для этого разглядите один из равных прямоугольных треугольников, образованных высотой.
3. Сторона, противолежащая прямому углу, будет являться гипотенузой, а две остальные – катетами. Значит, высота равностороннего треугольника будет одним из катетов меньшего прямоугольного треугольника . 2-й катет будет равняться половине стороны большого треугольника , потому что высота в положительном прямоугольнике делит ее напополам, являясь медианой.
4. Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов. Следственно для того, дабы узнать высоту, из квадрата гипотенузы (то есть из квадрата одной из сторон равностороннего треугольника ) вычтите квадрат катета, образованного половиной стороны равностороннего треугольника , позже чего неукоснительно из итога этого вычисления извлеките квадратный корень.
5. Сейчас, когда высота вестима, обнаружьте площадь фигуры, умножив высоту на длину стороны и поделив получившееся значение на два.
6. В случае, если вам знаменита только высота, то вновь разглядите один из прямоугольных треугольников, образующихся при проведении высоты, которая делит напополам угол и сторону положительного многоугольника. Опираясь на теорему Пифагора, составьте уравнение a² = c²-(1/2*с)², где a² – высота, c² – сторона равностороннего треугольника . В этом уравнении обнаружьте значение переменной a.
7. Узнав высоту, вычислите площадь положительного треугольника . Для этого умножьте высоту на сторону треугольника и поделите полученный позже умножения итог напополам.
Видео по теме
Обратите внимание!
Для начала абстрагируемся от частностей и посмотрим, как обнаружить основание треугольника, не являющегося ни равносторонним, ни равнобедренным, ни прямоугольным. Потому что основанием в такой фигуре может служить любая сторона, для начала предпочтем какую-то грань и «обзовём» её основанием. Соответственно, повернём треугольник так, дабы он на ней стоял, и будем искать её длину.
Полезный совет
Как обнаружить основание равнобедренного треугольника? Смотря, что дано в данном треугольнике. Если в равнобедренном треугольнике дана сторона и угол, тот, что находится наоборот основания, то можете провести из этого угла высоту треугольника. В итоге, по свойству равностороннего треугольника вы получите два равных прямоугольника.
