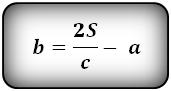
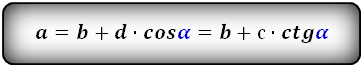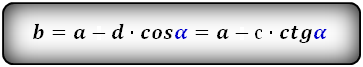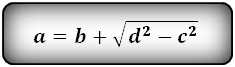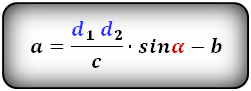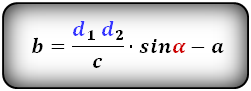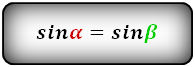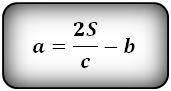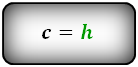1. Формула длины оснований прямоугольной трапеции через среднюю линию
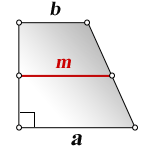
a – нижнее основание
b – верхнее основание
m – средняя линия
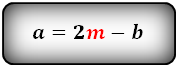
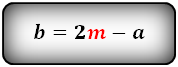
Формулы длины оснований :
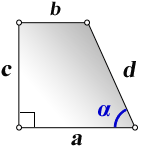
2. Формулы длины оснований через боковые стороны и угол при нижнем основании
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α – угол при нижнем основании
Формулы длины оснований :
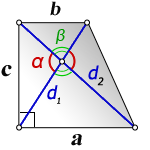
3. Формулы длины оснований трапеции через диагонали и угол между ними
a – нижнее основание
b – верхнее основание
c – боковая сторона под прямым углом к основаниям
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
Формулы длины оснований :
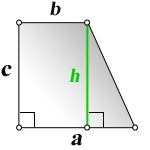
4. Формулы длины оснований трапеции через площадь
a – нижнее основание
b – верхнее основание
c – боковая сторона под прямым углом к основаниям
h – высота трапеции
Формулы длины оснований :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 15 октября 2013
-
Обновлено: 13 августа 2021
Как посчитать верхнее основание прямоугольной трапеции, зная только высоту и нижнее основание?
Alec Orlole
Знаток
(363),
на голосовании
5 лет назад
Трапеция получилась отсечением части прямоугольного треугольника
По факту нужно это для расчета высоты потолка мансарды в разных местах уклона крыши. Решение должно быть элементарным, но не нашел ответа
Дополнен 5 лет назад

Голосование за лучший ответ
Андрей Фогель
Мастер
(1971)
5 лет назад
Похоже, вы не один, кто не нашел ответа, или другим это не интересно.
99th
Знаток
(309)
5 лет назад
Никак, нужно знать еще и боковую сторону трапеции.
Alec OrloleЗнаток (363)
5 лет назад
Диагональ трапеции известна полностью в прямоугольном треугольнике
99thЗнаток (309)
5 лет назад
Из подобия треугольников: 1,1/2.5=x/2,2
отсюда меньшее основание равно 0,968
Рамзес
Мыслитель
(5171)
5 лет назад
2,5/(2,5-1,4) = 2,2/х; х=(1,1)(2,2)/2,5=0,97
Похожие вопросы
В данной публикации мы рассмотрим различные формулы, с помощью которых можно вычислить высоту прямоугольной трапеции.
Напомним, в прямоугольной трапеции одна из боковых сторон перпендикулярна ее основаниями, и потому одновременно является высотой фигуры.
-
Нахождение высоты прямоугольной трапеции
- Через длины сторон
-
Через основания и прилежащий угол
- Через боковую сторону и прилежащий угол
- Через диагонали и угол между ними
- Через площадь и основания
Нахождение высоты прямоугольной трапеции
Через длины сторон
Зная длины обоих оснований и большей боковой стороны прямоугольной трапеции, можно найти ее высоту (или меньшую боковую сторону):
Данная формула следует из теоремы Пифагора. В данном случае высота h – это неизвестный катет прямоугольного треугольника, гипотенуза которого равняется d, а известный катет – разности оснований, т.е. (a-b).
Через основания и прилежащий угол
Если даны длины оснований и любой из прилежащих к ним острых углов, то вычислить высоту прямоугольной трапеции можно по формуле:
Через боковую сторону и прилежащий угол
Если известна длина боковой стороны прямоугольной трапеции и прилежащий к ней угол (любой), найти высоту фигуры удастся таким образом:
Примечание: с помощью этой формулы можно, в т.ч., доказать, что меньшая боковая сторона – это и есть высота трапеции:
Через диагонали и угол между ними
При условии, что известны длины оснований прямоугольной трапеции, диагонали и угол между ними, рассчитать высоту фигуры можно так:
Если вместо суммы оснований известна длина средней линии, то формула примет вид:
m – средняя линия, которая равна половине суммы оснований, т.е.m = (a+b)/2.
Через площадь и основания
Если известна площадь прямоугольной трапеции и длина ее оснований (или средней линии), найти высоту можно таким образом:
Как найти основания прямоугольной трапеции
Математическая фигура с четырьмя углами называется трапецией, если пара противоположных ее сторон параллельна, а другая пара – нет. Параллельные стороны называют основаниями трапеции, две другие – боковыми. В прямоугольной трапеции один из углов при боковой стороне – прямой.
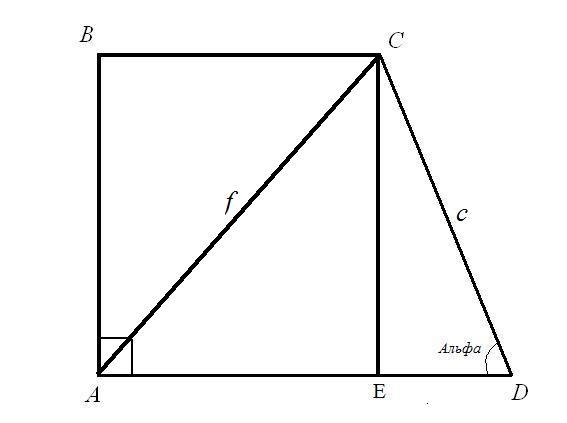
Инструкция
Задача 1.Найдите основания BC и AD прямоугольной трапеции, если известна длина диагонали AC = f; длина боковой стороны CD = c и угол при ней ADC = α.Решение:Рассмотрите прямоугольный треугольник CED. Известны гипотенуза c и угол между гипотенузой и катетом EDC. Найдите длины сторон CE и ED: по формуле угла CE = CD*sin(ADC); ED = CD*cos(ADC). Итак: CE = c*sinα; ED=c*cosα.
Рассмотрите прямоугольный треугольник ACE. Гипотенуза AC и катет CE вам известны, найдите сторону AE по правилу прямоугольного треугольника: сумма квадратов катетов равна квадрату гипотенузы. Итак: AE(2) = AC(2) – CE(2) = f(2) – c*sinα. Вычислите квадратный корень из правой части равенства. Вы нашли верхнее основание прямоугольной трапеции.
Длина основания AD является суммой длин двух отрезков AE и ED. AE = квадратный корень(f(2) – c*sinα); ED = c*cosα).Итак: AD = квадратный корень(f(2) – c*sinα) + c*cosα.Вы нашли нижнее основание прямоугольной трапеции.
Задача 2.Найдите основания BC и AD прямоугольной трапеции, если известна длина диагонали BD = f; длина боковой стороны CD = c и угол при ней ADC = α.Решение:Рассмотрите прямоугольный треугольник CED. Найдите длины сторон CE и ED: CE = CD*sin(ADC) = c*sinα; ED = CD*cos(ADC) = c*cosα.
Рассмотрите прямоугольник ABCE. По свойству прямоугольника AB = CE = c*sinα.Рассмотрите прямоугольный треугольник ABD. По свойству прямоугольного треугольника квадрат гипотенузы равен сумме квадратов катетов. Поэтому AD(2) = BD(2) – AB(2) = f(2) – c*sinα.Вы нашли нижнее основание прямоугольной трапеции AD = квадратный корень(f(2) – c*sinα).
По правилу прямоугольника BC = AE = AD – ED = квадратный корень(f(2) – c*sinα) – с*cosα.Вы нашли верхнее основание прямоугольной трапеции.
Все формулы основания прямоугольной трапеции
1. Формула длины оснований прямоугольной трапеции через среднюю линию
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины оснований :
2. Формулы длины оснований через боковые стороны и угол при нижнем основании
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α – угол при нижнем основании
Формулы длины оснований :
3. Формулы длины оснований трапеции через диагонали и угол между ними
a – нижнее основание
b – верхнее основание
c – боковая сторона под прямым углом к основаниям
d 1 , d 2 – диагонали трапеции
α , β – углы между диагоналями
Формулы длины оснований :
4. Формулы длины оснований трапеции через площадь
a – нижнее основание
b – верхнее основание
c – боковая сторона под прямым углом к основаниям
h – высота трапеции
Узнать ещё
Знание — сила. Познавательная информация
В прямоугольную трапецию вписана окружность
Если в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства.
1. Сумма оснований трапеции равна сумме боковых сторон.
2. Расстояния от вершины трапеции до точек касания вписанной окружности равны.
3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности.
4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.
5. Если точка касания делит боковую сторону на отрезки m и n, то радиус вписанной окружности равен
И еще два полезных свойства прямоугольной трапеции, в которую вписана окружность:
1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции — квадрат, сторона которого равна радиусу. (AMOE и BKOM — квадраты со стороной r).
2) Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований.
Площадь трапеции равна произведению полусуммы ее оснований на высоту:
Обозначим CF=m, FD=n. Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а
Свойства прямоугольной трапеции
В данной статье мы расскажем Вам о свойствах прямоугольной трапеции, как обычной, так и той, в которую вписана окружность.
Для начала напомним некоторые основные определения.
Трапеция – это четырехугольник, имеющий 2 параллельные друг другу стороны, причем 2 другие стороны параллельными не являются.
Прямоугольная трапеция – это такая трапеция, одна из боковых сторон которой перпендикулярна ее основаниям (изображена на рис.).
Средняя линия трапеции – это отрезок, который соединяет середины боковых сторон фигуры (на рис. EF).
Основные свойства прямоугольной трапеции
- Средняя линия EF равна половине суммы ее оснований BC и AD.
- точка пересечения (H) диагоналей прямоугольной трапеции AC и BD;
- точка пересечения (E) продолжений боковых сторон трапеции AB и CD;
- середины (F и G) оснований трапеции BC и AD.
Данным свойством обладает как прямоугольная, так и равносторонняя трапеция.
Свойства прямоугольной трапеции, в которую вписана окружность
SABCD = BC * AD
Узнать подробнее о свойствах трапеции с прямым углом, в которую вписана окружность, а также ознакомиться с доказательствами этих свойств, можно на сайте uznateshe.ru.
Понравилась статья, расскажите о ней друзьям:
[spoiler title=”источники:”]
http://people-ask.ru/nauki/geometriya/svojstva-pryamougolnoj-trapecii
[/spoiler]