1. Формула длины основания равнобедренной трапеции через среднюю линию
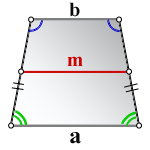
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины основания:
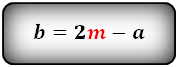
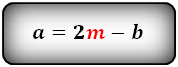
2. Формулы длины сторон через высоту и угол при нижнем основании
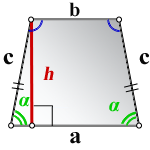
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α – угол при основании трапеции
h – высота трапеции
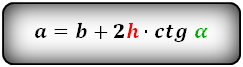
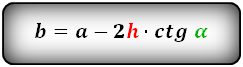
Формулы всех четырех сторон трапеции:
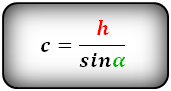
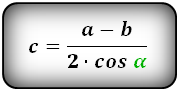
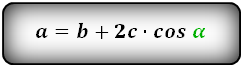
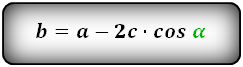
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
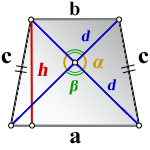
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
d – диагонали
α , β – углы между диагоналями
h – высота трапеции
Формулы длины сторон трапеции:
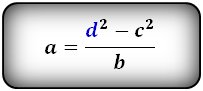
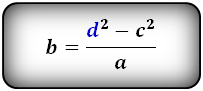

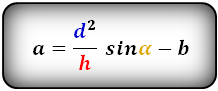
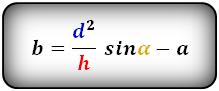
справедливо для данной ситуации:
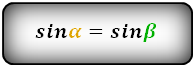
4. Формулы длины сторон равнобедренной трапеции через площадь
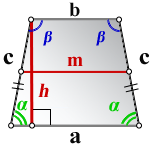
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α , β – углы при основаниях
m – средняя линия
h – средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
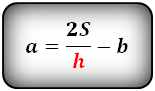
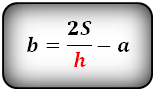
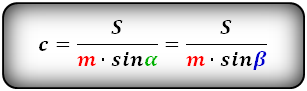

Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 08 октября 2013
-
Обновлено: 13 августа 2021
Как найти основание равнобедренной трапеции
Трапецией называют четырехугольник, основания которого лежат на двух параллельных прямых, при этом две другие стороны параллельными не являются. Нахождение основания равнобедренной трапеции требуется как при сдаче теории и решении задач в учебных заведениях, так и в ряде профессий (инженерных, архитектурных, дизайнерских).
Инструкция
У равнобедренной (или равнобокой) трапеции непараллельные стороны как и углы, которые образуются при пересечении нижнего основания, равны.
Трапеция имеет два основания, и чтобы их найти, нужно сначала обозначить фигуру. Пусть дана равнобедренная трапеция ABCD с основаниями AD и BC. При этом известны все параметры, кроме оснований. Боковая сторона AB=CD=a, высота BH=h и площадь равна S.
Для решения задачи об основании трапеции проще всего будет составить систему уравнений, чтобы через взаимосвязанные величины найти нужные основания.
Обозначьте отрезок BC за x, а AD за y, чтобы в дальнейшем было удобно обращаться с формулами и понимать их. Если не сделать этого сразу, можно запутаться.
Выпишите все формулы, которые пригодятся при решении поставленной задачи, используя известные данные. Формула площади равнобедренной трапеции: S=((AD+BC)*h)/2. Теорема Пифагора: a*a = h*h +AH*AH .
Вспомните свойство равнобедренной трапеции: высоты, выходящие из вершины трапеции, отсекают равные отрезки на большом основании. Отсюда следует, что два основания можно связать по формуле, вытекающей из этого свойства: AD=BC+2AH или y=x+2AH
Найдите катет AH, следуя теореме Пифагора, которую вы уже записали. Пусть он будет равен некому числу k. Тогда формула, вытекающая из свойства равнобедренной трапеции будет выглядеть так: y=x+2k.
Выразите через площадь трапеции неизвестную величину. У вас должно получиться: AD=2*S/h-BC или y=2*S/h-x.
После этого подставьте данные числовые значения в полученную систему уравнений и решите ее. Решение любой системы уравнений можно найти автоматически в программе MathCAD.
Полезный совет
Старайтесь всегда при решении задач максимально упростить обозначения и формулы. Так решение найдется гораздо быстрее.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти основание трапеции?
Ксения Колесникова
Знаток
(360),
закрыт
8 лет назад
Напишите, пожалуйста формулу, если известно, что трапеция равнобедренная, 1 из углов равен 60гр. , боковая сторона равна 8см. , и меньшее основание равно 7гр.
Заранее спасибо!
Лена Куликова
Профи
(592)
8 лет назад
Рисуешь трапецию ABCD, где BC и AD – основания, проводишь высоты – BK, CM. В треугольнике ABK угол А=60, по условию, тогда угол В =30, т. к. треугольник прямоугольный. Существует свойство, что в прямоугольном треугольнике катет лежащий напротив угла в 30гр. равен половине гипотенузы, тогда АК=AB/2=4см, СМ=4 аналогично, и КМ=BC=7cm(прямоугольник) . АК+КМ+МД=4+7+4=15см
Формулу я не знаю…
НатУша
Искусственный Интеллект
(197985)
8 лет назад
Нет такой формулы.
Есть формула для нахождения площади трапеции.
Полусумма оснований умноженная на высоту.
Значит нади найти большее основание и высоту.
Опусти из тупых углов высоты, посмотри на чертеж. В прямоугольном треугольнике катет, лежащий против угла в 30 градусов, равен половине гипотенузы.
Значит большее основание равно 4+7+4 = 15 см.
По теореме Пифагора найди высоту ( будет 4V3) и подставь все в формулу.
Все формулы сторон равнобедренной трапеции
1. Формула длины основания равнобедренной трапеции через среднюю линию
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины основания :
2. Формулы длины сторон через высоту и угол при нижнем основании
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α – угол при основании трапеции
h – высота трапеции
Формулы всех четырех сторон трапеции :
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
d – диагонали
α , β – углы между диагоналями
h – высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4. Формулы длины сторон равнобедренной трапеции через площадь
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α , β – углы при основаниях
m – средняя линия
h – средняя линия
Формулы длины сторон равнобедренной трапеции через площадь :
Формулы трапеции
Для расчёта всех основных параметров трапеции воспользуйтесь калькулятором.
Виды трапеции
- Произвольная трапеция – это четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна)
- Равнобедренная трапеция – это такая трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – это такая трапеция, у которой есть прямые углы при боковой стороне
Свойства трапеции
- Средняя линия трапеции (FE) параллельна основаниям и равна их полусумме $$ FE = $$
- Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне
Например: биссектриса AH отсекает на основании DC отрезок DH , который равен боковой стороне AD - Треугольники AOB и DOC, образованные отрезками диагоналей и основаниями трапеции, подобны
- Треугольники AOD и BOC, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь
- В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон (AD + BC = AB + DC)
- Отрезок (KL), соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии, т.е. $$ KL = $$
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой
- Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности
Свойства и признаки равнобедренной трапеции
- В равнобедренной трапеции углы при любом основании равны (∠ADC = ∠DCB и ∠DAB = ∠ABC)
- В равнобедренной трапеции длины диагоналей равны (AC = BD)
- Если трапецию можно вписать в окружность, то трапеция – равнобедренная
- Около равнобедренной трапеции можно описать окружность
- Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований
Формулы площади произвольной трапеции
Площадь трапеции через основания и высоту
Площадь трапеции через среднюю линию и высоту
Площадь трапеции через диагонали и угол между ними
Площадь трапеции через четыре стороны
Формулы площади равнобедренной трапеции
Площадь трапеции через стороны
Площадь трапеции через стороны и угол
$$ S = AD * sin(∠ADC) * (DC – AD * cos(∠ADC)) $$ $$ S = AD * sin(∠ADC) * (AB + AD * cos(∠ADC)) $$
Площадь трапеции через диагонали и угол между ними
Площадь трапеции через среднюю линию, боковую сторону и угол при основании
$$ S = FE * AD * sin(∠ADC) = FE * AD * sin(∠DAB) $$
Площадь трапеции если в нее вписана окружность
Формулы сторон произвольной трапеции
Основание через другое основание и среднюю линию
$$ AB = 2 * FE – DC $$ $$ DC = 2 * FE – AB $$
Основание через другое основание, диагонали и угол между ними
$$ DC = AB + AG * (ctg(∠ADC) + ctg(∠BCD)) $$ $$ AB = DC – AG * (ctg(∠ADC) + ctg(∠BCD)) $$ $$ DC = AB + AD * cos(∠ADC) + BC * cos(∠BCD) $$ $$ AB = DC – AD * cos(∠ADC) – BC * cos(∠BCD) $$ $$ AD = $$ $$ BC = $$
Формулы сторон равнобедренной трапеции
$$ AD = $$ $$ AD = $$ $$ DC = AB + 2 * AG * ctg(∠ADC) $$ $$ AB = DC – 2 * AG * ctg(∠ADC) $$ $$ DC = AB + 2 * AB * cos(∠ADC) $$ $$ AB = DC – 2 * AB * cos(∠ADC) $$
Длина основания через диагональ, боковую сторону и другое основание
Длина боковой стороны через диагональ и основания
Длина основания через высоту, другое основание, диагонали и угол между ними
Длина основания через высоту, другое основание и площадь трапеции
Длина боковой стороны через площадь трапеции, среднюю линию и угол при основании
Длина боковой стороны через площадь трапеции, основания и угол при основании
Формулы сторон прямоугольной трапеции
$$ DC = AB + BC * cos(∠BCD) = AB + AD * ctg(∠BCD) $$ $$ AB = DC – BC * cos(∠BCD) = DC – AD * ctg(∠BCD) $$ $$ DC = AB + sqrt $$ $$ AB = DC – sqrt $$
Длина основания через боковую сторону, другое основание, диагонали и угол между ними
Длина основания через площадь трапеции, другое основание и высоту
Высота в прямоугольной трапеции равна стороне, которая перпендикулярна основаниям (AD = AG) $$ DC = <2 * S over AD>- AB $$ $$ AB = <2 * S over AD>- DC $$
Формулы диагоналей произвольной трапеции
Длина диагоналей через четыре стороны
Длина диагоналей по теореме косинусов
Длина диагоналей через высоту
Длина диагоналей через стороны и другую диагональ
Длина диагоналей через высоту, основания, другую диагональ и угол между диагоналей
Длина диагоналей через площадь трапеции, другую диагональ и угол между диагоналей
Длина диагоналей через среднюю линию, высоту, другую диагональ и угол между диагоналей
Формулы диагоналей равнобедренной трапеции
Длина диагоналей через стороны
Длина диагоналей по теореме косинусов
Длина диагоналей через высоту основание и угол при основании
Длина диагоналей через сторону и высоту
Формулы диагоналей прямоугольной трапеции
Формулы средней линии произвольной трапеции
Длина средней линии через основания
Длина средней линии через основание, высоту и углы при нижнем основании
Длина средней линии через диагонали, высоту и угол между диагоналями
Длина средней линии через площадь и высоту
Формулы средней линии равнобедренной трапеции
Длина средней линии через основания
Длина средней линии через основание, высоту и углы при нижнем основании
$$ FE = DC – AG * ctg(∠ADC) = AB + AG * ctg(∠ADC) $$
Длина средней линии через основания, боковую сторону и высоту
Длина средней линии через диагонали, высоту и угол между диагоналями
Длина средней линии через площадь и боковую сторону
Формулы средней линии прямоугольной трапеции
Длина средней линии через основания, высоту и угол при нижнем основании
Длина средней линии через основания, боковую сторону и угол при нижнем основании
Длина средней линии через основания и боковые стороны
Длина средней линии через диагонали, высоту и угол между диагоналями
Формулы высоты произвольной трапеции
Длина высоты через четыре стороны
Длина высоты через боковую сторону и прилегающий угол к основанию
$$ AG = AD * sin(∠ADC) = BC * sin(∠BCD) $$
Длина высоты через диагонали и углы между ними
Длина высоты через среднюю линию, диагонали и углы между ними
Длина высоты через площадь и основания
Длина высоты через площадь и среднюю линию
Формулы высоты равнобедренной трапеции
Длина высоты через по сторонам
Длина высоты через боковую сторону и прилегающий угол к основанию
Длина высоты через основания и прилегающий угол к основанию
Длина высоты через диагонали и углы между ними
Длина высоты через площадь и основания
Длина высоты через площадь и среднюю линию
Формулы боковых сторон прямоугольной трапеции
Сторона AD в прямоугольной трапеции равна высоте, поэтому все формулы высоты произвольной трапеции актуальны для стороны AD прямоугольной трапеции.
Сторона BC по трём сторонам
Сторона BC через основания и угол ∠BCD
Сторона BC через Сторону AD
Сторона BC через площадь, среднюю линию и угол ∠BCD
Сторона BC через площадь, основания и угол ∠BCD
Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции
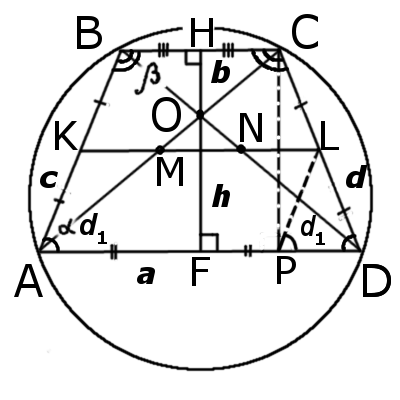 |
| Рис.1 |
Признаки равнобедренной трапеции
∠ABC = ∠BCD и ∠BAD = ∠ADC
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
Основные свойства равнобедренной трапеции
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) – равен полуразности оснований:
Стороны равнобедренной трапеции
Формулы длин сторон равнобедренной трапеции:
a = b + 2 h ctg α = b + 2 c cos α
b = a – 2 h ctg α = a – 2 c cos α
| c = | h | = | a – b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d 1 2 – c 2 | b = | d 1 2 – c 2 | c = √ d 1 2 – ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | – b b = | 2S | – a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
Средняя линия равнобедренной трапеции
Формулы длины средней линии равнобедренной трапеции:
m = a – h ctg α = b + h ctg α = a – √ c 2 – h 2 = b + √ c 2 – h 2
2. Формула средней линии трапеции через площадь и сторону:
Высота равнобедренной трапеции
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
| h = | 1 | √ 4 c 2 – ( a – b ) 2 |
| 2 |
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a – b | tg β | = c sin β |
| 2 |
Диагонали равнобедренной трапеции
Формулы длины диагоналей равнобедренной трапеции:
d 1 = √ a 2 + c 2 – 2 ac cos α
d 1 = √ b 2 + c 2 – 2 bc cos β
4. Формула длины диагонали через высоту и основания:
| d 1 = | 1 | √ 4 h 2 + ( a + b ) 2 |
| 2 |
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
1. Формула площади через стороны:
| S = | a + b | √ 4 c 2 – ( a – b ) 2 |
| 4 |
2. Формула площади через стороны и угол:
S = ( b + c cos α ) c sin α = ( a – c cos α ) c sin α
3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площади через основания и угол между основой и боковой стороной:
5. Формула площади ранобедренной трапеции в которую можно вписать окружность:
S = ( a + b ) · r = √ ab ·c = √ ab ·m
6. Формула площади через диагонали и угол между ними:
| S = | d 1 2 | · sin γ | = | d 1 2 | · sin δ |
| 2 | 2 |
7. Формула площади через среднюю линию, боковую сторону и угол при основании:
S = mc sin α = mc sin β
8. Формула площади через основания и высоту:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p – a )( p – c )( p – d 1) |
где
a – большее основание
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
[spoiler title=”источники:”]
http://calc-online24.ru/formula/trapez
http://ru.onlinemschool.com/math/formula/trapezium_isosceles/
[/spoiler]
Как найти основания трапеции
Основания трапеции можно найти несколькими способами, в зависимости от заданных параметров. При известной площади, высоте и боковой стороне равнобокой трапеции последовательность расчетов сводится к вычислениям стороны равнобедренного треугольника. А также к использованию свойства равнобокой трапеции.
Начертите равнобокую трапецию. Дана площадь трапеции – S, высота трапеции – h и боковая сторона – a. Опустите высоту трапеции на большее основание. Большее основание будет разделено на отрезки m и n.
Для определения длины обоих оснований (х, y) примените свойство равнобокой трапеции и формулу расчета площади трапеции.
Согласно свойству равнобокой трапеции отрезок n равен полуразности оснований х и y. Следовательно, меньшее основание трапеции y можно представить в виде разности большего основания и отрезка n, помноженного на два: y = x – 2*n.
Найдите неизвестный меньший отрезок n. Для этого вычислите одну их сторон получившегося прямоугольного треугольника. Треугольник образован высотой – h (катет), боковой стороной – a (гипотенуза) и отрезком – n (катет). Согласно теореме Пифагора неизвестный катет n² = a² – h². Подставьте известные числовые значения и высчитайте квадрат катета n. Возьмите корень квадратный из полученного значения – это и будет длина отрезка n.
Подставьте полученное значение в первое уравнение для вычисления y. Площадь трапеции высчитывается по формуле S = ((х + y)*h)/2. Выразите неизвестную переменную: y = 2*S/h – х.
Запишите оба полученных уравнения в систему. Подставляя известные значения, найдите две искомые величины в системе двух уравнений. Полученное решение системы х представляет собой длину большего основания, а y – меньшего основания.
