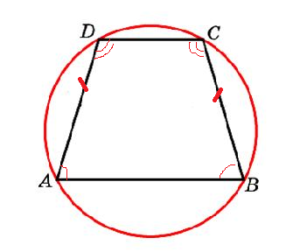
Вписанная в трапецию окружность
Когда в трапецию можно вписать окружность? Какими свойствами обладает вписанная в трапецию окружность? Где находится центр этой окружности? Чему равен ее радиус?
1. В трапецию можно вписать окружность тогда и только тогда когда суммы ее противоположных сторон равны.
1) В трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
2) Обратно, если AD+BC=AB+CD, то в трапецию ABCD можно вписать окружность.
2. Центр вписанной в трапецию окружности — точка пересечения её биссектрис.
O — точка пересечения
биссектрис трапеции ABCD.
3. По свойству биссектрис трапеции, прилежащие к её боковой стороне,
и точка O лежит на средней линии трапеции.
4. Точки касания, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины:
5.
6. Диаметр вписанной в трапецию окружности равен высоте трапеции, радиус — половине высоты:
Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции – параллельные стороны
- Боковые стороны – две другие стороны
- Средняя линия – отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция – трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a – h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a – c· cos α – d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 – 2 ad· cos β
d 2 = √ a 2 + c 2 – 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab – | a ( d 2 – c 2 ) |
| a – b |
| d 2 = | √ | c 2 + ab – | a ( c 2 – d 2 ) |
| a – b |
d 1 = √ h 2 + ( a – h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a – h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab – d 2 2
d 2 = √ c 2 + d 2 + 2 ab – d 1 2
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 – | ( | ( a – b ) 2 + c 2 – d 2 | ) | 2 |
| 2 | 2( a – b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p – a )( p – b )( p – a – c )( p – a – d ) |
| | a – b | |
где
| p = | a + b + c + d | – полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p – a )( p – c )( p – d 1) |
где
a – большее основание
Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Трапеция. Свойства трапеции
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то
Площадь
или где – средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
[spoiler title=”источники:”]
http://ru.onlinemschool.com/math/formula/trapezium/
[/spoiler]
Окружность, вписанная в трапецию
Что такое окружность, вписанная в трапецию
Окружность можно вписать в любой треугольник. Однако это утверждение нельзя применить к любому из четырехугольников.
Прежде чем приступить к рассмотрению темы о вписанной в трапецию окружности, дадим определение вписанной окружности.
Вписанной в многоугольник окружностью называют окружность, которая касается каждой из сторон многоугольника в одной точке. Многоугольник в этом случае называют описанным около окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Теорема 1
Теорема о вписанной окружности: в произвольный выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.
Доказательство: пусть имеется произвольный четырехугольник MNKL и вписанная в него окружность. Обозначим точки касания окружности со сторонами четырехугольника как O, P, R, S.
Если касательные проведены из одной точки, то отрезки, построенные от этой точки до точки касания с окружностью, равны. Тогда KS=KR, LS=LO, MO=MP, NR=NP. Вычислим суммы противоположных сторон: MN+KL=(MP+NP)+(KS+LS) и NK+ML=(NR+KR)+(MO+LO).
Из равенства отрезков получим, что MN+KL= NK+ML.
Примечание 1
Четырехугольник считают выпуклым, если он расположен в одной полуплоскости относительно линии, проходящей через любую из его сторон.
Трапеция является выпуклым четырехугольником. При этом две параллельные стороны трапеции называют основаниями, а две остальные — боковыми сторонами.
Тогда необходимым условием наличия вписанной окружности в трапецию будет равенство суммы ее оснований и боковых сторон.
Для обратного случая — окружность описана вокруг трапеции, трапеция должна быть равнобедренной, то есть ее боковые стороны должны быть равными.
Рассмотрим свойства вписанной в трапецию окружности.
Из свойства биссектрис при боковых сторонах трапеции следует, что радиусы вписанной окружности, проведенные к вершинам боковой стороны и лежащие на биссектрисах, образуют прямой угол.
Примечание 2
Биссектрисы трапеции пересекаются под углом 90°.
Радиус вписанной окружности, проведенный к точкам касания, перпендикулярен сторонам трапеции (по свойству перпендикулярности радиуса и касательной).
Из предыдущего свойства вытекает следующее: радиус вписанной окружности равен половине высоты трапеции, а диаметр — полной длине высоты.
Примечание 3
Высота трапеции — прямая, опущенная от одного основания к другому под прямым углом.
Где находится центр такой окружности
Для построения и решения задача необходимо определить, где расположен центр вписанной окружности.
Примечание 4
Центр окружности, вписанной в трапецию, лежит в точке пересечения биссектрис.
Биссектрисы трапеции пересекаются под прямым углом, отсюда можно сделать следующий вывод: треугольники MON и KOL — прямоугольные.
Формулы для расчета
Основными характеристиками любой окружности являются радиус и диаметр.
Точка касания окружности радиусом R и боковой стороны делит последнюю на два отрезка v и q. Тогда формула для вычисления радиуса будет иметь вид:
Формула 1
(R=sqrt{vcdot q})
Если трапеция равнобедренная и сумма длин оснований равна двум длинам боковой стороны, радиус вписанной окружности:
Формула 2
(R=frac{sqrt{vcdot q}}2)
Диаметр равен длине двух радиусов, значит:
Формула 3
(D=2sqrt{vcdot q})
Формула радиуса через высоту трапеции:
Диаметр через высоту:
Если значение высоты неизвестно, ее можно найти через длины диагоналей (d_1) и (d_2) и оснований a и b трапеции:
Формула 6
(h=frac{d_1cdot d_2}{a+b}singamma)
где γ — угол между диагоналями трапеции.
Площадь вписанной окружности через параметры трапеции (высоту, отрезки боковой стороны):
Формула 7
(S=pi R^2=frac14pi h^2)
или
Формула 8
(S=pi R^2=picdot vcdot q)
В случае равнобедренной трапеции:
Формула 9
(S=pi R^2=frac{picdot vcdot q}4)
Периметр вписанной окружности через параметры трапеции:
Формула 10
(P=2mathrm{πR}=mathrm{πh})
или
Формула 11
Если трапеция равнобедренная:
Формула 12
(P=2mathrm{πR}=mathrmpisqrt{mathrm{vq}})
Приведем формулы для вычисления произвольной и равнобедренной трапеции через радиус вписанной окружности R.
Площадь трапеции:
Формула 13
(S=frac{a+b}2h=(a+b)R)
Полусумма оснований a и b равна средней линии l, тогда:
Формула 14
(S=2cdot lcdot R)
Площадь равнобедренной трапеции:
Формула 15
( S=frac{4R^2}{sinalpha})
где α — угол между основанием и боковой стороной.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Трапеция. Формулы, признаки и свойства трапеции
Определение.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Элементы трапеции:
- Основы трапеции – параллельные стороны
- Боковые стороны – две другие стороны
- Средняя линия – отрезок, соединяющий середины боковых сторон.
Виды трапеций:
- Равнобедренная трапеция – трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
AB + CD = BC + AD
2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:
BC : AD = OC : AO = OB : DO
7. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c2 + d2
Сторона трапеции
Формулы определения длин сторон трапеции:
1. Формула длины оснований трапеции через среднюю линию и другую основу:
a = 2m – b
b = 2m – a
2. Формулы длины основ через высоту и углы при нижнем основании:
a = b + h · (ctg α + ctg β)
b = a – h · (ctg α + ctg β)
3. Формулы длины основ через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a – c·cos α – d·cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Определение.
Средняя линия – отрезок, соединяющий середины боковых сторон трапеции.
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
1. Формула высоты через сторону и прилегающий угол при основании:
h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| 2m | 2m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
1. Формулы диагоналей по теореме косинусов:
d1 = √a2 + d2 – 2ad·cos β
d2 = √a2 + c2 – 2ac·cos α
2. Формулы диагоналей через четыре стороны:
| d1 = | √ | d 2 + ab – | a(d 2 – c2) |
| a – b |
| d2 = | √ | c2 + ab – | a(c2 – d 2) |
| a – b |
3. Формула длины диагоналей через высоту:
d1 = √h2 + (a – h · ctg β)2 = √h2 + (b + h · ctg α)2
d2 = √h2 + (a – h · ctg α)2 = √h2 + (b + h · ctg β)2
4. Формулы длины диагонали через сумму квадратов диагоналей:
d1 = √c2 + d 2 + 2ab – d22
d2 = √c2 + d 2 + 2ab – d12
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
2. Формула площади через среднюю линию и высоту:
S = m · h
3. Формула площади через диагонали и угол между ними:
| S = | d1d2 | · sin γ | = | d1d2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c2 – | ( | (a – b)2 + c2 – d 2 | ) | 2 |
| 2 | 2(a – b) |
5. Формула Герона для трапеции
| S = | a + b | √(p – a)(p – b)(p – a – c)(p – a – d) |
| |a – b| |
где
| p = | a + b + c + d | – полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
P = a + b + c + d
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p – a)(p – c)(p – d1) |
где
a – большее основание
Окружность вписанная в трапецию
В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
a + b = c + d
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
25
Июл 2013
Категория: Справочные материалы
Трапеция. Свойства трапеции
2013-07-25
2016-06-15
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка —
и
, то
Площадь
или
где
– средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Смотрите также площадь трапеции.
Автор: egeMax |
комментарий 431
Печать страницы
Трапеция вписанная в окружность и ее свойства
Какими свойствами обладает трапеция, вписанная в окружность?
Трапеция — это четырехугольник. А четырехугольник можно вписать в окружность только тогда, когда сумма противолежащих углов составляет 180 градусов.
А это возможно только в равнобокой трапеции. То есть, только равнобокую трапецию можно вписать в окружность.
Давайте вспомним свойства равнобокой трапеции.
Свойства трапеции равнобокой и трапеции, вписанной в окружность, часто можно встретить при решении задач. Поэтому нужно их помнить.
Хотите иметь справочные материалы со свойствами основных геометрических фигур всегда под рукой?
Тогда скачайте справочник в видеоформате.
«Видеошпаргалки по геометрии»
Интересная статья? Поделитесь ею пожалуйста с другими: