Тупоугольный треугольник, элементы, свойства, признаки и формулы.
Тупоугольный треугольник – это треугольник, у которого один угол тупой.
Тупоугольный треугольник (понятие и определение)
Элементы тупоугольного треугольника
Свойства тупоугольного треугольника
Формулы тупоугольного треугольника
Остроугольный треугольник, прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, тупоугольный треугольник
Тупоугольный треугольник (понятие и определение):
Тупоугольный треугольник – это треугольник, у которого один угол тупой, т.е. один из его углов лежит в пределах между 90° и 180°.
Тупоугольный треугольник – это треугольник, у которого один угол тупой, а два других – острые. В свою очередь, тупой угол – это угол, градусная мера которого составляет 90° до 180°, а острый угол – это угол, градусная мера которого составляет менее 90 градусов
Рис. 1. Тупоугольный треугольник
∠ BАC– тупой угол треугольника,
∠ АВС, ∠ BСA – острые углы треугольника
По определению, тупоугольным треугольником не может быть правильный (равносторонний) треугольник, т.к. у него каждый угол составляет 60°.
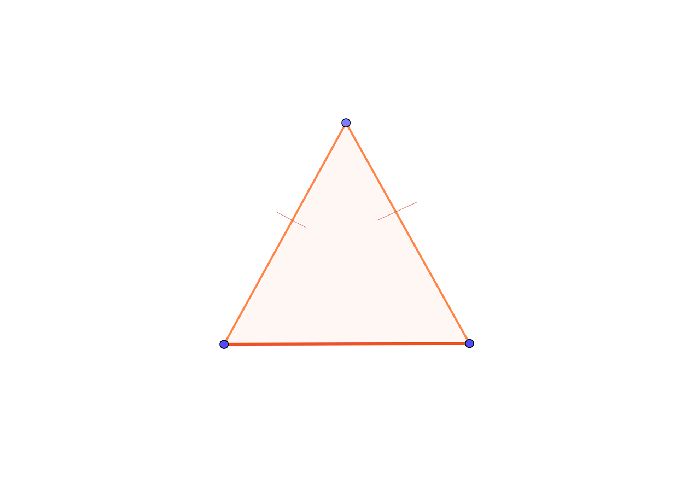
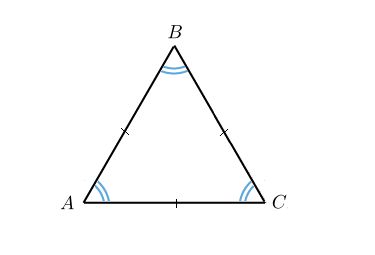
Рис. 2. Равносторонний треугольник
АВ = ВС = АС – стороны треугольника,
∠ АВС = ∠ BАC = ∠ BСA = 60° – углы треугольника
По определению, тупоугольным треугольником не может быть прямоугольный треугольник , т.к. у него один угол составляет 90° и сумма двух других углов также составляет 90°.
Рис. 3. Прямоугольный треугольник
Тупоугольный треугольник также может быть одновременно равнобедренным треугольником. Но не всякий равнобедренный треугольник тупой.
Рис. 4. Равнобедренный треугольник
АВ = AС – боковые стороны, BС – основание,
∠ ВАС – вершинный угол, ∠ АBC и ∠ BСA – углы при основании
Хотя в тупоугольном треугольнике тупой угол больше 90 градусов, сумма углов в треугольнике всегда равна 180 градусам.
Элементы тупоугольного треугольника:
Кроме сторон и углов у тупоугольного треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. тупоугольного, 6 внешних углов, по 2 на каждый внутренний. Внешний угол тупого угла тупоугольного треугольника всегда будет острым углом. Внешний угол острого угла тупоугольного треугольника всегда будет тупым углом.
Рис. 5. Тупоугольный треугольник и внешний угол
∠ ВAD – острый угол
Медиана тупоугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.
Рис. 6. Тупоугольный треугольник и медиана тупоугольного треугольника
MA – медиана тупоугольного треугольника
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Рис. 7. Тупоугольный треугольник и высота тупоугольного треугольника
MС – высота тупоугольного треугольника
Высота тупоугольного треугольника может лежать за пределами треугольника.
Биссектриса в тупоугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы пересекаются в точке, которая является центром вписанной окружности.
Рис. 8. Тупоугольный треугольник и биссектриса угла тупоугольного треугольника
MA – биссектриса тупого угла тупоугольного треугольника
Кроме того, биссектриса тупоугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Свойства тупоугольного треугольника:
Свойства тупоугольного треугольника аналогичны свойствам обычного треугольника:
1. Против большей стороны лежит больший угол, и наоборот.
Рис. 9. Тупоугольный треугольник
2. Против равных сторон лежат равные углы, и наоборот.
Рис. 10. Тупоугольный треугольник с равными боковыми сторонами
АВ = АС
3. Сумма углов тупоугольного треугольника равна 180°.
4. Любая сторона тупоугольного треугольника меньше суммы двух других сторон и больше их разности:
-
- a < b + c;
- a > b – c;
- b < a + c,
- b > a – c;
- c < a + b;
- c > a – b.
Квадрат
Овал
Остроугольный треугольник
Полукруг
Прямой угол
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Ромб
Трапеция
Тупой угол
Тупоугольный треугольник
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
20 504
Равнобедренный тупоугольный треугольник

4.8
Средняя оценка: 4.8
Всего получено оценок: 269.
4.8
Средняя оценка: 4.8
Всего получено оценок: 269.
Равнобедренный треугольник наиболее часто встречается в задачах по геометрии. Так сложилось, что равнобедренный треугольник не столь прост в решении, как правильный, но при этом обладает рядом интересных свойств, которые могут затруднить решение задачи.
Опыт работы учителем математики – более 33 лет.
Равнобедренный треугольник
Равнобедренным треугольником называется треугольник, две стороны которого равны между собой. Тогда третья сторона называется основанием, а равные стороны считаются боковыми.
Любой равнобедренный треугольник имеет ряд свойств:
- Углы при основании равнобедренного треугольника равны.
- Медиана, проведенная к основанию равнобедренного треугольника является биссектрисой и высотой.
Именно эти два свойства определяют специфические особенности равнобедренных треугольников. Как и произвольные треугольник, равнобедренные треугольники бывают 3 видов:
- Остроугольные
- Прямоугольные
- Тупоугольные.
Углы при основании равнобедренного треугольника равны, а сумма углов треугольника всегда равна 180 градусам. Поэтому в равнобедренном и тупоугольном треугольнике наибольший угол всегда лежит напротив основания. Если такой угол лежал бы при основании, то сумма углов превысила бы 180 градусов, а это невозможно.
Тупоугольный треугольник
Тупой угол это угол больше 90 градусов. Очень часто тупоугольный треугольник стараются изобразить так, чтобы тупой угол находился у основания треугольника. Такой подход облегчает восприятие фигуры.
В любой треугольник тупой угол добавляет несколько особенностей:
- Две высоты тупоугольного треугольника будут проходить вне треугольника. Они падают на продолжение одной из сторон.
- Ортоцентр, т.е. точка пересечения высот треугольника будет находится за пределами треугольника.
- Два других угла треугольника всегда будут острыми.
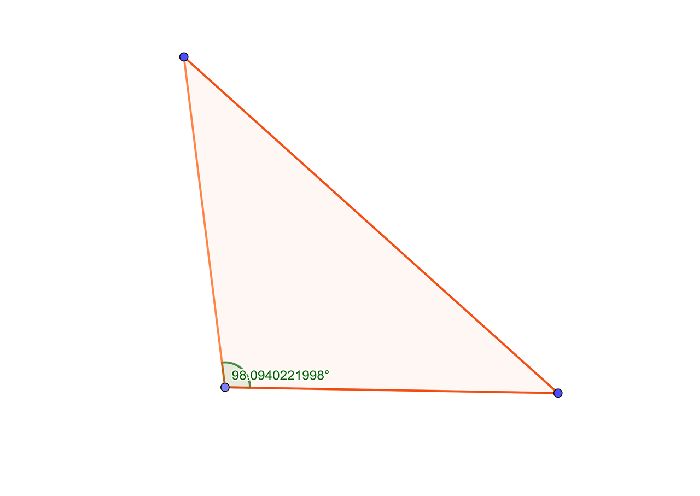
Равнобедренный тупоугольный треугольник
Равнобедренный треугольник – это треугольник, который с одной стороны содержит в себе тупой угол, а с другой стороны имеет две равные между собой стороны.
Такой равнобедренный треугольник сложно воспринимать визуально. Дело в том, что с одной стороны тупоугольные треугольники ученики часто изображают так, чтобы тупой угол был при основании.
Но если тупой угол начертить в основании, то реальное основание тупоугольного равнобедренного треугольника будет визуально совпадать с боковой стороной. Такой подход очень часто приводит к ошибкам. Поэтому равнобедренный тупоугольный треугольник лучше рисовать с тупым углом напротив основания, а сам угол подписывать прямо на чертеже.
С другой стороны, этот подход не всегда помогает воспринимать фигуру именно как тупоугольный треугольник. Поэтому и нужно подписывать углы, а при решении доказывать или проверять условие на наличие доказательств существования тупого угла в треугольнике.
Что мы узнали?
Мы узнали, что такое тупоугольный равнобедренный треугольник и какими особенностями он обладает. Поговорили о том, как лучше начертить тупоугольный треугольник и выделили проблемы, которые могут возникнуть с этим вопросом при решении задач.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-
Алексей Летаев
4/5
Оценка статьи
4.8
Средняя оценка: 4.8
Всего получено оценок: 269.
А какая ваша оценка?
Тупоугольный треугольник
Определение тупоугольного треугольника
ОПРЕДЕЛЕНИЕ
Тупоугольным треугольником называется треугольник, у которого один уз углов тупой (т.е. больше
(
90^{circ}
)).
Медиана тупоугольного треугольника, проведённая из вершины тупого угла, меньше половины стороны, на которую она опущена.
Примеры решения задач
ПРИМЕР 1
Выяснить, является ли треугольник тупоугольным, если его стороны равны (
mathrm{a}=9
) см, (
mathrm{b}=5
) см и (
c=6
) см.
Так в треугольнике против большего угла лежит большая сторона, то запишем теорему косинусов для стороны a:
(
a^{2}=b^{2}+c^{2}-2 b c cos alpha
)
(
81=25+36-2 cdot 5 cdot 6 cdot cos alpha
)
откуда (
cos alpha=-frac{1}{6}
) . Так как значение косинуса отрицательное, то угол а тупой.
Треугольник тупоугольный.
ПРИМЕР 2
Докажите, что в тупоугольном треугольнике основание высоты, проведенной из вершины тупого угла, лежит на стороне треугольника, а основания высот, проведенных из вершин острых углов, – на продолжениях сторон.
Предположим противное: пусть в треугольнике (
mathrm{ABC}
) с тупым углом (
mathrm{A}
) основание высоты (
mathrm{BK}
) лежит на стороне (
mathrm{AC}
). Тогда в прямоугольном треугольнике (
mathrm{AKB}
) есть тупой угол, что невозможно. Значит, основание высоты (
mathrm{BK}
) лежит на продолжении стороны (
mathrm{АС}
).
Теперь допустим, что в том же треугольнике основание высоты (
mathrm{AN}
) лежит на продолжении стороны (
mathrm{BC}
), например, за точкой C. Так как (
angle C
) – острый, то угол смежный с ним – тупой. Тогда в прямоугольном треугольнике (
mathrm{CNA}
) есть тупой угол. Это невозможно, поэтому точка (
mathrm{NH}
) лежит на стороне (
mathrm{BC}
).
Основание треугольника
Строгого определения понятия «основание треугольника» в геометрии не существует. Как правило, этим термином обозначается, сторона треугольника, к которой из противоположной вершины проведен перпендикуляр (опущена высота). Также этим термином принято называть «неравную» сторону равностороннего треугольника. Поэтому выберем из всего многообразия примеров, известного в математике под понятием «решение треугольников», варианты, в которых встречаются высоты и равносторонние треугольники.
Если известны высота и площадь треугольника, то для того чтобы найти основание треугольника (длину стороны, на которую опущена высота), воспользуемся формулой нахождения площади треугольника, утверждающей, что площадь любого треугольника можно посчитать, умножив половину длины основания на длину высоты:
S=1/2*c*h, где:
S — площадь треугольника,
с — длина его основания,
h — длина высоты треугольника.
Из этой формулы находим:
с=2*S/h.
Например, если площадь треугольника равняется 20 кв.см., а длина высоты — 10 см, то основание треугольника будет:
с=2*20/10=4 (см). 2 Если известны боковая сторона и периметр равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=Р-2*а, где:
Р — периметр треугольника,
а — длина боковой стороны треугольника,
с — длина его основания. 3 Если известны боковая сторона и величина противоположного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=а*√(2*(1-cosC)), где:
C — величина противоположного основанию угла равностороннего треугольника,
а — длина боковой стороны треугольника.
с — длина его основания.
(Формула является прямым следствием теоремы косинусов)
Имеется и более компактная запись этой формулы:
с=2*а*sin(B/2) 4 Если известны боковая сторона и величина смежного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей легко запоминающейся формуле:
с=2*а*cosA
A — величина смежного основанию угла равностороннего треугольника,
а — длина боковой стороны треугольника.
с — длина его основания.
Эта формула является следствием теоремы о проекциях. 5 Если известен радиус описанной окружности и величина противоположного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=2*R*sinC, где:
C — величина противоположного основанию угла равностороннего треугольника,
R — радиус описанной вокруг треугольника окружности,
с — длина его основания.
Эта формула является прямым следствием теоремы синусов.
Треугольник и его виды
Треугольник — это геометрическая фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, последовательно соединяющих эти точки. Указанные точки называются вершинами треугольника, а отрезки — сторонами.
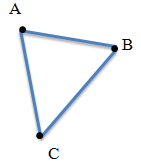
Данная фигура является треугольником (произносят: треугольник АВС, пишут: ∆ АВС). Точки А, В, С — вершины треугольника, а отрезки АВ, ВС, АС ‒ стороны.
Периметр треугольника — это сумма длин всех его сторон.
Виды треугольников
- Остроугольный треугольник — это треугольник, у которого всетри углаострые.
- Тупоугольный треугольник — это треугольник, у которого один из углов тупой.
- Прямоугольный треугольник — это треугольник, у которого один из углов прямой.
Сумма углов любого треугольника равна 180 0 .
По количеству равных сторон:
- Равнобедренный треугольник — это треугольник, у которого две стороны равны.
∆OXP — равнобедренный: XO = XP. Равные стороны на рисунке отмечают равным количеством чёрточек (в нашем случае одной чёрточкой). В равнобедренном треугольники равные стороны называют боковыми сторонами, а третью сторону — основанием, т.е. в ∆OXP: XO и XP — боковые стороны, а OP — основание.
- Равносторонний треугольник — это треугольник, у которого все стороны равны.
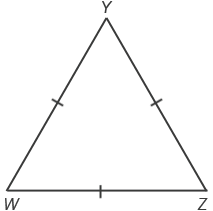
∆WYZ — равносторонний: WY = YZ = ZW. Равносторонний треугольник также называют правильным. Если сторона равностороннего треугольника равна 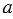
Оборудование: Компьютер, планшет или телефон с выходом в интернет
1. Организационный этап. Подготовка и подключение к сервису.
2. Этап целеполагания. (Отгадывание ребуса в видео уроке)
3. Актуализация опорных знаний. Вспомнить, что такое треугольник и виды углов.
Видео урок и выполните задания
https://learningapps.org/display?v=pzq4g08c521
Задания в видео уроке:
— Отгадайте ребус
— Задание на соотнесение видов треугольников
— Физическая минутка (гимнастика для глаз)
4. Обобщение и систематизация знаний и умений (решение задач, представленных в видео уроке).
Решение задач
1) Одна сторона 20 см, вторая сторона – на 16 см больше первой, третья сторона — в 2 раза меньше второй. Найдите периметр треугольника.
2) Найдите периметр равнобедренного треугольника, основание которого равно 15 см, а боковая сторона – 9 см.
3) Периметр треугольника равен р см, одна сторона – 20 см, вторая сторона b см. Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если р =70, b =31.
5. Повторение видов треугольников в видео
— Вставьте пропущенные слова
Если в треугольнике один из углов прямой, то такой треугольник называется -1-
Если в треугольнике один из углов тупой, то такой треугольник называется -2-
Если в треугольнике все углы острые, то такой треугольник называется -3-
Если в треугольнике все стороны равные, то такой треугольник называется -4-
Если в треугольнике все стороны разные, то такой треугольник называется -5-
Если в треугольнике только две стороны равны, то такой треугольник называется -6-
6. Информация о домашнем задании. Домашнее задание размещено в электронном дневнике (ссылка для выполнения теста).
Как найти основание треугольника
Для того, чтобы найти основание треугольника, можно воспользоваться одной из формул, обязательно должны быть заданы для этой формулы площадь и высота. Вообще, в геометрии и тригонометрии нет четкого обозначения того, какая именно сторона является основанием, так как его можно перевернуть на любую из них. Чтобы найти основание треугольника, его для начала нужно обозначить, а именно выделить ту сторону, на противоположном от которой углу расположена высота. Это перпендикуляр по отношению к основанию, и в зависимости от типа треугольника, он может делить основание пополам.
Есть ряд основных формул, по которым можно найти основание треугольника, в том числе и равнобедренного. Основная формула выглядит так:
- S – площадь треугольника;
- С – длина основания треугольника, которую надо найти;
- h – высота треугольника.
Исходя из тех данных, которые у нас есть, можно найти основание треугольника, если дана площадь и высота.
Как найти основание равнобедренного треугольника
По этой же формуле можно найти основание равнобедренного треугольника. Если известна одна сторона и значение угла напротив основания, то можно вывести по формуле высоту треугольника и потом найти основание по общей формуле.
Как найти основание равностороннего треугольника через косинус
Если известны боковая сторона и величина противоположного основанию угла, можно найти основание треугольника через формулу, где используется значение косинуса.
- С – величина противоположного основанию угла равностороннего треугольника;
- А – длина боковой стороны треугольника;
- с – длина основания.
Эта формула для того, чтобы найти основание треугольника, основана на теореме косинусов и имеет более известную и более простую для применения формулу с=2*а*sin(B/2).
А еще интересно знать, стоит ли покупать евро, так как валюта постоянно дорожает.
Как найти основание треугольника
Строгого определения понятия «основание треугольника» в геометрии не существует. Как правило, этим термином обозначается, сторона треугольника, к которой из противоположной вершины проведен перпендикуляр (опущена высота). Также этим термином принято называть «неравную» сторону равностороннего треугольника. Поэтому выберем из всего многообразия примеров, известного в математике под понятием «решение треугольников», варианты, в которых встречаются высоты и равносторонние треугольники.
Если известны высота и площадь треугольника, то для того чтобы найти основание треугольника (длину стороны, на которую опущена высота), воспользуемся формулой нахождения площади треугольника, утверждающей, что площадь любого треугольника можно посчитать, умножив половину длины основания на длину высоты:
S=1/2*c*h, где:
S — площадь треугольника,
с — длина его основания,
h — длина высоты треугольника.
Из этой формулы находим:
с=2*S/h.
Например, если площадь треугольника равняется 20 кв.см., а длина высоты — 10 см, то основание треугольника будет:
с=2*20/10=4 (см).
Если известны боковая сторона и периметр равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=Р-2*а, где:
Р — периметр треугольника,
а — длина боковой стороны треугольника,
с — длина его основания.
Если известны боковая сторона и величина противоположного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=а*√(2*(1-cosC)), где:
C — величина противоположного основанию угла равностороннего треугольника,
а — длина боковой стороны треугольника.
с — длина его основания.
(Формула является прямым следствием теоремы косинусов)
Имеется и более компактная запись этой формулы:
с=2*а*sin(B/2)
Если известны боковая сторона и величина смежного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей легко запоминающейся формуле:
с=2*а*cosA
A — величина смежного основанию угла равностороннего треугольника,
а — длина боковой стороны треугольника.
с — длина его основания.
Эта формула является следствием теоремы о проекциях.
Если известен радиус описанной окружности и величина противоположного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=2*R*sinC, где:
C — величина противоположного основанию угла равностороннего треугольника,
R — радиус описанной вокруг треугольника окружности,
с — длина его основания.
Эта формула является прямым следствием теоремы синусов.
- Медианы, биссектрисы и высоты треугольника
- Как вычислить основание равнобедренного треугольника
- Как найти основание у равнобедренного треугольника
- Как найти боковую сторону равнобедренного треугольника, если дано основание
Основание треугольника
Основание треугольника – это такая же сторона, как и две других. Основание редко имеет особое значение, но из-за визуальной обособленности от других сторон, ученики часто путаются и допускают ошибки. Разберем подробнее, как сторона треугольника может считаться основанием, и в каких случаях это действительно имеет значение
Стороны треугольника
У треугольника всегда три стороны. Одна из них считается основанием. Как правило, основание выделяется только построением, т.е. нижняя сторона треугольника, и приниматься за основание.
Иногда в решении указывают углы при основании произвольного треугольника. Это не совсем верно, поскольку в произвольном треугольнике все углы равнозначны, а значит не имеет смысла выделять углы при основании. Выделяются только углы при основании равнобедренного треугольника.
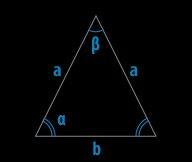
Нужно учитывать, что любой произвольный треугольник можно условно перевернуть, т.е. перечертить фигуру таким образом, чтобы основанием стала другая сторона. По этому разделять понятие боковых сторон и основания у произвольного треугольника не имеет смысла – это только добавит путаницы в решение задачи.
Уравнение основания треугольника, так же, как и уравнение любой из сторон треугольника, является уравнением прямой линии.
Равнобедренный треугольник
Равнобедренный треугольник – это единственный подвид треугольника, где основание имеет реальное практическое значение. Равнобедренным треугольником называется треугольник, у которого две стороны равны между собой. Равные стороны зовутся боковыми, а третья сторона считается основанием.
Существует две теоремы об основании равнобедренного треугольника. Это:
- Теорема о равенстве углов: в равнобедренном треугольнике углы при основании равны.
- Теорема о равенстве медианы, биссектрисы и высоты, проведенной к основанию. Теорема особенно подчеркивает, что из трех возможных медиан, высот и биссектрис, только проведенные к основанию окажутся равными между собой.
В равнобедренном треугольнике основание определяется значением сторон: равные стороны – боковые, неравная – основание.
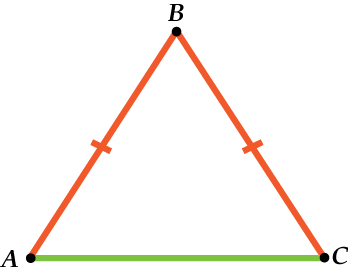
По ходу решения задачи может получится так, что основание окажется сбоку, не нужно этого пугаться. Стоит или привыкнуть к такому построению равнобедренного треугольника или каждый раз перечерчивать чертеж, разворачивая треугольник в нужную сторону.
Равносторонний треугольник
Равносторонний треугольник – это частный случай равнобедренного. У равнобедренного треугольника равны две стороны, а у равностороннего все три. Но именно из-за этого свойства значение основания равнобедренного треугольника теряется.
В равностороннем треугольнике какую сторону не выбери: две другие всегда будут равны между собой, а значит любая сторона может считаться основанием.
Рис. 3. Равносторонний треугольник.
Существует формула, где часто упоминается слово основание. Это формула площади, которая равна половине произведения основания треугольника на высоту, проведенную к этому основанию. Но в качестве основания может быть принята любая сторона, главное, чтобы именно на нее падала высота. Поэтому и в этом случае выбор стороны треугольника, которую можно считать основанием, некритичен.
Что мы узнали?
Мы узнали, что такое основание треугольника. Поговорили о ситуациях, когда стоит выделять основание среди других сторон треугольника, а когда это окажется напрасной тратой времени. Обсудили значимость основания равнобедренного треугольника.