Элементы конуса
Определение. Вершина конуса – это точка (K), из которой исходят лучи.
Определение. Основание конуса – это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.
Определение. Образующей конуса (L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.
Формула. Длина образующей (L) прямого кругового конуса через радиус R и высоту H (через теорему Пифагора):
L2 = R2 + H2
Определение. Направляющая конуса – это кривая, которая описывает контур основания конуса.
Определение. Боковая поверхность конуса – это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.
Определение. Поверхность конуса состоит из боковой поверхности и основания конуса.
Определение. Высота конуса (H) – это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.
Определение. Ось конуса (a) – это прямая, проходящая через вершину конуса и центр основания конуса.
Определение. Конусность (С) конуса – это отношение диаметра основания конуса к его высоте. В случае усеченного конуса – это отношение разности диаметров поперечных сечений D и d усеченного конуса к расстоянию между ними:
где C – конусность, D – диаметр основания, d – диаметр меньшего основания и h – расстояние между основаниями.
Конусность характеризует остроту конуса, то есть, угол наклона образующей к основанию конуса. Чем больше конусность, тем острее угол наклона. угол конуса α будет:
где R – радиус основы, а H – высота конуса.
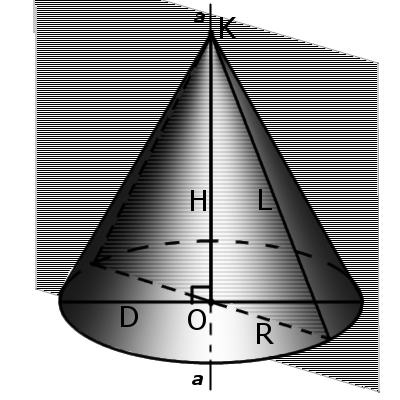
Определение. Осевое сечение конуса – это сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, у которого стороны образованы образующими, а основание треугольника – это диаметр основания конуса.
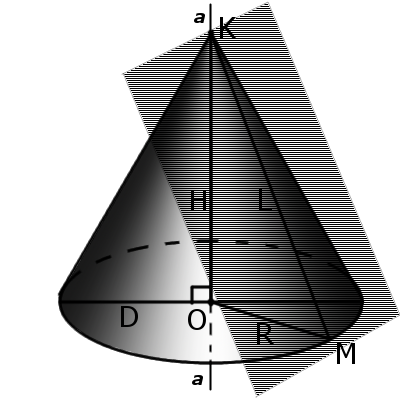
Определение. Касательная плоскость к конусу – это плоскость, проходящая через образующую конуса и перпендикулярна к осевому сечению конуса.
Определение. Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим или параболическим конусом (последние два имеют бесконечный объем).
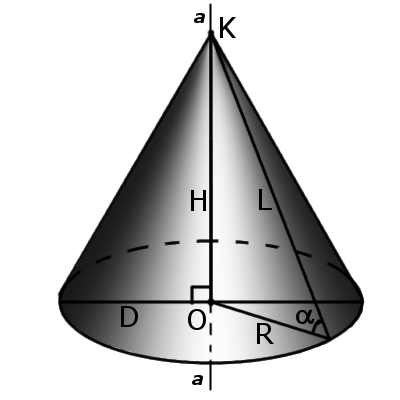
Определение. Прямой конус – это конус у которого ось перпендикулярна основе. У такого конуса ось совпадает с высотой, а все образующие равны между собой.
Формула. Объём кругового конуса:
где R – радиус основы, а H – высота конуса.
Формула. Площадь боковой поверхности (Sb) прямого конуса через радиус R и длину образующей L:
Sb = πRL
Формула. Общая площадь поверхности (Sp) прямого кругового конуса через радиус R и длину образующей L:
Sp = πRL + πR2
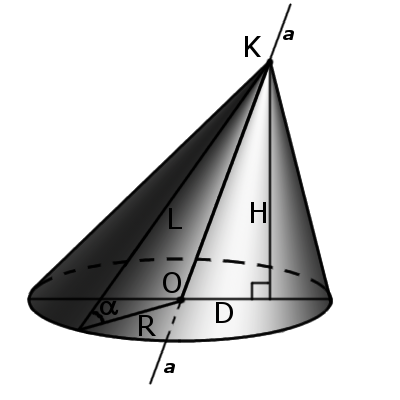
Определение. Косой (наклонный) конус – это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой.
Формула. Объём любого конуса:
где S – площадь основы, а H – высота конуса.
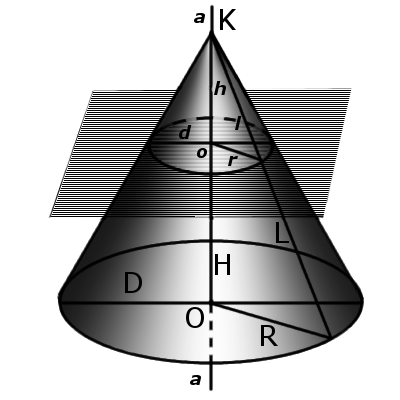
Определение. Усеченный конус – это часть конуса, которая находится между основанием конуса и плоскостью сечения, параллельная основе.
Формула. Объём усеченного конуса:
где S1 и S2 – площади меньшей и большей основы соответственно, а H и h – расстояние от вершины конуса до центра нижней и верхней основы соответственно.
Уравнение конуса
1. Уравнение прямого кругового конуса в декартовой системе координат с координатами (x, y, z):
| x2 | + | y2 | – | z2 | = 0 |
| a2 | a2 | c2 |
2. Уравнение прямого эллиптического конуса в декартовой системе координат с координатами (x, y, z):
| x2 | + | y2 | = | z2 |
| a2 | b2 | c2 |
Основные свойства кругового конуса
1. Все образующие прямого кругового конуса равны между собой.
2. При вращении прямоугольного треугольника вокруг своего катета на 360 ° образуется прямой круговой конус.
3. При вращении равнобедренного треугольника вокруг своей оси на 180 ° образуется прямой круговой конус.
4. В месте пересечения конуса плоскостью, параллельной основанию конуса, образуется круг. (см. Срезанный конус)
5. Если при пересечении плоскость не параллельна основе конуса и не пересекается с основанием, то в месте пересечения образуется эллипс (рис. 3).
6. Если плоскость сечения проходит через основание, то в месте пересечения образуется парабола (рис. 4).
7. Если плоскость сечения проходит через вершину, то в месте пересечения образуется равнобедренный треугольник (см. Осевое сечение).
8. Центр тяжести любого конуса находится на одной четвертой высоты от центра основы.
Прямой конус – это конус, у которого ось перпендикулярна основанию. У такого конуса ось совпадает с высотой, а все образующие равны между собой
Косой (наклонный) конус – это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой
Образующая конуса – это отрезок, который соединяет вершину конуса с границей основания конуса.
Длина образующей, L
$$
L = sqrt{R^2 + h^2}
$$
Площадь основания, SО
$$
S_О = pi * R^2
$$
Площадь боковой поверхности, SБ
$$
S_Б = pi * R * L
$$
Общая площадь поверхности, S
$$
S = pi * R * L + pi * R^2 = S_О + S_Б
$$
Объём прямого конуса, V
$$
V = {1 over 3} * pi * h * R^2
$$
Объём любого конуса
$$
V = {1 over 3} * S_О * h
$$
Угол ∠ f для развертки
$$
∠ f = 360° * {R over L}
$$
Конус — тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета.

Треугольник (POA) вращается вокруг стороны (PO).
(PO) — ось конуса и высота конуса.
(P) — вершина конуса.
(PA) — образующая конуса.
Круг с центром (O) — основание конуса.
(AO) — радиус основания конуса.
Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось (PO) конуса.
Осевое сечение конуса — это равнобедренный треугольник.
(APB) — осевое сечение конуса.
— углы между образующими и основанием конуса.
Для конуса построим развёртку боковой поверхности. Это круговой сектор.

Сектор имеет длину дуги, равную длине окружности в основании конуса
2πR
, угол развёртки боковой поверхности
α
.
В конусе нельзя обозначить угол развёртки.
На развёртке конуса нельзя обозначить высоту и радиус конуса.
Образующая конуса (l) является радиусом сектора.

Таким образом, боковая поверхность конуса является частью полного круга с радиусом (l):
Длина дуги также является частью длины полной окружности с радиусом (l), но в то же время длина дуги — это длина окружности основания конуса с радиусом (R).
Сравним выражения длины дуги и выразим
α
через (R):
2πl⋅α360°=2πR;α=2πR⋅360°2πl=R⋅360°l.
Получаем ещё одну формулу боковой поверхности конуса; не используется угол развёртки боковой поверхности:
.
Если провести сечение конуса плоскостью, перпендикулярной оси конуса, то эта плоскость разбивает конус на две части, одна из которых — конус, а другую часть называют усечённым конусом.

Также усечённый конус можно рассматривать как тело вращения, которое образовалось в результате вращения прямоугольной трапеции вокруг боковой стороны (которая перпендикулярна к основанию трапеции) или в результате вращения равнобедренной трапеции вокруг высоты, проведённой через серединные точки оснований трапеции.

— ось конуса и высота конуса.
Круги с центрами (O) и
O1
— основания усечённого конуса.
(AO) и
A1O1
— радиусы оснований конуса.
Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось
OO1
конуса.
Осевое сечение конуса — это равнобедренная трапеция.
— осевое сечение конуса.
Боковая поверхность определяется как разность боковой поверхности данного конуса и отсечённого конуса:
Sбок.=πR⋅PA−πr⋅PA1=πR⋅PA1+AA1−πr⋅PA1==πR⋅PA1+πR⋅AA1−πr⋅PA1==πR⋅l+πR−πr⋅PA1.
Так как
ΔPAO∼ΔPA1O1
, то стороны их пропорциональны:
PAPA1=Rr;l+PA1PA1=Rr;r⋅l+PA1=R⋅PA1;rl=R⋅PA1−r⋅PA1;PA1⋅R−r=rl;PA1=rlR−r.
Таким образом получаем формулу боковой поверхности усечённого конуса, которая содержит радиусы оснований и образующую усечённого конуса:
Sбок.=πRl+π⋅PA1⋅R−r=πRl+π⋅rlR−r⋅R−r;Sбок.=πRl+πrl=πl⋅R+r.
Конусом (прямым круговым конусом) называется тело, состоящее из круга (основания конуса), точки, не лежащей в плоскости этого круга (вершины конуса), и всех отрезков, соединяющих вершину конуса с точками основания.
Конус является телом вращения.
Конус
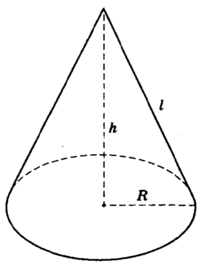
Рис.1
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.
Конус — тело, которое ограничено конической поверхностью и плоскостью, на которой лежат концы образующих конической поверхности.
Коническая поверхность — поверхность, которая образуется движением отрезка, один из концов которого неподвижен, а другой перемещается на плоскости вдоль некоторой кривой. Отрезки называют образующими конической поверхности, а кривую – направляющей. Неподвижная точка – вершина конической поверхности.
Боковая поверхность конуса — часть конической поверхности, ограниченная плоскостью.
Основание конуса — часть плоскости, отсекаемая боковой поверхностью конуса.
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания (См.Рис.1). В противном случае, конус называется наклонным. В школьном курсе изучается прямой круговой конус.
Круговой конус — конус, у которого в основании круг.
Прямой круговой конус (просто конус) — круговой конус, у которого прямая, соединяющая вершину конуса с центром круга, лежащего в основании, перпендикулярна плоскости основания.
Ось конуса — прямая, проходящая через вершину конуса и центр основания конуса.
Высота конуса — отрезок оси конуса, соединяющий вершину конуса с центром основания.
Конус можно рассматривать как тело, полученное вращением прямоугольного треугольника вокруг прямой, содержащей его катет.
Образующие конуса совпадают с образующими конической поверхности.
Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением. Плоскость, проходящая через образующую конуса и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью конуса.
См.Рис.2.
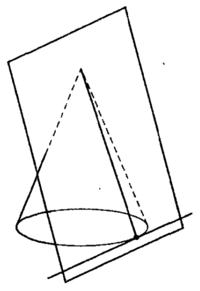
Рис.2
Развёртка боковой поверхности конуса — круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса.
Площадь боковой поверхности (круглого) конуса равна произведению половины длины окружности основания (C) на образующую (l):
$$S_{бок}=frac{1}{2}cdot Cl=picdot rl$$
, где r – радиус основания, l – длина образующей.
Площадь полной поверхности конуса — сумма площадей основания конуса и его боковой поверхности, которая записывается формулой:
$$S_{полн}=picdot r(l+r)$$
, где r — радиус основания, l — длина образующей.
Объем всякого конуса равен трети произведения площади основания (S) на высоту (h):
$$V=frac{1}{3}cdot Sh$$
Объем круглого конуса:
$$V=frac{1}{3}cdot Sh=frac{1}{3}cdotpi r^2 cdot h$$
Усеченный конус – это часть конуса, ограниченная его основанием и сечением, параллельным плоскости основания.
См.Рис.3.
Усечённый конус
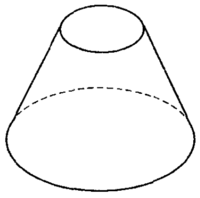
Рис.3
Формулы для усечённого конуса (См.Рис.4):
$$ S_{бок}=picdot lcdot (R+r)
\ S_{полн}=S_{бок}+pi(R^2+r^2)
\ V=frac{1}{3}picdot h(R^2+Rcdot r+r^2)
$$
Усечённый конус
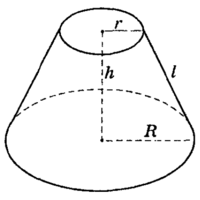
Рис.4

Пример 1. Высота конуса равна 4 , а длина образующей – 5. Найдите диаметр основания конуса.
Видео-решение.
Высота конуса равна 4 , а длина образующей – 5. Найдите диаметр основания конуса.

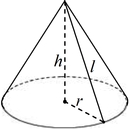
Конус – это геометрическая фигура, полученная вращением прямоугольного треугольника вокруг одного из катетов. У каждого конуса есть основание и боковая поверхность.
Любой конус характеризуется высотой h (осевой линией), радиусом r и образующей l (см. рисунок). Именно эти характеристики используются в формулах конуса при вычислении объема, площади поверхности и площади боковой поверхности.
Высота конуса (осевая линия) – это перпендикуляр, проведенный из вершины конуса к основанию.
Радиус конуса – это радиус его основания.
Образующая конуса – это отрезок, который соединяет вершину конуса с любой точкой, лежащей на линии окружности основания.
Формула образующей конуса
Образующую конуса можно найти, зная ее высоту H и радиус R:
L = √H2 + R2
Формула площади боковой поверхности конуса
Площадь боковой поверхности конуса можно получить, зная его радиус R и образующую L:
Sбок.пов = πRL
Формула площади основания конуса
Площадь основания конуса можно вычислить по его радиусу R:
Sосн = πR2
Формула площади конуса
Площадь поверхности конуса можно получить, сложив площадь боковой поверхности и площадь основания конуса:
S = Sбок.пов + Sосн = πRL + πR2
Формула объема конуса
Объем конуса можно вычислить, зная его высоту H и площадь основания:
V = 1/3 ⋅ Sосн ⋅ H = 1/3πR2H
