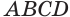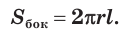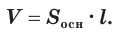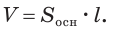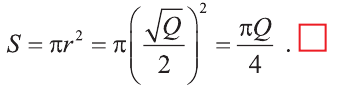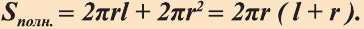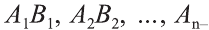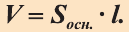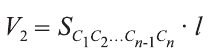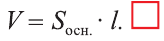Сечение цилиндра: определение, виды, его образующая
Содержание:
- Кратко о цилиндре
- Осевое сечение
- Как найти площадь сечения
- Осевое сечение наклонного цилиндра
-
Примеры задач
- Задача 1
- Задача 2
Кратко о цилиндре
Цилиндр — это геометрическая фигура, которая ограничена цилиндрической поверхностью и двумя плоскими окружностями.
Также можно сказать, что это тело вращения, возникающее при вращении прямоугольника вокруг его стороны.
Осевое сечение
Это сечение фигуры плоскостью, проходящей через ее ось. Оно является прямоугольником. Таким образом, любое сечение, параллельное оси цилиндра (и перпендикулярное его основанию), становится прямоугольником. Сторонами этой фигуры будет диаметр цилиндра и высота его оси.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как найти площадь сечения
Формула 1
(S = d*h,)
где (d) — диаметр, а (h) — высота всей фигуры.
Также есть формулы для расчета площади сечения, параллельного оси геометрического тела (но не пересекающего ее).
Формула 2
(S = a*h, )
где (a) — хорда.
Осевое сечение наклонного цилиндра
Сечение наклонного цилиндра по оси представляет собой параллелограмм. Его стороны нам уже известны: одна из них равна диаметру d, как и в случае с прямой фигурой. Другая — длина образующего отрезка. Ее мы можем обозначить буквой b.
Для точного определения всех параметров параллелограмма недостаточно знать только длины его сторон. Для расчета площади фигуры нам понадобится один из ее углов. Допустим, что острый угол между плоскостью и направляющий равен α. Тогда формула S параллелограмма будет выглядеть следующим образом:
(S = d * b * sin(α))
Примеры задач
Рассмотрим пару задач на осевое сечение с решениями.
Задача 1
Дан круглый прямой цилиндр. Его осевое сечение является квадратом. Вопрос: чему равна S сечения, если площадь поверхности всего цилиндра — 100 см²?
Решение
Чтобы найти S квадрата, нужно сначала определить радиус или диаметр окружности цилиндра. Для этого вспомним формулу для нахождения площади самого цилиндра:
(Sц = 2pi * r * (r + h))
Так как осевое сечение — квадрат, значит радиус основания в два раза меньше высоты фигуры. В таком случае, формула будет выглядеть так:
(Sц = 2pi * r * (r + 2r) = 6 * pi * r²)
Исходя из этого, будем выражать радиус:
(r = √(Sц / (6*pi)))
Если сторона квадратного сечения равна диаметру основания цилиндра, то для определения площади квадрата S используем формулу:
(S = (2*r)2 = 4*r2 = 2*Sц/ (3*pi))
Подставим известные данные ((Sц = 100см^2)) и получим площадь сечения (S = 21,23 см²).
Ответ: (S = 21,23 см²).
Задача 2
Дано: ABCD — осевое сечение цилиндра. Площадь сечения (Sc) равна (10 м²), а площадь основания (Sо— 5 м²). Найти высоту цилиндра.
Решение
Так как площадь основания — круг, то (Sо = pi * r²). Тогда (r = √(Sо/pi) = √(5/pi).)
Так как площадь сечения — прямоугольник, то (Sc = AB * BC = h * 2r.) Тогда (h = Sc/(2r) = 10/(2√(5/pi)) = 5√(pi/5) = √(5pi).)
Ответ: (h = √(5pi).)
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.
Прямоугольник
AOO1A1
вращается вокруг стороны
OO1
.
OO1
— ось симметрии цилиндра и высота цилиндра.
AA1
— образующая цилиндра, длина которой равна длине высоты цилиндра.
(AO) — радиус цилиндра.
Полученная цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги — основаниями цилиндра.
Осевое сечение цилиндра — это сечение цилиндра плоскостью, которая проходит через ось цилиндра. Это сечение является прямоугольником.
При сечении цилиндра плоскостью, параллельной оси цилиндра (т. е. перпендикулярной основанию), также получается прямоугольник.
На рисунке изображён цилиндр, пересечённый плоскостью, которая параллельна оси цилиндра
OO1
.
— прямоугольник.
(OA = OB = R) — радиусы.
(OC) — расстояние от оси цилиндра до плоскости сечения.
Дуга (AB) равна центральному углу (AOB).
При сечении цилиндра плоскостью, параллельной основанию, в сечении получаем круг, равный основаниям цилиндра.
Если представить, что боковая цилиндрическая поверхность разрезана по образующей
AA1
и развёрнута, получаем прямоугольник.
Сторона
AA1
равна высоте (H), а другую сторону образует развёрнутая окружность основания длиной
2πR
.
Так как развёртка — прямоугольник, то боковая поверхность определяется по формуле:
Основания цилиндра — два круга с общей площадью
2⋅πR2
.
Полная поверхность цилиндра определяется по формуле:
.
На этой странице вы узнаете
- Как вода в кружке иллюстрирует сечение цилиндра?
- Как лист бумаги превратить в цилиндр?
Что общего у джентльмена 19 века, Вилли Вонка из «Чарли и шоколадная фабрика», Шерлока Холмса в экранизации «Безобразная невеста» и некоторых сценических костюмов? Цилиндр! О нем, вернее о фигуре цилиндра и поговорим в статье.

Понятие цилиндра
Сейчас мы говорим про мужской головной убор, который был популярен в 19 веке и стал достаточно узнаваем в массовой культуре. Оказывается, в математике также существует цилиндр. И они похожи по форме.
Цилиндр — тело вращения, полученное при вращении прямоугольника вокруг одной из его сторон.
Возможно, для уточнения некоторых терминов вам захочется заглянуть в статью «Тела вращения».
Если посмотреть на форму шляпы, то она действительно будет похожа на геометрическую фигуру. Встретить цилиндр можно и в наше время. Обычная кружка является цилиндром.

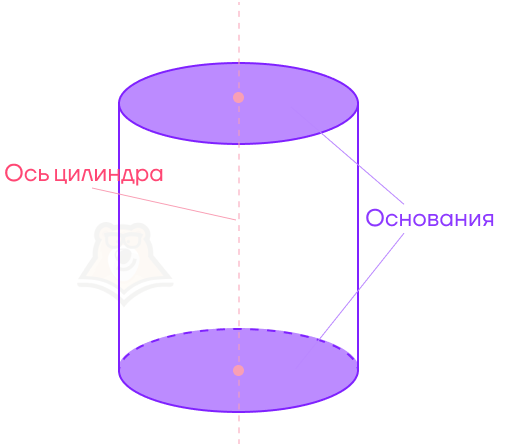
Прямая, вокруг которой мы крутили прямоугольник, чтобы получить цилиндр, — это ось цилиндра.
Также, как у Земли есть ось вращения, она есть и у цилиндра.
Наша кружка стоит на круглом дне. Это дно, как и самый верх кружки, будут называться основаниями цилиндра.
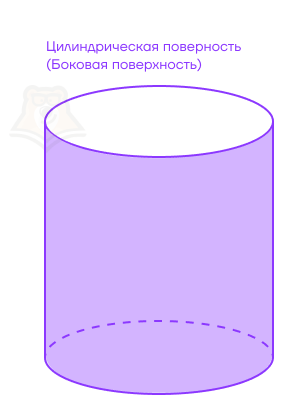
Снова посмотрим на стенки кружки. В цилиндре эта поверхность будет называться цилиндрической поверхностью. Ее также могут называть боковой поверхностью цилиндра.
Представим, что наша кружка раскрашена вертикальными линиями. Эти линии будут лежать на цилиндрической поверхности и перпендикулярны основаниям. У них есть название:
Образующая цилиндра — отрезок, соединяющий точки окружностей основания и перпендикулярный плоскостям оснований.
Все образующие, — а в цилиндре их очень-очень много, —лежат только на цилиндрической поверхности. Эта поверхность и состоит из множества образующих.
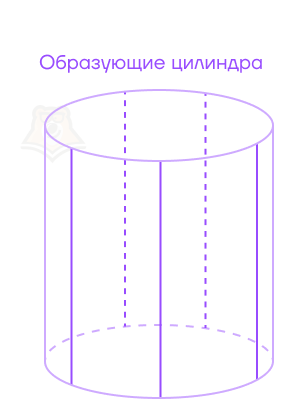
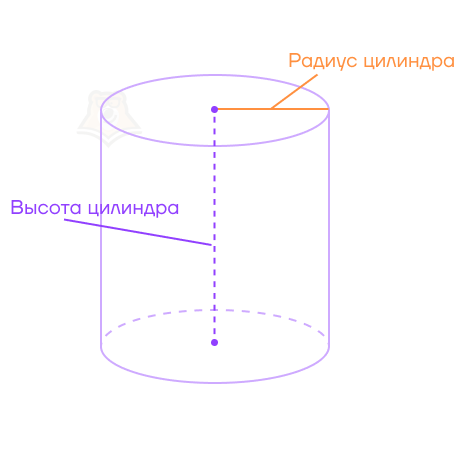
Узнаем ширину кружки. Для этого нужно измерить радиус дна. Этот же радиус будет радиусом основания, а в цилиндре он называется радиусом цилиндра.
Теперь найдем высоту кружки. Для этого нужно измерить расстояние от дна до самого верха кружки.
В математике это будет расстоянием между плоскостями, а ищется оно как длина перпендикуляра, опущенного из одной плоскости на другую. Подробнее про это можно прочесть в статье «Расстояния между фигурами».
Высота цилиндра — перпендикуляр, опущенный из плоскости одного основания на плоскость второго основания.
Свойства цилиндра
Рассмотрим, какими свойствами обладает цилиндр.
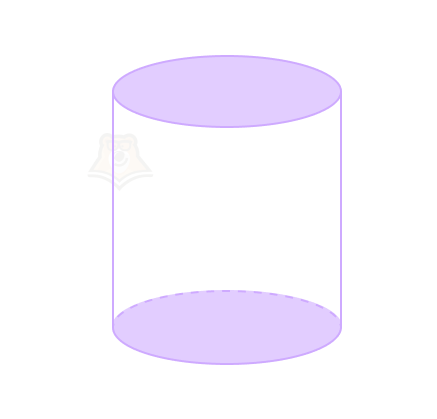
Свойство 1. Основания цилиндра равны и параллельны.
Это всегда два равных круга, лежащих в параллельных плоскостях.
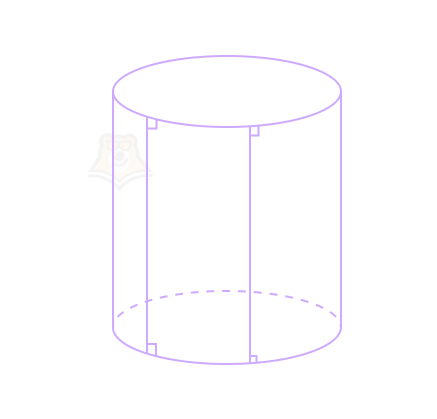
Свойство 2. Образующие цилиндра равны и параллельны.
Поскольку все образующие перпендикулярны основаниям, то они параллельны между собой по свойству прямой и перпендикулярной ей плоскости. Подробнее про это свойство можно прочесть в статье «Углы в пространстве».
А равны они потому, что являются перпендикуляром к основаниям, то есть равны высоте цилиндра.
Свойство 3. Сечение цилиндра, проходящее через ось цилиндра, является прямоугольником. Такое сечение в цилиндре будет называться осевым сечением цилиндра.
Например, если разрезать тортик по диаметру, то место среза как раз будет прямоугольником.
Подробности про сечения фигур можно найти в статье «Сечения».
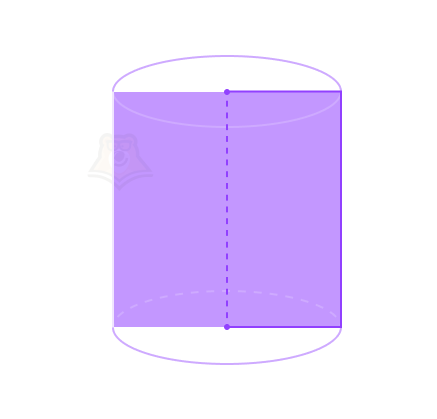
Свойство 4. Сечение цилиндра, проходящее параллельно оси цилиндра и перпендикулярно его основаниям, будет являться прямоугольником.
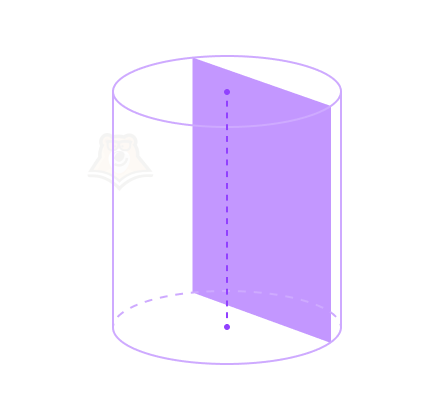
Свойство 5. Сечение цилиндра, перпендикулярное оси цилиндра, является кругом с радиусом, равным радиусу цилиндра. Такое сечение в цилиндре называется перпендикулярным сечением цилиндра.
Если налить в кружку воду, то ее поверхность примет круглую форму. При этом совершенно без разницы, сколько воды наливать: поверхность останется кругом.
Поскольку поверхность воды параллельна дну кружки, то есть основаниям цилиндра, то она является перпендикулярным сечением цилиндра.
Этим опытом можно подтвердить свойство 5.
Заметим, что все вышеописанные свойства относятся к прямому цилиндру.
Цилиндр также может быть наклонным. В этом случае ось цилиндра и его образующие не будут перпендикулярны основаниям.
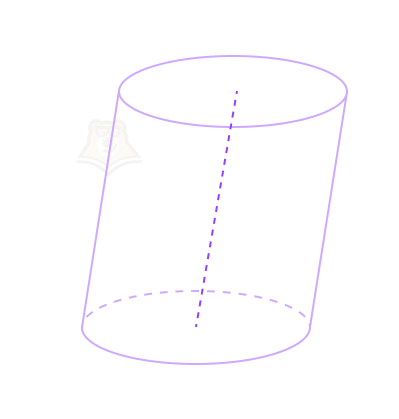
Если мы разрежем поверхность цилиндра по одной из его образующих и как бы “развернем” ее, у нас получится прямоугольник.
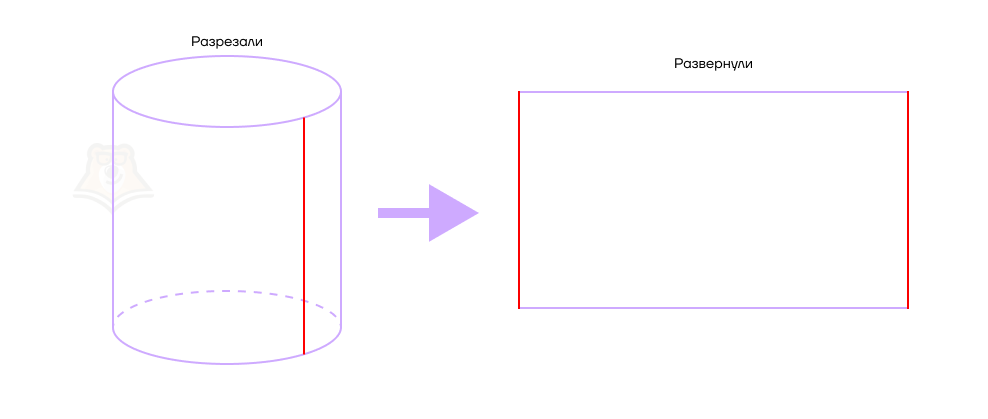
Это также легко увидеть, если вспомнить художников с тубусами. Тубус имеет форму цилиндра, и свернутый прямоугольный лист принимает такую же форму.

Развертка боковой поверхности цилиндра — прямоугольник, одна сторона которого равна высоте цилиндра, а вторая — длине окружности его основания.
Поскольку развертка боковой поверхности цилиндра — это прямоугольник, то любой лист бумаги можно превратить в цилиндр. Для этого достаточно скрутить его в трубочку. При этом чем тоньше будет трубочка, тем меньше будет радиус цилиндра.
Формулы цилиндра
А если это прямоугольник, то мы знаем, как найти его площадь. Нам нужно умножить его длину на высоту. Так мы получаем площадь боковой поверхности цилиндра.
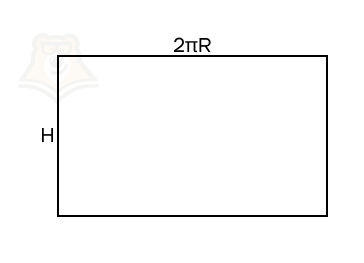
(S_{бок.} = 2 pi RH)
В этой формуле 2R — длина окружности основания, где R — его радиус, а Н — образующая (или высота) цилиндра. Подробнее про площадь прямоугольника и длину окружности (а также про площадь круга) можно прочесть в статьях «Параллелограмм» и «Окружность и круг».
Мы нашли площадь боковой поверхности. Как же теперь найти площадь полной поверхности?
Для этого нужно сложить площади боковой поверхности и оснований. Следовательно, мы получаем следующую формулу.
(S = S_{бок.} + 2S_{осн.} = 2 pi RH+2 pi R^2 = 2 pi R(H + R))
Допустим, мы решили сделать чашку очень вкусного чая, но чтобы правильно его заварить нам нужно знать точный объем воды. Для этого вычислим объем цилиндра. Воспользуемся следующей формулой:
(V = S_{осн.}H = pi R^2H)
В этой формуле R — радиус цилиндра, Н — высота.
Часто формулу объема можно применить для решения жизненных задач. Например, чтобы найти объем детали, погруженной в воду.
Пример 1. В цилиндрическом сосуде налито 1650 см3 жидкости. В этот сосуд опустили деталь. При этом уровень жидкости увеличился в 1,2 раза. Найдите объем детали. Ответ выразите в см3.
Решение.
Шаг 1. Выразим высоту жидкости в первый и второй раз. Пусть вначале уровень жидкости был равен х, значит после того, как в нее опустили деталь, он стал равен 1,2х.
Шаг 2. Вспомним физику и заметим, что объем жидкости в сосуде после того, как в него опустили деталь, будет равен сумме объемов жидкости и детали: V = Vж + Vд.
Шаг 3. С помощью объема жидкости выразим площадь основания сосуда:
Vж = Sосн.H
1650 = Sосн.x
(S_{осн} = frac{1650}{x})
Шаг 4. Подставим площадь основания в формулу объема жидкости после того, как в нее опустили деталь:
(V = S_{осн.}H = frac{1650}{x} * 1,2x = 1980)
Шаг 5. Тогда объем детали будет равен:
Vд = V — Vж
Vд = 1980 — 1650 =330
Ответ: 330 см3
Фактчек
- Цилиндр — тело вращения, полученное при вращении прямоугольника вокруг одной из его сторон. Цилиндр может быть прямым и наклонным. В наклонном цилиндре ось не перпендикулярна основаниям цилиндра.
- Цилиндр состоит из двух оснований и цилиндрической поверхности (боковой поверхности цилиндра). Основания имеют форму кругов, равны между собой и лежат в параллельных плоскостях. Развертка боковой поверхности имеет форму прямоугольника.
- Образующая цилиндра — отрезок, соединяющий точки окружностей основания и перпендикулярный плоскостям оснований. В прямом цилиндре образующая равна высоте цилиндра. Образующие равны и параллельны друг другу, а также образуют боковую поверхность цилиндра.
- Осевое сечение цилиндра проходит через его ось и является прямоугольником. Любое сечение, параллельное осевому, также будет являться прямоугольником. Перпендикулярное сечение проходит перпендикулярно оси цилиндра и параллельно его основаниям. Перпендикулярное сечение имеет форму круга.
Проверь себя
Задание 1.
Что такое образующая цилиндра?
- Ось вращения, с помощью которой получен цилиндр.
- Диаметр оснований цилиндра.
- Любой перпендикуляр, проведенный от одного основания к другому.
- Отрезок, соединяющий точки окружности основания.
Задание 2.
Площадь боковой поверхности цилиндра равняется 44. Его радиус равен 8. Найдите высоту цилиндра.
- 2,75
- 5,5
- (2,75 pi)
- 2
Задание 3.
Площадь основания цилиндра равна 16. Его высота равна 4. Найдите площадь полной поверхности цилиндра.
- 64
- (64 pi)
- 32
- (32 pi)
Задание 4.
Объем цилиндра равен 28, а его высота равняется 7. Найдите диаметр основания.
- 4
- 2
- 16
- 8
Ответы: 1. – 4 2. – 1 3. – 2 4. – 1
§ 17. Цилиндр
17.1. Определение цилиндра и его элементов
Определение. Тело, которое образуется при вращении прямоугольника вокруг прямой, содержащей его сторону, называется цилиндром (рис. 141).
Круги, образованные вращением сторон прямоугольника, перпендикулярных оси вращения, называются основаниями цилиндра (верхним и нижним). Так как противоположные стороны прямоугольника равны, то основаниями цилиндра являются равные круги.
Рис. 141
Поверхность, образованная вращением стороны прямоугольника, параллельной оси вращения, называется боковой поверхностью цилиндра, а её площадь — площадью боковой поверхности цилиндра и обозначается Sбок. Объединение боковой поверхности цилиндра и двух его оснований называется полной поверхностью цилиндра, а её площадь обозначается Sполн. Таким образом,
Sполн = Sбок + 2Sосн.(1)
Высотой цилиндра называется перпендикуляр, проведённый из какой-либо точки одного основания цилиндра к плоскости другого. Длину этого перпендикуляра также называют высотой цилиндра. Отрезок, соединяющий точки окружностей оснований и перпендикулярный к их плоскостям, называется образующей цилиндра вращения. Отрезок оси вращения, заключённый внутри цилиндра, называется осью цилиндра.

Если основания прямого кругового цилиндра подвергнуть сжатию так, чтобы окружность основания преобразовалась в эллипс, то получим цилиндр, который называется эллиптическим цилиндром (рис. 142, б).
Так как окружность при параллельном проектировании изображается эллипсом, то изображения кругового и эллиптического цилиндров совпадают.
Цилиндр, образующие которого не перпендикулярны плоскостям его оснований, называется наклонным цилиндром (рис. 142, в).
Рис. 142
Рис. 143
Нам предстоит изучать лишь прямой круговой цилиндр, поэтому слова «прямой круговой» опускаем.
Поверхность, образованную вращением прямой, параллельной оси вращения, называют цилиндрической поверхностью вращения (рис. 143).
Уравнение x2 + y2 = r2 (r > 0) задаёт цилиндрическую поверхность вращения с осью вращения Oz и радиусом основания r. Из этого уравнения следует, что цилиндрическая поверхность является поверхностью второго порядка. (Подробнее о поверхностях второго порядка можно прочитать в «Дополнениях» в конце этой книги.)
17.2. Свойства цилиндра
а) Сечения цилиндра плоскостью. Так как цилиндр является телом вращения, то любое его перпендикулярное сечение есть круг, а перпендикулярное сечение боковой поверхности цилиндра — окружность; центры этих окружностей и кругов — точки пересечения секущих плоскостей и оси цилиндра (рис. 144).
Рис. 144
Рис. 145
Рис. 146
Рис. 147
Рис. 148
Если секущая плоскость пересекает ось цилиндра и не перпендикулярна ей, то в сечении может получиться эллипс (рис. 145) или его некоторая часть (рис. 146, 147). Это следует из того, что параллельной проекцией окружности на плоскость, не параллельную плоскости окружности, является эллипс. (Вспомните: наклонив цилиндрический стеклянный сосуд с водой, вы видите на поверхности воды эллипс или его часть.)
Сечение цилиндра плоскостью, проходящей через ось, называется осевым сечением цилиндра. Так как поворот пространства вокруг прямой на угол 180° является осевой симметрией относительно оси вращения, то ось прямого кругового цилиндра является его осью симметрии. Значит, осевым сечением цилиндра вращения является прямоугольник, стороны которого равны диаметру основания и образующей цилиндра (рис. 148). При этом все осевые сечения цилиндра — равные между собой прямоугольники.
Цилиндр, осевое сечение которого — квадрат, называют равносторонним цилиндром (рис. 149).
Так как все образующие цилиндра равны и параллельны друг другу, то любое сечение цилиндра плоскостью, параллельной его оси, есть прямоугольник, высота которого равна образующей цилиндра (рис. 150).
б) Изображение цилиндра. Чтобы построить изображение цилиндра, достаточно построить: 1) прямоугольник AВB1A1 и его ось OO1 (рис. 151); 2) два равных эллипса, центрами которых являются точки O и O1 и осями — отрезки АВ и A1В1. Выделив штрихами невидимые линии, получаем искомое изображение цилиндра.
Рис. 149
Рис. 150
Рис. 151
в) Касательная плоскость к цилиндру.
Определение. Плоскость, проходящая через образующую цилиндра перпендикулярно плоскости осевого сечения, проведённой через эту образующую, называется касательной плоскостью к цилиндру (рис. 152).
Рис. 152
Говорят, что плоскость α касается цилиндра (цилиндрической поверхности) по образующей DD1, каждая точка образующей DD1 является точкой касания плоскости α и данного цилиндра.
Через любую точку боковой поверхности цилиндра проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности цилиндра можно провести лишь одну плоскость, касательную к данному цилиндру в этой точке.
17.3. Развёртка и площадь поверхности цилиндра
Следует заметить, что развёртка поверхности вращения — понятие в определённой мере интуитивное. К тому же не для каждой поверхности тела вращения можно построить её развёртку. Иными словами, не каждую поверхность можно «развернуть» на плоскости. Например, не существует развёртки сферы (см. раздел «Дифференциальная геометрия» в конце этой книги).
Рис. 153
Развёртку цилиндра мы также введём на интуитивном уровне.
Пусть R — радиус основания, h — высота цилиндра.
Рис. 154
Рис. 155
Полная поверхность цилиндра состоит из его боковой поверхности и двух оснований — равных кругов. Если эту поверхность «разрезать» по образующей DD1 (рис. 153) и по окружностям оснований, затем боковую поверхность развернуть на плоскости, то получим развёртку полной поверхности цилиндра (рис. 154), состоящую из прямоугольника и двух равных кругов, касающихся противоположных сторон этого прямоугольника (рис. 155).
Попробуйте изготовить развёртку цилиндра и склеить из неё цилиндр.
За площадь боковой поверхности цилиндра принимается площадь её развёртки, т. е. площадь боковой поверхности цилиндра равна площади прямоугольника, у которого одна сторона равна длине окружности основания цилиндра, а другая сторона — высоте цилиндра:
Sбок = 2πRh.
Таким образом, доказана следующая теорема.
Теорема 26. Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту. ▼
Площадь круга радиуса R равна πR2, поэтому Sосн = πR2. Тогда для нахождения площади полной поверхность цилиндра справедливо:
Sполн = Sбок + 2Sосн = 2πRh + 2πR2 = 2πR(R + h).
Следствие. Пусть цилиндр образован вращением прямоугольника ABCD вокруг его высоты AD (рис. 156). Тогда
Sбок = 2πDC•BC. (1)
Рис. 156
Если EF — серединный перпендикуляр к образующей BC, проведённый из точки F оси l цилиндра, то EF = CD. Учитывая, что ВС = AD, получаем: Sбок = 2πEF•AD, т. е. боковая поверхность цилиндра равна произведению высоты цилиндра на длину окружности, радиус которой равен длине серединного перпендикуляра его образующей, проведённого из точки оcu цилиндра.
Это следствие найдёт своё применение в п. 19.7.
17.4. Призмы, вписанные в цилиндр и описанные около цилиндра
Нам предстоит решать задачи, в которых рассматриваются многогранники, вписанные в фигуры вращения и описанные около них.
Для правильного и наглядного изображения конфигураций из таких многогранников и фигур вращения необходимо верно изображать правильные многоугольники, вписанные в окружность (круг) или описанные около неё.
Определение. Призма называется вписанной в цилиндр, если основания призмы вписаны в основания цилиндра (рис. 157).
Рис. 157
Цилиндр в этом случае называют описанным около призмы.
Боковые рёбра призмы соединяют соответственные вершины её оснований, вписанных в основания цилиндра. Эти вершины лежат на окружностях оснований цилиндра. Образующие цилиндра соединяют соответственные точки окружностей его оснований и параллельны боковым рёбрам призмы. Следовательно, боковые рёбра вписанной в цилиндр призмы — образующие цилиндра.
Определение. Призма называется описанной около цилиндра, если основания призмы описаны около оснований цилиндра.
Рис. 158
Цилиндр при этом называют вписанным в призму (рис. 158).
Так как соответственные стороны оснований призмы параллельны друг другу и перпендикулярны радиусам оснований цилиндра, проведённым в точки касания, то плоскости боковых граней призмы являются касательными плоскостями к цилиндру: эти плоскости касаются поверхности цилиндра по образующим, соединяющим точки, в которых стороны оснований призмы касаются окружностей оснований цилиндра.
При изображении правильных призм, вписанных в цилиндр, следует руководствоваться алгоритмами построений изображений правильных многоугольников, вписанных в окружность.
Итак, для построения изображения правильной призмы, вписанной в цилиндр: 1) строим изображение цилиндра; 2) строим изображение правильного многоугольника, вписанного в верхнее основание цилиндра; 3) через вершины построенного вписанного многоугольника проводим образующие цилиндра; 4) в нижнем основании цилиндра последовательно соединяем концы этих образующих; 5) выделяем видимые и невидимые линии (отрезки) изображаемых фигур.
Рис. 159
На рисунке 159 изображены вписанные в цилиндр: призма, в основании которой прямоугольный треугольник (рис. 159, а); правильная четырёхугольная призма (рис. 159, б); правильная треугольная призма (рис. 159, в); правильная шестиугольная призма (рис. 159, г).
ЗАДАЧА (3.029). Диагональ осевого сечения равностороннего цилиндра равна a
Рис. 160
Решение. Рассмотрим случай а). Пусть в равносторонний цилиндр вписана правильная призма ABCA1B1C1 (рис. 160); CDD1C1 — осевое сечение; OO1 = h — высота цилиндра; ОС = R — радиус основания цилиндра.
Так как цилиндр — равносторонний, то CDD1C1 — квадрат, значит, высота цилиндра равна диаметру его основания. Тогда в квадрате СDD1С1 находим CD = 
Далее, △ АВС — правильный, вписанный в основание, радиус которого R = 





Sосн = 

S
бок = 3SABB1A1 = 3AB•BB1 = 3•

Тогда
Sполн = Sбок + 2Sосн = 


Ответ: a) 

Рис. 161
ЗАДАЧА (3.032). В равносторонний цилиндр, высота которого равна a, вписана правильная призма. Найти расстояние и угол между диагональю боковой грани призмы и осью цилиндра, если призма: а) треугольная; б) четырёхугольная; в) шестиугольная.
Решение. Рассмотрим случай б). Пусть ABCDA1B1C1D1 — вписанная в цилиндр правильная призма (рис. 161). Найдём расстояние и угол между осью OO1 цилиндра и скрещивающейся с ней (почему?) диагональю АB1 боковой грани ABB1A1 данной призмы.
Расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, проведёнными через эти прямые.
Если точка Е — середина отрезка AD, то расстояние между скрещивающимися прямыми AB1 и OO1 равно расстоянию между плоскостью грани ABB1A1 и параллельной ей (почему?) плоскостью сечения EFF1E1. Это расстояние равно длине отрезка ОK (где точка K — середина АВ), так как OK ⟂ (ABB1) и (ABB1) || (EFF1).
Поскольку данный цилиндр — равносторонний, то BDD1B1 — квадрат со стороной BD = ВВ1 = a. Тогда АВ = 



Обозначим ∠ (OO1; AB1) = ϕ, M = AB1 ∩ A1B. Для нахождения угла ϕ проведём в грани ABB1A1 прямую KK1 || OO1. Тогда ϕ = ∠ (OO1; AB1) = ∠ (KK1; AB1). Так как KK1 || OO1, OO1 ⟂ (ABC), то MK ⟂ AB. Поэтому △ АKМ — прямоугольный. В этом треугольнике АK = 




Ответ: б) 


Действительно, Sбок. пов. призм = h•Pосн. призм, где Росн. призм — периметр основания призмы, h — длина её высоты. Для правильных вписанных в цилиндр призм h — постоянная величина, равная длине высоты цилиндра, а предел последовательности периметров правильных многоугольников, вписанных в окружность (основание цилиндра), равен длине этой окружности. Таким образом, мы вновь получаем: Sбок = 2πRh.
17.5. Объём цилиндра
Напомним принятое нами соглашение, основанное на принципе Кавальери.
«Пусть даны два тела и плоскость. Если каждая плоскость, параллельная данной плоскости и пересекающая одно из данных тел, пересекает также и другое, причём площади сечений, образованных при пересечении обоих тел, относятся как m : n, то и объёмы этих тел относятся как m : n».
Рис. 162
Расположим цилиндр, имеющий высоту h и радиус основания R, и прямоугольный параллелепипед с рёбрами h, R, R так, чтобы их основания находились на двух параллельных плоскостях, расстояние между которыми равно h (рис. 162). Каждая плоскость, параллельная данным плоскостям и пересекающая цилиндр, пересекает также прямоугольный параллелепипед, причём площади образованных при пересечении обоих тел сечений относятся как π•R2 : R2 = π : 1. Тогда и для объёмов этих тел справедливо: Vцил : Vпарал = π : 1 или Vцил : (R2•h) = π : 1, откуда
Vцил = π•R2•h.
Если цилиндр высотой h пересечь плоскостью, параллельной его оси, то этот цилиндр разобьётся на два тела (рис. 163). Объёмы этих тел относятся как площади сегментов, образовавшихся в основании цилиндра (докажите это на основании принципа Кавальери). Следовательно, объём каждого из этих тел может быть вычислен по формуле
V = Sсегм•h.
Рис. 163
Рис. 164
Любая плоскость, проведённая через середину оси цилиндра, разбивает этот цилиндр на два равновеликих тела (рис. 164), объём V каждого из которых равен половине объёма данного цилиндра, т. е. V = 
Попробуйте, исходя из этой формулы, доказать, что в таком случае объём каждой части цилиндра (см. рис. 164) может быть вычислен по формуле:
V= 
где a и b — длины отрезков, на которые образующая цилиндра делится секущей плоскостью.
Содержание:
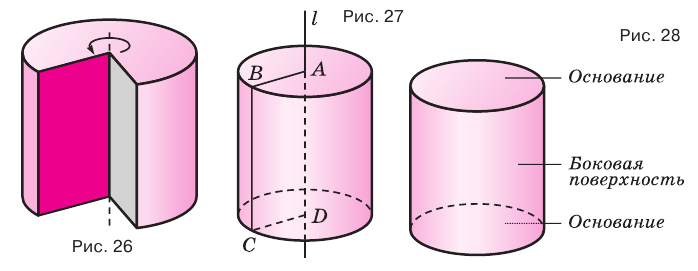
Цилиндром называется тело, полученное вращением прямоугольника вокруг оси, проходящей через его сторону (рис. 26). На рисунке 27 показано образование цилиндра при вращении прямоугольника
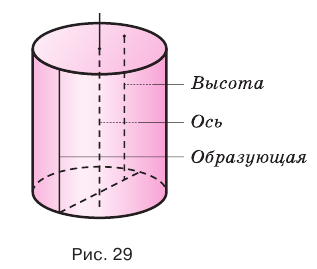
Образующая цилиндра является его высотой.
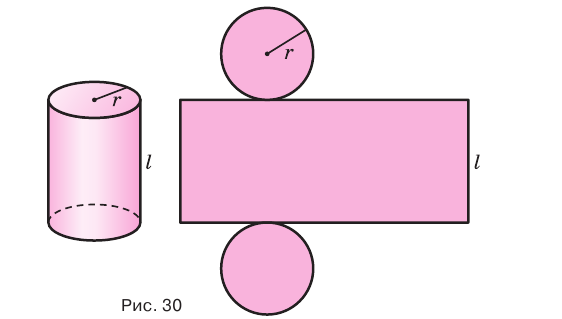
Поверхность цилиндра можно развернуть на плоскость, в результате получится прямоугольник, представляющий боковую поверхность цилиндра, и два круга, представляющих его основания. На рисунке 30 показан цилиндр и его развертка.
Теорема 4.
Боковая поверхность цилиндра равна произведению длины окружности основания и образующей:
На плоскости важной конфигурацией, которая часто встречается в задачах, является сочетание окружности с прямой. Подобной пространственной конфигурацией является сочетание цилиндра с плоскостью.
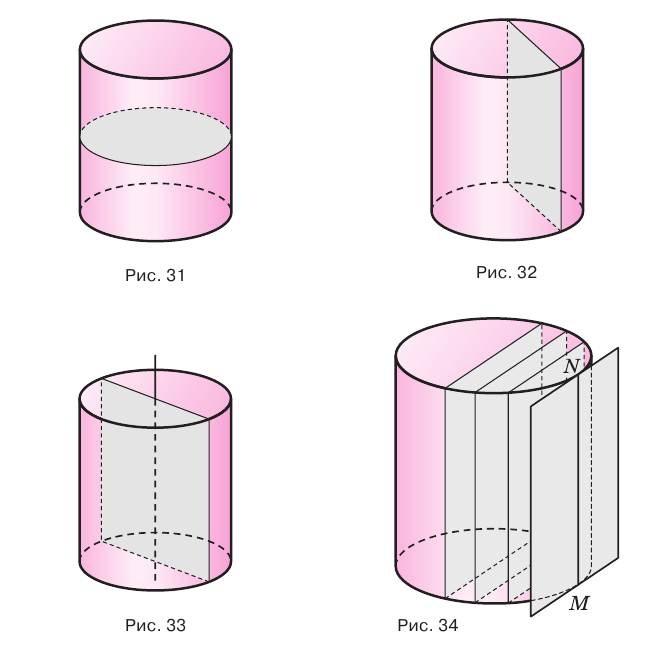
Если цилиндр пересечь плоскостью, параллельной основанию, то получится круг, равный основанию (рис. 31), а если плоскостью, перпендикулярной основанию, то — прямоугольник, одна сторона которого равна высоте цилиндра (рис. 32). Осевое сечение цилиндра, т. е. сечение плоскостью, проходящей через ось цилиндра, является прямоугольником, стороны которого равны высоте цилиндра и диаметру его основания (рис. 33).
Будем двигать плоскость, проходящую через ось цилиндра, параллельно самой себе (рис. 34). При этом две противолежащие стороны прямоугольника-сечения цилиндра, являющиеся хордами оснований, будут уменьшаться, а две другие стороны, которые являются образующими цилиндра, — сближаться до того момента, пока не совпадут. Получим плоскость, содержащую образующую 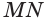
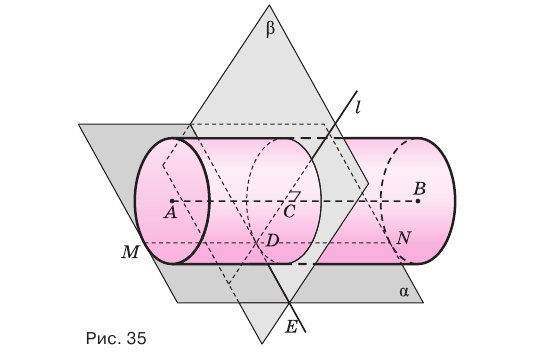
Теорема 5.
Если плоскость касается цилиндра по некоторой образующей, то ей перпендикулярна плоскость, проходящая через эту образующую и ось цилиндра.
Доказательство:
Пусть плоскость 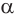
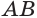
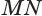
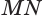
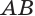
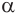
Проведем прямую 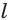
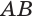
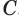
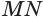
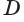
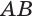
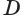
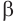
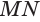
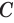
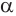
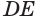
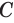
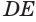
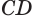
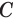
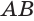
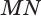
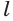
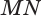
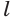
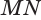
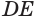
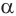
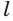
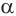
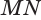
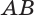
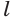
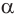
Теорема 5 выражает свойство касательной плоскости цилиндра.
Теорема 6.
Плоскость касается цилиндра, если она проходит через его образующую и перпендикулярна плоскости, содержащей эту образующую и ось цилиндра.
Доказательство:
Пусть плоскость 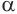
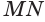
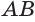
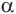
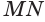
Пусть 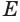
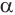
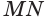
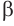
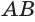
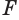
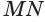
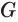
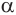
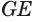
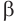
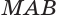
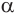
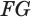
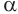
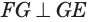
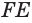
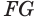
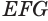
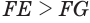
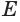
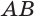
Теорема 6 выражает признак касательной плоскости цилиндра.
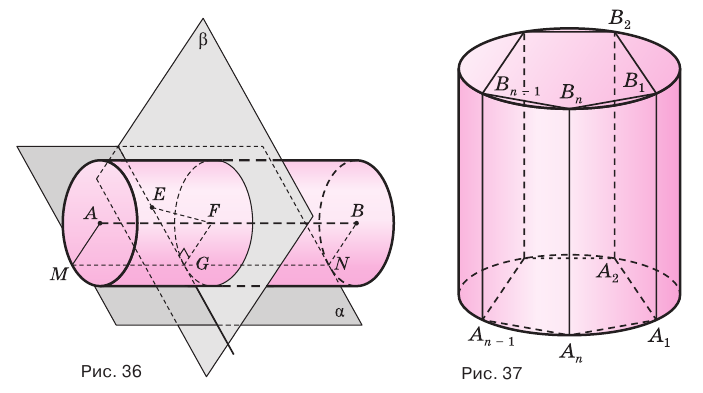
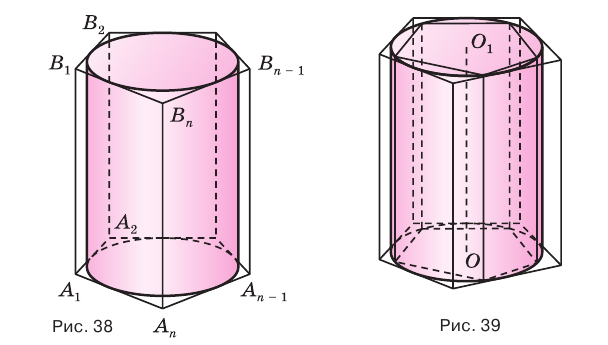
Пусть имеется цилиндр (рис. 37). Впишем в одно из оснований цилиндра многоугольник 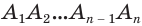
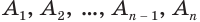
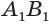
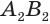
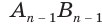
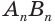
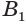
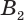
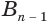
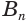
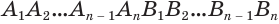
Если цилиндр описан около призмы, то основания цилиндра описаны около оснований призмы, а боковая поверхность цилиндра содержит боковые ребра призмы.
Подобным образом вводится понятие призмы, описанной около цилиндра, и цилиндра, вписанного в призму (рис. 38). Если призма описана около цилиндра, то ее основания описаны около оснований цилиндра, а боковые грани касаются боковой поверхности цилиндра.
Теорема 7.
Объем цилиндра равен произведению площади его основания и образующей:
Доказательство:
Пусть имеется цилиндр с осью 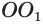
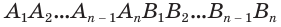
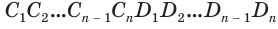
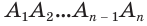
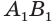
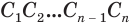
Будем количество 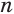
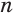
В описанном процессе высота 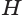
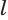
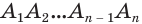
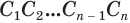
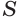
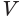
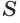
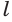
Поверхность цилиндра
Ещё один важный класс пространственных фигур – тела вращения. Цилиндр является одним из них, мы познакомимся с ним глубже. Свойства цилиндра похожи на свойства призм, мы последовательно изучим их.
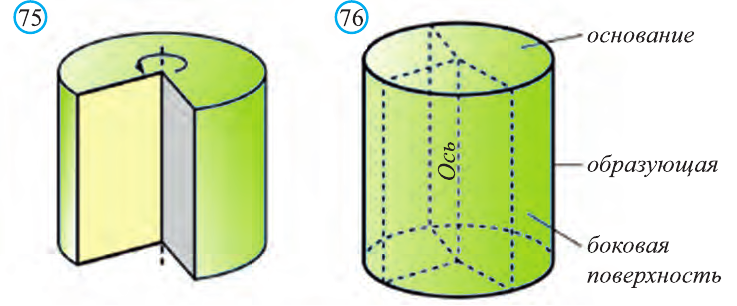
Тело, полученное вращением прямоугольника вокруг одной из его сторон называют цилиндром (точнее, прямой круговой цилиндр) (рис. 75). При вращении прямоугольника одна его сторона остаётся неподвижной. Её называют осью цилиндра. Поверхность, образованную при вращении противоположной стороны прямоугольника называют цилиндрической поверхностью, а саму сторону образующей цилиндра. Две другие стороны прямоугольника при этом вращении образуют два равных круга, которые называют основаниями цилиндра (рис. 76).
Замечание. Тело, полученное вращением прямоугольника вокруг одной из его сторон называют прямым круговым цилиндром. Более широкое понятие цилиндра вводят следующим образом.
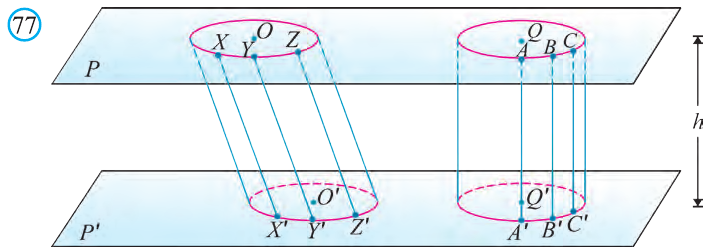
Пусть в пространстве параллельный перенос переводит плоскую фигуру F1, в фигуру F2. Тело, состоящее из этих фигур и отрезков, соединяющих их соответствующие точки, называют цилиндром (рис. 77).
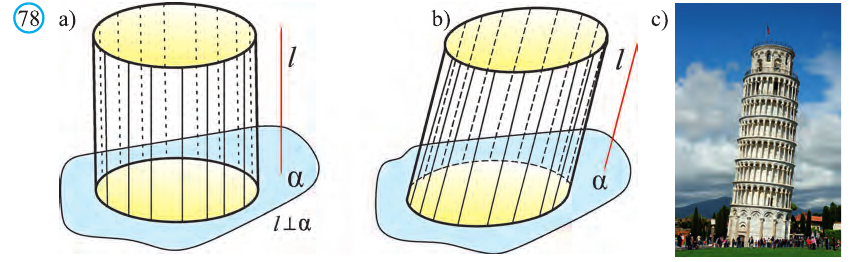
Если при параллельном переносе образующая перпендикулярна плоскости фигуры F1 , цилиндр называют прямым (рис. 78.а), в противном случае наклонным цилиндром (рис. 78.b). На рисунке 78.с изображена Пизанская башня, имеющая вид наклонного цилиндра.
Если фигура F1 является кругом, то цилиндр называют круговым цилиндром.
Только прямой круговой цилиндр является телом вращения. В дальнейшем мы будем рассматривать прямые круговые цилиндры, которые для краткости будем называть цилиндрами.
Основания цилиндра являясь равными кругами, лежат на параллельных плоскостях. Перпендикуляр, опущенный из некоторой точки одного основания на другое, называют его высотой.
Расстояние между параллельными плоскостями равно высоте цилиндра. Ось цилиндра также является его высотой.
Образующие цилиндра параллельны и равны. Точно также, длины высоты, оси и образующих цилиндра будут равны между собой.
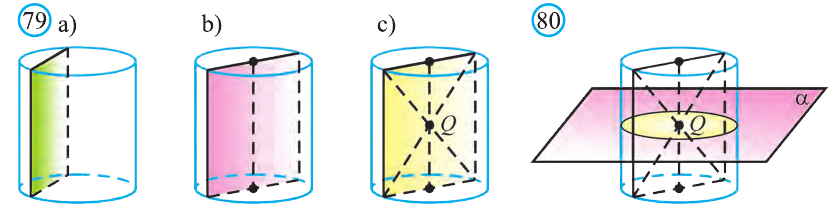
Сечением цилиндра плоскостью параллельной его оси является прямоугольник (рис.79.а). Две противоположные его стороны – это образующие цилиндра, а две другие стороны – соответствующие параллельные хорды оснований цилиндра.
В частности, осевое сечение также прямоугольник, образованный сечением цилиндра плоскостью, проходящей через его ось (рис. 79.b).
Диагонали осевого сечения цилиндра проходят через точку являющуюся серединой отрезка, соединяющего центры оснований цилиндра. Следовательно, эта точка Q есть центр симметрии цилиндра (рис. 79.с).
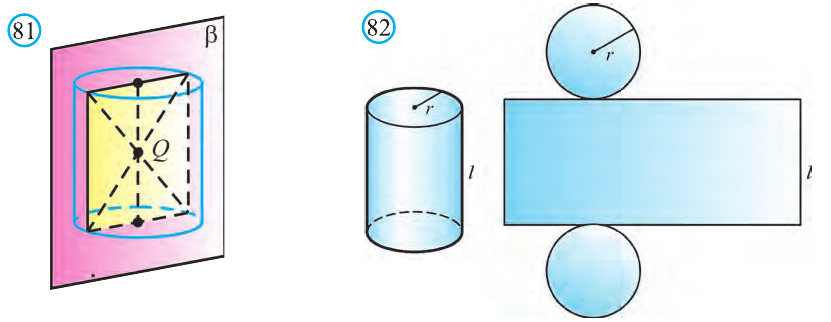
Плоскость, проходящая через точку Q перпендикулярно оси цилиндра является его плоскостью симметрии (рис. 80). Любая плоскость, проходящая через ось цилиндра также будет ось симметрии цилиндра (рис. 81).
Пример:
Осевое сечение цилиндра – квадрат, площадь которого Q. Найдите площадь основания цилиндра.
Решение:
Сторона квадрата равна 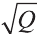
основания. Поэтому его площадь равна
Докажите самостоятельно эту теорему пользуясь рисунком 82.
Следствие. Полная поверхность цилиндра равна сумме его боковой поверхности и площадей двух его оснований:
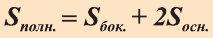
Пусть дан произвольный цилиндр. Впишем в одно из его оснований многоугольник 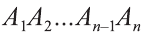
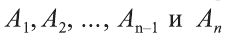
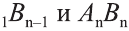
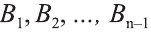
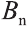
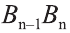
Ясно, что если вокруг основания призмы можно описать окружность, то вокруг призмы можно описать цилиндр.
Аналогично вводятся понятия призмы, описанной вокруг цилиндра и цилиндра, вписанного в призму (рис. 84). Если призма описана вокруг цилиндра, то основание призмы будет описано вокруг основания цилиндра и боковые грани призмы будут касаться боковой поверхности цилиндра.
Ясно, что если в основание призмы можно вписать окружность, то вокруг цилиндра можно описать призму.
Объём цилиндра
Теорема. Объём цилиндра равен произведению площади его основания и образующей цилиндра:
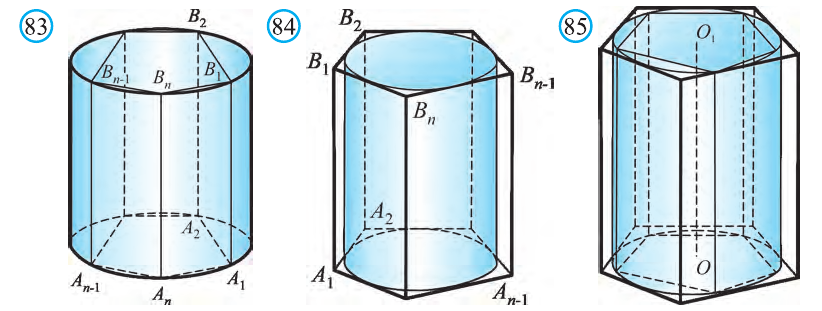
Доказательство. Пусть дан цилиндр с осью ОО1 (рис. 85). Впишем в него призму 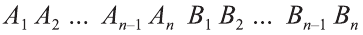
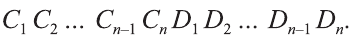
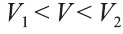
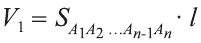
Будем всё больше и больше увеличивать число n сторон оснований призм. Тогда объём вписанной призмы будет увеличиваться, а объём описанной призмы уменьшаться. Если число n сторон увеличивать неограниченно, то разность между объёмами будет стремится к нулю. Число, к которому приближаются объёмы вписанной и описанной призм, принимают за объём данной призмы. При этом площади многогранников 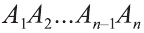
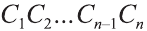
Исторические сведения:
В произведении Абу Райхна Беруни «Книга о началах искусства астрономии» («Астрономия») как введение в стереометрию в разделе о геометрии приводятся следующие определения фигур:
Куб – физическая фигура, похожая на кубик для игры в нарды, ограниченная с шести сторон квадратами.
Призма – представляет собой фигуру, ограниченную по бокам плоскостями в форме квадрата или прямоугольника, а сверху и снизу -двумя треугольниками. В этом определении Беруни приведено описание частного вида призмы, а именно треугольной призмы.
Книга Беруни «Канон Масьуда» написана в 1037 году. В ней приведены правила нахождения объёмов параллелепипеда и призмы: «Если тело не четырёхугольное или другого вида, то его расчёт таков: найди площадь, умножь его на глубину, в итоге получишь объём». В произведении Абу Али ибн Сино «Книга знания» в разделе «Основы изучения геометрических тел» дано описание тела и треугольной призмы. А также описаны условия взаимного равенства двух призм. Ибн Сино даёт следующее определение призмы: «Призма – тело, ограниченное двумя плоскими треугольными сторонами.»
В произведении Аль Каши «Книга счёта» приведёт много примеров расчета площадей поверхностей и объёмов тел. Благодаря своим глубоким знаниям в математике, геометрии, тригонометрии, механике и астрономии он пользовался вниманием и уважением Улугбека. Аль Каши наряду с многоугольниками изучачл призмы, пирамиды, цилиндры, конусы, усечённые конусы.
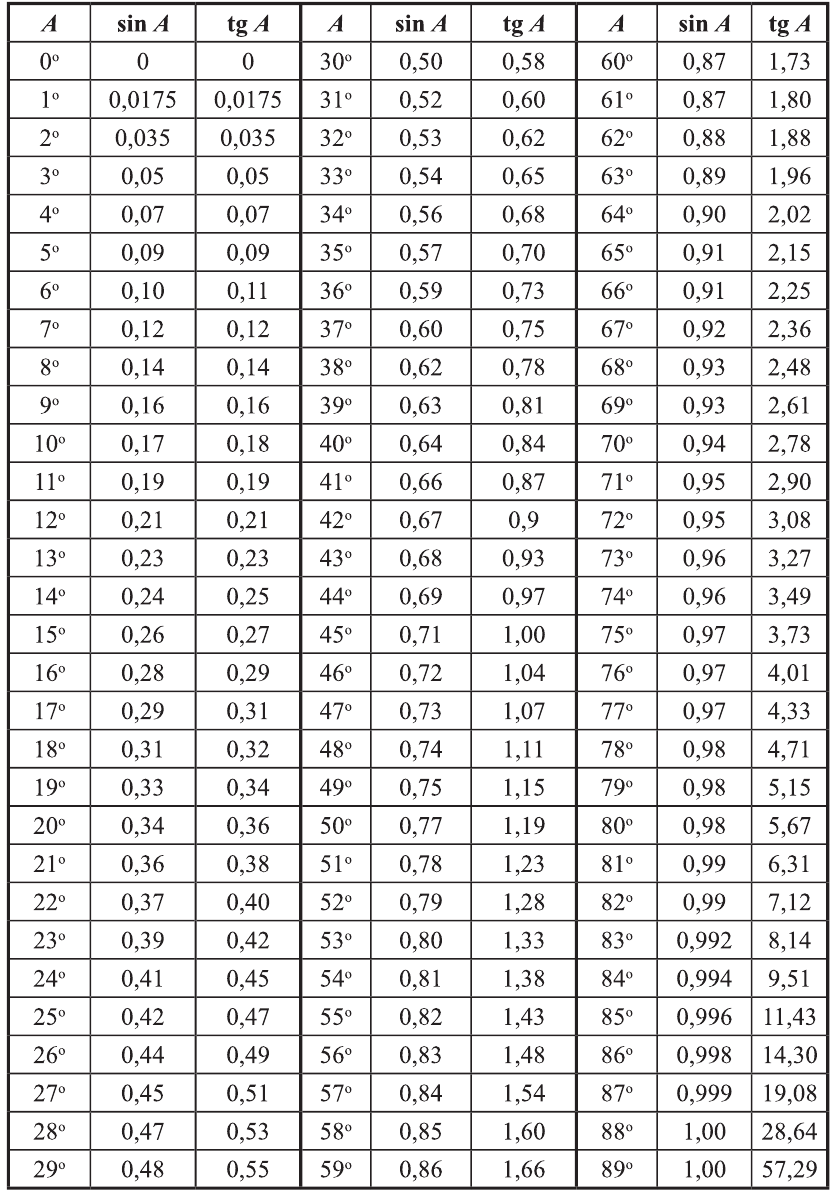
Таблица приближенных значений тригонометрических функций:
- Пирамида в геометрии
- Конус в геометрии
- Сфера в геометрии
- Шар в геометрии
- Возникновение геометрии
- Призма в геометрии
- Планиметрия – формулы, определение и вычисление
- Стереометрия – формулы, определение и вычисление